Next Article in Journal
The Question of Studying Information Entropy in Poetic Texts
Next Article in Special Issue
Nonextraction Orthodontic Treatment of Severely Impacted Maxillary Canines through Transalveolar Transplantation in a 10-Year-Old Patient: A Case Report with a 6-Year Follow-Up Period
Previous Article in Journal
An Improved Nested Named-Entity Recognition Model for Subject Recognition Task under Knowledge Base Question Answering
Previous Article in Special Issue
Is There a Difference in Mid-Palatal Suture Density after Rapid Maxillary Expansion, Surgically Assisted Rapid Maxillary Expansion, and Miniscrew-Assisted Rapid Palatal Expansion? A Systematic Review and Meta-Analysis
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 13
Issue 20
10.3390/app132011256
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The Center of Resistance of an Impacted Maxillary Canine: A Finite Element Analysis

by
Sewoong Oh
1,2,
Youn-Kyung Choi
3,
Yong-Il Kim
1,2,
Seong-Sik Kim
1,2,
Soo-Byung Park
1,2 and
Sung-Hun Kim
1,2,*
1
Department of Orthodontics, Dental and Life Science Institute, School of Dentistry, Pusan National University, Yangsan 50612, Republic of Korea
2
Dental Research Institute, Pusan National University Dental Hospital, Yangsan 50612, Republic of Korea
3
(Bio)medical Research Institute, Pusan National University Hospital, Busan 49241, Republic of Korea
*
Author to whom correspondence should be addressed.
Appl. Sci. 2023, 13(20), 11256; https://doi.org/10.3390/app132011256
Submission received: 23 September 2023 / Revised: 10 October 2023 / Accepted: 12 October 2023 / Published: 13 October 2023
(This article belongs to the Special Issue Clinical Applications of Orthodontic TSADs and CBCT)
Browse Figures
Versions Notes

Abstract

:
The aim of this study was to calculate the center of resistance (COR) of an impacted maxillary canine according to the stages of pericoronal tissue healing using the finite element method (FEM). The maxillary canine model was three-dimensionally scanned, and the structures surrounding the tooth were modeled using a computer-aided design program. The COR was calculated in the buccolingual (BL) and mesiodistal (MD) directions using the FEM. After applying a single force to a specific point of the tooth, several counter moments were applied to compensate for this at the same point. Thereafter, the displacement curve of the tooth axis for each counter moment was plotted. The intersection points between the displacement curves corresponded to the COR. At the beginning of healing, the COR of the MD and BL direction was located at 38.1% and 38.7% of the root length from the cementoenamel junction, respectively. At the end of healing, the COR of the MD and BL direction was located at 44.6% and 49.8% of the crown length from the cementoenamel junction, respectively. The COR of the impacted maxillary canine gradually shifts to the coronal side as the healing of the pericoronal tissue occurs.

1. Introduction

There are many definitions of an impacted tooth [1,2]. Kokich et al. [1] called a tooth impacted when the tooth did not erupt in the proper position of the dental arch during normal growth. Thilander et al. [2] defined an impacted tooth as a case in which tooth eruption was significantly delayed or there were no clinical or radiological findings that further eruption was in progress.
Surveys on the prevalence of impacted teeth was conducted on all permanent teeth except the third molars in Italy [3], Korea [4], and Turkey [5]. The prevalence of impacted teeth was found to be 2.9~8.6% [3,4,5]. The prevalence of impacted teeth in the maxilla was 10 to 20 times higher than in the mandible [6]. In the maxilla, the canine showed the highest ratio with 69%, and in the mandible, the premolar showed the highest ratio with 56% [6]. The etiologies of the impacted teeth were diverse [7,8], and about 70% of cases were caused by abnormal eruption pathways or localized pathologic lesions [9].
Impacted teeth require orthodontic treatment because they cause not only aesthetic problems, such as midline displacement due to the inclination of adjacent teeth, but also degenerative changes, such as root resorption of adjacent teeth, cyst formation, and loss of tooth alignment space [10]. Treatment methods include surgical exposure followed by orthodontic traction, extraction of the impacted tooth, surgical replantation, and extraction of the deciduous tooth [11]. In many cases, surgical exposure followed by orthodontic traction is performed [11]. There are two types of surgical exposure: open and closed [12]. Open surgical exposure removes the bone and soft tissue around the impacted tooth and opens the impacted area to induce a spontaneous eruption of the impacted tooth or bonds an attachment a few days after the procedure. On the other hand, closed surgical exposure is a procedure that opens the flap, bonds an attachment to the impacted tooth, and then covers the flap again and applies orthodontic forces immediately [12]. Therefore, closed surgical exposure requires more careful consideration of the orthodontic force applied to the impacted teeth than open surgical exposure.
Knowing the center of resistance (COR) in the orthodontic traction of impacted teeth is important. If the orthodontic force is given to the impacted tooth without considering the COR, it may be moved in an undesirable direction or rotated, resulting in traction failure or a longer treatment period [13]. However, since the impacted tooth is inside the bone, it may be different from the COR of the erupted tooth. There have been many studies [14,15,16,17] on the COR of erupted teeth. Gandhi et al. [14] calculated the three-dimensional COR positions of about 50 maxillary first molars using the finite element method (FEM). As a result, the COR was located below and slightly distal to the trifurcation area, and the location of the COR varied as the shape of the molars varied. Above all, it was shown that the COR was a point that could vary depending on the direction of force. Choy et al. [15] proved using mathematical analysis that the position of the COR moved nonlinearly depending on the shape of the root of the erupted tooth, the height of the alveolar bone, and the length of the root.
However, few studies have reported on the COR of impacted teeth despite its clinical importance. Moreover, in the case of the closed surgical exposure of an impacted tooth, the COR may change depending on the stage of pericoronal tissue healing around the crown.
Previous studies [18,19,20] on the COR of impacted teeth have been conducted on impacted teeth with exposed crowns. Prasad et al. [18] used the FEM to calculate the von Mises stress of the impacted canine and surrounding teeth when a palatally impacted canine with an exposed crown was pulled from a 0.019 × 0.025 stainless steel archwire. In addition, the side effects that may occur in surrounding teeth were predicted using the FEM. Zeno et al. [19] divided 21 patients with a palatally impacted canine exposed using the open method into two groups according to severity. Then, they analyzed how the stress on the periodontal ligament (PDL) of an impacted canine varied depending on the severity and traction direction. As a result, it was concluded that it was preferable to perform vertical traction first, as the largest initial movement could be expected when traction was performed vertically. Sezici et al. [20] analyzed the stress generated in the PDL when pulling a palatally impacted canine with an exposed crown with the same force using a 0.016 SS Kilroy spring and a NiTi spring on a 0.019 × 0.025 stainless steel archwire. As a result, it was found that even though the same traction force was used, a larger PDL stress distribution appeared on the impacted canine and the surrounding anchor teeth in the 0.016 SS Kilroy spring.
There are several methods [21,22,23] for calculating the COR of the tooth, but the FEM is widely used [14,15,16,17,18,19,20]. The FEM is a method of analyzing the stress distribution of an object against external force after creating an accurate model of the anatomical structure and physical properties of the object using a computer [16,24,25].
The aim of this study was to calculate the COR of the impacted maxillary canine according to the stages of pericoronal tissue healing using the FEM. That is, after the closed surgical exposure, we attempted to establish a basis for selecting an appropriate point of action in the traction of impacted teeth by confirming whether the COR changes depended on the healing stage.

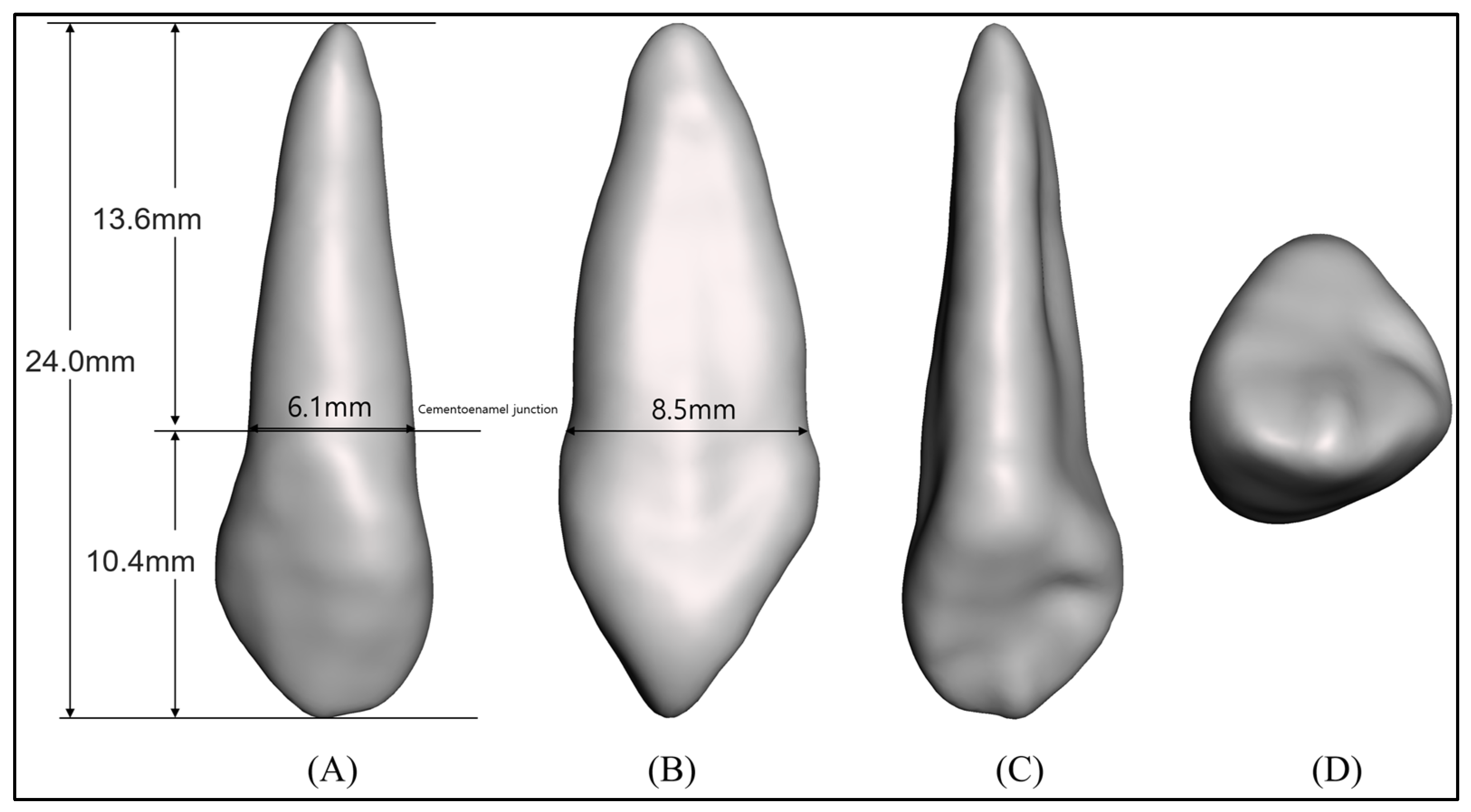
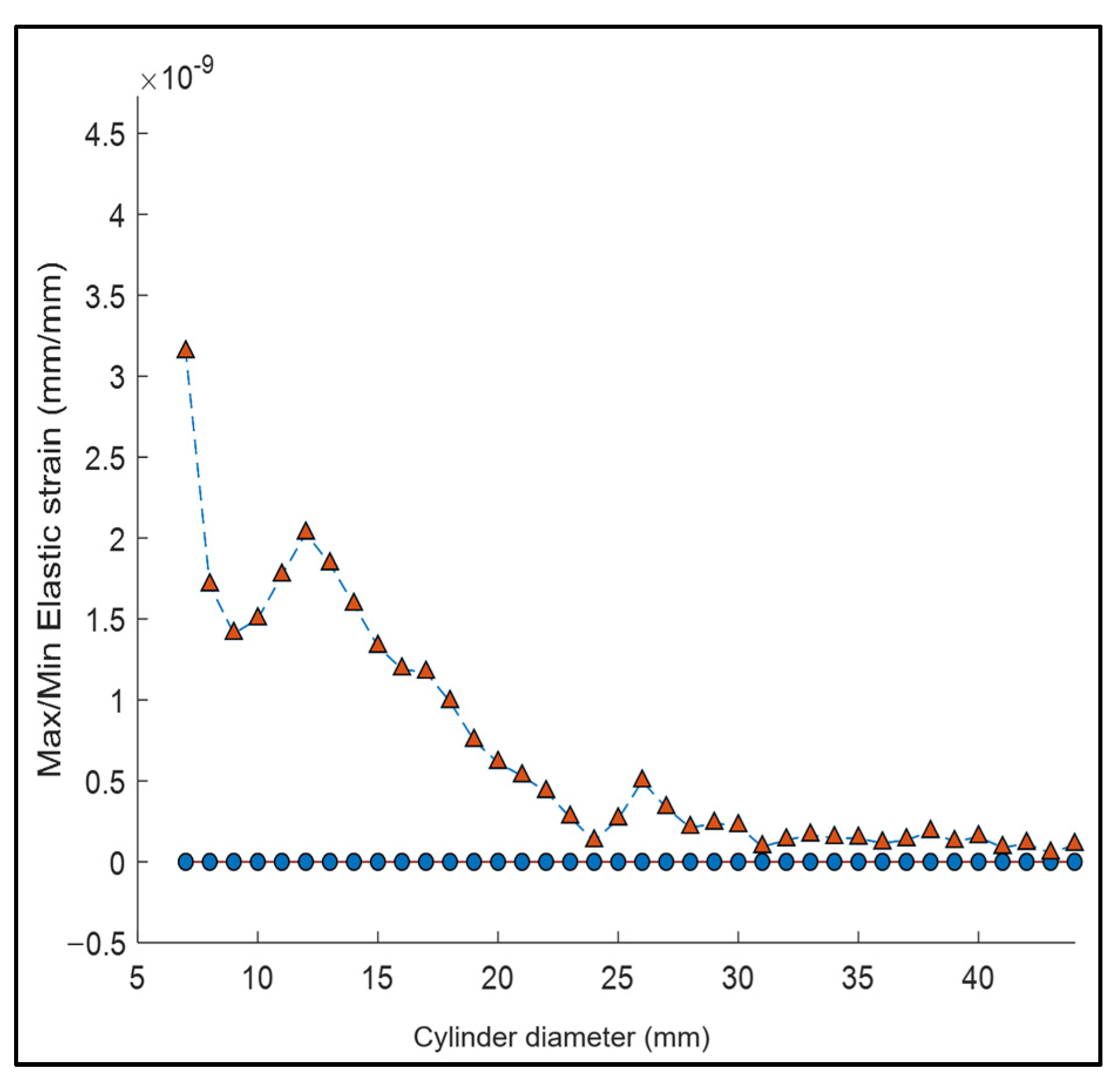
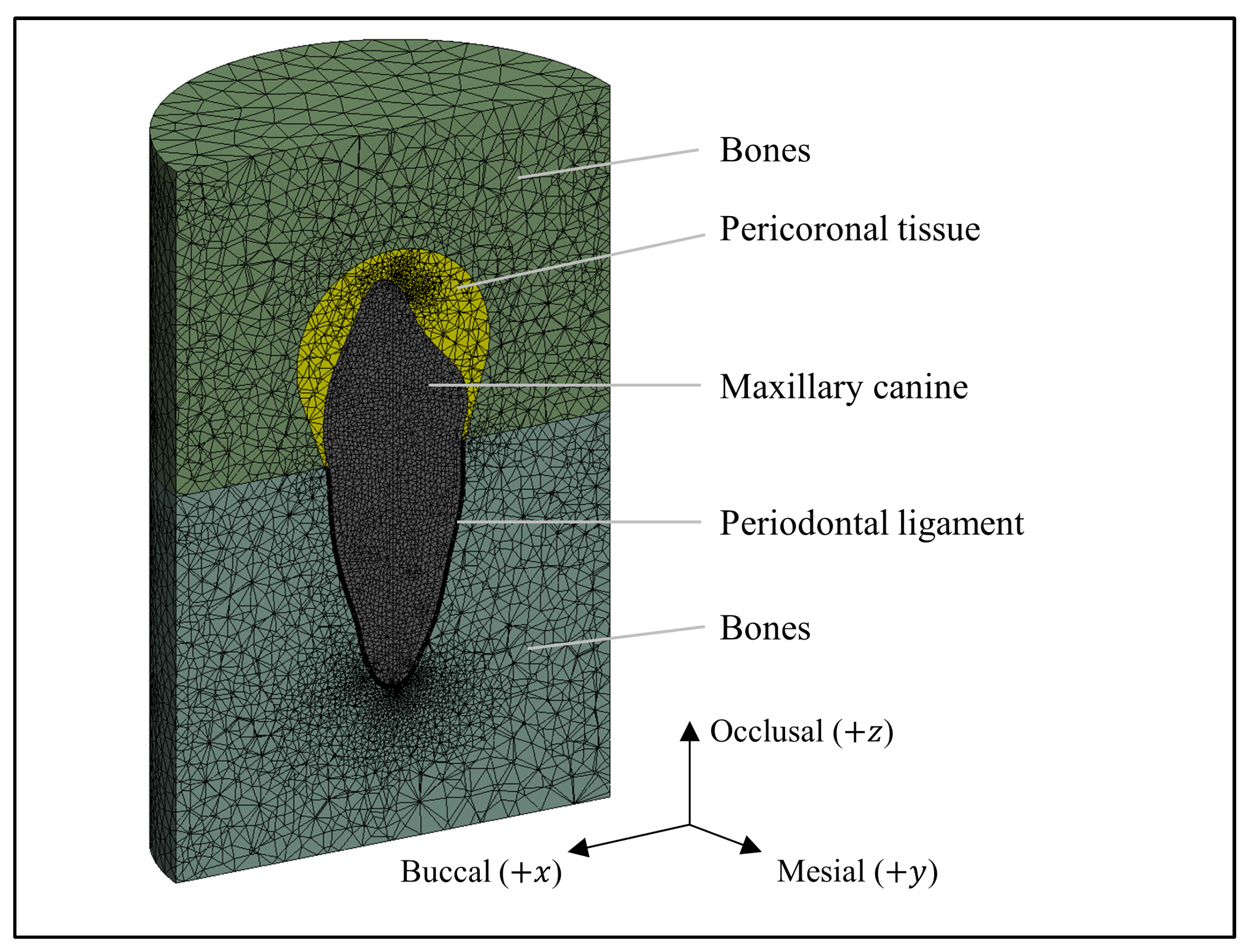
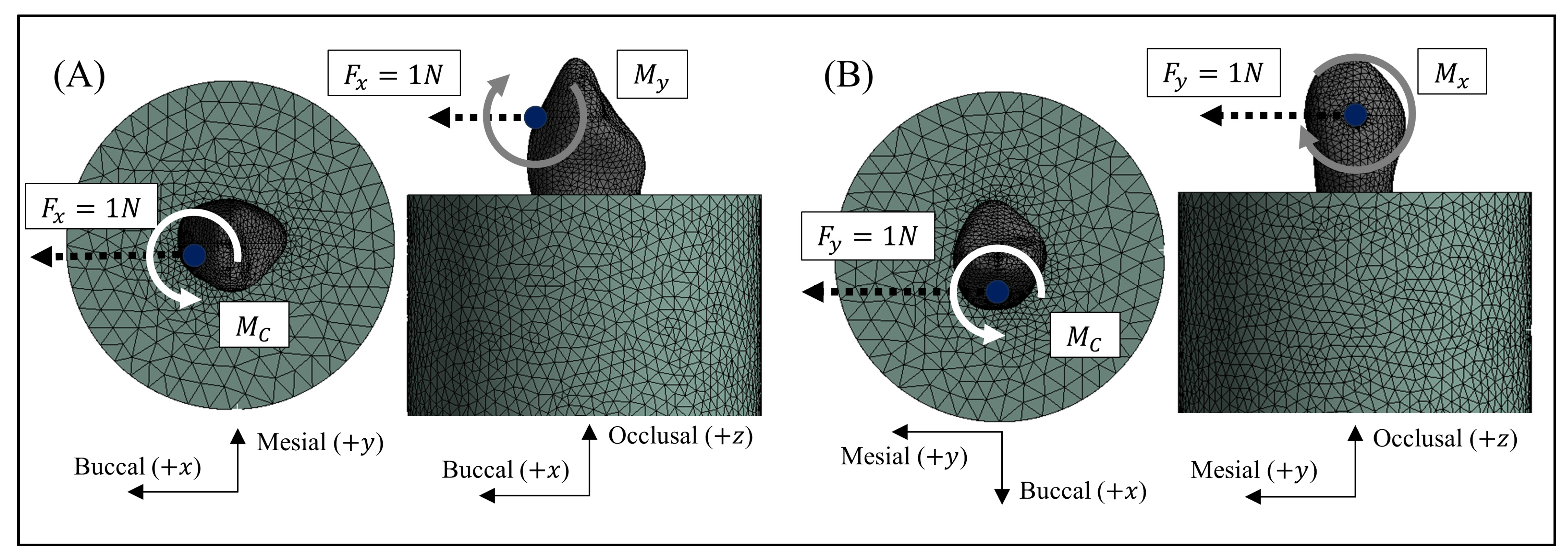
2. Materials and Methods

For impacted maxillary canine modeling, the maxillary canine model (NISSIN B3-305, Nissin Dental Product, Kyoto, Japan) was three-dimensionally scanned (TRIOS 4, 3Shape TRIOS A/S, Copenhagen, Denmark) and saved in Standard Template Library (STL) format. The triangular mesh was re-meshed using the STL file editing program (Autodesk Inc., San Rafael, CA, USA). The crown length was 10.4 mm, and the root length was 13.6 mm. The total length was 24.0 mm. At the cementoenamel junction (CEJ), the mesiodistal (MD) diameter was 6.1 mm, and the buccolingual (BL) diameter was 8.5 mm. The tooth shape and size are shown in Figure 1. Then, the structures surrounding the tooth were modeled using a computer-aided design program (Spaceclaim, Ansys Inc., Canonsburg, PA, USA). To reduce the complexity of the calculation, the PDL was modeled in the form of a uniform film with a thickness of 0.25 mm, and the bone around the tooth was modeled in the form of a cylinder to reduce the computation time [26]. The diameter and height of the cylinder were set to 24 mm in diameter and 42 mm in height, which is the size at which the stress at the boundary is reduced below the error range by performing a FEM pretest (Figure 2). The pericoronal tissue was designed in a circular dome shape with a radius of 6 mm to blend naturally with the PDL so that there were no sharp edges (Figure 3).
The material properties (Table 1) were obtained from the previous literature [14,27,28,29]. The alveolar bone and teeth were assumed to consist of linear elastic, isotropic, and homogeneous materials. However, since the nonlinearity of the PDL can significantly change the finite element analysis results, the PDL implemented nonlinear and hyperelastic properties using the Ogden 1st model. (μ1 = 0.07277; α1 = 16.95703; D1 = 3 × 107, specific density = 1.00 g/cm3) [14,27]. To simulate the histological changes in the pericoronal tissue after closed surgical exposure, it was assumed that the stages of healing would occur sequentially in the order of granulation tissue, fibrous tissue, immature woven bone, and mature woven bone [30].
ANSYS Mechanical (Ansys Inc., Canonsburg, PA, USA) was used for finite element analysis. The meshing was performed using 4-node tetrahedral elements, and the number of tetrahedral elements used for each maxillary canine, PDL, bone, and pericoronal tissue was 72,677, 786,367, 266,335, and 55,831, respectively. As a boundary condition, the nodes lining the outermost part of the cylinder restricted three-dimensional movement.
The moment-to-force ratio (M/F) for pure translation is equal to the distance from the known line of action of the applied force to the COR. The Cartesian coordinate system was set with the cusp tip as the origin, the positive x-axis as buccal, the positive y-axis as mesial, and the positive z-axis as occlusal (Figure 4).
The method proposed by Meyer [31] was used to determine the COR using the FEM (Figure 5). First, after applying a single force to a specific point of the tooth, several counter moments were applied to compensate for this at the same point. Thereafter, the displacement curve of the tooth axis for each counter moment was plotted. The intersection points between the displacement curves corresponded to the COR. However, since each displacement curve may not intersect at one point, the point with the minimum distance from all curves was defined as the intersection point and obtained using the least square method.
Specifically, to estimate the COR in the BL direction, a buccal force (Fx = 1 N) was applied 4.5 mm below the cusp tip, and then a counter moment (My = 1, 3, 5, 7, 11 N-mm, or equivalently My/Fx = 1, 3, 5, 7, 11 mm) was applied.
In the same way, a mesial force (Fy = 1 N) was applied 4.5 mm below the cusp tip, and then a counter moment (Mx = 1, 3, 5, 7, 11 N-mm, or equivalently Mx/Fy = 1, 3, 5, 7, 11 mm) was applied to obtain the COR in the MD direction. In this case, to prevent mesial-in rotation, an additional z-direction moment (Mc = −3.45 N-mm) was applied (Figure 4).
For visibility of each axis graph, one marker was assigned to each of the five nodes.

3. Results

Figure 6 and Figure 7 show the changes in the displacement curve of the tooth axis in the BL and MD directions according to the counter moment, respectively. The tooth bending deformations are amplified by the discrepancies in the horizontal and vertical axis scales.
Table 2 and Figure 8 show the location of the COR from the CEJ according to the pericoronal tissue and their relative locations to the root and crown. The COR gradually shifts to the coronal side as the healing of the pericoronal tissue occurs.
In the case of the granulation tissue, the COR of the MD and BL directions was located at 5.18 mm (38.1% of the root length) and 5.26 mm (38.7% of the root length) from the CEJ to the root apex side, respectively.
In the case of the fibrous tissue, the COR of the MD and BL directions was located at 2.82 mm (20.8% of the root length) and 3.46 mm (25.5% of the root length) from the CEJ to the root apex side, respectively. This COR of the MD and BL directions was moved 2.36 mm and 1.80 mm coronally from the COR of the granulation tissue, respectively.
In the case of the immature woven bone, the COR of the MD and BL direction was located at 4.25 mm (40.8% of the crown length) and 4.30 mm (41.3% of the crown length) from the CEJ to the coronal side, respectively. This COR of the MD and BL directions was moved 9.43 mm and 9.56 mm coronally from the COR of the granulation tissue, respectively.
In the case of the mature woven bone, the COR of the MD and BL direction was located at 4.64 mm (44.6% of the crown length) and 5.18 mm (49.8% of the crown length) from the CEJ to the coronal side, respectively. This COR of the MD and BL directions was moved 9.82 mm and 10.44 mm coronally from the COR of the granulation tissue, respectively.

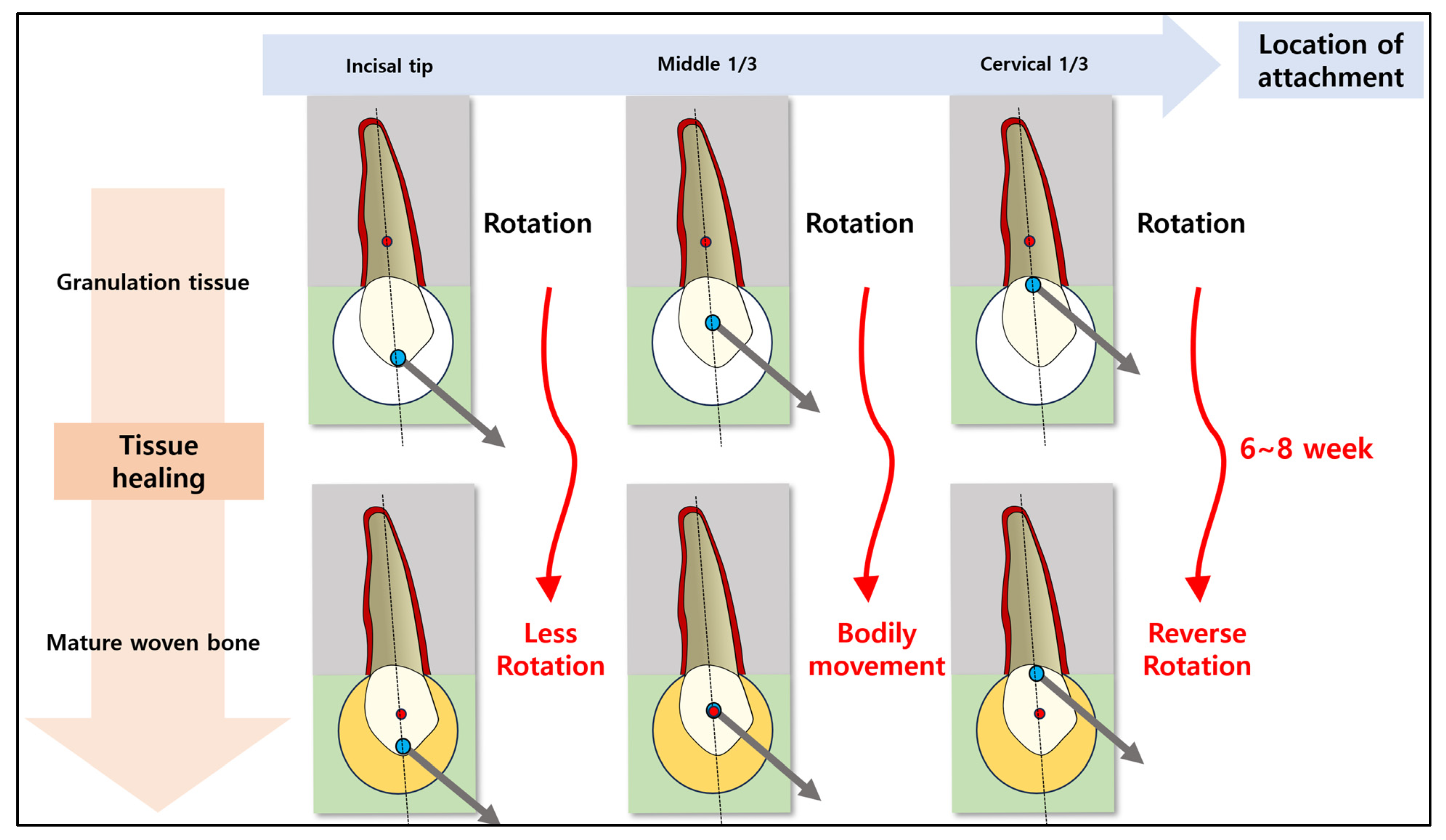
4. Discussion

In classical mechanics, a force refers to an action that can change the motion, direction, or shape of an object. The force consists of three factors: magnitude, line of action, and point of action, and all three factors are involved in interaction with an object. In other words, the action is not determined solely by the magnitude of the force, but depends on the line of action and the point of action.
Fish [32] recognized the importance of the point of action and first introduced the concept of the COR from rigid body mechanics into dentistry in 1917. He concluded that when a horizontal force is applied to a tooth with a single root, there will be an action point that causes the bodily movement somewhere between the root apex and the alveolar crest, and he stated that it might probably exist at the midpoint between the alveolar crest and the apex. Since then, the COR has been defined in various ways, such as the point of action that shows the greatest resistance to tooth movement, or the point of action that shows only pure translation regardless of the direction of force [33,34].
For effective orthodontic treatment, it is important to apply appropriate force to the teeth to control tooth movement. Orthodontic tooth movement consists of rotation, translation, and a combination of the two. This is achieved due to the relationship between the orthodontic force and the COR. If the COR is accurately known, the orthodontic force that generates a specific tooth movement can be predicted, enabling efficient tooth movement.
A common definition of the COR is the point at which the object will be translated when a single force is applied. The COR of the tooth is determined using the material properties of the tooth and surrounding supporting structures [35]. In particular, it is crucial to accurately know the COR of the impacted tooth because an impacted tooth is an isolated tooth, so inappropriate tooth movement easily occurs due to an erroneous force. If the COR of the impacted tooth can be accurately identified, the probability of success in the orthodontic traction of the impacted tooth will increase, and the treatment period will be shortened, improving the quality of life of the patient.
Various analytical or experimental methods [21,22,23] have been used to find the COR of the tooth. Burstone et al. [21] used three-dimensional laser holography to determine the COR of the maxillary central incisors. Choy et al. [22] used an electrical resistance strain gauge method to determine the COR of the upper anterior segment. Woo et al. [23] used a laser reflection technique to find the COR of the maxillary anterior teeth. However, most studies [14,15,16,17,18,19,20] have used the FEM. The advantage of the FEM is that the model setting is free and that even complex shapes can be modeled. In addition, any external force can be handled, and load or restraint conditions can be arbitrarily selected [36].
There are several techniques to find the COR of the tooth using the FEM [21]. The first technique is to find the point of application of the force when the tooth is purely translated while changing the point where the force is applied. In the case of teeth with multiple roots, this method is difficult to use because the COR may exist outside the tooth. The second technique is to find the counter moment when the tooth is purely translated after applying a force to an arbitrary point and then changing the counter moment. That is, when a single force that does not pass through the COR is applied to the teeth, combined rotation and translation occur. The rotational movement can be compensated for by changing the amount of the counter moment. We used the second technique, which was modified by Meyer [31]. Figure 6 and Figure 7 show that at a certain M/F ratio, a rotational movement using a single force is compensated for and only a translational movement occurs, confirming that the displacement curve is parallel to the y-axis.
In this study, the COR of the impacted maxillary canine according to the stages of pericoronal tissue healing was measured in two directions (MD and BL directions) using the FEM. As a result, the COR gradually moved toward the crown tip as the healing of the pericoronal tissue occurred. When the pericoronal tissue, which corresponds to a completely exposed crown state, was air, the COR was located near 38% of the root in the MD direction, similar to previous studies [21,35] on erupted teeth. Burstone et al. [21] showed that the COR of single-rooted teeth was located 33% from the alveolar crest and Provatidis et al. [35] showed the COR was located 38.9% away from it.
When the pericoronal tissue was mature woven bone, the COR was 44.6% of the crown length in the MD direction. It is speculated that when the pericoronal tissue is filled with hard materials like mature woven bones, the influence of the root being surrounded by soft tissues like the PDL is reduced, and the COR of the impacted tooth becomes closer to the COR of the crown.
Because the COR changes according to the stages of pericoronal tissue healing, it is important to know the change in tooth movement depending on the timing of applying orthodontic force to the impacted tooth. When an attachment is bonded to the incisal tip of an impacted canine tooth and an orthodontic force is applied in the distal direction after closed surgical exposure, a rotational movement occurs if the pericoronal tissue is granulation tissue. As time passes and the pericoronal tissue changes to mature woven bone, the direction of rotation does not change and only the moment decreases (Figure 9). When an attachment is attached to the middle 1/3 of crown and an orthodontic force is applied in the distal direction after closed surgical exposure, a rotational movement occurs if the pericoronal tissue is granulation tissue. As time passes and the pericoronal tissue changes to mature woven bone, the rotational movement disappears and a bodily movement appears. When an attachment is attached to the cervical 1/3 of crown and an orthodontic force is applied in the distal direction after closed surgical exposure, a rotational movement occurs if the pericoronal tissue is granulation tissue. As time passes and the pericoronal tissue changes to mature woven bone, a reverse rotational movement occurs.
Specifically, if this is used clinically for pure translation of the impacted tooth in the MD direction after closed surgical exposure and the end of healing, the orthodontic force should be applied after bonding an attachment above 44.6% of the crown length. Also, in the case of impacted maxillary canines, where the root apex is located on the maxillary first premolar side, uncontrolled tipping is required to move the root apex to the desired position, so bond an attachment above 44.6% of the crown length and apply orthodontic forces.
It is generally known that the COR varies depending on the direction in which the force is applied. Meyer et al. [30] analyzed the COR of six mandibular incisors using the FEM and found that the COR in the BL direction was located more apically than that in the MD direction. This was because the tooth roots in the BL direction have a wider shape. In this study, the location of the COR in the two directions was not consistent, which was similar to the results of previous studies [26,31] on erupted teeth. This is estimated to come from the difference in geometry for each side of the tooth [31]. That is, the root shape on the MD side was less tapered than the root shape on the BL side (Figure 10). Therefore, the COR in the MD direction was slightly closer to the cementoenamel junction than that in the BL direction.
Despite the good research results, this study has limitations. First, although the PDL was assumed to be an isotropic, homogenous, and uniform thickness of 0.25 mm, the actual PDL is not of a uniform thickness and is anisotropic and inhomogeneous [37], so the location of the COR may be estimated differently. Second, the FEM is an analysis of the initial movement of teeth in response to an applied force and does not reflect the movement of the teeth over time. Third, the average shape and size of the maxillary canines were modeled, so they do not match the COR of individual maxillary canines. It is necessary to find changes in the COR of canines with different volumes and root shapes. Fourth, there has been no histological study on how the pericoronal tissue changes after closed surgical exposure, and although the healing of the pericoronal tissue may vary with stress or strain on the tissue due to traction of an impacted tooth, we assumed that the healing of the closed surgical exposure might be the same as the healing of a normal extraction socket. Lastly, clinical data are needed to validate these simulated outcomes.

5. Conclusions

The COR gradually shifts to the coronal side as the healing of the pericoronal tissue occurs.
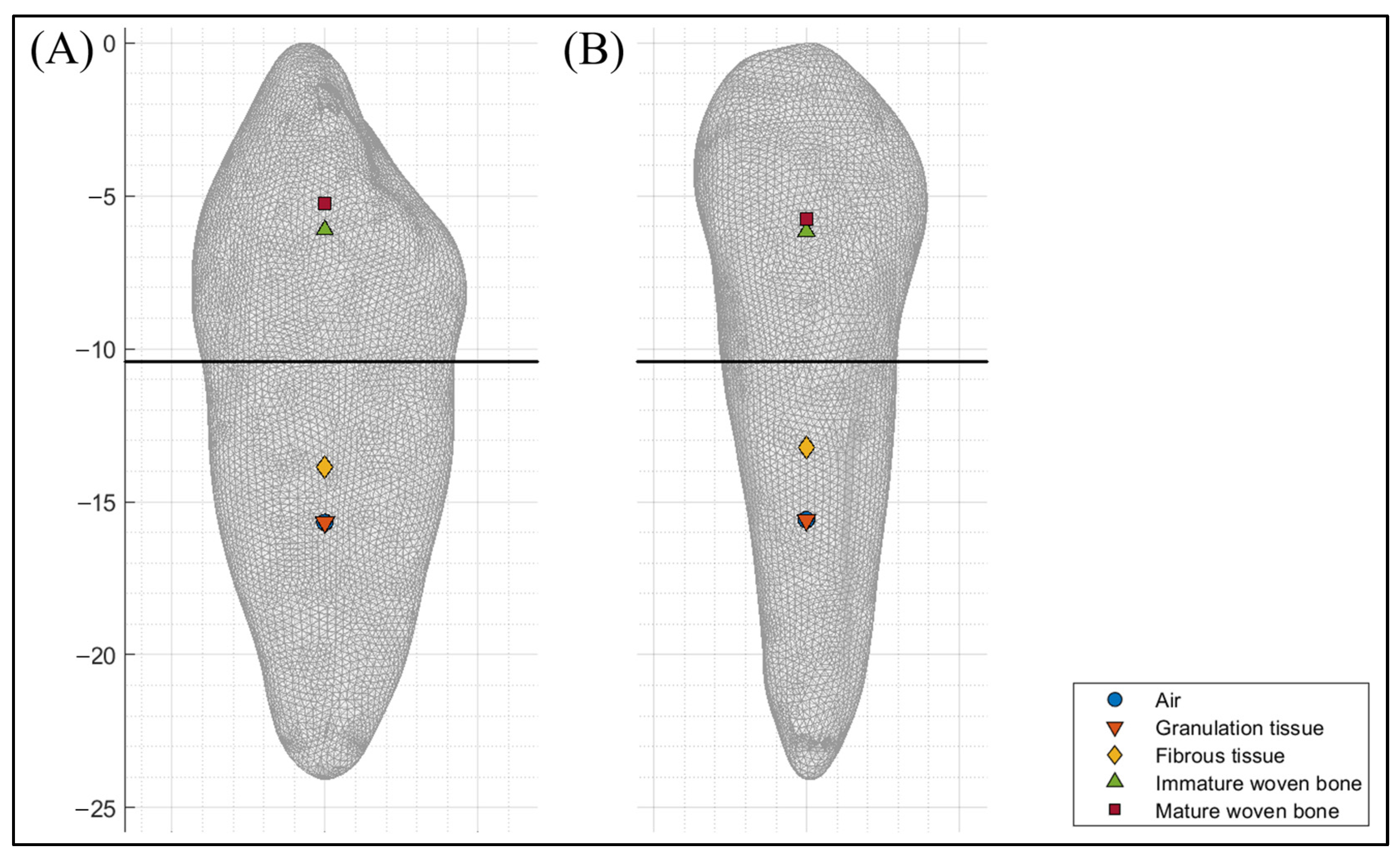
  • At the beginning of healing, the COR of the MD and BL direction was located at 38.1% and 38.7% of the root length from the cementoenamel junction, respectively.
  • At the second stage of healing, the COR of the MD and BL direction was located at 20.8% and 25.5% of the root length from the cementoenamel junction, respectively.
  • At the third stage of healing, the COR of the MD and BL direction was located at 40.8% and 41.3% of the crown length from the cementoenamel junction, respectively.
  • At the end of healing, the COR of the MD and BL direction was located at 44.6% and 49.8% of the crown length from the cementoenamel junction, respectively.
The COR varies depending on the direction in which the force is applied. The COR in MD direction was slightly closer to the cementoenamel junction than that in the BL direction.
We establish a basis for selecting an appropriate point of action in the traction of impacted teeth.

Author Contributions

Conceptualization, S.-H.K.; methodology, S.O.; software, S.O.; validation, Y.-K.C.; formal analysis, Y.-I.K.; data curation, S.-S.K.; writing—original draft preparation, S.-H.K.; writing—review and editing, S.-H.K.; visualization, S.O.; supervision, S.-B.P.; project administration, S.-H.K.; funding acquisition, S.-H.K. All authors have read and agreed to the published version of the manuscript.

Funding

This study was supported by Dental Research Institute (PNUDH DRI-2023-01), Pusan National University Dental Hospital.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Kokich, V.G.; Mathews, D.P. Surgical and orthodontic management of impacted teeth. Dent. Clin. North Am. 1993, 37, 181–204. [Google Scholar] [CrossRef] [PubMed]
  2. Thilander, B.; Jakobsson, S. Local factors in impaction of maxillary canines. Acta Odontol. Scand. 1968, 26, 145–168. [Google Scholar] [CrossRef] [PubMed]
  3. Laganà, G.; Venza, N.; Borzabadi-Farahani, A.; Fabi, F.; Danesi, C.; Cozza, P. Dental anomalies: Prevalence and associations between them in a large sample of non-orthodontic subjects, a cross-sectional study. BMC Oral Health 2017, 17, 1–7. [Google Scholar] [CrossRef] [PubMed]
  4. Ku, J.H.; Han, B.; Kim, J.; Oh, J.; Kook, Y.-A.; Kim, Y. Common dental anomalies in Korean orthodontic patients: An update. Korean J. Orthod. 2022, 52, 324–333. [Google Scholar] [CrossRef]
  5. Uslu, O.; Akcam, M.O.; Evirgen, S.; Cebeci, I. Prevalence of dental anomalies in various malocclusions. Am. J. Orthod. Dentof. Orthop. 2009, 135, 328–335. [Google Scholar] [CrossRef]
  6. Patil, S.; Maheshwari, S. Prevalence of impacted and supernumerary teeth in the North Indian population. J. Clin. Exp. Dent. 2014, 6, e116–e120. [Google Scholar] [CrossRef]
  7. Mucedero, M.; Rozzi, M.; Di Fusco, G.; Danesi, C.; Cozza, P. Morphometric analysis of the palatal shape and arch dimension in subjects with buccally displaced canine. Eur. J. Orthod. 2020, 42, 544–550. [Google Scholar] [CrossRef]
  8. Oh, S.; Kim, Y.I.; Kim, S.S.; Park, S.B.; Kim, S.H. Comparison of root apex’s position between unilateral and bilateral palatally impacted canines: A pilot study. Am. J. Orthod. Dentof. Orthop. 2023, 163, 311–318. [Google Scholar] [CrossRef]
  9. Jo, W.; Lee, N.; Lee, S. A statistical study on characteristics and treatment of child and adolescent patients with tooth impaction. J. Korean Acad. Pediatr. Dent. 2014, 41, 306–313. [Google Scholar] [CrossRef]
  10. Bishara, S.E.; Kommer, D.D.; McNeil, M.H.; Montagano, L.N.; Oesterle, L.J.; Youngquist, H.W. Management of impacted canines. Am. J. Orthod. 1976, 69, 371–387. [Google Scholar] [CrossRef]
  11. Cruz, R.M. Orthodontic traction of impacted canines: Concepts and clinical application. Dental Press J. Orthod. 2019, 24, 74–87. [Google Scholar] [CrossRef]
  12. Cassina, C.; Papageorgiou, S.N.; Eliades, T. Open versus closed surgical exposure for permanent impacted canines: A systematic review and meta-analyses. Eur. J. Orthod. 2018, 40, 1–10. [Google Scholar] [CrossRef]
  13. Kapila, S.D. Cone Beam Computed Tomography in Orthodontics; Wiley-Blackwell: Ann Arbor, MI, USA, 2014. [Google Scholar]
  14. Gandhi, V.; Luu, B.; Dresner, R.; Pierce, D.; Upadhyay, M. Where is the center of resistance of a maxillary first molar? A 3-dimensional finite element analysis. Am. J. Orthod. Dentof. Orthop. 2021, 160, 442–450. [Google Scholar] [CrossRef]
  15. Choy, K.; Pae, E.K.; Park, Y.; Kim, K.H.; Burstone, C.J. Effect of root and bone morphology on the stress distribution in the periodontal ligament. Am. J. Orthod. Dentof. Orthop. 2000, 117, 98–105. [Google Scholar] [CrossRef] [PubMed]
  16. Vollmer, D.; Bourauel, C.; Maier, K.; Jäger, A. Determination of the centre of resistance in an upper human canine and idealized tooth model. Eur. J. Orthod. 1999, 21, 633–648. [Google Scholar] [CrossRef] [PubMed]
  17. Liu, X.; Liu, M.; Wu, B.; Liu, J.; Tang, W.; Yan, B. Effect of the Maxillary Sinus on Tooth Movement during Orthodontics Based on Biomechanical Responses of Periodontal Ligaments. Appl. Sci. 2022, 12, 4990. [Google Scholar] [CrossRef]
  18. Prasad, K.N.; Shivamurthy, P.; Sagarkar, R. Orthodontic Displacement and Stress Assessment: A Finite Element Analysis. World J. Dent. 2017, 8, 407–412. [Google Scholar] [CrossRef]
  19. Zeno, K.G.; Mustapha, S.; Ayoub, G.; Ghafari, J.G. Effect of force direction and tooth angulation during traction of palatally impacted canines: A finite element analysis. Am. J. Orthod. Dentof. Orthop. 2020, 157, 377–384. [Google Scholar] [CrossRef]
  20. Lena Sezici, Y.; Gediz, M.; Akış, A.A.; Sarı, G.; Duran, G.S.; Dindaroğlu, F. Displacement and stress distribution of Kilroy spring and nickel-titanium closed-coil spring during traction of palatally impacted canine: A 3-dimensional finite element analysis. Orthod. Craniofac. Res. 2020, 23, 471–478. [Google Scholar] [CrossRef]
  21. Burstone, C.J.; Pryputniewicz, R.J. Holographic determination of centers of rotation produced by orthodontic forces. Am. J. Orthod. 1980, 77, 396–409. [Google Scholar] [CrossRef]
  22. Choy, K.; Kim, K.H.; Burstone, C.J. Initial changes of centres of rotation of the anterior segment in response to horizontal forces. Eur. J. Orthod. 2006, 28, 471–474. [Google Scholar] [CrossRef] [PubMed]
  23. Woo, J.Y.; Park, Y.C. Experimental study of the vertical location of the centers of resistance for maxillary anterior teeth during retraction using the laser reflection technique. Korean J. Orthod. 1993, 23, 375–389. [Google Scholar]
  24. Kwak, K.H.; Oh, S.; Choi, Y.K.; Kim, S.H.; Kim, S.S.; Park, S.B.; Kim, Y.I. Effects of different distalization directions and methods on maxillary total distalization with clear aligners: A finite element study. Angle Orthod. 2023, 93, 348–356. [Google Scholar] [CrossRef]
  25. Zhu, G.Y.; Zhang, B.; Yao, K.; Lu, W.X.; Peng, J.J.; Shen, Y.; Zhao, Z.H. Finite element analysis of the biomechanical effect of clear aligners in extraction space closure under different anchorage controls. Am. J. Orthod. Dentof. Orthop. 2023, 163, 628–644. [Google Scholar] [CrossRef]
  26. Geiger, M.E.; Lapatki, B.G. Locating the center of resistance in individual teeth via two-and three-dimensional radiographic data. J. Orofac. Orthop. 2014, 75, 96–106. [Google Scholar] [CrossRef] [PubMed]
  27. Huang, H.; Tang, W.; Yan, B.; Wu, B.; Cao, D. Mechanical responses of the periodontal ligament based on an exponential hyperelastic model: A combined experimental and finite element method. Comput. Methods Biomech. Biomed. Engin. 2016, 19, 188–198. [Google Scholar] [CrossRef] [PubMed]
  28. Ghiasi, M.S.; Chen, J.E.; Rodriguez, E.K.; Vaziri, A.; Nazarian, A. Computational modeling of human bone fracture healing affected by different conditions of initial healing stage. BMC Musculoskelet. Disord. 2019, 20, 1–14. [Google Scholar] [CrossRef]
  29. Liu, L.; Zhan, Q.; Zhou, J.; Kuang, Q.; Yan, X.; Zhang, X.; Shan, Y.; Li, X.; Lai, W.; Long, H. Effectiveness of an anterior mini-screw in achieving incisor intrusion and palatal root torque for anterior retraction with clear aligners: A finite element study. Angle Orthod. 2021, 91, 794–803. [Google Scholar] [CrossRef]
  30. Araújo, M.G.; Silva, C.O.; Misawa, M.; Sukekava, F. Alveolar socket healing: What can we learn? Periodontol. 2000 2015, 68, 122–134. [Google Scholar] [CrossRef]
  31. Meyer, B.N.; Chen, J.; Katona, T.R. Does the center of resistance depend on the direction of tooth movement? Am. J. Orthod. Dentof. Orthop. 2010, 137, 354–361. [Google Scholar] [CrossRef]
  32. Fish, G.D. Some Engineering Principles of Possible Interest to Orthodontists; SS White Dental Manufacturing Company: Philadelphia, PA, USA, 1917. [Google Scholar]
  33. Mulligan, T.F. Common sense mechanics. J. Clin. Orthod. 1979, 13, 676–683. [Google Scholar] [PubMed]
  34. Smith, R.J.; Burstone, C.J. Mechanics of tooth movement. Am. J. Orthod. 1984, 85, 294–307. [Google Scholar] [CrossRef] [PubMed]
  35. Provatidis, C.G. Numerical estimation of the centres of rotation and resistance in orthodontic tooth movement. Comput. Methods Biomech. Biomed. Engin. 1999, 2, 149–156. [Google Scholar] [CrossRef] [PubMed]
  36. Bourauel, C.; Keilig, L.; Rahimi, A.; Reimann, S.; Ziegler, A.; Jäger, A. Computer-aided analysis of the biomechanics of tooth movements. Int. J. Comput. Dent. 2007, 10, 25–40. [Google Scholar] [PubMed]
  37. Berkovitz, B. The structure of the periodontal ligament: An update. Eur. J. Orthod. 1990, 12, 51–76. [Google Scholar] [CrossRef] [PubMed]
Applsci 13 11256 g001
Figure 1. Three-dimensionally scanned model for maxillary canine. (A) labial side, (B) mesial side, (C) lingual side, (D) occlusal side.
Figure 1. Three-dimensionally scanned model for maxillary canine. (A) labial side, (B) mesial side, (C) lingual side, (D) occlusal side.
Applsci 13 11256 g001
Applsci 13 11256 g002
Figure 2. Minimum and maximum elastic strain at the outermost boundary according to the diameter of the cylinder. Triangle point, maximum elastic strain; circle point, minimum elastic strain.
Figure 2. Minimum and maximum elastic strain at the outermost boundary according to the diameter of the cylinder. Triangle point, maximum elastic strain; circle point, minimum elastic strain.
Applsci 13 11256 g002
Applsci 13 11256 g003
Figure 3. Finite element model for impacted maxillary canine. Pericoronal tissues consist of air, granulation tissue, fibrous tissue, immature woven bone, or mature woven bone.
Figure 3. Finite element model for impacted maxillary canine. Pericoronal tissues consist of air, granulation tissue, fibrous tissue, immature woven bone, or mature woven bone.
Applsci 13 11256 g003
Applsci 13 11256 g004
Figure 4. Coordinate system and loading conditions of each direction. (A) Buccolingual direction, (B) Mesiodistal direction.
Figure 4. Coordinate system and loading conditions of each direction. (A) Buccolingual direction, (B) Mesiodistal direction.
Applsci 13 11256 g004
Applsci 13 11256 g005
Figure 5. Schematic diagram for calculating the center of resistance. After applying a single force (F = 1 N) to a specific point of the tooth, several counter moments (M/F = 1, 3, 5, 7 mm) are applied to compensate for this at the same point. Dark green, blue, light green, and red lines signify the displacement curve of the tooth axis.
Figure 5. Schematic diagram for calculating the center of resistance. After applying a single force (F = 1 N) to a specific point of the tooth, several counter moments (M/F = 1, 3, 5, 7 mm) are applied to compensate for this at the same point. Dark green, blue, light green, and red lines signify the displacement curve of the tooth axis.
Applsci 13 11256 g005
Applsci 13 11256 g006
Figure 6. Buccolingual displacement of the tooth axial path. (A) Air, (B) granulation tissue, (C) fibrous tissue, (D) immature woven bone, and (E) mature woven bone. Horizontal dotted lines indicate the height of the cementoenamel junction of the maxillary canine.
Figure 6. Buccolingual displacement of the tooth axial path. (A) Air, (B) granulation tissue, (C) fibrous tissue, (D) immature woven bone, and (E) mature woven bone. Horizontal dotted lines indicate the height of the cementoenamel junction of the maxillary canine.
Applsci 13 11256 g006
Applsci 13 11256 g007
Figure 7. Mesiodistal displacement of the tooth axial path. (A) Air, (B) granulation tissue, (C) fibrous tissue, (D) immature woven bone, and (E) mature woven bone. Horizontal dotted lines indicate the height of the cementoenamel junction of the maxillary canine.
Figure 7. Mesiodistal displacement of the tooth axial path. (A) Air, (B) granulation tissue, (C) fibrous tissue, (D) immature woven bone, and (E) mature woven bone. Horizontal dotted lines indicate the height of the cementoenamel junction of the maxillary canine.
Applsci 13 11256 g007
Applsci 13 11256 g008
Figure 8. Center of resistance of the impacted maxillary canine according to the stages of pericoronal tissue healing. (A) Buccolingual direction and (B) mesiodistal direction.
Figure 8. Center of resistance of the impacted maxillary canine according to the stages of pericoronal tissue healing. (A) Buccolingual direction and (B) mesiodistal direction.
Applsci 13 11256 g008
Applsci 13 11256 g009
Figure 9. Changes in tooth movement depending on the location of an attachment and the timing of applying orthodontic force to the impacted tooth. Red circle, center of resistance; blue circle, the location of an attachment; arrow, the direction of an orthodontic force.
Figure 9. Changes in tooth movement depending on the location of an attachment and the timing of applying orthodontic force to the impacted tooth. Red circle, center of resistance; blue circle, the location of an attachment; arrow, the direction of an orthodontic force.
Applsci 13 11256 g009
Applsci 13 11256 g010
Figure 10. Root shape on the mesiodistal and buccolingual side. (A) Mesiodistal side and (B) buccolingual side.
Figure 10. Root shape on the mesiodistal and buccolingual side. (A) Mesiodistal side and (B) buccolingual side.
Applsci 13 11256 g010
Table 1. Material properties of the finite element model.
Table 1. Material properties of the finite element model.
Young’s Modulus (MPa)Poisson’s Ratio
Periodontal ligament0.05Ogden 1st model
Tooth19,6000.3
Bone17,0000.3
Granulation tissue0.0010.17
Fibrous tissue20.17
Immature woven bone10000.3
Mature woven bone60000.3
Table 2. Center of resistance according to the stages of pericoronal tissue healing: locations from the cementoenamel junction and root/crown length percentages.
Table 2. Center of resistance according to the stages of pericoronal tissue healing: locations from the cementoenamel junction and root/crown length percentages.
Pericoronal TissueLocation from the Cementoenamel Junction (mm)Percentage of Root/Crown Length (%)
MDBLMDBL
Air−5.18 *−5.26 *38.1% †38.7% †
Granulation tissue−5.18 *−5.26 *38.1% †38.7% †
Fibrous tissue−2.82 *−3.46 *20.8% †25.5% †
Immature woven bone4.254.3040.8% ‡41.3% ‡
Mature woven bone4.645.1844.6% ‡49.8% ‡
* Negative means root apex direction; † percentage of root length; ‡ percentage of the crown length; BL, buccolingual direction; MD, mesiodistal direction.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Oh, S.; Choi, Y.-K.; Kim, Y.-I.; Kim, S.-S.; Park, S.-B.; Kim, S.-H. The Center of Resistance of an Impacted Maxillary Canine: A Finite Element Analysis. Appl. Sci. 2023, 13, 11256. https://doi.org/10.3390/app132011256

AMA Style

Oh S, Choi Y-K, Kim Y-I, Kim S-S, Park S-B, Kim S-H. The Center of Resistance of an Impacted Maxillary Canine: A Finite Element Analysis. Applied Sciences. 2023; 13(20):11256. https://doi.org/10.3390/app132011256

Chicago/Turabian Style

Oh, Sewoong, Youn-Kyung Choi, Yong-Il Kim, Seong-Sik Kim, Soo-Byung Park, and Sung-Hun Kim. 2023. "The Center of Resistance of an Impacted Maxillary Canine: A Finite Element Analysis" Applied Sciences 13, no. 20: 11256. https://doi.org/10.3390/app132011256

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop