Improved Reptile Search Optimization Algorithm: Application on Regression and Classification Problems
Abstract
1. Introduction
1.1. Contributions and Organization
- An improved reptile search algorithm (IRSA) based on a sine operator and Levy flight was proposed to enhance the performance of the original RSA.
- The proposed IRSA was evaluated using 23 benchmark test functions. Various qualitative, quantitative, comparative, statistical, and complexity analyses were performed to validate the positive effects of the improvisations.
- This research also proposed a hybrid methodology that integrates Multi-Layer Perceptron Neural Network with the improvised RSA for solving various classification problems.
- Finally, the IRSA was applied to train a radial basis function neural network (RBFNN) for short-term wind and solar power predictions.
1.2. Literature Survey
2. Proposed Methodology
2.1. Reptile Search Algorithm
2.1.1. Initialization
2.1.2. Encircling Phase (Exploration)
2.1.3. Hunting Phase (Exploitation)
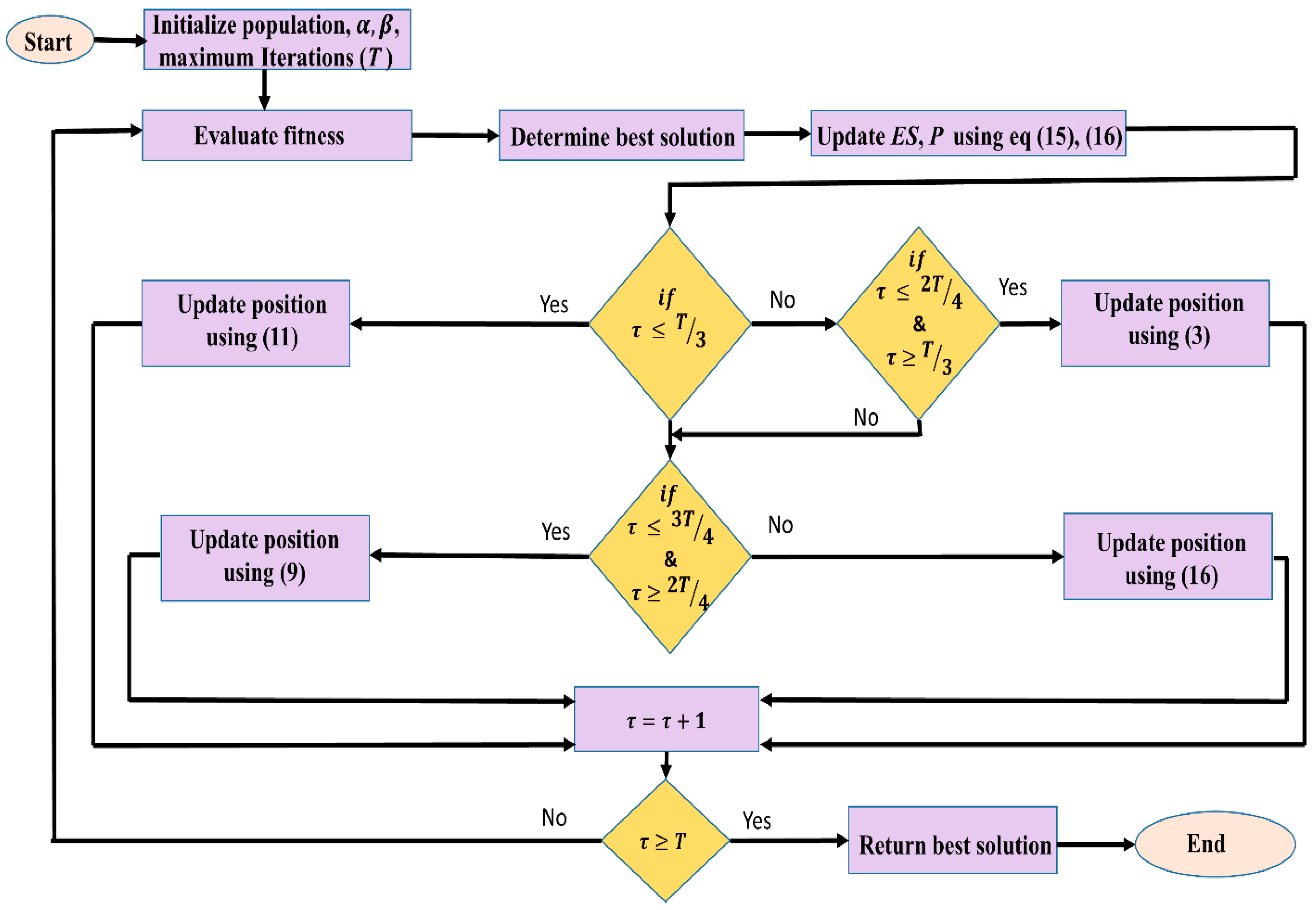
2.2. Proposed Improved Reptile Search Algorithm (IRSA)
| Algorithm 1 Pseudocode of IRSA |
| Initialize random population x Initialize iteration counter= 0, maximum iteration T, alpha, beta while< T Evaluate fitness of potential candidates Determines the best solution Update Es,using Equations (6) and (7) for j = 1: p for k = 1: n If Solve using Equation (11) else if Solve using Equation (3) else if Solve using Equation (9) else Solve using Equation (16) end if end for end for t = t + 1 end while Return best solution |
3. Experimental Verification Using Benchmark Test Functions
3.1. Qualitative Analysis
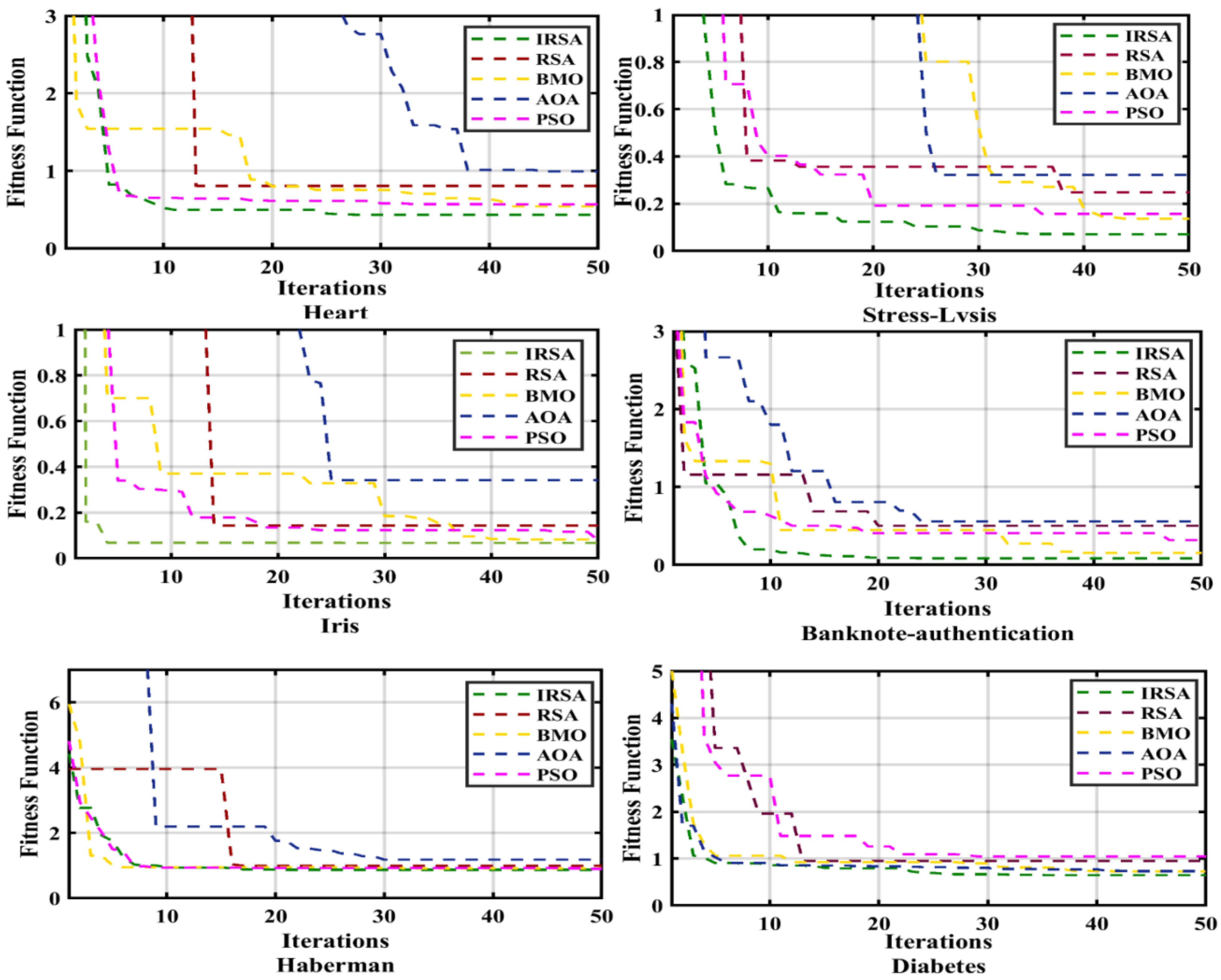
3.2. Comparative Analysis
3.3. Time Complexity Analysis
4. IRSA for Neural Network Training
4.1. Multi-Layer Perceptron Neural Network (MLPNN)
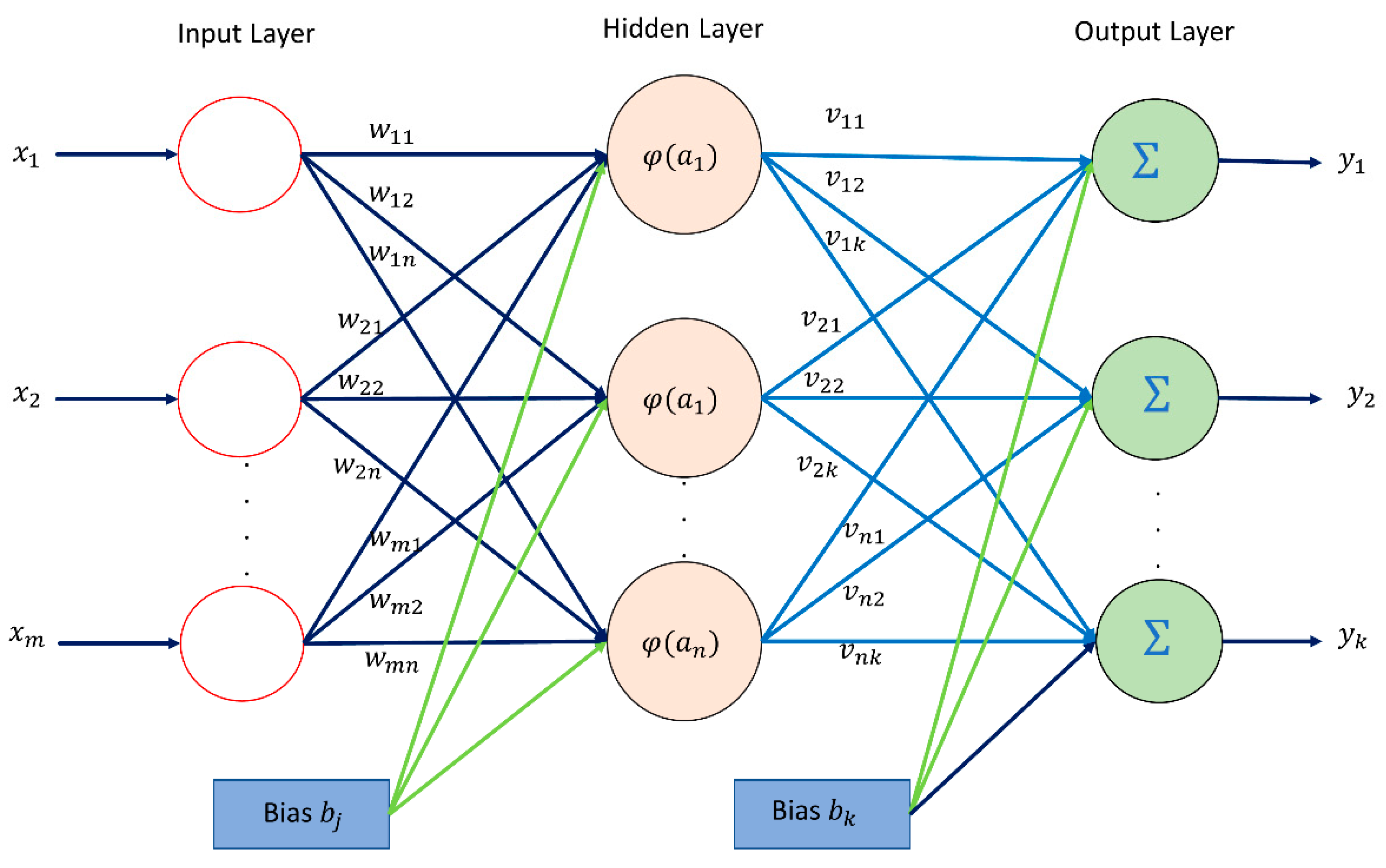
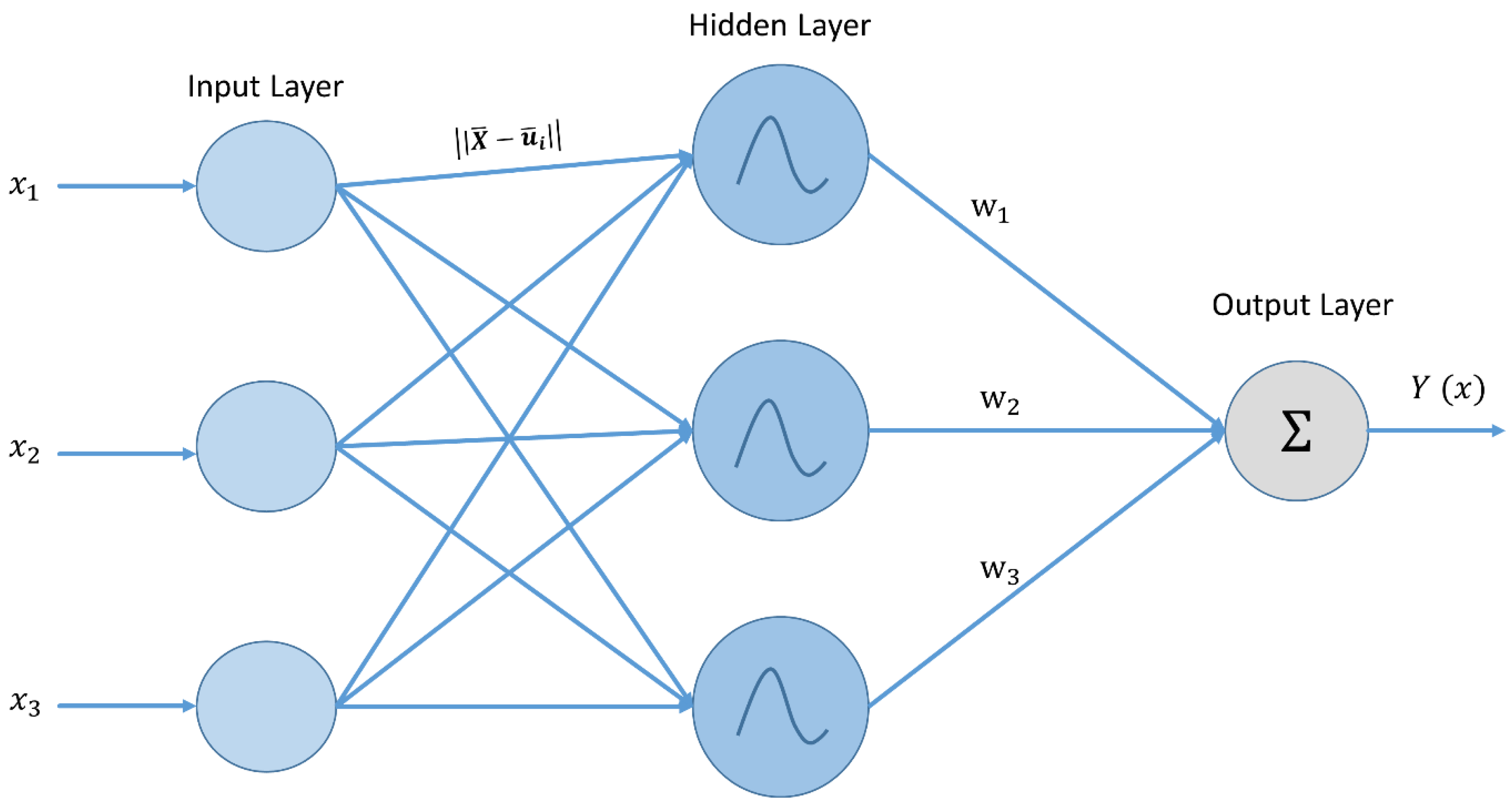
4.2. Radial Basis Function Neural Network (RBFNN)
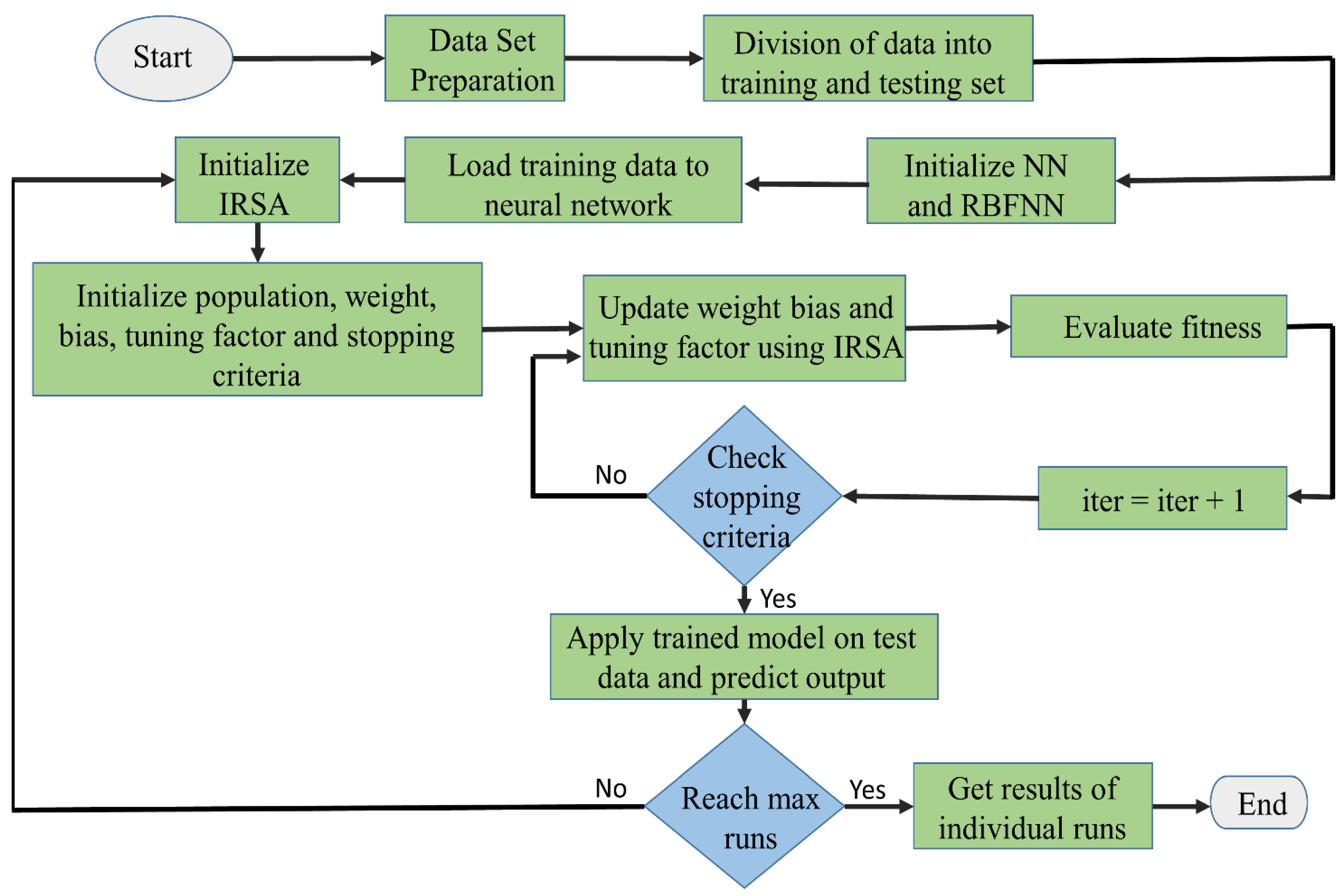
4.3. Training of MLPNN and RBFNN Using the Proposed IRSA
5. IRSA for Solving Classification Problems
Statistical Indicators for Classification
6. IRSA for Solving the Regression Problems
6.1. Wind Power Prediction
6.2. Solar Power Prediction
6.3. Statistical Indicators for Regression
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Function Description | Dim | Range | |
|---|---|---|---|
| 500, 100, 50, 30 | [−100, 100] | 0 | |
| 500, 100, 50, 30 | [−10, 10] | 0 | |
| 500, 100, 50, 30 | [−100, 100] | 0 | |
| 500, 100, 50, 30 | [−100, 100] | 0 | |
| 500, 100, 50, 30 | [−30, 30] | 0 | |
| 500, 100, 50, 30 | [−100, 100] | 0 | |
| 500, 100, 50, 30 | [−1.28, 1.28] | 0 |
| Function Description | Dim | Range | |
|---|---|---|---|
| 500, 100, 50, 30 | [−100, 100] | −418.980 × Dim | |
| 500, 100, 50, 30 | [−10, 10] | 0 | |
| 500, 100, 50, 30 | [−100, 100] | 0 | |
| 500, 100, 50, 30 | [−100, 100] | 0 | |
here, , | 500, 100, 50, 30 | [−30, 30] | 0 |
| 500, 100, 50, 30 | [−100, 100] | 0 |
| Function Description | Dim | Range | |
|---|---|---|---|
| 2 | [−65, 65] | 0.998 | |
| 4 | [−1, 1] | 0 | |
| 2 | [−5, 5] | −1.0316 | |
| 2 | [−4, 4] | 0.398 | |
| 2 | [−5, 5] | 3 | |
| 3 | [−5, 5] | −3.86 | |
| 6 | [−5, 5] | −1.170 | |
| 4 | [−5, 5] | −10.153 | |
| 4 | [−5, 5] | −10.4028 | |
| 4 | [−1, 1] | −10.536 |
| Function | Description | Range | Dim | |
|---|---|---|---|---|
| CEC-1 | Storn’s Chebyshev polynomial fitting problem | 1 | [−8192, 8192] | 9 |
| CEC-2 | Inverse Hilbert matrix problem | 1 | [−16,384, 16,384] | 16 |
| CEC-3 | Lennard–Jones minimum energy cluster | 1 | [−4, 4] | 18 |
| CEC-4 | Rastrigin function | 1 | [−100, 100] | 10 |
| CEC-5 | Grienwank function | 1 | [−100, 100] | 10 |
| CEC-6 | Weierstrass function | 1 | [−100, 100] | 10 |
| CEC-7 | Modified Schwefel function | 1 | [−100, 100] | 10 |
| CEC-8 | Expanded Schaffer function | 1 | [−100, 100] | 10 |
| CEC-9 | Happy CAT function | 1 | [−100, 100] | 10 |
References
- Chong, H.Y.; Yap, H.J.; Tan, S.C.; Yap, K.S.; Wong, S.Y. Advances of metaheuristic algorithms in training neural networks for industrial applications. Soft Comput. 2021, 25, 11209–11233. [Google Scholar] [CrossRef]
- Osaba, E.; Villar-Rodriguez, E.; Del Ser, J.; Nebro, A.J.; Molina, D.; LaTorre, A.; Suganthan, P.N.; Coello, C.A.C.; Herrera, F. A Tutorial On the design, experimentation and application of metaheuristic algorithms to real-World optimization problems. Swarm Evol. Comput. 2021, 64, 100888. [Google Scholar] [CrossRef]
- Khan, M.K.; Zafar, M.H.; Mansoor, M.; Mirza, A.F.; Khan, U.A.; Khan, N.M. Green energy extraction for sustainable development: A novel MPPT technique for hybrid PV-TEG system. Sustain. Energy Technol. Assess. 2022, 53, 102388. [Google Scholar]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Knowles, J.; Corne, D. The Pareto archived evolution strategy: A new baseline algorithm for Pareto multiobjective optimization. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999. [Google Scholar]
- Mansoor, M.; Mirza, A.F.; Ling, Q. Harris hawk optimization-based MPPT control for PV Systems under Partial Shading Conditions. J. Clean. Prod. 2020, 274, 122857. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Wu, Q.; Ma, Z.; Xu, G.; Li, S.; Chen, D. A novel neural network classifier using beetle antennae search algorithm for pattern classification. IEEE Access 2019, 7, 64686–64696. [Google Scholar] [CrossRef]
- Amari, S.; Wu, S. Improving support vector machine classifiers by modifying kernel functions. Neural Netw. 1999, 12, 783–789. [Google Scholar] [CrossRef]
- Peterson, L.E. K-nearest neighbor. Scholarpedia 2009, 4, 1883. [Google Scholar] [CrossRef]
- Rish, I. An empirical study of the I Bayes classifier. In Proceedings of the IJCAI 2001 Workshop on Empirical Methods in Artificial Intelligence, Seattle, WA, USA, 8 August 2001. [Google Scholar]
- El Naqa, I.; Murphy, M. What Is Machine Learning? In Machine Learning in Radiation Oncology: Theory and Applications; El Naqa, I., Li, R., Murphy, M., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 3–11. [Google Scholar]
- Shanmuganathan, S. Artificial Neural Network Modelling: An Introduction. In Artificial Neural Network Modelling; Shanmuganathan, S., Samarasinghe, S., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 1–14. [Google Scholar]
- Sinha, A.K.; Hati, A.S.; Benbouzid, M.; Chakrabarti, P. ANN-based pattern recognition for induction motor broken rotor bar monitoring under supply frequency regulation. Machines 2021, 9, 87. [Google Scholar] [CrossRef]
- D’Addona, D.M.; Ullah, A.M.M.S.; Matarazzo, D. Tool-wear prediction and pattern-recognition using artificial neural network and DNA-based computing. J. Intell. Manuf. 2017, 28, 1285–1301. [Google Scholar] [CrossRef]
- Wu, J.; Xu, C.; Han, X.; Zhou, D.; Zhang, M.; Li, H.; Tan, K.C. Progressive Tandem Learning for Pattern Recognition with Deep Spiking Neural Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 7824–7840. [Google Scholar] [CrossRef] [PubMed]
- Kiranyaz, S.; Avci, O.; Abdeljaber, O.; Ince, T.; Gabbouj, M.; Inman, D.J. 1D convolutional neural networks and applications: A survey. Mech. Syst. Signal Process. 2021, 151, 107398. [Google Scholar] [CrossRef]
- Poznyak, A.; Chairez, I.; Poznyak, T. A survey on artificial neural networks application for identification and control in environmental engineering: Biological and chemical systems with uncertain models. Annu. Rev. Control. 2019, 48, 250–272. [Google Scholar] [CrossRef]
- Hussain, M.; Dhimish, M.; Titarenko, S.; Mather, P. Artificial neural network based photovoltaic fault detection algorithm integrating two bi-directional input parameters. Renew. Energy 2020, 155, 1272–1292. [Google Scholar] [CrossRef]
- Veerasamy, V.; Wahab, N.I.A.; Othman, M.L.; Padmanaban, S.; Sekar, K.; Ramachandran, R.; Hizam, H.; Vinayagam, A.; Islam, M.Z. LSTM Recurrent Neural Network Classifier for High Impedance Fault Detection in Solar PV Integrated Power System. IEEE Access 2021, 9, 32672–32687. [Google Scholar] [CrossRef]
- Jiang, J.; Li, W.; Wen, Z.; Bie, Y.; Schwarz, H.; Zhang, C. Series Arc Fault Detection Based on Random Forest and Deep Neural Network. IEEE Sens. J. 2021, 21, 17171–17179. [Google Scholar] [CrossRef]
- Han, F.; Jiang, J.; Ling, Q.H.; Su, B.Y. A survey on metaheuristic optimization for random single-hidden layer feedforward neural network. Neurocomputing 2019, 335, 261–273. [Google Scholar] [CrossRef]
- Spurlock, K.; Elgazzar, H. A genetic mixed-integer optimization of neural network hyper-parameters. J. Supercomput. 2022, 78, 14680–14702. [Google Scholar] [CrossRef]
- Abd Elaziz, M.; Dahou, A.; Abualigah, L.; Yu, L.; Alshinwan, M.; Khasawneh, A.M.; Lu, S. Advanced metaheuristic optimization techniques in applications of deep neural networks: A review. Neural Comput. Appl. 2021, 33, 14079–14099. [Google Scholar] [CrossRef]
- Darwish, A.; Hassanien, A.E.; Das, S. A survey of swarm and evolutionary computing approaches for deep learning. Artif. Intell. Rev. 2020, 53, 1767–1812. [Google Scholar] [CrossRef]
- Ho, Y.-C.; Pepyne, D.L. Simple explanation of the no-free-lunch theorem and its implications. J. Optim. Theory Appl. 2002, 115, 549–570. [Google Scholar] [CrossRef]
- Abualigah, L.; Abd Elaziz, M.; Sumari, P.; Geem, Z.W.; Gandomi, A.H. Reptile Search Algorithm (RSA): A nature-inspired meta-heuristic optimizer. Expert Syst. Appl. 2022, 191, 116158. [Google Scholar] [CrossRef]
- Bou-Rabee, M.; Lodi, K.A.; Ali, M.; Ansari, M.F.; Tariq, M.; Sulaiman, S.A. One-month-ahead wind speed forecasting using hybrid AI model for coastal locations. IEEE Access 2020, 8, 198482–198493. [Google Scholar] [CrossRef]
- Farayola, A.M.; Sun, Y.; Ali, A. ANN-PSO Optimization of PV systems under different weather conditions. In Proceedings of the 2018 7th International Conference on Renewable Energy Research and Applications (ICRERA), Paris, France, 14–17 October 2018; IEEE: Piscataway, NJ, USA, 2018. [Google Scholar]
- Abdolrasol, M.G.; Mohamed, R.; Hannan, M.A.; Al-Shetwi, A.Q.; Mansor, M.; Blaabjerg, F. Artificial neural network based particle swarm optimization for microgrid optimal energy scheduling. IEEE Trans. Power Electron. 2021, 36, 12151–12157. [Google Scholar] [CrossRef]
- Banadkooki, F.B.; Ehteram, M.; Ahmed, A.N.; Teo, F.Y.; Ebrahimi, M.; Fai, C.M.; Huang, Y.F.; El-Shafie, A. Suspended sediment load prediction using artificial neural network and ant lion optimization algorithm. Environ. Sci. Pollut. Res. 2020, 27, 38094–38116. [Google Scholar] [CrossRef]
- Wongsinlatam, W.; Buchitchon, S. Criminal cases forecasting model using a new intelligent hybrid artificial neural network with cuckoo search algorithm. IAENG Int. J. Comput. Sci. 2020, 47, 481–490. [Google Scholar]
- Mehrabi, P.; Honarbari, S.; Rafiei, S.; Jahandari, S.; Alizadeh Bidgoli, M. Seismic response prediction of FRC rectangular columns using intelligent fuzzy-based hybrid metaheuristic techniques. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 10105–10123. [Google Scholar] [CrossRef]
- Anand, A.; Suganthi, L. Hybrid GA-PSO optimization of artificial neural network for forecasting electricity demand. Energies 2018, 11, 728. [Google Scholar] [CrossRef]
- Faris, H.; Aljarah, I.; Mirjalili, S. Improved monarch butterfly optimization for unconstrained global search and neural network training. Appl. Intell. 2018, 48, 445–464. [Google Scholar] [CrossRef]
- Zafar, M.H.; Khan, N.M.; Mansoor, M.; Mirza, A.F.; Moosavi, S.K.R.; Sanfilippo, F. Adaptive ML-based technique for renewable energy system power forecasting in hybrid PV-Wind farms power conversion systems. Energy Convers. Manag. 2022, 258, 115564. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, J.S. Improved salp swarm algorithm based on levy flight and sine cosine operator. IEEE Access 2020, 8, 99740–99771. [Google Scholar] [CrossRef]
- Iacca, G.; Junior, V.C.D.S.; de Melo, V.V. An improved Jaya optimization algorithm with Lévy flight. Expert Syst. Appl. 2021, 165, 113902. [Google Scholar] [CrossRef]
- Dahou, A.; Abd Elaziz, M.; Chelloug, S.A.; Awadallah, M.A.; Al-Betar, M.A.; Al-qaness, M.A.; Forestiero, A. Intrusion Detection System for IoT Based on Deep Learning and Modified Reptile Search Algorithm. Comput. Intell. Neurosci. 2022, 2022, 6473507. [Google Scholar] [CrossRef]
- Xiong, J.; Peng, T.; Tao, Z.; Zhang, C.; Song, S.; Nazir, M.S. A dual-scale deep learning model based on ELM-BiLSTM and improved reptile search algorithm for wind power prediction. Energy 2023, 266, 126419. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl. Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Chechkin, A.; Metzler, R.; Klafter, J.; Gonchar, V.Y. Introduction to the Theory Lévy Flights. In Anomalous Transport: Foundations and Applications; Wiley-VCH: Weinheim, Germany, 2008. [Google Scholar]
- Yang, X.-S.; Deb, S. Multiobjective cuckoo search for design optimization. Comput. Oper. Res. 2013, 40, 1616–1624. [Google Scholar] [CrossRef]
- Xin, Y.; Yong, L.; Guangming, L. Evolutionary programming made faster. IEEE Trans. Evol. Comput. 1999, 3, 82–102. [Google Scholar] [CrossRef]
- Sulaiman, M.H.; Mustaffa, Z.; Saari, M.M.; Daniyal, H. Barnacles mating optimizer: A new bio-inspired algorithm for solving engineering optimization problems. Eng. Appl. Artif. Intell. 2020, 87, 103330. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The Arithmetic Optimization Algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Fouad, M.M.; El-Desouky, A.I.; Al-Hajj, R.; El-Kenawy, E.S.M. Dynamic Group-Based Cooperative Optimization Algorithm. IEEE Access 2020, 8, 148378–148403. [Google Scholar] [CrossRef]
- Zafar, M.H.; Khan, N.M.; Moosavi, S.K.R.; Mansoor, M.; Mirza, A.F.; Akhtar, N. Artificial Neural Network (ANN) trained by a Novel Arithmetic Optimization Algorithm (AOA) for Short Term Forecasting of Wind Power. In Proceedings of the International Conference on Intelligent Technologies and Applications (INTAP), Grimstad, Norway, 11–13 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 197–209. [Google Scholar]
- Liang, J.J.; Suganthan, P.N.; Chen, Q. Problem definitions and evaluation criteria for the CEC 2013 special session on real-parameter optimization. Comput. Intell. Lab. Zhengzhou Univ. Zhengzhou China Nanyang Technol. Univ. Singap. Tech. Rep. 2013, 201212, 281–295. [Google Scholar]
- Mansoor, M.; Ling, Q.; Zafar, M.H. Short Term Wind Power Prediction using Feedforward Neural Network (FNN) trained by a Novel Sine-Cosine fused Chimp Optimization Algorithm (SChoA). In Proceedings of the 2022 5th International Conference on Energy Conservation and Efficiency (ICECE), Lahore, Pakistan, 16–17 March 2022; IEEE: Piscataway, NJ, USA, 2022. [Google Scholar]
- Available online: https://archive.ics.uci.edu/ml/index.php (accessed on 17 September 2022).
- Available online: https://www.kaggle.com/datasets (accessed on 30 September 2022).
- Al-Dahidi, S.; Ayadi, O.; Alrbai, M.; Adeeb, J. Ensemble approach of optimized artificial neural networks for solar photovoltaic power prediction. IEEE Access 2019, 7, 81741–81758. [Google Scholar] [CrossRef]
- Şahin, S.; Türkeş, M. Assessing wind energy potential of Turkey via vectoral map of prevailing wind and mean wind of Turkey. Theor. Appl. Climatol. 2020, 141, 1351–1366. [Google Scholar] [CrossRef]
- Available online: https://www.kaggle.com/datasets/berkerisen/wind-turbine-scada-dataset (accessed on 13 October 2022).
- Available online: https://www.kaggle.com/datasets/anikannal/solar-power-generation-data (accessed on 10 October 2022).
- Zafar, M.H.; Khan, U.A.; Khan, N.M. Hybrid Grey Wolf Optimizer Sine Cosine Algorithm based Maximum Power Point Tracking Control of PV Systems under Uniform Irradiance and Partial Shading Condition. In Proceedings of the 2021 4th International Conference on Energy Conservation and Efficiency (ICECE), Lahore, Pakistan, 16–17 March 2021; IEEE: Piscataway, NJ, USA, 2021. [Google Scholar]
- Zafar, M.H.; Khan, N.M.; Mirza, A.F.; Mansoor, M.; Akhtar, N.; Qadir, M.U.; Khan, N.A.; Moosavi, S.K.R. A novel meta-heuristic optimization algorithm based MPPT control technique for PV systems under complex partial shading condition. Sustain. Energy Technol. Assess. 2021, 47, 101367. [Google Scholar]
- Mansoor, M.; Mirza, A.F.; Duan, S.; Zhu, J.; Yin, B.; Ling, Q. Maximum energy harvesting of centralized thermoelectric power generation systems with non-uniform temperature distribution based on novel equilibrium optimizer. Energy Convers. Manag. 2021, 246, 114694. [Google Scholar] [CrossRef]
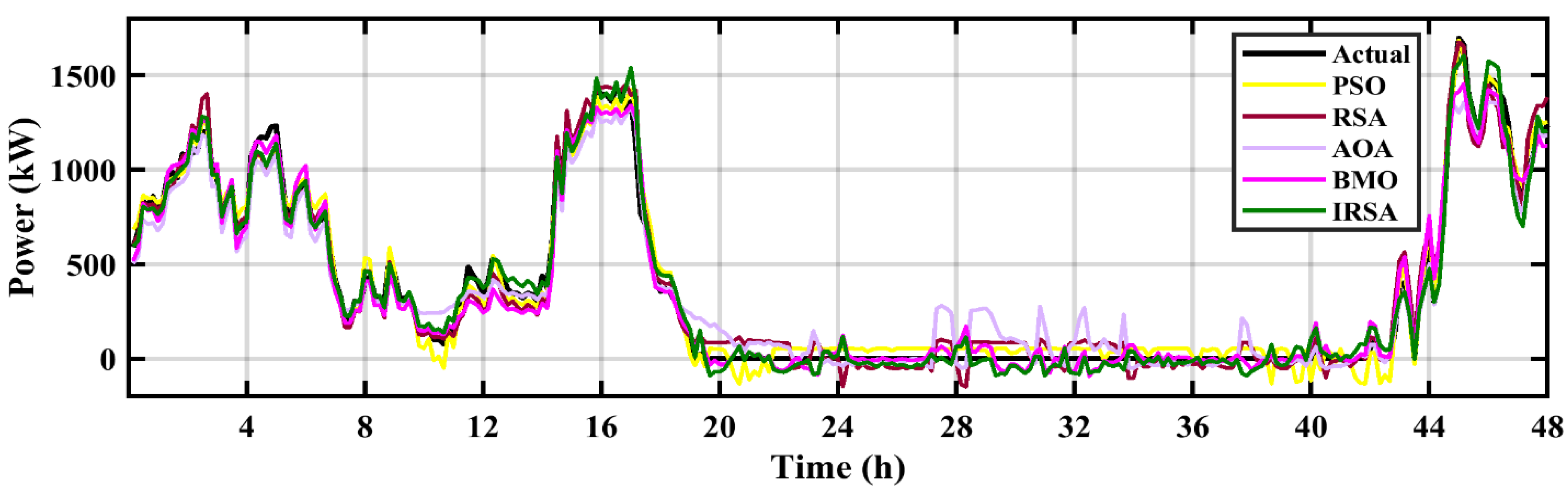

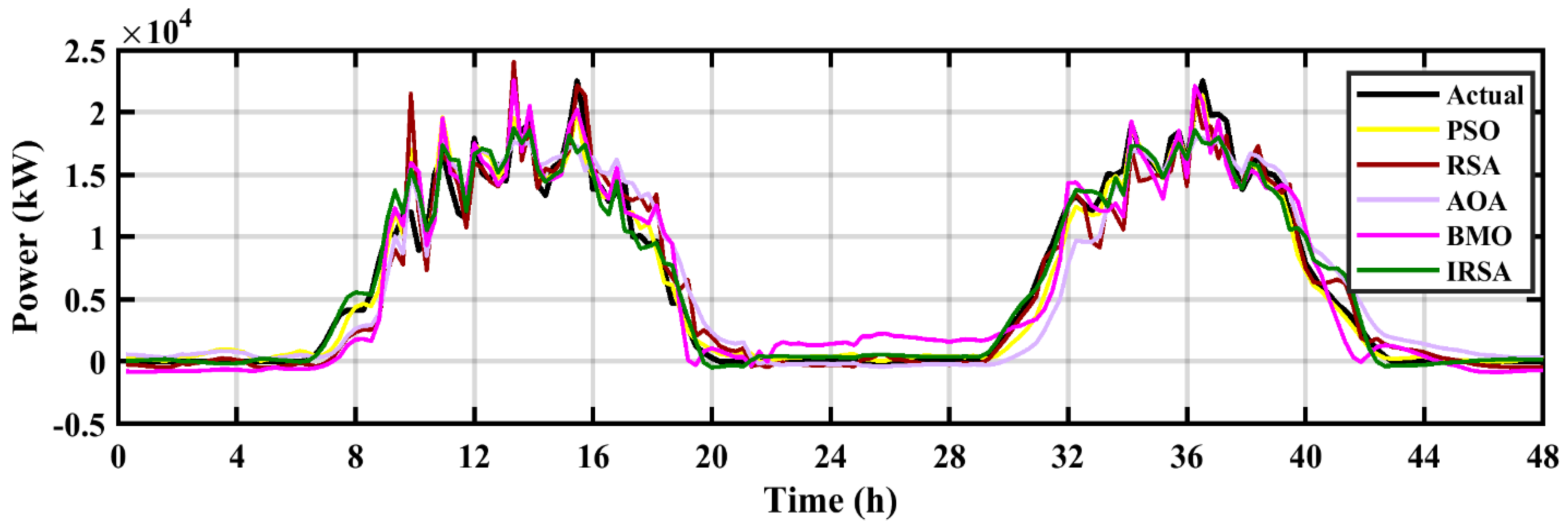
| Fun | Measure | IRSA | RSA | BMO | PSO | GWO | AOA | DGCO |
|---|---|---|---|---|---|---|---|---|
| F1 | Best | 0 | 0 | 6.030e-129 | 32.4203 | 4.7922e-35 | 6.706e-284 | 1.238e-21 |
| Worst | 0 | 0 | 1.961e-121 | 63.6854 | 8.0427e-33 | 1.2838e-114 | 2.1218e-19 | |
| Average | 0 | 0 | 2.712e-122 | 43.2608 | 1.4545e-33 | 1.2838e-115 | 4.7446e-20 | |
| STD | 0 | 0 | 6.153e-122 | 9.48589 | 2.4625e-33 | 4.0598e-115 | 7.9075e-20 | |
| F2 | Best | 0 | 0 | 1.393e-67 | 2.35817 | 1.7406e-20 | 0 | 3.7704e-14 |
| Worst | 0 | 0 | 7.383e-65 | 5.32663 | 9.4593e-20 | 0 | 4.68526e-13 | |
| Average | 0 | 0 | 1.841e-65 | 3.31147 | 4.5301e-20 | 0 | 1.10333e-13 | |
| STD | 0 | 0 | 2.663e-65 | 0.89717 | 2.2708e-20 | 0 | 1.29549e-13 | |
| F3 | Best | 0 | 0 | 4.0313e-92 | 5.5826e+03 | 4.5340e-04 | 0.0286 | 0.0025 |
| Worst | 0 | 0 | 2.9026e-76 | 9.1971e+03 | 0.0201 | 0.5838 | 25.4054 | |
| Average | 0 | 0 | 1.1183e-76 | 7.8891e+03 | 0.0074 | 0.1907 | 5.7823 | |
| STD | 0 | 0 | 1.5330e-76 | 1.3842e+03 | 0.0074 | 0.2277 | 10.9998 | |
| F4 | Best | 0 | 0 | 7.3742e-58 | 5.43665 | 7.5397e-09 | 4.6289e-88 | 4.97610e-06 |
| Worst | 0 | 0 | 2.5295e-52 | 14.1279 | 4.4114e-08 | 0.05287 | 0.000247 | |
| Average | 0 | 0 | 4.1512e-53 | 8.305702 | 1.8813e-08 | 0.024560 | 5.9520e-05 | |
| STD | 0 | 0 | 8.765e-53 | 2.59027 | 1.274e-08 | 0.02222 | 7.3133e-05 | |
| F5 | Best | 45.4705 | 48.9824 | 48.9417 | 5.7675e+03 | 46.1950 | 48.6070 | 46.1974 |
| Worst | 47.7889 | 48.9903 | 48.9984 | 1.0132e+04 | 47.8430 | 48.9439 | 47.8660 | |
| Average | 46.4656 | 48.9883 | 48.9721 | 8.1573e+03 | 47.0300 | 48.7869 | 47.0569 | |
| STD | 0.6506 | 0.0032 | 0.0173 | 2.0349e+03 | 0.8086 | 0.1402 | 0.5917 | |
| F6 | Best | 1.58 | 11.97 | 11.39 | 150.00 | 2.25 | 6.43 | 3.48 |
| Worst | 2.67 | 12.25 | 12.44 | 284.60 | 2.89 | 7.44 | 5.78 | |
| Average | 2.37 | 12.22 | 11.935 | 214.76 | 2.5 | 6.90 | 4.67 | |
| STD | 0.25 | 0.0878 | 0.4067 | 47.02 | 0.27 | 0.34 | 0.66 | |
| F7 | Best | 7.6084e-06 | 2.6639e-05 | 1.5133e-04 | 0.1347 | 4.8839e-04 | 1.6821e-07 | 0.0014 |
| Worst | 2.8963e-05 | 6.7811e-05 | 3.8440e-04 | 0.2985 | 0.0037 | 5.2418e-05 | 0.0154 | |
| Average | 8.7740e-05 | 9.0710e-05 | 4.1659e-04 | 0.2155 | 0.0022 | 2.3443e-05 | 0.0071 | |
| STD | 9.3116e-05 | 5.2933e-05 | 2.3023e-04 | 0.0592 | 0.0012 | 2.0923e-05 | 0.0055 | |
| F8 | Best | −1.0646e+4 | −8.845e+3 | −5.358e+3 | −1.0646e+4 | −9.14e+3 | −8.0208e+03 | −1.0548e+04 |
| Worst | −6.8637e+3 | −4.57e+3 | −2.928e+03 | −6.8637e+3 | −6.13e+3 | −6.8298e+03 | −7.3571e+03 | |
| Average | −8.7577e+3 | −6.04e+3 | −3.867e+03 | −8.7577e+3 | −7.32e+3 | −7.2473e+03 | −8.5385e+03 | |
| STD | 1.0697e+3 | 1.2009e+3 | 863.4437 | 1.0697e+3 | 902.38 | 427.9226 | 849.1905 | |
| F9 | Best | 0 | 0 | 0 | 114.0457 | 5.6843e-13 | 0 | 4.4338e-12 |
| Worst | 0 | 0 | 0 | 140.5094 | 5.42412 | 0 | 1.4080e-09 | |
| Average | 0 | 0 | 0 | 131.6173 | 3.0390 | 0 | 4.7419e-10 | |
| STD | 0 | 0 | 0 | 15.2178 | 2.7705 | 0 | 8.0872e-10 | |
| F10 | Best | 8.8817e-16 | 8.8817e-16 | 8.8817e-16 | 2.98933 | 3.9968e-14 | 8.8817e-16 | 2.0863e-12 |
| Worst | 8.8817e-16 | 8.8817e-16 | 8.8817e-16 | 4.25557 | 5.0626e-14 | 8.8817e-16 | 20.2605 | |
| Average | 8.8817e-16 | 8.8817e-16 | 8.881e-16 | 3.62755 | 4.3520e-14 | 8.8817e-16 | 4.04392 | |
| STD | 0 | 0 | 0 | 0.38752 | 3.3495e-15 | 0 | 8.52536 | |
| F11 | Best | 0 | 0 | 0 | 1.18496 | 0 | 0.009543 | 0 |
| Worst | 0 | 0 | 0 | 1.75459 | 0.014698 | 0.428251 | 0.019779 | |
| Average | 0 | 0 | 0 | 1.39448 | 0.00368 | 0.159273 | 0.001977 | |
| STD | 0 | 0 | 0 | 0.177805 | 0.006091 | 0.138820 | 0.006254 | |
| F12 | Best | 0.0868 | 1.1349 | 0.7756 | 0.1567 | 0.0373 | 1.0089 | 0.1162 |
| Worst | 0.1513 | 1.4160 | 1.1959 | 0.2635 | 0.0583 | 1.0286 | 0.2057 | |
| Average | 0.1534 | 1.3680 | 1.1688 | 0.2182 | 0.0459 | 1.0395 | 0.2604 | |
| STD | 0.0373 | 0.1246 | 0.2121 | 0.0552 | 0.0110 | 0.0316 | 0.1348 | |
| F13 | Best | 4.5760e-08 | 1.8359 | 0.1800 | 0.1624 | 0.8989 | 4.7901 | 2.8443 |
| Worst | 2.9444 | 3.8301 | 0.2521 | 0.3925 | 1.6895 | 4.9737 | 3.4369 | |
| Average | 1.9711 | 3.0760 | 0.2071 | 0.2657 | 1.1783 | 4.9183 | 3.0976 | |
| STD | 1.6991 | 0.7882 | 0.0293 | 0.0835 | 0.3008 | 0.0811 | 0.2333 |
| Fun | Measure | IRSA | RSA | BMO | PSO | GWO | AOA | DGCO |
|---|---|---|---|---|---|---|---|---|
| F14 | Best | 0.9980 | 2.9821 | 2.0481 | 1.913 | 0.9980 | 7.8740 | 0.9980 |
| Worst | 2.9834 | 3.0006 | 11.7187 | 2.981 | 10.7632 | 12.6705 | 2.9821 | |
| Average | 2.1313 | 2.9901 | 6.4665 | 2.523 | 5.1025 | 10.7579 | 2.1964 | |
| STD | 0.8325 | 0.0139 | 3.0067 | 0.7341 | 4.9092 | 1.7957 | 0.6274 | |
| F15 | Best | 0.00030 | 0.00068 | 0.00033 | 0.00038 | 0.00030 | 0.00036 | 0.00035 |
| Worst | 0.01550 | 0.00896 | 0.00654 | 0.00142 | 0.02036 | 0.05758 | 0.001224 | |
| Average | 0.00406 | 0.00180 | 0.001710 | 0.000813 | 0.004417 | 0.009030 | 0.000709 | |
| STD | 0.00548 | 0.00253 | 0.00223 | 0.00043 | 0.008408 | 0.018280 | 0.000237 | |
| F16 | Best | −1.03162 | −1.03159 | −1.03162 | −1.03162 | −1.03162 | −1.03162 | −1.03162 |
| Worst | −1.03162 | −0.99552 | −0.91896 | −1.03162 | −1.03162 | −1.03162 | −1.03162 | |
| Average | −1.03162 | −1.02159 | −1.01681 | −1.03162 | −1.03162 | −1.03162 | −1.03162 | |
| STD | 2.8338e-08 | 0.01150 | 0.03493 | 5.4218e-08 | 1.6501e-08 | 4.1202e-09 | 3.1308e-09 | |
| F17 | Best | 0.39788 | 0.40742 | 0.39788 | 0.39788 | 0.39788 | 0.39788 | 0.39788 |
| Worst | 0.397897 | 1.27099 | 0.42696 | 0.39788 | 0.39788 | 0.39788 | 0.39788 | |
| Average | 0.397891 | 0.64371 | 0.40330 | 0.39788 | 0.39788 | 0.39788 | 0.39788 | |
| STD | 3.8146e-06 | 0.25782 | 0.01085 | 7.2909e-07 | 4.2567e-07 | 4.3534e-08 | 3.6445e-07 | |
| F18 | Best | 3.00000 | 3.00000 | 2.99999 | 3.00000 | 3.00000 | 3.00000 | 3.000000 |
| Worst | 3.000001 | 3.39511 | 42.1054 | 3.00011 | 3.00002 | 95.1885 | 3.000000 | |
| Average | 3.000000 | 3.04555 | 10.1188 | 3.00002 | 3.00001 | 23.1248 | 3.00000 | |
| STD | 5.1797e-07 | 0.12303 | 13.0276 | 3.477e-05 | 7.920e-06 | 28.7189 | 6.458e-10 | |
| F19 | Best | −3.86277 | −3.85920 | −3.85436 | −3.86276 | −3.86277 | −3.86277 | −3.86278 |
| Worst | −3.85374 | −3.57053 | −1.28898 | −3.86201 | −3.85315 | −1.00081 | −3.86277 | |
| Average | −3.86101 | −3.75028 | −3.44530 | −3.86263 | −3.86034 | −1.85933 | −3.86277 | |
| STD | 0.00367 | 0.09664 | 0.81662 | 0.00024 | 0.00403 | 1.38235 | 3.6601e-06 | |
| F20 | Best | −3.32086 | −2.89690 | −2.45549 | −3.32121 | −3.20304 | −3.32194 | −3.32189 |
| Worst | −3.20101 | −0.17365 | −0.54213 | −3.19851 | −3.08259 | −3.15098 | −3.13200 | |
| Average | −3.27287 | −1.54187 | −1.24769 | −3.22497 | −3.17957 | −3.27776 | −3.21025 | |
| STD | 0.06116 | 1.03850 | 0.75791 | 0.05061 | 0.04241 | 0.071964 | 0.06482 | |
| F21 | Best | −10.1206 | −5.0552 | −4.9619 | −10.2512 | −10.0712 | −10.1531 | −10.1494 |
| Worst | −5.0552 | −5.0552 | −1.8717 | −5.0552 | −5.0552 | −5.0552 | −5.0549 | |
| Average | −9.0840 | −5.0552 | −3.8482 | −6.0943 | −6.0745 | −6.0747 | −7.0926 | |
| STD | 2.2573 | 3.8458e-07 | 1.3134 | 2.7922 | 2.2793 | 2.2798 | 2.7900 | |
| F22 | Best | −10.3586 | −5.08767 | −5.05414 | −10.4029 | −10.4024 | −10.4029 | −10.3960 |
| Worst | −3.72361 | −5.08766 | −2.32919 | −3.72365 | −5.08765 | −3.72429 | −3.72380 | |
| Average | −8.44500 | −5.08766 | −3.83632 | −5.87780 | −9.33904 | −7.60893 | −6.66468 | |
| STD | 2.83980 | 1.0352e-06 | 0.98429 | 2.449069 | 2.24067 | 2.97300 | 3.25225 | |
| F23 | Best | −10.52251 | −5.128480 | −4.99447 | −10.53637 | −10.5361 | −10.5363 | −10.5309 |
| Worst | −3.83461 | −5.12847 | −2.49710 | −3.83472 | −5.12845 | −2.29603 | −3.83496 | |
| Average | −8.48605 | −5.12847 | −3.77437 | −6.62130 | −8.91314 | −7.34602 | −6.50874 | |
| STD | 2.94732 | 2.3686e-06 | 0.76135 | 2.73097 | 2.61167 | 3.32172 | 3.45155 |
| Fun | Dim | IRSA | RSA | BMO | PSO | GWO | AOA | DGCO |
|---|---|---|---|---|---|---|---|---|
| F1 | 30 | 0 | 0 | 2.9729e-75 | 100.429274 | 5.806e-20 | 1.74296e-76 | 5.93134e-10 |
| 100 | 0 | 0 | 7.502e-46 | 2951.7571 | 0.0012668 | 0.023492033 | 47.4212010 | |
| 500 | 0 | 0 | 5.948e-41 | 91703.5649 | 109.12381 | 0.5862142 | 113.8580 | |
| F2 | 30 | 0 | 0 | 1.0065e-39 | 4.59976602 | 7.467e-11 | 0 | 2.10414e-07 |
| 100 | 0 | 0 | 4.6351e-25 | 53.7327530 | 0.0134880 | 4.19883e-60 | 0.268447521 | |
| 500 | 0 | 0 | 3.3724e-23 | 487.76760 | 10.64367 | 0.00161 | 2.519646 | |
| F3 | 30 | 0 | 0 | 1.1399e-52 | 1321.79087 | 0.0001101 | 6.9638e-104 | 7.97466788 |
| 100 | 0 | 0 | 3.164e-28 | 50712.1407 | 14820.47 | 1.531983171 | 80032.5400 | |
| 500 | 0 | 0 | 6.6866e-19 | 1303817.56 | 513880.05 | 36.035904 | 104.83 | |
| F4 | 30 | 0 | 0 | 5.6171e-32 | 8.65232085 | 4.478e-05 | 3.51206e-13 | 0.04110228 |
| 100 | 0 | 0 | 3.1527e-20 | 31.480699 | 5.7402399 | 0.100756622 | 82.157639 | |
| 500 | 0 | 0 | 5.7108e-18 | 43.134284 | 65.76152 | 0.17991607 | 0.09866121 | |
| F5 | 30 | 25.72424 | 28.99171 | 28.995762 | 1300.12057 | 27.136822 | 28.59270148 | 26.21687570 |
| 100 | 96.8983 | 98.9901048 | 98.9698060 | 226496.089 | 98.343648 | 98.90012672 | 97.5081886 | |
| 500 | 498.3830 | 499.6902 | 499.0781 | 27910234.5 | 9445.0271 | 499.1341156 | 4392.7 | |
| F6 | 30 | 0.576633 | 7.0346180 | 6.97472880 | 111.668505 | 0.7535595 | 3.03144018 | 1.25053679 |
| 100 | 11.05309 | 24.7513018 | 24.5099804 | 2069.85282 | 9.4928888 | 18.4072873 | 13.8718994 | |
| 500 | 111.5654 | 124.751626 | 123.355451 | 64419.3854 | 268.90391 | 117.2773220 | 145.94373 | |
| F7 | 30 | 9.50e-05 | 1.9397e-05 | 0.00050276 | 0.05970424 | 0.0019118 | 3.78351e-05 | 0.00390436 |
| 100 | 3.97e-05 | 2.2064e-05 | 0.0004319 | 1.2096514 | 0.0097439 | 5.96465e-06 | 0.0300833 | |
| 500 | 8.21e-05 | 0.00046135 | 0.00080821 | 235.665342 | 0.7073979 | 0.000119979 | 0.292147 | |
| F8 | 30 | −5214.04 | −3431.1934 | −2834.3518 | −6549.69516 | −6277.543 | −4918.30201 | −5573.32119 |
| 100 | −64809.8 | −36018.762 | −18000.185 | −56587.461 | −16611.13 | −47550.1316 | −34933.7702 | |
| 500 | −80242.2 | −44205.61 | −12898.155 | −36269.793 | −58117.96 | −22872.6112 | −24663.3214 | |
| F9 | 30 | 0 | 0 | 0 | 103.812346 | 1.9054417 | 0 | 5.86970e-09 |
| 100 | 0 | 0 | 0 | 587.205492 | 58.233470 | 0 | 20.62413137 | |
| 500 | 0 | 0 | 0 | 4309.97279 | 902.54104 | 0 | 466.7469966 | |
| F10 | 30 | 8.881e-16 | 8.8817e-16 | 8.8817e-16 | 5.2518904 | 1.724e-10 | 8.88178e-16 | 1.63626e-06 |
| 100 | 8.881e-16 | 8.881e-16 | 8.8817e-16 | 7.8262077 | 5.792e-05 | 8.88178e-16 | 20.523618 | |
| 500 | 8.881e-16 | 8.881e-16 | 4.440e-15 | 12.927665 | 2.140639 | 0.0083857 | 20.881255 | |
| F11 | 30 | 0 | 0 | 0 | 1.8485067 | 0.0298839 | 0.23855046 | 1.26669e-10 |
| 100 | 0 | 0 | 0 | 28.3884325 | 0.0349668 | 897.847451 | 0.04874511 | |
| 500 | 0 | 0 | 0 | 867.60304 | 3.1100432 | 13134.6129 | 162.849911 | |
| F12 | 30 | 0.048112 | 1.59700365 | 0.93494039 | 0.01698208 | 0.0712204 | 0.81438277 | 0.045133459 |
| 100 | 0.374642 | 1.28994163 | 1.19529976 | 0.64770498 | 0.1179354 | 1.20962184 | 0.389415151 | |
| 500 | 0.9743 | 1.2075 | 1.1980 | 2.0190 | 0.5999 | 1.1800 | 1.2411 | |
| F13 | 30 | 1.280496 | 1.970635 | 2.6705939 | 0.15916980 | 0.1018868 | 2.9785990 | 1.600784929 |
| 100 | 7.876407 | 9.878585 | 9.993848 | 4.57433449 | 5.5499672 | 9.963623491 | 8.44409492 | |
| 500 | 49.99682 | 49.99734 | 49.99725 | 82.318 | 46.351 | 49.998 | 54.177 |
| Fun | T IRSA | T RSA | T FDO | T BMO | T AOA | T PSO | T GWO | T DGCO | T FPA | T DFA |
|---|---|---|---|---|---|---|---|---|---|---|
| CEC01 | 440.04 | 498.64 | 9569.9 | 512.80 | 468.96 | 472.38 | 472.49 | 472.884 | 702.73 | 901.60 |
| CEC02 | 51.562 | 158.97 | 303.77 | 26.603 | 9.7899 | 10.097 | 11.746 | 14.144 | 420.60 | 858.17 |
| CEC03 | 66.843 | 192.89 | 491.69 | 35.672 | 17.950 | 18.158 | 19.011 | 22.222 | 481.66 | 1018.4 |
| CEC04 | 33.761 | 99.078 | 514.31 | 26.605 | 9.1060 | 10.075 | 11.035 | 12.389 | 266.56 | 627.08 |
| CEC05 | 34.373 | 99.519 | 744.31 | 27.667 | 9.4832 | 10.545 | 11.180 | 12.966 | 267.42 | 491.911 |
| CEC06 | 175.14 | 240.27 | 5176.0 | 189.23 | 165.30 | 169.64 | 168.52 | 170.18 | 423.23 | 641.59 |
| CEC07 | 34.831 | 99.440 | 384.83 | 24.768 | 9.7759 | 10.604 | 11.566 | 12.993 | 266.66 | 483.13 |
| CEC08 | 34.733 | 99.406 | 369.56 | 25.428 | 9.7797 | 10.683 | 11.522 | 12.848 | 267.13 | 481.31 |
| CEC09 | 33.670 | 98.69 | 383.27 | 23.551 | 8.3110 | 9.1362 | 10.298 | 11.728 | 266.52 | 492.78 |
| Fun | T1 | IRSA | RSA | FDO | BMO | AOA | PSO | GWO | DGCO | FPA | DFA |
|---|---|---|---|---|---|---|---|---|---|---|---|
| CEC01 | 0.0105 | 43.017 | 48.736 | 934.10 | 50.118 | 45.839 | 46.173 | 46.184 | 46.222 | 68.655 | 88.065 |
| CEC02 | 0.0042 | 5.101 | 15.584 | 29.717 | 2.665 | 1.024 | 1.054 | 1.215 | 1.449 | 41.120 | 83.826 |
| CEC03 | 0.0044 | 6.5924 | 18.895 | 48.058 | 3.5501 | 1.8205 | 1.84077 | 1.9240 | 2.2374 | 47.079 | 99.466 |
| CEC04 | 0.0031 | 3.3636 | 9.7386 | 50.266 | 2.6652 | 0.9572 | 1.05189 | 1.1456 | 1.2777 | 26.085 | 61.272 |
| CEC05 | 0.0035 | 3.4234 | 9.7816 | 72.714 | 2.7688 | 0.9940 | 1.09774 | 1.1597 | 1.3340 | 26.169 | 48.079 |
| CEC06 | 0.0068 | 17.163 | 23.519 | 505.25 | 18.538 | 16.202 | 16.6257 | 16.517 | 16.679 | 41.376 | 62.688 |
| CEC07 | 0.0044 | 3.4681 | 9.7739 | 37.628 | 2.4859 | 1.0226 | 1.10349 | 1.1974 | 1.3367 | 26.095 | 47.222 |
| CEC08 | 0.0045 | 3.4585 | 9.7706 | 36.138 | 2.5503 | 1.0230 | 1.1112 | 1.1931 | 1.3225 | 26.141 | 47.044 |
| CEC09 | 0.0036 | 3.3547 | 9.7015 | 37.476 | 2.3671 | 0.8796 | 0.9602 | 1.0736 | 1.2132 | 26.081 | 48.164 |
| Data Set | # Classes | # Features | No. of training samples | No. of testing samples |
|---|---|---|---|---|
| Iris | 3 | 4 | 100 | 50 |
| Heart | 2 | 13 | 203 | 100 |
| Stress-Lysis | 3 | 3 | 1340 | 661 |
| Banknote-authentication | 2 | 4 | 919 | 453 |
| Blood-transfusion | 2 | 4 | 501 | 247 |
| Cryotherapy | 2 | 6 | 60 | 30 |
| Diabetes | 2 | 8 | 514 | 254 |
| Dataset | Training Accuracy (%) | ||||
|---|---|---|---|---|---|
| PSONN | BMOANN | AOANN | RSANN | IRSANN | |
| Iris | 97 | 94 | 93 | 88.02 | 97 |
| Heart | 72.60726 | 66.9967 | 59.73597 | 42.24422 | 88 |
| Stress-Lysis | 91.75412 | 95.8021 | 70.16492 | 59.37031 | 99.42171 |
| Banknote-authentication | 94.42623 | 97.9235 | 85.68306 | 84.48087 | 99.45355 |
| Blood-transfusion | 79.95992 | 78.15631 | 77.35471 | 75.1503 | 77.55511 |
| Cryotherapy | 90 | 92 | 71.66667 | 81.66667 | 96.66667 |
| Diabetes | 74.80469 | 75 | 72.07031 | 66.79688 | 78.10156 |
| Haberman | 75 | 75 | 78.43137 | 79.41176 | 78.43137 |
| Dataset | Testing Accuracy (%) | ||||
|---|---|---|---|---|---|
| PSONN | BMOANN | AOANN | RSANN | IRSANN | |
| Iris | 94 | 98.66 | 92 | 91 | 98.23 |
| Heart | 70.9571 | 75.90759 | 58.08581 | 46.53465 | 85 |
| Stress-Lysis | 91.90405 | 97.0015 | 70.01499 | 57.12144 | 99.7121 |
| Banknote-authentication | 93.43545 | 96.49891 | 83.3698 | 85.33917 | 99.56236 |
| Blood-transfusion | 77.51004 | 77.91165 | 74.6988 | 79.11647 | 80.72289 |
| Cryotherapy | 93.33333 | 86.66667 | 80 | 76.66667 | 93.33333 |
| Diabetes | 67.57813 | 75.78125 | 76.1718867 | 69.92188 | 77.26563 |
| Haberman | 67.47059 | 76.47059 | 76.64706 | 70.09804 | 80.54902 |
| Dataset | Cost Function Comparison | |||||
|---|---|---|---|---|---|---|
| PSONN | BMOANN | AOANN | RSANN | IRSANN | ||
| Iris | Best | 0.078788 | 0.082034 | 0.342085 | 0.143403 | 0.072572 |
| Avg | 0.137949 | 0.087161 | 0.742686 | 0.327073 | 0.115797 | |
| Std | 0.083667 | 0.00569 | 0.484778 | 0.159949 | 0.108159 | |
| Heart | Best | 0.56952 | 0.545925 | 0.995477 | 0.808033 | 0.472722 |
| Avg | 0.640322 | 0.581627 | 1.372587 | 0.853887 | 0.517036 | |
| Std | 0.062089 | 0.030938 | 0.53151 | 0.076074 | 0.038613 | |
| Stress-Lysis | Best | 0.156856 | 0.136333 | 0.321634 | 0.248556 | 0.0911631 |
| Avg | 0.159272 | 0.142592 | 0.353229 | 0.627416 | 0.268016 | |
| Std | 0.003418 | 0.007051 | 0.027562 | 0.328421 | 0.055127 | |
| Banknote-authentication | Best | 0.318751 | 0.154256 | 0.556654 | 0.503623 | 0.085457 |
| Avg | 0.331262 | 0.170783 | 0.764328 | 0.836328 | 0.145555 | |
| Std | 0.017693 | 0.016899 | 0.207149 | 0.288424 | 0.054529 | |
| Blood-transfusion | Best | 0.823567 | 0.882403 | 0.960614 | 0.958203 | 0.887161 |
| Avg | 0.830233 | 0.888582 | 1.260426 | 0.976322 | 0.895859 | |
| Std | 0.009426 | 0.008437 | 0.259695 | 0.015692 | 0.009459 | |
| Cryotherapy | Best | 0.357101 | 0.756437 | 0.234832 | 0.542086 | 0.28827 |
| Avg | 0.362329 | 0.888982 | 0.292911 | 0.764291 | 0.305118 | |
| Std | 0.007394 | 0.129127 | 0.050999 | 0.192532 | 0.127465 | |
| Diabetes | Best | 1.048615 | 0.725924 | 0.730482 | 0.947266 | 0.646058 |
| Avg | 1.076385 | 0.743759 | 0.7562 | 0.982109 | 0.724891 | |
| Std | 0.042824 | 0.019733 | 0.036372 | 0.040968 | 0.07128 | |
| Haberman | Best | 0.892895 | 0.906456 | 0.977251 | 0.994621 | 0.881229 |
| Avg | 0.936445 | 0.931774 | 1.269601 | 0.998591 | 0.925252 | |
| Std | 0.061589 | 0.00719 | 0.14037 | 0.003469 | 0.038883 | |
| Data Set | Technique | Training | Testing | ||||
|---|---|---|---|---|---|---|---|
| Precision | Recall | F1 Score | Precision | Recall | F1 Score | ||
| Iris | IRSA | 0.979142 | 0.979923 | 0.979533 | 0.962222 | 0.967178 | 0.969693 |
| RSA | 0.891866 | 0.875316 | 0.883513 | 0.832602 | 0.796296 | 0.814045 | |
| BMO | 0.944356 | 0.943915 | 0.944136 | 0.977778 | 0.977778 | 0.977778 | |
| AOA | 0.680918 | 0.647619 | 0.663851 | 0.695926 | 0.655556 | 0.675138 | |
| PSO | 0.972973 | 0.969697 | 0.971332 | 0.964912 | 0.958333 | 0.961612 | |
| Heart | IRSA | 0.888428 | 0.884587 | 0.88503 | 0.848726 | 0.851251 | 0.854971 |
| RSA | 0.462116 | 0.462022 | 0.462069 | 0.60397 | 0.603725 | 0.603848 | |
| BMO | 0.73858 | 0.636917 | 0.683992 | 0.740629 | 0.660205 | 0.698108 | |
| AOA | 0.480976 | 0.481498 | 0.481237 | 0.482877 | 0.486242 | 0.484554 | |
| PSO | 0.657688 | 0.651564 | 0.654612 | 0.602002 | 0.577957 | 0.589735 | |
| Stress-Lysis | IRSA | 0.862953 | 0.869583 | 0.866255 | 0.831595 | 0.842565 | 0.837044 |
| RSA | 0.551258 | 0.515412 | 0.514234 | 0.55435 | 0.508844 | 0.61734 | |
| BMO | 0.959656 | 0.951436 | 0.955528 | 0.975669 | 0.96373 | 0.969663 | |
| AOA | 0.768447 | 0.674813 | 0.718593 | 0.784879 | 0.673437 | 0.7249 | |
| PSO | 0.879358 | 0.895391 | 0.887302 | 0.889297 | 0.905763 | 0.897455 | |
| Banknote-authentication | IRSA | 0.995792 | 0.994563 | 0.995225 | 0.995902 | 0.995349 | 0.995625 |
| RSA | 0.844413 | 0.838669 | 0.841531 | 0.85288 | 0.852147 | 0.852513 | |
| BMO | 0.97761 | 0.98115 | 0.979377 | 0.963706 | 0.967257 | 0.965478 | |
| AOA | 0.57296 | 0.57642 | 0.694746 | 0.809533 | 0.812795 | 0.811161 | |
| PSO | 0.942964 | 0.944103 | 0.943533 | 0.933375 | 0.934613 | 0.933994 | |
| Blood-transfusion | IRSA | 0.729753 | 0.595356 | 0.655739 | 0.691121 | 0.570559 | 0.62508 |
| RSA | 0.627282 | 0.508097 | 0.561434 | 0.730453 | 0.531909 | 0.615567 | |
| BMO | 0.683964 | 0.579004 | 0.627122 | 0.652637 | 0.552494 | 0.598405 | |
| AOA | 0.761869 | 0.511741 | 0.612243 | 0.624494 | 0.505248 | 0.558578 | |
| PSO | 0.739583 | 0.621758 | 0.675572 | 0.686359 | 0.564815 | 0.619683 | |
| Cryotherapy | IRSA | 0.950774 | 0.943611 | 0.957148 | 0.95 | 0.916667 | 0.933036 |
| RSA | 0.818449 | 0.806561 | 0.812462 | 0.766667 | 0.767857 | 0.767261 | |
| BMO | 0.915882 | 0.928276 | 0.912064 | 0.819444 | 0.830144 | 0.824759 | |
| AOA | 0.699177 | 0.690236 | 0.694678 | 0.638889 | 0.633333 | 0.636099 | |
| PSO | 0.897321 | 0.902715 | 0.90001 | 0.944444 | 0.928571 | 0.936441 | |
| Diabetes | IRSA | 0.772165 | 0.7483 | 0.760045 | 0.683296 | 0.676977 | 0.690122 |
| RSA | 0.626005 | 0.601743 | 0.613634 | 0.66266 | 0.610454 | 0.635487 | |
| BMO | 0.724919 | 0.726392 | 0.725655 | 0.699808 | 0.722159 | 0.710808 | |
| AOA | 0.651455 | 0.614956 | 0.632679 | 0.670297 | 0.643082 | 0.656407 | |
| PSO | 0.704908 | 0.676813 | 0.734665 | 0.765362 | 0.699496 | 0.730948 | |
| Haberman | IRSA | 0.714555 | 0.561729 | 0.638992 | 0.677083 | 0.54118 | 0.623362 |
| RSA | 0.519912 | 0.501389 | 0.510477 | 0.650000 | 0.517637 | 0.576316 | |
| BMO | 0.700376 | 0.56504 | 0.625471 | 0.632979 | 0.550607 | 0.588927 | |
| AOA | 0.655914 | 0.574148 | 0.612313 | 0.662338 | 0.58316 | 0.620232 | |
| PSO | 0.674919 | 0.605186 | 0.638153 | 0.662837 | 0.58249 | 0.620072 | |
| Data Set | Technique | Training | Testing | Cost | ||||
|---|---|---|---|---|---|---|---|---|
| RE | RMSE | R2 | RE | RMSE | R2 | |||
| Wind power prediction(winter) | PSO | 0.0157 | 11.8303 | 0.9835 | 0.0886 | 55.6747 | 0.9081 | 0.0121 |
| RSA | 0.0170 | 16.6071 | 0.9657 | 0.1065 | 61.2748 | 0.8890 | 0.0326 | |
| BMO | 0.0959 | 32.5220 | 0.8278 | 0.2318 | 107.9345 | 0.5259 | 0.0444 | |
| AOA | 0.0356 | 26.9534 | 0.8961 | 0.1135 | 59.1465 | 0.8749 | 0.0373 | |
| IRSA | 0.0049 | 8.3396 | 0.9918 | 0.0642 | 32.7880 | 0.9665 | 0.0105 | |
| Wind power prediction(summer) | PSO | 0.0049 | 2.8918 | 0.9907 | 0.0772 | 9.5937 | 0.9780 | 0.0193 |
| RSA | 0.0055 | 4.4855 | 0.9778 | 0.6042 | 38.7233 | 0.6423 | 0.0251 | |
| BMO | 0.0808 | 5.8582 | 0.9460 | 0.2983 | 22.3706 | 0.8291 | 0.0428 | |
| AOA | 0.0339 | 4.0871 | 0.9779 | 0.4688 | 30.6282 | 0.7565 | 0.0208 | |
| IRSA | 0.0015 | 2.8416 | 0.9912 | 0.0632 | 9.3401 | 0.9801 | 0.0184 | |
| PV power prediction | PSO | 0.0235 | 94.9000 | 0.9649 | 0.0762 | 298.7930 | 0.9420 | 0.0535 |
| RSA | 0.0144 | 119.6847 | 0.9626 | 0.0440 | 223.8701 | 0.9656 | 0.0410 | |
| BMO | 0.0359 | 148.5061 | 0.9150 | 0.1148 | 232.2480 | 0.9545 | 0.0827 | |
| AOA | 0.0429 | 183.5005 | 0.8987 | 0.1111 | 383.4890 | 0.8913 | 0.0963 | |
| IRSA | 0.0146 | 90 | 0.9761 | 0.1285 | 260.8531 | 0.9611 | 0.0234 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, M.K.; Zafar, M.H.; Rashid, S.; Mansoor, M.; Moosavi, S.K.R.; Sanfilippo, F. Improved Reptile Search Optimization Algorithm: Application on Regression and Classification Problems. Appl. Sci. 2023, 13, 945. https://doi.org/10.3390/app13020945
Khan MK, Zafar MH, Rashid S, Mansoor M, Moosavi SKR, Sanfilippo F. Improved Reptile Search Optimization Algorithm: Application on Regression and Classification Problems. Applied Sciences. 2023; 13(2):945. https://doi.org/10.3390/app13020945
Chicago/Turabian StyleKhan, Muhammad Kamran, Muhammad Hamza Zafar, Saad Rashid, Majad Mansoor, Syed Kumayl Raza Moosavi, and Filippo Sanfilippo. 2023. "Improved Reptile Search Optimization Algorithm: Application on Regression and Classification Problems" Applied Sciences 13, no. 2: 945. https://doi.org/10.3390/app13020945
APA StyleKhan, M. K., Zafar, M. H., Rashid, S., Mansoor, M., Moosavi, S. K. R., & Sanfilippo, F. (2023). Improved Reptile Search Optimization Algorithm: Application on Regression and Classification Problems. Applied Sciences, 13(2), 945. https://doi.org/10.3390/app13020945





