Abstract
For the purpose of determining whether vacant taxis are supposed to use high-occupancy vehicle (HOV) lanes, this paper builds a framework to explore the performances of a network before and after vacant taxis use HOV lanes and to detect the optimal deployment of HOV lanes. We use a variational inequality (VI) to describe travelers’ mode choice following a logit model and the route choice abided by the user equilibrium principle on the network. A simple network is adopted to explore the network performances when vacant taxis are allowed to use/forbidden from using HOV lanes. Then we propose a framework presented by a bi-level model for the optimal deployment of HOV lanes in which the lower level is the variational inequality and the upper level aims at maximization of social welfare. This bi-level programming with a genetic algorithm combined with a surrogate assistant approach is applied to the simple network and a Sioux Falls network to analyze the network performances in the cases allowing/forbidding vacant taxis from using HOV lanes. The results reveal the paradox that social welfare may decrease when allowing vacant taxis to use HOV lanes compared to when forbidding vacant taxis from using HOV lanes. Considering optimal HOV lane deployment, this paradox still exists. However, it does not always happen due to the different parameters, e.g., flag–fall price. Therefore, the qualification of vacant taxis to use HOV lanes depends on the topology, attributes, and travel demand of the network. The results display that the models and the algorithm are effective in reality.
1. Introduction
Taxis play a significant role in traffic systems since many travelers are willing to choose taxi mode due to the speediness, convenience, scarcity of parking, pricing, and door-to-door 24 h service. Numerous countries have regulated their own taxi market. For example, Belgium, Denmark, Germany, Japan, etc., have fare regulations, and Switzerland, Italy, Korea, and Romania have entry regulations in their own taxi markets for the benefits of this industry. Some studies have conducted research on regulatory policies to explore the effects [1,2,3]. However, little attention has been paid to the regulation that vacant taxis use HOV lanes. On one hand, vacant taxis belong to transit, which means they are qualified to enter HOV lanes. On the other hand, vacant taxis account for congestion externalities like regular vehicles, which implies that they are supposed to be forbidden from using HOV lanes. In recent years, taxi demand has become increasingly higher, with non-negligible impacts on traffic systems. Therefore, exploring the effects of the scheme that vacant taxis use HOV lanes is necessary.
Abundant studies have been conducted in the field of the taxi market. In terms of an aggregated model, Douglas first dealt with taxi studies by modeling the taxicab market with scheduled fares and free entry [4]. Daganzo proposed a model taking into account the travel and waiting time as physical variables for the optimization of taxi fleet size [5]. Arnott built the first structure model considering a uniform customer demand distribution and demonstrated the shadow cost of taxis, concluding that subsidization is necessary under the idea of the decentralization of the social optimum [6]. During the years from 1997 to 2010, Yang and Huang finished a series of work on the equilibrium of the taxi market. For instance, they provided a model to describe how vacant and occupied taxis cruise and serve customers at the urban level [7]. Wong et al. considered traffic congestion and elastic demand in the model and proposed a method to calculate the waiting time [8]. Yang et al. detected the consequences of externalities in different markets [9]. They concluded that in the competitive market the second-best solution brings a more efficient taxi utilization in the condition of high demand with a smaller fleet and higher fare [10]. Yang et al. proposed a non-linear fare structure to explore the impacts on the taxi market [11]. This series of work widely extended the equilibrium model of the taxi market. In addition, Yang et al. analyzed the economics of equilibrium properties of the taxi market, taking both bilateral taxi–customer search frictions and congestion externalities into consideration [12], and Li et al. detected the specific area design for taxi service [13]. With technological development, some studies detected the impacts from new technologies or new markets formed by new technologies on the taxi market. He et al. proposed a model to describe the taxi market in the presence of an e-hailing application through a smartphone [14]. Wang et al. evaluated the pricing scheme of an e-hailing platform [15]. Nie proposed an empirical study of the impacts from the ride-sourcing market on the taxi market by collecting real data from Shenzhen city [16]. There is a tide of ride-sourcing market research caused by new technologies.
Since the 1990s, HOV lanes have been implemented in many places around the world, such as the United States, Germany, Norway, Australia, and China, for the purpose of the alleviation of traffic congestion. Abundant studies have emerged investigating the impacts of HOV lanes on the efficiency, emission, and safety performance of traffic networks as well as the optimal design of HOV lanes. The results show that HOV lanes bring different effects in various situations. On one hand, HOV lanes show positive performance on routes and whole traffic networks [17,18]. For example, Giuliano et al. [19] confirmed that the Route 55 HOV facility encouraged more travelers to carpool during peak hours. Chang et al. [20] revealed the success of the HOV lanes in terms of maximizing people throughout, managing congestion, offering travel time saving, and reliability. On the other hand, some studies demonstrated that HOV lanes failed to reduce traffic congestion. Kwon and Varaiya [21] conducted an investigation on the performances of the HOV lanes in California. The results showed the ineffectiveness of the HOV lanes on mitigating congestion, namely, reducing total travel time. The most likely reason is that insufficient travelers are willing to choose carsharing mode, leading to lower HOV lane usage. Dahlgren [22] also stated that HOV lanes are not always better than general purpose (GP) lanes in alleviating congestion. From the perspective of the environment, HOV lanes are partially effective [23,24]. Therefore, several approaches, involving converting HOV lanes to HOT lanes, optimal deployment design of lanes, and allowing other types of vehicles like plug-in electric vehicles to use HOV lanes, were proposed to remedy the drawbacks of HOV lanes [25,26,27,28,29,30]. Most of the studies above proposed models based on theoretical analysis.
Note that variational inequality is a useful tool to analyze traffic networks. It can be used to describe travelers’ mode and route choice. Dafermos first introduced VI into transportation network analysis [31]. Nagurney finished a series of work on the application to transportation networks involving models and algorithms [32]. VI has been widely used in the field of transportation research, with various cases such as ridesharing [33,34]; the ride-sourcing market [35]; equilibrium, including autonomous vehicle [36]; etc. Therefore, VI is an appropriate choice for ridesharing equilibrium, taxi market equilibrium, and analysis.
Nevertheless, the impacts of HOV lanes on networks with the presence of taxis are unclear. In other words, few studies have investigated the effects of the network when allowing/forbidding vacant taxis from using HOV lanes. We propose a framework including the variational inequality (VI) model and bi-level programming to explore the performance of the network and the optimal deployment of HOV lanes, respectively, in which VI is used to describe the travelers’ mode and route choice when vacant taxis are allowed to use/forbidden from using HOV lanes, respectively, and bi-level programming aiming at maximal social welfare based on the two situations. We explain the procedures to solve VI and bi-level programming and use numerical examples to examine the performances of the network to demonstrate the feasibility of our models and algorithms. The rests of this paper is organized as follows: Section 2 introduces the preliminaries of this paper. Section 3 demonstrates the formulations, including cost functions, principles, constrains, and the VI model. Section 4 explores the performances of the network in a given network with/without the scheme allowing/forbidding vacant taxis from using HOV lanes as a numerical example. Bi-level programming for the optimization of the HOV lane deployment is provided in Section 5 and the algorithm of the bi-level model is explained in Section 6, both of which are applied as a simple network and a Sioux Falls network in Section 7 to detect the performances. The conclusions and further research directions are outlined in Section 8.
2. Preliminaries
Limited-access HOV lanes are common. For simplicity, we assume that there only exist limited-access HOV lanes. Under this assumption, each HOV lane or GP lane is regarded as a link. Consider a general network , where is the set of nodes, is the set of GP links, and is the set of HOV lanes. are the sets of origins, destinations, and travel modes respectively, where , , and . In this paper we assume that there are three types of travel modes: solo driving, carpooling, and taxi, denoted as , respectively. Vacant taxi mode is denoted as . represents the set of paths used by travelers, and represents the set of the paths used by vacant taxis. The notations are listed as follows:
- the demand between OD pair
- the demand for travel mode between OD pair
- the demand for vacant taxis between OD pair
- the value of time of travelers
- the value of waiting time of taxi passengers
- the area of origin
- the length of link
- the capacity of link
- the operation cost per unit distance of solo-driving travelers
- the flag–fall price per ride
- the mileage-based fare per ride
- the delay-based fare per ride
- the operation cost per unit distance of vacant taxis
- travel time function on link , which is strictly increasing, convex, and continuous with the flow on link
- A binary constant that equals 1 when link is on the path between OD pair and 0 otherwise.
- the flow of travel mode on path between OD pair
- the flow of vacant taxis on path between OD pair
- the vehicle flow on link
- the vehicle flow of mode on link
- the vehicle flow of vacant taxis on link
3. Formulations
3.1. Cost Functions
The generalized path cost functions of solo-driving travelers, carpooling travelers, and taxi passengers are defined respectively as follows:
where is the average occupancy in a carpooling vehicle; is the aggregate carpooling additional cost, which includes convenience, privacy, and so on [30]; and is the financial carpooling cost. is an endogenous variable representing the customer waiting time in origin . It is worth noticing that the taxi cost function is not strictly linearly increasing due to the flag–fall price. However, the inaccuracy can be eliminated by longer distance. For simplicity, we adopted the linear assumption for the taxi cost function [9,37,38]. The waiting time can be calculated as:
where is the corrected parameter, is the number of vacant taxis in origin , and is the searching time of vacant taxis in origin . If vacant taxis have access to HOV lanes, the cost function of vacant taxis is denoted as:
On the contrary, if vacant taxis are forbidden from using HOV lanes, the cost function of vacant taxis is:
Then the total generalized path cost function of vacant taxis is:
3.2. Model Constraints
Based on [8], the movements of occupied taxis and vacant taxis follow some mathematical relationships. The relationship between the total demand and the demands of the modes is supposed to satisfy the following equation:
The demand of occupied taxi mode is satisfied with:
where and are the demands of occupied taxis from origin zone and to the destination zone , respectively. The relationships between flow patterns and demands satisfy:
Meanwhile, the flow patterns must be non-negative:
In the taxi market the distribution of vacant taxis corresponds to that of occupied taxis. To be specific, it satisfies the following equations:
where is the probability of vacant taxis traveling to origin from all the destinations belonging to , which is calculated by:
where is the non-negative uncertain parameter. Equations (15)–(17) imply that after the occupied taxis travel from origins to destinations, they turn into vacant taxis. Then the vacant taxis, whose distribution yields to the description expressed by the equations, travel from the destinations to the origins to take passengers. Therefore, Equation (9) can be rewritten as:
In the taxi market the occupied taxis and vacant taxis abide by following constraints [8]:
where is the taxi fleet size, and , represented as , is the average travel time from to and , and vice versa. Equation (19) demonstrates that the total service time of taxi demand, including occupied taxi demand and vacant taxi demand, is the total service time of the whole taxi market in a 1 h duration.
3.3. Travel Mode Split and Path Choice
In this paper it is assumed that the trips follow elastic demand, which can be described as:
where is the coefficient and is the generalized minimal cost between OD pair . The travelers follow the principles of a logit travel mode split and the UE principle. The logit formulation can be expressed as:
where is the sensitive coefficient, is the minimal cost of travelers with mode between OD pair , and is the attraction of mode between OD pair . The UE principle for the travelers of the three modes is expressed as follows:
Likewise, the UE principle for vacant taxis is described as:
The UE principle states that each type of traveler always chooses the path with the minimal travel cost for this type of travel mode. No one chooses the paths with a travel cost larger than the minimum.
3.4. Varational Inequality
Since the cost functions are asymmetric, namely, , , , a VI is used to describe the traffic system as below:
The VI above can be proven to be equivalent to a logit mode split and the traffic assignment following the UE principle simultaneously. Note that in the situations that allow or forbid vacant taxis from using HOV lanes, the VI above can be used to describe the traffic systems, just with different sets. The constrains (8)~(16) and (19) are non-negative and linear, whereas the decision variables are non-negative, which implies that at least one solution to the VI above exists [8]. Several approaches to solving the VI problem have emerged, such as a projection algorithm, a diagonalization algorithm, an approach with a gap function to transfer a VI problem into equivalent mathematical programming, and so on. In this paper we adopt the block Gauss–Seidel decomposition approach combined with the method of successive averages and a diagonalization algorithm to solve the VI above. The flow patterns and demands can be captured. Readers may be interested in [38] for the proof and the steps of this algorithm. According to [39], the overall computational complexity of the block Gauss–Seidel decomposition approach combined with the method of successive averages and diagonalization algorithm is and for the projection method, in which and are the convergence error for the two algorithms, respectively. Therefore, the projection method is more effective than the solving method we adopt, especially in the large-scale network. However, the approach we adopt is still effective in solving the VI and easier to implement. In this paper we still choose to use the block Gauss–Seidel decomposition algorithm for simplicity.
If differentiating , we can obtain the following equations:
then we know that . Note that and are Lagrange multipliers, and Wong et al. pointed out that is not unique since the expression exists. However, should be unique due to the time conservation equation for vacant taxi movements [37]. Therefore, Wong et al. proposed the methods to calculate the searching and waiting time based on the equations above on the condition of single taxi mode [10]. In this paper, referring to [38], we adopt this method in the multi-mode condition. We represent in Equation (17) as:
is an arbitrary constant. Then the searching time for vacant taxis can be expressed as:
we use to represent , so can be denoted as:
Let , and , from Equation (17), so we obtain:
Then the passenger waiting time can be calculated by:
Proposition 1.
Let vector denote the set of the potential demand . Ifis non-empty, there is at least one optimal solution of P1. Namely, there is at least one optimal travel-demand pattern and flow pattern.
Proof of Proposition 1.
The problem P1 can be rewritten as:
where is the optimal solution vector. Specifically, . Since is non-empty and , we can always find an OD pair between which . From Equation (8) it can be guaranteed that between this OD pair there is always . In addition, we can find at least one path flow satisfying . Therefore, we know that is non-empty and bounded, which can guarantee the compactness of the solution space. The VI can be seen as ; thus, is a continuous function. From the well-known Weierstrass theorem, the existence of the optimal solution can be guaranteed. □
Proposition 2.
The optimal travel-demand pattern and the aggregate link flow patternfollowing the logit mode split and user equilibrium principle can be obtained by solving the above VI problem.
Proof of Proposition 2.
Since P1 is a VI, the Karush–Kuhn–Tucker (KKT) points of P1 are identical to the optimal solution. Thus, the KKT conditions are given by:
By mathematical manipulations, the logit mode split and user equilibrium can be derived from the KKT conditions. Readers may refer to the similar process in [38] for the details. Therefore, the optimal solutions and from the KKT points follow the logit mode split and the user equilibrium. Since the KKT conditions are the necessary and sufficient conditions of the P1 problem, the optimal solution is also the solution of the VI above. □
According to the propositions, we are able to detect the network performances by solving the P1 problem. In next section we will construct the criterion based on the optimal solutions to evaluate the network when vacant taxis are allowed to use/forbidden from using HOV lanes.
4. The Network Performance
The VI and algorithm are applied to a numerical example in this section. As shown in Figure 1, the network has six nodes and 14 links. Each link consists of a HOV lane and a GP lane. As mentioned above, each lane is considered a link. The OD pairs and demands are listed in Table 1 and attributes of the links are shown in Table 2. We adopt the traditional BPR function as the travel time function.
where denotes the free-flow travel time. is the flow on link , which satisfies:
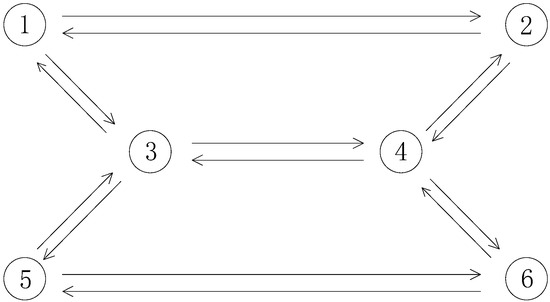
Figure 1.
Topology of the network.

Table 1.
Travel demand of the network.

Table 2.
Free-flow travel time, capacity, and length of lanes.
Generally, the system performances are measured by the social welfare of the network. To be specific, in this paper the social welfare in the case allowing vacant taxis to use HOV lanes is expressed as:
In the case of forbidding vacant taxis from using HOV lanes, the total cost is written as:
Referring to [38], the parameters are set as:
For simplicity, hereafter we denote the case allowing vacant taxis to enter HOV lanes as case 1, and the case forbidding vacant taxis from using HOV lanes as case 2.
Table 3 shows that the social welfare decreases slightly, and the demand of private cars, carpooling vehicles, and occupied taxis varies mildly. It is a paradox that the social welfare decreases in case 1 comparing to in case 2. There are two possible reasons: (i) allowing vacant taxis to enter HOV lanes increases the number of vehicles in HOV lanes and thereby urges some travelers to use GP lanes, which may intensify the congestion of some GP lanes, Or (ii) allowing vacant taxis to use HOV lanes is akin to adding new roads for vacant taxis, in which the network capacity is limited by the bottleneck, like in the Braess paradox. Figure 2 illustrates that the ratios of the flow to the capacity in each HOV lane, showing that the ratio in case 2 is smaller than that in case 1 for each HOV lane and none of the HOV are congested (the ratios are less than one). This proves that the congestion does not derive from the HOV lanes. The impacts of the scheme allowing vacant taxis to use HOV lanes is not apparent since the number of vacant taxis in the HOV lanes is not too many. Therefore, the scheme is able to elevate the usage of HOV lanes, although it gives rise to the paradox with a given network.

Table 3.
The network performance in case 1 and case 2.
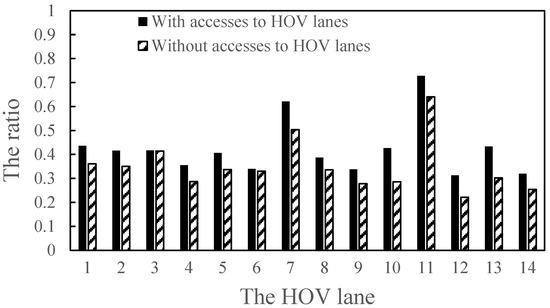
Figure 2.
Ratio of flow on the HOV lane to the capacity versus the HOV lane.
5. Optimal Deployment of HOV Lanes
Allowing or forbidding vacant taxis from using HOV lanes means changing the topology of the network with the demand pattern. It is worth detecting the optimal design of HOV lanes with or without access of vacant taxis to HOV lanes. However, we know that adding new links may lead to a Braess paradox. In this paper we assume that an HOV lane is separated from a link. The construction cost is negligible since the cost of separating a lane is low.
We use a binary variable to denote the determination of the deployment of the HOV lanes. If we deploy a HOV lane on link , , and otherwise. Then the capacities of the lanes would alter, which leads to various travel times. When no HOV lane is on the link, the travel time on consisting of GP lanes can be expressed as:
When an HOV lane is separated from the link, the travel time on is denoted as:
and the travel time on is:
where is the proportion of the link capacity and .
Thus, the travel time on is calculated by:
and the travel time on is:
Based on the calculation above, we propose a bi-level programming for optimal design. The lower level is the VI above, describing the travel mode and route choice, whereas the upper level aims at maximizing the social welfare. With or without the accesses of vacant taxis to HOV lanes, the upper level can be expressed as and , respectively. We use max (Z) to denote upper level aiming at or , and the bi-level model is written as:
The flow patterns are defined by the VI above.
In this procedure, the decision variable is . In terms of the variation of , the capacity change and the link travel time change, which has an impact on the topology of the network. With or without the access of vacant taxis to HOV lanes in the network, the social welfare varies. Therefore, the deployment design aims to find the optimal value of the binary variable to determine whether the HOV lane is supposed to be constructed on link for the purpose of maximal social welfare.
6. Algorithm
The HOV lane-design problem belongs to the discrete network-design problem since it is assumed that the HOV lanes are individual links in this paper. Abundant studies have been conducted in this filed. The widespread model is the bi-level mode, and the algorithms refer to the branch and bound algorithm [40], the decomposition method with support function [41], the chaotic optimization approach [42], etc. Readers may refer to [43] for specific information. In this paper, we adopt a genetic algorithm to solve our model due to the binary variable . However, the computation of the lower level for the large networks is expensive. Chen et al. [44] demonstrated the effectiveness of the surrogate assistant approach on application and explained various surrogate functions; thus, we are able to select the surrogate assistant algorithm combined with genetic algorithm to lower the price of computation. Here we adopt a quadratic polynomial function to evaluate the lower level for beneficial computation for simplicity. The algorithm meets the procedure later.
Step 1. Generate sufficient unduplicated feasible solutions of and compute the VI problem to obtain various social welfare.
Step 2. Built on the results received from Step 1, construct the quadratic polynomial function.
Step 3. Use the genetic algorithm to solve the bi-level programming. Note that the evaluation function is the function constructed in step 2 instead of the social welfare obtained through solving the VI problem.
Step 4. Compute the real value of the objective function with the optimal solution.
The flowchart describing the procedure is shown in Figure 3.
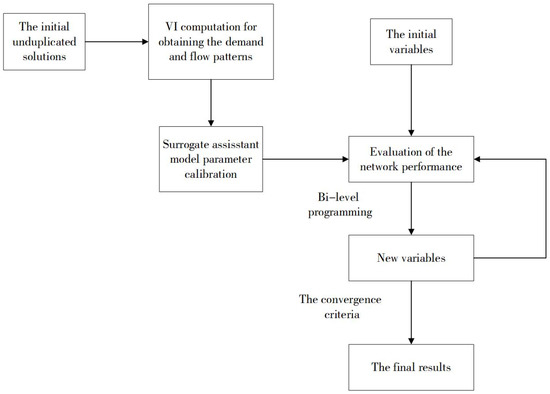
Figure 3.
The algorithm flowchart.
7. Numerical Examples
7.1. Simple Network Example
We apply the model and the algorithm to the simple network in Figure 1 to capture the optimal HOV lane deployment and detect the performances. The topology of the network, the parameters, and the demands are shown above.
Figure 4 shows the negative relevance of the ratio Ψ to the taxi fleet size, where the ratio is the maximum social welfare in case 1 to that in case 2. The reason is the existence of the paradox. The growing taxi fleet size enlarges the impact of the paradox on social welfare, which implies that allowing vacant taxis to use HOV lanes affects the network more negatively with increasing taxi fleet size. We examine the ratio of the flow to the capacity on the HOV links and show the example when in Figure 5, and the result shows that no flow on the HOV lane is greater than the capacity, implying that the social welfare decrease derives from GP lanes instead of the congestion on HOV links.
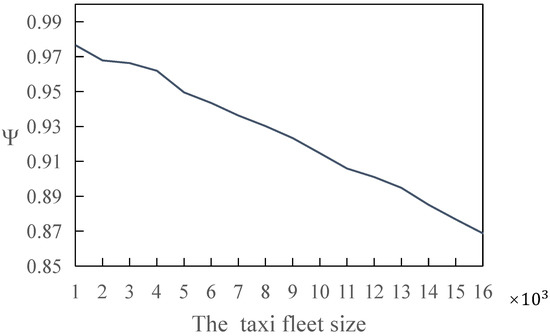
Figure 4.
Ratio of maximum social welfare in case 1 to that in case 2 against various taxi fleet sizes.
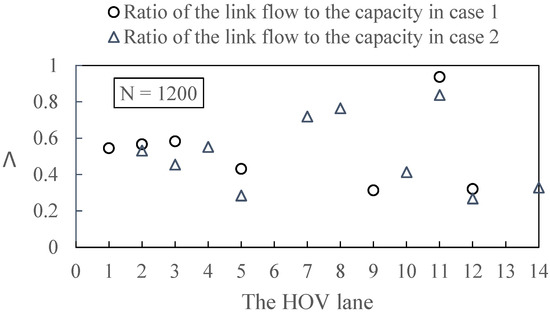
Figure 5.
Ratio of the link flow to the capacity on the HOV links.
Figure 6 shows that with the increase in the flag–fall price, the Ψ ratio of maximum social welfare in case 1 to that in case 2 initially decreases dramatically. This is because a higher flag–fall price reduces the demand on taxis, resulting in decreasing the external cost of taxis. When the flag–fall price is extremely high, the taxi demand is too small to affect the network performance, and thus the Ψ ratio keeps steady. Note that when the flag–fall price is 5 and 6, the social welfare in case 1 is higher than that in case 2. This means that the paradox does not always happen. The flag–fall price is an element that influences social welfare.
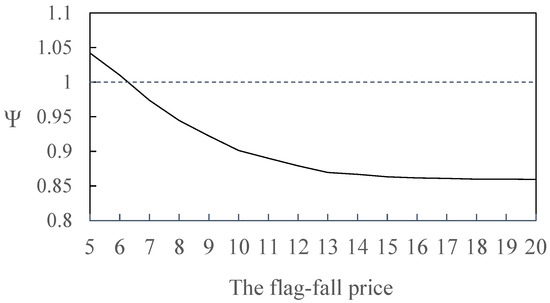
Figure 6.
Ratio of maximum social welfare in case 1 to that in case 2 versus the flag–fall price of taxis.
7.2. Sioux Falls Network Example
In this example we use the Sioux Falls network to demonstrate the feasibility of the model and algorithm. The topology and parameters of the Sioux Falls network follows [45] and the demand follows [46]. According to reality, the other parameters of the traffic system are set by . For example, the value of time is set according to the average salary and the working time in a month. The optimal deployment of the HOV lanes is illustrated in Figure 7. The blue dashed lines represent the HOV lanes, for which we know that the optimal deployment schemes are different with/without the schemes.
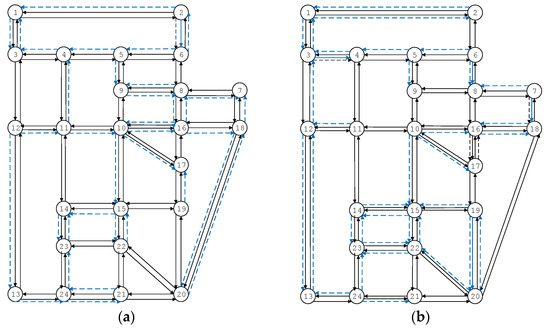
Figure 7.
The optimal deployment of HOV lanes.
Figure 7a shows the optimal deployment of HOV lanes in case 1, whereas Figure 7b shows the deployment in case 2 in the Sioux Falls network. From Table 4 we see that the social welfare in case 1 is lower than that in case 2, which means this scheme is invalid for increasing social welfare in this Sioux Falls network due to the paradox. The social welfare and the demand pattern vary slightly, since the optimal HOV lane deployment adjust the objective. Although the elastic demand exists, the paradox is still possible. Thus, the topology and the parameters of the network can determine whether the paradox happens. The results in the Sioux Falls network demonstrate that the models and the algorithms we proposed can be use in reality since it is the simulative network from a real case.

Table 4.
The social welfare of case 1 and case 2 in the Sioux Falls network.
8. Conclusions
This paper tries to state the issue of whether vacant taxis are supposed to use HOV lanes. We propose a framework including a VI describing the travel mode and route choice of travelers for the purpose of exploring the network performance with/without the access of vacant taxis to HOV lanes, as well as bi-level programming for optimal deployment of HOV lanes as a bi-level programming for maximum social welfare. Due to the binary variables and the expensive computation, the genetic algorithm combined with a surrogate assistant approach is adopted to solve the bi-level model. The models and the algorithms are applied to numerical examples to demonstrate the feasibility and effectiveness. The main findings are listed as follows:
- (1)
- A paradox similar to the Braess paradox is revealed. Given HOV lane deployment, allowing vacant taxis to use HOV lanes may be negative for maximization of social welfare with intensive usage of HOV lanes. This paradox may derive from the congestion in GP lanes and the capacity limits of the bottlenecks, instead of the congestion in HOV lanes. Allowing vacant taxis to use HOV lanes can intensify the utilization of the HOV lanes while decreasing social welfare.
- (2)
- Considering optimization of HOV lane deployment, allowing vacant taxis to use HOV lanes is more likely negative to social welfare due to the paradox, although the optimal deployments are different in two cases.
- (3)
- The paradox depends on the topology and the parameters of the network, e.g., the flag–fall price of taxis. If the paradox is inexistent, the scheme may be beneficial to the traffic system. Therefore, specific information and analysis are necessary to determine whether to forbid or allow vacant taxis to use HOV lanes.
- (4)
- The models and the algorithms can be used in reality.
This study offers a framework for decision-makers to determine the access of vacant taxis to HOV lanes. Road managers can apply this framework to determine whether vacant taxis are supposed to use HOV lanes in specific situations. They also may notice the possible paradox and the network performances displayed in our results. A more efficient algorithm would be helpful for the model, and real traffic network and data will be tested in further research.
Author Contributions
Conceptualization, D.D.; methodology, F.G. and D.D.; software, F.G. and K.L.; validation, F.G. and D.D.; formal analysis, F.G.; investigation, F.G.; resources, D.D.; writing—original draft preparation, F.G. and D.D.; writing—review and editing, F.G., K.L. and D.D.; visualization, F.G.; supervision, K.L. and D.D.; project administration, D.D.; funding acquisition, D.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Special Postdoctoral Science Fund Project for basic research and frontier exploration of Chongqing Science and Technology Bureau, grant number cstc2021jcyj-bsh0210, and jointly supported by the National Social Science Foundation of China, grant number 22BGL276; the National Natural Science Foundation of China: 52262045; and the Natural Science Foundation of Gansu Province, China, grant number 20JR5RA398.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors thank the anonymous reviewers and editors for their valuable and constructive suggestions for improving this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Schroeter, J.R. A model of taxi service under fare structure and fleet size regulation. Bell J. Econ. 1983, 14, 81–96. [Google Scholar] [CrossRef]
- Moore, A.T.; Balaker, T. Do economists reach a conclusion on taxi deregulation? Econ. J. Watch. 2006, 3, 109. [Google Scholar]
- Loo, B.P.Y.; Leung, B.S.Y.; Wong, S.C.; Yang, H. Taxi license premiums in Hong Kong: Can their fluctuations be explained by taxi as a mode of public transport? Int. J. Sustain. Transp. 2007, 1, 249–266. [Google Scholar] [CrossRef]
- Douglas, G.W. Price regulation and optimal service standards: The taxicab industry. J. Transp. Econ. Policy 1972, 6, 116–127. [Google Scholar]
- Daganzo, C.F. An approximate analytic model of many-to-many demand responsive transportation systems. Transp. Res. 1978, 12, 325–333. [Google Scholar] [CrossRef]
- Arnott, R. Taxi travel should be subsidized. J. Urban Econ. 1996, 40, 316–333. [Google Scholar] [CrossRef]
- Yang, H.; Wong, S.C. A network model of urban taxi services. Transp. Res. B-Methodol. 1998, 32, 235–246. [Google Scholar] [CrossRef]
- Wong, K.I.; Wong, S.C.; Yang, H. Modeling urban taxi services in congested road networks with elastic demand. Transp. Res. B-Methodol. 2001, 35, 819–842. [Google Scholar] [CrossRef]
- Yang, H.; Ye, M.; Tang, W.H.; Wong, S.C. Regulating taxi services in the presence of congestion externality. Transp. Res. A-Policy 2005, 39, 17–40. [Google Scholar] [CrossRef]
- Wong, K.I.; Wong, S.C.; Yang, H.; Wu, J.H. Modeling urban taxi services with multiple user classes and vehicle modes. Transp. Res. B-Methodol. 2008, 42, 985–1007. [Google Scholar] [CrossRef]
- Yang, H.; Fung, C.S.; Wong, K.I.; Wong, S.C. Nonlinear pricing of taxi services. Transp. Res. A-Policy 2010, 44, 337–348. [Google Scholar] [CrossRef]
- Yang, H.; Leung, C.W.Y.; Wong, S.C.; Bell, M.G. Equilibria of bilateral taxi–customer searching and meeting on networks. Transp. Res. B-Methodol. 2010, 44, 1067–1083. [Google Scholar] [CrossRef]
- Li, B.; Szeto, W.Y. Taxi service area design: Formulation and analysis. Transp. Res. E-Logist. 2019, 125, 308–333. [Google Scholar] [CrossRef]
- He, F.; Shen, Z.-J.M. Modeling taxi services with smartphone-based e-hailing applications. Transp. Res. C-Emerg. 2015, 58, 93–106. [Google Scholar] [CrossRef]
- Wang, X.; He, F.; Yang, H.; Gao, H.O. Pricing strategies for a taxi-hailing platform. Transp. Res. E-Logist. 2016, 93, 212–231. [Google Scholar] [CrossRef]
- Nie, Y.M. How can the taxi industry survive the tide of ridesourcing? Evidence from Shenzhen, China. Transp. Res. C-Emerg. 2017, 79, 242–256. [Google Scholar] [CrossRef]
- McMullen, B.S.; Gut, T. HOV lane effectiveness in controlling traffic congestion. Transp. Q. 1992, 46, 429–434. [Google Scholar]
- Stamos, I.; Kitis, G.; Basbas, S.; Tzevelekis, I. Evaluation of a high occupancy vehicle lane in central business district Thessaloniki. Procedia-Soc. Behav. Sci. 2012, 48, 1088–1096. [Google Scholar] [CrossRef]
- Giuliano, G.; Levine, D.W.; Teal, R.F. Impact of high occupancy vehicle lanes on carpooling behavior. Transportation 1990, 17, 159–177. [Google Scholar] [CrossRef]
- Chang, M.; Wiegmann, J.; Smith, A.; Bilotto, C. A Review of HOV Lane Performance and Policy Options in the United States; No. FHWA-HOP-09-029; Federal Highway Administration: Washington, DC, USA, 2008.
- Kwon, J.; Varaiya, P. Effectiveness of California’s high occupancy vehicle (HOV) system. Transp. Res. C-Emerg. 2008, 16, 98–115. [Google Scholar] [CrossRef]
- Dahlgren, J. High occupancy vehicle lanes: Not always more effective than general purpose lanes. Transp. Res. A-Policy 1998, 32, 99–114. [Google Scholar] [CrossRef]
- Fontes, T.; Fernandes, P.; Rodrigues, H.; Bandeira, J.M.; Pereira, S.R.; Khattak, A.J.; Coelho, M.C. Are HOV/eco-lanes a sustainable option to reducing emissions in a medium-sized European city? Transp. Res. A-Policy 2014, 63, 93–106. [Google Scholar] [CrossRef]
- Nesamani, K.S.; Lianyu, C.H.U.; Recker, W. Policy implications of incorporating hybrid vehicles into high-occupancy vehicle lanes. J. Transp. Syst. Eng. Inf. Technol. 2010, 10, 30–41. [Google Scholar] [CrossRef]
- Sheldon, T.L.; DeShazo, J.R. How does the presence of HOV lanes affect plug-in electric vehicle adoption in California? A generalized propensity score approach. J. Environ. Econ. Manag. 2017, 85, 146–170. [Google Scholar] [CrossRef]
- Tal, G.; Nicholas, M.A.; Davies, J.; Woodjack, J. Charging behavior impacts on electric vehicle miles traveled: Who is not plugging in? Transp. Res. Rec. 2014, 2454, 53–60. [Google Scholar] [CrossRef]
- Song, Z.; Yin, Y.; Lawphongpanich, S. Optimal deployment of managed lanes in general networks. Int. J. Sustain. Transp. 2015, 9, 431–441. [Google Scholar] [CrossRef]
- Gardner, L.M.; Bar-Gera, H.; Boyles, S.D. Development and comparison of choice models and tolling schemes for high-occupancy/toll (HOT) facilities. Transp. Res. B-Methodol. 2013, 55, 142–153. [Google Scholar] [CrossRef]
- Dahlgren, J. High-occupancy/toll lanes: Where should they be implemented? Transp. Res. A-Policy 2002, 36, 239–255. [Google Scholar] [CrossRef]
- Yang, H.; Huang, H.J. Carpooling and congestion pricing in a multilane highway with high-occupancy-vehicle lanes. Transp. Res. A-Policy 1999, 33, 139–155. [Google Scholar] [CrossRef]
- Dafermos, S. Traffic equilibrium and variational inequalities. Transp. Sci. 1980, 14, 42–54. [Google Scholar] [CrossRef]
- Nagurney, A. Network Economics: A Variational Inequality Approach; Springer Science & Business Media: Berlin, Germany, 1998. [Google Scholar]
- Ma, J.; Xu, M.; Meng, Q.; Cheng, L. Ridesharing user equilibrium problem under OD-based surge pricing strategy. Transp. Res. B-Methodol. 2020, 134, 1–24. [Google Scholar] [CrossRef]
- Ma, J.; Meng, Q.; Cheng, L.; Liu, Z. General stochastic ridesharing user equilibrium problem with elastic demand. Transp. Res. B-Methodol. 2022, 162, 162–194. [Google Scholar] [CrossRef]
- Ni, L.; Chen, C.; Wang, X.C.; Chen, X.M. Modeling network equilibrium of competitive ride-sourcing market with heterogeneous transportation network companies. Transp. Res. C-Emerg. 2021, 130, 103277. [Google Scholar] [CrossRef]
- Xie, T.; Liu, Y. Impact of connected and autonomous vehicle technology on market penetration and route choices. Transp. Res. C-Emerg. 2022, 139, 103646. [Google Scholar] [CrossRef]
- Yang, H.; Wong, S.C.; Wong, K.I. Demand–supply equilibrium of taxi services in a network under competition and regulation. Transp. Res. B-Methodol. 2002, 36, 799–819. [Google Scholar] [CrossRef]
- Zhu, J.; Xiao, F.; Liu, X. Taxis in road pricing zone: Should they pay the congestion charge? J. Adv. Transp. 2015, 49, 69–113. [Google Scholar] [CrossRef]
- Wang, X.; Wang, J.; Guo, L.; Liu, W.; Zhang, W. A convex programming approach for ridesharing user equilibrium under fixed driver/rider demand. Transp. Res. B-Methodol. 2021, 149, 33–51. [Google Scholar] [CrossRef]
- Long, J.; Gao, Z.; Zhang, H.; Szeto, W.Y. A turning restriction design problem in urban road networks. Eur. J. Oper. Res. 2010, 206, 569–578. [Google Scholar] [CrossRef]
- Gao, Z.; Wu, J.; Sun, H. Solution algorithm for the bi-level discrete network design problem. Transp. Res. B-Methodol. 2005, 39, 479–495. [Google Scholar] [CrossRef]
- Wu, J.J.; Sun, H.J.; Gao, Z.Y.; Zhang, H.Z. Reversible lane-based traffic network optimization with an advanced traveller information system. Eng. Optim. 2009, 41, 87–97. [Google Scholar] [CrossRef]
- Farahani, R.Z.; Miandoabchi, E.; Szeto, W.Y.; Rashidi, H. A review of urban transportation network design problems. Eur. J. Oper. Res. 2013, 229, 281–302. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, L.; He, X.; Xiong, C.; Li, Z. Surrogate-based optimization of expensive-to-evaluate objective for optimal highway toll charges in transportation network. Comput.-Aided Civ. Infrastruct. Eng. 2014, 29, 359–381. [Google Scholar] [CrossRef]
- Yan, C.Y.; Jiang, R.; Gao, Z.Y.; Shao, H. Effect of speed limits in degradable transport networks. Transp. Res. C-Emerg. 2015, 56, 94–119. [Google Scholar] [CrossRef]
- Tam, M.L.; Lam, W.H.K. Analysis of demand for road-based transport facilities: A bi-level programming approach. Transp. Res. Rec. 1999, 1685, 73–80. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).