Abstract
This paper deals with the model reference tracking control problem of linear systems based on the observer for Markov jump systems with unknown transition rates. The main contributions are as follows: Firstly, we designed a descriptor observer for a given model by the matrix transformation. Then, a tracking control law composed of a feedforward compensator and feedback control law was designed by calculating variations based on the designed observer. The feedback part can stabilize the system. The feedforward part is the complete parametric feedforward tracking compensator. The two parts can be solved separately, and a controller that can make the system stable is proposed under the condition that transition rates are partially unknown through the Lyapunov stability theory. The feedforward parametric solution is given by the generalized Sylvester equation. The algorithm and criteria are proved by several examples and compared with the existing conclusions.
1. Introduction
Markov jump systems are composed of a series of continuous time or discrete time subsystems, and the jump between the modes is determined by the Markov chain. Many practical stochastic mutation systems can be modeled using Markov jump systems. Thus, the jump systems have been extensively studied and many useful results have been obtained. The stochastic stability of a Markov jump system was proposed by Yuandong Ji and Howard Jay Chizeck [1]. Many researchers have discussed the problems surrounding stochastic stability and stochastic admissibility for Markov jump systems, such as stability for discrete-time systems [2,3,4]. For continuous-time systems, Boukas solved stability and stabilization problems [5]; the stability of singular hybrid systems was discussed in [6] and a nonlinear Markov system was discussed in [7,8,9]. On the other hand, a model reference adaptive control (MRAC) constructs a reference model to characterize the desired control performance of a closed-loop system [10], which has been widely used in the industry and theoretical control. The authors of [11] designed a tracking controller for the switched systems based on a reference model. There are some applications used in different fields of MRAC, such as economics [12], vehicles [13,14], sleep monitoring [15], polysolenoid linear motors [16], and the visual servo system [17]. In [18], the model reference control problem for the Markov system was first discussed. However, the model reference controls for Markov jump systems with circular or elliptical orbits, such as satellites, did not appear until 2017 (in [19]). However, he does not take the incompleteness of the state and unknown transition rates (TRs) into consideration. In practical engineering, the state of the system is difficult to obtain. Thus, the observer that obtains the system state by the output is also widely used in the control field for a traditional system, e.g., the traditional Luenberger observer [20,21,22,23] or the robust observer [24,25]. In [26], a novel robust observer was designed, moreover, some sliding observers were reviewed in [27,28]. For Markov systems, observers were designed, such as a proportional integral observer [29], whose performance is excellent but does not fit high-order systems. Wu studied the state estimation and sliding mode control of the Markov jump system [30] and the mode-dependent observer [31] for the discrete Markov system. Yang designed an observer for Markov jump systems [32], which can directly obtain the state estimation without any supplementary design. In this paper, the state was obtained by a series of transformations.
Many studies are based on the condition that the transition matrix is completely known. In engineering, some values of transition matrices are hard to obtain, while some are completely inaccessible. Thus, the unknown part of the transition matrix comes into view, e.g., the information is incomplete in Markov chains or games [33,34,35], and the TRs are partially unknown [36,37,38,39,40]. In [38], the author assumed that the lower bound of the unknown self-transition rate was known and successfully solved the stability problem. However, in practical applications, the above conditions are difficult to meet. In 2014, Kao attempted to solve the problem of a completely unknown situation of the self-transition rate in [41], but the proof process was wrong. In [42], Park proposed sufficient and necessary conditions for the resolution with partly unknown transition rates. However, the author just set up a new function that was still a sufficient condition. 2021, In [43], the author solved the H∞ filtering of a discrete Markov jump system with unknown transition rates, where the self-transition rate could be absolutely unknown. However, the self-transition rate of a discrete jump system is positive, while the self-transition rate of a continuous jump system is negative, so the above method does not apply to the continuous system.
Although there are many studies on the control problem of a Markov jump system, very few studies have investigated the problem of the model reference tracking control of a Markov jump system. Because different reference models correspond to completely different algorithms, it is difficult to guarantee the tracking effects of different models. The model reference tracking problem is much more complicated than the analysis or stability of Markov jump systems only. Partly unknown transition rates and state incompleteness are still open issues. Therefore, this motivated us to address this problem subject to partially unknown TRs based on the observer.
In this paper, we studied the observer-based model reference tracking control along with partly unknown transition rates. Firstly, an observer was designed for a given system by a descriptor augmentation transformation. Then the controller was designed by using the properties of the observer and variational methods, which consist of two parts: a feedback controller and feedforward compensator. We propose sufficient conditions for the stochastic stability of the system under the condition where the self-transition rate can be completely unknown; moreover, the parametric solution of the feedback controller is given using the above condition. Finally, the parametric solution of the feedforward compensator is given using the generalized Sylvester equation. The feasibility of the above theorem and algorithm is proved via several numerical examples in the last part.
The notations adopted in this paper are standard. is the n-dimensional real Euclidean space. is the normed linear space of all m by n real matrices. represent the Euclidean norm of or the operator norm of . is the transpose of a matrix (or vector) A. mean A is a negative(semi-) definite symmetric matrix. In symmetric block matrices, we use “*” as an ellipsis for the terms induced by symmetry, for a block-diagonal matrix, and .
2. Problem Description and Preliminaries
Consider the continuous-time Markov jump system. The model of the system is defined by the following differential equations:
where , and are the parameter matrices of the system. , , are the state vector, input vector, and output vector, respectively. is the Markov process that represents the jump mode of system (1), which takes values in a finite set . Moreover, the transition probability matrix is given by:
where > 0. , . Denote the transition rate from i to j and for i, j. When transition rates are partly unknown, the transition matrix can be described as follows:
where the “?” denotes the unknown transition rates. To facilitate the future discussion, for all , the set denotes
Moreover, if . It is further described as . Where represent the jth bounded-known element with the index in the ith row of . Denote , , and to replace , , and , when .
Definition 1
([44]). The closed loop system with is stochastically stable (SS) if for every initial condition and the following holds
represents the mathematical expectation operator. This paper researches the model reference tracking control problem for continuous-time systems with a circular-like orbit. Without losing generality, the reference signal can be generated by the following reference model:
where , are the state vector and output vector of the reference mode. and are the known matrices with appropriate dimensions. The purpose is to design a controller that can make the output track the reference model’s output in the meaning square:
For arbitrary initial values , , and . The following problem needs to be done to realize the purpose of the paper. For systems (1) and (7), a controller is designed in the form of
Using this algorithm, the closed-loop system can be stochastic stable and can track in the meaning square.
3. Observer and Control Law Design
3.1. Observer Design
In order to apply a generalized augmented transform to the system. First, we must define the following variables and augmented matrices.
Based on the definitions above, the descriptor system can be constructed as:
where , , , .
Let be an orthogonal matrix of , which means . We define a coordinate transformation matrix
where .
We can easily obtain . For convenience, we denote as
where , , , with
where , ,, . Further, we use , obviously,
We define a new matrix as follows:
We rank( n+p, multiplying on both sides of (14):
It can be seen that ,, further denote as:
where , we can further derived as , thus we have:
By decomposing , Equation (17) can be rewritten as:
Then we derive:
Similarly, use the decomposing that , obtain the following equation:
The reduced linear observer is designed as follows, based on the above:
In the above equation, and are the estimations of and . z(t) is the intermediate variable.
Lemma 1.
By the process above, we have the following equations:
| (1), | (2), |
| (3), | (4), |
| (5), | (6). |
The proof of Lemma 1 is shown in Appendix A.
3.2. Control Law Design
According to Section 2, in order to design a feedback controller and feedforward compensator, the existence conditions of the controllers should be determined first. The following theorem gives the existing conditions of the controller.
Theorem 1.
The problem has a solution if the system is SS and matrices exist, , and , satisfying the following equations:
Proof of Theorem 1.
Let
After, we take the derivatives on both sides of the first expression, and we obtain the following equation:
We substitute (t) to the original formula:
We substitute by (22) in the above equation:
Similarly, we substitute from the above equation:
By (22), we can conclude that , which means equation above is:
By (4) and (5) in Lemma 1 and Equation (23), and the equation above, we have:
By (1) of Lemma 1, . Combined with (2) in Lemma 1, , we plug into the above equation
□
By Theorem 1 and Equations (3) and (6) in Lemma 1, we are able to show that:
Clearly, system (23) and system (1) have the same structures and, hence, the state feedback control law , which can stabilize system (1), and the state feedback can also stabilize system (21), which is to say that the system
is stochastically stable; thus, (6) holds, and then (22) and (24). The controller can be rewritten as
combined with (24). The following can be obtained . Next, we design the state feedback controller and the feedforward tracking compensator.
4. Parameter Solutions
The above theorem gives the existence conditions of the controller. In this section, we will solve the feedback controller and the feedforward compensator, respectively.
4.1. State Feedback Control Law Design
From (25) and (26), the state feedback control law involves making the system SS. In the following theorem, based on the stability theory and LMI method, we propose a sufficient condition for SS of the system when the transition rates are partially unknown, and the parameter solution of the controller can be derived from the above condition.
Theorem 2.
System (1) with and partly unknown TRs is stochastically stable if there exists a set of symmetric and positive-definite matrices , and a set of matrices , satisfying:
Moreover, if the above inequations are solvable, the controller gain can be computed from the relation , where
.
.
.
.
.
.
To prove Theorem 2, we first introduce the following lemma.
Lemma 2
([44]). The unforced system (1) () is SS if and only if there exists a set of symmetric and positive-definite matrices , satisfying:
Lemma 2 shows the SS of the Markov jump systems. System (1) with can be rewritten as . It can be concluded from Lemma 2 that the SS condition of the system with the feedback controller can be obtained simply by replacing with .
Proof of Theorem 2.
Consider two cases: and .
Case 1: .
Since , the SS inequality of the system with can be rewritten as:
Denote
Thus, can be guaranteed by
Multiply on both sides of (36), which hold by using (28) and (30) through the Schur complement.
Case 2: Similarly, we denote
Thus, can be guaranteed by
We multiply on both sides of (39) Thus, can be guaranteed by (29)–(31) by using the Schur complement. □
Note that the controller derived from Theorem 2 can stochastically stabilize system (1).
4.2. Feedforward Control Law Design
Since , and can be obtained by Section 4.1. The key to solving the feedforward compensator is to find matrices and satisfied (23). According to the generalized Sylvester equation, the matrix in the form of (23) has a complete parametric solution, which can be solved by the following Lemmas.
Lemma 3
([45]). If the matrix pair is controllable, there exists a unimodular matrix , satisfying
where is the generalized inverse matrix of matrix , such that . is a diagonal matrix and satisfies . We partition the unimodular matrix as:
,,, can be written in the following form:
Lemma 4
([19]). Four polynomial matrices , , , and are as above. If the matrix pair is controllable, the parameter solutions of , can be obtained as follows:
where is an arbitrary parameter matrix, which represents the degree of freedom with appropriate dimensions in the solution. In the calculation, we judge whether the matrix pair is controllable. If it is controllable, we decompose the matrix according to Lemma 3, and then solve and through Lemma 4.
4.3. Algorithm for Solving the Controller
Given the reference model coefficient matrices , , and , , for every , and the transition probability matrix , then the following algorithm can be presented as follow:
- According to Theorem 2, compute the state feedback gain matrix.
- Judge whether the matrix pair is controllable. If it is controllable, solve Lemma 3, and go on to the next step; otherwise, the feedforward compensator does not exist.
- Compute and based on Lemma 4, then compute the gain matrix of the feedforward compensator.
5. Numerical Example
Several examples are presented to explain the feasibility of the algorithm.
Example 1.
Consider plant (1) and give the system parameters in the following form to illustrate the effectiveness of our results.
, ,
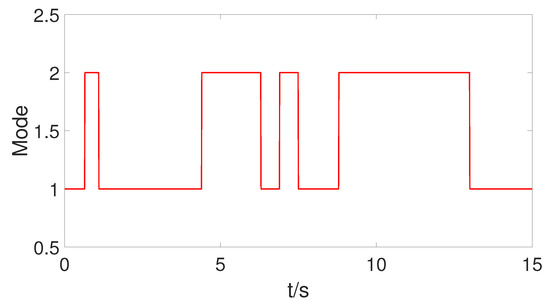
, ,
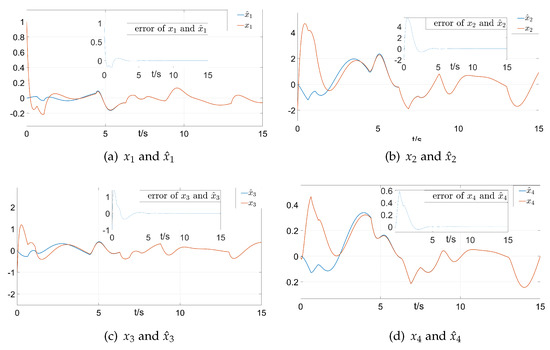
, . The control input . The transition rate matrix Π is chosen in and the transition rate is shown in Figure 1. Following the observer design process, the simulation results are presented in Figure 2 with the initial value . Figure 2a–d are the trajectories of the system states and their estimated states. It can be seen that the achieved observer performance is ideal. From the error image—after about 1.6 s, the error between the estimated value and the actual value is very small. However, the matrix is not a full rank. So this model is unable to complete the model reference tracking control; whatever the reference model is, the controller does not exist. This example shows that the effect of the observer is ideal, but the algorithm is not suitable for all systems.

Figure 1.
Transition rates.

Figure 2.
Results of the observer under initial conditions .
Example 2.
Consider the following satellite tracking system with three modes.
, , , where the transition rate . The matrices and in the reference model are designed as , =.. . If the output of the satellite model can track the circular signal generated by the reference model, the orbiting motion can be completed. Set the simulation time at 5000 s.
After computations by the LMI Toolbox in Matlab,
.
.
.
. .
.
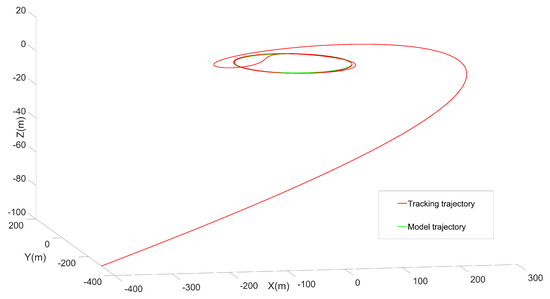
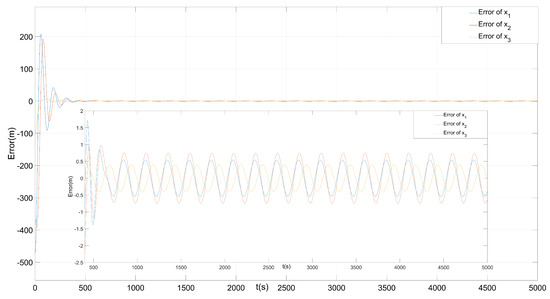
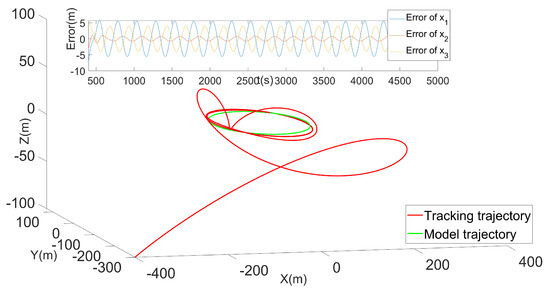
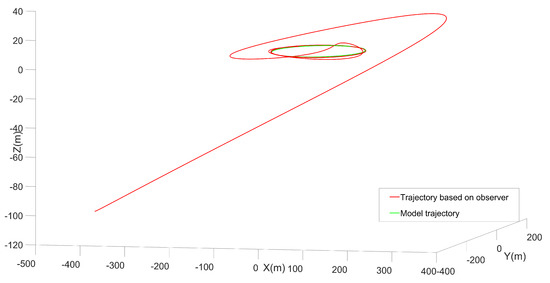
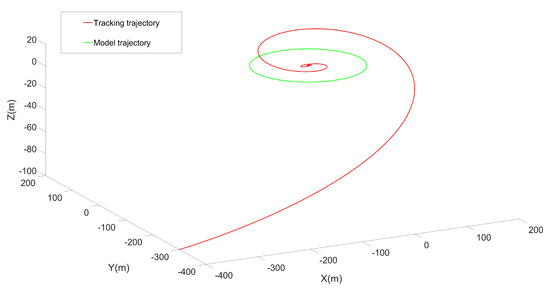
The trajectory of the system under initial conditions is shown in Figure 3. The trajectory of the system and position error between the system and model is shown in Figure 4. As can be seen from the Figure 4, the error between the system and the reference model is about 0.5 m after 400 s. In addition, it can be seen from Figure 3 that the system trajectory perfectly tracks the reference model, and the reason for the errors is that, to a certain extent, the system lags in the phase. The controller in [5] is selected as the contrast test. Since this control law is based on the completely known transition rates, we may as well set the known transition rate matrix to obtain the results as shown in Figure 5. We can see that the system error is about 10 times in this paper after almost 500 s. It can be seen that although the transition rates are partly unknown in this paper, the results are better. Figure 6 is the trajectory of the system based on the observer. The observer-based system tracking control can also meet the conditions. The trajectory without a feedforward compensator is shown in Figure 7, which embodies the superiority of the algorithm compared with the feedforward compensator only. This example verifies the tracking performance of the algorithm, and the effects are ideal in the observer-based case.

Figure 3.
Trajectory.

Figure 4.
Error between the system and model.

Figure 5.
Contrast test.

Figure 6.
Trajectory based on the observer.

Figure 7.
Trajectory without the feedforward compensator.
6. Conclusions
In this paper, the observer-based model reference tracking control problem with partly unknown TRs was studied. For a given system, a descriptor observer was designed by the matrix transformation, which solved the estimation problem. A tracking controller composed of a state feedback controller and the feedforward of the state of the model that has a complete parametric form was designed for the given reference model. The parametric solution of the controller was given by analyzing the stochastic stability of the system with transition rates partly unknown, and the self-transition rate of the system can be unknown. A parametric method was established for the feedforward part of the tracking problem based on the theory of the generalized Sylvester equations. The performance of the observer, the stability of the control system, and the tracking effect were verified by several numerical examples. It has fewer errors compared to the existing conclusions.
Author Contributions
Methodology, W.S.; Software, W.S.; Validation, W.S.; Formal analysis, W.S.; Investigation, W.S.; Resources, A.J.; Data curation, A.J.; Writing—original draft, W.S.; Writing—review & editing, W.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Most of the data is given in the text.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Proof of Lemma 1.
Define the following matrices:
| (1), | (2), |
| (3), | (4), |
| (5), | (6), |
| (7), | (8). |
Moreover, (1)–(4) can be obtained by the equivalence of corresponding terms of the following equation:
Thus, (1)–(4) hold. Using (2) and (4), we have:
Thus, (5) holds, then
By the equivalence of corresponding terms, we have . So (6) hold
Thus, . So (7) hold.
Thus, (8) holds. From the above equation, it can be seen that the equations in Lemma 1 are true. The proof is finished. □
References
- Ji, Y.; Chizeck, H.J. Controllability, stabilizability, and continuous-time Markovian jump linear quadratic control. IEEE Trans. Autom. Control 1990, 35, 777–788. [Google Scholar] [CrossRef]
- Hou, T.; Liu, Y.; Deng, F. Stability for discrete-time uncertain systems with infinite Markov jump and time-delay. Sci. China Inf. Sci. 2021, 64, 152202. [Google Scholar] [CrossRef]
- Wang, P.; Wang, W.; Su, H.; Feng, J. Stability of stochastic discrete-time piecewise homogeneous Markov jump systems with time delay and impulsive effects. Nonlinear Anal. Hybrid Syst. 2020, 38, 100916. [Google Scholar] [CrossRef]
- Rakkiyappan, R.; Chandrasekar, A.; Lakshmanan, S.; Park, J. Exponential stability for markovian jumping stochastic BAM neural networks with mode-dependent probabilistic time-varying delays and impulse control. Complex 2015, 20, 39–65. [Google Scholar] [CrossRef]
- Zhang, L.; Boukas, E.K. Stability and stabilization of Markovian jump linear systems with partly unknown transition probabilities. Automatica 2009, 45, 463–468. [Google Scholar] [CrossRef]
- Xia, Y.; Boukas, E.K.; Shi, P.; Zhang, J. Stability and stabilization of continuous-time singular hybrid systems. Automatica 2009, 45, 1504–1509. [Google Scholar] [CrossRef]
- Zhang, X.; Baron, L.; Liu, Q.; Boukas, E.K. Design of Stabilizing Controllers With a Dynamic Gain for Feedforward Nonlinear Time-Delay Systems. IEEE Trans. Autom. Control 2011, 56, 692–697. [Google Scholar] [CrossRef]
- Boukas, E.K. Stabilization of stochastic singular nonlinear hybrid systems. Nonlinear-Anal.-Theory Methods Appl. 2006, 64, 217–228. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Q.; Baron, L.; Boukas, E.K. Feedback stabilization for high order feedforward nonlinear time-delay systems. Automatica 2011, 47, 962–967. [Google Scholar] [CrossRef]
- Ji, H.; Cui, B.; Liu, X. Adaptive control of Markov jump distributed parameter systems via model reference. Fuzzy Sets Syst. 2020, 392, 115–135. [Google Scholar]
- Tan, M.; Mai, J.; Song, Z. Exponential H∞ output tracking control for coupled switched systems with states of different dimensions. Int. J. Control 2021, 94, 190–201. [Google Scholar] [CrossRef]
- Carravetta, F.; Sorge, M.M. Model reference adaptive expectations in Markov-switching economies. Econ. Model. 2013, 32, 551–559. [Google Scholar] [CrossRef]
- Chen, Z.; Hu, H.; Wu, Y.; Zhang, Y.; Li, G.; Liu, Y. Stochastic model predictive control for energy management of power-split plug-in hybrid electric vehicles based on reinforcement learning. Energy 2020, 211, 118931. [Google Scholar] [CrossRef]
- Zhao, X.; Guo, G. Model Reference Adaptive Control of Vehicle Slip Ratio Based on Speed Tracking. Appl. Sci. 2020, 10, 3459. [Google Scholar] [CrossRef]
- Peng, L.; Yin, A.; Song, W.; Yao, W.; Ren, H.; Yang, L. Sleep Monitoring With Hidden Markov Model for Physical Conditions Tracking. IEEE Sens. J. 2021, 21, 14232–14239. [Google Scholar] [CrossRef]
- Nguyen, H.Q. Observer-Based Tracking Control for Polysolenoid Linear Motor with Unknown Disturbance Load. Actuators 2020, 9, 23. [Google Scholar] [CrossRef]
- Lala, T.; Chirla, D.; Radac, M. Model Reference Tracking Control Solutions for a Visual Servo System Based on a Virtual State from Unknown Dynamics. Energies 2021, 15, 267. [Google Scholar] [CrossRef]
- Boukas, E.K. On reference model tracking for Markov jump systems. Int. J. Syst. Sci. 2009, 40, 393–401. [Google Scholar] [CrossRef]
- Fu, Y.; Lu, Y.; Zhang, M. Model reference tracking control of continuous-time periodic linear systems with actuator jumping fault and its applications in orbit maneuvering. Int. J. Control. Autom. Syst. 2017, 15, 2182–2192. [Google Scholar] [CrossRef]
- Afri, C.; Andrieu, V.; Bako, L.; Dufour, P. State and Parameter Estimation: A Nonlinear Luenberger Observer Approach. IEEE Trans. Autom. Control 2017, 62, 973–980. [Google Scholar] [CrossRef]
- CastroRego, F.; Pu, Y.; Alessandretti, A.; Aguiar, A.; Pascoal, A.M.; Jones, C.N. A Distributed Luenberger Observer for Linear State Feedback Systems With Quantized and Rate-Limited Communications. IEEE Trans. Autom. Control 2021, 66, 3922–3937. [Google Scholar]
- Yin, Z.; Bai, C.; Du, N.; Du, C.; Liu, J. Research on Internal Model Control of Induction Motors Based on Luenberger Disturbance Observer. IEEE Trans. Power Electron. 2021, 36, 8155–8170. [Google Scholar] [CrossRef]
- Bejarano, F.J.; Mera, M. Robust Luenberger-like observer for control of linear switched systems under arbitrary unknown switched function. Asian J. Control. 2020, 23, 2527–2536. [Google Scholar] [CrossRef]
- Rincón, A.; Restrepo, G.M.; Velasco, F.E. A Robust Observer-Based Adaptive Control of Second—Order Systems with Input Saturation via Dead-Zone Lyapunov Functions. Computation 2021, 5, 82. [Google Scholar] [CrossRef]
- Al-Gabalawy, M.; Mahmoud, K.; Darwish, M.M.; Dawson, J.A.; Lehtonen, M.; Hosny, N.S. Reliable and Robust Observer for Simultaneously Estimating State-of-Charge and State-of-Health of LiFePO4 Batteries. Appl. Sci. 2021, 11, 3609. [Google Scholar] [CrossRef]
- Hua, H.; Fang, Y.; Zhang, X.; Lu, B. A Novel Robust Observer-Based Nonlinear Trajectory Tracking Control Strategy for Quadrotors. IEEE Trans. Control. Syst. Technol. 2021, 29, 1952–1963. [Google Scholar] [CrossRef]
- Yao, D.; Lu, R.; Xu, Y.; Ren, H. Observer-based sliding mode control of Markov jump systems with random sensor delays and partly unknown transition rates. Int. J. Syst. Sci. 2017, 48, 2985–2996. [Google Scholar] [CrossRef]
- Jiang, B.; Shi, P.; Mao, Z. Sliding Mode Observer-Based Fault Estimation for Nonlinear Networked Control Systems. Circuits, Syst. Signal Process. 2011, 30, 1–16. [Google Scholar] [CrossRef]
- Vijayakumar, M.; Sakthivel, R.; Mohammadzadeh, A.; Karthick, S.A.; Anthoni, S.M. Proportional integral observer based tracking control design for Markov jump systems. Appl. Math. Comput. 2021, 410, 126467. [Google Scholar] [CrossRef]
- Wu, L.; Shi, P.; Gao, H. State Estimation and Sliding-Mode Control of Markovian Jump Singular Systems. IEEE Trans. Autom. Control 2010, 55, 1213–1219. [Google Scholar]
- Huo, S.; Ge, L.; Li, F. Robust H∞ Consensus for Markov Jump Multiagent Systems Under Mode-Dependent Observer and Quantizer. IEEE Syst. J. 2020, 15, 2443–2450. [Google Scholar] [CrossRef]
- Yang, H.; Yin, S. Descriptor Observers Design for Markov Jump Systems with Simultaneous Sensor and Actuator Faults. IEEE Trans. Autom. Control 2019, 64, 3370–3377. [Google Scholar] [CrossRef]
- Lei, C.; Zhang, H.; Wang, L.; Liu, L.; Ma, D. Incomplete information Markov game theoretic approach to strategy generation for moving target defense. Comput. Commun. 2018, 116, 184–199. [Google Scholar] [CrossRef]
- Ashkenazi-Golan, G.; Rainer, C.; Solan, E. Solving two-state Markov games with incomplete information on one side. Games Econ. Behav. 2020, 122, 83–104. [Google Scholar] [CrossRef]
- Cui, D.; Wang, Y.; Su, H.; Xu, Z.; Que, H. Fuzzy-model-based tracking control of Markov jump nonlinear systems with incomplete mode information. J. Frankl. Inst. 2021, 358, 3633–3650. [Google Scholar] [CrossRef]
- Fang, H.; Zhu, G.; Stojanovic, V.; Nie, R.; He, S.; Luan, X.; Liu, F. Adaptive optimization algorithm for nonlinear Markov jump systems with partial unknown dynamics. Int. J. Robust Nonlinear Control 2021, 31, 2126–2140. [Google Scholar] [CrossRef]
- Li, F.; Xu, S.; Shen, H.; Ma, Q. Passivity-Based Control for Hidden Markov Jump Systems With Singular Perturbations and Partially Unknown Probabilities. IEEE Trans. Autom. Control 2020, 65, 3701–3706. [Google Scholar] [CrossRef]
- Zhang, L.; Lam, J. Necessary and Sufficient Conditions for Analysis and Synthesis of Markov Jump Linear Systems With Incomplete Transition Descriptions. IEEE Trans. Autom. Control 2010, 55, 1695–1701. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Q. Finite-time H∞ control for singular Markovian jump systems with partly unknown transition rates. Appl. Math. Model. 2016, 40, 302–314. [Google Scholar] [CrossRef]
- Shen, M.; Park, J.; Ye, D. A Separated Approach to Control of Markov Jump Nonlinear Systems with General Transition Probabilities. IEEE Trans. Cybern. 2016, 46, 2010–2018. [Google Scholar] [CrossRef]
- Kao, Y.; Xie, J.; Wang, C. Stabilization of Singular Markovian Jump Systems With Generally Uncertain Transition Rates. IEEE Trans. Autom. Control 2014, 59, 2604–2610. [Google Scholar] [CrossRef]
- Park, C.; Kwon, N.K.; Park, I.S.; Park, P. H∞ filtering for singular Markovian jump systems with partly unknown transition rates. Automatica 2019, 109, 108528. [Google Scholar] [CrossRef]
- Shen, A.; Li, L.; Li, C. H∞ Filtering for Discrete-Time Singular Markovian Jump Systems with Generally Uncertain Transition Rates. Circuits, Syst. Signal Process. 2021, 40, 3204–3226. [Google Scholar] [CrossRef]
- Boukas, E.K. Stochastic Switching Systems: Analysis and Design; Birkhauser: Basel, Switzerland; Berlin, Germany, 2005. [Google Scholar]
- Horn, R.A.; Johnson, C.R. Matrix analysis. In Statistical Inference for Engineers and Data Scientists; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).