Progressive Formation of Retrogressive Landslide and the Lateral Length of Instability
Abstract
1. Introduction
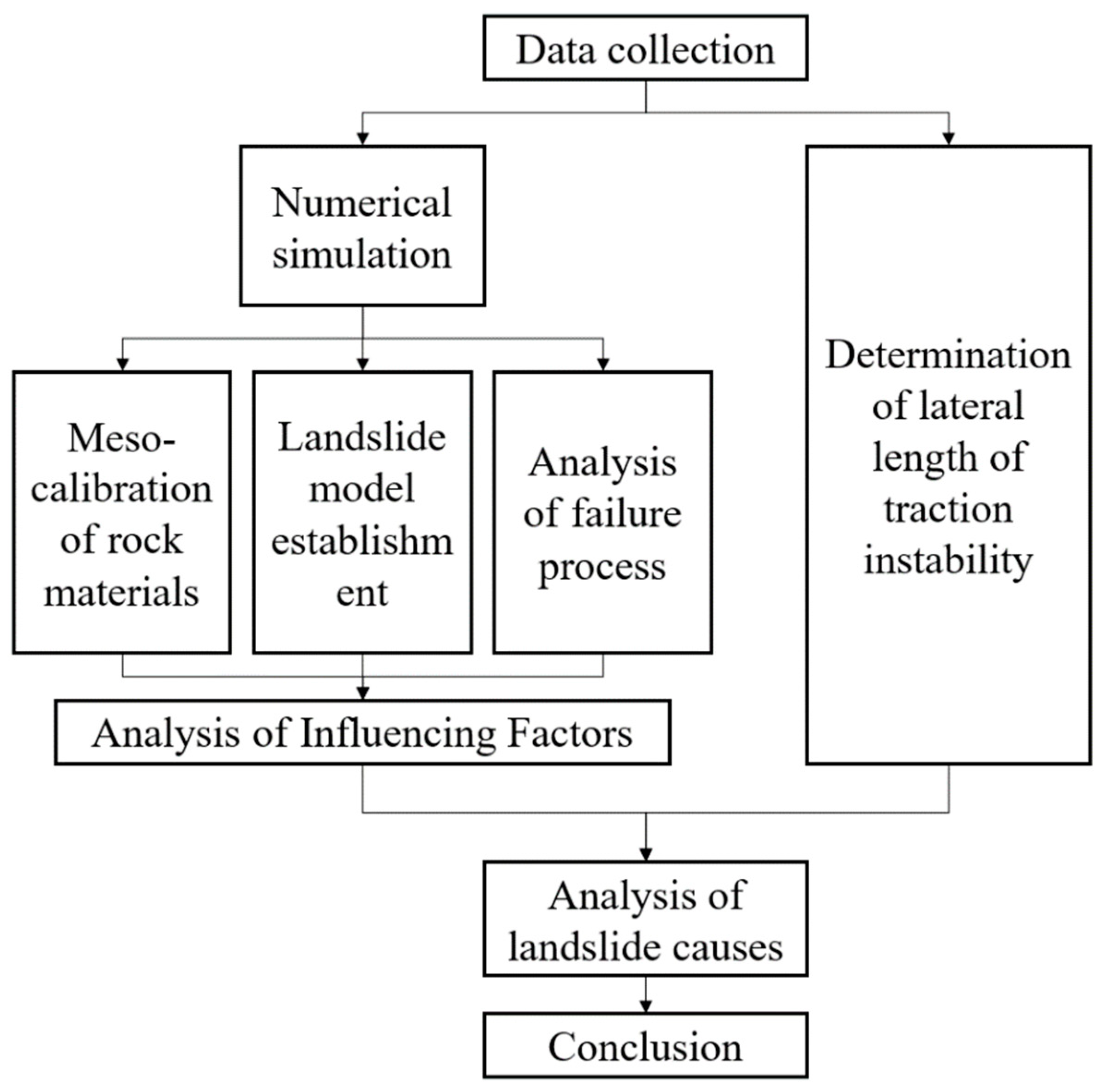
2. Numerical Simulation of Landslide Failure Process
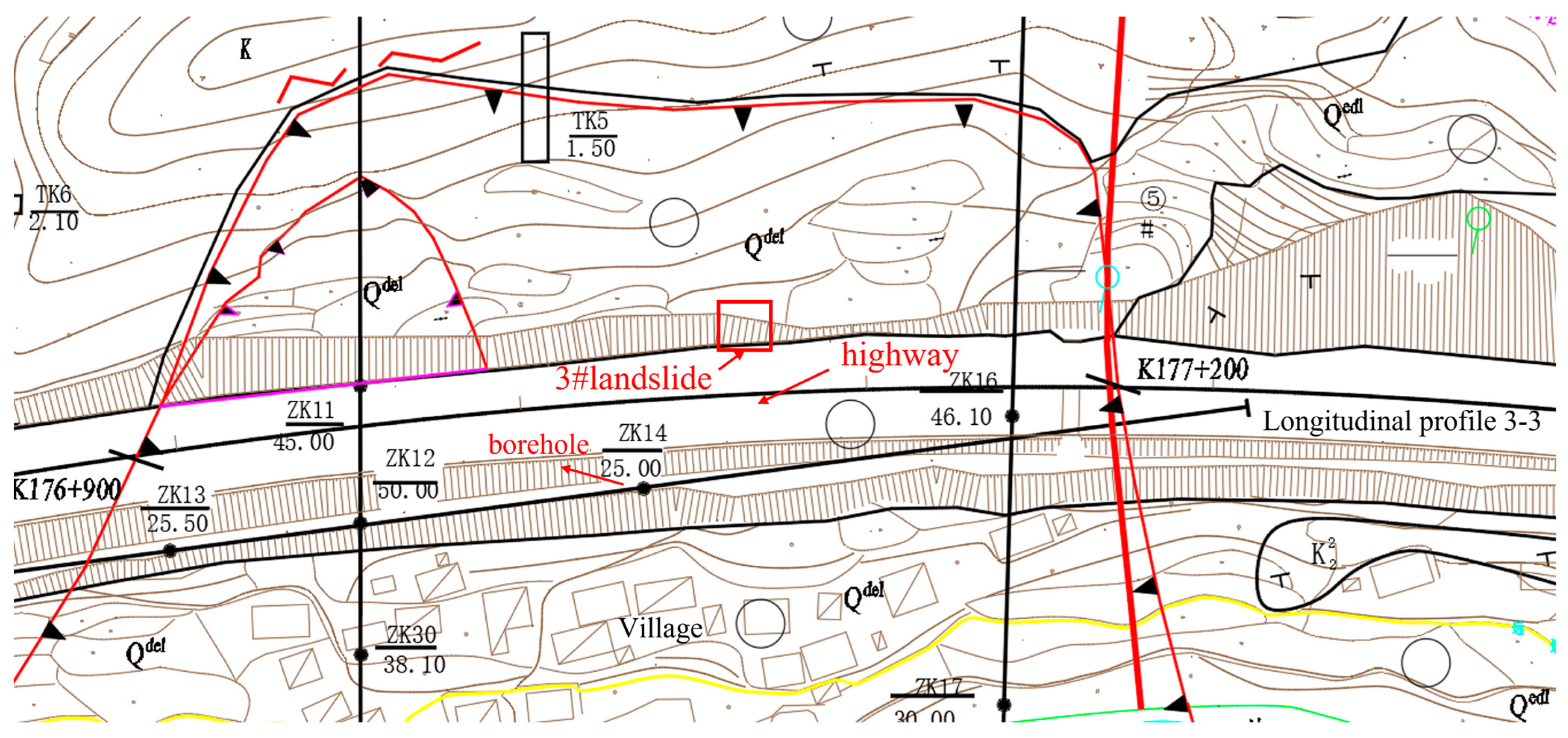
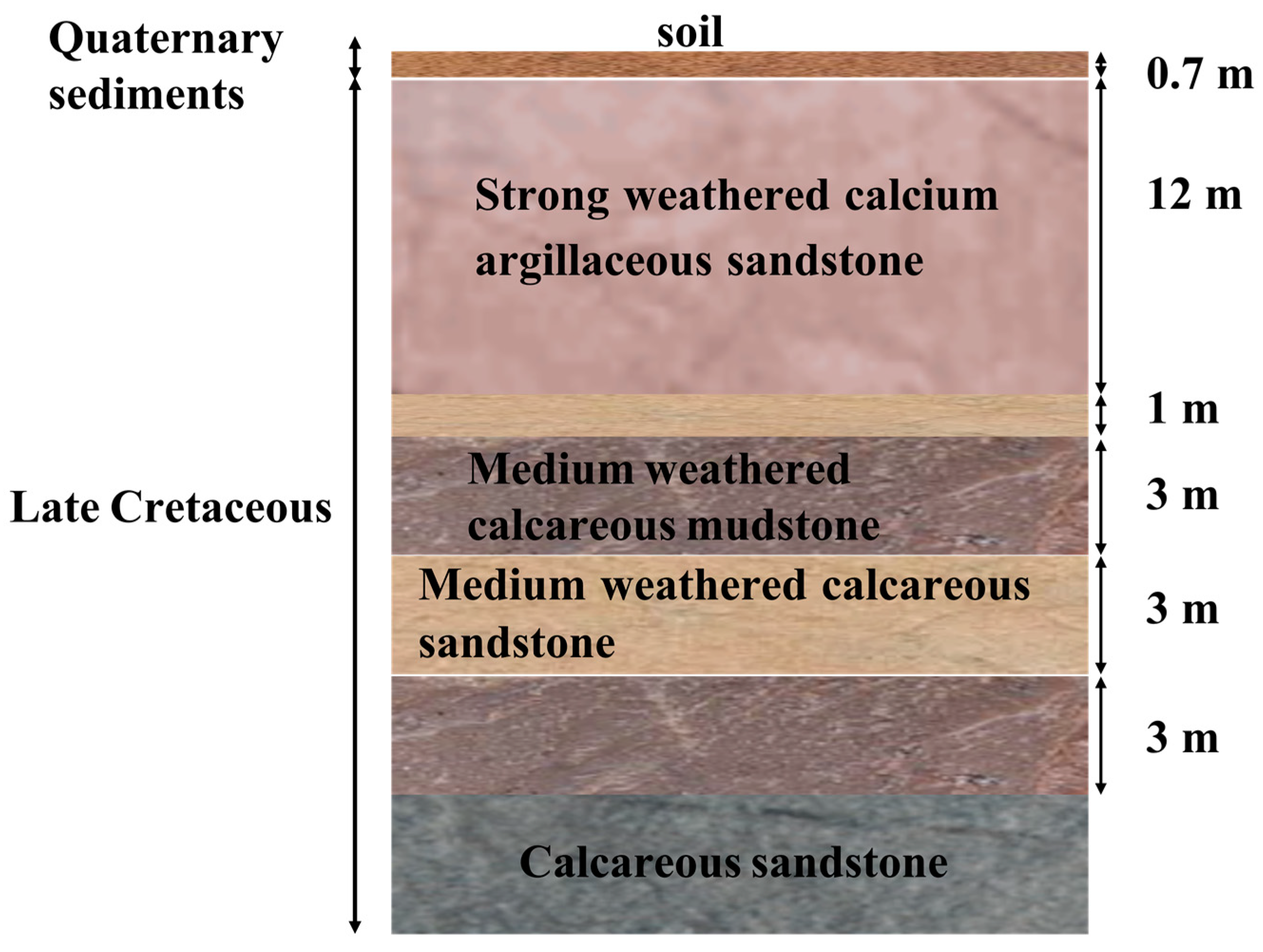
2.1. Geological Background
- (1)
- Quaternary sediments: up to 0.5 m gray-brown soil, widely distributed on the hillside surface.
- (2)
- Late Cretaceous: medium-thick layered argillaceous sandstone, calcareous mudstone, and calcareous sandstone, etc. [34]. The calcareous sandstone and calcareous mudstone are alternately deposited, and there are weak interlayers of mud films with different thicknesses between the layers. The interlayer lithology is strongly weathered mudstone or plastic clay, and the properties are poor. A detailed summary is as follows:
2.2. PFC Introduction
2.3. Meso-Calibration of Rock Materials
2.4. Landslide Model Establishment
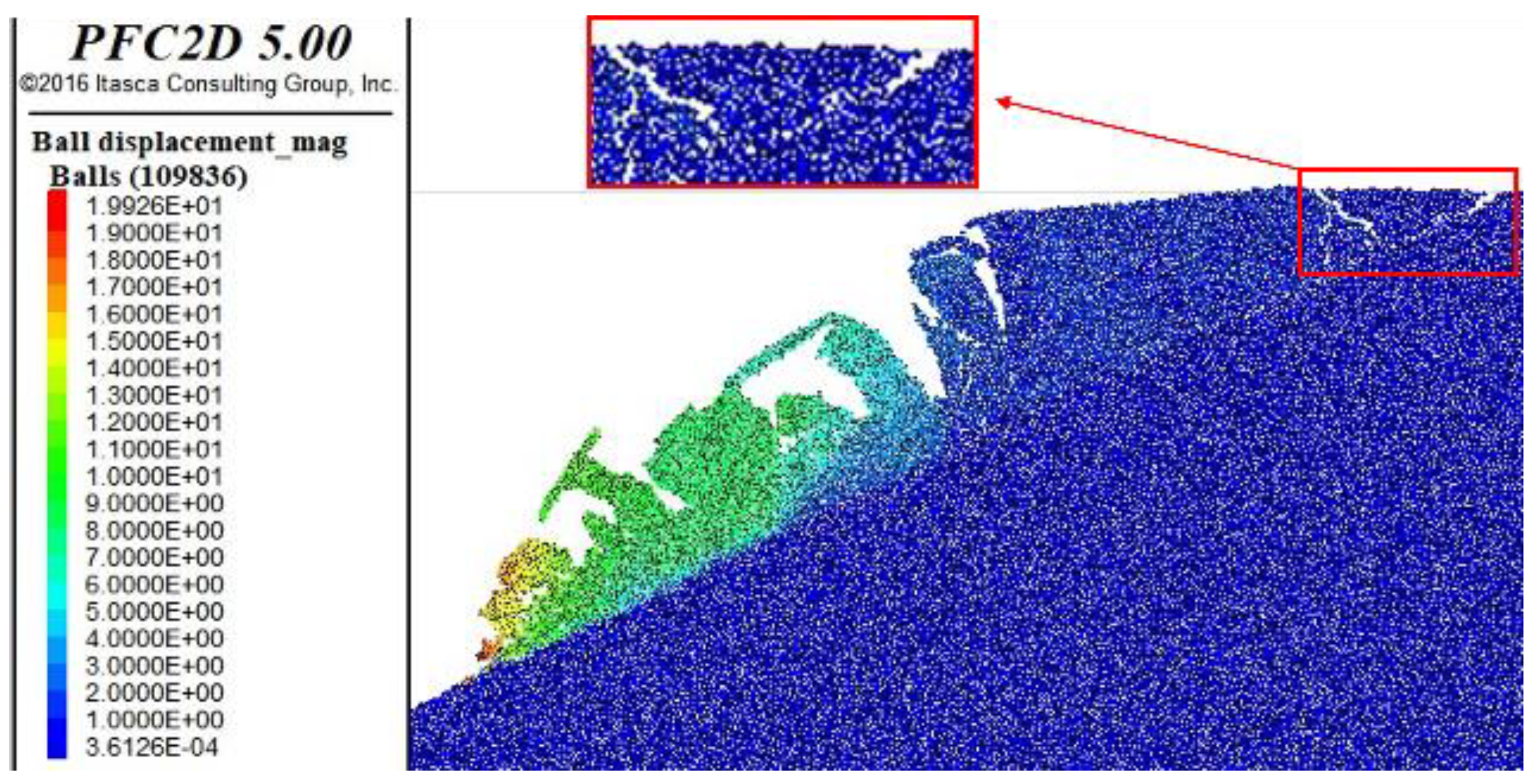
2.5. Analysis of Landslide Failure Mode
3. Determination of Lateral Length of Traction Instability and Analysis of Influencing Factors
3.1. Determination of Lateral Length of Traction Instability
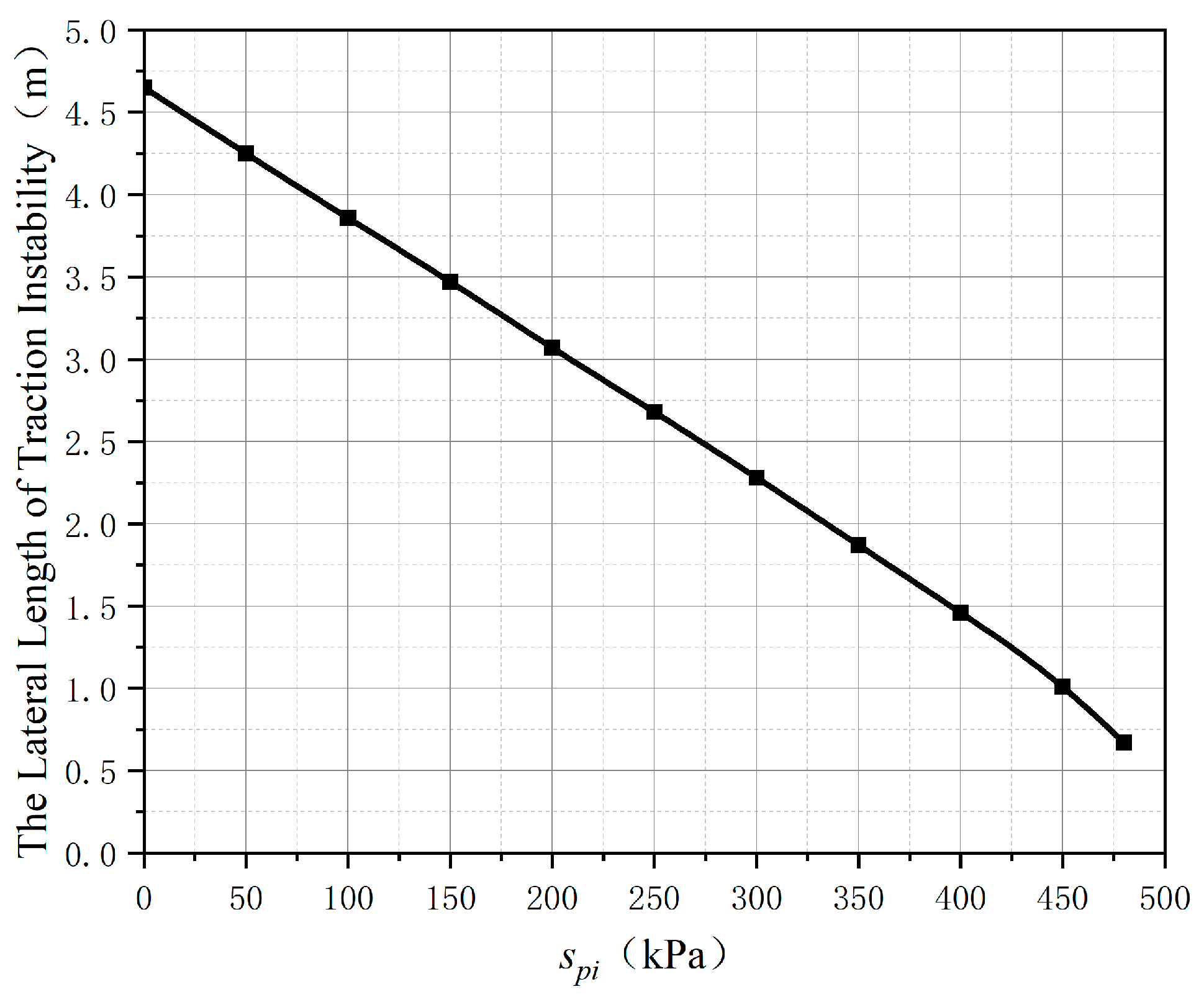
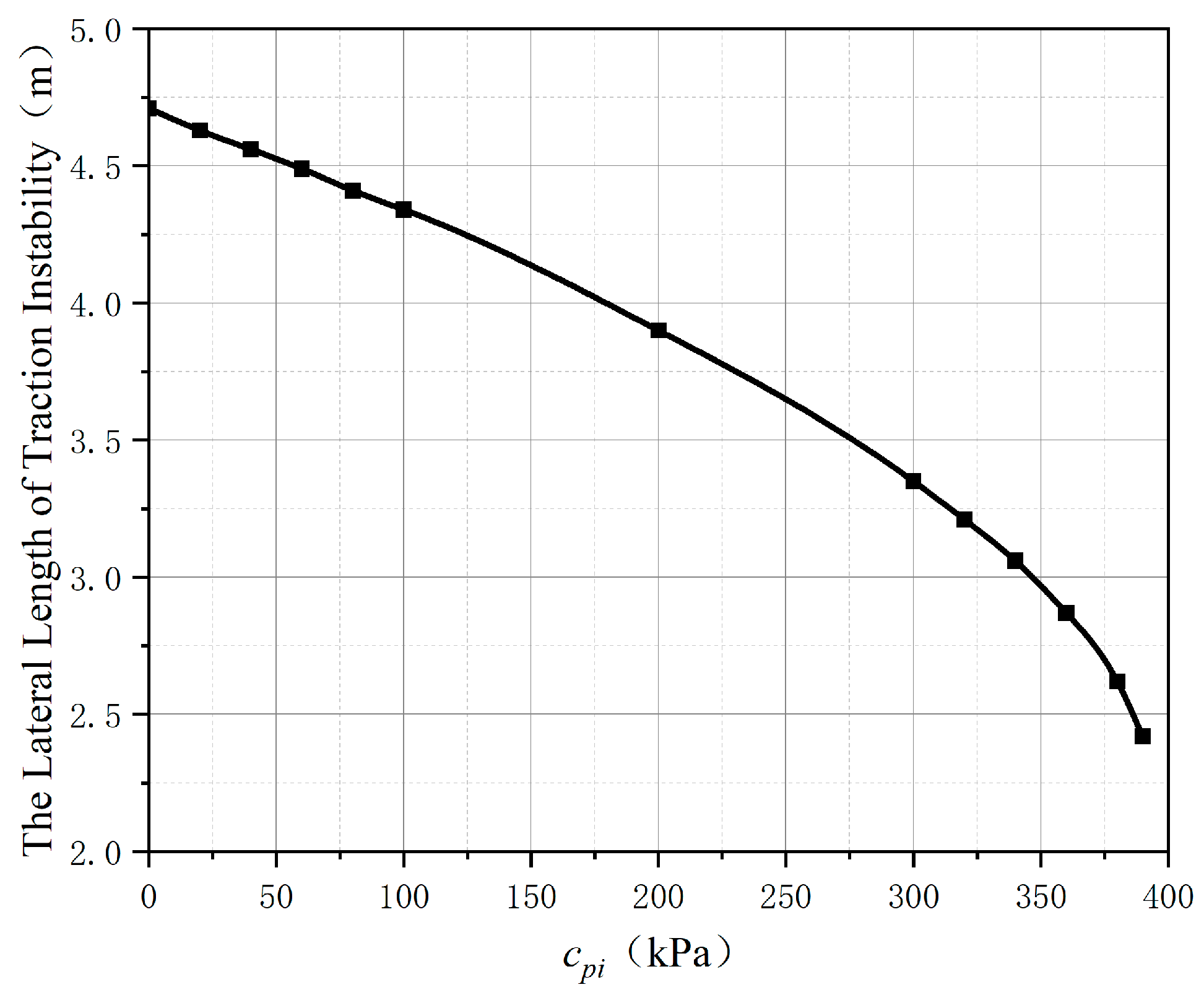
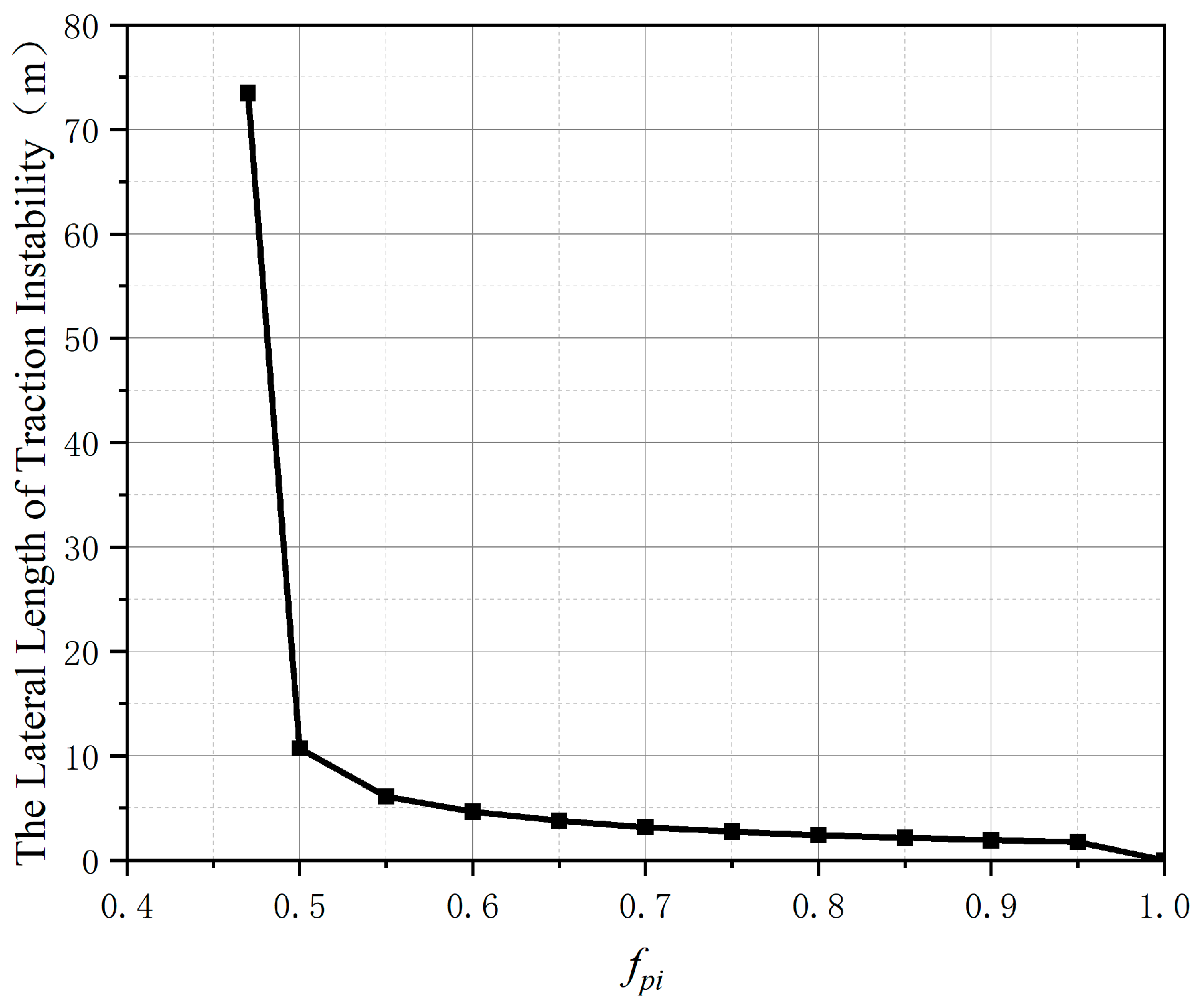
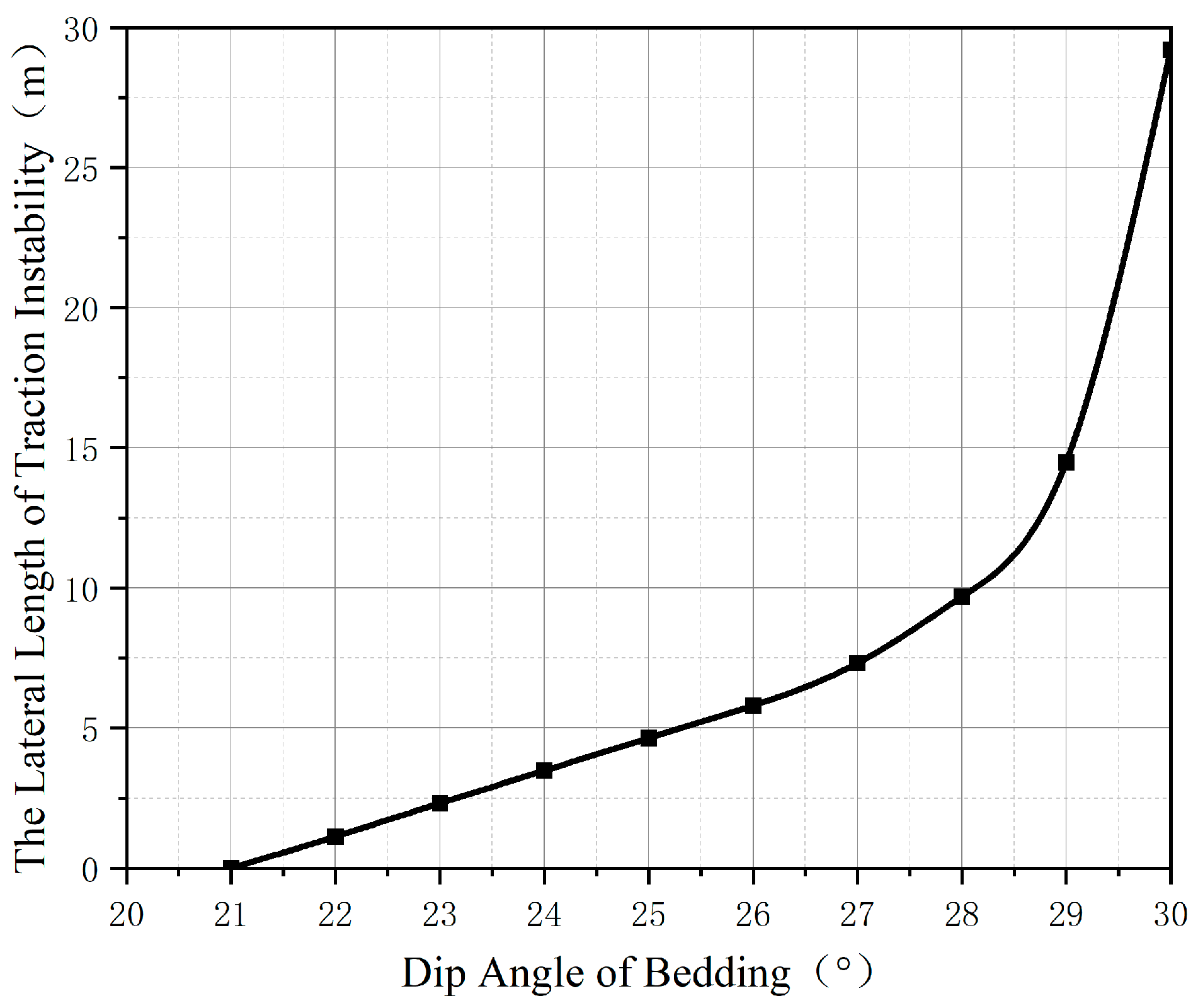
3.2. Analysis of Influence Factors on Lateral Length of Traction Instability
4. Conclusions
- (1)
- The particle flow discrete element is used to simulate the complex geological conditions of the slope, and the total failure process of the retrogressive landslide is analyzed, and the mechanism of the slope failure is slip-pull crack according to previous research. The range of the first section of the slope is 4.54 m, that is, the first section of the slide area is located in the front 8.63% of the slope. This kind of slope will be pulled and split into multiple blocks when it slips, and the lower part of the slope will shift and cause the upper part to be unstable, and eventually slide along the sliding surface. The particle flow method has good applicability to simulate the failure movement process of the landslide.
- (2)
- When the retrogressive landslide is treated in engineering practice, the lateral length of the traction instability can be obtained according to the stability theory of the sliding pull-crack failure slope, and the accurate judgment of the traction failure range of the sliding body can be estimated.
- (3)
- The dip angle of bedding and the coefficient of friction are the main factors affecting the lateral length of the slope traction instability. In engineering practice, they should be mainly paid attention to when roughly judging slope instability.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fan, H.; Lu, Y.; Hu, Y.; Fang, J.; Lv, C.; Xu, C.; Feng, X.; Liu, Y. A Landslide Susceptibility Evaluation of Highway Disasters Based on the Frequency Ratio Coupling Model. Sustainability 2022, 14, 7740. [Google Scholar] [CrossRef]
- Feng, T.; Chen, H.; Wang, K.; Nie, Y.; Zhang, X.; Mo, H. Assessment of underground soil loss via the tapering grikes on limestone hillslopes. Agric. Ecosyst. Environ. 2020, 297, 106935. [Google Scholar] [CrossRef]
- He, Y.; Zhong, G.; Wang, L.; Kuang, Z. Characteristics and occurrence of submarine canyon-associated landslides in the middle of the northern continental slope, South China Sea. Mar. Pet. Geol. 2014, 57, 546–560. [Google Scholar] [CrossRef]
- Lacroix, P.; Araujo, G.; Hollingsworth, J.; Taipe, E. Self-Entrainment Motion of a Slow-Moving Landslide Inferred From Landsat-8 Time Series. J. Geophys. Res. Earth Surf. 2019, 124, 1201–1216. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, L.; Krabbenhoft, K.; Tinti, S. A case study and implication: Particle finite element modelling of the 2010 Saint-Jude sensitive clay landslide. Landslides 2020, 17, 1117–1127. [Google Scholar] [CrossRef]
- Yuan, Z.; Zhao, J.; Li, S.; Jiang, Z.; Huang, F. A Unified Solution for Surrounding Rock of Roadway Considering Seepage, Dilatancy, Strain-Softening and Intermediate Principal Stress. Sustainability 2022, 14, 8099. [Google Scholar] [CrossRef]
- Chen, C.; Peng, Z.; Gu, J.; Peng, Y.; Huang, X.; Wu, L. Exploring Environmentally Friendly Biopolymer Material Effect on Soil Tensile and Compressive Behavior. Int. J. Environ. Res. Public Health 2020, 17, 9032. [Google Scholar] [CrossRef]
- Zhu, C.; Long, S.; Zhang, J.; Wu, W.; Zhang, L. Time Series Multi-Sensors of Interferometry Synthetic Aperture Radar for Monitoring Ground Deformation. Front. Environ. Sci. 2022, 10, 929958. [Google Scholar] [CrossRef]
- Chigira, M.; Wang, W.-N.; Furuya, T.; Kamai, T. Geological causes and geomorphological precursors of the Tsaoling landslide triggered by the 1999 Chi-Chi earthquake, Taiwan. Eng. Geol. 2003, 68, 259–273. [Google Scholar] [CrossRef]
- Lian, B.; Peng, J.; Zhan, H.; Huang, Q.; Wang, X.; Hu, S. Formation mechanism analysis of irrigation-induced retrogressive loess landslides. Catena 2020, 195, 104441. [Google Scholar] [CrossRef]
- Richer, B.; Saeidi, A.; Boivin, M.; Rouleau, A. Overview of Retrogressive Landslide Risk Analysis in Sensitive Clay Slope. Geosciences 2020, 10, 279. [Google Scholar] [CrossRef]
- Del Gaudio, V.; Wasowski, J.; Pierri, P.; Mascia, U.; Calcagnile, G. Gravimetric Study of a Retrogressive Landslide in Southern Italy. Surv. Geophys. 2000, 21, 391–406. [Google Scholar] [CrossRef]
- Guo, C.; Zhang, Y.; Li, X.; Ren, S.; Yang, Z.; Wu, R.; Jin, J. Reactivation of giant Jiangdingya ancient landslide in Zhouqu County, Gansu Province, China. Landslides 2020, 17, 179–190. [Google Scholar] [CrossRef]
- Lollino, P.; Santaloia, F.; Amorosi, A.; Cotecchia, F. Delayed failure of quarry slopes in stiff clays: The case of the Lucera landslide. Géotechnique 2011, 61, 861–874. [Google Scholar] [CrossRef]
- Shan, Z.; Zhang, W.; Wang, D.; Wang, L. Numerical investigations of retrogressive failure in sensitive clays: Revisiting 1994 Sainte-Monique slide, Quebec. Landslides 2021, 18, 1327–1336. [Google Scholar] [CrossRef]
- Yang, T.; Rao, Y.; Wu, Y.; Wang, H.; Yu, Q.; Li, H.; Chen, H. Water softening-induced retrogressive landslides: Experiments and theoretical calculations of back scarp inclination. Geomorphology 2021, 389, 107800. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, D. Stability analysis of cut slope with shear band propagation along a weak layer. Comput. Geotech. 2020, 125, 103676. [Google Scholar] [CrossRef]
- Lin, H.; Yu, Y.; Li, G.; Yang, H.; Peng, J. A Simplified Numerical Approach for the Prediction of Rainfall-Induced Retrogressive Landslides. Acta Geol. Sin.-Engl. Ed. 2016, 90, 1471–1480. [Google Scholar] [CrossRef]
- Marko, K.; Tiit, H.; Peeter, T.; Volli, K. Analysis of a retrogressive landslide in glaciolacustrine varved clay. Eng. Geol. 2010, 116, 109–116. [Google Scholar] [CrossRef]
- Lin, H.C.; Yu, Y.Z.; Li, G.X.; Peng, J.B. Developing Processes of Rainfall-induced Retrogressive Landslide by Model Experiments. Disaster Adv. 2012, 5, 861–865. [Google Scholar]
- Morandi, M.; Farabegoli, E.; Onorevoli, G. Root reinforcement and its implications in shallow landsliding susceptibility on a small alpine catchment. In Proceedings of the EGU General Assembly 2012, Conference Abstracts, Vienna, Austria, 22–27 April 2012; p. 4214. [Google Scholar]
- Li, Q.; Wang, Y.M.; Zhang, K.B.; Yu, H.; Tao, Z.Y. Field investigation and numerical study of a siltstone slope instability induced by excavation and rainfall. Landslides 2020, 17, 1485–1499. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, C.; Liu, T.; Xia, K.; Sun, C.; Chen, L. Analysis of a retrogressive landslide with double sliding surfaces: A case study. Environ. Earth Sci. 2020, 79, 21. [Google Scholar] [CrossRef]
- Li, J.; Chen, S.; Yu, F.; Jiang, L. Reinforcement Mechanism and Optimisation of Reinforcement Approach of a High and Steep Slope Using Prestressed Anchor Cables. Appl. Sci. 2020, 10, 266. [Google Scholar] [CrossRef]
- Liu, D.; Yang, X.; Wang, J. Study on Anti-Slide Pile Spacing in Slope Reinforcement Using Anti-Slide Pile with Geocell and Influencing Factors. In Proceedings of the 4th International Conference on Digital Manufacturing and Automation (ICDMA), Qingdao, China, 29–30 June 2013; IEEE: Piscataway Township, NJ, USA, 2013; pp. 1258–1260. [Google Scholar]
- Liu, Z.; Qiu, H.; Ma, S.; Yang, D.; Pei, Y.; Du, C.; Sun, H.; Hu, S.; Zhu, Y. Surface displacement and topographic change analysis of the Changhe landslide on September 14, 2019, China. Landslides 2021, 18, 1471–1483. [Google Scholar] [CrossRef]
- Zhou, T.; Luo, X.; Hou, Y.; Xiang, Y.; Peng, S. Quantifying the effects of road width on roadside vegetation and soil conditions in forests. Landsc. Ecol. 2020, 35, 69–81. [Google Scholar] [CrossRef]
- Li, M.; Lv, H.; Lu, Y.; Wang, D.; Shi, S.; Li, R. Instantaneous discharge characteristics and its methane ignition mechanism of coal mine rock damage. Environ. Sci. Pollut. Res. 2022, 29, 62495–62506. [Google Scholar] [CrossRef]
- Li, Y.; Zeng, X.; Lin, Z.; Su, J.; Gao, T.; Deng, R.; Liu, X. Experimental study on phosphate rock modified soil-bentonite as a cut-off wall material. Water Supply 2021, 22, 1676–1690. [Google Scholar] [CrossRef]
- Zhang, Y.; Ren, B.; Hursthouse, A.S.; Deng, R.; Hou, B. An Improved SWAT for Predicting Manganese Pollution Load at the Soil-Water Interface in a Manganese Mine Area. Pol. J. Environ. Stud. 2018, 27, 2357–2365. [Google Scholar] [CrossRef]
- Xie, Q.; Ren, B.; Hursthouse, A.; Shi, X. Effects of mining activities on the distribution, controlling factors, and sources of metals in soils from the Xikuangshan South Mine, Hunan Province. Integr. Environ. Assess. Manag. 2022, 18, 748–756. [Google Scholar] [CrossRef]
- Luo, X.; Ren, B.; Hursthouse, A.S.; Thacker, J.R.M.; Wang, Z. Soil from an Abandoned Manganese Mining Area (Hunan, China): Significance of Health Risk from Potentially Toxic Element Pollution and Its Spatial Context. Int. J. Environ. Res. Public Health 2020, 17, 6554. [Google Scholar] [CrossRef]
- Yu, S.; Chen, Y.; Zhao, J.; Fu, S.; Li, Z.; Xia, H.; Zhou, L. Temperature sensitivity of total soil respiration and its heterotrophic and autotrophic components in six vegetation types of subtropical China. Sci. Total Environ. 2017, 607, 160–167. [Google Scholar] [CrossRef] [PubMed]
- Yu, W.; Li, K.; Liu, Z.; An, B.; Wang, P.; Wu, H. Mechanical characteristics and deformation control of surrounding rock in weakly cemented siltstone. Environ. Earth Sci. 2021, 80, 1–15. [Google Scholar] [CrossRef]
- Zou, S.-H.; Li, K.-Q.; Han, Q.-Y.; Yu, C.W. Numerical simulation of the dynamic formation process of fog-haze and smog in transport tunnels of a hot mine. Indoor Built Environ. 2017, 26, 1062–1069. [Google Scholar] [CrossRef]
- Zhao, Y.; Luo, S.; Wang, Y.; Wang, W.; Zhang, L.; Wan, W. Numerical Analysis of Karst Water Inrush and a Criterion for Establishing the Width of Water-resistant Rock Pillars. Mine Water Environ. 2017, 36, 508–519. [Google Scholar] [CrossRef]
- Xie, W.; Ren, B.; Hursthouse, A.S.; Wang, Z.; Luo, X. Simulation of Manganese Transport in Groundwater Using Visual MODFLOW: A Case Study from Xiangtan Manganese Ore Area in Central China. Pol. J. Environ. Stud. 2020, 30, 1409–1420. [Google Scholar] [CrossRef] [PubMed]
- Potyondy, D.O. The bonded-particle model as a tool for rock mechanics research and application: Current trends and future directions. Geosyst. Eng. 2015, 18, 1–28. [Google Scholar] [CrossRef]
- Cundall, P.A. A computer model for simulating progressive, large-scale movement in blocky rock system. In Proceedings of the International Symposium on Rock Mechanics, Nancy, France, 4–6 October 1971. [Google Scholar]
- Cundall, P.A. Formulation of a three-dimensional distinct element model—Part I. A scheme to detect and represent contacts in a system composed of many polyhedral blocks. Int. J. Rock Mech. Mining Sci. Geomech. Abstr. 1988, 25, 107–116. [Google Scholar]
- Hart, R.; Cundall, P.A.; Lemos, J. Formulation of a three-dimensional distinct element model—Part II. Mechanical calculations for motion and interaction of a system composed of many polyhedral blocks. Int. J. Rock Mech. Mining Sci. Geomech. Abstr. 1988, 25, 117–125. [Google Scholar]
- Itasca Consulting Group, Inc. Universal Distinct Element Code, Version 5.0; Itasca Consulting Group, Inc.: Minneapolis, MN, USA, 2011. [Google Scholar]
- Liu, S.; Liu, H.; Liu, H.; Xia, Z.; Zhao, Y.; Zhai, J. Numerical simulation of mesomechanical properties of limestone containing dissolved hole and persistent joint. Theor. Appl. Fract. Mech. 2022, 122, 103572. [Google Scholar] [CrossRef]
- Ríos-Bayona, F.; Johansson, F.; Mas-Ivars, D.; Sánchez-Juncal, A.; Bolin, A. Using PFC2D to simulate the shear behaviour of joints in hard crystalline rock. Bull. Eng. Geol. Environ. 2022, 81, 1–19. [Google Scholar] [CrossRef]
- Li, B.; Gong, W.; Tang, H.; Zou, Z.; Bowa, V.M.; Juang, C.H. Probabilistic analysis of a discrete element modelling of the runout behavior of the Jiweishan landslide. Int. J. Numer. Anal. Methods Geomech. 2021, 45, 1120–1138. [Google Scholar] [CrossRef]
- Yin, Z.; Li, R.; Lin, H.; Chen, Y.; Wang, Y.; Zhao, Y. Analysis of Influencing Factors of Cementitious Material Properties of Lead–Zinc Tailings Based on Orthogonal Tests. Materials 2023, 16, 361. [Google Scholar] [CrossRef]
- Zhang, N.-C.; Zhang, N.; Esterle, J.; Kan, J.-G.; Zhao, Y.-M.; Xue, F. Optimization of gateroad layout under a remnant chain pillar in longwall undermining based on pressure bulb theory. Int. J. Mining Reclam. Environ. 2016, 30, 128–144. [Google Scholar] [CrossRef]
- Liu, S.; Nie, Y.; Hu, W.; Ashiru, M.; Li, Z.; Zuo, J. The Influence of Mixing Degree between Coarse and Fine Particles on the Strength of Offshore and Coast Foundations. Sustainability 2022, 14, 9177. [Google Scholar] [CrossRef]
- Wu, H.; Jia, Q.; Wang, W.; Zhang, N.; Zhao, Y. Experimental Test on Nonuniform Deformation in the Tilted Strata of a Deep Coal Mine. Sustainability 2021, 13, 13280. [Google Scholar] [CrossRef]
- Lu, Y.; Liu, Y.; Shi, S.; Wang, G.G.; Li, H.; Wang, T. Micro-particles stabilized aqueous foam for coal spontaneous combustion control and its flow characteristics. Process Saf. Environ. Prot. 2020, 139, 262–272. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, C.; Wang, Y.; Lin, H. Shear-related roughness classification and strength model of natural rock joint based on fuzzy comprehensive evaluation. Int. J. Rock Mech. Min. Sci. 2021, 137, 104550. [Google Scholar] [CrossRef]
- Chen, W.; Wan, W.; Zhao, Y.; Peng, W. Experimental Study of the Crack Predominance of Rock-Like Material Containing Parallel Double Fissures under Uniaxial Compression. Sustainability 2020, 12, 5188. [Google Scholar] [CrossRef]
- Zhao, Y.; Tang, J.; Chen, Y.; Zhang, L.; Wang, W.; Wan, W.; Liao, J. Hydromechanical coupling tests for mechanical and permeability characteristics of fractured limestone in complete stress–strain process. Environ. Earth Sci. 2017, 76, 1–18. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, Q.; Zhang, C.; Liao, J.; Lin, H.; Wang, Y. Coupled seepage-damage effect in fractured rock masses: Model development and a case study. Int. J. Rock Mech. Min. Sci. 2021, 144, 104822. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, Y.; Tan, T.; Zhang, L.; Zhu, S.; Xu, F. Evolution and modeling of mine water inflow and hazard characteristics in southern coalfields of China: A case of Meitanba mine. Int. J. Min. Sci. Technol. 2022, 32, 513–524. [Google Scholar] [CrossRef]
- Peng, Y.; Liu, G.; Wu, L.; Zuo, Q.; Liu, Y.; Zhang, C. Comparative study on tunnel blast-induced vibration for the underground cavern group. Environ. Earth Sci. 2021, 80, 1–13. [Google Scholar] [CrossRef]
- Tang, H.; Yong, R.; Ez Eldin, M.A.M. Stability analysis of stratified rock slopes with spatially variable strength parameters: The case of Qianjiangping landslide. Bull. Eng. Geol. Environ. 2017, 76, 839–853. [Google Scholar] [CrossRef]
- Xia, G.Q.; Liu, C.; Xu, C.; Le, T.C.; Foong, L. Dynamic Analysis of the High-Speed and Long-Runout Landslide Movement Process Based on the Discrete Element Method: A Case Study of the Shuicheng Landslide in Guizhou, China. Adv. Civ. Eng. 2021, 2021, 1–16. [Google Scholar] [CrossRef]
- Wang, F.; Sassa, K. Landslide simulation by a geotechnical model combined with a model for apparent friction change. Phys. Chem. Earth, Parts A/B/C 2010, 35, 149–161. [Google Scholar] [CrossRef]
- Tang, C.-L.; Hu, J.-C.; Lin, M.-L.; Angelier, J.; Lu, C.-Y.; Chan, Y.-C.; Chu, H.-T. The Tsaoling landslide triggered by the Chi-Chi earthquake, Taiwan: Insights from a discrete element simulation. Eng. Geol. 2009, 106, 1–19. [Google Scholar] [CrossRef]









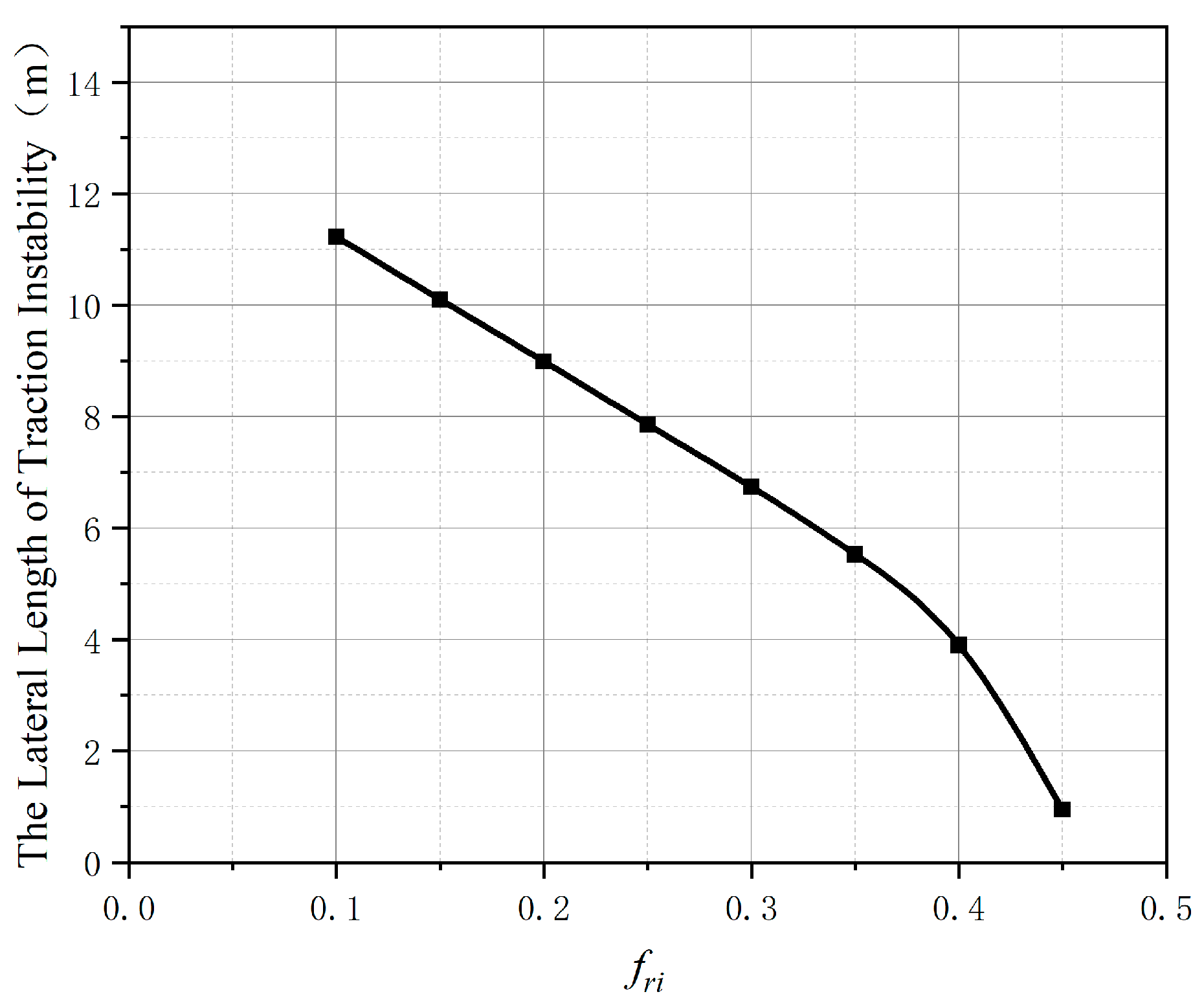
| Simulation Parameters | Numerical Value |
|---|---|
| Normal stiffness | 2.28 |
| Linear method deform friction angle (°) | 21 |
| Linear method deform tensile strength (MP) | 3.0 |
| Linear method deform adhesion (MP) | 3.0 |
| Particle density (kg/m3) | 2600 |
| Simulation Parameters | Numerical Value |
|---|---|
| Normal stiffness | 2.0 |
| Linear method deform friction angle (°) | 21 |
| Linear method deform tensile strength (MP) | 2.48 |
| Linear method deform adhesion (MP) | 2.4 |
| Particle density (kg/m3) | 2600 |
| Simulation Parameters | Numerical Value |
|---|---|
| Normal stiffness | 2.0 |
| Linear method deform friction angle (°) | 21 |
| Linear method deform tensile strength (MP) | 35 |
| Linear method deform adhesion (MP) | 35 |
| Particle density (kg/m3) | 2600 |
| Simulation Parameters | Numerical Value |
|---|---|
| Normal stiffness | 1.52 |
| Linear method deform friction angle (°) | 21 |
| Linear method deform tensile strength (MP) | 54 |
| Linear method deform adhesion (MP) | 54 |
| Particle density (kg/m3) | 2600 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; Xie, L.; Tang, Y.; Chen, Y.; Hu, H.; Lu, G.; Chen, C.; Lin, H. Progressive Formation of Retrogressive Landslide and the Lateral Length of Instability. Appl. Sci. 2023, 13, 799. https://doi.org/10.3390/app13020799
Zhu X, Xie L, Tang Y, Chen Y, Hu H, Lu G, Chen C, Lin H. Progressive Formation of Retrogressive Landslide and the Lateral Length of Instability. Applied Sciences. 2023; 13(2):799. https://doi.org/10.3390/app13020799
Chicago/Turabian StyleZhu, Xiongpeng, Linglin Xie, Yi Tang, Yifan Chen, Huihua Hu, Guangyin Lu, Changfu Chen, and Hang Lin. 2023. "Progressive Formation of Retrogressive Landslide and the Lateral Length of Instability" Applied Sciences 13, no. 2: 799. https://doi.org/10.3390/app13020799
APA StyleZhu, X., Xie, L., Tang, Y., Chen, Y., Hu, H., Lu, G., Chen, C., & Lin, H. (2023). Progressive Formation of Retrogressive Landslide and the Lateral Length of Instability. Applied Sciences, 13(2), 799. https://doi.org/10.3390/app13020799








