Abstract
This paper addresses the problem of time difference of arrival (TDOA) based passive target localizationand proposes an improved chaos-driven hybrid differential evolution (DE) algorithm and butterfly optimization algorithm (BOA), named ICDEBOA, to solve this complex optimization problem. The proposed algorithm consists of a new mutation strategy with the mechanisms of the BOA algorithm incorporated into the DE algorithm. To boost optimization effectiveness, chaos theory is employed to adjust the control parameter values. The considered localization problem is formulated using the maximum likelihood estimator. To perform the accuracy comparison, the convex constrained weighting least squares algorithm is applied to the considered localization problem as the widely used method in literature. The statistical analysis shows that the proposed modifications to the ICDEBOA algorithm improve its optimization performance, as demonstrated by the improved performance on the CEC2014 benchmark problems. The ICDEBOA algorithm is also shown to be more robust than existing algorithms in noisy environments. Numerical simulation results show that the proposed ICDEBOA algorithm meets the CRLB and achieves better performance than the CWLS, DE, and BOA algorithms.
1. Introduction
Accurate localization based on difference of arrival (TDOA) data collected from a single receiver and a set of transmitters is essential for many wireless sensor network (WSN) applications [1,2]. The majority of localization technologies that have been developed and are widely in usage, such as the global positioning system (GPS) [3], ultrasonic-based systems [4], infrared-based systems [5], and RF-based systems [6], require the attachment of an additional device with its own power source to localize the target. Systems such as these are known as “active localization systems,” since the target directly obtains the range measurements, thus being directly involved in localization. Recent research focuses on device-free passive localization, in which the target to be located does not need to be equipped with additional devices or take any active part in the localization process and simply reflects the signals coming from the transmitters [7]. In practice, the GPS, as a prominent active system, shows significant drawbacks, such as excessive power consumption and poor localization performance in cases with weak satellite signals such us indoor areas [3]. Passive target localization has become one of the most popular techniques used to locate the passive targets in a variety of applications, including emergency rescue, intelligent transportation systems, radar, and mobile phone localization, due to its effectiveness as a replacement for GPS and other traditional positioning systems [8,9]. The vast majority of TDOA-based localization techniques in the literature are classified as “active systems”. In this paper, we outline the development of a device-free passive target localization system for real-world environments based on TDOA measurements, along with the appropriate design of a metaheuristic hybrid algorithm to obtain a solution to the considered problem.
Therefore, this work considers the passive target localization model, where the positioning is performed based on TDOA measurements under the noisy conditions. The TDOA measurements are produced by subtracting the required time propagation of a signal emitted from the transmitter over the target reflected to a receiver from the direct signal propagation time captured at the receiver. Due to a nonlinear connection between the measured distances and the target’s true location, estimating the target’s unknown position is a difficult process. A reasonable assumption for the error distribution of TDOA measurements when modelling the considered passive target localization problem in a line of sight (LOS) environment is to model the measurement error as Gaussian-distributed random variables [2]. A number of estimation techniques, including nonlinear least squares (NLS) [10] and maximum likelihood (ML) [11] estimators, that do not have a closed form solution, are used in literature to tackle localization problems. With the linear least squares (LLS) and weighed linear least squares (WLS) methods, the NLS method’s nonlinear objective function can be made linear, thus providing a closed-form solution [12]. The constrained weighted least squares (CWLS) approach is introduced to provide a solution, in closed form, that has higher quality [13]. In this regard, the relationship between the target location and an auxiliary variable is introduced into the CWLS optimization problem as the equality constraint that has the highest term of the second order.
The ML estimator is another widely used estimation method that can improve estimation accuracy. When the statistical information regarding the distribution of the error in measurements is identified, the ML estimator method is straightforward to apply [11]. Due to the pronounced nonentities and complex landscape of the ML objective function, it is difficult to obtain a global optimum solution. In order to solve this type of optimization problem, various efficient optimization algorithms have been suggested in the literature. The semidefinite programming (SDP), which transforms the multimodal optimization problem into a convex one by applying the corresponding relaxations, is commonly used [2]. It has been demonstrated, however, that the SDP approach has some drawbacks that impact the accuracy of the global optimal solution, particularly when the measurement noise level is high [14]. In this context, obtaining a high precision solution that represents global optimum to the nonlinear, non-convex ML objective function has become a formidable obstacle.
This paper presents evolutionary algorithms (EAs) as a way to overcome these limitations while searching for the global optimum solution of a multimodal and complex target estimation problem [15,16,17]. In the development of the EAs, the exploration and exploitation phases have a crucial impact on the obtained solutions [18]. EAs perform exploration in searching for a promising location of the global optimum, whereas exploitation is performed when looking to improve the obtained global best solution. Therefore, to achieve a promising solution, the optimization algorithm must provide an effective balance between these two phases.
Various metaheuristic algorithms, such as the genetic algorithm (GA) [19], particle swarm optimization (PSO) [20], butterfly optimization algorithm (BOA) [21], differential evolutionary (DE) [22], cuckoo search algorithm (CS) [23], artificial bee colony (ABC) [24], gray wolf optimizer (GWO) [25], whale optimization algorithm (WOA) [26], and firefly algorithm (FA) [27], have been developed and applied to various optimization problems using key characteristics of these biological systems. BOA and DE algorithms have been successfully used in recent years to identify the global optimal solution to a variety of complex optimization problems due to their advantages such as ease of development and fast convergence [28,29,30].
Differential evolution is a stochastic population-based evolutionary algorithm that employs the recombination approach, which creates new solutions depending upon the weighted difference between two randomly selected population members added to a third population member to direct the search in the solution space. Storn and Price [22] first proposed this method for minimizing nonlinear functions that are not differentiable. Since then, DE has proven to be highly effective in a wide range of scientific optimization problems thanks to its ability to prevent premature and encourage rapid convergence as well as guarantee population diversity [16,31]. Like other EAs, it employs a population of candidate solutions and searches stochastically by applying mutation, crossover, and selection operators to guide the population toward the promising solutions. The simplicity of conventional DE lies in the fact that the crossover rate, scale factor, and population size are the only three control parameters that need to be adjusted. The mutation technique and the selection of the control parameters have a significant impact on the efficiency with which DE solves a given optimization problem [28]. In certain optimization situations, DE is prone to converge prematurely to local optima and exhibits poor convergence late in the search process, motivating researchers to develop new enhanced variants of the DE algorithm to improve the optimization performance of the DE to overcome these challenges [32,33]. There are a variety of mutation strategies in the literature. This is because the choice of mutation strategy has a strong effect on how well an optimization problem is solved. In this way, DE/rand/1 and DE/rand/2 are better for exploration, whereas the DE/current-to-best/1 and DE/current-to-best/2 are better for local searches because they focus on the best candidate in the current population [28]. To boost optimization effectiveness, a new DE algorithm, JADE [33], has been proposed, with a new mutation strategy, “DE/current-to-p best” as an extension to the traditional “DE/current-to-best/1”, along with an optional external archive. Parameter adaptation eliminates the need for experts to be aware of the specifics of optimization problems by automatically updating the control parameters to suitable values. Results from simulations demonstrate that JADE is superior to both traditional DE algorithms and adaptive variants. Built upon the JADE, the researchers developed a parameter adaptive DE algorithm (SHADE) that stores the parameters used in previous successful evolution rounds [34]. jDE (self-adaptive tuning parameters) is another well-known variant of DE algorithm that has shown acceptable performance on benchmark problems, which uses an evolution process to fine tune the optimization algorithm parameters [35].
BOA is a novel optimization technique that is based on the foraging and mating behaviour of butterflies [21]. As they search for food, butterflies emit a fragrance, the intensity of which is proportional to the abundance of food sources. Other butterflies in the swarm can detect the strength of the fragrance released by other butterflies to estimate the likely location of a food supply or mate. Therefore, the BOA algorithm imitates feeding and mating habits of biological butterflies, assuming that a butterfly would produce a fragrance of varying strength, which is associated with the butterfly’s objective function value. The fragrance will propagate over a distance, and other butterflies can sense it. This is how the butterflies can share their personal information with other butterflies and form a collective social knowledge network. Due to its simplicity and effectiveness, BOA has been suggested to solve a variety of engineering applications, from WSN sensor localization [29], engineering design problems [36], and neural network training [30], etc. Despite the fact that the BOA has shown better performance in real-world applications compared to other meta-heuristic algorithms, it also faces many challenging issues. For instance, the basic BOA is easy to fall into the local optimum when solving highly complex problems, and the convergence speed will reduce greatly in the late iteration process [37]. Therefore, many improved variants of BOA have been suggested to overcome the two aspects [36,38].
In order to further improve the optimization performance on complex optimization problems, researchers resorted to hybridizing two or more algorithms, thus creating one new algorithm that exploits the complementary strengths of each method. Some examples of the combination of two meta-heuristic algorithms include: the HFPSO [39] algorithm, where the FA and PSO algorithms are hybridized with the aim of increasing accuracy and improving convergence; a DE/WOA [26] hybrid algorithm, which combines local search abilities of WOA with DE global search; HPSOBOA [40], which combines BOA and PSO algorithms; etc. In a recent study, it was proposed to combine the butterfly optimization algorithm (BOA) and differential evolution (DE), named HBODEA [41], in order to more effectively utilise each method’s advantages. Two enhancements—mutation and crossover operations of DE and dynamic adaptive operators—are added to the original BOA in the proposed identification strategy to increase global search capability and decrease the risk of being trapped in a local optimum. However, this hybridization left a lot of different improvements and variations to be performed. As a result, all of these papers demonstrate that the hybridization of EAs speeds up the process of achieving the best solution, prevents the issue of premature convergence, and yields better answers.
Numerous applications of nonlinear dynamics, especially those incorporating chaos, have gained prominence as a consequence of the development of nonlinear dynamics and are now commonly employed to enhance the effectiveness of various optimization techniques [42]. The infinitely unstable periodic motions that characterise the bounded dynamic behaviour of non-linear systems is characterised as chaos [43]. One of the most effective methods for improving the performance of metaheuristic algorithms is to use chaos maps, which generate bounded random numbers based on initial conditions. In the literature, there are various chaos maps, such as the piecewise map, iterative map, logistic map, sine map, Tent map, and so on [44]. Chaos has been used in the self-adaptive chaos differential evolution (SACDE) [45], where the mutation factor is controlled using chaos maps and dynamically changing weighting factors and crossover factors are also introduced. Recently, a new hybrid optimization method based on differential evolution (DE) and chaos theory was made [46]. This method uses chaotic sequences to change DE parameters automatically in order to help the algorithm to escape local minimums and improve global convergence. For the purpose of tackling three engineering optimization problems, Arora and Singh [36] suggested an enhanced butterfly optimization technique with several chaotic maps. Here, three chaotic BOA algorithms were created. The first one used chaos maps to generate initial solutions, the second used chaos to control switch probability p, and the third was a combination of the previous two. The results showed that BOA modified with chaotic maps shows improved performance in terms of avoiding local optima and accelerating convergence. To prove that the suggested chaotic BOA is correct, engineering design issues, benchmark test functions, and both multimodal and unimodal benchmarks are used. As a result, the pseudo-randomness, ergodicity, and irregularity of chaos maps make them an ideal addition to EAs, helping to boost the efficiency of optimization and the quality of the solutions they provide [36,47].
Motivated by the above considerations, we recognise the importance of passive localization, especially in the indoor environment, where the traditional techniques cannot be applied with the required accuracy. By also looking at the above strengths and weaknesses of the BOA and DE algorithms, we can see that the DE algorithm has a good ability to explore, which depends on the mutation scheme chosen, and that the BOA algorithm has a good ability to search locally. Therefore, in this study, we suggest ICDEBOA, a hybridization between BOA and DE, to effectively tackle the passive target localization problem. In the suggested approach, we add a new composite roulette wheel-based mutation operator into the DE algorithm. To take advantage of the BOA algorithm’s good local search ability, a hybrid algorithm is created by using BOA expressions for particle movement to produce a mutant vector in the DE algorithm. Furthermore, an adaptive technique incorporating chaos map is used to update the BOA algorithm’s sensory fragrance.
In the context of range-based target localization, the CRLB is usually utilised to access the statistical performance of various localization algorithms. As a result, determining CRLB as an optimality criterion for the considered localization problem is a critical issue [48]. In this aspect, the CRLB establishes the physical impossibility of an unbiased estimator’s variance being less than the given bound. Consequently, in this research, we define the CRLB for the investigated localization problem and use it to evaluate the root-mean-square error (RMSE) of the presented ICDEBOA technique and compare against that of several other widely used methods.
Given the aforementioned information, the primary goals of this work were as follows:
- To formulate a new problem of localization of a passive target using the obtained TDOA measurements.
- To present a new global optimization method that is a hybridization of BOA and DE algorithms, named ICDEBOA, so that the passive target localization problem can be solved successfully.
- To validate the proposed algorithm’s performance on benchmark test functions by comparing simulation results to a number of state-of-the-art methods.
- To show how well the proposed method works by comparing simulation results on an example localization system to well-known approaches and derived CRLB.
The remaining sections of the paper are structured as follows. In Section 2, relevant work on localization and the application of evolutionary algorithms to localization problems is presented. In Section 3, the general localization problem of a passive target using TODA measurements is formulated. In Section 4, the derivation of the appropriate ML estimator for the considered localization problem is presented. In Section 5, the formulation of the CWLS is outlined. Section 6 describes differential evolution algorithm with the employed improvements. The procedure of the BOA algorithm along with the improvements is given in Section 7. The derivation of ICDEBOA is proposed in Section 8. Section 9 describes the CRLB in the context of the considered localization. In Section 10, numerical experiment results are presented. In Section 11, conclusions and future work are stated. The detailed derivation of CRLB for passive TDOA-based localization is presented in Appendix A, while the detiled derivation of CWLS is provided in Appendix B.
2. Background and Related Work
Finding a passive target has gained interest in recent years due to its wide applications, especially in indoor positioning and defensive systems where GPS signals are unavailable [3]. In general, solutions for indoor localization fall into two categories: range-based and range-free. Lateration, such as trilateration and multilateration, is the most widely employed range-based localization approach. Here, the range is defined as the distance between the target and the receivers. It can be derived from multiple signal parameters, including time of arrival (TOA) [49], TODA, received signal strength (RSS) [50], angle of arrival (AOA) [51], or a combination of these parameters [52]. It has been demonstrated that the TDOA parameter delivers more accurate and straightforward localization compared to localization techniques based on other parameters [13]. As an alternative to range-based localization techniques for indoor environments, range-free localization techniques such as the Distance Vector Hop (DV-Hop) [53], centroid or weighted centroid approach [54], and approximation point-in-triangulation test (APIT) [55] are extensively utilised. These technologies are both affordable and easy to apply since they do not necessitate complicated equipment structure. However, the range-based localization methods for indoor positioning are more accurate compared to range-free methods [56].
The formulated passive target localization problem using TDOA measurements is a nontrivial task due to its high nonlinearity and nonconvexity. In order to solve such complex localization problems, in the literature, the most widely used methods include the NLS [10] and ML [11] estimators. The NLS estimator is based on finding the extremum of the objective function, which is formulated as the sum of the squared measurement errors. However, when solving the NLS estimator with conventional gradient based methods, it can be shown to have some convergence issues, and there is a need for a promising intial solution. LLS methods are often used to linearize the NLS estimation problem so that it can be solved in closed form [12]. However, it has been shown that the CRLB can only be reached with LLS methods when the measurement errors are small enough. To improve the accuracy and provide a closed-form solution to the localization problem, a two-step weighted least-squares (2WLS) method is put forward to approximate the NLS function [12]. The two-step WLS method rearranges the nonlinear TDOA equations into a set of linear equations by introducing an auxiliary variable [57]. In the first step, it estimates the source position and auxiliary variable independently, and then in the second step it refines the estimate by considering their connection. To further improve the accuracy and avoid ill-matrix problems, the CWLS method is proposed, which explicitly incorporates the relationship between the source position and the auxiliary variable as a constraint [58]. In this way, the CWLS method formulates the quadratically constrained quadratic problem (QCQP), which is a non-convex problem. However, it can be converted to a convex problem by exploiting the hidden convexity in the constraint.
Another widely applied estimator is the ML estimator, which has been regarded as an optimal method for target estimation [11]. However, the formulation of the ML target localization problem using TDOA measurements is a non-convex optimization problem. To address this issue, a SDP method is proposed, which relaxes the non-convex ML optimization to a convex SDP problem [59]. However, as shown in the literature, the performance of the SDP method is not satisfactory in the presence of a large measurement error. In the literature, evolutionary algorithms (EAs) are used to deal with the fact that the ML estimation problem is not convex. This is because EAs can find the best global solution to such problems.
Different kinds of EAs, including FA, PSO, and BOA, etc., have been successfully utilized during the last few years in solving different localization problems [29]. Since the performance of a wireless sensor network is significantly impacted by the accuracy of the sensor node localization, Arora and Singh [29] proposed the BOA method, a nature-inspired optimization algorithm, to reduce localization errors when calculating the position of sensor nodes in WSNs. In comparison to the PSO and FA based node localization systems, the proposed method demonstrates more consistent and precise node positioning resuls. Researchers suggested using PSO and TDOA combined, which significantly improves positioning accuracy [60]. Comparisons with established methods like WLS and LLS demonstrate that PSO is superior. In addition, the ML estimator is utilised to create the objective function for the hybrid TDOA/AOA location estimation issue, and the PSO improved with chaos is offered as a solution [15]. Comparative investigation demonstrates that the upgraded PSO algorithm outperforms the traditional optimization algorithms in terms of global search capability. To improve localization accuracy in WSNs while using fewer power and resources, researchers presented a two-stage PSO algorithm for locating wireless sensor nodes in concave space [61]. The authors proposed employing a TDOA passive positioning sensor selection approach based on the tabu search to balance the positioning accuracy of the sensor network and system utilization [62]. Consideration is given to the passive TDOA model, with sensor position errors taken into consideration, and the tabu search method is used to solve the transformed sensor selection problem. Simulation findings demonstrate that the performance of the suggested sensor optimization approach closely resembles that of the exhaustive search. A genetic algorithm with the flexibility to be modified for varied circumstances and ground models is proposed to select the appropriate node localization in order to decrease the CRLB in each sensor of an asynchronous TDOA architecture [63]. The proposed methodology allows for the optimization of a passive A-TDOA architecture’s 3D sensor deployment, including ground modeling flexibility and the reduction of spatial discretization to achieve better results, which is critical for precision applications and indoor and outdoor navigation of automatic vehicles such as automatic ground vehicles and unmanned aerial vehicles.
It has been established that combining two or more EAs can improve solution quality and boost optimization performance. Combining the WLS and FA algorithms, the Hybrid Firefly Algorithm (hybrid-FA) is proposed for estimating target coordinates from TDOA data [27]. According to the simulation findings, the hybrid-FA approach provides better performance and localization accuracy than the state-of-the-art localization approaches. Furthermore, the improved DE algorithm has been successfully hybridised with the FA method and deployed to address the passive target localization problem utilising TOA measurements [16]. The results reveal that the proposed method outperforms the standard algorithms in terms of localization performance. GA is hybrdized with the DE algorithm in order to improve the perofrmance in the WSN localization problem [64]. In addition, combining the DE algorithm with the standard direct search Nelder-Mead approach yielded higher quality solutions for an objective function defined using the ML method [65]. Moreover, a number of hybrid EA variants, such as DE and FA (HFDLA) [66], HPSOVNS [67], and PSO and variable neighbourhood search (HPSOVNS), are used successfully to improve positioning accuracy.
The techniques for passive localization have found a wide range of applications in recent years due to their ability to accurately locate a target without relying on active sensors or emitting radio signals. Based on TDOA data, the authors provided an experimental evaluation of multipath mitigation in two distinct interior settings utilizing a beam steering broadband circular polarization antenna (BSBCPA) in an indoor passive localization system [68]. Experiments are proposed using LOS and complicated multipath while delivering a signal with a 20 MHz bandwidth via WLAN. Compared to traditional omnidirectional linear polarization antennas, they discovered that the BSBCPA can enhance positioning accuracy by at least 51%. The experimental findings demonstrate that the proposed BSBCPA mitigates multipath propagation for TDOA-based indoor passive localization in a considerable manner. Passive localization found application during the launch mission of a launch vehicle. Using ground-based telemetry stations increases the reliability of the launch vehicle’s flight safety control system [69]. The authors applied passive TDOA/AOA localization utilizing two ground telemetry stations and developed a strategy to increase the accuracy of its localization based on second-order polynomial regression. By comparing the findings of the suggested approach to the measured data from an on-board GPS utilized during the third flight of the Korea Space Launch Vehicle-1, the localization accuracy has been enhanced. For security applications, the authors presented a passive localization method based on TOA measurements on the most recent 802.11ac WiFi standard, taking advantage of the widespread deployment of WiFi systems, which typically use RSS parameters for localization [70]. Using the experimental setting, a prototype was created that demonstrated a considerable improvement in positioning accuracy over previous methods. Furthermore, by leveraging the WiFi standard, the authors propose a passive localization tracking system to predict the footprints of suspects. Using ultra-wideband radio signals is widely used for the implementation of passive localization systems. For the passive localization of fixed targets based on the hybrid RSS/TDoA method, the authors presented an algorithm for the optimal estimation of the amplitude and propagation delay time of an ultra-wideband radio signal [71]. An algorithm has been developed for the optimal estimation of distances from the radiation source to base stations, based on the results of the measurements of the amplitude and the propagation delay time of the UWB radio signal. Localization in crowded urban areas is another intriguing application area. Here, sensors are carried by flying unmanned aerial vehicles to precisely locate the signal source passively, making it possible to establish a wireless sensor network with the ideal geometry configuration [72]. According to the min-max criterion, the authors presented a condensed formulation of the TDOA localization method. The nonlinear equations are relaxed using semidefinite programming to produce an initial solution, which is then used as the starting point of the iterative algorithm to refine the solution in order to determine the source’s location with accuracy.
Based on the previous, this paper proposes an enhanced ICDEBOA method as the hybridization of two well-proven EAs, with the aim of improving the accuracy of estimating passive target location based on solving an ML objective function formulated using TDOA measurements, particularly when measurement noise is high.
3. Localization Problem
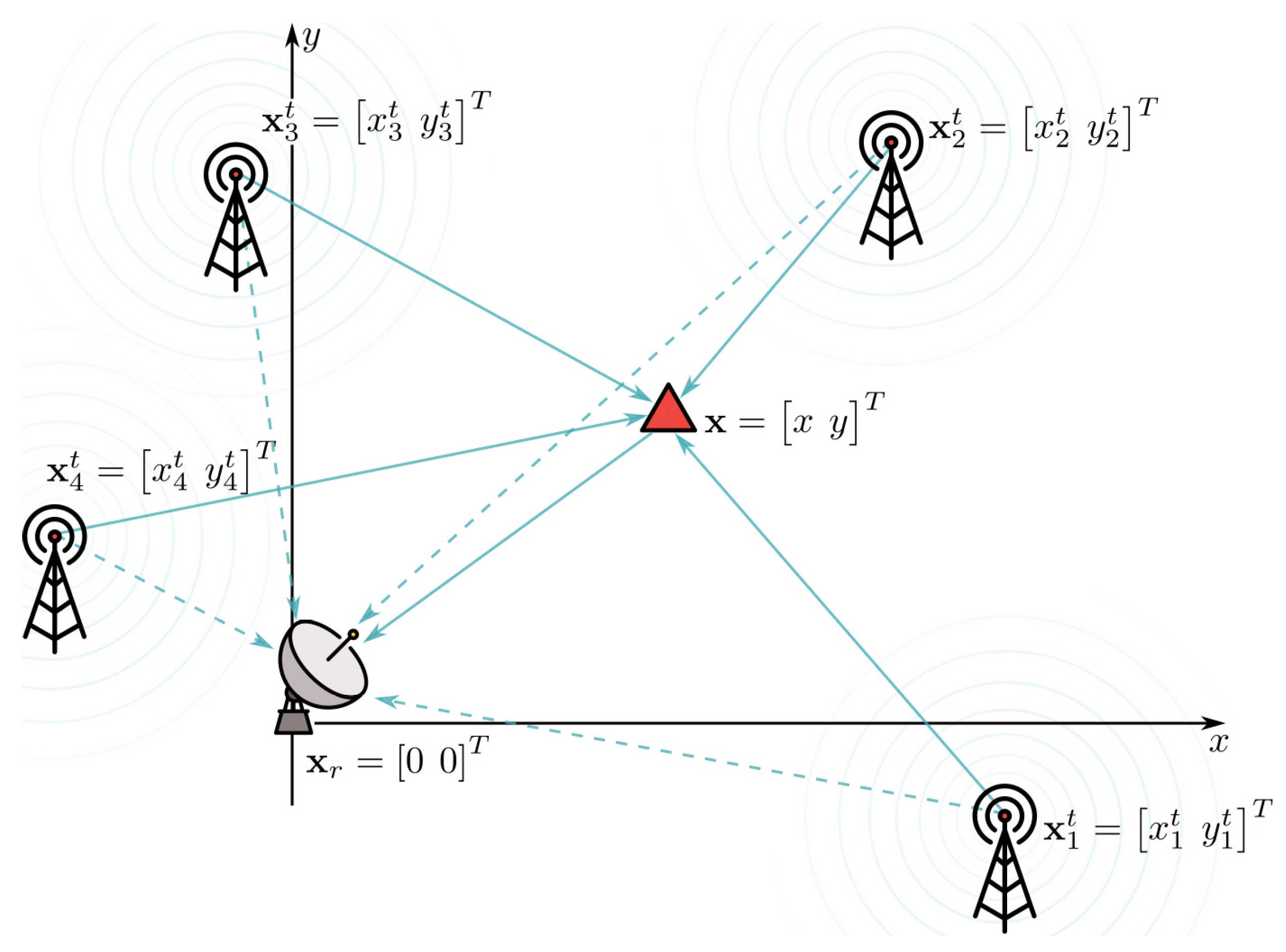
The proposed passive target localization problem uses TDOA signal parameter to estimate the passive target’s unknown position under the conditions of LOS environment. Figure 1 illustrates the considered localization system, which consists of a set of transmitters , whose positions are previously known and the passive target at the unknown coordinates x and y. The target is illuminated by the signals coming from the transmitters, which is then reflected from the target and captured at the receiver, which is, without the loss of generality, placed in the origin .
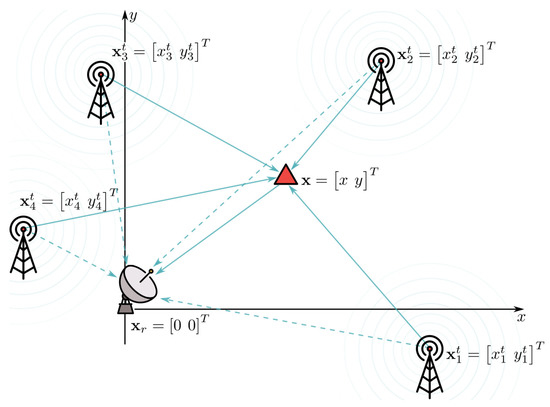
Figure 1.
Illustration of the plaement of transmitters, receiver and a target and a distribution of signals in a considered localization problem.
Here, we model TDOA measurement error using the Gaussian distribution, which in a LOS context, is a justified proposition [2]. Assuming the time synchronisation of and is obtained and that the passive target simply reflects signals back and forth between and [48], the noisy TDOA measurements are obtained as the signal time difference
where denotes the TOA of a signal which is reflected from the target coming from the ith transmitter and captured at the receiver, and is the TOA of a signal which is directly coming from the ith transmitter to a receiver. Then, by substituting the coordinates of receiver, transmitters and target the TDOA measurement is represented as
where denotes the two-dimensional Euclidean distance, c denotes propagation speed of light, and is the Gaussian modelled measurement noise. Eliminating the term c, the range measurement of the signal coming from ith transmitter is obtained
where is Gaussian zero-mean distributed variable. Since the distance between each of the transmitters and receiver is previously known, we introduce a new variable to rearrange a range measurement as follows
Therefore, the Equation (3) can be rewritten as
Which is represented in the corresponding vector form
in which
and is the measurement noise vector, under assumption that each component of a vector is independent and an identically distributed zero-mean Gaussian variable. The denotes the appropriate matrix of covariance, whose elements can be calculated using the expectation operator as . Taking into consideration that the measurement noise is the zero-mean Gaussian variable, it can be simplified to [48].
This paper aims to accurately predict the passive target’s location, which is unknown, using TDOA parameters under the presence of noise. This is achieved solving the ML estimation problem, which is in general nonlinear and has multiple optima, which is outlined in the following section.
4. Formulation of Maximum Likelihood Estimator
To estimate the position of a passive target the Maximum Likelihood estimator is employed, since the probability density functions of measurement errors are known. A zero-mean Gaussian distribution is assumed for the TDOA measurement errors in the formulation of the localization issue [2]. Therefore, the likelihood function is obtained as
Then, taking the logarithm of the Equation (8), log-likelihood function is yielded
in which is neglected as a constant independent of . As the solution to the minimization problem, we obtain the estimated target position
with objective function of ML estimator
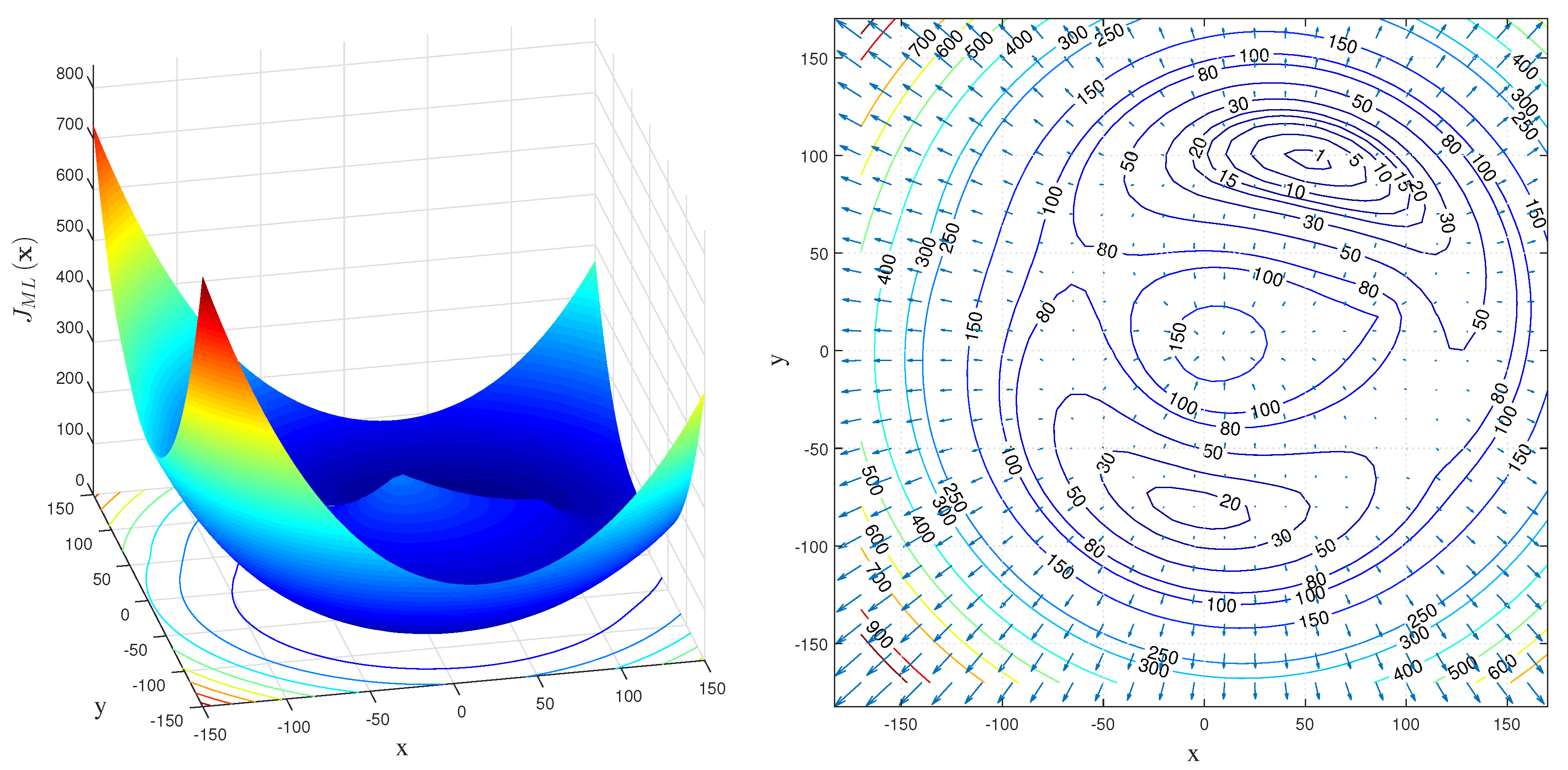
The corresponding objective function of the formulated ML estimation problem is depicted on Figure 2.

Figure 2.
The plot of the considered ML objective function .
Based on an examination of the topology of the function depicted in Figure 2, it is determined that is a multi-modal function with pronounced nonlinearities. Wherever the global minimum of a function occurs is where the target should be located, due to the difficulty of the function, it is important to use advanced algorithms for finding the best possible solution globally.
5. Constrained Weighted Least-Squares
In this section, the CWLS algorithm is developed for the considered passive target localization problem. Therefore, the nonlinear TDOA equations can be transformed into a set of linear equations, by introducing the variable , neglecting and squaring the Equation (5) giving the following expression
The following constrained optimization problem can be used to estimate the coordinates of the target in the presence of measurement errors
where is a matrix of weights that is symetric, is a diagonal and orthonormal matrix. It is possible to approximatively determine the elements of matrix of weights under conditions of sufficiently low measurement noise, as
where
The optimization problem (18) is a quadratically constrained quadratic program (QCQP), which can be solved using the Lagrange multiplier method. Therefore, the Lagrangian function of the optimization problem (18) is given by
where is the Lagrange multiplier. The minimum of Equation (22) is obtained by differentiating with respect to , as follows
Solving the Equation (23) for , the following CWLS solution, denoted by , is obtained
where the value of is unknown, and can be determined as a root of the 4th-order polynomial, which is obtained by substituting Equation (25) into Equation (24) (see Appendix B), given as
where and are given in Appendix B. Then, the procedure based on CWLS method is
- Step 1:
- Initialize elements of matrix of weights as .
- Step 2:
- Using the standard root finding algorithm determine all real-valued roots of the Equation (26).
- Step 3:
- Substitute obtained in previous step into Equation (25), and determine all sub estimates of for which the is minimal.
- Step 4:
- Using the Equation (20) construct the weighting matrix .
- Step 5:
- Repeat steps 2–4 until satisfies the stopping criterion.
6. Differential Evolution Algorithm and Improvements
6.1. Conventional DE
The DE method belongs to group of evolutionary optimization algorithms that are capable of obtaining a global optimum of difficult multimodal optimization problems [22]. Initialization, mutation, crossover, and selection are the four cornerstone operators of the DE algorithm’s optimization procedure. These operators are discussed briefly in the following subsections.
6.1.1. Initialization
The DE algorithm begins its search for the global optimum with a population of candidate solutions that are randomly positioned in the feasible search space. Each member of the population in the Gth generation is vector of components , where denotes the jth component of the ith vector, of nth dimension. For the considered localization problem, the component of each individual in the population is initialized as follows
where denotes a random number generated in the range . Here, and denote the maximum and minimum bounds of the feasible search space for each vector component.
6.1.2. Mutation
The mutation is a crucial operator in the DE algorithm, which promotes the exploration of the search space to locate the region of the global minimum and improves the quality of the solutions. In this regard, for each target vector , the DE algorithm creates the corresponding mutant vector . The vector is usually created as a combination of weighted vector differences between randomly chosen vectors. Numerous mutation techniques have been presented in the literature with the intent of enhancing exploration, exploitation, or both. The most prominent mutation schemes include [73]:
DE/rand/1
DE/rand/2
DE/best/1
DE/best/2
DE/current-to-best/1
where and are mutually distinct integers randomly generated from the set the denotes the individual with the best objective function value in the entire population at the current generation G and F is the scale factor that controls the scaling ratio of the difference vector. It has been shown that besides choosing the appropriate mutation scheme the value of scale factor plays a significant role in the optimization outcome [28].
6.1.3. Crossover
The crossover operator is used in the DE algorithm to promote population diversity. In this operator, the algorithm generates a trial vector component by combining the elements of the target vector and the matching mutant vector , created in the previous step, as follows
where is a uniformly generated random number from the range and is a crossover rate, a parameter controlling the number of components from the mutant vector is injected into the trial vector, and is an integer selected randomly. It has been demonstrated that the number of vector components chosen for crossover varies depending on the stage of the optimization process [74]. Adaptively changing the crossover rate during optimization is, thus, essential.
6.1.4. Selection
Finally, in the selection operator, the DE algorithm determines which vector poses the qualities required to solve the considered optimization problem and is chosen to form a population for the next generation. As the measure of the quality of the solution, the objective function value at the trial vector and matching target vector is employed. Therefore, the individual with the lower objective function value is retained for the next generation according to
where denotes the target vector selected to the next generation.
Repeated iterations of mutation, selection, and crossover are carried out until the maximum number of generations specified by the termination criteria has been reached.
6.2. Improvement of the Differential Evolution Algorithm
SHADE is a powerful variant of the DE algorithm that emerged as an improvement on the well-known JADE algorithm [34]. Therefore, in this study, we suggest using the SHADE method to provide specific control parameters for each population member. In this regard, for each individual the scale factor and crossover rate are produced according to the Cauchy and normal distributions, respectively, as follows
where represents a random number drawn according with the Cauchy distribution whose median is denoted as and the scale parameter is fixed to , and is a random number drawn from the normal distribution with mean value denoted as and standard deviation .
Both and are initialized to . Since the domains of the scale factor and crossover rate in DE algorithm are usually defined as and [73], the in the cases when the values generated according to Equations (35) and (36) are out of bounds the following truncation rules are applied: When scale factor is , we truncate to 1,otherwise in case , is regenerated using Equation (35) and domain is checked again. For the crossover rate check if , and if satisfied truncate to 1, in the case truncate to 0.
The SHADE algorithm has introduced a set where the successful previous versions of generated parameters are stored in order to influence the generation of new values in the next generation. Therefore, the and values which have proven to be successful are stored in the sets and , respectively in each iteration. Then, in the next generation the and parameters are generated according to
where c denotes learning rate, a constant that controls the amount of previous experience taken for new parameter generation, which is set to [34], while and are the weighted Lehmer mean and weighted arithmetic mean, respectively, which are determined as
where the size of the sets and is , and coefficients are determined as
6.3. Mutation Scheme DE/current-to-pbest/1
The popular JADE method includes a mutation operator, DE/current-to-pbest/1, that narrows the search to the top percentile of population members and quickens convergence [33]. This operator is an extended with improved parameter adaption scheme introduced in the SHADE algorithm. This demonstrates the significance of the mutation strategy to the performance of optimization. The following may be stated about the accompanying mutation vector based on the suggested DE/current-to-pbest/1 mutation operator:
where is randomly selected from the top ( ) individuals in the current population with and is generated to Equation (35).
Analysing the Eq., we observe that the search ability of the algorithm is enhanced, particularly in the latter stages of the evolution process, when the mutation vector explores the neighborhood of each in the direction of the solution.
7. Butterfly Optimization Algorithm and Improvements
7.1. Original BOA Algorithm
BOA is a novel metaheuristic optimization technique that was inspired by butterfly foraging and butterfly mating [21]. The BOA algorithm’s algorithmic representation of the biological system is based on three hypotheses:
- All butterflies attract each-other by emitting a scent.
- Their flight is random or aimed to the best butterfly emitting more intense scent.
- Butterfly stimulus strength is determined by the objective function value at the considered butterfly.
There are three stages to BOA algorithm’s optimization process: startup, iteration, and final optimization. In each execution of BOA, the initialization phase is conducted first, followed by iteration, and the algorithm is finished after the optimal solution has been identified in the final optimization phase. The objective function and solution space are specified during the phase of initialization. In this phase, the BOA parameters are initialized, and the method then generates a random initial butterfly population within the upper and lower bounds calculating and storing their fragrance and fitness values. The iteration phase of BOA follows the initialization step and with it is when the optimum solution is found via a series of iterations. During each iteration, the value of the objective function is calculated for each butterfly, and then the butterflies use that value to influence the amount of scent they produce in their current positions
in which a denotes the power exponent chosen as and c is the sensory fragrance in the range , and I is the stimulus intensity. The change in fragrance absorption is governed by the parameter a value. Given two limit scenarios, i.e., when , there is no absorption of scent, i.e., the same amount of fragrance is recognized by all butterflies. Consequently, a fragrant butterfly can be discovered anywhere within the region, and a global solution can be reached. In contrast, when , the scent cannot be sensed by other butterflies, thus impacting the algorithm’s optimization behaviour. The algorithm’s convergence rate can be controlled by the value of the parameter c, which is usually chosen based on the properties of the objective function to be optimized. The values of a and c, have a considerable effect on the algorithm’s convergence rate and optimization performance. The value of the stimulus intensity I depends on the objective function value at the considered butterfly, as follows
where is the objective function value of ith butterfly at Gth generation. In the iteration phase, the BOA evaluates two steps, i.e., global and local search. The butterfly with the highest obj. function value, indicated by , is moved in the step of global search using the formula
where is the randomly selected number. The next step, which deals with the local search, assumes movement of the butterfly in the vicinity of other neighbouring butterflies, as follows
where and denote the appropriate butterflies taken from the solution space.
7.2. Chaos Enhanced BOA Algorithm
Literature shows that the traditional BOA method has high local search ability, but it often prematurely converges to local optima, which degrades optimization efficiency, particularly when dealing with the complicated and multi-modal optimization [37]. Therefore there is a need to modify original BOA and improve optimization performance. This is why some academics have recommended incorporating chaos into BOA in order to boost overall optimization efficiency and avoid the issues in performance [36]. In nonlinear dynamic systems, we can observe a bounded dynamic behavior called chaos, which is described with chaos maps, which generate a limited series of random integers in response to a given starting condition.
By analyzing Equation (43), we see that the butterfly’s ability to detect the scents emitted off by other butterflies is one of the most crucial aspects in BOA, since it directs their flight throughout the search phase. Thus, when solving complex optimization problems, parameter c should not be kept constant during the optimization process. Searching with a small c may cause premature convergence, while a large constant value of c early in the search phase increases the risk of missing the region of global optimum, which affects optimization performance. Therefore, we propose an adaptive mechanism to change value of sensory fragrance c during the optimization process which is based on the use of chaos maps, which can be written in the following form
where represents the chaotic motion produced by chosen chaos map in the Gth generation. The Equation (48) describes a parameter which has the chaotic motion but is upper bounded by the fator .
Numerous distinct chaos maps may be found in literature. The five most popular chaotic maps have been utilised in the current study to change the value of parameter c and to identify which one is most appropriate for the task at hand.
Piecewise map: The Piecewise map is described as
Iterative map: The expression for the Iterative map can be written as
where P is the parameters choosen as .
Logistic map: The Logistic map is written as
Sine map: The expression for Sine map can be written as
where the chaotic motion is achieved for .
Tent map: The Tent map is written acording to the equation
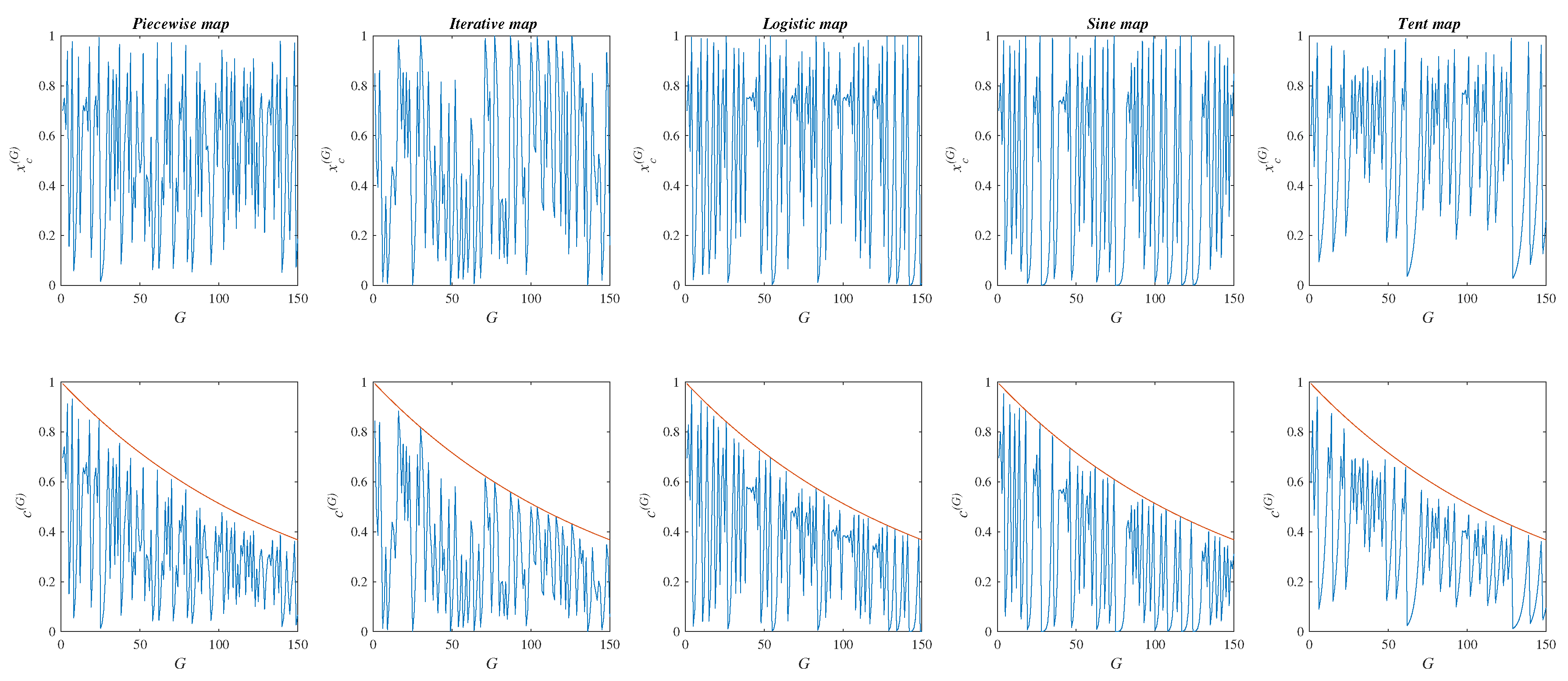
In this respect, Figure 3 illustrates the changes of the employed chaos maps given in Equations (49)–(54), with the increase in generations, and the plot chaos based sensory fragrance from Equation (48) with the employment of each chaos map expression for setting the value of .

Figure 3.
Plot of the employed chaos maps and corresponding chaos based sensory fragrance as a function of generation number.
From the Figure 3, we find that the considered chaos maps generate a number sequence that is both ergodic and irregular, but each considered map has unique properties that are visible on the graph. Moreover, we observe that the exponential factor serves as the top boundary for the chaos-based sensory scent . As a result, at the beginning of the optimization process, the considered chaotic sequences have higher values, and as more generations are added, the value of the resulting sequence of numbers decreases. Higher values at the start of the optimization process are beneficial for encouraging solution space exploration. The lower values at the end of the optimization process, however, are important for the improvement of local search in the later stage of the optimization process.
In order to determine which of the considered chaos maps is best suited to increase the performance of BOA algorithm, in this paper the statistical analysis is applied, which is explained in detail in Section 10.1.1. Based on the results of the Friedman’s test, presented in Table 1 we observe that the introduction of chaos maps into the BOA algorithm leads to an increase in optimization performance compared to conventional BOA. Furthermore, it is concluded that the BOA algorithm enhanced with sine map has achieved the best performance (best rank). Therefore the chaos-based sensory fragrance can be obtained using the following equations:
where a is the parameter which determines the chaotic motion.

Table 1.
Summary of the statistical findings of the Friedman test comparing the performance of the five chaos-improved BOA algorithms and the conventional BOA algorithm.
8. Improved Chaos-Driven Hybrid Differential Evolution and Butterfly Optimization Algorithm
In Section 4, it has been demonstrated that the considered passive target localization problem is a non-convex complex problem, which cannot be solved using conventional algorithms. According to a review of the literature, the DE algorithm often performs well in a global search but poorly in a local search [32]. However, applying these tactics throughout the whole evolution process might result in premature convergence. The authors have suggested utilising DE/best/1, DE/best/2, and more recently DE/current-to-p-best/1 mutation strategies to enhance local search [33]. Conversely, BOA algorithm shows excellent local search ability, however, it often prematurely converges to local optima of complex problems [37]. Therefore, the main idea of this paper is to combine good local search abilities of BOA with excellent global search of DE algorithm. In the proposed ICDEBOA algorithm, this is achieved by introducing the BOA particle movement equations into the mutation strategies of DE algorithm. Furthermore, the improvements of DE and BOA algorithms, outlined in the previous subsections, are introduced into the ICDEBOA algorithm.Therefore, in order to improve the exploration abilities of the proposed ICDEBOA algorithm, in this paper we propose the uses of the following two mutation strategies for exploration:
- DE/rand/1 mutation strategy with adaptive scale factor , which is calculated according to the Equation (35). Therefore the expression for calculating the mutation vector is
- Novel DE/rand-global-BOA/2 mutation strategy, which is produced by introducing the parts of BOA global search step into the DE/rand/2 mutation strategy. Therefore, to achieve this the term in Equation (29) is replaced with the term from Equation (45). Furthermore, the adaptive scale factor given in Equation (35) is introduced instead the conventional scale factor F. Additionally, the sine chaos map-based sensory fragrance is employed in determining the term . Therefore, the DE/rand-global-BOA/2 mutation strategy has the form
Next, the modification is performed in order to perform local search and improve the solution accuracy. The use of the following two mutation operators is proposed
- The usage of DE/best/1 mutation strategy with adaptive scale factor from Equation (35) is proposed, which can be expressed as
- A new DE/best-local-BOA/2, produced by hybridizing the mutation operator DE/best/2 form DE algorithm with the local search step of BOA algorithm given in Equation (46). In this regard, the term from the Equation (31) is replaced with the term from Equation (46). Furthermore, the adaptive scale factor from Equation (35) and sine chaos map-based sensory fragrance from Equation (48) have been introduced, providing the following expression
A lot of research has been proposed, which deals with the introduction of new mutation operators into the DE algorithm. In JADE, authors proposed using the DE/current-to-p-best/1 mutation scheme to improve optimization performance [33]. Moreover, authors proposed using multiple mutation strategies [75]. In this way, the suggested technique presents a novel triangular mutation rule based on the convex combination vector of the triplet created by the three randomly selected vectors and the difference vector between the best and poorest individuals from the three randomly picked vectors. Combining the mutation rule with the standard mutation approach via a non-linear decreasing probability rule, authors proposed using a reflection-based mutation operation inspired by the Nelder–Mead technique and two additional fundamental mutation strategies to preserve population diversity [76]. In order to choose mutation strategies, their probabilities of success for each individual are employed using a roulette wheel selection method. Recently, the authors proposed hybridization between DE and FA algorithms with multiple mutation strategies, where the FA is introduced into the mutation scheme of DE and then randomly applied during the evolution process [16].
In this paper, we proposed using the roulette wheel selection, in order to perform the choice of the mutation operator, which is appropriate to the current optimization stage. Initially, each of the mutation operators are assigned random success rates in the range such that . During the evolution process, the kth mutation operator, which is used to produce mutant vector of the ith individual, is assigned value 1 if the produced mutant vector lead to the improvement in the optimization process, e.g., the success rate is calculated as follows
Then, the total probability of choosing the appropriate mutation scheme is calculated as follows
where denotes the total number of individuals that are assigned the kth mutation operator in the current generation. Therefore, if the value of of kth mutation operator is higher, the probability of choosing that mutation scheme increases.
In this way, the pseudocode of the proposed ICDEBOA algorithm is presented in Algorithm 1, for the considered passive target localization problem.
| Algorithm 1 ICDEBOA algorithm pseudo-code |
Initialize parameters , Generation of initial population of individual Generate sine map for Initialize values of for whiledo Determine the probability of choosing the appropriate mutation scheme Update sensory fragrance using the Equation (55) for do Generate three random integers such that Use roulette wheel to select k switch k do case k = 1 Apply mutation operator in Equation (57) case k = 2 Apply hybrid mutation operator DE/rand-global-BOA/2 in Equation (58) case k = 1 Apply mutation operator in Equation (59) case k = 1 Apply hybrid mutation operator DE/best-local-BOA/2 in Equation (60) end switch Calculate the success rate using Equation (61) Perform crossover Generate random number for do end for Perform selection end for end while |
9. Cramer-Rao Lower Bound
In this section, the overview of the estimation error measure and the derivation of the appropriate CRLB is provided, which is used to assess the performance of considered estimation methods. The CRLB, which is given by the inverse of the Fisher information matrix (FIM), denoted as , sets the lower limit for the variance (or covariance matrix) of any unbiased estimator [48]. The FIM represents a measure of the knowledge contained in the observed data about the unknown parameter vector, and it may be computed as follows
with the corresponding elements of the matrix determined according to the expressions
The process of deriving the Equations (64)–(66) is described in detail in Appendix A. Therefore, the CRLB inequality bound of the unbiased estimator of parameter is represented with the relationship between covariance and the inverse of the FIM, as follows
where denotes the estimated value of .
10. Experimental Analysis
Experiments were carried out to evaluate the accuracy of the proposed ICDEBOA method on the localization problem and to compare the optimization performance of the proposed algorithm with the performance of state-of-the-art algorithms in the literature on a set of CEC2014 benchmark problems. The results of these experiments are presented in this section. The results collected may be broken down into two categories: (1) an assessment of various EAs’ performances on the CEC2014 benchmark, and (2) an examination of localization’s effectiveness.
10.1. Statistical Comparisons on CEC2014 Problems
According to [77], the CEC2014 benchmark problems include 30 optimization problems with one objective that are defined on real numbers with the search space dimensions of , and 100. Based on objective functions characteristics, the CEC2014 benchmark problems can be put into four groups:
- Unimodal functions (1–3),
- Simple multimodal functions (4–16),
- Hybrid objective functions(17–22),
- Composition functions (23–30).
In order to compare how well the algorithms performs, the solution error measure was created. This is defined as the difference between the solution , which has the lowest objective function value and was obtained in a single simulation run and solution , which is previously known for the considered objective function. The termination criterion for the subsequent numerical experiments was set at , 100 individual in each algorithm’s population is employed, and each algorithm was run 51 times for each of the test functions. Two non-parametric statistical hypothesis tests, such as the Wilcoxon signed-rank test and the Friedman test, have been used to analyze and evaluate the quality of the solutions from a statistical perspective.
The Wilcoxon signed-rank is used to compare the optimization performance of each of the algorithms under consideration. This test provides information whether the first algorithm performs statistically better than the second algorithm, and was performed with significance. Therefore, ”there is no difference between the mean results of the two samples” [78] represents the null hypothesis. The hypothesis is rejected when , and then ”there is a difference in the mean results of the two samples” represents inverse hypothesis.
Here, denotes accomulated ranks where first algorithm had a superior performance to second one taken to test, and denotes the accomulated ranks for the case when the second tested algorithm achieved better performance.
The Friedman test was employed to determine differences in performance between each algorithm taken for comaprison form the statistical point. This is achieved by obtaining the ranks of each algorithm over each CEC2014 problem on all considered D. Here, the best performing algorithm is the one with the lowest rank. This test is taken with a significance level , and the null hypothesis ”there is no difference among the performance of all algorithms” is rejected for . Conversely, the alternative is ”there is a difference among the performance of all algorithms” [78].
In the obtained results, the signs +, ≈, − (better, equal, and worse) denote: (+) that the first algorithm had significantly better optimization performance than the second, (−) that the first algorithm performed significantly worse than the second, and (≈) that there is no significant difference in optimization performance between the two algorithms.
10.1.1. Analyzing the Effectiveness of the Chaos Maps on BOA Performance
To evaluate the effectiveness of the chaos theory-based sensory fragrance, as proposed in Section 7.2 in Equation (55), on the optimization performance of the BOA algorithm we have performed the following statistical analysis. The performance of the BOA algorithm is evaluated with five chaos maps, as shown in Figure 3, and compared to the conventional BOA algorithm using the Friedman test. The following variations of BOA algorithm were considered, which have the same operators as conventional BOA, except that the sensory fragrance is set according to Equation (48) with the following chaos map:
Table 1 shows a summary of the Friedman test’s statistical results of the performance comparison between the five chaos-improved BOA algorithms and the conventional BOA.
According to the results in Table 1, we conclude that the chaos-enhanced BOA algorithms have significantly better performance than the conventional BOA. Moreover, the results demonstrate that the best performance among the tested algorithms is achieved with the BOA-c-Sine algorithm, which demonstrates the effectiveness of the proposed modification. Therefore, we conclude that the improved chaos-based sensory fragrance given in Equation (55) will be taken in hybridization with the DE algorithm with the sine map given in Equation (53).
10.1.2. Analyzing the Effectiveness of the Proposed Hybridization
In this section, we present the results of performing the statistical comparison between the performance of the proposed ICDEBOA algorithm and several state-of-the-art algorithms in literature, including original BOA [21], SHADE [34], HPSOBOA [40], and jDE [35], evaluated over 30 objective functions defined in the CEC2014 benchmark.
The obtained mean (Mean) and standard (STD) deviation values of the best results of each algorithm obtained on each test objective function over each dimension are shown in Table 2. In addition, an appropriate sign is assigned to each tested algorithm, except the proposed ICDEBOA, to indicate whether the current algorithm achieved better +, worse − or a similar ≈ solution to the proposed algorithm.

Table 2.
Mean and standard deviation of the best objective function value obtained by the considered algorithms on a set of the CEC2014 test functions.
Based on the findings in Table 2, we observe that the proposed ICDEBOA algorithm outperforms other well-known algorithms on the large number of considered benchmark objective functions, and only on several isolated cases does the proposed algorithm has worse or similar performance to other considered algorithms. It should be noted that the ICDEBOA algorithm outperformed the SHADE algorithm on all considered problems. Results demonstrated that the HPSOBOA algorithm is in terms of performance right behind the ICDEBOA algorithm in the majority of cases, and successfully outperformed the ICDEBOA algorithm on and over all dimensions, and on HPSODEBOA showed similar performance to ICDEBOA. On and , the HPSOBOA achieved better solutions on functions and . Over dimensions and , the HPSOBOA showed better performance over composition functions . The proposed and HPSOBOA algorithm achieved similar performance for and 50 over simple multi-modal functions and , as well as for and 100 over functions and . The jDE algorithm performed better than ICDEBOA on and 50 on composite functions and , while the algorithms demonstrated similar performance on function . The original BOA algorithm outperformed the proposed method on and functions over all dimensions, and and on and 50. Since the proposed method ICDEBOA had significantly better performance than other algorithms in the majority of cases, especially compared to BOA and SHADE, it further proves the validity of the proposed hybridization.
Using the Wilcoxon signed-rank test, the performance of the proposed ICDEBOA algorithm is compared to the performance of other algorithms that have been considered. Table 3 displays the statistical and comparative findings of the Wilcoxon signed-rank test applied to the CEC2014 benchmark problems.

Table 3.
The results of performing Wilcoxon test on CEC2014 objective functions for all considered methods.
Based on the obtained results in Table 3, we observe that the ICDEBOA algorithm provides significantly better performance comapred to other considered algorithms on all dimensions. Compared to conventional BOA and SHADE algorithms, we observe improvement of performance, which further confirms the validity of the proposed hybridization. On and ICDEBOA achieved similar performance to HPSOBOA algorithm; however, the proposed algorithm has the higher value compared to .
Moreover, the Friedman test is used to assess if there is a statistically significant difference between performance of considered algorithms. In this way, Table 4 shows the average rankings of the Friedman test for each method studied on the different functions and dimensions of the CEC2014 benchmark problems. Here, the first-place rank is displayed in bold, and underline id used to denoted second one.

Table 4.
Results of the performance comparison using Friedman test with significance on CEC2014 test problems.
The results in Table 4, show that the obtained Friedman p values are less than significance in each considered case. The results demonstrate that the proposed ICDEBOA algorithm has the best performance among all the algorithms taken for considerations. The HPSOBOA algorithm shows the second-best performance. According to statistical analysis, hybridising DE and BOA algorithms improves optimization performance while overcoming their drawbacks. The expanded mutation operators, which incorporate butterfly algorithms equations for position updating, and the inclusion of a chaotic map to the sensory fragrance greatly improve the ICDEBOA method, proving the usefulness of the introduced changes.
10.2. Evaluation of Accuracy of Localization
This section presents the results of the numerical simulations of localization performance comparison between the ICDEBOA alg., proposed in this work, and the widely applied CWLS, DE, and BOA methods on the considered TDOA based passive target localization problem. The goal of this section is to verify the proposed improvements introduced in ICDEBOA algorithm and its efficiency on the considered localization problem. In order to measure the localization efficiency, the algorithms are evaluated through RMSE performance and compared to the derived CRLB, as it represents the lower bound on the variance of any unbiased estimator. To measure the localization accuracy, the RMSE is employed, which can be calculated as
where is the location of target which is known, is the estimate of the target position and denotes how much Monte Carlo simulation iterations are made for fixed .
It has been shown that some algorithms are sensitive to relative target–transmitter–receiver positions in the localization process, which leads to the singularity and bad solutions. To analyze how this relative position affects the localization performance of the considered algorithms, we consider three characteristic cases in the simulation. Thus, in the first four simulations, the transmitters are fixed to locations m, m, m, and m, and as stated in Section 3, we place the receiver in the center of the introduced coordinate system. The arrangement of transmitters forms a convex polygon, and we firstly consider how the placement of the target near the centroid of the figure formed by transmitter locations, at , affect the localization. Then, in the second simulation the position of the target is moved outside the convex figure formed by transmitters at . Finally, we consider the case when we assign the target a random location in the area in each run of the simulation.
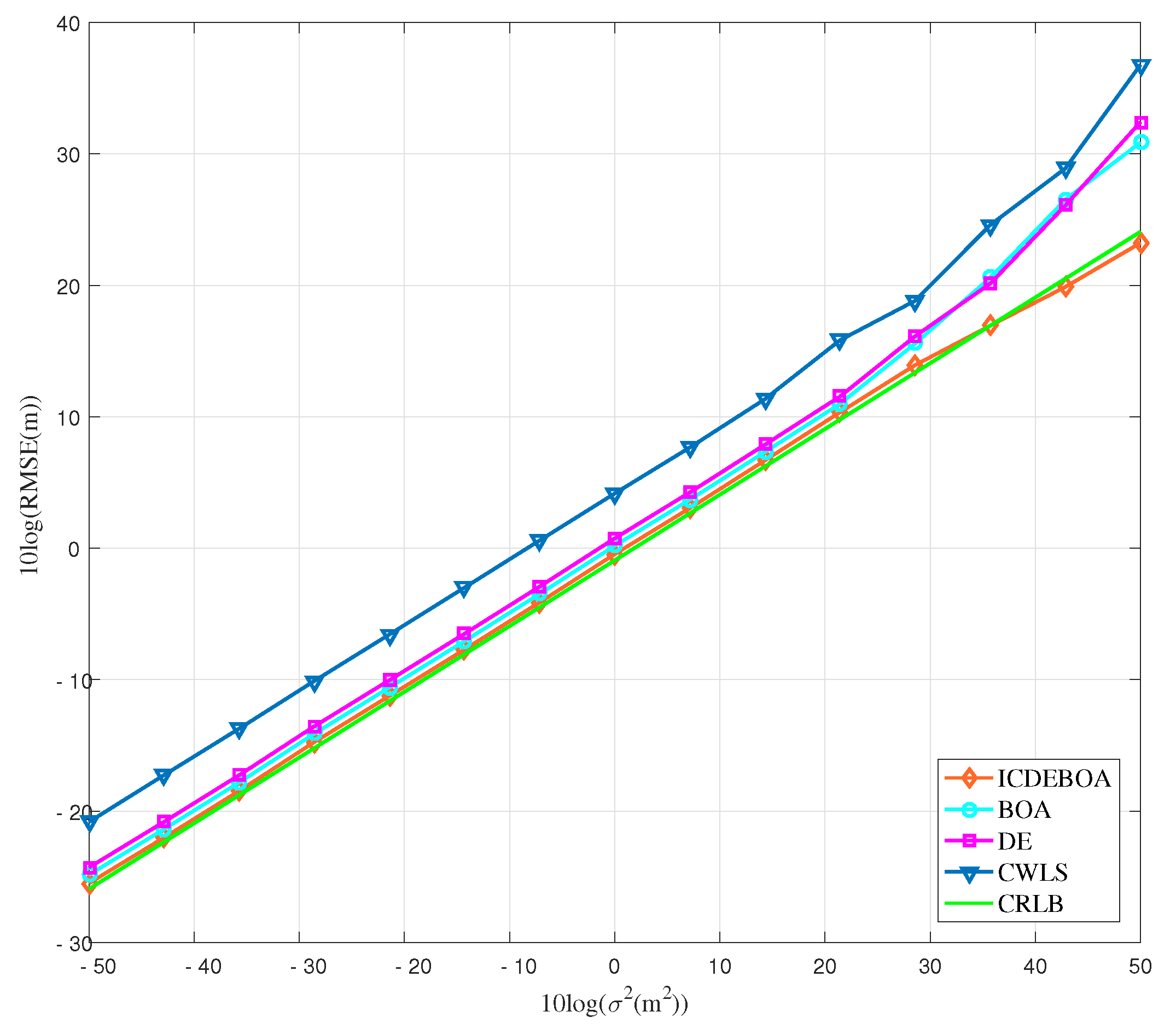
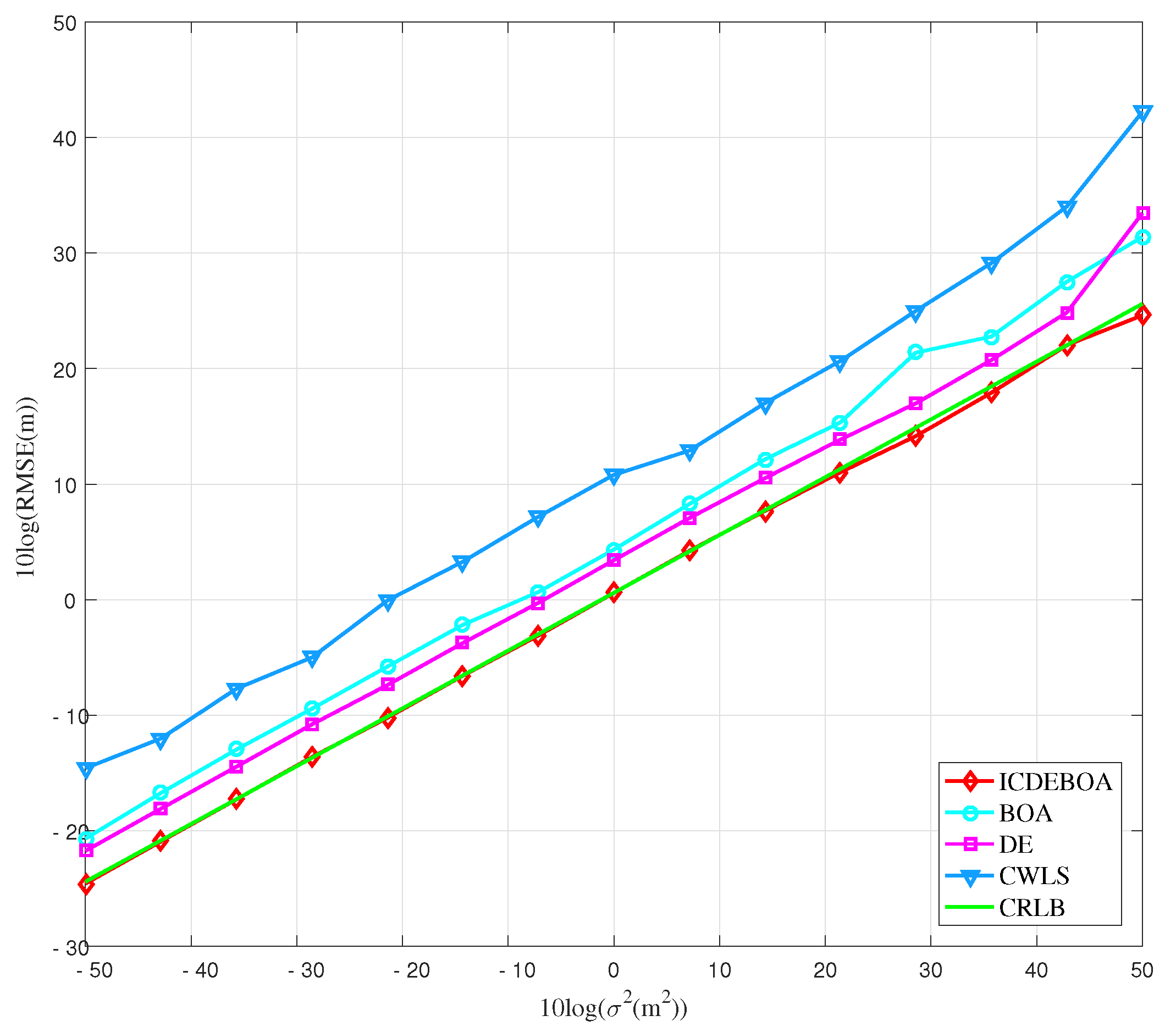
The results of the first simulation scenario are depicted in the Figure 4 as the functional relationship between the measurement noise and RMSE performance and compared to the CRLB.

Figure 4.
RMSE performance of different algorithms vs. p for first simulation case.
From the Figure 4 it can be concluded that the proposed ICDEBOA algorithm attains the CRLB and outperforms other considered methods on a whole considered range of measurement noise p. The performance of DE and BOA algorithms is slightly above the CRLB, while the CWLS algorithm showed the worse performance, especially when dB.
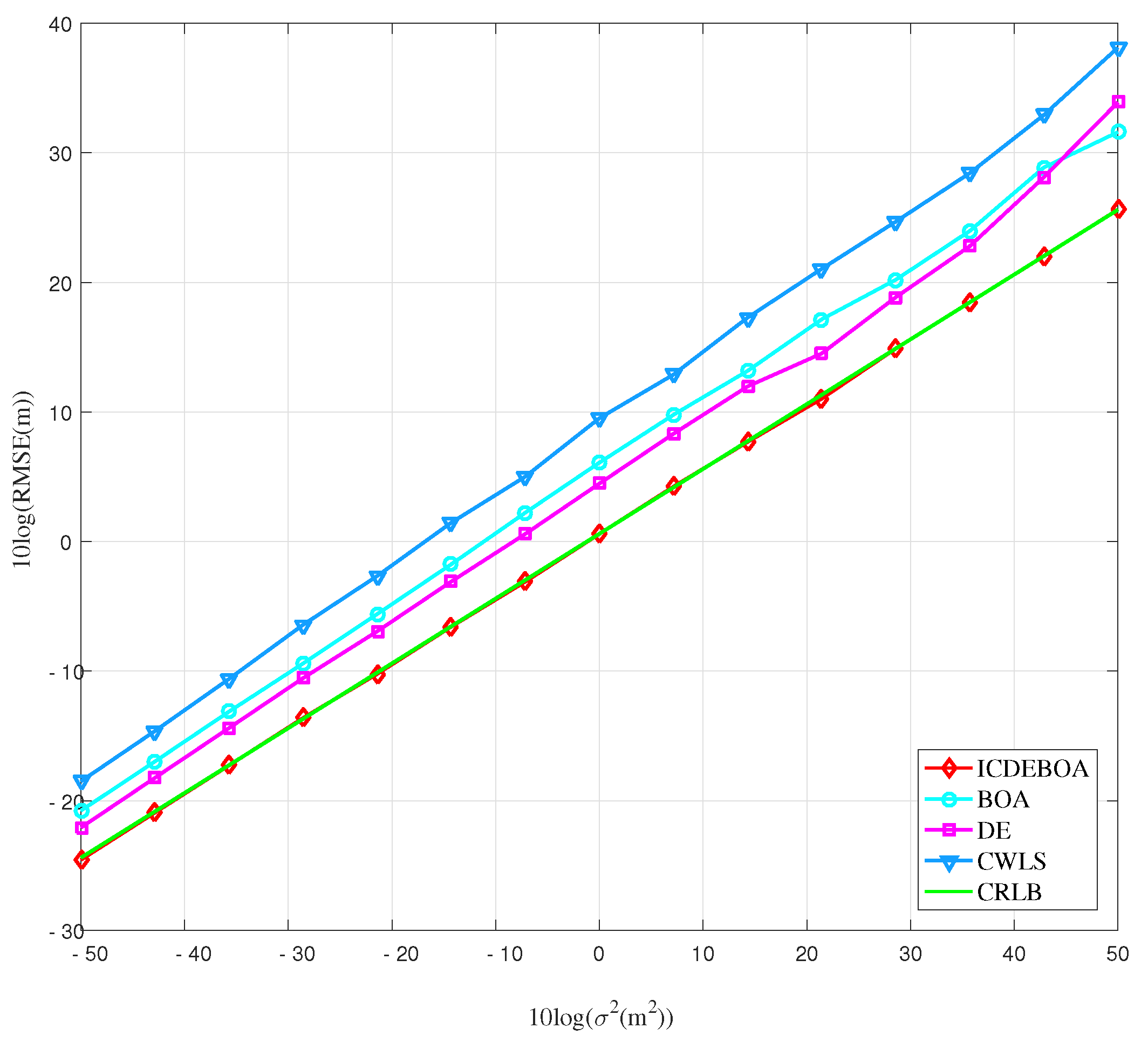
Figure 5 presents the results of the second scenario, where we place the target in the position outside of polygon formed by transmitter locations. Here, the RMSE performances of considered algorithms are plotted as a function of the measurement noise, and compared to the CRLB.
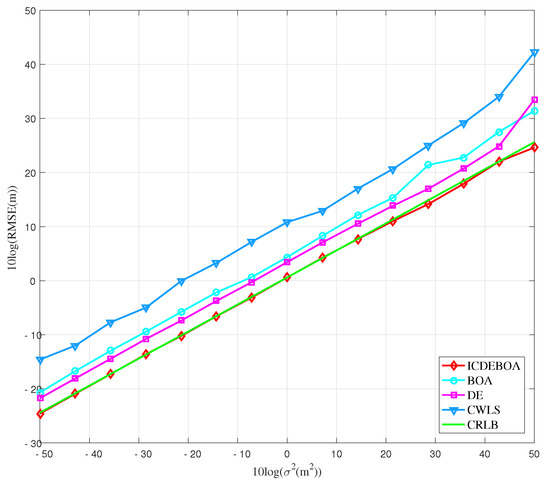
Figure 5.
Plot of the obtained RMSE curves in relation to the measurement noise for second simulation case.
Based on the results in Figure 5 we observe that even in this case the proposed ICDEBOA algorithm is able to attain the CRLB accuracy and show better performance with regard to other algorithms taken for simulation. In this case, the DE and BOA algorithm show a slight degradation in performance, compared to the previous case, which is observed in the bigger discrepancy from the CRLB. Again, the CWLS method has the worst performance among all algorithms.
In Figure 6 the results of the third simulation case, which considers a random placement of target in the area in each simulation iteration, are depicted as a function RMSE of p.
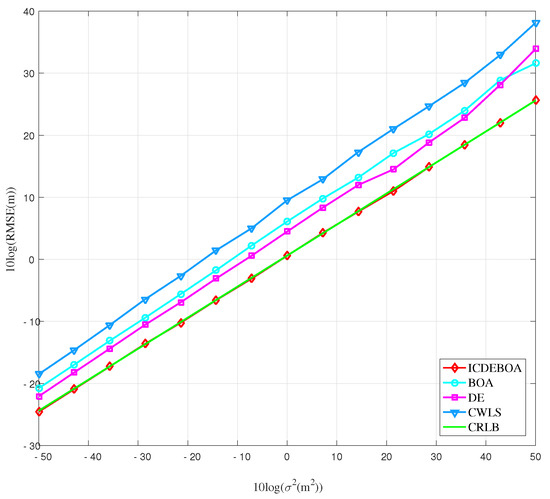
Figure 6.
The results obtained for the third simulation case depicted in the form of RMSE performance of different algorithms vs. p.
Based on the results of the third simulation scenario depicted in Figure 6, we observe that the ICDEBOA algorithm is able to reach the CRLB accuracy, while outperforming CWLS, DE and BOA algorithms. In this case, it is notable that there is a higher discrepancy between the CRLB and the DE, BOA, and CWLS algorithms’ RMSE performance curves. As in previous cases, the CWLS showed the lowest accuracy, with the curve high above the CRLB.
If we compare the results in Figure 4 through Figure 6 and analyze the obtained RMSE values under different conditions, we find that the considered algorithms had the performance closest to the CRLB in the first simulation case when we placed the target in the area surrounded by transmitters. Alternatively, we observe the biggest descrepency from the CRLB in the case when the target is not surrounded by transmitters, as shown in Figure 5. In addition, it is observed that the proposed ICDEBOA algorithm holds the CRLB accuracy for the entire considered range of p in all of the scenarios that have been considered for simulation.
Further investigation into the localization performance of different approaches is conducted by considering the localization error of considered algorithm trough the cumulative distribution functions (CDFs) when the measurement noise is . The localization error (LE) is introduced for CDF analysis as the Euclidean norm of the actual and estimated positions discrepancy, and it is computed as
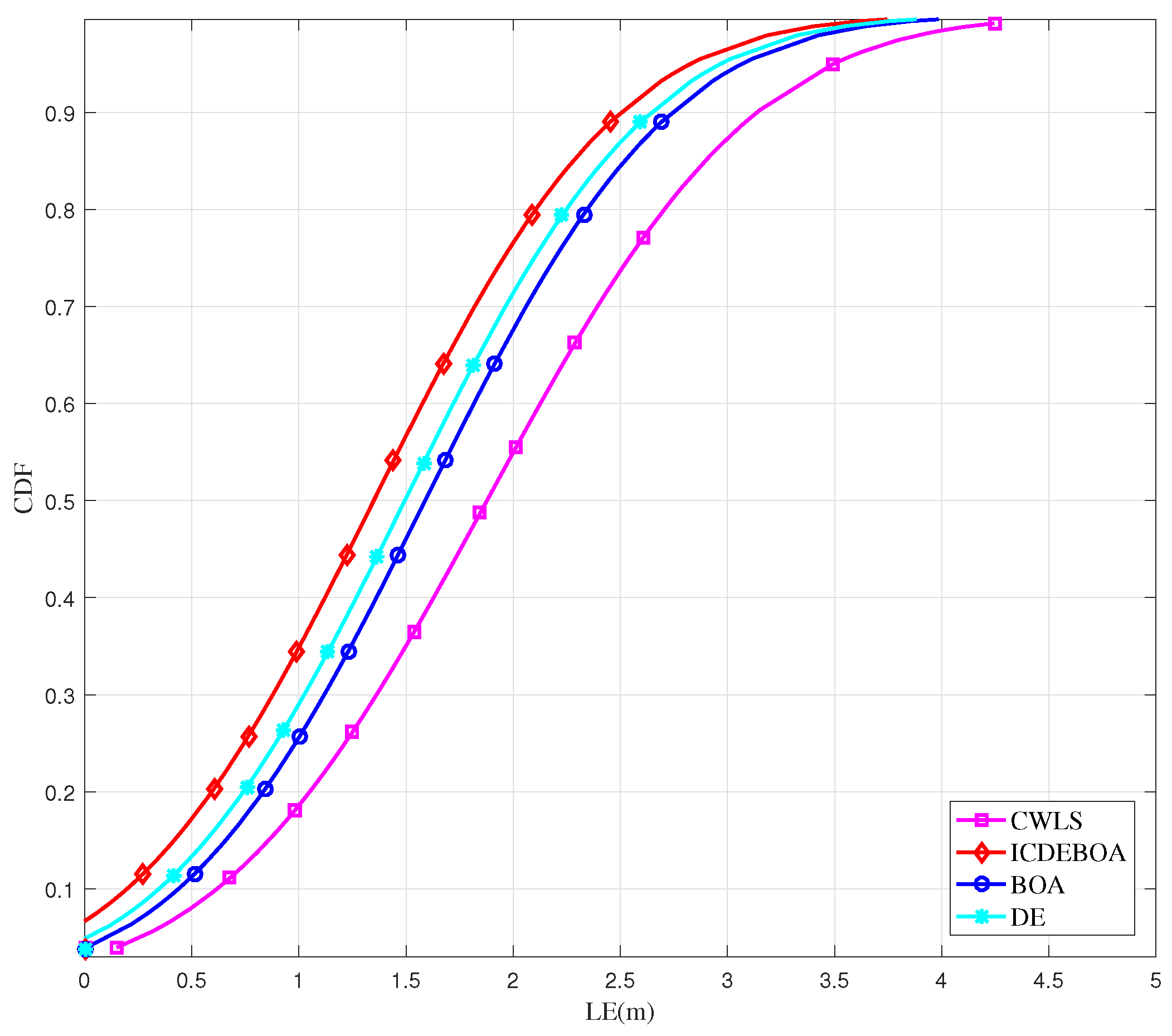
The CDFs of the localization error for the considered algorithms for the passive target positioned as in the first simulation scenario are presented in Figure 7 as a function of LE.
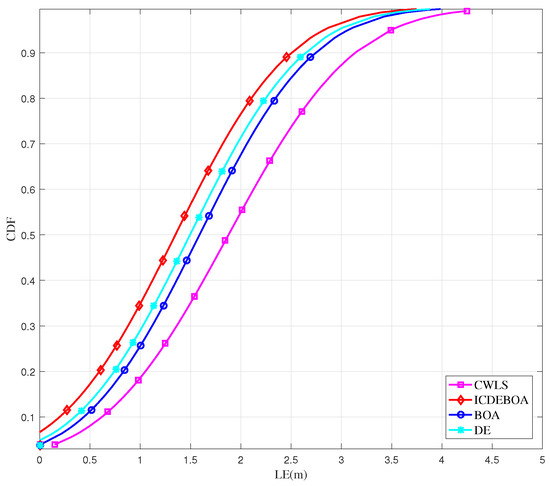
Figure 7.
The obtained CDFs of for considered passive TDOA-based localization problem.
Based on the results shown in Figure 7, we can observe that the proposed ICDEBOA algorithm provides localization accuracy of less than m for the CDF percentile, while the BOA, DE, and CWLS algorithms achieve s of less than m, m, and m, respectively, for the same case. So, we can say that the ICDEBOA algorithm improves LE by compared to BOA, by compared to DE, and by compared to the CWLS method, proving that it has improved performance.
Lastly, we look at how the accuracy of the localization changes as the number of transmitters involved in localization increases. Consider transmitters that are uniformly dispersed on a circle of a radius , such that the coordinate of each transmitter can be obtained as
where we fix the target inside the circle formed by transmitters near the center at the coordinates m.
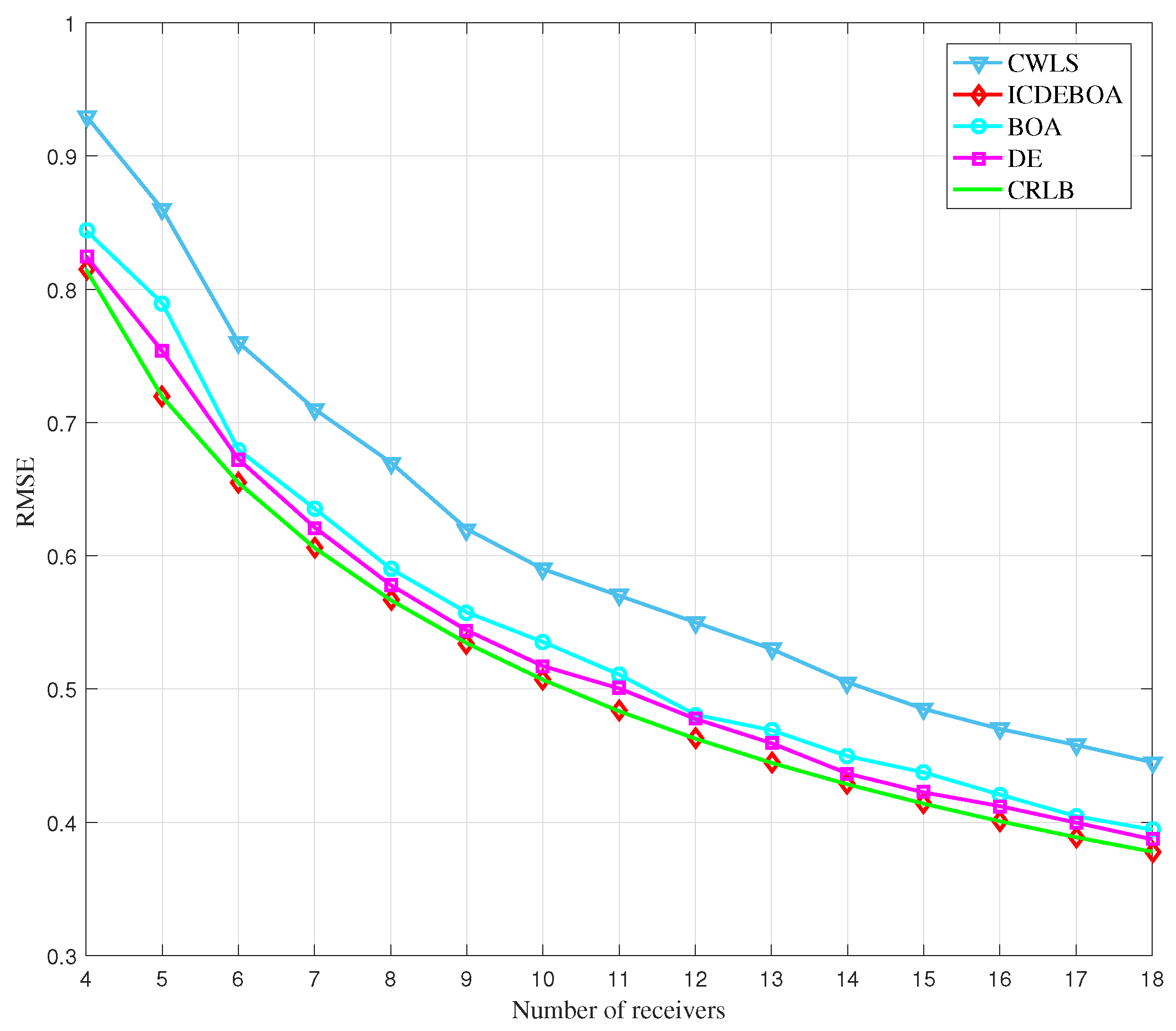
The functional changes of RMSE curves with the change of the number of transmitters employed in the localization for the considered algorithms are displayed in Figure 8, along with the appropriate CRLB, for the variance of measurement noise .

Figure 8.
The change in RMSE performance of the considered algorithms with the increase in the participating transmitters for measurement noise variance .
Figure 8 shows that as the number of transmitters grows from 4 to 10, the RMSE performance of all algorithms under consideration improves noticeably. We observe that the proposed method is able to reach CRLB accuracy in each of the cases. Furthermore, we observe that CWLS algorithm deviates from the CRLB accuracy. If we consider the cases of lowest number of employed transmitters (4) and the case of highest number of transmitters (18) taken for simulation, we observe the improvement in accuracy of location estimation of 52.4% in the proposed method.
Based on simulation results, we came to the conclusion that the proposed ICDEBOA algorithm’s performance was less affected by large-scale changes in measurement noise and network topologies than other algorithms we looked at.
11. Conclusions
This paper investigates the TDOA-based localization of a passive target in the presence of noise, which is in general a complex and multimodal problem. To solve this problem, the evolutionary algorithms DE and BOA are hybridized, resulting in the ICDEBOA algorithm. This paper aims to investigate the proposed ICDEBOA algorithm’s performance and capabilities on the considered passive localization problem, with a focus on the high measurement noise case, where conventional algorithms perform poorly. In the ICDEBOA algorithm, a composite roulette wheel is introduced to the DE algorithm and employed in a new mutation operator to choose the appropriate mutation scheme for current optimization state. Using BOA expressions for particle movement to generate a mutant vector in the DE algorithm yields a hybrid algorithm that takes advantage of the BOA algorithm’s strong local search capability. In addition, an adaptive method incorporating chaos theory is used to update the BOA algorithm’s sensory fragrance, and adaptive parameter adjudication strategies from the SHADE algorithm are implemented in the DE algorithm. In order to perform the comparison of the localization performance with several well-known algorithms, the CRLB is derived for the considered problem of localization. In addition, to evaluate the optimization performance of the ICDEBOA algorithm and compare to state-of-the-art methods, a set of CEC2014 test functions are employed and statistical comparison is performed.
In the results of statistical comparison performed on CEC2014 test problems we observe that the algorithm proposed in this paper shows improved optimization performance. Regarding the localization accuracy, the proposed ICDEBOA algorithm successfully attains the CRLB and outperforms the CWLS, BOA, and SHADE algorithms in that aspect. In the case of a variation of the network topology, we observe that the ICDEBOA algorithm always achieves CRLB and is not affected with the network topology change.
The focus of upcoming research will be on energy-efficient network structure and performance evaluation in a non-line-of-sight environment. Analyzing the sensitivity to parameter changes can help the optimization process be further improved.
Author Contributions
Conceptualization, M.R. and M.S. (Miloš Sedak); Methodology and Validation, M.R.; Formal Analysis, Software, Investigation, Data Curation, M.R. and M.S. (Miloš Sedak); Resources, M.S. (Mirjana Simić) and P.P.; Writing—Original Draft Preparation, M.R. and M.S. (Miloš Sedak); Writing—Review and Editing, M.S. (Mirjana Simić) and P.P.; Visualization, M.R.; Supervision, M.S. (Mirjana Simić) and P.P. All authors have read and agreed to the published version of the manuscript.
Funding
The research of M. Rosić was supported by the Serbian Ministry of Education and Science under Grant TR35029. The research of M. Sedak was supported by the Serbian Ministry of Education and Science under Grant No. TR35006. The work of M. Simić was supported in part by Serbian Ministry of Education and Science under Grant TR32028.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Based on the expression in Equation (A1), we conclude that the componental partial derivative is
Then, the first element of matrix is
Analogus to this the remaining elements of are
If we take , the following is obtained
Appendix B
Using eigenvalue decomposition, the matrix can be diagonalized as follows
where and are the eigenvalues of the matrix , and is the matrix composed of the eigenvectors. Substituting Equation (A13) into yields the following equation
References
- Sachs, J. Handbook of Ultra-Wideband Short-Range Sensing: Theory, Sensors, Applications; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar] [CrossRef]
- Chalise, B.K.; Zhang, Y.D.; Amin, M.G.; Himed, B. Target localization in a multi-static passive radar system through convex optimization. Signal Process. 2014, 102, 207–215. [Google Scholar] [CrossRef]
- Shen, L.; Zhang, Q.; Pang, J.; Xu, H.; Li, P.; Xue, D. ANTspin: Efficient Absolute Localization Method of RFID Tags via Spinning Antenna. Sensors 2019, 19, 2194. [Google Scholar] [CrossRef] [PubMed]
- Shen, M.; Wang, Y.; Jiang, Y.; Ji, H.; Wang, B.; Huang, Z. A new positioning method based on multiple ultrasonic sensors for autonomous mobile robot. Sensors 2019, 20, 17. [Google Scholar] [CrossRef] [PubMed]
- Siegele, D.; Staso, U.D.; Piovano, M.; Marcher, C.; Matt, D.T. State of the art of non-vision-based localization technologies for AR in facility management. In Proceedings of the International Conference on Augmented Reality, Virtual Reality and Computer Graphics, Lecce, Italy, 7–10 September 2020; pp. 255–272. [Google Scholar]
- Ulusar, U.D.; Celik, G.; Al-Turjman, F. Cognitive RF-based localization for mission-critical applications in smart cities: An overview. Comput. Electr. Eng. 2020, 87, 106780. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Y.; Zhou, M.; Nie, W.; Yang, X. Indoor Passive Localization With Channel State Information Using a Single Access Point. IEEE Sens. J. 2021, 21, 17085–17095. [Google Scholar] [CrossRef]
- Choi, K.H.; Ra, W.S.; Park, S.Y.; Park, J.B. Robust least squares approach to passive target localization using ultrasonic receiver array. IEEE Trans. Ind. Electron. 2014, 61, 1993–2002. [Google Scholar] [CrossRef]
- Noroozi, A.; Sebt, M.A. Target localization from bistatic range measurements in multi-transmitter multi-receiver passive radar. IEEE Signal Process. Lett. 2015, 22, 2445–2449. [Google Scholar] [CrossRef]
- Zekavat, R.; Buehrer, R.M. Handbook of Position Location: Theory, Practice and Advances; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 27. [Google Scholar] [CrossRef]
- Destino, G.; Abreu, G. On the maximum likelihood approach for source and network localization. IEEE Trans. Signal Process. 2011, 59, 4954–4970. [Google Scholar] [CrossRef]
- Noroozi, A.; Sebt, M.A. Weighted least squares target location estimation in multi-transmitter multi-receiver passive radar using bistatic range measurements. IET Radar Sonar Navig. 2016, 10, 1088–1097. [Google Scholar] [CrossRef]
- Jin, B.; Xu, X.; Zhang, T. Robust time-difference-of-arrival (TDOA) localization using weighted least squares with cone tangent plane constraint. Sensors 2018, 18, 778. [Google Scholar] [CrossRef]
- Wang, G.; Li, Y.; Ansari, N. A semidefinite relaxation method for source localization using TDOA and FDOA measurements. IEEE Trans. Veh. Technol. 2013, 62, 853–862. [Google Scholar] [CrossRef]
- Yue, Y.; Cao, L.; Hu, J.; Cai, S.; Hang, B.; Wu, H. A Novel Hybrid Location Algorithm Based on Chaotic Particle Swarm Optimization for Mobile Position Estimation. IEEE Access 2019, 7, 58541–58552. [Google Scholar] [CrossRef]
- Rosić, M.B.; Simić, M.I.; Pejović, P.V. An improved adaptive hybrid firefly differential evolution algorithm for passive target localization. Soft Comput. 2021, 25, 5559–5585. [Google Scholar] [CrossRef]
- Lalama, Z.; Boulfekhar, S.; Semechedine, F. Localization Optimization in WSNs Using Meta-Heuristics Optimization Algorithms: A Survey. Wirel. Pers. Commun. 2022, 122, 1197–1220. [Google Scholar] [CrossRef]
- Mohamed, A.W.; Almazyad, A.S. Differential evolution with novel mutation and adaptive crossover strategies for solving large scale global optimization problems. Appl. Comput. Intell. Soft Comput. 2017, 2017, 7974218. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, Y.I. Multiple sources localization by the WSN using the direction-of-arrivals classified by the genetic algorithm. IEEE Access 2019, 7, 173626–173635. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S.; Ji, G. A comprehensive survey on particle swarm optimization algorithm and its applications. Math. Probl. Eng. 2015, 2015, 931256. [Google Scholar] [CrossRef]
- Arora, S.; Singh, S. Butterfly optimization algorithm: A novel approach for global optimization. Soft Comput. 2019, 23, 715–734. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Cheng, J.; Xia, L. An effective Cuckoo search algorithm for node localization in wireless sensor network. Sensors 2016, 16, 1390. [Google Scholar] [CrossRef]
- Arora, S.; Singh, S. An Effective Hybrid Butterfly Optimization Algorithm with Artificial Bee Colony for Numerical Optimization. Int. J. Interact. Multimed. Artif. Intell. 2017, 4, 14–21. [Google Scholar] [CrossRef]
- Devika, E.; Saravanan, A. Enhanced gray wolf optimization for estimation of time difference of arrival in WSNs. Int. J. Pervasive Comput. Commun. 2022. [Google Scholar] [CrossRef]
- Xiong, G.; Zhang, J.; Yuan, X.; Shi, D.; He, Y.; Yao, G. Parameter extraction of solar photovoltaic models by means of a hybrid differential evolution with whale optimization algorithm. Sol. Energy 2018, 176, 742–761. [Google Scholar] [CrossRef]
- Wu, P.; Su, S.; Zuo, Z.; Guo, X.; Sun, B.; Wen, X. Time Difference of Arrival (TDoA) Localization Combining Weighted Least Squares and Firefly Algorithm. Sensors 2019, 19, 2554. [Google Scholar] [CrossRef]
- Opara, K.R.; Arabas, J. Differential Evolution: A survey of theoretical analyses. Swarm Evol. Comput. 2019, 44, 546–558. [Google Scholar] [CrossRef]
- Arora, S.; Singh, S. Node localization in wireless sensor networks using butterfly optimization algorithm. Arab. J. Sci. Eng. 2017, 42, 3325–3335. [Google Scholar] [CrossRef]
- Tan, L.S.; Zainuddin, Z.; Ong, P. Wavelet neural networks based solutions for elliptic partial differential equations with improved butterfly optimization algorithm training. Appl. Soft Comput. 2020, 95, 106518. [Google Scholar] [CrossRef]
- Najarro, L.A.C.; Song, I.; Kim, K. Differential evolution with opposition and redirection for source localization using RSS measurements in wireless sensor networks. IEEE Trans. Autom. Sci. Eng. 2020, 17, 1736–1747. [Google Scholar] [CrossRef]
- Deng, W.; Shang, S.; Cai, X.; Zhao, H.; Song, Y.; Xu, J. An improved differential evolution algorithm and its application in optimization problem. Soft Comput. 2021, 25, 5277–5298. [Google Scholar] [CrossRef]
- Zhang, J.; Sanderson, A.C. JADE: Adaptive differential evolution with optional external archive. IEEE Trans. Evol. Comput. 2009, 13, 945–958. [Google Scholar] [CrossRef]
- Tanabe, R.; Fukunaga, A. Success-history based parameter adaptation for differential evolution. In Proceedings of the Evolutionary Computation (CEC), Cancun, Mexico, 20–23 June 2013; pp. 71–78. [Google Scholar]
- Brest, J.; Greiner, S.; Boskovic, B.; Mernik, M.; Zumer, V. Self-adapting control parameters in differential evolution: A comparative study on numerical benchmark problems. IEEE Trans. Evol. Comput. 2006, 10, 646–657. [Google Scholar] [CrossRef]
- Arora, S.; Singh, S. An improved butterfly optimization algorithm with chaos. J. Intell. Fuzzy Syst. 2017, 32, 1079–1088. [Google Scholar] [CrossRef]
- Fan, Y.; Shao, J.; Sun, G.; Shao, X. A self-adaption butterfly optimization algorithm for numerical optimization problems. IEEE Access 2020, 8, 88026–88041. [Google Scholar] [CrossRef]
- Li, G.; Shuang, F.; Zhao, P.; Le, C. An improved butterfly optimization algorithm for engineering design problems using the cross-entropy method. Symmetry 2019, 11, 1049. [Google Scholar] [CrossRef]
- Aydilek, I.B. A hybrid firefly and particle swarm optimization algorithm for computationally expensive numerical problems. Appl. Soft Comput. 2018, 66, 232–249. [Google Scholar] [CrossRef]
- Zhang, M.; Long, D.; Qin, T.; Yang, J. A Chaotic Hybrid Butterfly Optimization Algorithm with Particle Swarm Optimization for High-Dimensional Optimization Problems. Symmetry 2020, 12, 1800. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, G.; Wang, X.; Ni, P.; Zhang, J. A hybrid identification method on butterfly optimization and differential evolution algorithm. Smart Struct. Syst. 2020, 26, 345–360. [Google Scholar]
- Yang, D.; Li, G.; Cheng, G. On the efficiency of chaos optimization algorithms for global optimization. Chaos Solitons Fractals 2007, 34, 1366–1375. [Google Scholar] [CrossRef]
- Thompson, J.M.T.; Stewart, H.B. Nonlinear Dynamics and Chaos; John Wiley & Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Tavazoei, M.S.; Haeri, M. Comparison of different one-dimensional maps as chaotic search pattern in chaos optimization algorithms. Appl. Math. Comput. 2007, 187, 1076–1085. [Google Scholar] [CrossRef]
- Zhenyu, G.; Bo, C.; Min, Y.; Binggang, C. Self-adaptive chaos differential evolution. In Proceedings of the International Conference on Natural Computation, Xi’an, China, 24–28 September 2006; pp. 972–975. [Google Scholar]
- Mandal, S.; Mandal, K.K. Optimal energy management of microgrids under environmental constraints using chaos enhanced differential evolution. Renew. Energy Focus 2020, 34, 129–141. [Google Scholar] [CrossRef]
- Tian, D.; Zhao, X.; Shi, Z. Chaotic particle swarm optimization with sigmoid-based acceleration coefficients for numerical function optimization. Swarm Evol. Comput. 2019, 51, 100573. [Google Scholar] [CrossRef]
- Li, W.; Wei, P.; Xiao, X. A robust TDOA-based location method and its performance analysis. Sci. China Ser. F Inf. Sci. 2009, 52, 876–882. [Google Scholar] [CrossRef]
- Shen, J.; Molisch, A.F.; Salmi, J. Accurate passive location estimation using TOA measurements. IEEE Trans. Wirel. Commun. 2012, 11, 2182–2192. [Google Scholar] [CrossRef]
- Hu, Y.; Leus, G. Robust differential received signal strength-based localization. IEEE Trans. Signal Process. 2017, 65, 3261–3276. [Google Scholar] [CrossRef]
- Xu, S.; Doğançay, K. Optimal sensor placement for 3-D angle-of-arrival target localization. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1196–1211. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M.; Dinis, R.; Bernardo, L. On target localization using combined RSS and AoA measurements. Sensors 2018, 18, 1266. [Google Scholar] [CrossRef]
- Xiao, H.; Zhang, H.; Wang, Z.; Gulliver, T.A. An RSSI based DV-hop algorithm for wireless sensor networks. In Proceedings of the 2017 IEEE Pacific Rim Conference on Communications, Computers and Signal Processing (PACRIM), Shanghai, China, 21–25 September 2017; pp. 1–6. [Google Scholar]
- Shen, J.; Wang, A.; Wang, C.; Hung, P.C.; Lai, C.F. An efficient centroid-based routing protocol for energy management in WSN-assisted IoT. IEEE Access 2017, 5, 18469–18479. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Z.; Yao, M.; Qiu, Z. VN-APIT: Virtual nodes-based range-free APIT localization scheme for WSN. Wirel. Netw. 2016, 22, 867–878. [Google Scholar] [CrossRef]
- Halder, S.; Ghosal, A. A survey on mobile anchor assisted localization techniques in wireless sensor networks. Wirel. Netw. 2016, 22, 2317–2336. [Google Scholar] [CrossRef]
- Chen, J.; Zhao, Y.; Zhao, C.; Zhao, Y. Improved two-step weighted least squares algorithm for TDOA-based source localization. In Proceedings of the 2018 19th International Radar Symposium (IRS), Bonn, Germany, 20–22 June 2018; pp. 1–6. [Google Scholar]
- Lin, L.; So, H.C.; Chan, F.K.; Chan, Y.T.; Ho, K. A new constrained weighted least squares algorithm for TDOA-based localization. Signal Process. 2013, 93, 2872–2878. [Google Scholar] [CrossRef]
- Biswas, P.; Liang, T.C.; Toh, K.C.; Ye, Y.; Wang, T.C. Semidefinite programming approaches for sensor network localization with noisy distance measurements. IEEE Trans. Autom. Sci. Eng. 2006, 3, 360–371. [Google Scholar] [CrossRef]
- Cakir, O.; Kaya, I.; Yazgan, A.; Cakir, O.; Tugcu, E. Emitter location finding using particle swarm optimization. Radioengineering 2014, 23, 252–258. [Google Scholar]
- Meng, Y.; Zhi, Q.; Zhang, Q.; Yao, N. A Two-Stage Particle Swarm Optimization Algorithm for Wireless Sensor Nodes Localization in Concave Regions. Information 2020, 11, 488. [Google Scholar] [CrossRef]
- Li, Q.; Chen, B.; Yang, M. Time Difference of Arrival Passive Localization Sensor Selection Method Based on Tabu Search. Sensors 2020, 20, 6547. [Google Scholar] [CrossRef]
- Díez-González, J.; Álvarez, R.; González-Bárcena, D.; Sánchez-González, L.; Castejón-Limas, M.; Perez, H. Genetic algorithm approach to the 3D node localization in TDOA systems. Sensors 2019, 19, 3880. [Google Scholar] [CrossRef]
- Srideviponmalar, P.; Jawahar Senthil Kumar, V.; Harikrishnan, R. Hybrid Genetic Algorithm–Differential Evolution Approach for Localization in WSN. In Intelligent Engineering Informatics; Springer: Cham, Switzerland, 2018; pp. 263–271. [Google Scholar]
- Rosić, M.B.; Simić, M.I.; Pejović, P.V. Passive target localization problem based on improved hybrid adaptive differential evolution and Nelder-Mead algorithm. J. Sens. 2020, 2020, 3482463. [Google Scholar] [CrossRef]
- Harikrishnan, R.; Kumar, V.J.S.; Ponmalar, P.S. A Comparative Analysis of Intelligent Algorithms for Localization in Wireless Sensor Networks. Wirel. Pers. Commun. 2016, 87, 1057–1069. [Google Scholar] [CrossRef]
- Gumaida, B.F.; Luo, J. A hybrid particle swarm optimization with a variable neighborhood search for the localization enhancement in wireless sensor networks. Appl. Intell. 2019, 49, 3539–3557. [Google Scholar] [CrossRef]
- Su, C.; Liu, Y.; Liu, L.; Yang, M.; Zhao, H.; Yin, X. Experimental Evaluation of Multipath Mitigation in TDOA-Based Indoor Passive Localization System Using A Beam Steering Broadband Circular Polarization Antenna. Electronics 2018, 7, 362. [Google Scholar] [CrossRef]
- Kwon, S.; Choi, Y.; Moon, S.; You, C.; Liu, H.; Kim, J.H.; Kim, D.J.; Park, H.; Kim, J.Y.; Hwang, I. Performance enhancement of hybrid TDOA/AOA using multipath delay estimation. Wirel. Pers. Commun. 2020, 115, 2551–2568. [Google Scholar] [CrossRef]
- Tsai, M.H.; Luo, J.N.; Yang, M.H.; Lo, N.W. Location Tracking and Forensic Analysis of Criminal Suspects’ Footprints. In Proceedings of the 2019 IEEE 2nd International Conference on Information and Computer Technologies (ICICT), Kahului, HI, USA, 14–17 March 2019; pp. 210–214. [Google Scholar]
- Ivanov, S.; Kuptsov, V.; Badenko, V.; Fedotov, A. RSS/TDoA-Based Source Localization in Microwave UWB Sensors Networks Using Two Anchor Nodes. Sensors 2022, 22, 3018. [Google Scholar] [CrossRef] [PubMed]
- Wan, P.; Ni, Y.; Hao, B.; Li, Z.; Zhao, Y. Passive localization of signal source based on wireless sensor network in the air. Int. J. Distrib. Sens. Netw. 2018, 14, 1550147718767371. [Google Scholar] [CrossRef]
- Wu, G.; Shen, X.; Li, H.; Chen, H.; Lin, A.; Suganthan, P.N. Ensemble of differential evolution variants. Inf. Sci. 2018, 423, 172–186. [Google Scholar] [CrossRef]
- Zhou, Y.Z.; Yi, W.C.; Gao, L.; Li, X.Y. Adaptive differential evolution with sorting crossover rate for continuous optimization problems. IEEE Trans. Cybern. 2017, 47, 2742–2753. [Google Scholar] [CrossRef]
- Mohamed, A.W. An improved differential evolution algorithm with triangular mutation for global numerical optimization. Comput. Ind. Eng. 2015, 85, 359–375. [Google Scholar] [CrossRef]
- Qian, W.; Chai, J.; Xu, Z.; Zhang, Z. Differential evolution algorithm with multiple mutation strategies based on roulette wheel selection. Appl. Intell. 2018, 48, 3612–3629. [Google Scholar] [CrossRef]
- Liang, J.J.; Qu, B.Y.; Suganthan, P.N. Problem definitions and evaluation criteria for the CEC 2014 special session and competition on single objective real-parameter numerical optimization. Comput. Intell. Lab. Zhengzhou Univ. Zhengzhou China Tech. Rep. Nanyang Technol. Univ. Singap. 2013, 635, 490. [Google Scholar]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).