Hydrothermal Reservoir and Electrical Anisotropy Investigated by Magnetotelluric Data, Case Study of Asal Rift, Republic of Djibouti
Abstract
1. Introduction
2. Geological Background
3. Methods
3.1. Magnetotelluric Data Acquisition and Processing
3.2. Dimensionality Analysis of MT Data
3.2.1. Phase Tensor
3.2.2. Geoelectric Strike Angle from Impedance Invariants
3.2.3. Strike Angle from Decomposition Model
3.2.4. Induction Vectors
3.3. Electrical Anisotropy
3.4. Static Shift Correction and Strategy for 2D Inversion Models
4. Results
4.1. Dimensionality
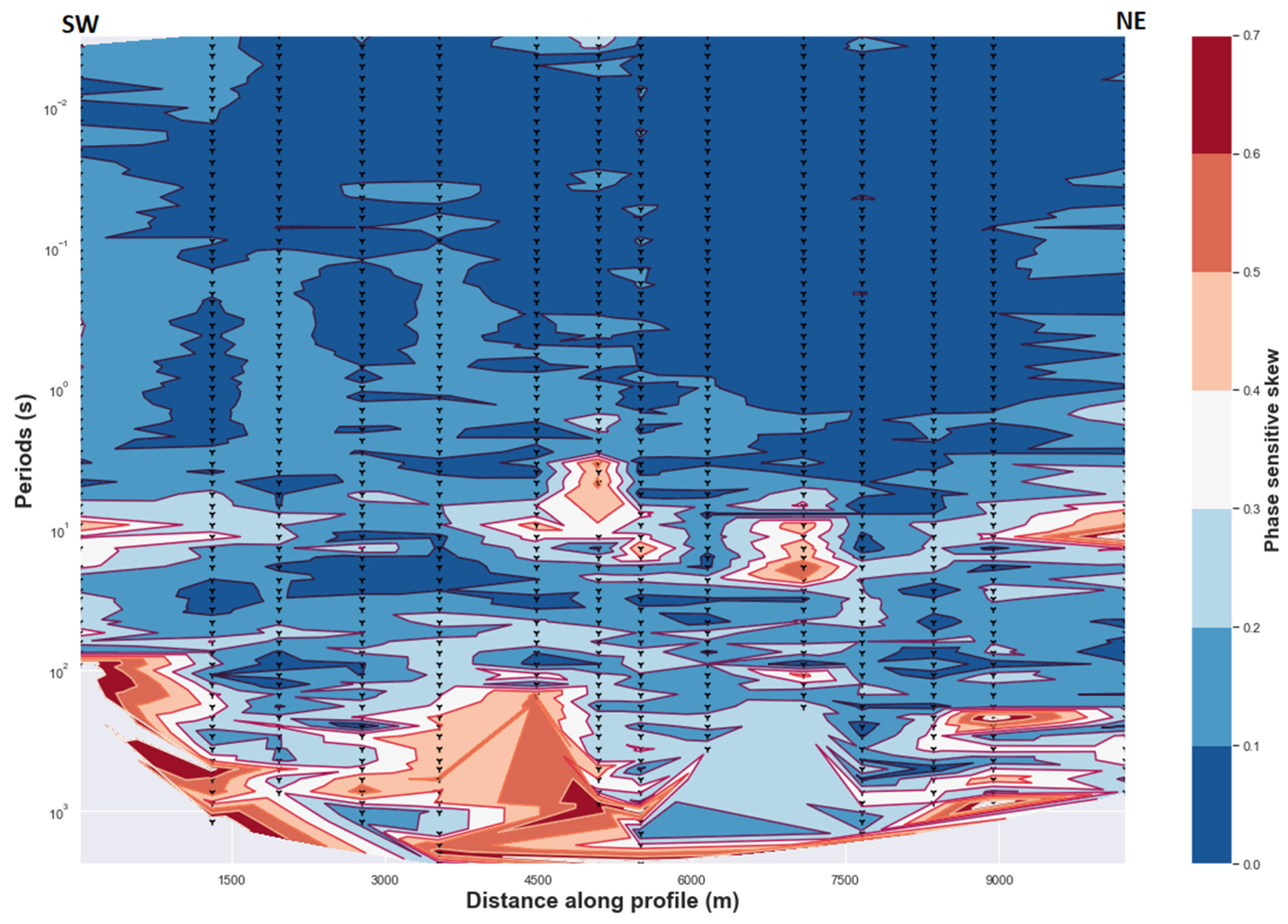
4.1.1. Extent of 2D Regional Conductivity and the Regional Skew
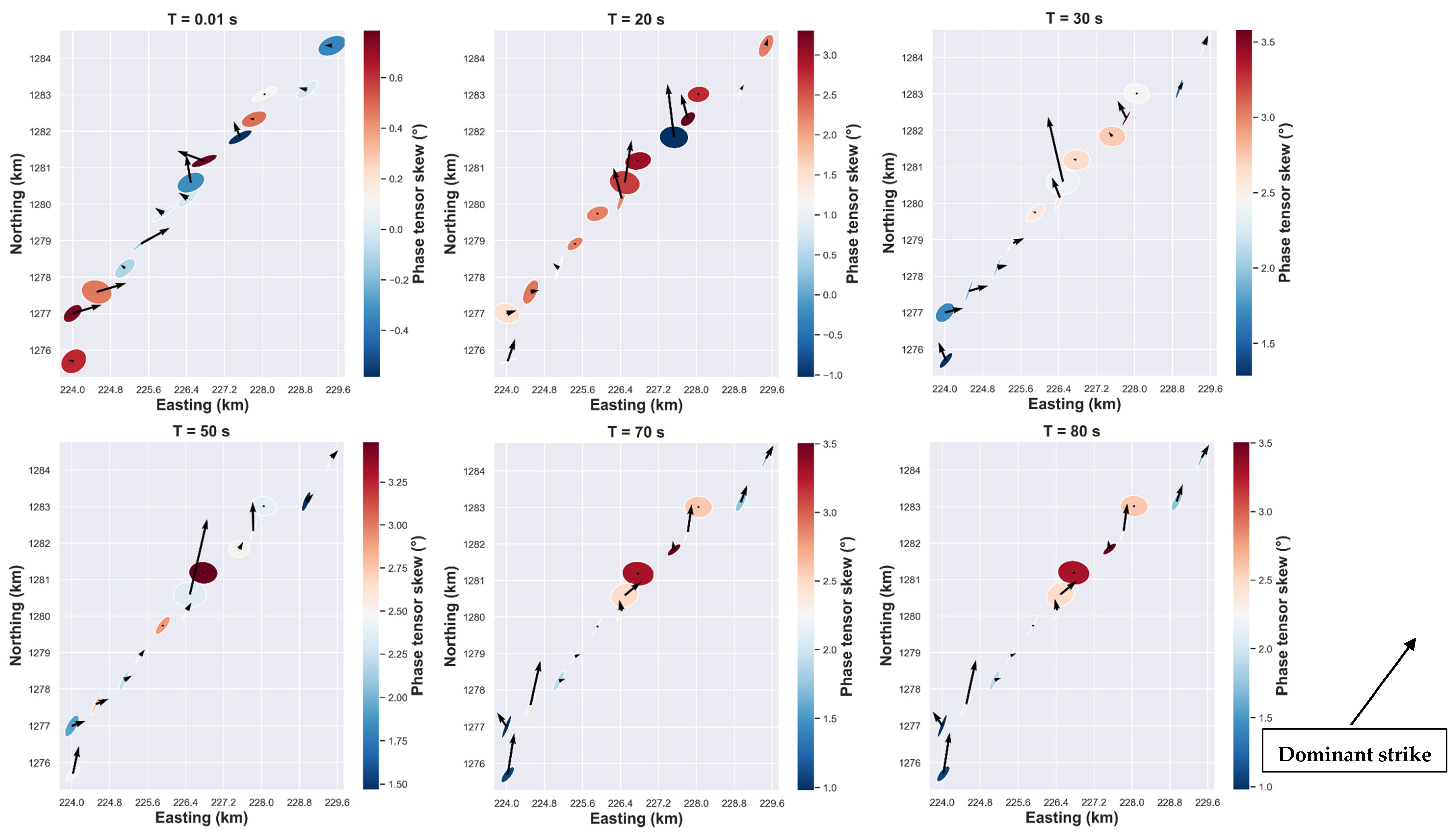
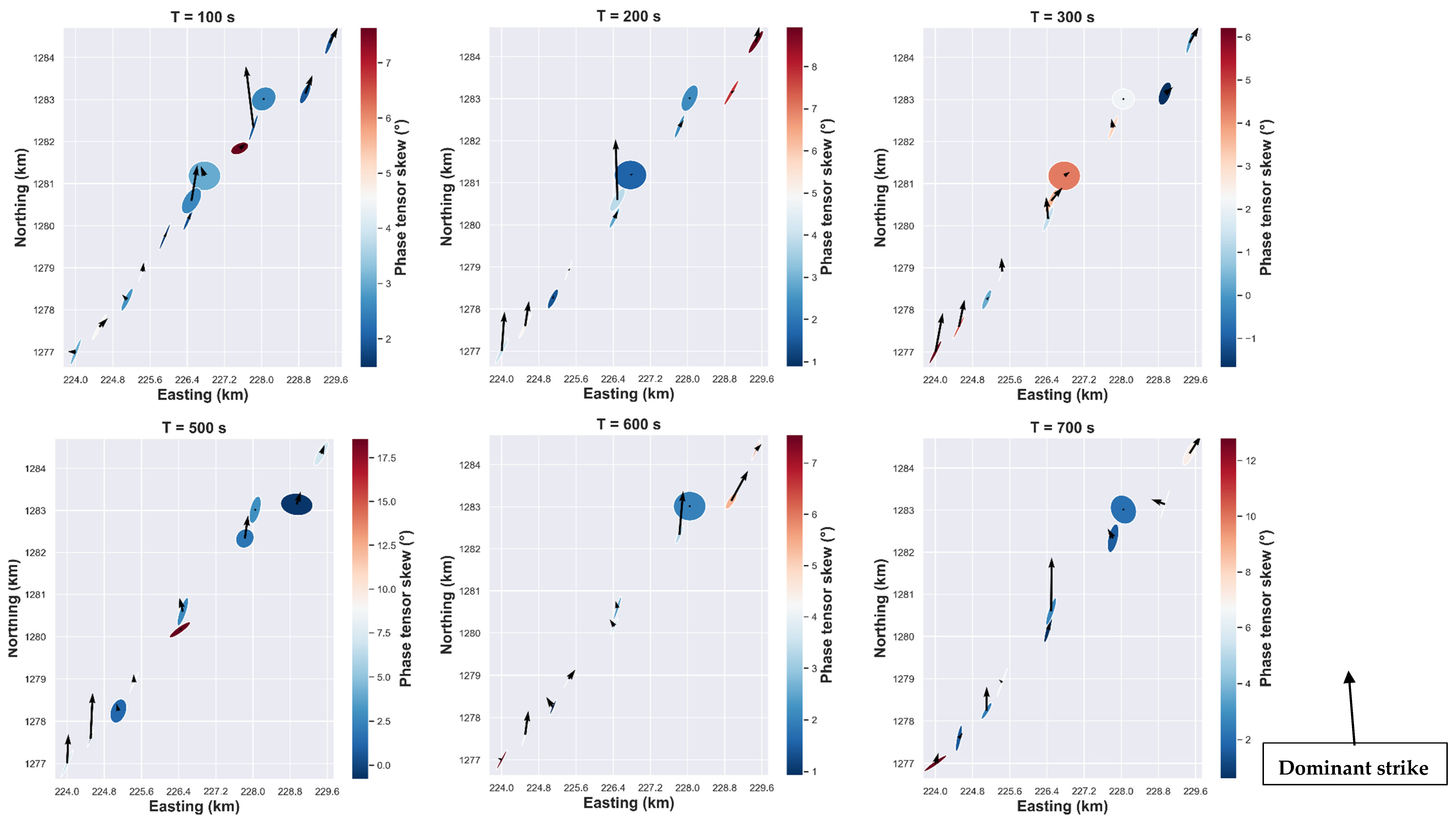
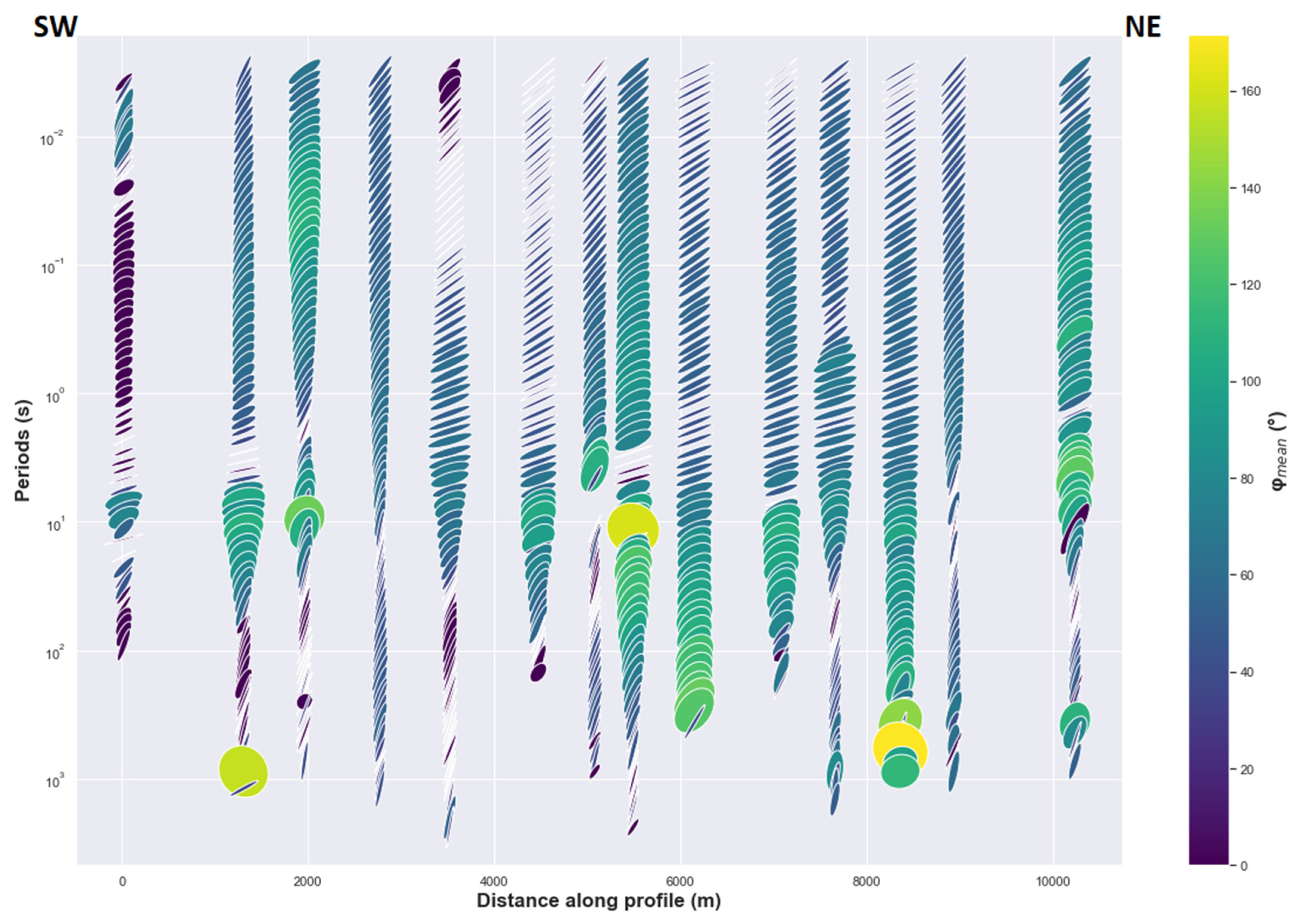
4.1.2. Phase Tensor Analysis
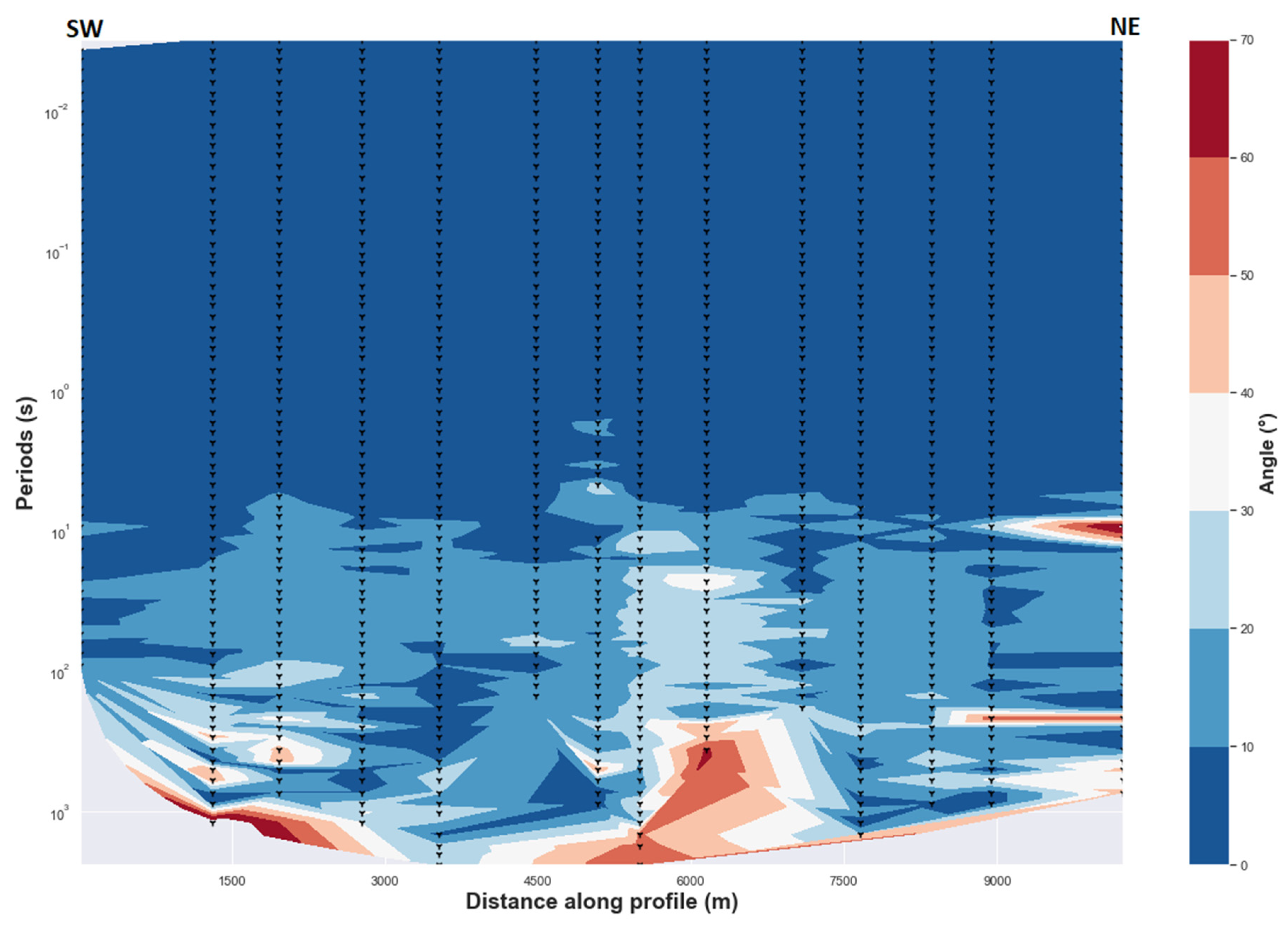
4.1.3. Impedance Invariant and Decomposition Model
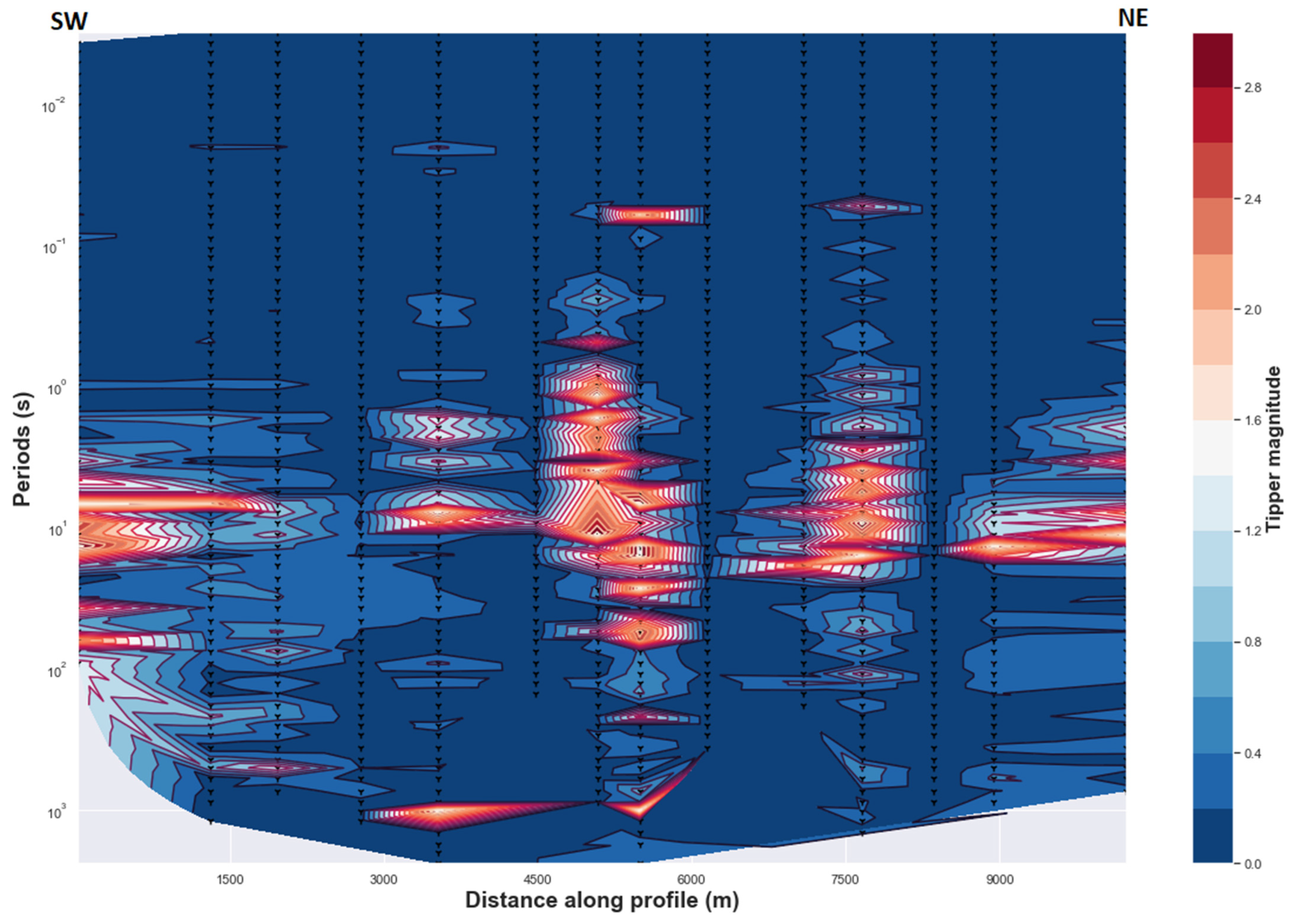
4.1.4. Tipper Orientation with Phase Tensor Ellipse
4.2. Electrical Anisotropy
4.2.1. Impedance Phase Split
4.2.2. The Ellipticity of the Phase Tensor
4.2.3. Induction Vectors
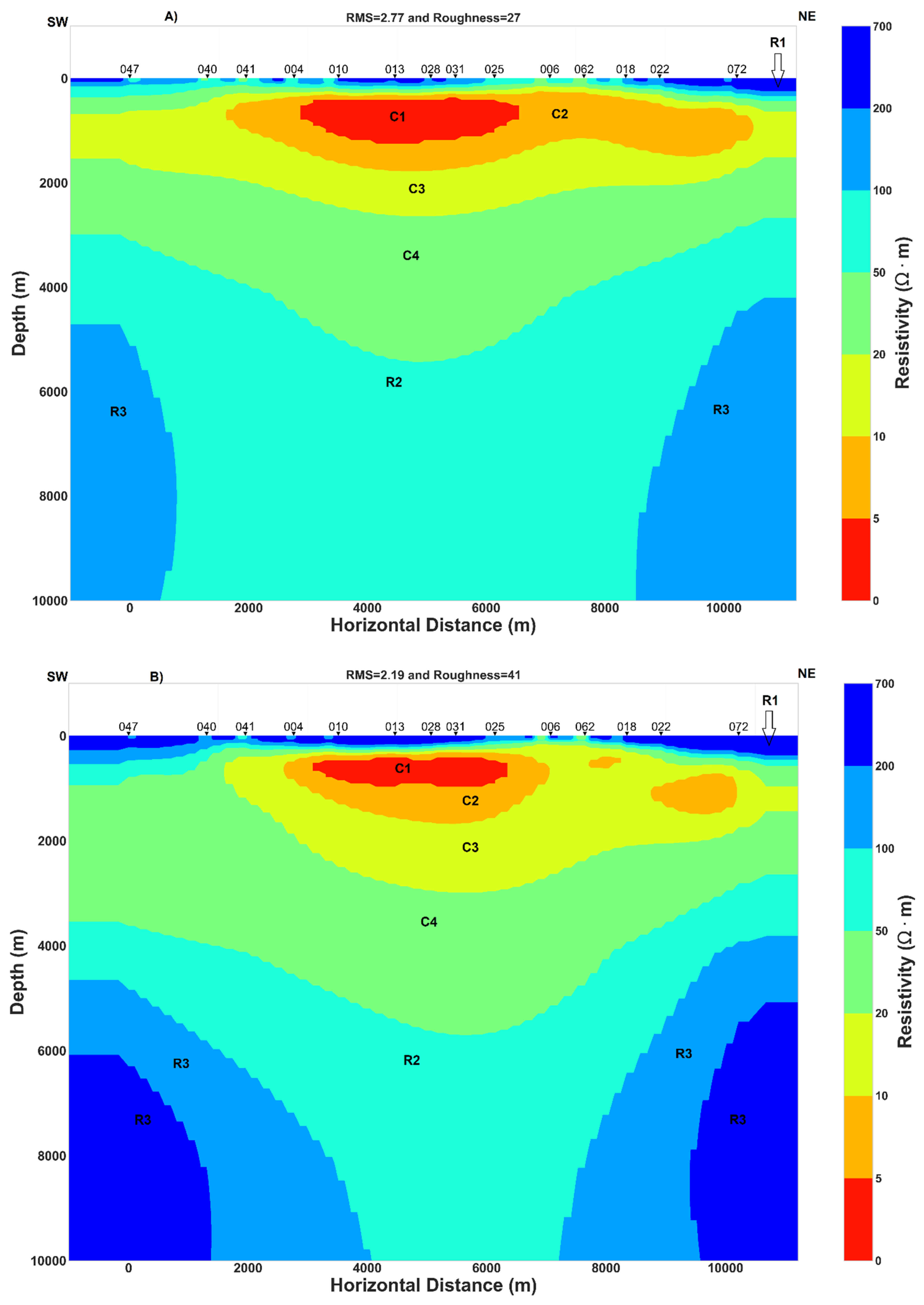
4.3. 2D Inversion Models
5. Discussion
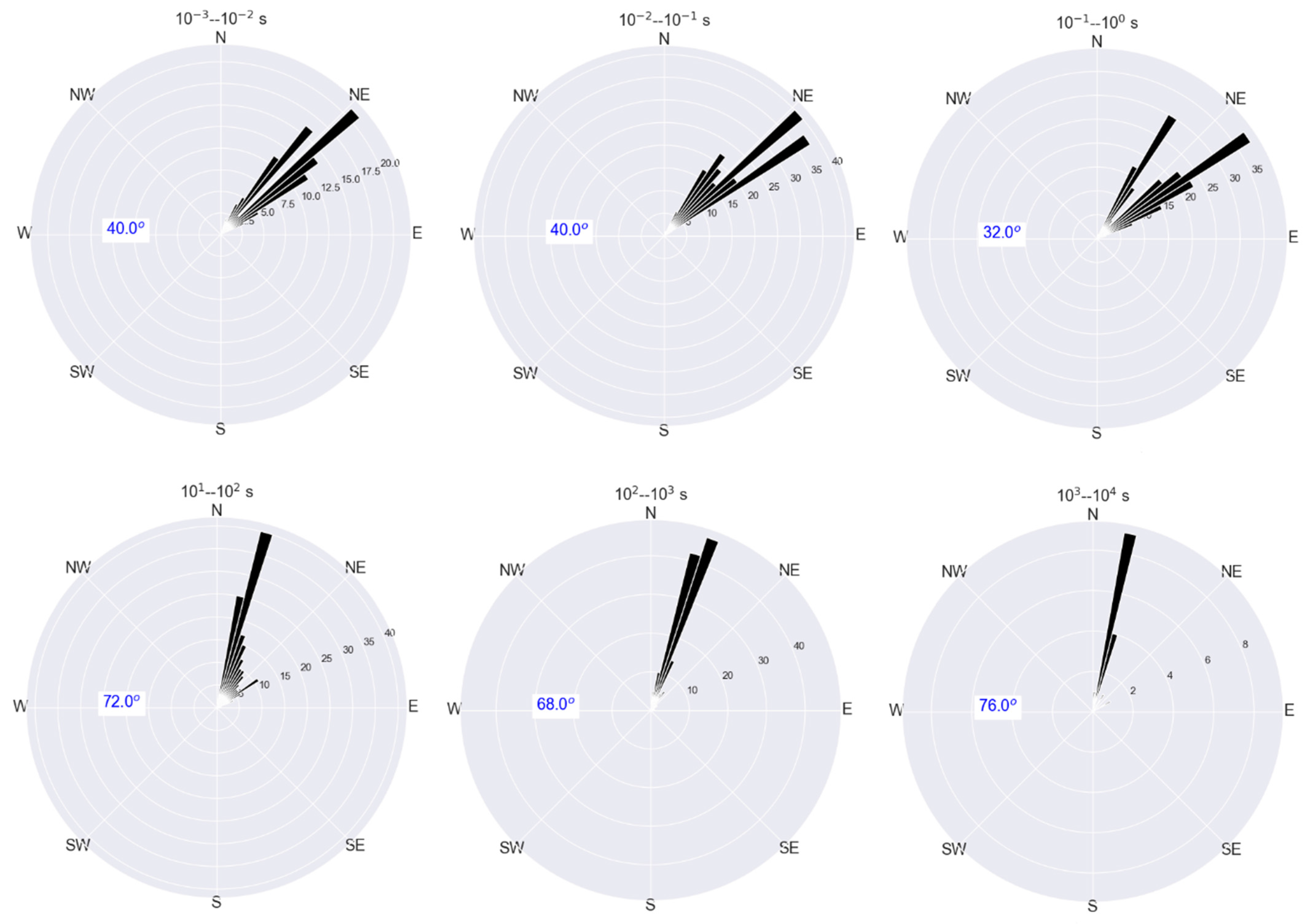
5.1. Geoelectric Strike Direction Dependent of the Periods
5.1.1. Comparison of Geoelectric Strike with Strike Determined from Other Studies
5.1.2. Origin and Possible Mechanism Inducing Geoelectric Strike in a Rift Context
5.2. Two Main Directions of Anisotropy Varying with Depth
5.2.1. Presence of 2D Anisotropic Structure
5.2.2. Origin of Electrical Anisotropy and the Role of Stress Field
5.2.3. Electrical Anisotropy Direction Related to the Plates Motion
5.2.4. Electrical Anisotropy Direction Related to the Fluid-Filled in Oriented Fractures
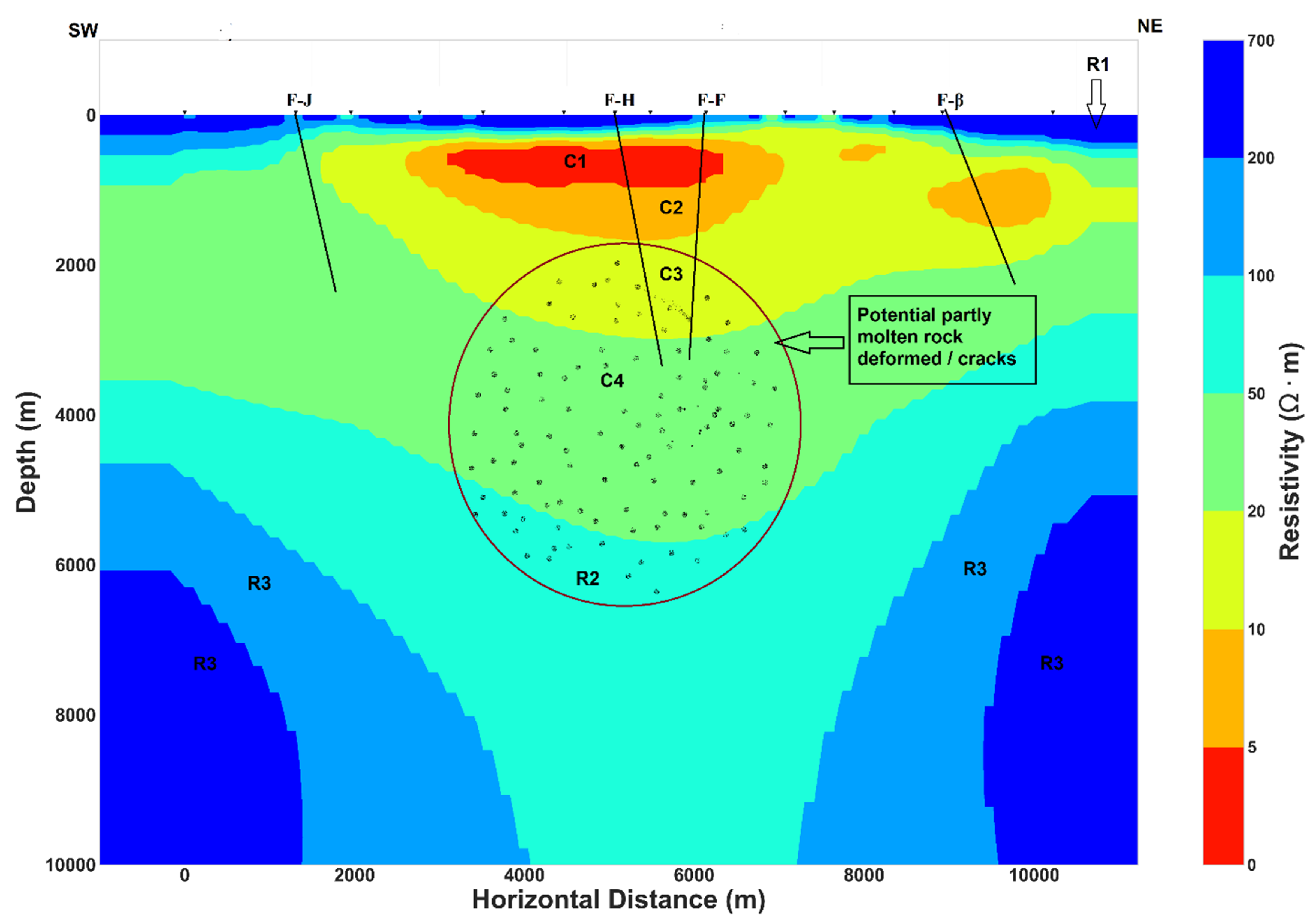
5.3. Subsurface Conductivity Structure and Associated Interpretations
5.3.1. Hydrothermal System and Fluid Circulation
5.3.2. The Importance of Conductive Major Normal Fault H
5.3.3. Potential Magma Reservoir Inferred from Joint Interpretation
6. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

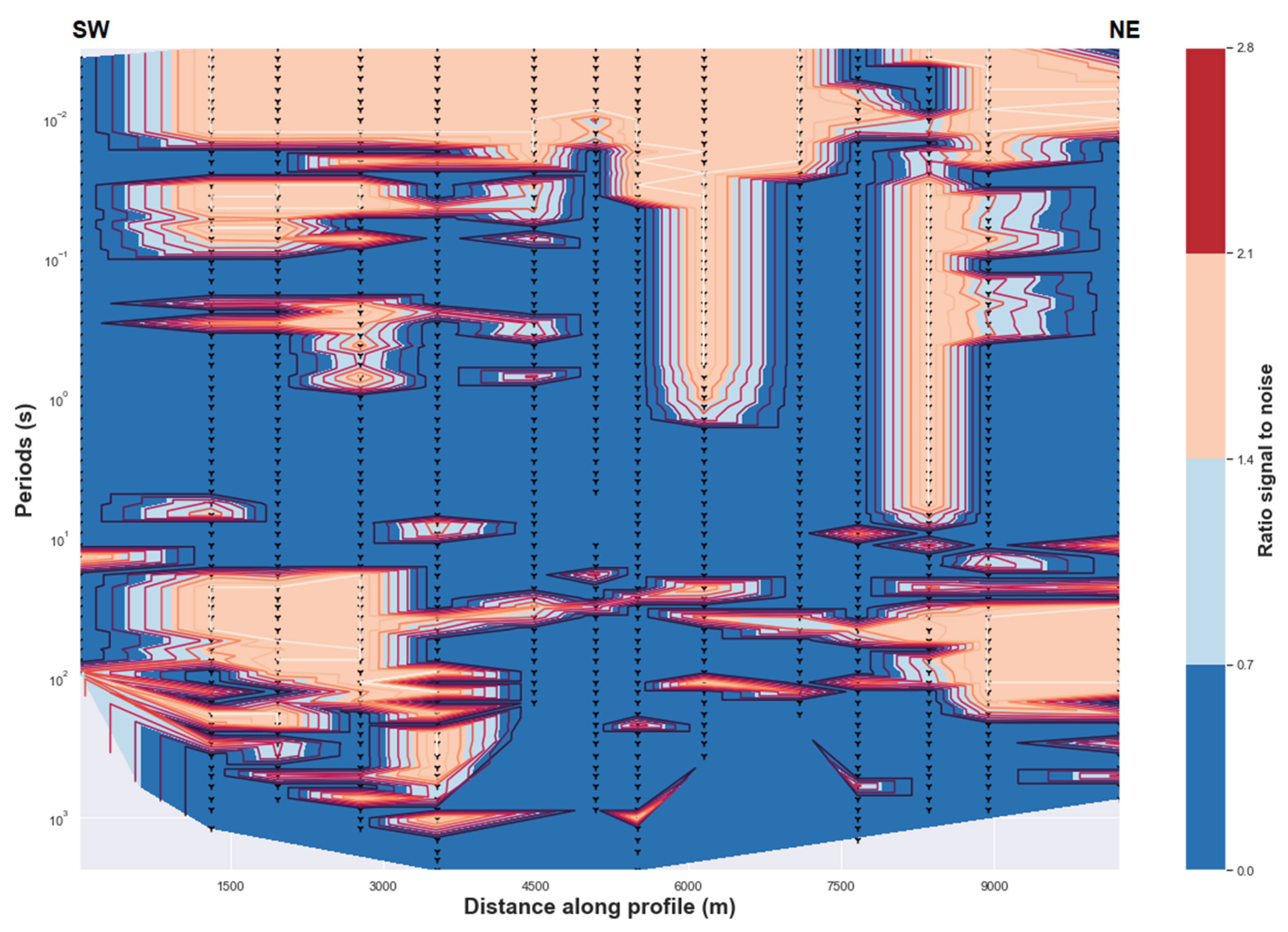

References
- Sanjuan, B.; Michard, G.; Michard, A. Origine des substances dissoutes dans les eaux des sources thermales et des forages de la région Asal-Ghoubbet (République de Djibouti). J. Volcanol. Geotherm. Res. 1990, 43, 333–352. [Google Scholar] [CrossRef]
- Manighetti, I.; Tapponnier, P.; Courtillot, V.; Gruszow, S.; Gillot, P.-Y. Propagation of rifting along the Arabia-Somalia Plate Boundary: The Gulfs of Aden and Tadjoura. J. Geophys. Res. Solid Earth 1997, 102, 2681–2710. [Google Scholar] [CrossRef]
- Doubre, C.; Peltzer, G. Fluid-controlled faulting process in the Asal Rift, Djibouti, from 8 yr of radar interferometry observations. Geol 2007, 35, 69. [Google Scholar] [CrossRef]
- Doubre, C.; Manighetti, I.; Dorbath, L.; Dorbath, C.; Bertil, D.; Delmond, J.C. Crustal structure and magmato-tectonic processes in an active rift (Asal-Ghoubbet, Afar, East Africa): 2. Insights from the 23-year recording of seismicity since the last rifting event. J. Geophys. Res. Solid Earth 2007, 112. [Google Scholar] [CrossRef]
- Mlynarski, M.; Zlotnicki, J. Fluid circulation in the active emerged Asal rift (east Africa, Djibouti) inferred from self-potential and Telluric–Telluric prospecting. Tectonophysics 2001, 339, 455–472. [Google Scholar] [CrossRef]
- Hassan Aden, A.; Raymond, J.; Giroux, B.; Sanjuan, B. New Insights into Hydrothermal Fluid Circulation Affected by Regional Groundwater Flow in the Asal Rift, Republic of Djibouti. Energies 2021, 14, 1166. [Google Scholar] [CrossRef]
- Giroux, B.; Chouteau, M.; Descloîtres, M.; Ritz, M. Use of the magnetotelluric method in the study of the deep Maestrichtian aquifer in Senegal. J. Appl. Geophys. 1997, 38, 77–96. [Google Scholar] [CrossRef]
- Meju, M.A. Geoelectromagnetic Exploration for Natural Resources: Models, Case Studies and Challenges. Surv. Geophys. 2002, 23, 133–206. [Google Scholar] [CrossRef]
- Spichak, V.; Manzella, A. Electromagnetic sounding of geothermal zones. J. Appl. Geophys. 2009, 68, 459–478. [Google Scholar] [CrossRef]
- Piña-Varas, P.; Ledo, J.; Queralt, P.; Marcuello, A.; Perez, N. On the detectability of Teide volcano magma chambers (Tenerife, Canary Islands) with magnetotelluric data. Earth Planets Space 2018, 70, 14. [Google Scholar] [CrossRef]
- Simpson, F. A three-dimensional electromagnetic model of the southern Kenya Rift: Departure from two dimensionality as a possible consequence of a rotating stress field. J. Geophys. Res. Solid Earth 2000, 105, 19321–19334. [Google Scholar] [CrossRef]
- Houssein, D.E.; Axelsson, G. Geothermal resources in the Asal Region, Republic of Djibouti: An update with emphasis on reservoir engineering studies. Geothermics 2010, 39, 220–227. [Google Scholar] [CrossRef]
- Manighetti, I.; Tapponnier, P.; Gillot, P.Y.; Jacques, E.; Courtillot, V.; Armijo, R.; Ruegg, J.C.; King, G. Propagation of rifting along the Arabia-Somalia Plate Boundary: Into Afar. J. Geophys. Res. Solid Earth 1998, 103, 4947–4974. [Google Scholar] [CrossRef]
- Gasse, F.; Fontes, J.-C. Palaeoenvironments and palaeohydrology of a tropical closed lake (Lake Asal, Djibouti) since 10,000 yr B.P. Palaeogeogr. Palaeoclimatol. Palaeoecol. 1989, 69, 67–102. [Google Scholar] [CrossRef]
- Stein, R.S.; Briole, P.; Ruegg, J.-C.; Tapponnier, P.; Gasse, F. Contemporary, Holocene, and Quaternary deformation of the Asal Rift, Djibouti: Implications for the mechanics of slow spreading ridges. J. Geophys. Res. Solid Earth 1991, 96, 21789–21806. [Google Scholar] [CrossRef]
- De Chabalier, J.-B.; Avouac, J.-P. Kinematics of the Asal Rift (Djibouti) Determined from the Deformation of Fieale Volcano. Science 1994, 265, 1677–1681. [Google Scholar] [CrossRef]
- Vigny, C.; de Chabalier, J.-B.; Ruegg, J.-C.; Huchon, P.; Kurt, L.F.; Cattin, R.; Asfaw, L.; Kanbari, K. Twenty-five years of geodetic measurements along the Tadjoura-Asal rift system, Djibouti, East Africa. J. Geophys. Res. Solid Earth 2007, 112. [Google Scholar] [CrossRef]
- Cattin, R.; Doubre, C.; de Chabalier, J.-B.; King, G.; Vigny, C.; Avouac, J.-P.; Ruegg, J.-C. Numerical modelling of quaternary deformation and post-rifting displacement in the Asal–Ghoubbet rift (Djibouti, Africa). Earth Planet. Sci. Lett. 2005, 239, 352–367. [Google Scholar] [CrossRef]
- Audin, L.; Manighetti, I.; Tapponnier, P.; Métivier, F.; Jacques, E.; Huchon, P. Fault propagation and climatic control of sedimentation on the Ghoubbet Rift Floor: Insights from the Tadjouraden cruise in the western Gulf of Aden. Geophys. J. Int. 2001, 144, 391–413. [Google Scholar] [CrossRef]
- Sakindi, G.U.G.T.P. (Iceland) Three-Dimensional Inversion of Magnetotelluric Data: Geological-Geothermal Interpretation of Asal Geothermal Field, Djibouti; United Nations University: Reykjavic, Iceland, 2015. [Google Scholar]
- Bahr, K. Interpretation of the magnetotelluric impedance tensor: Regional induction and local telluric distortion. J. Geophys. 1987, 62, 119–127. [Google Scholar]
- Caldwell, T.G.; Bibby, H.M.; Brown, C. The magnetotelluric phase tensor. Geophys. J. Int. 2004, 158, 457–469. [Google Scholar] [CrossRef]
- Weaver, J.T.; Agarwal, A.K.; Lilley, F.E.M. The relationship between the magnetotelluric tensor invariants and the phase tensor of Caldwell, Bibby, and Brown. ASEG Ext. Abstr. 2003, 2003, 1–8. [Google Scholar] [CrossRef]
- Heise, W.; Caldwell, T.G.; Bibby, H.M.; Brown, C. Anisotropy and phase splits in magnetotellurics. Phys. Earth Planet. Inter. 2006, 158, 107–121. [Google Scholar] [CrossRef]
- Booker, J.R. The Magnetotelluric Phase Tensor: A Critical Review. Surv. Geophys. 2014, 35, 7–40. [Google Scholar] [CrossRef]
- Szarka, L.; Menvielle, M. Analysis of rotational invariants of the magnetotelluric impedance tensor. Geophys. J. Int. 1997, 129, 133–142. [Google Scholar] [CrossRef]
- Lilley, F.E.M. Magnetotellurics: The CBB or phase tensor and Bahr’s 1988 analysis. Explor. Geophys. 2020, 51, 401–421. [Google Scholar] [CrossRef]
- Eisel, M.; Haak, V.; Pek, J.; Červ, V. A magnetotelluric profile across the German Deep Drilling Project (KTB) area: Two- and three-dimensional modeling results. J. Geophys. Res. Solid Earth 2001, 106, 16061–16073. [Google Scholar] [CrossRef]
- García Juanatey, M.A.; Hübert, J.; Tryggvason, A.; Juhlin, C.; Pedersen, L.B.; Bauer, T.E.; Dehghannejad, M. 2D and 3D MT in the central Skellefte Ore District, northern Sweden. Tectonophysics 2019, 764, 124–138. [Google Scholar] [CrossRef]
- Tournerie, B.; Chouteau, M.; Marcotte, D. Magnetotelluric static shift: Estimation and removal using the cokriging method. Geophysics 2007, 72, F25. [Google Scholar] [CrossRef]
- Arnason, K. The Static Shift Problem in MT Soundings. In Proceedings of the World Geothermal Congress, Melbourne, Australia, 19–25 April 2015. [Google Scholar]
- Gómez-Treviño, E.; Esparza, F.J.; Muñiz, Y.; Calderón, A. The magnetotelluric transverse electric mode as a natural filter for static effects: Application to the COPROD2 and COPROD2S2 data sets. Geophysics 2014, 79, E91–E99. [Google Scholar] [CrossRef]
- Moorkamp, M.; Avdeeva, A.; Basokur, A.T.; Erdogan, E. Inverting magnetotelluric data with distortion correction—Stability, uniqueness and trade-off with model structure. Geophys. J. Int. 2020, 222, 1620–1638. [Google Scholar] [CrossRef]
- Pellerin, L.D.; Hohmann, G.W. Transient electromagnetic inversion; a remedy for magnetotelluric static shifts. Geophysics 1990, 55, 1242–1250. [Google Scholar] [CrossRef]
- Krivochieva, S.; Chouteau, M. Integrating TDEM and MT methods for characterization and delineation of the Santa Catarina aquifer (Chalco Sub-Basin, Mexico). J. Appl. Geophys. 2003, 52, 23–43. [Google Scholar] [CrossRef]
- Nam, M.J.; Kim, H.J.; Song, Y.; Lee, T.J.; Suh, J.H. Three-dimensional topographic and bathymetric effects on magnetotelluric responses in Jeju Island, Korea. Geophys. J. Int. 2009, 176, 457–466. [Google Scholar] [CrossRef]
- Eisel, M.; Bahr, K. Electrical Anisotropy in the Lower Crust of British Columbia: An Interpretation of a Magnetotelluric Profile after Tensor Decomposition. J. Geomagn. Geoelec. 1993, 45, 1115–1126. [Google Scholar] [CrossRef]
- Bibby, H.M.; Caldwell, T.G.; Brown, C. Determinable and non-determinable parameters of galvanic distortion in magnetotellurics. Geophys. J. Int. 2005, 163, 915–930. [Google Scholar] [CrossRef]
- Kellett, R.L.; Mareschal, M.; Kurtz, R.D. A model of lower crustal electrical anisotropy for the Pontiac Subprovince of the Canadian Shield. Geophys. J. Int. 1992, 111, 141–150. [Google Scholar] [CrossRef]
- Heise, W.; Pous, J. Effects of anisotropy on the two-dimensional inversion procedure. Geophys. J. Int. 2001, 147, 610–621. [Google Scholar] [CrossRef]
- Tong, X.; Liu, J.; Li, A. Two-dimensional regularized inversion of AMT data based on rotation invariant of Central impedance tensor. Earth Planet. Phys. 2018, 2, 430–437. [Google Scholar] [CrossRef]
- Wannamaker, P.E.; Hasterok, D.P.; Johnston, J.M.; Stodt, J.A.; Hall, D.B.; Sodergren, T.L.; Pellerin, L.; Maris, V.; Doerner, W.M.; Groenewold, K.A.; et al. Lithospheric dismemberment and magmatic processes of the Great Basin–Colorado Plateau transition, Utah, implied from magnetotellurics. Geochem. Geophys. Geosyst. 2008, 9. [Google Scholar] [CrossRef]
- Pedersen, L.B.; Engels, M. Routine 2D inversion of magnetotelluric data using the determinant of the impedance tensor. Geophysics 2005, 70, G33–G41. [Google Scholar] [CrossRef]
- Bahr, K.; Bantin, M.; Jantos, C.; Schneider, E.; Storz, W. Electrical anisotropy from electromagnetic array data: Implications for the conduction mechanism and for distortion at long periods. Phys. Earth Planet. Inter. 2000, 119, 237–257. [Google Scholar] [CrossRef]
- Smittarello, D.; Grandin, R.; Chabalier, J.-B.D.; Doubre, C.; Deprez, A.; Masson, F.; Socquet, A.; Saad, I.A. Transient deformation in the Asal-Ghoubbet Rift (Djibouti) since the 1978 diking event: Is deformation controlled by magma supply rates? J. Geophys. Res. Solid Earth 2016, 121, 6030–6052. [Google Scholar] [CrossRef]
- Padilha, A.L.; Vitorello, Í.; Pádua, M.B.; Bologna, M.S. Lithospheric and sublithospheric anisotropy beneath central-southeastern Brazil constrained by long period magnetotelluric data. Phys. Earth Planet. Inter. 2006, 158, 190–209. [Google Scholar] [CrossRef]
- Pinzuti, P.; Humler, E.; Manighetti, I.; Gaudemer, Y. Petrological constraints on melt generation beneath the Asal Rift (Djibouti) using quaternary basalts. Geochem. Geophys. Geosyst. 2013, 14, 2932–2953. [Google Scholar] [CrossRef]
- Bahr, K.; Simpson, F. Electrical Anisotropy below Slow- and Fast-Moving Plates: Paleoflow in the Upper Mantle? Science 2002, 295, 1270–1272. [Google Scholar] [CrossRef] [PubMed]
- Brasse, H.; Kapinos, G.; Li, Y.; Mütschard, L.; Soyer, W.; Eydam, D. Structural electrical anisotropy in the crust at the South-Central Chilean continental margin as inferred from geomagnetic transfer functions. Phys. Earth Planet. Inter. 2009, 173, 7–16. [Google Scholar] [CrossRef]
- Frederiksen, A.W.; Ferguson, I.J.; Eaton, D.; Miong, S.-K.; Gowan, E. Mantle fabric at multiple scales across an Archean–Proterozoic boundary, Grenville Front, Canada. Phys. Earth Planet. Inter. 2006, 158, 240–263. [Google Scholar] [CrossRef]
- Shalivahan; Bhattacharya, B.B. Electrical anisotropy of asthenosphere in a region of window to mantle underneath Eastern Indian Craton. Phys. Earth Planet. Inter. 2005, 152, 43–61. [Google Scholar] [CrossRef]
- Wannamaker, P.E. Anisotropy versus Heterogeneity in Continental Solid Earth Electromagnetic Studies: Fundamental Response Characteristics and Implications for Physicochemical State. Surv. Geophys. 2005, 26, 733–765. [Google Scholar] [CrossRef]
- Prawirodirdjo, L.; Bock, Y. Instantaneous global plate motion model from 12 years of continuous GPS observations. J. Geophys. Res. Solid Earth 2004, 109. [Google Scholar] [CrossRef]
- Einarsson, P. Earthquakes and present-day tectonism in Iceland. Tectonophysics 1991, 189, 261–279. [Google Scholar] [CrossRef]
- Medynski, S.; Pik, R.; Burnard, P.; Dumont, S.; Grandin, R.; Williams, A.; Blard, P.-H.; Schimmelpfennig, I.; Vye-Brown, C.; France, L.; et al. Magmatic cycles pace tectonic and morphological expression of rifting (Afar depression, Ethiopia). Earth Planet. Sci. Lett. 2016, 446, 77–88. [Google Scholar] [CrossRef]
- Cox, S.F.; Knackstedt, M.A.; Braun, J. Principles of Structural Control on Permeability and Fluid Flow in Hydrothermal Systems. Rev. Econ. Geol. 2001. [Google Scholar] [CrossRef]
- Karato, S. The role of hydrogen in the electrical conductivity of the upper mantle. Nature 1990, 347, 272–273. [Google Scholar] [CrossRef]
- Duba, A.; Constable, S. The electrical conductivity of lherzolite. J. Geophys. Res. 1993, 98, 11885–11899. [Google Scholar] [CrossRef]
- Roux, E.; Moorkamp, M.; Jones, A.G.; Bischoff, M.; Endrun, B.; Lebedev, S.; Meier, T. Joint inversion of long-period magnetotelluric data and surface-wave dispersion curves for anisotropic structure: Application to data from Central Germany: Joint Inversion of Mt and Sw Data. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Gatzemeier, A.; Tommasi, A. Flow and electrical anisotropy in the upper mantle: Finite-element models constraints on the effects of olivine crystal preferred orientation and microstructure. Phys. Earth Planet. Inter. 2006, 158, 92–106. [Google Scholar] [CrossRef]
- Heise, W.; Caldwell, T.G.; Bertrand, E.A.; Hill, G.J.; Bennie, S.L.; Ogawa, Y. Changes in electrical resistivity track changes in tectonic plate coupling. Geophys. Res. Lett. 2013, 40, 5029–5033. [Google Scholar] [CrossRef]
- Kirkby, A.; Heinson, G.; Holford, S.; Thiel, S. Mapping fractures using 1D anisotropic modelling of magnetotelluric data: A case study from the Otway Basin, Victoria, Australia. Geophys. J. Int. 2015, 201, 1961–1976. [Google Scholar] [CrossRef]
- Nurhasan; Ogawa, Y.; Ujihara, N.; Tank, S.B.; Honkura, Y.; Onizawa, S.; Mori, T.; Makino, M. Two electrical conductors beneath Kusatsu-Shirane volcano, Japan, imaged by audiomagnetotellurics, and their implications for the hydrothermal system. Earth Planets Space 2006, 58, 1053–1059. [Google Scholar] [CrossRef]
- Usui, Y.; Ogawa, Y.; Aizawa, K.; Kanda, W.; Hashimoto, T.; Koyama, T.; Yamaya, Y.; Kagiyama, T. Three-dimensional resistivity structure of Asama Volcano revealed by data-space magnetotelluric inversion using unstructured tetrahedral elements. Geophys. J. Int. 2017, 208, 1359–1372. [Google Scholar] [CrossRef]
- Ebinger, C.J.; Casey, M. Continental breakup in magmatic provinces: An Ethiopian example. Geology 2001, 29, 527–530. [Google Scholar] [CrossRef]
- Doubre, C.; Geoffroy, L. Rift-zone development around a plume-related magma centre on the Isle of Skye (Scotland): A model for stress inversions. Terra Nova 2003, 15, 230–237. [Google Scholar] [CrossRef]
- Keir, D.; Hamling, I.J.; Ayele, A.; Calais, E.; Ebinger, C.; Wright, T.J.; Jacques, E.; Mohamed, K.; Hammond, J.O.S.; Belachew, M.; et al. Evidence for focused magmatic accretion at segment centers from lateral dike injections captured beneath the Red Sea rift in Afar. Geology 2009, 37, 59–62. [Google Scholar] [CrossRef]
- Zan, L.; Gianelli, G.; Passerini, P.; Troisi, C.; Haga, A.O. Geothermal exploration in the republic of djibouti: Thermal and geological data of the hanlé and asal areas. Geothermics 1990, 19, 561–582. [Google Scholar] [CrossRef]
- Triahadini, A.; Aizawa, K.; Teguri, Y.; Koyama, T.; Tsukamoto, K.; Muramatsu, D.; Chiba, K.; Uyeshima, M. Magnetotelluric transect of Unzen graben, Japan: Conductors associated with normal faults. Earth Planets Space 2019, 71, 28. [Google Scholar] [CrossRef]
- Usui, Y.; Uyeshima, M.; Ogawa, T.; Yoshimura, R.; Oshiman, N.; Yamaguchi, S.; Toh, H.; Murakami, H.; Aizawa, K.; Tanbo, T.; et al. Electrical Resistivity Structure around the Atotsugawa Fault, Central Japan, Revealed by a New 2-D Inversion Method Combining Wideband-MT and Network-MT Data Sets. J. Geophys. Res. Solid Earth 2021, 126, e2020JB020904. [Google Scholar] [CrossRef]
- Partzsch, G.M.; Schilling, F.R.; Arndt, J. The influence of partial melting on the electrical behavior of crustal rocks: Laboratory examinations, model calculations and geological interpretations. Tectonophysics 2000, 317, 189–203. [Google Scholar] [CrossRef]
- Abdallah, S.; Utsugi, M.; Aizawa, K.; Uyeshima, M.; Kanda, W.; Koyama, T.; Shiotani, T. Three-dimensional electrical resistivity structure of the Kuju volcanic group, Central Kyushu, Japan revealed by magnetotelluric survey data. J. Volcanol. Geotherm. Res. 2020, 400, 106898. [Google Scholar] [CrossRef]
- Hassan Aden, A.; Raymond, J.; Giroux, B. Numerical Modeling of Hydrothermal System Circulation Beneath Asal Rift, Republic of Djibouti. Energies 2022, 15, 9310. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hassan Aden, A. Hydrothermal Reservoir and Electrical Anisotropy Investigated by Magnetotelluric Data, Case Study of Asal Rift, Republic of Djibouti. Appl. Sci. 2023, 13, 1157. https://doi.org/10.3390/app13021157
Hassan Aden A. Hydrothermal Reservoir and Electrical Anisotropy Investigated by Magnetotelluric Data, Case Study of Asal Rift, Republic of Djibouti. Applied Sciences. 2023; 13(2):1157. https://doi.org/10.3390/app13021157
Chicago/Turabian StyleHassan Aden, Abdek. 2023. "Hydrothermal Reservoir and Electrical Anisotropy Investigated by Magnetotelluric Data, Case Study of Asal Rift, Republic of Djibouti" Applied Sciences 13, no. 2: 1157. https://doi.org/10.3390/app13021157
APA StyleHassan Aden, A. (2023). Hydrothermal Reservoir and Electrical Anisotropy Investigated by Magnetotelluric Data, Case Study of Asal Rift, Republic of Djibouti. Applied Sciences, 13(2), 1157. https://doi.org/10.3390/app13021157



