Viscoelastic Strains of Palaeozoic Shales under the Burger’s Model Description
Abstract
:1. Introduction
2. Characteristics of the Material
3. Laboratory Rheological Analyses of Paleozoic Rocks
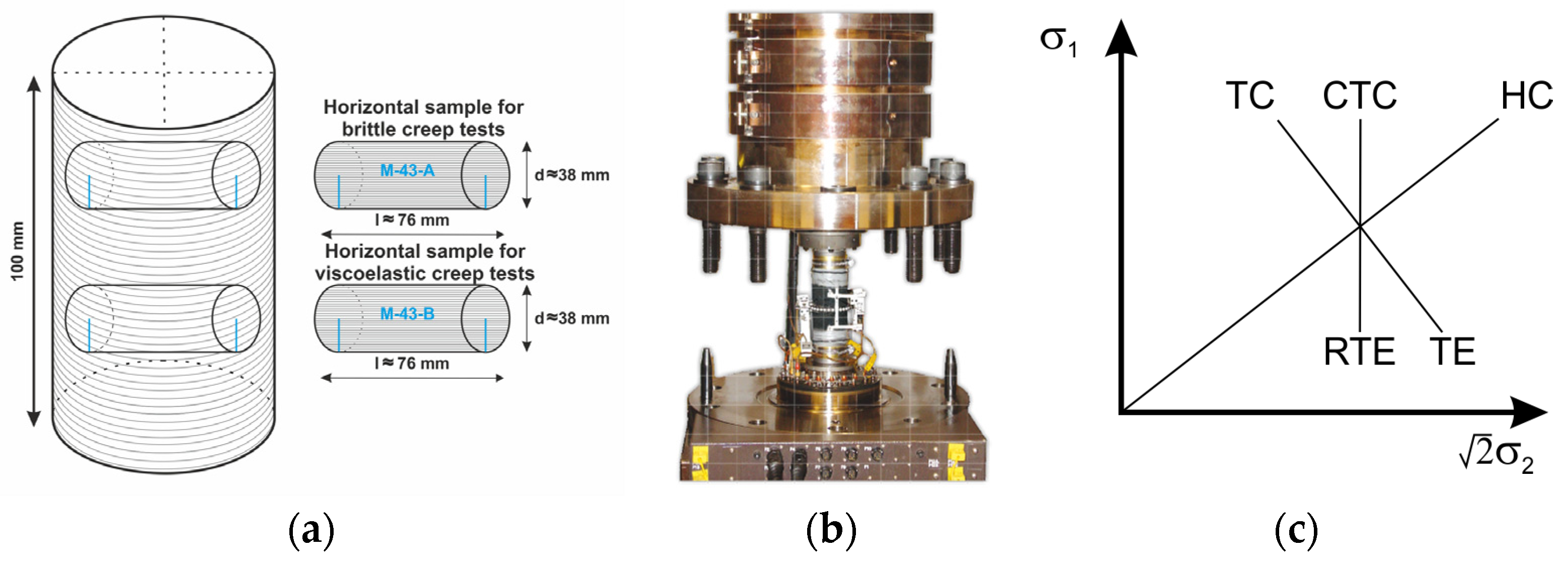
3.1. Experimental Equipment
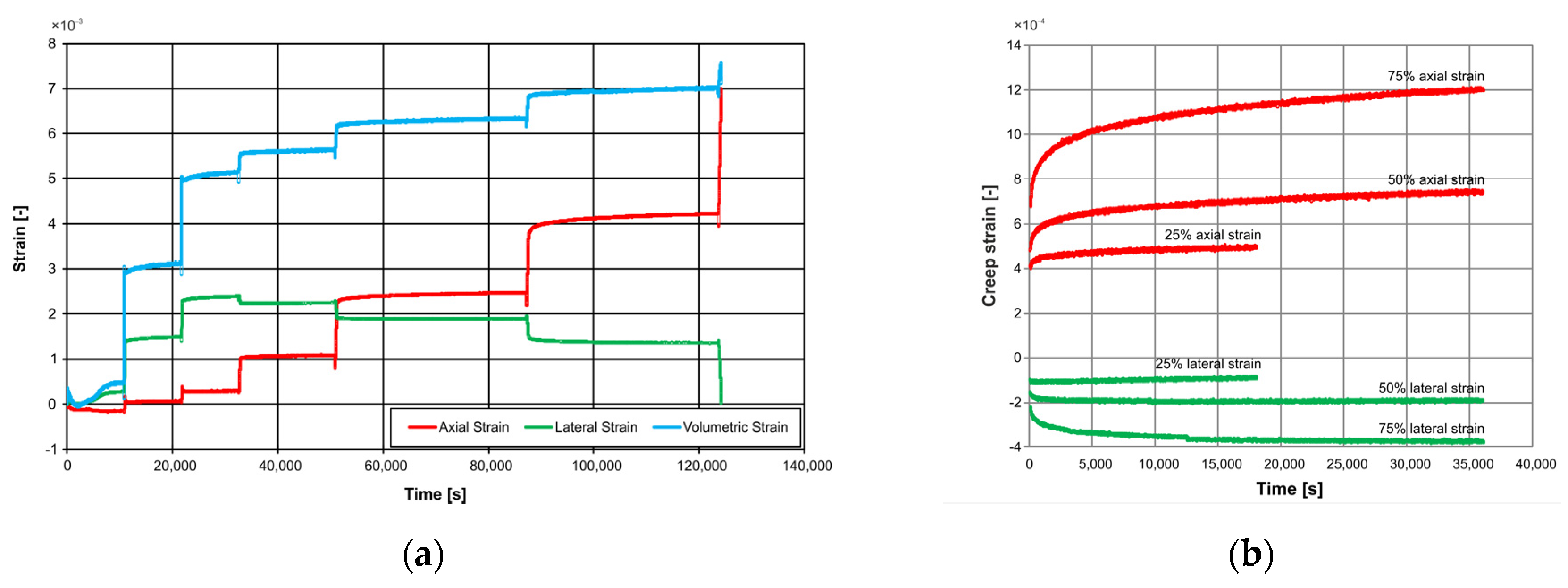
3.2. Initial Creep Analysis in Paleozoic Shales on 1D Models
4. Theoretical Basics of Rock Rheology in Triaxial Test Conditions for the Burger’s Model
- σm is axiator of the stress tensor σm = (σ1 + σ2 + σ3)/3 = σokt,
- εm is axiator of the strain tensor εm = (ε1 + ε2 + ε3)/3 = εokt,
- Sij is deviatoric stress tensor,
- eij is deviatoric strain tensor.
- and are the first and second derivative of the average stress, respectively,
- vol and vol are the first and second derivatives of the volumetric strain, respectively,
- ij and ij are the first and second derivatives of deviatoric stress tensor, respectively,
- ij and ij are the first and second derivatives of the deviatoric strain tensor, respectively.

4.1. Parameters of Burger’s Model for the Paleozoic Shales from the Baltic Basin
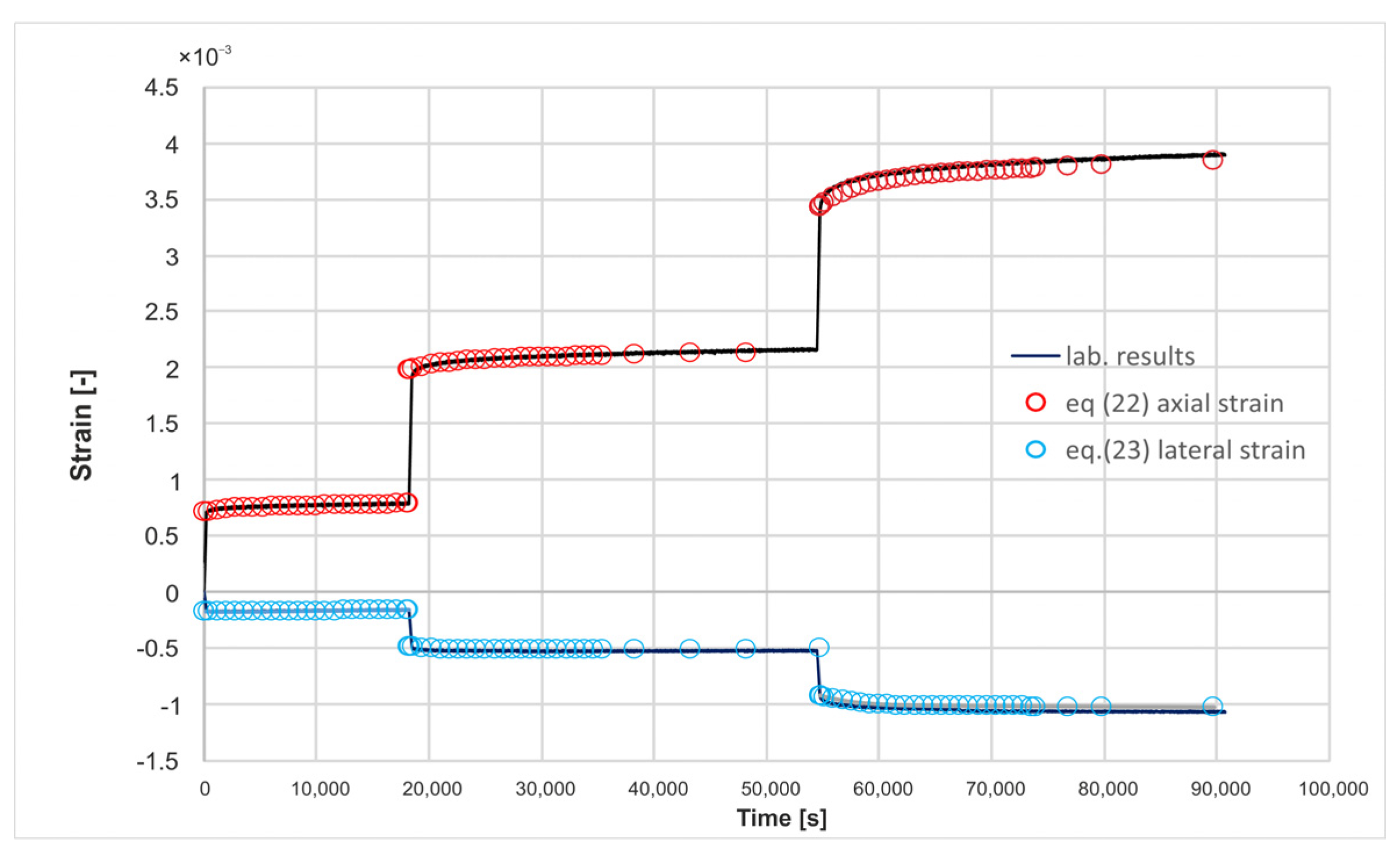
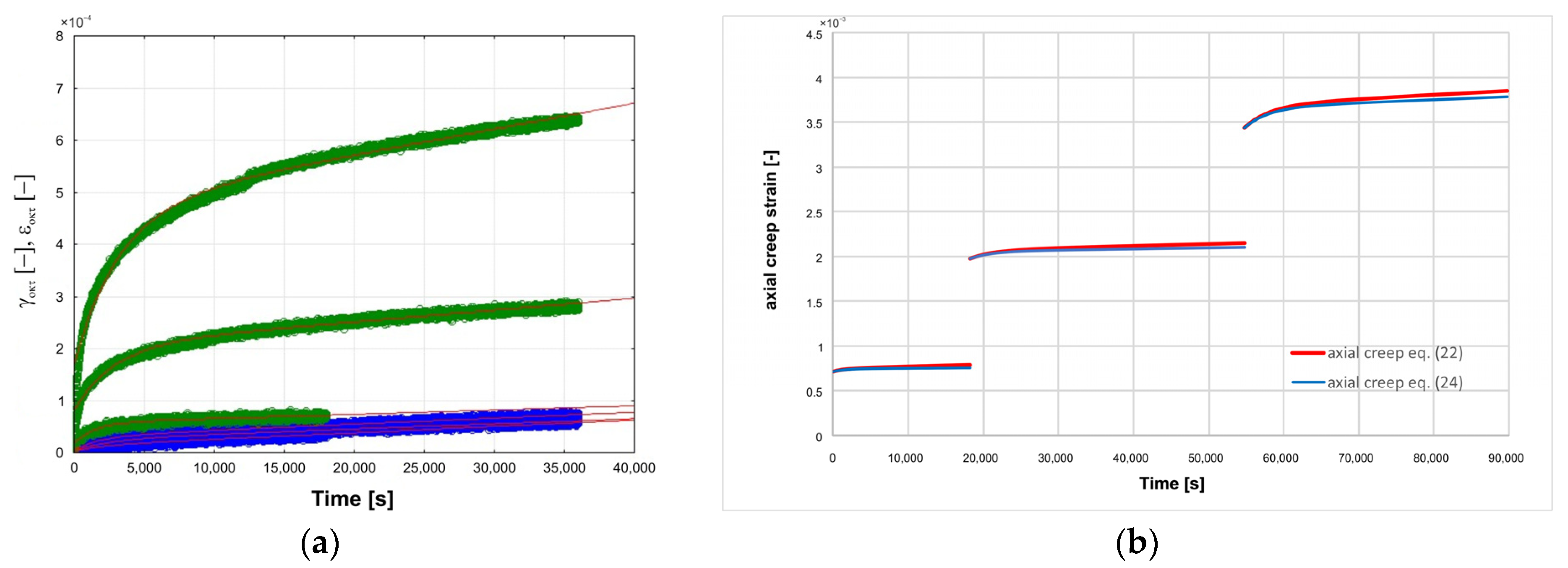
5. Verification of Burger’s Model for Creep Description in Paleozoic Shales in Conventional Triaxial Loading Conditions
6. Assessing the Significance of Volumetric Creep Description in Paleozoic Shales
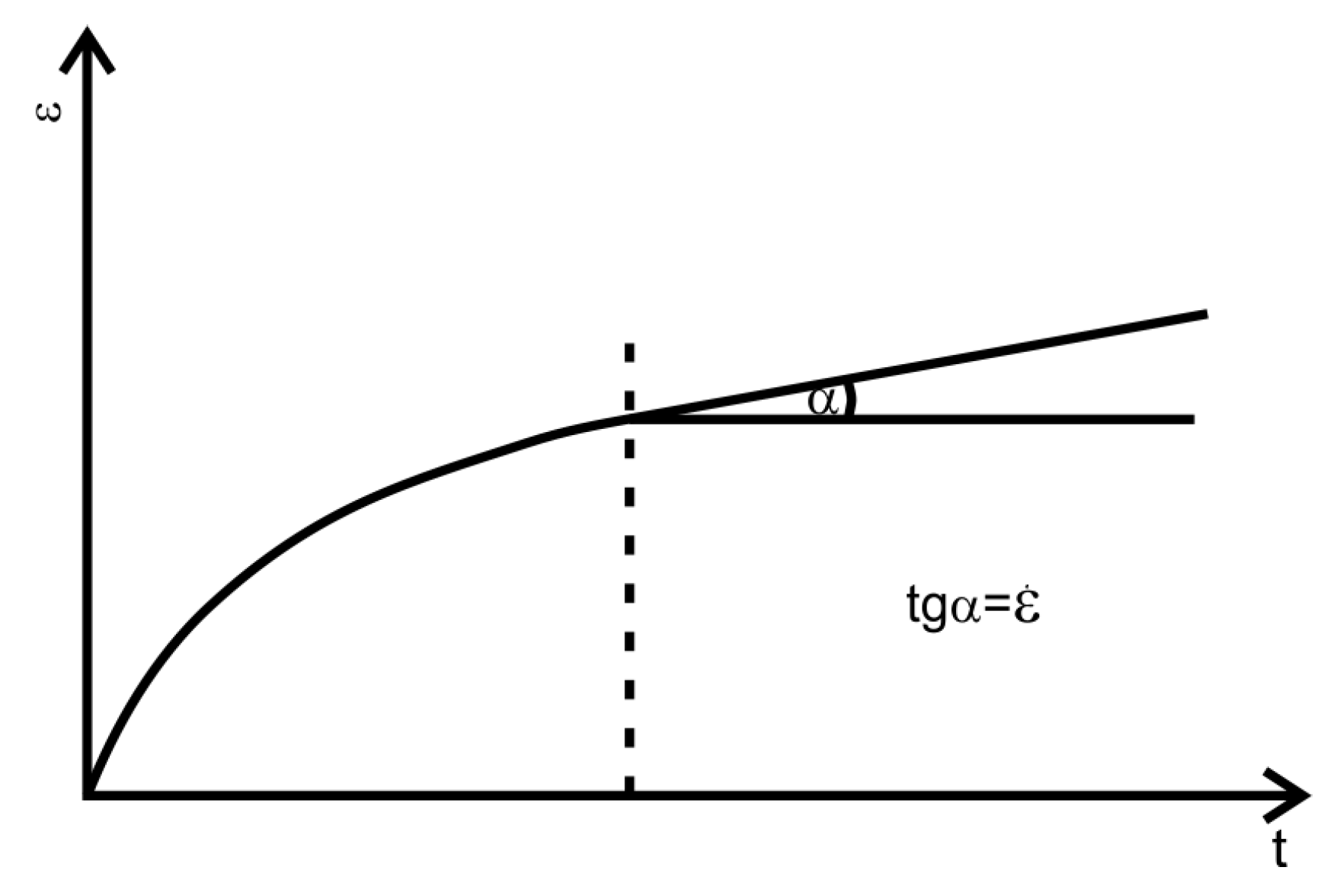
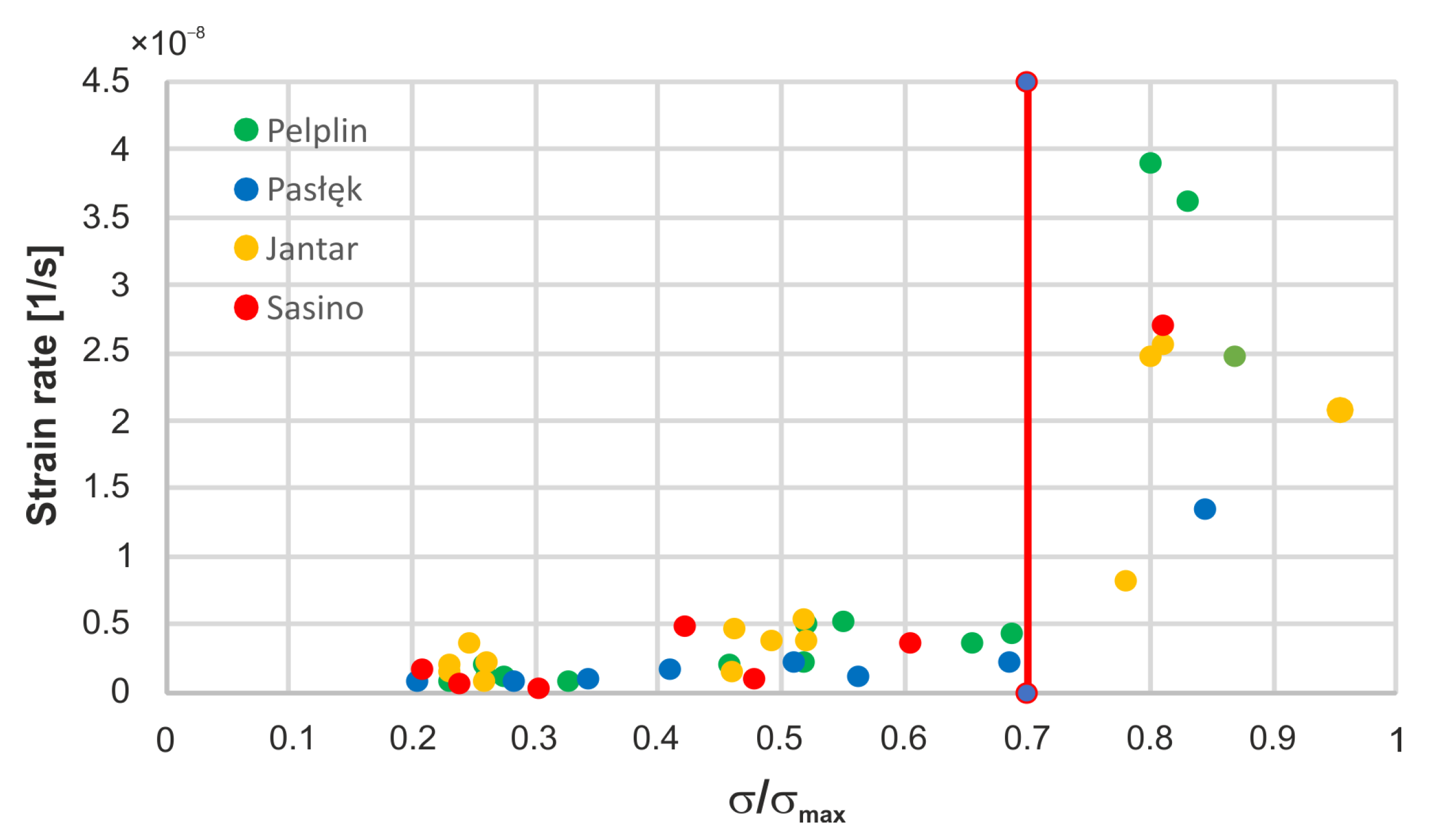
7. Linear Creep Limit in Paleozoic Shales
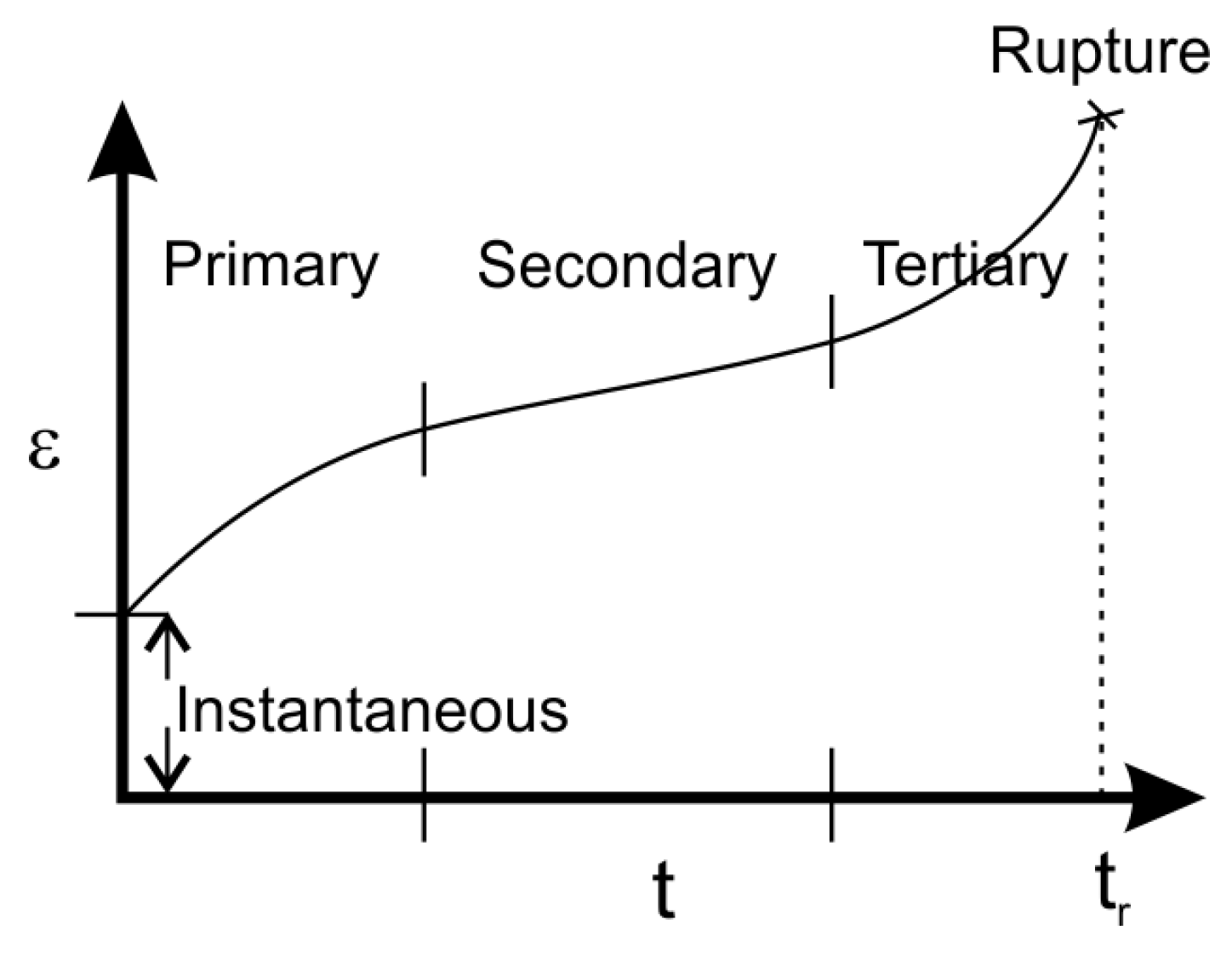
8. Summary and Remarks on Creep in Shales with Regard to Loadings Exceeding Secondary Creep
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, H.; Su, T.; Deng, H.; Wang, R.; Zhao, J.; Sun, X.; An, L. Characterizing three-dimensional creep of Beishan granite by the variable-coefficient Abel dashpot. Mech. Time-Depend. Mater. 2021, 25, 85–100. [Google Scholar] [CrossRef]
- Frenelus, W.; Peng, H.; Zhang, J. Creep Behavior of Rocks and Its Application to the Long-Term Stability of Deep Rock Tunnels. Appl. Sci. 2022, 12, 8451. [Google Scholar] [CrossRef]
- Xue, W.; Wang, Y.; Chen, Z.; Liu, H. An integrated model with stable numerical methods for fractured underground gas storage. J. Clean. Prod. 2023, 393, 136268. [Google Scholar] [CrossRef]
- Jin, J.; Cristescu, N.D. Anelasticviscoplastic model for transient creep of rock salt. Int. J. Plast. 1998, 41, 85–107. [Google Scholar] [CrossRef]
- Zhou, H.W.; Wang, C.P.; Han, B.B.; Duan, Z.Q. A creep constitutive model for salt rock based on fractional derivatives. Int. J. Rock Mech. Min. 2011, 48, 116–121. [Google Scholar] [CrossRef]
- Yang, C.; Wang, T.; Li, Y.; Yang, H.; Li, J.; Qu, D.; Xu, B.; Yang, Y.; Daemen, J. Feasibility analysis of using abandoned salt caverns for large-scale underground energy storage in China. Appl. Energy 2015, 137, 467–481. [Google Scholar] [CrossRef]
- Wu, F.; Chen, J.; Zou, Q.L. A nonlinear creep damage model for salt rock. Int. J. Damage Mech. 2019, 28, 758–771. [Google Scholar] [CrossRef]
- Vernik, L.; Nur, A. Ultrasonic velocity and anisotropy of hydrocarbon source rocks. Geophysics 1992, 57, 727–735. [Google Scholar] [CrossRef]
- Sarout, J.; Guéguen, Y. Anisotropy of elastic wave velocities in deformed shales: Part 1—Experimental results. Geophysics 2008, 73, 75–89. [Google Scholar] [CrossRef]
- Kohli, A.H.; Zoback, M.D. Frictional properties of shale reservoir rocks. J. Geophys. Res. Solid Earth 2013, 118, 5109–5125. [Google Scholar] [CrossRef]
- Dewhurst, D.N.; Siggins, A.F. Impact of fabric, microcracks and stress field on shale anisotropy. Geophys. J. Int. 2006, 165, 135–148. [Google Scholar] [CrossRef]
- Sone, H.; Zoback, M.D. Mechanical properties of shale-gas reservoir rocks—Part 1: Static and dynamic elastic properties and anisotropy. Geophysics 2013, 78, 381–392. [Google Scholar] [CrossRef]
- Rybacki, E.; Reinicke, A.; Meier, T.; Makasi, M.; Dresen, G. What controls the mechanical properties of shale rocks?—Part I: Strength and Young’s modulus. J. Pet. Sci. Eng. 2015, 135, 702–722. [Google Scholar] [CrossRef]
- Kamali-Asl, A.; Ghazanfari, E.; Newell, P.; Stevens, M. Elastic, viscoelastic, and strength properties of Marcellus Shale specimens. J. Pet. Sci. Eng. 2018, 171, 662–679. [Google Scholar] [CrossRef]
- Liang, Z.; Chen, Z.; Rahman, S.S. Experimental investigation of the primary and secondary creep behavior of shale gas reservoir rocks from deep sections of the Cooper Basin. J. Nat. Gas Sci. Eng. 2020, 73, 103044. [Google Scholar] [CrossRef]
- Sone, H.; Zoback, M.D. Mechanical properties of shale-gas reservoir rocks -part 2:ductile creep, brittle strength, and their relation to the elastic modulus. Geophysics 2013, 78, 393–402. [Google Scholar] [CrossRef]
- Herrmann, J.; Rybacki, E.; Sone, H.; Dresen, G. Deformation Experiments on Bowland and Posidonia Shale—Part II: Creep Behavior at In Situ pc–T Conditions. Rock Mech. Rock Eng. 2020, 53, 755–779. [Google Scholar] [CrossRef]
- Mighani, S.; Bernabé, Y.; Boulenouar, A.; Mok, U.; Evans, B. Creep Deformation in Vaca Muerta Shale From Nanoindentation to Triaxial Experiments. JGR Solid Earth 2019, 124, 7842–7868. [Google Scholar] [CrossRef]
- Liu, K.; Rassouli, F.S.; Liu, B.; Ostadhassan, M. Creep Behavior of Shale: Nanoindentation vs. Triaxial Creep Tests. Rock Mech. Rock Eng. 2020, 54, 321–335. [Google Scholar] [CrossRef]
- Gupta, N.; Mishra, B. Experimental Investigation of the Influence of Bedding Planes and Differential Stress on Microcrack Propagation in Shale Using X-ray CT Scan. Geotech. Geol. Eng. 2021, 39, 213–236. [Google Scholar] [CrossRef]
- Trzeciak, M.; Sone, H.; Dąbrowski, M. Long-term creep tests and viscoelastic constitutive modeling of lower Paleozoic shales from the Baltic Basin, N Poland. Int. J. Rock Mech. Min. Sci. 2018, 112, 139–157. [Google Scholar] [CrossRef]
- Ding, X.; Zhang, F.; Zhang, G.; Yang, L.; Shao, J. Modeling of hydraulic fracturing in viscoelastic formations with the fractional Maxwell model. Comput. Geotech. 2020, 126, 103723. [Google Scholar] [CrossRef]
- Yang, Y.; Zoback, M.D. Viscoplastic Deformation of the Bakken and Adjacent Formations and Its Relation to Hydraulic Fracture Growth. Rock Mech. Rock Eng. 2016, 49, 689–698. [Google Scholar] [CrossRef]
- Rybacki, E.; Herrmann, J.; Wirth, R.; Dresen, G. Creep of Posidonia shale at elevated pressure and temperature. Rock Mech. Rock Eng. 2017, 50, 3121–3140. [Google Scholar] [CrossRef]
- Kang, J.; Zhou, F.; Liu, C.; Liu, Y. A fractional non-linear creep model for coal considering damage effect and experimental validation. Int. J. Non-Linear Mech. 2015, 76, 20–28. [Google Scholar] [CrossRef]
- Hu, K.; Feng, Q.; Li, H.; Hu, Q. Study on Creep Characteristics and Constitutive Model for Thalam Rock Mass with Fracture in Tunnel. Geotech Geol. Eng. 2018, 36, 827–834. [Google Scholar] [CrossRef]
- Sone, H.; Zoback, M.D. Time-dependent deformation of shale gas reservoir rocks and its long-term effect on the in situ state of stress. Int. J. Rock Mech. Min. Sci. 2014, 69, 120–132. [Google Scholar] [CrossRef]
- Mandal, P.P.; Sarout, J.; Rezaee, R. Triaxial Deformation of the Goldwyer Gas Shale at In Situ Stress Conditions—Part II: Viscoelastic Creep/Relaxation and Frictional Failure. Rock Mech. Rock Eng. 2023, 56, 7441–7474. [Google Scholar] [CrossRef]
- Haghighat, E.; Rassouli, F.S.; Zoback, M.D.; Juanes, R. A viscoplastic model of creep in shale. Geophysics 2020, 85, MR155–MR166. [Google Scholar] [CrossRef]
- Yin, Q.; Liu, Y.; Borja, R.I. Mechanisms of creep in shale from nanoscale to specimen scale. Comput. Geotech. 2021, 136, 104138. [Google Scholar] [CrossRef]
- Modliński, Z.; Podhalańska, T. Outline of the lithology and depositional features of the lower Paleozoic strata in the Polish part of the Baltic region. Geol. Q. 2010, 54, 109–121. [Google Scholar]
- Wilczynski, P.M.; Domonik, A.; Lukaszewski, P. Anisotropy of Strength and Elastic Properties of Lower Paleozoic Shales from the Baltic Basin, Poland. Energies 2021, 14, 2995. [Google Scholar] [CrossRef]
- Leśniak, G.; Sowiżdżał, K.; Stadtmuller, M.; Lis-Śledziona, A.; Kaczmarczyk, W.; Słota-Valim, M.; Kasza, P. Performing Non-Standard Comprehensive Petrophysical and Geomechanical Studies on Samples and Data from Lower Palaeozoic Shales; Technical Report Shalemech No. 3; INiG–PIB: Kraków, Poland, 2017. (In Polish) [Google Scholar]
- Wilczynski, P.M.; Domonik, A.; Lukaszewski, P. Brittle Creep and Viscoelastic Creep in Lower Palaeozoic Shales from the Baltic Basin, Poland. Energies 2021, 14, 4633. [Google Scholar] [CrossRef]
- Jaeger, J.C.; Cook, N.G.W. Fundamentals of Rock Mechanics; Methuen & Co., Ltd.: London, UK, 1969. [Google Scholar]
- Tajduś, A. Maintenance of Roadways in the Light of the Influence of Time on Stresses, Strains and Zones of Destruction in the Rock Mass. In ZN Górnictwo; AGH: Kraków, Poland, 1990; Volume 154. (In Polish) [Google Scholar]
- Lakes, R.S. Viscoelastic Materials; Cambridge University Press: New York, NY, USA, 2009. [Google Scholar]
- Ganczarski, A.; Skrzypek, J. Mechanics of Modern Materials, 1st ed.; Cracow University of Technology: Kraków, Poland, 2013; p. 308. (In Polish) [Google Scholar]
- Cristescu, N.D.; Hunsche, U. Time Effects in Rock Mechanics; Wiley & Sons: Chichester, QC, Cananda, 1998. [Google Scholar]
- Kwaśniewski, M. Nonlinear model of rock creep. Zesz. Nauk. Politech. Śląskiej 1987, 157, 151–186. (In Polish) [Google Scholar]
- Zheng, H.; Feng, X.-T.; Hao, X. A creep model for weakly consolidated porous sandstone including volumetric creep. Int. J. Rock Mech. Min. Sci. 2015, 78, 99–107. [Google Scholar] [CrossRef]
- Flisiak, J.; Mazurek, J.; Tajduś, A. Rheological properties of Krakowiec clays. In ZN Górnictwo; AGH: Kraków, Poland, 1992; Volume 16, pp. 273–298. (In Polish) [Google Scholar]
- Chen, W.F.; Mizuno, E. Nonlinear Analysis in Soil Mechanics; Elsevier: Amsterdam, The Netherlands; Oxford, UK; New York, NY, USA; Tokyo, Japan, 1990. [Google Scholar]
- Tibco Statistica™, version 13.1. 2022. Product Documentation. Tibco: Palo Alto, CA, USA, 2023.
- Sone, H.; Zoback, M.D. Visco-Plastic Properties of Shale Gas Reservoir Rocks. ARMA. 2011. ARMA-11-417. Available online: https://pangea.stanford.edu/departments/geophysics/dropbox/STRESS/publications/MDZ%20PDF's/2011/2011_Visco_plastic_propoerties_Sone_Zoback.pdf (accessed on 30 September 2023).
- Feng, X. Experiment and Numerical Simulation on Creep Mechanical Behaviors of Mudstone under Unloading Condition. Hindawi Geofluids 2022, 2022, 7175774. [Google Scholar] [CrossRef]
- Huang, P.; Zhang, J.; Spearing, A.J.S.; Chai, J.; Dong, C. Experimental study of the creep properties of coal considering initial damage. Int. J. Rock Mech. Min. Sci. 2021, 139, 104629. [Google Scholar] [CrossRef]
- Zhao, Y.; Cao, P.; Wang, W.; Wan, W.; Liu, Y. Viscoelasto-plastic rheological experiment under circular increment step load and unload and nonlinear creep model of soft rocks. J. Cent. South Univ. Technol. 2009, 16, 488–494. [Google Scholar] [CrossRef]
- Wang, W.; Lv, J.; Wang, H. A creep-damage constitutive model for sandstone. Appl. Mech. Mater. 2012, 170–173, 289–294. [Google Scholar] [CrossRef]
- Kranz, R.L.; Scholz, C.H. Critical dilatant volume of rocks at the onset of tertiary creep. J. Geophys. Res. 1977, 82, 893–898. [Google Scholar] [CrossRef]
- Lockner, D. Room Temperature Creep in Saturated Granite. J. Geophys. Res. 1993, 98, 475–487. [Google Scholar] [CrossRef]
- Brantut, N.; Heap, M.; Meredith, P.; Baud, P. Time-dependent cracking and brittle creep in crustal rocks: A review. J. Struct. Geol. 2013, 52, 17–43. [Google Scholar] [CrossRef]


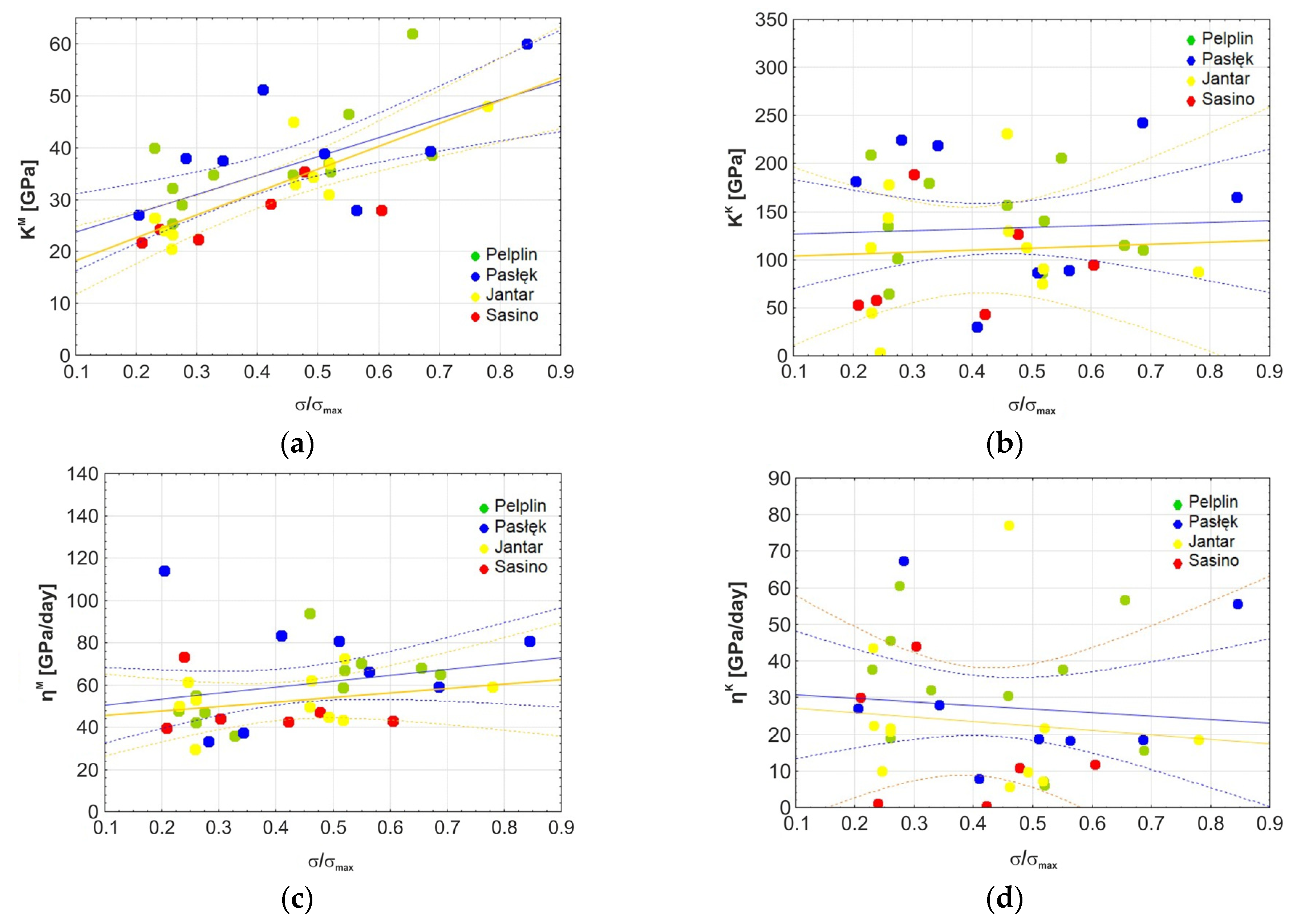
| Deviatoric Creep | Volumetric Creep | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sample | Sample | (σ1 − σ3) | GK | GM | R2 | KK | KM | R2 | ||||
| Location | Number | [GPa] | [GPa] | [GPa/day] | [GPa/day] | [GPa] | [GPa] | [GPa/day] | [GPa/day] | |||
| Pelplin | W260A | 0.23 | 473 | 25 | 8.0 | 292 | 0.89 | 420 | 40 | 38 | 48 | 0.87 |
| 0.46 | 237 | 19 | 7.6 | 167 | 0.98 | 315 | 35 | 31 | 94 | 0.90 | ||
| 0.69 | 81 | 16 | 3.0 | 63 | 0.99 | 221 | 39 | 16 | 65 | 0.89 | ||
| W264A | 0.27 | 242 | 20 | 4.7 | 192 | 0.96 | 203 | 29 | 61 | 47 | 0.93 | |
| 0.55 | 166 | 20 | 3.0 | 63 | 0.99 | 413 | 46 | 38 | 70 | 0.90 | ||
| B211A | 0.33 | 400 | 18 | 7.1 | 205 | 0.91 | 359 | 35 | 32 | 36 | 0.90 | |
| 0.65 | 133 | 18 | 2.2 | 86 | 0.99 | 231 | 62 | 57 | 68 | 0.91 | ||
| M30B | 0.26 | 282 | 18 | 4.1 | 166 | 0.95 | 130 | 32 | 46 | 55 | 0.83 | |
| 0.52 | 118 | 15 | 2.7 | 60 | 0.98 | 281 | 35 | 6 | 67 | 0.87 | ||
| W260B | 0.26 | 268 | 19 | 5.1 | 107 | 0.98 | 269 | 25 | 19 | 42 | 0.92 | |
| 0.52 | 128 | 17 | 6.1 | 145 | 0.98 | 174 | 37 | 7 | 59 | 0.89 | ||
| Pasłęk | W278A | 0.28 | 372 | 20 | 7.4 | 224 | 0.90 | 450 | 38 | 67 | 33 | 0.90 |
| 0.56 | 162 | 17 | 4.7 | 191 | 0.97 | 178 | 28 | 18 | 66 | 0.92 | ||
| 0.84 | 15 | 13 | 1.1 | 20 | 0.99 | 331 | 60 | 56 | 81 | 0.95 | ||
| W278B | 0.34 | 185 | 16 | 3.7 | 194 | 0.88 | 439 | 38 | 28 | 37 | 0.85 | |
| 0.69 | 20 | 12 | 0.6 | 43 | 0.98 | 485 | 39 | 19 | 59 | 0.82 | ||
| B236A | 0.20 | 711 | 24 | 9.1 | 195 | 0.96 | 363 | 27 | 27 | 114 | 0.92 | |
| 0.41 | 257 | 21 | 5.3 | 138 | 0.90 | 61 | 51 | 16 | 117 | 0.88 | ||
| W277B | 0.51 | 68 | 17 | 1.1 | 71 | 0.92 | 173 | 39 | 19 | 81 | 0.90 | |
| Jantar | W305A | 0.25 | 244 | 18 | 1.8 | 76 | 0.96 | 6 | 24 | 10 | 61 | 0.78 |
| 0.49 | 123 | 14 | 1.3 | 32 | 0.98 | 226 | 34 | 10 | 45 | 0.89 | ||
| W306A | 0.26 | 260 | 19 | 4.6 | 104 | 0.97 | 357 | 23 | 22 | 53 | 0.91 | |
| 0.52 | 110 | 14 | 3.3 | 80 | 0.99 | 182 | 37 | 22 | 73 | 0.94 | ||
| 0.78 | 42 | 10 | 1.3 | 31 | 0.99 | 175 | 48 | 19 | 59 | 0.95 | ||
| B275B | 0.26 | 246 | 15 | 4.1 | 155 | 0.88 | 287 | 20 | 21 | 30 | 0.90 | |
| 0.52 | 98 | 12 | 1.6 | 34 | 0.94 | 150 | 31 | 7 | 43 | 0.90 | ||
| B279D | 0.23 | 329 | 19 | 5.7 | 119 | 0.96 | 226 | 26 | 44 | 164 | 0.73 | |
| 0.46 | 145 | 17 | 3.0 | 67 | 0.98 | 464 | 45 | 77 | 50 | 0.81 | ||
| M43BB | 0.23 | 285 | 20 | 2.8 | 110 | 0.95 | 90 | 26 | 22 | 50 | 0.83 | |
| 0.46 | 142 | 16 | 3.0 | 60 | 0.90 | 261 | 33 | 6 | 62 | 0.78 | ||
| Sasino | M60B | 0.30 | 336 | 18 | 7.1 | 105 | 0.92 | 378 | 22 | 22 | 44 | 0.90 |
| 0.60 | 169 | 16 | 3.1 | 62 | 0.98 | 191 | 28 | 28 | 12 | 0.92 | ||
| W320B | 0.21 | 314 | 18 | 1.9 | 185 | 0.92 | 106 | 22 | 44 | 39 | 0.82 | |
| 0.42 | 161 | 15 | 3.2 | 144 | 0.98 | 87 | 29 | 12 | 43 | 0.84 | ||
| M62A | 0.24 | 319 | 22 | 3.7 | 257 | 0.88 | 116 | 24 | 30 | 73 | 0.64 | |
| 0.48 | 304 | 20 | 7.4 | 219 | 0.94 | 254 | 35 | 1 | 47 | 0.66 | ||
| Sample | Sample | (σ1 − σ3) | B | n | R2 |
|---|---|---|---|---|---|
| Location | Number | [MPa−1] × 10−5 | [-] | ||
| Pelplin | B-211-A | 0.65 | 1.6 | 0.043 | 0.93 |
| M-30-B | 0.52 | 2.0 | 0.044 | 0.94 | |
| W-260-A | 0.46 | 1.6 | 0.037 | 0.97 | |
| W-260-B | 0.52 | 1.7 | 0.045 | 0.97 | |
| W-264-A | 0.55 | 1.8 | 0.044 | 0.93 | |
| Average | 1.7 | 0.043 | |||
| Standard dev. | 0.11 | 4.4 × 10−5 | |||
| Pasłęk | B-236-A | 0.41 | 1.7 | 0.023 | 0.94 |
| W-277-B | 0.46 | 1.8 | 0.029 | 0.98 | |
| W-278-A | 0.56 | 1.9 | 0.032 | 0.98 | |
| W-278-B | 0.69 | 1.6 | 0.048 | 0.98 | |
| Average | 1.8 | 0.033 | |||
| Standard dev. | 0.06 | 3.4 × 10−4 | |||
| Jantar | B-275-B | 0.52 | 2.6 | 0.040 | 0.99 |
| B-279-D | 0.46 | 1.8 | 0.039 | 0.99 | |
| M-43B-B | 0.46 | 2.0 | 0.036 | 0.97 | |
| W-305-A | 0.49 | 2.0 | 0.048 | 0.76 | |
| W-306-A | 0.52 | 2.0 | 0.046 | 0.93 | |
| Average | 2.1 | 0.042 | |||
| Standard dev. | 0.37 | 1.1 × 10−4 | |||
| Sasino | M-60-B | 0.60 | 1.9 | 0.036 | 0.96 |
| M-62-A | 0.48 | 1.8 | 0.020 | 0.91 | |
| W-320-B | 0.42 | 2.4 | 0.027 | 0.82 | |
| Average | 2.0 | 0.028 | |||
| Standard dev. | 0.17 | 1.3 × 10−4 |
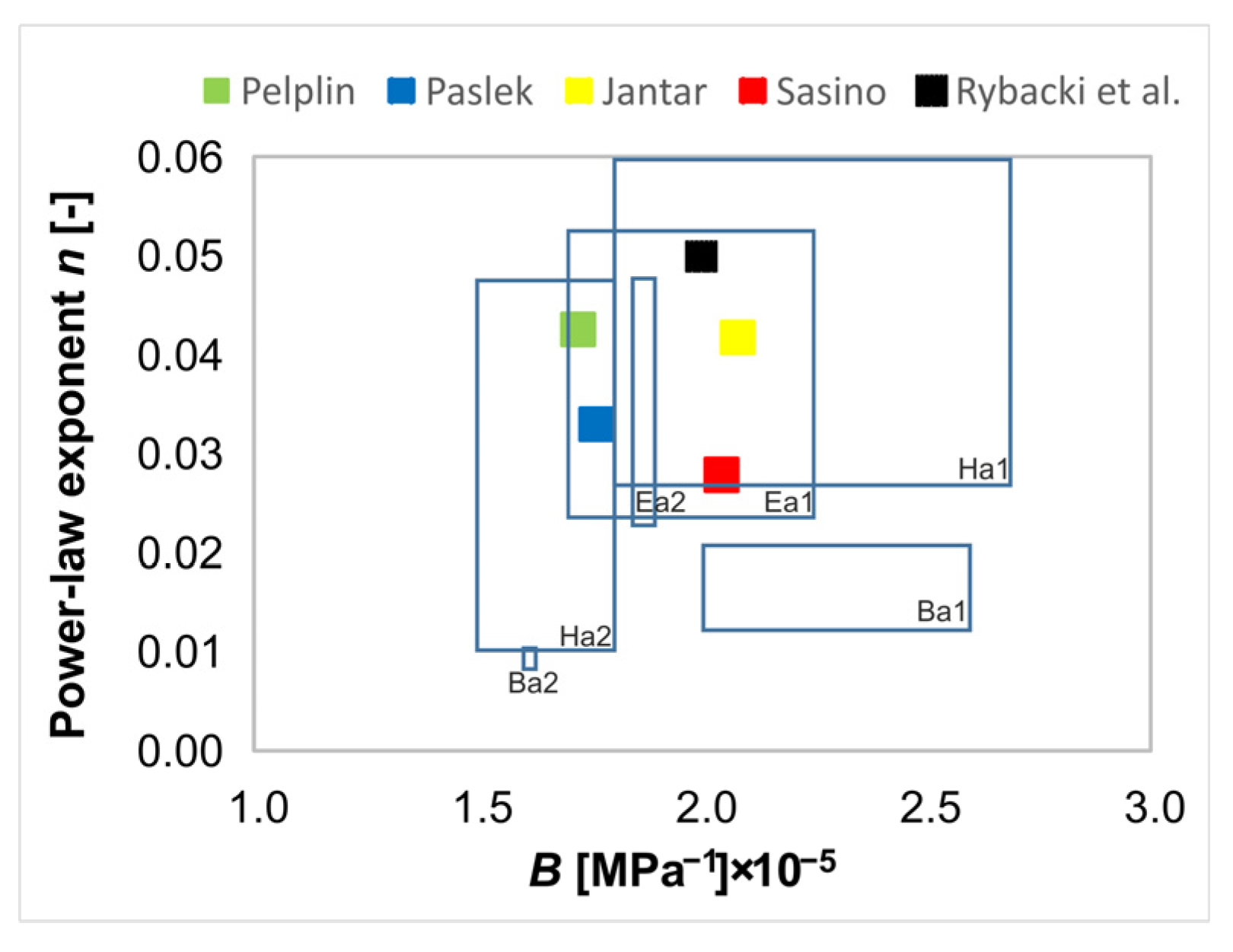
| Shale | Ref. | B | n | QFP | Cb | Clay | σTCS | pc | Temp. |
|---|---|---|---|---|---|---|---|---|---|
| [MPa−1] × 10−5 | [-] | vol% | vol% | vol% | [MPa] | [MPa] | [oC] | ||
| Barnett-1 (Ba1) | a | 2.0–2.6 | 0.012–0.021 | 48 | 2 | 50 | 210 | <30 | room |
| Barnett-2 (Ba2) | a | 1.6–1.6 | 0.009–0.010 | 42 | 48 | 10 | 325 | <30 | room |
| Hayneville-1 (Ha1) | a | 1.8–2.7 | 0.027–0.062 | 32 | 20 | 48 | 145 | <30 | room |
| Hayneville-2 (Ha2) | a | 1.5–1.8 | 0.011–0.049 | 23 | 49 | 28 | 240 | <30 | room |
| Eagle Ford-1 (Ea1) | a | 1.7–2.3 | 0.024–0.053 | 24 | 46 | 30 | 200 | <30 | room |
| Eagle Ford-2 (Ea2) | a | 1.7–1.8 | 0.023–0.049 | 14 | 66 | 20 | 175 | <30 | room |
| Pos_Dot | b | 2 | 0.05 | 14 | 42 | 43 | 175 | 20 | 20 |
| Pelplin | c | 1.7 | 0.043 | 40 | 14 | 46 | 215 | 50 | 85 |
| Paslek | c | 1.8 | 0.033 | 36 | 7 | 57 | 155 | 50 | 85 |
| Jantar | c | 2.1 | 0.042 | 31 | 22 | 46 | 215 | 50 | 85 |
| Sasino | c | 2 | 0.028 | 51 | 3 | 45 | 222 | 50 | 85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wilczynski, P.M.; Cieslik, J.; Domonik, A.; Lukaszewski, P. Viscoelastic Strains of Palaeozoic Shales under the Burger’s Model Description. Appl. Sci. 2023, 13, 10981. https://doi.org/10.3390/app131910981
Wilczynski PM, Cieslik J, Domonik A, Lukaszewski P. Viscoelastic Strains of Palaeozoic Shales under the Burger’s Model Description. Applied Sciences. 2023; 13(19):10981. https://doi.org/10.3390/app131910981
Chicago/Turabian StyleWilczynski, Przemyslaw Michal, Jerzy Cieslik, Andrzej Domonik, and Pawel Lukaszewski. 2023. "Viscoelastic Strains of Palaeozoic Shales under the Burger’s Model Description" Applied Sciences 13, no. 19: 10981. https://doi.org/10.3390/app131910981
APA StyleWilczynski, P. M., Cieslik, J., Domonik, A., & Lukaszewski, P. (2023). Viscoelastic Strains of Palaeozoic Shales under the Burger’s Model Description. Applied Sciences, 13(19), 10981. https://doi.org/10.3390/app131910981