An Optimized Flexible Accelerator for Elliptic Curve Point Multiplication over NIST Binary Fields

Abstract

This article proposes a flexible hardware accelerator optimized from a throughput and area point of view for the computationally intensive part of elliptic curve cryptography. The target binary fields, defined by the National Institute of Standards and Technology, are $GF\left(2^{163}\right)$, $GF\left(2^{233}\right)$, $GF\left(2^{283}\right)$, $GF\left(2^{409}\right)$, and $GF\left(2^{571}\right)$. For the optimization of throughput, the proposed accelerator employs a digit-parallel multiplier. The size of the digit is 41 bits. The proposed accelerator has reused the multiplication and squaring circuit for area optimization to compute modular inversions. Flexibility is included using three additional buffers on top of the proposed accelerator architecture to load different input parameters. Finally, a dedicated controller is used to optimize control signal handling. The architecture is modeled using Verilog and implemented up to the post-place-and-route level on a Xilinx Virtex-7 field-programmable gate array. The area utilization of our accelerator in slices is 1479, 1998, 2573, 3271, and 4469 for $m=163$ to 571. The time needed to perform one-point multiplication is 7.15, 10.60, 13.26, 20.96, and 30.42 μs. Similarly, the throughput over area figures for the same key lengths are 94.56, 47.21, 29.30, 14.58, and 7.35. Consequently, achieved results and a comprehensive performance comparison show the suitability of the proposed design for constrained environments that demand throughput/area-efficient implementations.

1. Introduction

The two well-known examples of public-key cryptography (PKC) are Elliptic curve cryptography (ECC) [1] and RSA [2]. Comparatively, the advantages of ECC include but are not limited to power efficiency, bandwidth optimization, and improved area utilization. The reason behind these advantages is the ability of ECC to provide a similar amount of security as RSA but with smaller lengths of the target key [3]. Considering larger key lengths contribute to maximizing security, however, for hardware accelerators, operating larger lengths of the target key with a low-area constraint poses serious challenges. Examples of these environments (operating larger lengths of the target key with a low-area constraint) include ubiquitous computing [4,5,6], radio-frequency-identification (RFID) networks [7,8], and safe autonomous robots [9]. Therefore, this work aims to provide a hardware accelerator optimizing both throughput and area simultaneously for elliptic curve point multiplication.

The point multiplication is the most computationally intensive part of ECC. Many organizations have accepted ECC as a standardization. One such organization is the National Institute of Standards and Technology (NIST). The NIST has offered two fields for ECC to ensure secure and efficient communications [10]: prime fields, denoted as $GF\left(P\right)$, and binary fields, represented as $GF\left(2^m\right)$. Moreover, NIST has specifically recommended various key lengths for these fields.

For deployments, ECC includes a four-layer model [3]. The first layer encompasses essential operations such as encryption, decryption, signature generation, signature verification, and so on. The second layer operations are point addition (PA) and doubling (PD). The third-layer operation is the crucial operation in ECC, known as point multiplication (PM), and relies on the second-layer operations. Finally, the first layer is built upon modular arithmetic operators, including adders, squares, multipliers, and inversions. The performance of ECC’s PM operation depends upon the implementation of first-layer operations.

In addition to the four layers of ECC, there are two main alternatives for implementing ECC: a software implementation and a hardware implementation. Generally, software implementations such as microcontrollers offer higher flexibility with limited performance. On the other hand, field-programmable gate arrays (FPGAs) and application-specific integrated circuits (ASICs) are used for hardware implementations [11]. The FPGAs are reconfigurable, while ASICs are application-specific. These hardware implementation platforms provide higher performance with limited flexibility. Moreover, hardware implementations are also beneficial for higher security because optimizing hardware circuits is much more crucial than software implementations written in C/C++, Python, or assembly. There is always a trade-off between performance and flexibility. Concerning the aforementioned advantages, we have preferred FPGA-based hardware implementations.

The NIST-recommended binary fields are better suited for hardware implementation, while prime fields offer advantages in software-based platforms [3]. Prime fields require a carry bit when implementing polynomial addition. In addition, implementing polynomial additions with a carry bit utilizes a more complex circuit, increasing the hardware resources and maximizing the critical path delay. Polynomial addition can be performed for binary fields using a bitwise exclusive-OR operation, which avoids the carry bit during the implementation. The carry-free polynomial additions lead to improved computation time with optimized hardware resources and critical path delay. Thus, binary fields are implemented in this work.

Another important aspect of ECC is the choice of a basis for point representation. Consequently, polynomial and normal [3] bases are employed. As far as the polynomial basis is concerned, it is generally preferred for optimized modular multiplications. On the other hand, the normal basis is well-suited for frequent modular square computations. In addition to the choice of a basis in ECC, the selection of an appropriate coordinate system is equally important. The two commonly used coordinate systems are affine and projective. A suitable choice of the coordinate system also impacts performance. The limitation of the affine coordinates system is that it requires an inversion operation during every point addition and point doubling operation. Therefore, it is considered a relatively more computationally intensive option. On the other hand, projective coordinates are better suited for maximizing the throughput of ECC-based accelerators [3,11]. Therefore, in this article, we have selected a polynomial basis along with a projective coordinates system for implementation.

1.1. Pm Hardware Accelerators and Limitations

The latest advancements in hardware accelerators for PM computation in ECC are detailed in the state-of-the-art literature [12,13,14,15,16,17,18,19,20,21,22,23]. In [12], a highly efficient implementation of ECC is presented over $GF\left(2^{163}\right)$ with a focus on minimizing area utilization. They used a digit serial multiplier architecture for modular multiplication computation, which reduces hardware resources. To cater to low-cost cryptographic applications and enable integration with 8-bit processors, they incorporate an 8-bit input-output interface. Notably, their implementation of Montgomery PM on Virtex-5 utilizes 473 slices and computes one PM in 0.11 ms. Similar to [12], an interesting work is found in [13], where low-area implementation of PM for ECC over $GF\left(2^{163}\right)$ is illustrated. The authors employ the Lopez-Dahab algorithm and achieve low area utilization on FPGA. The optimization is achieved due to the use of a hybrid Karatsuba multiplier. With different digit sizes, a digit serial modular multiplier is utilized in [14] over $GF\left(2^m\right)$ with $m=163,233,283,409$ and 571 to realize the PM computation.

A crypto engine over $GF\left(2^{233}\right)$ is described in [15] for wireless sensor nodes. Here, the authors have focused on digit-by-digit computations for arithmetic operations while optimizing hardware resource utilization on the targeted FPGA device. Another notable work is described in [16], where a coprocessor design technique is employed to simultaneously leverage the advantages of symmetric and public-key cryptography. Their approach incorporates an Advanced Encryption Standard (AES-128) algorithm for symmetric cryptography, ECC over $GF\left(2^{163}\right)$ for elliptic curve operations in PKC, and a secure hash algorithm (SHA-256) for hash computations in digital signature, authentication, and random key generation.

A pipelined architecture with two stages is presented in [17]. The authors have proposed an efficient scheduling scheme for point addition and point doubling operations. It has minimized the total number of required clock cycles. The results have shown that the achieved frequencies are 369, 357, and 337 MHz for key lengths of 163, 233, and 283 bits, respectively. Similarly, the work in [18] is also based on pipelining technique with two stages. The authors have focused on reducing the total processing time. The reduction in total processing time is achieved through an optimized scheduling policy for point addition and point doubling operations. The efficient utilization of memory locations and an efficient multiplier, working on the principles of the digit-parallel scheme, contribute to reducing the area.

Instead of the binary field accelerators, a prime field processor is proposed in [19]. The size of the proposed processor is 256 bits. The authors employed Jacobian coordinates to overcome the computational overhead of modular inversion. Additionally, the design incorporates an interleaved modular multiplier, contributing to reductions in both area utilization and delay. The point addition and point doubling operations are optimized along with the multiplication algorithm. On prime fields, high-speed PM accelerators are described in [20,21]. In the hardware accelerator of [22], a particular model of ECC (i.e., Edward curves) is utilized for PM computation which offers unified PA and PD formulations, which are secured against side-channel attacks. Another high-speed PM accelerator over $GF\left(p\right)$ field with $p=256$ is illustrated in [23].

In the existing PM accelerators, throughput has been optimized by employing various optimization techniques such as pipelining [17], digit-serial modular multipliers [14], bit-parallel Karatsuba-based modular multiplications, combined Karatsuba and schoolbook-based modular multiplications [13], rescheduling of PA and PD operations [17,18], and many more. For area optimizations, the existing accelerators use bit-serial and digit-serial-based modular multiplication approaches [12]. While there have been several accelerators for PM computations [13,15,16,19,20,21,22,23], these focus on area or throughput optimization for specific key-lengths, such as 163, 233, 256, etc. However, some architectures consider both throughput and area optimizations simultaneously, as seen in recent designs [12,17,18]. These PM designs can be further optimized using different modular multiplication architectures.

1.2. Objective, Contributions and Significance

This work aims to implement an efficient hardware accelerator for PM computations in ECC that simultaneously considers throughput and area optimization. Our contributions are summarized as follows:

• Proposed PM architecture: we have proposed an optimized hardware accelerator that improves throughput and minimizes area for PM computation in ECC over $GF\left(2^m\right)$, where m can take values of 163, 233, 283, 409, and 571.
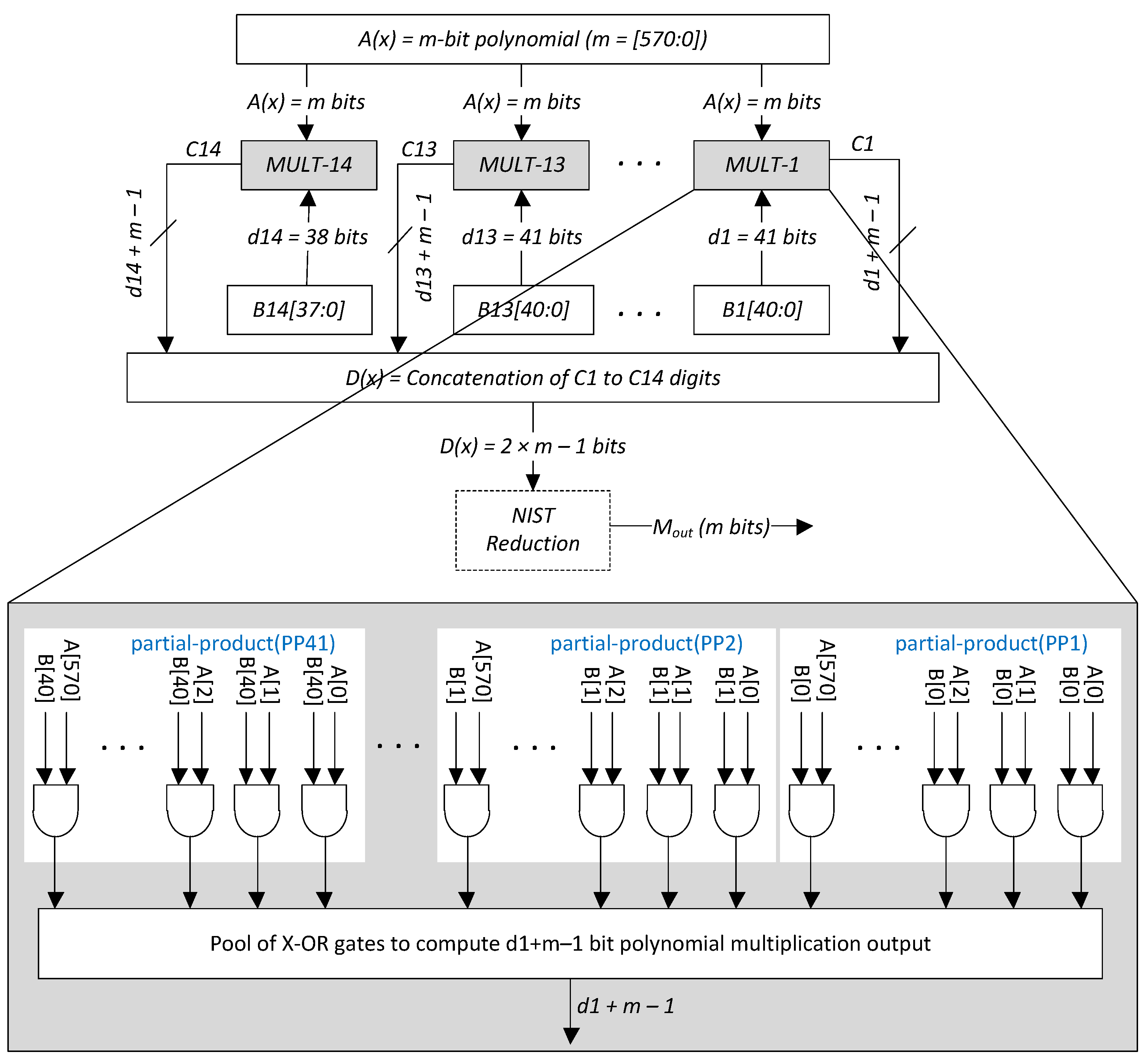
• gProposed digit-parallel multiplier architecture: to improve the throughput and reduce clock cycles for polynomial multiplications, we have proposed a multiplier circuit. The proposed circuit works on the digit-parallel principles such that the size of the digit is 41.
• Re-using the hardware resources: to implement the inversion operation, we have re-utilized the allocated area of the square unit and the digit-parallel multiplier unit, which reduces overall hardware area utilization.
• Flexibility: we have utilized two 571-bit input/output buffers on top of the proposed PM architecture to load different input parameters. Similarly, one 3-bit buffer is also used to provide read/write addresses. Using these three buffers, we have encountered flexibility in our accelerator architecture, which means different input parameters can be used for computations.
• Dedicated-controller: we have designed a controller circuit for efficient handling of control signals. The behavior of the controller circuit is described through a state machine.

We have validated the aforementioned contributions by implementing our proposed accelerator architecture on Xilinx Virtex-7 FPGA. We have written (all) the codes in Verilog (a hardware description language). The achieved results demonstrate that the proposed accelerator architecture utilizes 1479, 1998, 2573, 3271, and 4469 slices for a key length of 163, 233, 283, 409, and 571, respectively. The time needed for our accelerator architecture for these key lengths is 7.15, 10.60, 13.26, 20.96, and 30.42 μs. Similarly, for the same binary field lengths, the overall ratio between throughput and area is 94.56, 47.21, 29.30, 14.58, and 7.35. A comparison with existing techniques reveals the efficacy of the proposed solution.

This article is arranged in various subsections: Section 2 presents the mathematical background of the Lopez-Dahab projective coordinate system. The next section describes the proposed PM architecture. The implementation of the proposed design is made in Section 4. Consequently, the achieved results and a comprehensive performance comparison are presented. The article is concluded in the last section (Section 5).

2. Lopez-Dahab Projective Form of ECC over $\mathit{G}\mathit{F}\left({\mathbf{2}}^{\mathit{m}}\right)$

In projective coordinates, a starting point P over the binary field is shown with a combination of three variables (X, Y, and Z). The X and Y correspond to the affine x and y coordinates. The variable Z ensures a projective point with $Z\ne 0$. The variables X, Y, and Z represent the elements of the Lopez-Dahab coordinate system. Additionally, a and b are the curve constants, with $b\ne 0$.

$$\begin{array}{c}\hfill E:Y^2+XYZ=X^{3}Z+a{X}^2{Z}^2+b{Z}^4\end{array}$$

(1)

In order to execute the point multiplication, the PA and PD operations are essential. Let us illustrate these operations with an example: consider an initial and final point on the curve. These initial and final points are represented as P and Q, respectively. The PA operation denoted as $R=P+Q$, generates a new point R. Similarly, adding a point with itself, i.e., $P+P$, represents the PD operation, denoted as $2P$. Consequently, the point multiplication simply adds k copies of PA and PD operations. This phenomenon is shown in Equation (2).

$$\begin{array}{c}\hfill Q=k.P=k.(P+P\cdots +P)\end{array}$$

(2)

In the above equation, P is the starting point. The value of the scalar multiplier is represented by k. Similarly, the variable Q represents the resultant point. Various PM algorithms have been proposed for the implementation of the above equation. A discussion on these existing algorithms can be found in [11]. According to the findings of [11], the Montgomery PM algorithm is considered a better choice. The reason behind the preference for the Montgomery PM algorithm over other existing algorithms is its ability to offer uniform PA and PD instructions. In other words, the Montgomery algorithm inherently offers protection against various side-channel attacks. Consequently, we have also opted Montgomery PM algorithm to achieve a side-channel-protected solution.

Algorithm 1 takes a starting point P along with a sequence of binary numbers. In addition to it, there is another input k that represents the scalar multiplier. It outputs the coordinates of the endpoint (Q). The coordinates of the endpoint are x and y. The first line of the Algorithm handles the conversions operations. The conversion is made from affine coordinates to Lopez-Dahab coordinates. Inside the $for$ loop, the $if$ and $else$ portions of the algorithm determine whether a PA or PD operation should be performed. The instructions labeled from $Ins{t}_1$ to $Ins{t}_7$ are used for PA computations, while $Ins{t}_8$ to $Ins{t}_{14}$ are dedicated to PD computations. The selection between the $if$ and $else$ statements is based on the status of k. Finally, the Algorithm reconverts the coordinate system. The reconversion is made from Lopez-Dahab coordinates to affine coordinates.

Algorithm 1: Montgomery PM Algorithm [17].

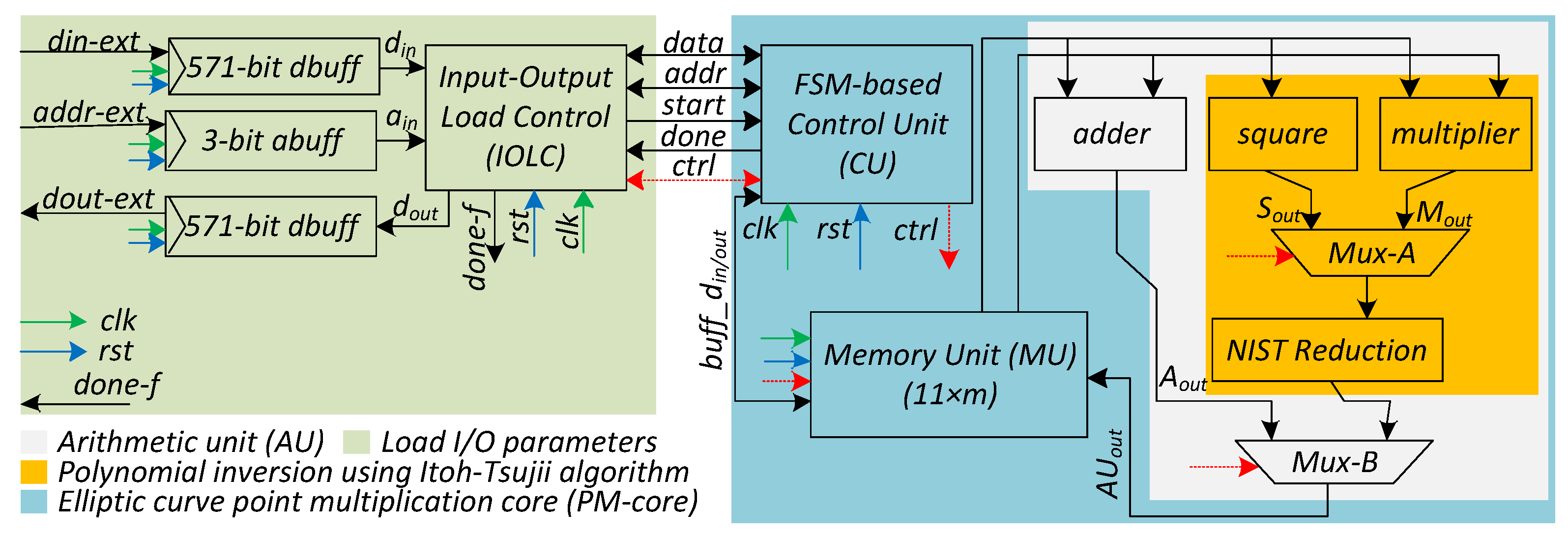
3. Proposed Hardware Accelerator Architecture

Figure 1 illustrates our proposed architecture for a PM accelerator over $GF\left(2^m\right)$, where m is set to 571. The architecture has two components: (i) load I/O parameters and (ii) elliptic curve point multiplication core (PM-core). The following subsections elaborate on various components of the proposed architecture.

3.1. Loading I/O Parameters to Our Accelerator

As mentioned before, our accelerator is flexible, which means different input parameters can be provided from outside to perform the PM operation of ECC. In other words, the proposed accelerator is not dedicated to specific input parameters. We have employed two 571-bit data buffers (denoted with 571-$bitdbuff$) and one 4-bit address buffer (represented with 4-$bitabuff$) to achieve this flexibility. Amongst the NIST-recommended binary field lengths, the longer key length is 571. Therefore, we prefer to choose a buffer length of 571 bits for a constant-time implementation. These three buffers operate serially. It implies that the corresponding 571-bit input buffer serially loads the input parameters bit-by-bit. After loading the one input parameter, the corresponding read/write address is loaded into 4-$bitabuff$. This process repeats until all the input parameters are provided to the PM-core for computations. Similarly, the corresponding 571-bit output buffer serially shifts the bits of the output. As seen in the block diagram of the proposed architecture, the data and address buffers correspond to the input-output load control (IOLC) block. This acts similarly to a controller between the buffers and the control unit of the PM-core to pass/collect data, read/write addresses, and other related control signals. We employ a 3-bit $ctr{l}_{ext}$ signal for efficient control functionalities. The encoding of IOLC block using $ctr{l}_{ext}$ signal is given below:

• Data read and write: we use $ctr{l}_{ext}$ = 000, which specify the bit-by-bit output data read from 571-$bitdbuff$ using one-bit $dout$-$ext$ signal. Similarly, we have encoded $ctr{l}_{ext}$ = 001 for input data write on a 571-$bitdbuff$ using one-bit $din$-$ext$ signal.
• Loading the coordinates of starting point: we set $ctr{l}_{ext}$ = 010 and $ctr{l}_{ext}$ = 011 to input the x and y components of the starting point P on a 571-$bitdbuff$ using one-bit $din$-$ext$ signal.
• Loading the values of constant and a scalar multiplier: we use $ctr{l}_{ext}$ = 100 and $ctr{l}_{ext}$ = 101 to load the curve constant parameter and a scalar multiplier on a 571-$bitdbuff$ using one-bit $din$-$ext$ signal.
• Collecting bits of final point: we use $ctr{l}_{ext}$ = 110 and $ctr{l}_{ext}$ = 111 to collect the bits of x and y components of the final point Q, respectively.

After loading each input parameter and the corresponding address, the IOLC unit passes data and address using data and addr signals to the control unit of the PM-core. Subsequently, the data is written on the used memory block. Similarly, the next input parameter is written on the memory block. Once writing all input parameters on the memory block is finished, the IOLC unit generates the $start$ signal for the control unit of the PM-core to start computations. After computing the PM operation, the control unit of the PM-core corresponds to the IOLC block by setting a $done$ signal, as shown in Figure 1. Based on this $done$ signal, the IOLC unit communicates to the control unit of the PM-core for reading final data from the memory block. Once reading the resultant data from the memory unit is finished, the IOLC unit generates a one-bit $done$-f signal. It ensures that the final results have been read.

It is important to note that we must load the x, y components of the starting point P, the constant b, and a secret key in a memory unit. All these input parameters need to load in a sequential style, one after another. This serial data loading is the initialization and needs $(4\times m)+4$ clock cycles. Out of $(4\times m)+4$ cycles, $4\times m$ cycles are needed to load four input parameters ($x_p$, $y_p$, b and secret key k) serially. Moreover, an additional four cycles are needed to reset the 571-$bitdbuff$ after loading each corresponding 571-bit value into the buffer. Similarly, we also need to load the corresponding read/write address, which takes five clock cycles; four for the address and an additional cycle to reset the 4-$bit$ $abuff$. This (serial data loading to the memory unit) enables the flexibility feature of our proposed accelerator design. Therefore, different ECC parameters can be loaded into our design for PM computation. The next subsection elaborates on the PM-core of the proposed accelerator architecture.

3.2. PM-Core

As shown in Figure 1, the PM-core has three main components. The first component is the memory unit that stores the initial, intermediate, and end results during the computation of the PM operation in ECC. The second unit is the arithmetic unit (AU) that executes the arithmetic operations required for PM computation, including addition, squaring, multiplication, reduction, and inversion. Finally, the last unit is the control unit (CU) which plays a crucial role in the accelerator’s operation by generating the control signals necessary for efficient control functionalities. Moreover, it communicates to the IOLC unit for read/write data on the memory block and (also for) other essential controls. In addition, the CU block of our PM-core ensures proper synchronization and coordination between the memory unit, an arithmetic unit, and other components, enabling the accelerator to execute the PM operation effectively. An in-depth discussion of the three components of the PM-core is given in the following subsections.

3.2.1. Memory Unit (MU)

The data memory in our proposed design is implemented as an array of registers as shown in Figure 1. It has a size of $11\times m$. Here, the number 11 depicts the number of addresses. The variable m denotes the number of bits stored in each address. The number of locations in the memory unit varies depending on the specific value of m. This value can be 163, 233, 283, 409, or 571. For example, if the accelerator is designed for $GF\left(2^{163}\right)$, the memory size would be $11\times 163$. Similarly, for $GF\left(2^{571}\right)$, the memory size would be $11\times 571$. Nevertheless, the total number of addresses remains the same across different values of m. On the other hand, the total number of stored bits in each memory location varies according to the key length, represented by m. Amongst 11 memory addresses, four addresses are dedicated to storing ECC curve parameters: $x_p$ (the x component of the starting point P), $y_p$ (the y component of the starting point P), b (the constant of the curve), and a secret key. These parameters are essential for performing computations and are inputs to Algorithm 1. The remaining seven addresses hold intermediate and end results. The internal structure of the data memory consists of two multiplexers with sizes of $11\times 1$ and one demultiplexer of $1\times 11$ size. They take inputs from the data memory. On the other hand, the demultiplexer allows one to write on a specific register using $A{U}_{out}$ signal. The corresponding control signals related to read and write operations are marked with red dotted lines in Figure 1.

3.2.2. Arithmetic Unit (AU)

The gray filled area in Figure 1 represents the AU, which consists of an adder, square block, multiplier, a reduction block, and two multiplexers ($Mux-A$ and $Mux-B$). The description of these architectural components is as follows:

Adder, Square and Routing Multiplexers

To implement a modular adder circuit over the binary field, a simple technique is employed as utilized in [16,17,18]. The adopted technique is based on using bitwise exclusive OR gates. More precisely, when adding two m-bit inputs, two-input m exclusive OR gates are required [3,14]. Since the adder circuit provides output as a combination of inputs, a single addition is completed within a single cycle. The square block takes an m-bit polynomial and produces a $2\times m-1$ bits output. Internally, the square block inserts an additional 0-bit between every two successive data bits. A combinational circuit can produce a polynomial square in just one clock cycle. After the polynomial square operation, the $2\times m-1$ bits size output must be transformed into an m-bit polynomial. Hence, polynomial reduction is necessary to achieve this transformation, which will be discussed later in the paper. For data routing purposes, the two multiplexers ($Mux-A$ and $Mux-B$) play a crucial role by selecting appropriate operands for the NIST reduction unit and data memory, which allows the results to be written back. Polynomial multiplication is a crucial operation in the PM computation of ECC. Therefore, the following text will comprehensively describe polynomial multiplication, reduction, and inversion.

Proposed Digit-Parallel Multiplier Architecture

Before delving into the details of our proposed polynomial multiplication design, exploring the various polynomial multiplication approaches described in the literature is essential. Notably, four frequently employed methods are bit-serial, digit-serial, bit-parallel, and digit-parallel. Recently in 2021, an academic tool was proposed in [24], to generate Verilog codes for various aforementioned multipliers. A comprehensive performance comparison over different field lengths is provided in [25]. The aforementioned methods come with its own set of advantages and limitations. For instance, bit and digit-serial circuits are optimized for hardware resources and power efficiency [12,14]. Conversely, bit-parallel and digit-parallel techniques are preferable for high-speed operations [17,18]. The computational cost also varies across these approaches. For instance, when given 2 m-bit inputs, bit-serial multipliers necessitate $m^2$ cycles, while the digit-serial technique needs $\frac{m}{n}$ cycles. Here, n is the size of the digit. On the other hand, digit and bit-parallel methods offer a computational cost of just one clock cycle. Nevertheless, the additional area resources along with increased power consumption are the drawbacks.

To minimize (overall) clock cycles for computations, we have chosen a digit-parallel polynomial multiplication approach in this work. Our implemented multiplier involves three main steps: creating digits, polynomial multiplication of the created digits, and concatenation to generate the final polynomial output. Moreover, we have kept the operand-one (i.e., polynomial $A\left(x\right)$) and created digits of the second operand (i.e., polynomial $B\left(x\right)$). Then, we multiplied each bit of the $A\left(x\right)$ with each bit of the created digits in parallel and produced digits of C1 to C14 as output. Later, we concatenate the outputs of the digit multiplications to generate the resultant output. Figure 2 shows our proposed digit-parallel multiplier architecture over $GF\left(2^{571}\right)$ with a digit size of 41 bits. The polynomial $A\left(x\right)$ is the first input to the multiplier, and as shown in Figure 2, the digits of polynomial $B\left(x\right)$ are created, i.e., B1 to B14. From digits B1 to B13 are 41 bits while the last digit is with a size of 38 bits. After the digits multiplication of B1 to B14 with a polynomial $A\left(x\right)$, the generated C1 to C14 digits are concatenated with each other to generate the final multiplication output of $D\left(x\right)$ of size $2\times m-1$ bits.

Reduction

As depicted in Figure 2, the resultant polynomial after each square and multiplication has a $2\times m-1$ bits length. To produce a polynomial of length m-bit, polynomial reduction is necessary. In this work, we have implemented NIST-recommended reduction algorithms for polynomial reduction after each square and multiplier unit, as described in [3]. Some existing accelerators, such as the one in [17], utilize separate reduction units after each square and multiplier block. However, we have employed only one reduction block to conserve hardware resources with an additional $2\times 1$ multiplexer, as illustrated in Figure 2. This decision enables us to minimize hardware requirements while achieving the desired polynomial reduction in the same clock cycle. For complete details about the reduction algorithms specific to $GF\left(2^{163}\right)$ to $GF\left(2^{571}\right)$, we refer interested readers to algorithms 2.41 to 2.45 of [3]. The computational cost, including the square/multiplication and reduction, is one clock cycle, as we have used combinational logic for the design implementation.

Inversion

Apart from polynomial addition, square, and multiplication, implementing Algorithm 1 for PM computation also requires polynomial inversion computations, as shown in the last two lines of Algorithm 1. Therefore, we have utilized a square version of the Itoh-Tsujii algorithm [26], which requires $m-1$ times repeated squares followed by 9, 10, 10, 11, and 12 modular multiplications over $GF\left(2^{163}\right)$, $GF\left(2^{233}\right)$, $GF\left(2^{283}\right)$, $GF\left(2^{409}\right)$, and $GF\left(2^{571}\right)$ fields. The Itoh-Tsujii algorithm is used because it only needs square and multiplication computations for modular inversion. Therefore, it is better to utilize the hardware resources of the square and multiplier to compute the inversion, which benefits minimizing the overall hardware resources. In our architecture, we have utilized the design components marked in orange in Figure 1 to implement the Itoh-Tsujii inversion algorithm. As described, the computational cost for one modular square and multiplier, including reduction, is one clock cycle. Thus, implementing the Itoh-Tsujii algorithm for modular inversion over $GF\left(2^{163}\right)$ requires 162 clock cycles for square computations and 9 clock cycles for modular multiplications. Hence, the total cycles required over $GF\left(2^{163}\right)$ field is 171 (162 for $m-1$ square operations and nine for nine modular multiplications). Similarly, the total cycles required for one modular inversion computation over $GF\left(2^{233}\right)$, $GF\left(2^{283}\right)$, $GF\left(2^{409}\right)$, and $GF\left(2^{571}\right)$ fields is 242, 292, 509, and 582.

3.2.3. Controller Circuit and Formulation for Clock Cycles

Our accelerator incorporates a controller circuit to execute Algorithm 1 for PM computation. Before initiating the PM computation, it is necessary to load the input parameters into the data memory. Using the 571-bit buffer of Figure 1, it loads four $m-1$ bits inputs. This initial loading into the data memory requires $(4\times m)+4$ clock cycles. Once the input parameters are loaded, the controller generates the $start$ signal. It allows the proposed accelerator to proceed with the PM computation. It involves various states. These states are responsible for various operations, e.g., the conversion from affine coordinate system to projective coordinate system, execution of PM operation, and reconversion from projective coordinate system to affine coordinate system.

The algorithm starts with the initialization step. Here, it converts affine coordinates to projective coordinates. The operators, including the adder, square, and multiplier, efficiently compute results in just one clock cycle. Consequently, for the statements in the first line of Algorithm 1, which involve addition and square operations, we can complete the computations in an efficient way. Specifically, for the computation of affine to projective coordinates, the statements $X_1=x_p$, $Z_1=1$, $Z_2=x_p^2$, and $X_2=x_p^4+b$ can be efficiently processed in our accelerator, requiring only five clock cycles for all field lengths ranging from $GF\left(2^{163}\right)$ to $GF\left(2^{571}\right)$.

Algorithm 1 utilizes a $for$ loop to perform PM operation in Lopez-Dahab projective form. Within the $for$ loop, the $if$ and $else$ portions contain statements for point addition and point doubling steps, respectively. The instructions $Ins{t}_1$ to $Ins{t}_7$ correspond to point addition, while $Ins{t}_8$ to $Ins{t}_{14}$ relate to point doubling. The $if$ or $else$ parts of the algorithm depends on the value of $k_i$. When the value is equal to one, the $if$ part is executed. When the value is not equal to one, the $else$ part is executed. It is important to note that the $if$ and $else$ sections consist of 14 instructions. Out of these 14 instructions, 11 instructions are reserved for squaring and multiplication. Similarly, three out of these 14 instructions are dedicated to modular addition. As a result, the $if$ and $else$ portions together need $14\times m$ cycles for PM computation in projective coordinates, where the value of m corresponds to the key length (e.g., 163, 233, 283, 409, or 571). For the proposed accelerator, the number of clock cycles utilized is as follows: 2282 cycles for $GF\left(2^{163}\right)$, 3262 cycles for $GF\left(2^{233}\right)$, 3962 cycles for $GF\left(2^{283}\right)$, 5726 cycles for $GF\left(2^{409}\right)$, and 7994 cycles for $GF\left(2^{571}\right)$.

The last part of the algorithm generates the x and y components of the final point Q. Moreover, a reconversion is made from the Lopez-Dahab coordinate system to the affine coordinate system. We have previously described the computational cost of one modular addition, square, multiplication, and inversion operations for the NIST-recommended field lengths. Therefore, our proposed accelerator requires $2\times$ inversion + 24 clock cycles to perform the Lopez-Dahab projective to affine conversion. Here, $2\times$ inversion indicates the clock cycles needed for executing two modular inversions. An additional 24 cycles are necessary to implement the other modular operations in the last two lines of Algorithm 1. As a result, our accelerator performs the Lopez-Dahab to affine conversion in 366 cycles for $GF\left(2^{163}\right)$, 508 cycles for $GF\left(2^{233}\right)$, 608 cycles for $GF\left(2^{283}\right)$, 1042 cycles for $GF\left(2^{409}\right)$, and 1188 cycles for $GF\left(2^{571}\right)$ fields. The total clock cycles for our accelerator can be calculated across different field lengths of 163, 233, 283, 409, and 571 using Equation (3). The corresponding values for clock cycles are 2653, 3775, 4575, 6773, and 9187. It is essential to mention that these clock cycles are for our PM-core, excluding the loading parameters’ cost.

$$\begin{array}{c}\hfill TotalClockCycles\left(TCC\right)=5+(14\times m)+2\times \left(inversion\right)+24\end{array}$$

(3)

4. Achieved Results and Performance Comparison

The achieved results are presented in Section 4.1, while a comprehensive performance comparison is given in Section 4.2.

4.1. Achieved Results

We have implemented our accelerator architecture over binary fields. The employed key lengths are 163, 233, 283, 409 and 571. The Verilog is chosen for functional modeling. As previously mentioned, the input parameters, namely $x_p$ and $y_p$, along with the value of constant b, have been taken from the NIST [10]. The achieved implementation results after the post-place-and-route level on the Xilinx Virtex-7 FPGA platform are summarized in

Table 1. Implementation results of the proposed design (after post-place-and-route level) for binary field on Xilinx Virtex-7 (xc7vx690t) [27].

m	Area Utilization			Results for Time			PM Algorithm
	Slices	LUTs	FFs	TCC	Freq (MHz)	Latency (μs)
163	1479	3862	1749	2653	371	7.15	Montgomery (Algorithm 1)
233	1998	6079	2431	3775	356	10.60
283	2573	6341	2925	4575	345	13.26
409	3271	9583	3981	6773	323	20.96
571	4469	11871	5692	9187	302	30.42

. The table provides implementation details across each key length in the following manner: the initial column represents the implemented length of the key. The next three columns (two, three, and four) display the utilized area in terms of slices, look-up tables (LUTs), and flip-flops (FFs). Similarly, the next three columns (five, six, seven) present the implementation results that are related to timing. These are presented in terms of total clock cycles (TCC), operating frequency (Freq) in MHz, and computation time (latency) in microseconds (μs). Lastly, column eight indicates the implemented PM algorithm within our accelerator. The area results are extracted from the synthesis tool. The total clock cycles are computed from Equation (3). The operating frequency is the ratio of one over provided time period to the Vivado tool for synthesis. Latency is the computation time and can be calculated using Equation (4).

$$\begin{array}{c}\hfill Latency\left(\mu s\right)=\frac{Clockcycles}{Clockfrequency\left(MHz\right)}\end{array}$$

(4)

If we consider only the hardware resources for comparison, the utilized FPGA slices over the binary fields of $GF\left(2^{163}\right)$, $GF\left(2^{233}\right)$, $GF\left(2^{283}\right)$, $GF\left(2^{409}\right)$, and $GF\left(2^{571}\right)$ are 1479, 1998, 2573, 3271, and 4469. Our accelerator utilizes 3862, 6079, 6341, 9583, and 11871 LUTs for similar binary fields. This increase in slices and LUTs is due to the increase in the implemented key lengths (i.e., 163, 233, 283, 409, and 571). If we consider the increase in the key lengths, i.e., from 163 to 233 (ratio of 163 with 233), this increase results in a value of 1.42, which means that the 233-bit key length is 1.42 times higher than the 163-bit key length. Using the same method, 283-bit key length is 0.82 times higher than 233; 409-bit key length is 0.69 times higher than 283; and the 571-bit key length is 0.71 times higher than 409-bit key length. Similarly, for all key lengths, if we consider the increase in the FPGA slices, i.e., from 163 to 233, this increase results in a value of 0.74 (ratio of 1479 with 1998), which means that the slices for 233-bit key length are 0.74 times higher than the utilized slices for 163-bit key length. With this strategy, the slices for 283-bit key length are 0.77 times higher than the slices of 233-bit key length; the slices for 409-bit key length are 0.78 times higher than the slices of 283-bit key length; and the slices for 571-bit key length are 0.73 times higher than the slices of 409-bit key length. Therefore, it can be observed that the increase in key length is higher than the corresponding utilized slices of our accelerator architecture. In other words, the calculated average increase in key length, i.e., $\frac{1.42+0.82+0.69+0.71}{4}$, is 0.91, which is higher than the average increase in slices (which is 0.75 and calculated using $\frac{0.74+0.77+0.78+0.73}{4}$). Subsequently, the techniques considered in this work for area optimizations are meaningful and can be utilized in other ECC-related accelerators.

In contrast to the hardware resources, the increase in key length also increases the required number of clock cycles, as indicated in the timing results of Table 1. Furthermore, the higher key length decreases the circuit frequency. This is because of a relatively more significant critical path in the computation. The critical path is the longest path that determines the maximum operating frequency of the circuit. As key lengths increase, the critical path becomes longer, significantly reducing clock frequency. To address this issue, our accelerator can utilize pipelining to minimize the critical path, although it may come with some area overhead. Similar pipelining techniques have been employed in ECC accelerators, such as those described in [17,18]. Column seven of Table 1 shows the increase in latency with the increase in the binary field length. It is important to note that this computation time is for PM operation without the cost of loading I/O parameters to our accelerator.

We have already described the clock cycle calculation of our accelerator for loading I/O parameters in Section 3.1. Therefore, the numerical values of the clock cycles for loading I/O parameters over $GF\left(2^{163}\right)$, $GF\left(2^{233}\right)$, $GF\left(2^{283}\right)$, $GF\left(2^{409}\right)$, and $GF\left(2^{571}\right)$ are 661, 941, 1141, 1645, and 2293. Column six of Table 1 shows the operating frequency, >300 MHz, for implemented binary field key lengths. The I/O parameters cannot load on our accelerator architecture using higher operating frequencies because we used serial data and address loading strategy. Therefore, for loading I/O parameters, a 5 MHz operating frequency can be used. Hence, on this slower 5 MHz, the computation cost of the proposed accelerator for loading I/O parameters is 132.2, 188.2, 228.2, 329, and 458.6 μs over $GF\left(2^{163}\right)$, $GF\left(2^{233}\right)$, $GF\left(2^{283}\right)$, $GF\left(2^{409}\right)$, and $GF\left(2^{571}\right)$. It can be observed that the cost of loading I/O parameters is much higher than the actual computation cost of the PM operation of ECC. This highlights the limitation of our proposed accelerator architecture.

4.2. Comparisons

We have compared our results with existing designs in

Table 2. Comparison to most recent state-of-the-art PM hardware accelerators.

Ref. #	Algorithm (or) PM Method	Device	Slices	LUTs Cycles	Clock	Freq MHz	Latency (μs)	Thrpt (Kbps)	T/Area	m
Area-optimized PM accelerators
[12]	Montgomery Ladder	Virtex-5	473	–	–	359	110	9.09	19.21	163
[12]	Binary	Virtex-5	420	–	–	362	830	1.20	2.85	163
[12]	Frobenius Map	Virtex-5	710	–	–	165	300	3.33	4.69	163
[13]	Lopez-Dahab	Virtex-7	3657	10,128	3426	135	25	40	10.93	163
[15]	Montgomery Ladder	Artix-7	442	–	1,553,782	190	8177	0.12	0.27	233
[16]	Frobenius Map	Artix-7	–	8577	55,068	150	367	2.72	0.31	163
Throughput and area-optimized PM architectures
[17]	Montgomery Ladder	Virtex-7	2207	9965	3960	369	10	100	45.31	163
[17]	Montgomery Ladder	Virtex-7	5120	18,953	5634	357	15	66.66	13.01	233
[17]	Montgomery Ladder	Virtex-7	5207	20,202	6850	337	20	50	9.60	283
[18]	Montgomery Ladder	Virtex-7	1529	4162	3798	383	9	111.11	72.66	163
[18]	Montgomery Ladder	Virtex-7	2048	6407	5402	379	14	71.42	34.87	233
[18]	Montgomery Ladder	Virtex-7	2623	6753	6568	377	17	58.82	22.42	283
[18]	Montgomery Ladder	Virtex-7	3373	10,083	9454	342	27	37.03	10.97	409
[18]	Montgomery Ladder	Virtex-7	4560	12,691	12,329	340	36	27.77	6.08	571
Throughput/speed-optimized PM designs
[14]	Montgomery Ladder	Virtex-5	6150	22,936	1371	250	5	200	32.52	163
[14]	Montgomery Ladder	Virtex-5	8134	28,683	2889	145	20	50	6.14	233
[14]	Montgomery Ladder	Virtex-5	7069	25,030	6347	189	33	30.30	4.28	283
[14]	Montgomery Ladder	Virtex-5	10,236	28,503	16,541	161	102	9.80	0.95	409
[14]	Montgomery Ladder	Virtex-5	11,640	32,432	44,047	127	348	2.87	0.24	571
[19]	Double and Add	Virtex-7	–	50,789	65,783	91	722	1.38	0.02	256
[20]	Montgomery Ladder	Virtex-7	2234	5478	–	170	352	2.84	1.27	E25519
[21]	NAF	Virtex-7	–	46.63k	7.955k	40	200	5	0.10	256
[22]	Double and Add	Virtex-7	6543	25,898	198,715	104	1903	0.52	0.07	256
[23]	Montgomery Ladder	Virtex-7	6909	–	32.3k	232	139	7.19	1.04	256
TW	Montgomery Ladder	Virtex-5	1773	4359	2653	339	7.82	127.87	72.12	163
			2291	6581	3775	321	11.76	85.03	37.11	233
			2869	6896	4575	303	15.09	66.26	23.09	283
			3543	10,081	6773	287	23.59	42.39	11.96	409
			4758	12,269	9187	269	34.15	29.82	4.31	571
		Virtex-7	1479	3862	2653	371	7.15	139.86	94.56	163
			1998	6079	3775	356	10.60	94.33	47.21	233
			2573	6341	4575	345	13.26	75.41	29.30	283
			3271	9583	6773	323	20.96	47.70	14.58	409
			4469	11,871	9187	302	30.42	32.87	7.35	571

In [16], ECC-163, AES-128, and SHA-256 algorithms have been implemented in a coprocessor design. For [15,19], we have calculated the latency value by the ratio of clock cycles over circuit frequency. In addition to slices and LUTs in [20], 40 DSP and nine BRAM blocks are also utilized. Similarly, in addition to slices in [23], 136 DSP and 15 BRAM blocks are also utilized. Thrpt determines the throughput and T/Area denotes the ratio of throughput over area, we employed area as slices for all works but for accelerators of [16,19,21], we utilized LUTs as slices are not reported in the reference designs. E25519 is the special form of ECC, named Edward 25519curve. TW specifies this work.

. Column one provides the reference number for the design that is going to be compared with the proposed design. The implemented PM algorithm (or) method for PM computation is given in the next column. Subsequently, the information about the target platform is shown in column three. The next two columns (four and five) show the information about consumed resources. The number of clock cycles for one PM computation is provided in column six. The next two columns (seven and eight) provide the frequency and latency for one PM execution. The next two columns (nine and ten) show the values for throughput and throughput over area. The architectural details regarding supported key lengths are given in the last column of the table.

Comparison to area-optimized PM implementations [12,13,15,16]. In comparison to the Virtex-5 implementation of [12], our accelerator over $GF\left(2^{163}\right)$ utilizes more hardware resources in slices as this work aims to optimize both throughput and area at the same time, while in the case of [12], the design premise was only the area optimizations. Another reason is the digit-serial multiplier architecture in the reference design, while we employed a digit-parallel modular multiplier. The comparison to LUTs and clock cycles is impossible as this information is not given in the reference design; see columns five and six in Table 2. The operating frequency for Montgomery and Binary PM algorithms in reference design is 359 and 362 MHz, which are comparatively 1.05 and 1.06 times higher than our Virtex-5 FPGA implementation. On the other hand, our accelerator is 2.05 times faster in circuit frequency against the Frobenius Map implementations of [12]. Even if our design utilizes higher resources and operates on lower circuit frequencies, our accelerator is 14.06, 106.13, and 38.36 times faster (in computation time or latency) as compared to Montgomery, Binary, and Frobenius Map implementations of [12].

For $GF\left(2^{163}\right)$, the Virtex-7 implementations of [13] is 2.47 times more resource intensive than our $GF\left(2^{163}\right)$ accelerator. In other words, our accelerator is more efficient in hardware resources (i.e., slices and LUTs). The reason is the use of a hybrid Karatsuba modular multiplier in the reference design, while we have utilized a digit-parallel modular multiplier with a digit size of 41 bits. Instead of hardware area, our accelerator is faster in clock cycles, frequency, and latency; see columns six to eight in Table 2.

We consider our Virtex-7 implementation for comparison to Artix-7 accelerators of [15,16]. In comparison to accelerator of [15] over $GF\left(2^{233}\right)$, our accelerator utilizes more resources in slices as the reference design optimizes for specific applications related to wireless-sensor-networks while we consider throughput and area at the same time for implementations. Although our accelerator utilizes higher resources, the clock cycle, frequency, and latency values are much lower than the reference design; we refer readers to follow the sixth, seventh, and eighth columns of Table 2. Specifically, our accelerator is 771.41 times faster in latency than the reference design. The design of [16] over $GF\left(2^{163}\right)$ utilizes 8577 LUTs which are comparatively 2.22 times higher than our accelerator architecture (i.e., 3862). Similarly, our accelerator is 20.75, 2.47, and 51.32 times faster in clock cycles, circuit frequency, and latency compared to the accelerator of [16].

Comparison to throughput and area-optimized PM accelerators [17,18]. A two-stage pipelined accelerator of [17] utilizes 2207, 5120, and 5207 slices for $GF\left(2^{163}\right)$, $GF\left(2^{233}\right)$, and $GF\left(2^{283}\right)$ on the Virtex-7 device; these slices on similar Virtex-7 FPGA are comparatively 1.49, 2.56, and 2.02 times higher than our accelerator for identical binary field lengths. The structural hazards due to pipelining in [17] cause higher clock cycle utilization than our accelerator, shown in column six of Table 2. Column seven in Table 2 confirms the higher circuit frequency due to pipelining in the reference design compared to our architecture. The lower clock cycle utilization in our work causes lower computation time than the reference accelerator. In comparison to another pipelined accelerator of [18] over Virtex-7 FPGA, our design utilizes lower slices and LUTs for all $GF\left(2^{163}\right)$ to $GF\left(2^{571}\right)$ binary fields, which can be seen in columns four and five of Table 2. Instead of hardware resources, our accelerator is faster in clock cycles and computation time, while the design of [18] is faster in circuit frequency due to a two-stage pipelining method.

Comparison to throughput/speed-optimized PM designs [14,19,20,21,22,23]. On Virtex-5 FPGA, the high-speed hardware design of [14] utilizes higher slices and LUTs over $GF\left(2^{163}\right)$ to $GF\left(2^{571}\right)$ binary fields as compared to our hardware accelerator. For $GF\left(2^{163}\right)$, the reference design is faster in clock cycles and computation time than our architecture on the same binary field of length 163. On the other hand, the proposed accelerator utilizes lower clock cycles and computation time over $GF\left(2^{233}\right)$ to $GF\left(2^{571}\right)$ binary fields. This is due to a digit-serial multiplier architecture in the reference design while we employed a bit-parallel modular polynomial multiplier. Additionally, for all binary field lengths of $GF\left(2^{163}\right)$ to $GF\left(2^{571}\right)$, our accelerator is faster in operating frequency; see column seven in Table 2.

Instead of the binary field hardware accelerators, we will compare our results to some recent prime field accelerators. It is essential to mention that an accurate comparison to prime field accelerators is impossible; however, we will provide the most reasonable comparison. In comparison to the 256-bit prime field accelerator of [19] over Virtex-7 FPGA, our binary field accelerators over $GF\left(2^{163}\right)$ to $GF\left(2^{571}\right)$ utilizes lower LUTs. The slices are impossible to compare as the slices are not reported in the reference design. Instead of hardware resources, our accelerators over $GF\left(2^{163}\right)$ to $GF\left(2^{571}\right)$ are faster in clock cycles, operating frequency, and computation time. The reason is the utilization of a digit-parallel multiplier in our work, while in the reference design, authors utilize an interleaved modular multiplier. In comparison to 256-bit prime field hardware accelerators of [20,21,22,23] on Virtex-7 FPGA, our accelerator over $GF\left(2^{283}\right)$ is faster in clock cycles, operating frequency and latency. On the other hand, the area utilization in slices and LUTs is also comparable to these accelerators.

4.3. Throughput and Throughput/Area Comparison

To comprehensively compare state-of-the-art designs, we have computed the throughput and throughput/area values, as shown in columns nine and ten of Table 2. The throughput, denoted as Thrpt, is presented in kilobits per second (Kbps) and is calculated using Equation (5). Additionally, the throughput over area values is calculated using Equation (6), where we utilized slices as the area metric. For the designs in [20,21,22,23], slices are not reported; therefore, we have used LUTs as the area metric in Equation (6) to compute the throughput/area ratio.

$$\begin{array}{c}\hfill Thrpt\left(Kbps\right)=\frac{1}{Latency\left(\mu s\right)}=\frac{1}{Latency}\times {10}^3\end{array}$$

(5)

$$\begin{array}{c}\hfill T/Area=\frac{Thrpt\left(Kbps\right)}{Area}=\frac{Thrpt\left(bps\right)}{Slices}\times {10}^3\end{array}$$

(6)

It is crucial to emphasize that a higher throughput/area ratio indicates better performance for the cryptographic circuit. Based on the values in columns nine and ten of Table 2, it is evident that the proposed accelerator over $GF\left(2^{163}\right)$, $GF\left(2^{233}\right)$, $GF\left(2^{283}\right)$, $GF\left(2^{409}\right)$, and $GF\left(2^{571}\right)$ achieves superior throughput and throughput/area ratio metrics on both Virtex-5 and Virtex-7 FPGA devices. This comparison demonstrates that the proposed accelerator is well-suited for cryptographic applications that require efficient implementations of ECC with a balance between high throughput and optimized area utilization.

5. Conclusions

This article has presented a hardware accelerator design for PM computation of ECC over $GF\left(2^{163}\right)$, $GF\left(2^{233}\right)$, $GF\left(2^{283}\right)$, $GF\left(2^{409}\right)$, and $GF\left(2^{571}\right)$, to optimize throughput and area simultaneously. A digit-parallel multiplier with a digit size of 41 bits is employed to enhance throughput. Additionally, we minimized hardware resources by re-using the hardware area of square and multiplier circuits to compute modular inversions. The implementation results on Xilinx Virtex-7 FPGA demonstrate that an increase in key length results in higher hardware resource utilization, including slices, LUTs, and FFs. Furthermore, longer key lengths (i.e., 409 and 571 bits) demand more computation time, leading to decreased operating frequencies compared to key lengths of 163, 233, and 283 bits. When compared to state-of-the-art approaches, the proposed accelerator over $GF\left(2^{163}\right)$, $GF\left(2^{233}\right)$, $GF\left(2^{283}\right)$, $GF\left(2^{409}\right)$, and $GF\left(2^{571}\right)$ achieves higher throughput and throughput/area ratio metrics. Consequently, our results and comparison to the state-of-the-art work demonstrate that the proposed accelerator is well-suited for applications that demand efficient implementations of ECC with a balanced emphasis on high throughput and optimized area utilization.