Abstract
Lung cancer is one of the most dangerous cancers in the world, and its early clinical manifestation is malignant nodules in the lungs, so nodule detection in the lungs can provide the basis for the prevention and treatment of lung cancer. In recent years, the development of neural networks has provided a new paradigm for creating computer-aided systems for pulmonary nodule detection. Currently, the mainstream pulmonary nodule detection models are based on convolutional neural networks (CNN); however, as the output of a CNN is based on a fixed-size convolutional kernel, it can lead to a model that cannot establish an effective long-range dependence and can only model local features of CT images. The self-attention block in the traditional transformer structures, although able to establish long-range dependence, are as ineffective as CNN structures in dealing with irregular lesions of nodules. To overcome these problems, this paper combines the self-attention block with the learnable regional attention block to form the multifaceted attention block, which enables the model to establish a more effective long-term dependence based on the characteristics of pulmonary nodules. And the multifaceted attention block is intermingled with the encoder–decoder structure in the CNN to propose the 3D multifaceted attention encoder–decoder network (MAED), which is able to model CT images locally while establishing effective long-term dependencies. In addition, we design a multiscale module to extract the features of pulmonary nodules at different scales and use a focal loss function to reduce the false alarm rate. We evaluated the proposed model on the large-scale public dataset LUNA16, with an average sensitivity of 89.1% across the seven predefined FPs/scan criteria. The experimental results show that the MAED model is able to simultaneously achieve efficient detection of pulmonary nodules and filtering of false positive nodules.
1. Introduction
According to data published by the World Health Organization’s Agency for Research on Cancer, in 2020 alone, 2.21 million people suffered from lung cancer and 1.8 million people died from lung cancer. Lung cancer is the second most common cancer globally and the number one cause of death. Lung cancer has no apparent complications in its early stages, so many patients are diagnosed with advanced lung cancer and miss out on the best time to cure it. The early clinical manifestation of lung cancer is a malignant nodule in the lung, so early detection and effective treatment of pulmonary nodules can significantly improve the survival rate of patients [1].
Quantitative CT imaging of the lungs can detect potential lung cancer patients better than standard chest X-ray screening [2], making CT images one of the main tools to assist physicians in diagnosing pulmonary nodules. However, radiologists must look at hundreds or even thousands of CT slices for each patient to reach an accurate conclusion. Due to the physician’s ability, work experience, and work status limitations, the results are often not objective enough and are prone to misses and misdiagnoses. Many researchers have therefore worked to develop efficient computer-aided detection systems to achieve accurate and effective detection of pulmonary nodules in low-dose CT scans. Early computer-aided diagnostic systems, such as morphological thresholds, relied on a priori knowledge. They required manual extraction of low-level features of pulmonary nodules, making it challenging to discriminate complex nodules after specific lesions have occurred [3]. According to Wani et al. [4], AI can improve the knowledge of healthcare professionals, enabling them to spend more time on direct patient care and reduce fatigue. In recent years, deep learning of AI has demonstrated powerful learning capabilities in processing raw image tasks. The advantage of deep learning-based models is that they can learn the intrinsic representation of the data despite the absence of prior knowledge.
There are many deep learning-based approaches to achieve pulmonary nodule detection [5], primarily based on a two-stage strategy: 1. candidate pulmonary nodule detection and 2. false positive pulmonary nodule filtering. For example, Zhao et al. [6] combined multiscale blocks with Faster R-CNN blocks to construct a pulmonary nodule detection model and proposed a 3D convolution-based MSM-CNN model to filter false positive pulmonary nodules. Zhang et al. [7] incorporated a multiscale attention block into an encoder–decoder network as the backbone of a Faster R-CNN model for pulmonary nodule detection. And the 3D multiscale attention block was incorporated into the Res2Net structure for a false positive reduction in pulmonary nodules. Peng et al. [8] combined Res2Net and the channel self-attention mechanism as the backbone of the model for the detection of lungs and the false positive reduction in nodules. Although the same network structure is adopted for different tasks, the features that the two networks advance for each other do not share with each other and still need to be trained multiple times. For multi-stage network models, features are extracted from the original dataset and predicted at each stage. However, the repetitive feature extraction will bring much computational cost [9]. Therefore, many scholars have begun constructing single-stage models for detecting lung nodules. For example, Li et al. [10] designed a feature extraction network with an encoding–decoding structure. They combined it with a 3D region suggestion network (RPN) to effectively detect pulmonary nodules. The single-stage pulmonary nodule detection task, without the false positive nodule screening component, necessitates that the network has a more robust feature extraction capability to identify pulmonary nodules more accurately. Most feature extraction networks are based on convolutional neural networks (CNNs). However, the limited receptive fields of CNNs make establishing long-range dependence on the model challenging. However, long-range dependence can provide information on the location and relationship of the target across the scene, which is crucial for detecting pulmonary nodules.
Inspired by the field of natural language processing (NLP), many scholars have fused the transformer module with CNNs to overcome the inherent weakness of CNN structures that cannot establish long-range dependencies. The transformer module weights and maps each token to all other tokens through a self-attention block to obtain the dependencies between different locations [11]. Due to its unique ability to model the global context, it has been widely used in medical images [12]. However, as with traditional CNN structures, the transformer structure itself is inflexible, where each pixel point must interact with all other pixel points, inevitably introducing a portion of redundant information [13]. In particular, in the pulmonary nodule detection task, as pulmonary nodules account for a tiny proportion of the whole CT image, global modeling using the transformer introduces many lung features into the computation (nodule features account for a tiny proportion). In addition, transformer-based models can also require more data to fit than traditional CNN models, and researchers often cannot collect enough data to fit a pure transformer model [14]. In order to establish long-range dependencies with the help of transformer structures under limited datasets, often the following two approaches can be used: 1. training the model on large datasets and applying the feature extraction capabilities obtained from the training to a new task (transfer learning) [15] and 2. using CNN structures instead of positional coding to achieve a more efficient inductive bias [16].
To address the above challenges, this paper introduces local learnable region attention (LRA) [17] into the transformer model. It combines it with traditional CNN models and 3D RPN models to propose the MAED model. LRA can form irregular receptive fields according to the specific conditions of the target and combines with traditional self-attention to form multifaceted attention, enabling the model to identify well irregularly lesioned pulmonary nodules. The multiscale fusion block (MSF) enables the model to better extract pulmonary nodule features of different sizes/diameters. The MAED model utilizes dynamic scaling with cross-entropy loss [18] to cope with the imbalance between positive and negative sample sizes. Overall, the MAED model can extract the texture information of nodules while also establishing efficient long-range dependence, enabling more accurate single-step pulmonary nodule detection.
The main points of the contribution of this paper are as follows:
- We propose a novel pulmonary nodule detection model, which can change the size of the receptive field according to the characteristics of the detection target and can effectively deal with various irregular lesions of pulmonary nodules.
- We use CNN structures to optimize the inherent shortcomings of the transformer-based model and enable the MAED model to effectively extract local features of nodules and establish long-range dependencies, improving the reliability and generalization of the model.
- We evaluate the MAED model on LUNA16 data, and the results of our experiments show that our model achieved both accurate detections of pulmonary nodules and the screening of false positive nodules in 3D CT scans compared to existing methods.
2. Related Works
2.1. Three-Dimensional Pulmonary Nodule Detection
The early detection of pulmonary nodules is the best way to prevent and treat cancer. With the gradual increase in lung cancer patients in recent years, there has been much interest in using computer-aided diagnosis (CAD) systems to improve radiologists’ efficiency. Most CAD systems have two stages: 1. candidate pulmonary nodule detection and 2. false positive pulmonary nodule filtering. Most previous work has used 2D anchor-point detection networks [3]. However, 2D or multi-view 2D models can lose important information from the original image and fail to identify pulmonary nodules accurately. Therefore, the use of 2D anchor-point detection networks is often combined with 3D networks to screen for false positive nodules and achieve more accurate detection. In recent years, many scholars have constructed 3D candidate nodule detection networks that do not need to be coupled with a false positive nodule filtering network to achieve higher accuracy. For example, Khosravan et al. [19] extended the DenseNet model to a pulmonary nodule detection task. They achieved a competitive performance metric (CPM) of 0.897 on the LUNA16 dataset by combining five 3D dense blocks and the maximum pooling layer. Huang et al. [20] incorporated a one-shot aggregation block, the receptive field block, and a feature fusion scheme into the YOLOV3 model. They eliminated duplicate detection by a non-polar depressed value algorithm, achieving a CPM of 0.905 on the LUNA16 dataset. Luo et al. [9] proposed a centroid matching model (SCPM-Net) based on a 3D sphere representation. SCPM-Net, compared to traditional pulmonary nodule detection models, does not require the manual setting of anchor parameters to achieve good outcomes.
2.2. Variable Attention
The transformer model can obtain larger receptive fields than the traditional CNN model and establish a long-range dependence between pixels. Dosovitskiy et al. [21] proposed the vision transformer (ViT). By cutting the image into different patches and transforming them into different tokens through linear mapping, the dependencies between the different tokens are established with the help of the self-attention block, successfully introducing the transformer struct into the vision domain. The transformer-based models have shown strong competitiveness in various vision tasks and are gradually being extended to medical imaging. For example, Cheng et al. [22] added a pre-trained ViT module between the encoder and decoder of the network for 2D medical image segmentation. Yang et al. [23] achieved the first multi-instance learning of pulmonary nodule features by using a transformer model to simultaneously learn multiple pulmonary nodule features from the same patient. The transformer builds long-range dependencies through self-attention while also introducing higher spatial and temporal complexity, and there are many redundant calculations in global modeling. Therefore, many scholars have attempted to construct non-global long-range dependencies. Beltagy et al. modified the traditional self-attention mechanism to propose the Longformer model [24]. In the Longformer model, each token performs local attention only for tokens in a fixed window size, and only a small number of tokens perform global attention computations. Swin-transformer divides the image into different windows, computes self-attention within each window, and devises a way to interact across windows [25]. However, most methods are based on setting a fixed-size local window, which requires the artificial setting of the window size and is poorly robust to scale-varying targets. Lin et al. [15] provided new ideas, and they extended variable attention into learnable attention by proposing the LRA block, which can dynamically generate different size perceptual fields for each target.
3. Methods
In this section, we focus on the overall architecture of the MAED model, as shown in Figure 1, and provide details of the specific implementation of the MAED model. The following four main areas include the encoder–decoder network, learnable region attention (LRA), multiscale fusion block (MSF), and 3D RPN block for regression prediction. All abbreviations for this paper are shown in Table 1.
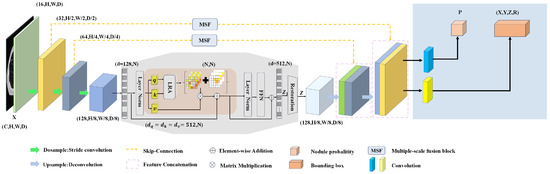
Figure 1.
The main structure of MAED, where the red modules are the LRA and self-attention blocks, the grey section shows the complete process of building long-range dependencies, and the blue section shows the regression prediction network.

Table 1.
List of abbreviations.
3.1. Three-Dimensional Encoder Network
The LRA block is based on transformer implementation, and because the computational complexity of the transformer is quadratic concerning the number of tokens (sequence lengths), directly treating each pixel point of the image as a token would introduce a large amount of computation. If one follows the ViT model (segmenting the image into fixed patches and then linearly mapping them into tokens), the model loses the ability to model local information about the image in space and depth [26]. In this paper, we remedy these deficiencies by designing a set of downsampled convolutions and combining them into an encoder network that progressively encodes the input image to produce a low-resolution representation of high-level features. In this way, the feature map will be rich in local contextual information with relatively little computational effort. Each downsampling block can take the form of
where and represent a 3D convolution with a convolution kernel of (padding of 1 and step size of 1, without changing the number of channels in the feature map), which models the feature map locally at the spatial level. Re represents an activation function to the non-linear map which is ReLU. After local modeling of the feature map with two 3D convolutions, the original features are summed with the extracted features using a residual join to prevent gradient dispersion. represents a 3D convolutional kernel of with a step size of 2 and a padding of 1. This step downsamples the input feature map and expands the number of channels of the feature to twice the original. It is worth noting that we use an additional convolution with a convolution kernel of (step size 1, padding 1) in front of the first module of the encoder to expand the input single-channel image into a feature map with a channel number of 16 as a way to obtain a richer feature set of the feature map.
3.2. Long-Range Dependence
As shown in Figure 2, models with different structures have different receptive fields. Because a fixed-size convolution kernel and an attention mechanism with predefined ranges cannot adequately learn spatial information between different scales [27], this paper introduces local learnable region attention (LRA), in which each feature is dynamically assigned attention. The basic idea of LRA is to introduce a learnable mask on top of the transformer global receptive field (global self-attention o mask, o is the Hadamard product) to avoid each pixel point having to interact with all other pixel points.
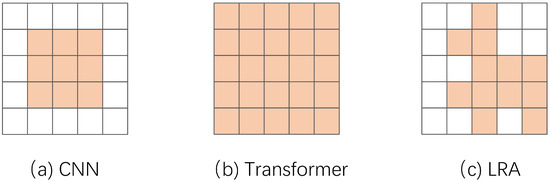
Figure 2.
Comparison of the perceived wildness of different structures.
3.2.1. Global Self-Attention
The original image was passed through the 3D encoder block to obtain a highly compressed feature map . In order to allow the transformer to model the spatiality and depth of the 3D image more comprehensively, we combine the spatial and depth dimensions of the image to obtain a set of feature maps . After a linear mapping layer, h generates three feature vectors, , , and . Then, vector Q is dotted with vector K to obtain the similarity matrix and normalized to obtain the weight matrix. Finally, the weight matrix is multiplied by the vector V to complete the global modeling of the feature map. The following equation shows global self-attention.
3.2.2. Local Learnable Region Attention
For each feature on the feature map, the LRA block generates a different irregular perceptual field . Firstly, for a given vector Q and vector K, two graphs , of predicted coverage are generated by the four learnable parameter matrices . The form is as follows:
Each value on the prediction maps represents the probability that the corresponding pixel point belongs to the mask region. To obtain a learnable three-dimensional attention map, we adjusted and to the four-dimensional tensor of the form , i.e., for each feature the corresponding prediction coverage map will be generated. In order to obtain the exact region of the mask, for , a cumulative distribution function will be used to integrate each of the predicted probability maps from the lower left (bl) to the upper right (ur). The integrates from the opposite direction, and the resulting integrated regions are multiplied to obtain the learnable mask regions. The formalization is as follows:
where and refer to any one of the feature maps, and p refers to or at any point on the feature map. Suppose that and , i.e., assuming that and are the result of the calculation of the above equation. The following equation shows the formal definition of the mask region.
where o denotes the Hadamard product, .
Due to the inclusion of the softmax function in the calculation of the probability plot, the probability plot may contain a large number of zeros, and the Hadamard product can effectively extract the overlapping part of the two probability maps (mask region). However, if the predicted non-zero values are concentrated in the image’s corners, it may result in fewer overlapping parts, as shown in the first row of Figure 3. Therefore, it is necessary to integrate from the top right to the bottom left again using the cumulative distribution function and using the opposite direction, i.e., repeat the above steps using the opposite direction of integration and sum up, as shown in Figure 3. The complete masked area is as follows:
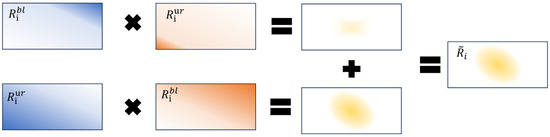
Figure 3.
An example of the learnable region filter mechanism.
The learnable areas of self-attention are as follows:
Subsequent experiments demonstrated that the global perceptual information is still non-negligible, so we summed the LAR with the global self-attention to retain the global information (the global self-attention weighting is small). The complete attention struct used in this paper is as follows:
3.2.3. Feedforward Layer
We keep the feedforward layer of the transformer module and use it to transform the features. The feedforward layer consists of 2 main fully connected layers. The first fully connected layer will map the token dimension to twice the original. The second fully connected layer will then map it back to the token dimension. This process can be abstracted into a function as follows:
3.3. Multiple-Scale Fusion
The purpose of the multiscale fusion (MSF) block is to extract node features of different sizes/diameters without reducing the resolution of the feature map. This paper extracts and fuses features using different dilated rates and convolution. The MSF block effectively prevents the loss of features, and its main structure is as follows:
where is a convolution, and are two 3D convolutions with dilation rates of 1 and 2, respectively (convolution kernel of , step size of 1, and padding of 1). After contacting the feature channels, a bottleneck layer (a convolution kernel of ) fuses the features and reduces the model’s parameters. Finally, the original features are summed with the extracted features via a residual block to preserve the original features, as shown in Figure 4. Dilated convolutions with different dilation rates result in different receptive fields. Therefore, combining convolutions with different dilation rates can improve the feature learning ability of the network for different scales of pulmonary nodules.
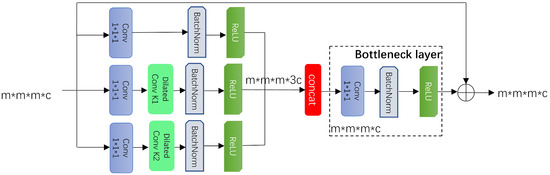
Figure 4.
Main structure of the MSF module.
3.4. Three-Dimensional Decoder Network
Because pulmonary nodules comprise a small proportion of the lung image, regressing predictions directly on a highly compressed feature map is challenging. Hence, this paper introduces a decoder block of a 3D CNN for upsampling to extend the resolution of the feature map, as shown on the right-hand side of Figure 2. Each of the upsampling modules can be abstracted as follows:
The function amplifies the resolution of the feature map and models the combination of feature maps at the corresponding positions in the encoder using a jump connection. and represent 3D convolutions with the kernel, which compresses the number of channels of the original feature map to half. is a transposed convolution with the 3D kernel, which extends the resolution of the original feature map by a factor of two. refers to the input of the jump connection. consists mainly of two 3D convolutions and residual links, which are used to further learn the feature map. The first part of the decoder has no upsampling and no jump connections, so the block without residual connections is used instead of the block.
3.5. Three-Dimensional Region Generation Network
We use a 3D region generation network (RPN) to achieve the final discrimination of pulmonary nodule classes (positive and negative nodules), predict each nodule bounding box, and merge overlapping candidate boxes using non-maximal suppression. Specifically, two sets of vectors are generated for each pixel point using two convolutional layers (with a convolutional kernel of ) predictions , where is a one-dimensional vector indicating the probability that the pixel point is a positive nodule, and is a four-dimensional vector predicting the offset of the anchor point of the spatial location and radius prediction. Because negative nodules will be much more significant than positive ones, we use a focal loss function to match positive and negative samples. The focal loss function is defined as follows:
In this study, when the label contains an accurate sample, ; otherwise, . is the balance factor and is the focusing parameter ().
The regression loss function on the nodal bounding box is
where denote the predicted offsets and denotes the defined anchor point, and denote the true label. s denotes the smoothed L1 regularization function.
4. Experiment
4.1. Data and Pre-Processing of Data
In this paper, the proposed model was evaluated comprehensively using the publicly available dataset LUNA16 [28], a filtered subset of the LIDC/IDRI dataset. The researchers excluded nodules with slice thicknesses greater than 2.5 mm and less than 3 mm from the LIDC/IDRI dataset and gave accurate annotation information. The LUNA16 dataset is a more suitable model for assessing the detection and segmentation of pulmonary nodules than the LIDC/IDRI dataset. In the LUNA16 dataset, there are 1186 pulmonary nodules from 888 different CT scans with a mean nodule size of 8.31 mm (standard deviation of 4.76 mm).
The original LDCT images contain many background areas besides the lung region that cannot be used directly in the experiment. This paper’s input images were finely segmented using a binary segmentation masking method (the LUNA16 dataset provided masking) to extract the complete lung tissue structure. All the pixel points were then cropped to the range [−1200,600] and normalized. The LUNA16 dataset is derived from devices made by different manufacturers, and inter-device differences lead to differences in the parameters of the images. For example, the slice thickness of CT scans varies (between 0.45 and 5.0 mm); the spacing of image pixels (in millimeters) also varies. The authors of this paper, therefore, resampled the cropped area, normalized the voxel spacing to 1 mm, and finally scaled all the images to .
4.2. Implementation Details
The experiments in this paper are based on implementing the PyTorch framework and running on a server with four NVIDIA Tesla V100 SXM2 GPUs. All the experiments in this paper were set with a random number seed of 0, a batch size of 24, and a learning rate of 0.001 and used an SGD optimizer (momentum of 0.9 and weight decay of ) to optimize the training process. In the training phase of the model, we used random cropping, random flipping, and scaling (in the range of 0.9 to 1.1) to enhance the data. For the training of anchors, the authors of this paper considered bounding boxes with an IoU (intersection and merging ratio) greater than 0.5 as positive examples and those with an IoU less than 0.02 as negative examples, as suggested by Li et al. [10]. The values of the anchor points were predefined as (5,10,20). The model’s performance is evaluated in this paper using the free-response receiver operating characteristic (FROC) script provided with the LUNA16 dataset. The FROC measures the detector’s performance by calculating the average number of false alarms per scan (sensitivity) and has seven predefined FPs/scan rates: 0.125, 0.25, 0.5, 1, 2, 4, and 8. All hyperparameters of the model are shown in Table 2.

Table 2.
Hyperparameters optimization results.
4.3. Comparison with State-of-the-Art Models
In this paper, we further analyze the LUNA16 dataset to compare our method with several published state-of-the-art methods for pulmonary nodule detection. Dou et al. [29] extended the FCN and residual network, which have relatively good results in the visual tasks, into a 3D network for pulmonary nodule detection and false positive reduction, respectively. Zhu et al. [30] extended the 2D Faster R-CNN into 3D and designed a U-net-like structure as the backbone network of the model. Li et al. [10] incorporated channel attention into an encoder–decoder network to achieve pulmonary nodule detection and false positive reduction. Tang et al. [31] proposed a joint multi-tasking framework using a single network to simultaneously achieve pulmonary nodule detection, false positive reduction, and segmentation. Wang et al. [32] used a network with an FPN structure to detect pulmonary nodules and proposed an attention 3D-CNN network to reduce false positives in detection. Song et al. [33] developed an anchorless network for the detection of pulmonary nodules. All the models were evaluated on the LUNA16 dataset, but the pre-processing may differ. The comparative results of the experiments are shown in Table 3. The MAED model proposed in this paper achieved both the detection of pulmonary nodules and the reduction in false positives using only one network, and the overall performance of the model is at the level of the state-of-the-art methods.

Table 3.
Comparison results with other state-of-the-art models.
4.4. Ablation Experiments
In order to verify the effectiveness of the proposed module, we designed different network structures for the ablation experiments, and the effects of attentional mechanisms, local attention, LRA, and MSF on the models were analyzed, respectively. Specifically, we designed the following four variants of the model:
- Encoder–decoder: This model consists only of an encoder responsible for downsampling and a decoder responsible for upsampling. The intermediate attention blocks are replaced using the same number of residual blocks.
- Encoder–decoder+transformer: This model inserts four transformer modules between the encoder and decoder, i.e., the image is modeled using global self-attention.
- Encoder–Decoder + LRA: This model inserts four LRA blocks (with feedforward network layers) between the encoder and decoder.
- MAED model without MSF: This model does not use multiscale modules at the jump links of the encoder and decoder compared to the completed model proposed in this paper.
4.5. Results
Table 4 shows all the results of the ablation experiments, and the model proposed in this paper outperforms the other baseline models in nearly all metrics. Adding an attention mechanism to the encoder–decoder structure, i.e., adding long-term dependencies to the local modeling, can improve some of the model’s performance. Models that use only the regionally learnable attention mechanism use more parameters than if only global self-attention is used. However, performance improvement in the model is not significant. However, the model performance can be significantly improved when the two attention mechanisms are used together (with a slight weighting of the global self-attention). According to Figure 5, the FROC curve of the MAED model covers a larger area than all the other models in the ablation experiment, further demonstrating the superiority of the MAED model.

Table 4.
The results of the ablation experiment.
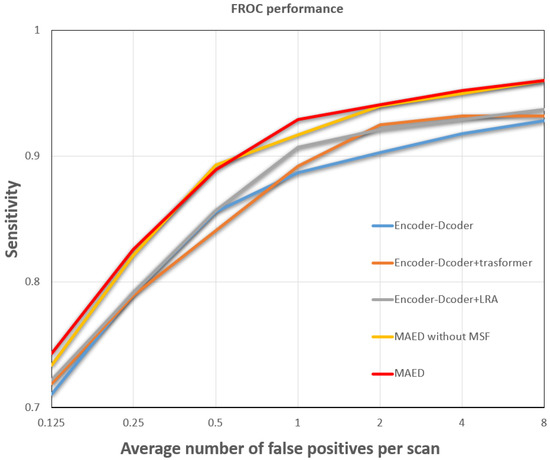
Figure 5.
Comparison of FROC curves for different networks.
To better understand the process of model inference and the assignment of weights by the model, we visualized the mask generated by the local learnable region attention (LRA), as shown in Figure 6. In the visualization, the white areas are the pulmonary nodules to be detected, with brighter colors in the plot indicating that the area will be given more weight in the calculation. As shown in Figure 6, the LRA block can accurately assign more weight to the area around the pulmonary nodule, allowing the model to focus more on the area around the pulmonary nodule and to establish practical long-range dependence on the area. However, the mask regions generated are not necessarily contiguous, i.e., irrelevant regions are accounted for when establishing long-term dependence. In future work, we will continue to investigate further to establish more accurate and valid region perception fields and extend this to other clinical applications.
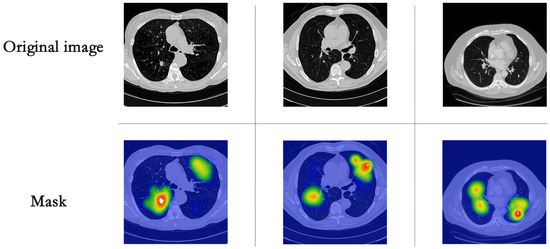
Figure 6.
Visualization of the results of LRA-generated masks.
5. Conclusions
This paper proposes a multi-task deep learning algorithm, the MAED model, for pulmonary nodule detection and false positive nodule screening. We combined the self-attention module with the LRA block to form the multifaceted attention block, which enabled the model to establish irregular long-range dependencies based on the features of the nodules, making the model better able to deal with the irregular lesions of pulmonary nodules. We integrated the multifaceted self-attention block with the encoder–decoder structure in the CNN with each other, which enabled the proposed model to model the local texture features of nodules while establishing an effective long-range dependency, making the model better able to identify the fine nodules. The performance of the model was further improved using methods, such as multiscale modules and focal loss functions. We conducted extensive experiments on the LUNA16 dataset to validate that the MAED model had the effectiveness of each component, and the overall performance of the model had an average sensitivity of 89.1% at seven predefined FPs/scans. The model proposed in this paper has better performance compared to state-of-the-art single- or multi-stage detection methods.
Representativeness/racial bias will occur when the datasets used to develop AI algorithms are not sufficiently diverse to represent many different population groups and/or characteristics. Therefore, in future work, we will collect more clinical data from different regions/countries to avoid the over-concentration of data leading to representativeness/ethnicity bias of the model. In addition, we will further expand the pulmonary nodule detection model into a pulmonary nodule segmentation model to provide more help to radiologists in their diagnostic work.
Author Contributions
Conceptualization, K.C.; Methodology, K.C. and Z.W.; Validation, Z.W.; Data Curation, H.T. and Z.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wood, D.E.; Kazerooni, E.A.; Baum, S.L.; Eapen, G.A.; Ettinger, D.S.; Hou, L.; Jackman, D.M.; Klippenstein, D.; Kumar, R.; Lackner, R.P.; et al. Lung cancer screening, version 3.2018, NCCN clinical practice guidelines in oncology. J. Natl. Compr. Cancer Netw. 2018, 16, 412–441. [Google Scholar] [CrossRef] [PubMed]
- Kramer, B.S.; Berg, C.D.; Aberle, D.R.; Prorok, P.C. Lung cancer screening with low-dose helical CT: Results from the National Lung Screening Trial (NLST). J. Med. Screen. 2011, 18, 109–111. [Google Scholar] [CrossRef]
- Ding, J.; Li, A.; Hu, Z.; Wang, L. Accurate pulmonary nodule detection in computed tomography images using deep convolutional neural networks. In Proceedings of the Medical Image Computing and Computer Assisted Intervention-MICCAI 2017: 20th International Conference, Quebec City, QC, Canada, 11–13 September 2017; Proceedings, Part III 20. Springer International Publishing: Cham, Switzerland, 2017; pp. 559–567. [Google Scholar]
- Wani, S.U.D.; Khan, N.A.; Thakur, G.; Gautam, S.P.; Ali, M.; Alam, P.; Alshehri, S.; Ghoneim, M.M.; Shakeel, F. Utilization of artificial intelligence in disease prevention: Diagnosis, treatment, and implications for the healthcare workforce. Healthcare 2022, 10, 608. [Google Scholar] [CrossRef]
- Li, R.; Xiao, C.; Huang, Y.; Hassan, H.; Huang, B. Deep learning applications in computed tomography images for pulmonary nodule detection and diagnosis: A review. Diagnostics 2022, 12, 298. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Z.; Liu, X.; Chen, Q.; Li, C.; Zhao, H.; Wang, Z. Pulmonary Nodule Detection Based on Multiscale Feature Fusion. Comput. Math. Methods Med. 2022, 2022, 8903037. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Peng, Y.; Guo, Y. Pulmonary nodules detection based on multi-scale attention networks. Sci. Rep. 2022, 12, 1466. [Google Scholar] [CrossRef] [PubMed]
- Peng, H.; Sun, H.; Guo, Y. 3D multi-scale deep convolutional neural networks for pulmonary nodule detection. PLoS ONE 2021, 16, e0244406. [Google Scholar] [CrossRef]
- Luo, X.; Song, T.; Wang, G.; Chen, J.; Chen, Y.; Li, K.; Metaxas, D.N.; Zhang, S. SCPM-Net: An anchor-free 3D lung nodule detection network using sphere representation and center points matching. Med. Image Anal. 2022, 75, 102287. [Google Scholar] [CrossRef]
- Li, Y.; Fan, Y. DeepSEED: 3D squeeze-and-excitation encoder-decoder convolutional neural networks for pulmonary nodule detection. In Proceedings of the 2020 IEEE 17th International Symposium on Biomedical Imaging (ISBI), Iowa City, IA, USA, 3–7 April 2020; pp. 1866–1869. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Oktay, O.; Schlemper, J.; Folgoc, L.L.; Lee, M.; Heinrich, M.; Misawa, K.; Mori, K.; McDonagh, S.; Hammerla, N.Y.; Kainz, B.; et al. Attention u-net: Learning where to look for the pancreas. arXiv 2018, arXiv:1804.03999. [Google Scholar]
- Cao, K.; Tao, H.; Wang, Z.; Jin, X. MSM-ViT: A multi-scale MobileViT for pulmonary nodule classification using CT images. J. X-ray Sci. Technol. 2023, 31, 731–744. [Google Scholar] [CrossRef] [PubMed]
- Matsoukas, C.; Haslum, J.F.; Söderberg, M.; Smith, K. Is it time to replace cnns with transformers for medical images? arXiv 2021, arXiv:2108.09038. [Google Scholar]
- Wu, Y.; Qi, S.; Sun, Y.; Xia, S.; Yao, Y.; Qian, W. A vision transformer for emphysema classification using CT images. Phys. Med. Biol. 2021, 66, 245016. [Google Scholar] [CrossRef] [PubMed]
- Mehta, S.; Rastegari, M. Mobilevit: Light-weight, general-purpose, and mobile-friendly vision transformer. arXiv 2021, arXiv:2110.02178. [Google Scholar]
- Lin, H.; Ma, Z.; Ji, R.; Wang, Y.; Hong, X. Boosting crowd counting via multifaceted attention. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 19628–19637. [Google Scholar]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollar, P. Focal loss for dense object detection. IEEE Trans. PAMI 2018, 42, 318–327. [Google Scholar] [CrossRef]
- Khosravan, N.; Bagci, U. S4ND: Single-shot single-scale lung nodule detection. In Proceedings of the Medical Image Computing and Computer Assisted Intervention-MICCAI 2018: 21st International Conference, Granada, Spain, 16–20 September 2018; Proceedings, Part II 11. Springer International Publishing: Cham, Switzerland, 2018; pp. 794–802. [Google Scholar]
- Huang, Y.S.; Chou, P.R.; Chen, H.M.; Chang, Y.C.; Chang, R.F. One-stage pulmonary nodule detection using 3-D DCNN with feature fusion and attention mechanism in CT image. Comput. Methods Programs Biomed. 2020, 220, 106786. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Chen, J.; Lu, Y.; Yu, Q.; Luo, X.; Adeli, E.; Wang, Y.; Lu, L.; Yuille, A.L.; Zhou, Y. Transunet: Transformers make strong encoders for medical image segmentation. arXiv 2021, arXiv:2102.04306. [Google Scholar]
- Yang, J.; Deng, H.; Huang, X.; Ni, B.; Xu, Y. Relational learning between multiple pulmonary nodules via deep set attention transformers. In Proceedings of the 2020 IEEE 17th International Symposium on Biomedical Imaging (ISBI), Iowa City, IA, USA, 3–7 April 2020; pp. 1875–1878. [Google Scholar]
- Beltagy, I.; Peters, M.E.; Cohan, A. Longformer: The long-document transformer. arXiv 2020, arXiv:2004.05150. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 10012–10022. [Google Scholar]
- Li, J.; Wang, W.; Chen, C.; Zhang, T.; Zha, S.; Yu, H.; Wang, J. Transbtsv2: Wider instead of deeper transformer for medical image segmentation. arXiv 2022, arXiv:2201.12785. [Google Scholar]
- Zhang, P.; Dai, X.; Yang, J.; Xiao, B.; Yuan, L.; Zhang, L.; Gao, J. Multi-scale vision longformer: A new vision transformer for high-resolution image encoding. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 2998–3008. [Google Scholar]
- Setio, A.A.A.; Traverso, A.; De Bel, T.; Berens, M.S.; Van Den Bogaard, C.; Cerello, P.; Chen, H.; Dou, Q.; Fantacci, M.E.; Geurts, B.; et al. Validation, comparison, and combination of algorithms for automatic detection of pulmonary nodules in computed tomography images: The LUNA16 challenge. Med. Image Anal. 2017, 42, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Dou, Q.; Chen, H.; Jin, Y.; Lin, H.; Qin, J.; Heng, P.A. Automated pulmonary nodule detection via 3d convnets with online sample filtering and hybrid-loss residual learning. In Proceedings of the Medical Image Computing and Computer Assisted Intervention-MICCAI 2017: 20th International Conference, Quebec City, QC, Canada, 11–13 September 2017; Proceedings, Part III 20. Springer International Publishing: Cham, Switzerland, 2017; pp. 630–638. [Google Scholar]
- Zhu, W.; Liu, C.; Fan, W.; Xie, X. Deeplung: Deep 3d dual path nets for automated pulmonary nodule detection and classification. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018; pp. 673–681. [Google Scholar]
- Tang, H.; Zhang, C.; Xie, X. Nodulenet: Decoupled false positive reduction for pulmonary nodule detection and segmentation. In Proceedings of the Medical Image Computing and Computer Assisted Intervention-MICCAI 2019: 22nd International Conference, Shenzhen, China, 13–17 October 2019; Proceedings, Part VI 22. Springer International Publishing: Cham, Switzerland, 2019; pp. 266–274. [Google Scholar]
- Wang, B.; Qi, G.; Tang, S.; Zhang, L.; Deng, L.; Zhang, Y. Automated pulmonary nodule detection: High sensitivity with few candidates. In Proceedings of the Medical Image Computing and Computer Assisted Intervention-MICCAI 2018: 21st International Conference, Granada, Spain, 16–20 September 2018; Proceedings, Part II. Springer International Publishing: Cham, Switzerland, 2018; pp. 759–767. [Google Scholar]
- Song, T.; Chen, J.; Luo, X.; Huang, Y.; Liu, X.; Huang, N.; Chen, Y.; Ye, Z.; Sheng, H.; Zhang, S.; et al. CPM-Net: A 3D center-points matching network for pulmonary nodule detection in CT scans. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention 2020, Lima, Peru, 4–8 October 2020; Springer: Cham, Switzerland, 2020; pp. 550–559. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).