Research on the Water Entry of the Fuselage Cylindrical Structure Based on the Improved SPH Model
Abstract
:1. Introduction
2. Improved SPH Model
2.1. Low-Dissipation Godunov SPH (GSPH) Method for Fluid
2.2. TL-SFPM (Total Lagrangian Smoothed Particle Hydrodynamics) Method for Solids
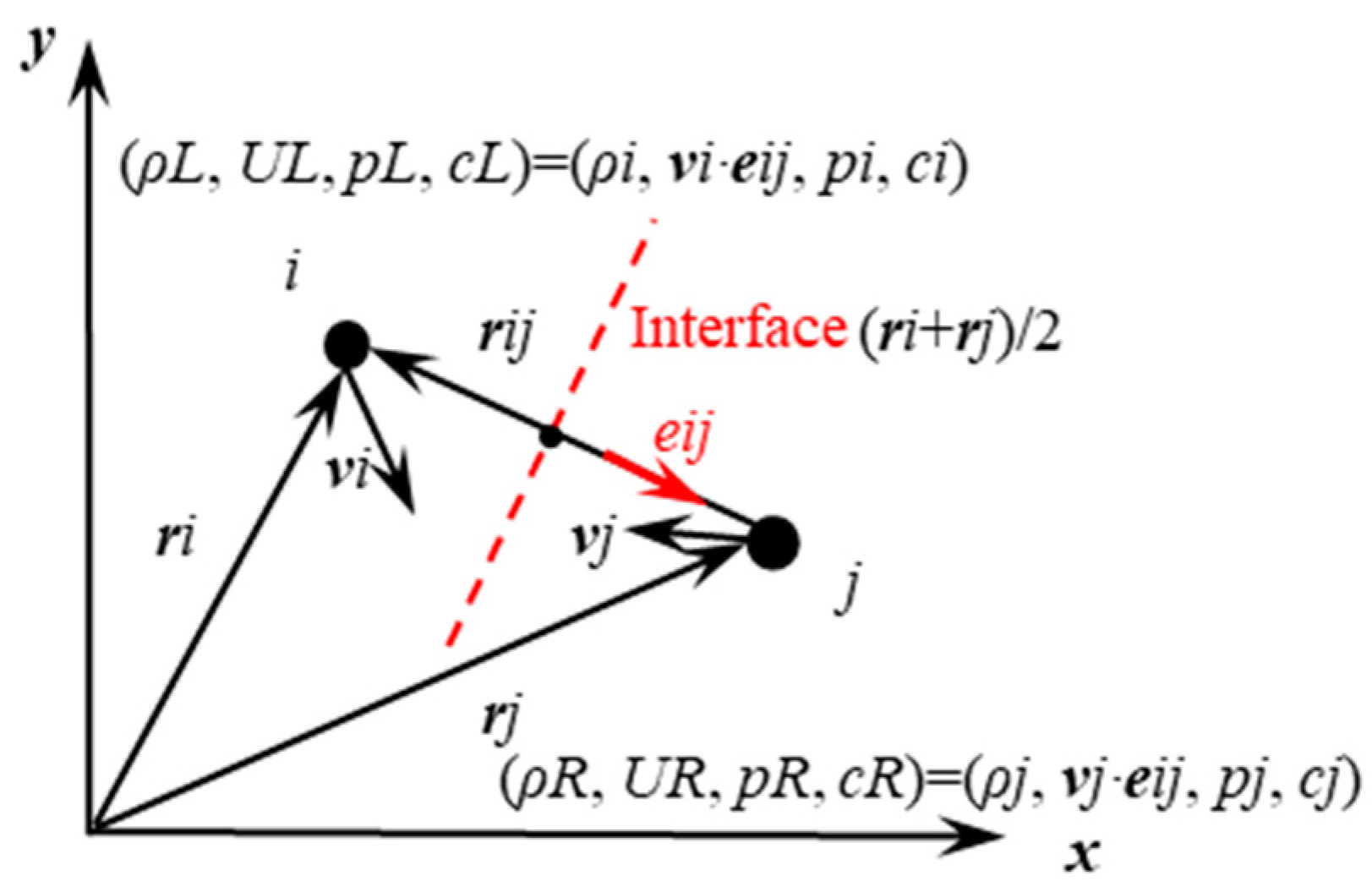
2.3. Riemann-Based Contact Algorithm for Fluids and Solids
3. Damage Model
4. Numerical Simulation of Water Entry of a Cylinder Structure
4.1. Validation through Numerical Simulation
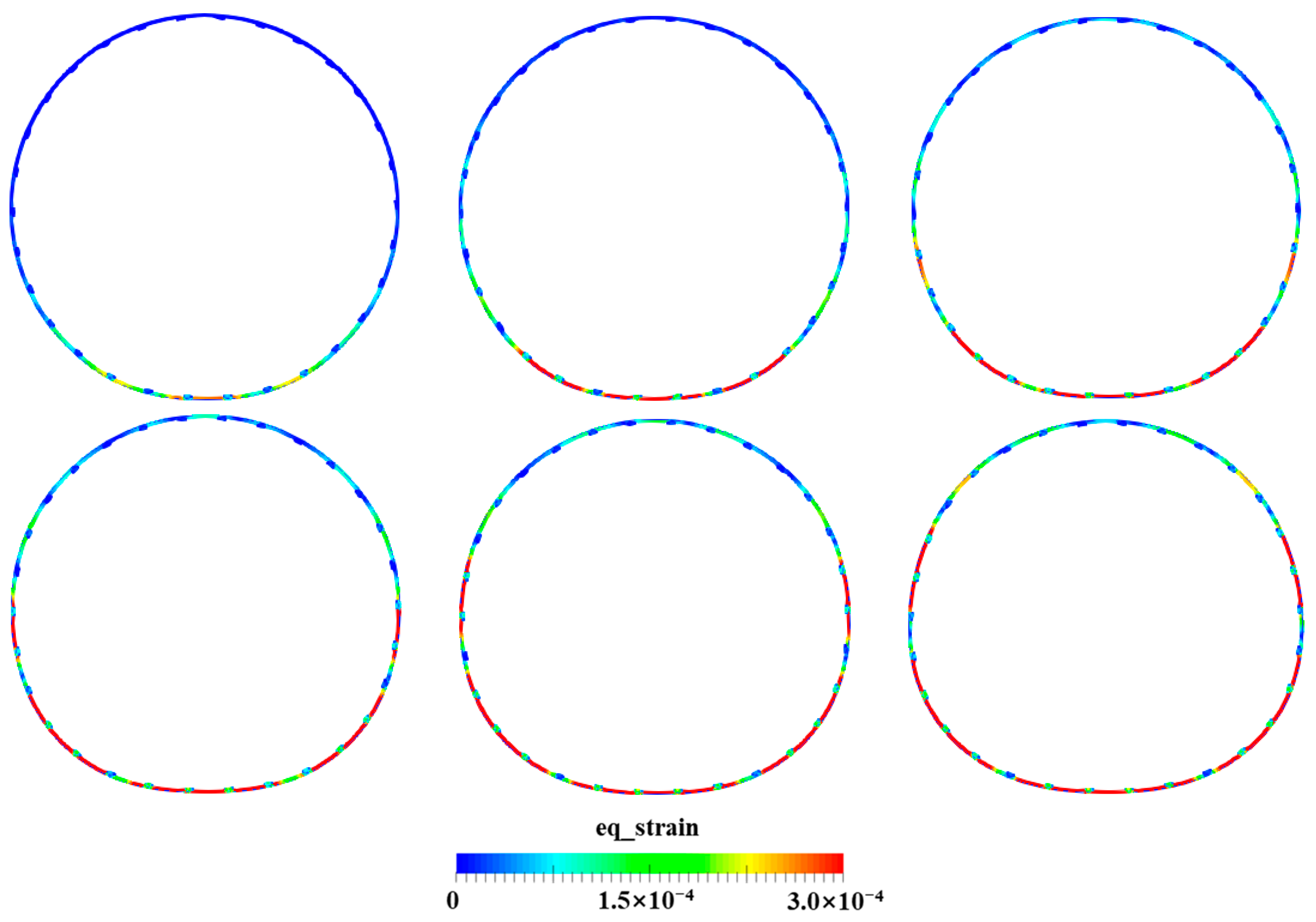
4.2. Water Entry of the Skin Cylinder
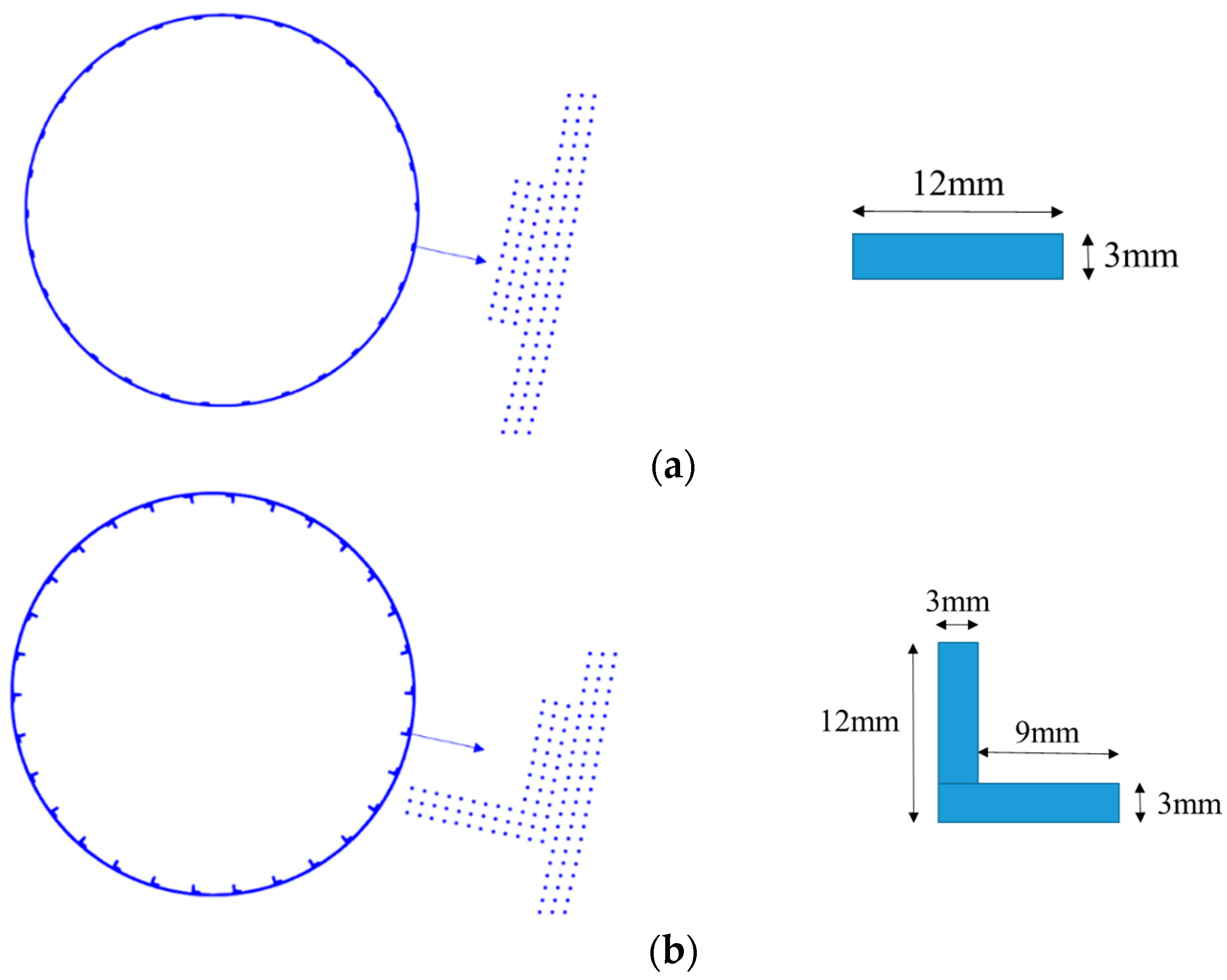
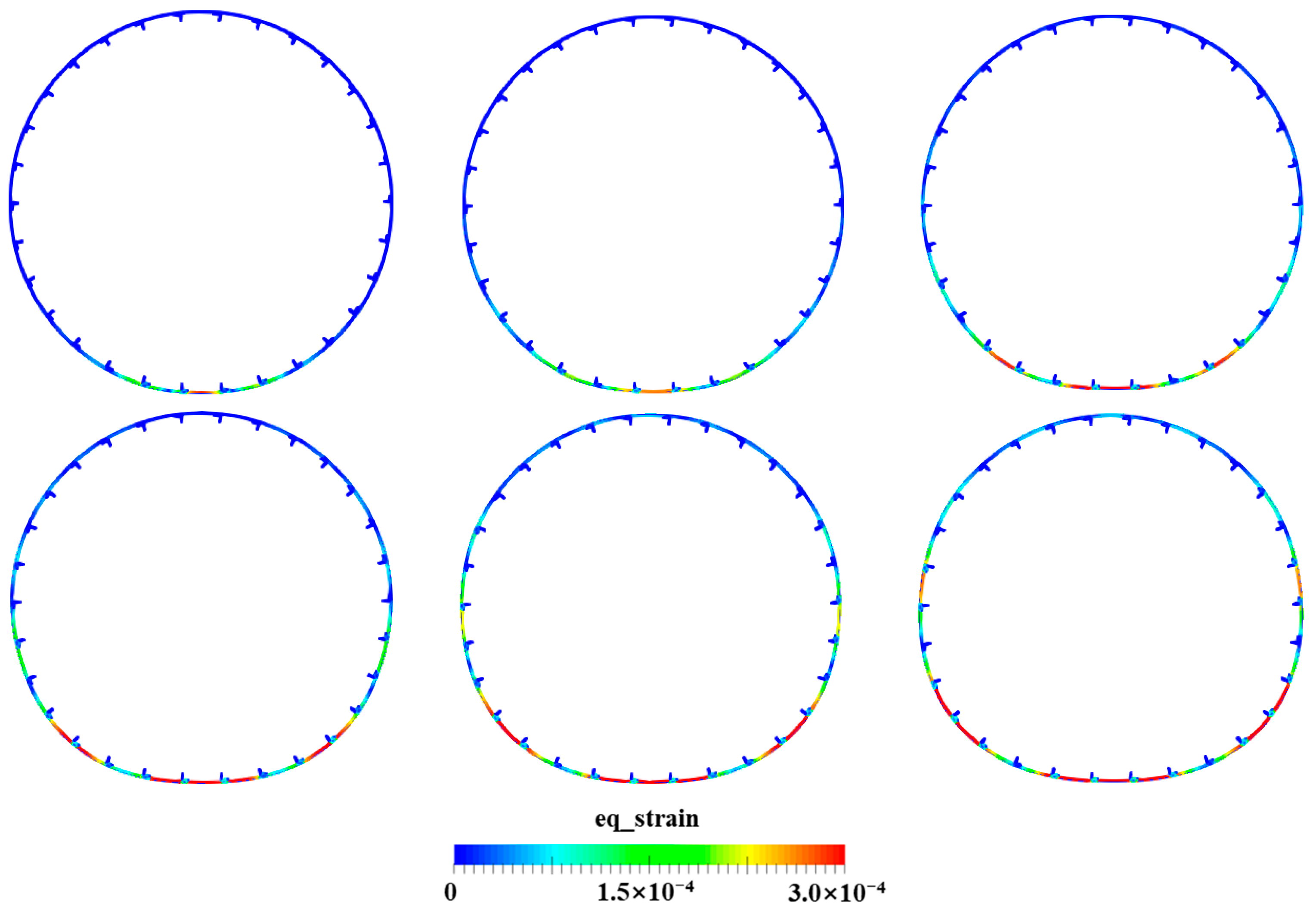
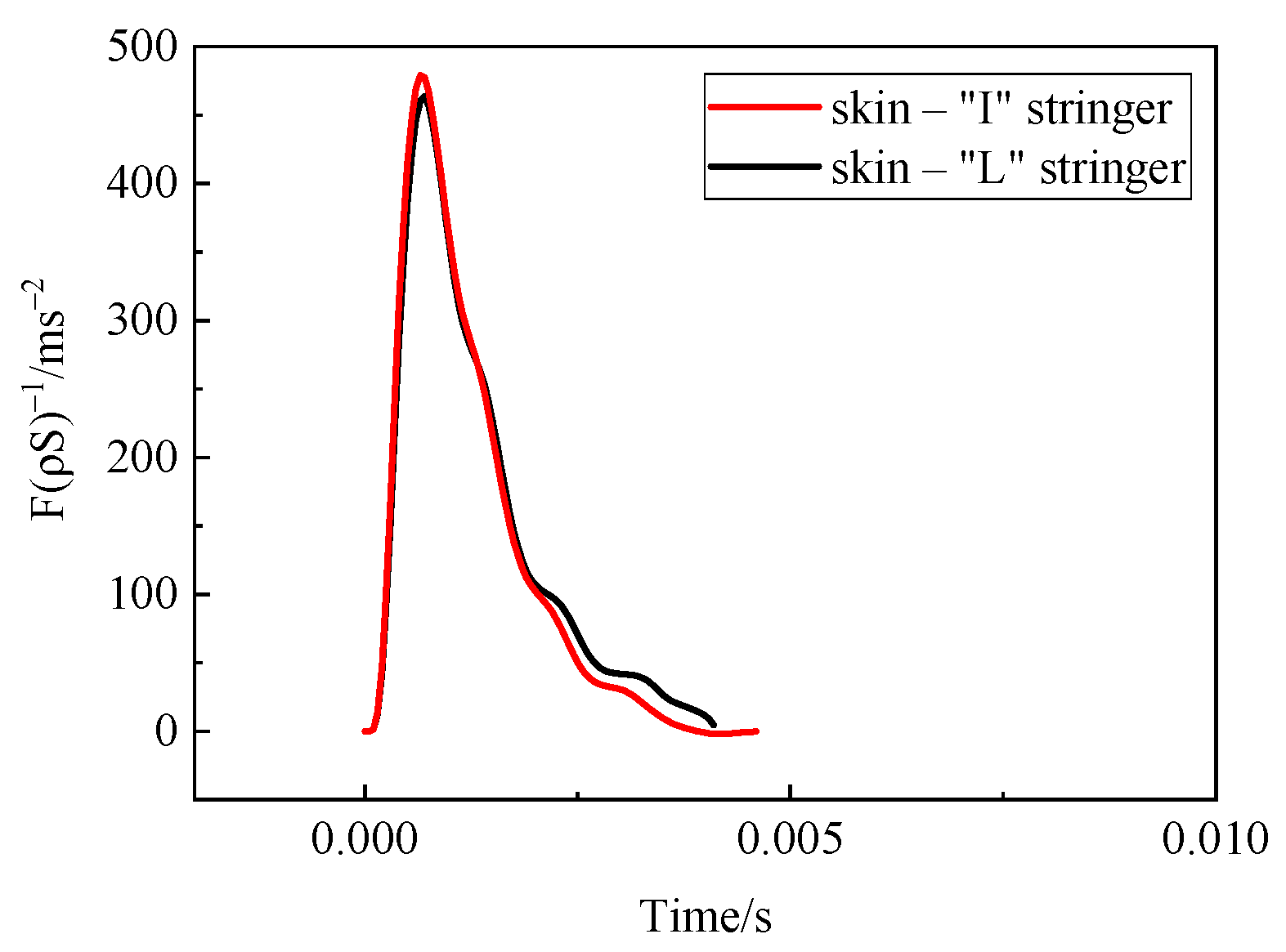
4.3. Water Entry of the Skin–Stringer Cylindrical Structure
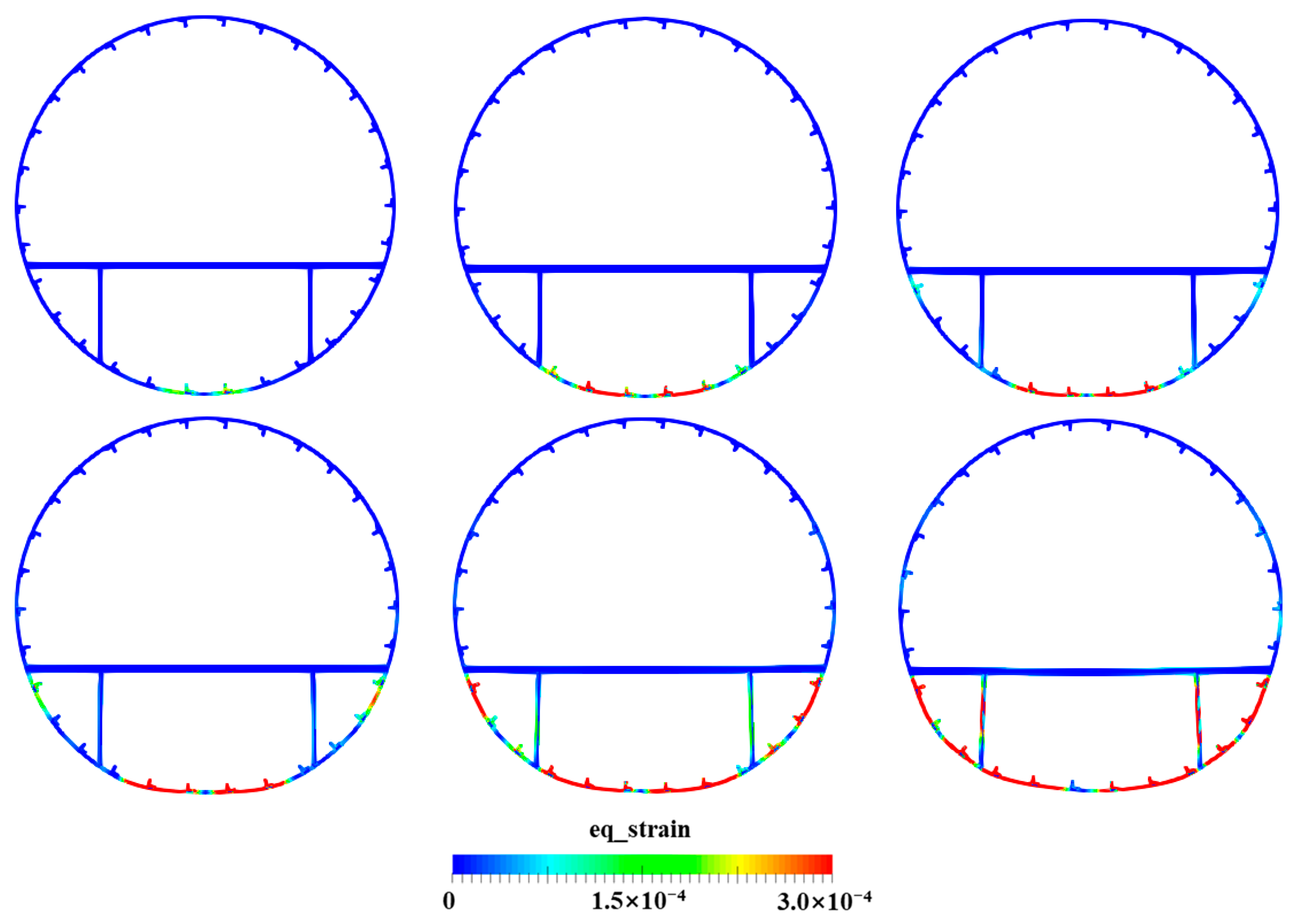
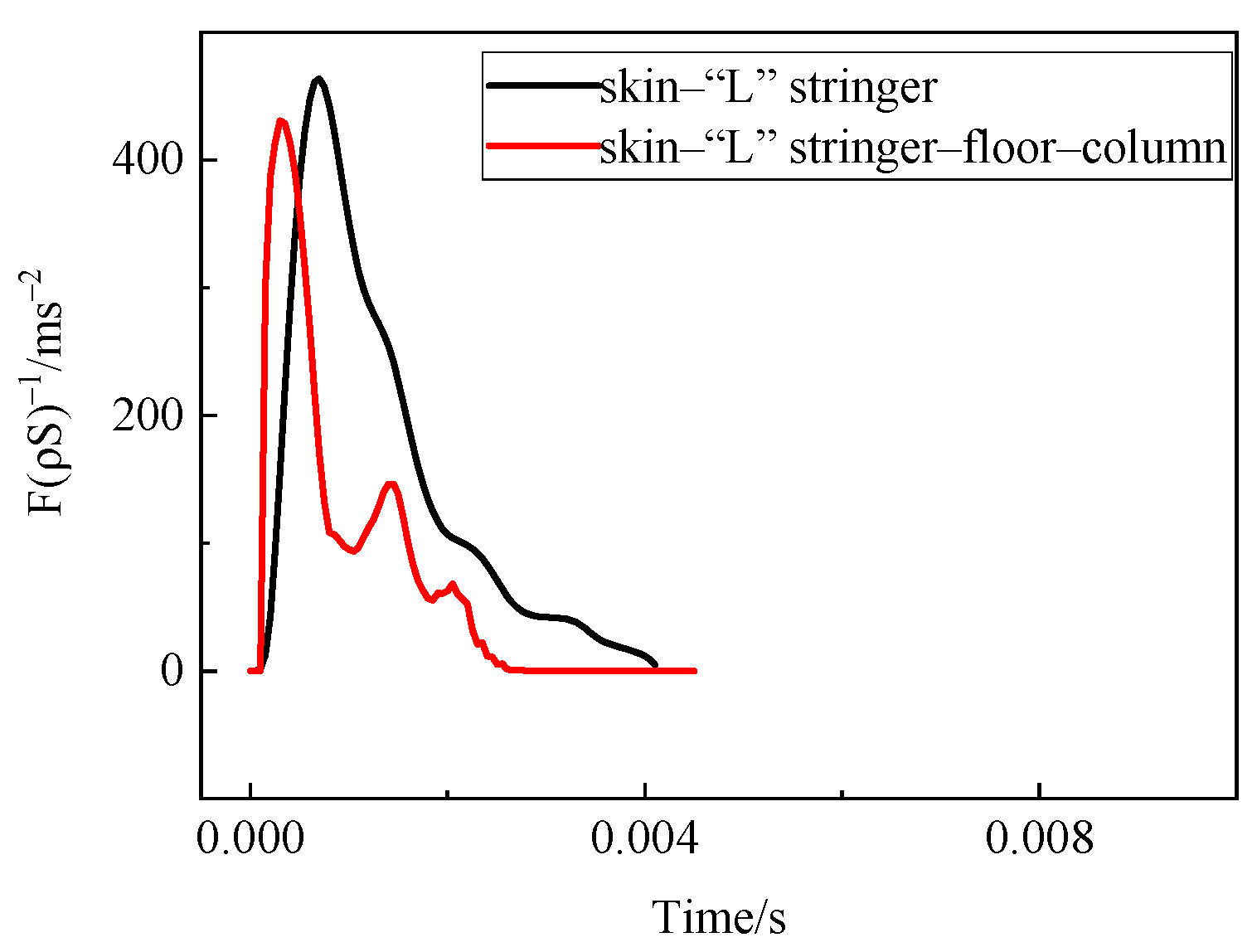
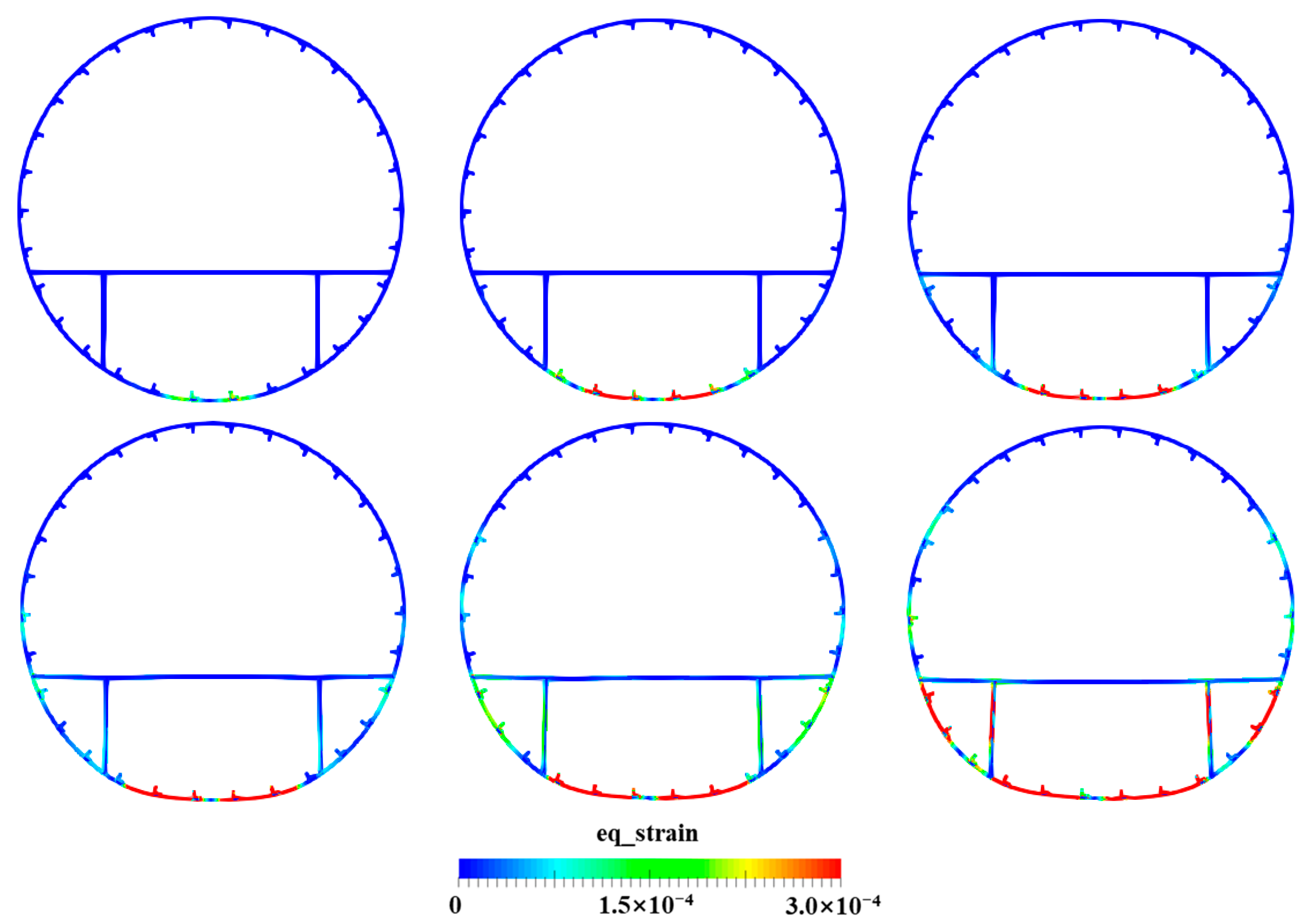
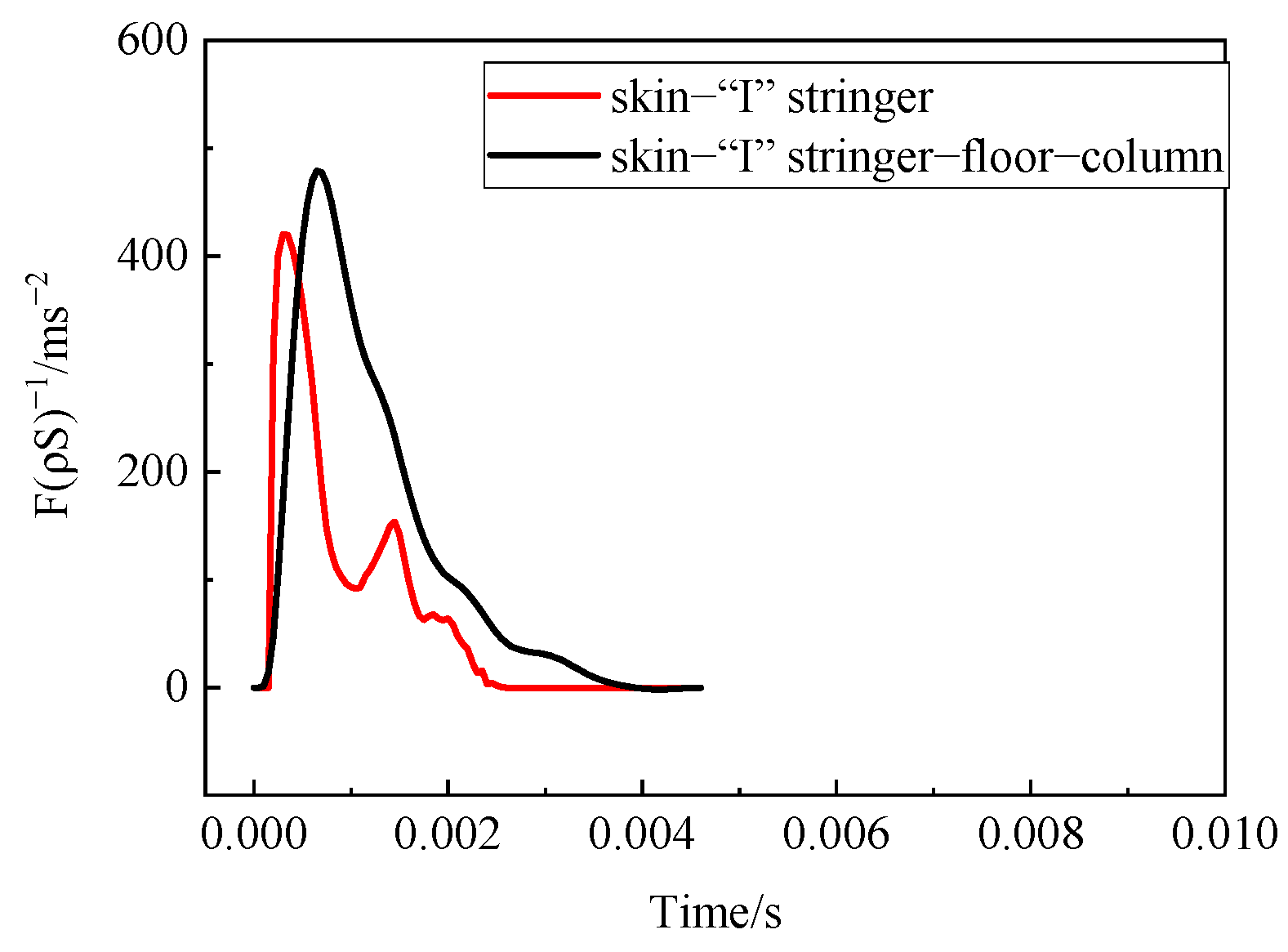
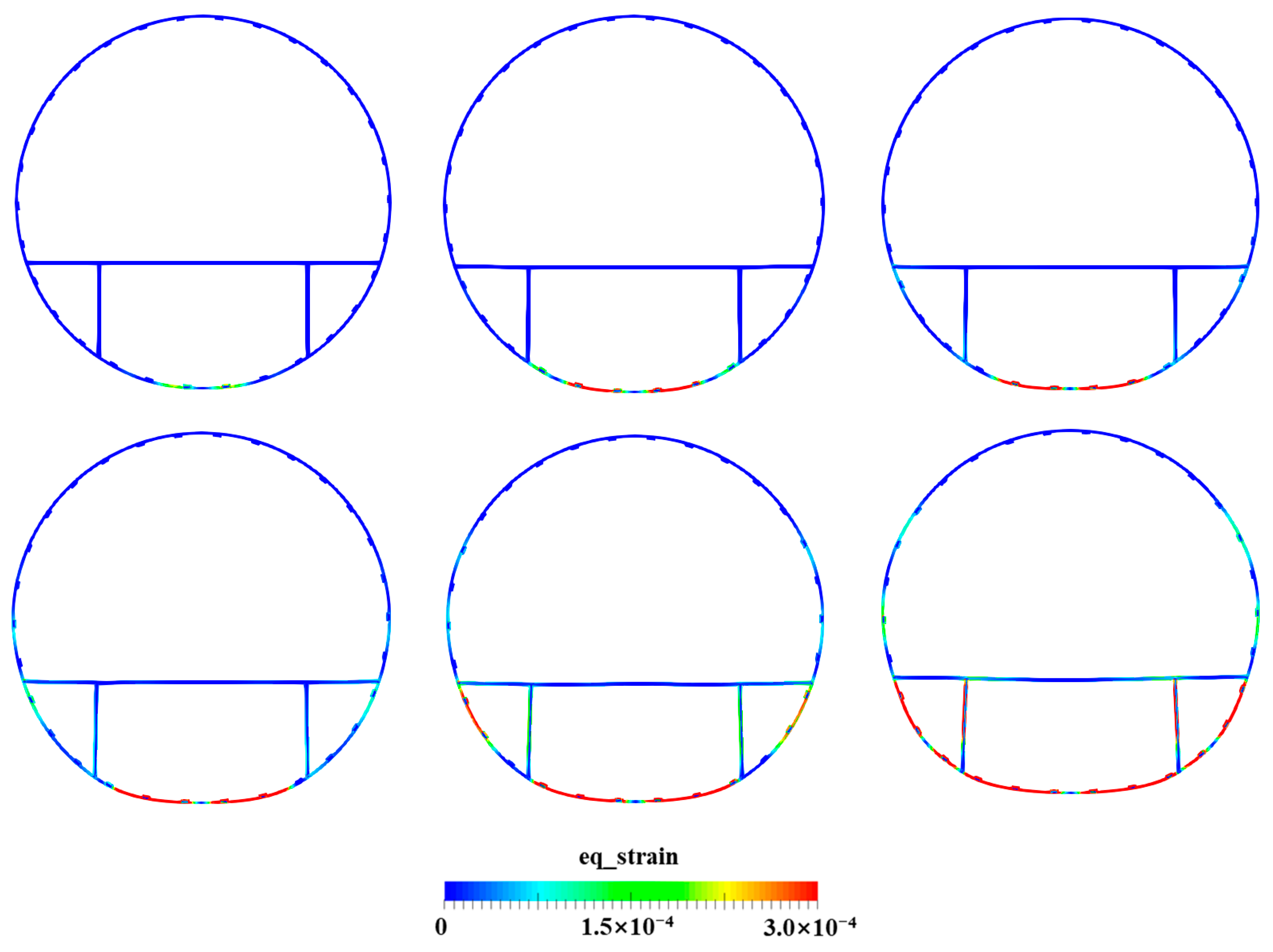
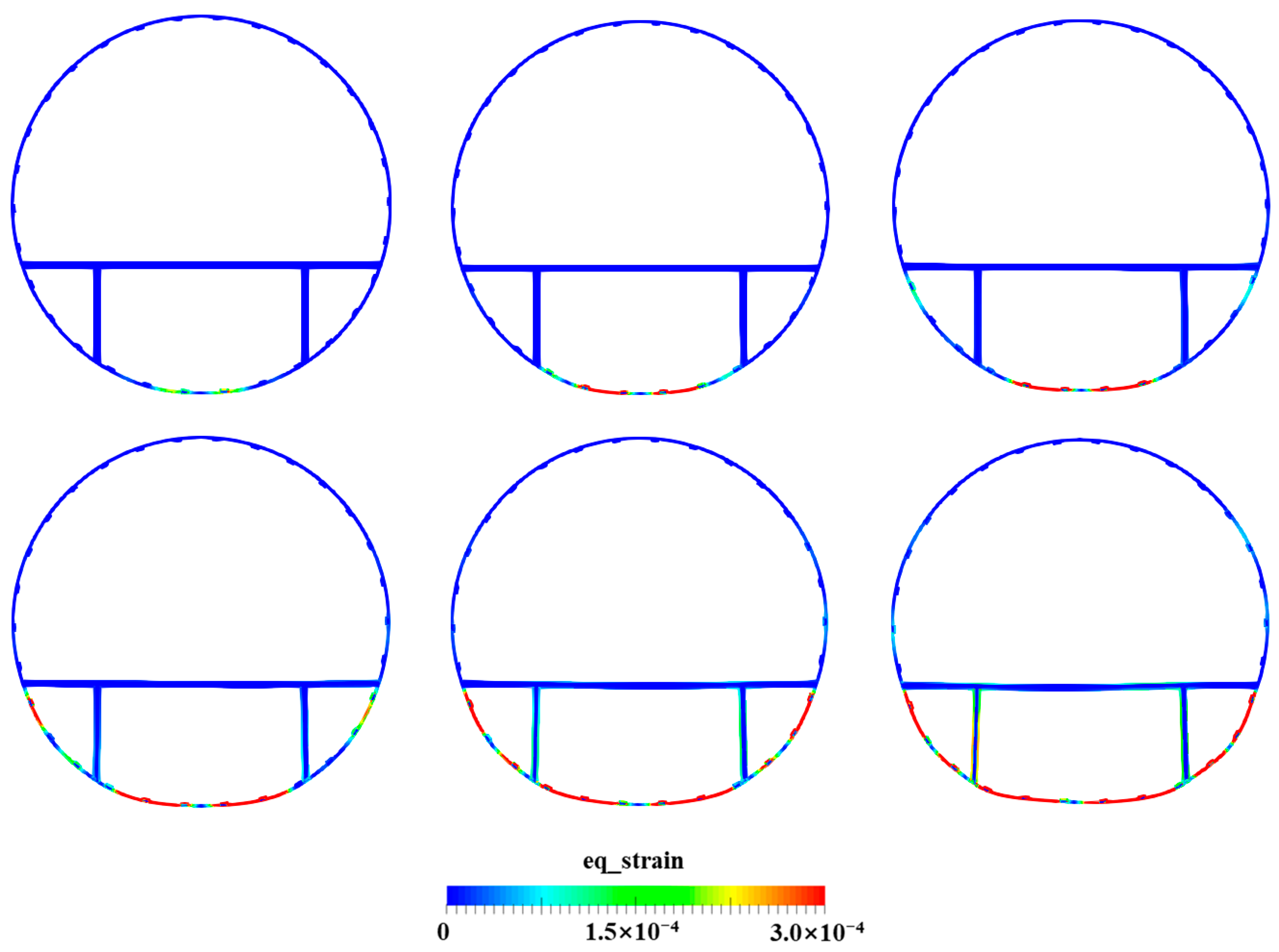
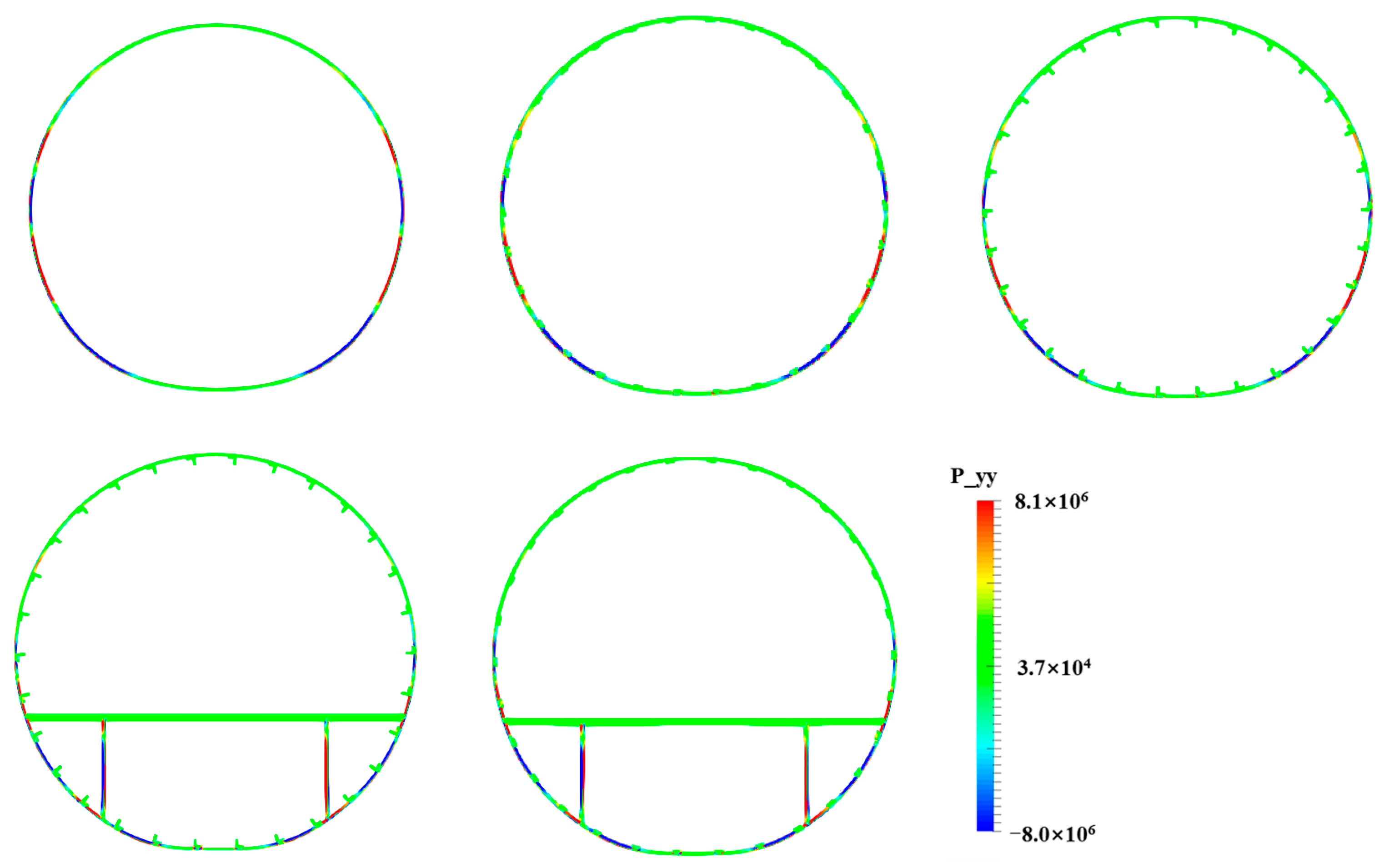
4.4. Water Entry of the Elastic Skin–Stringer–Floor–Column Structure
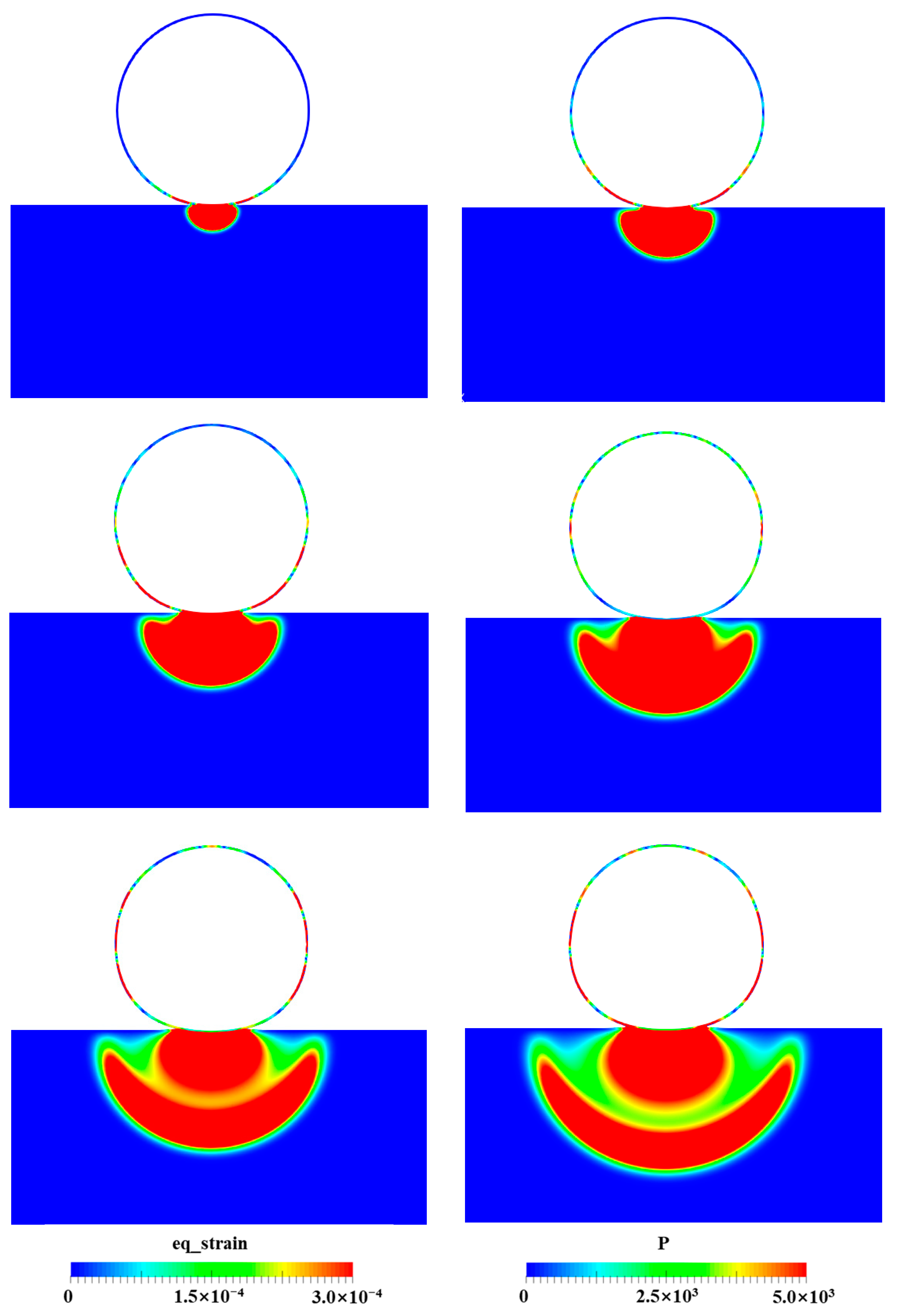
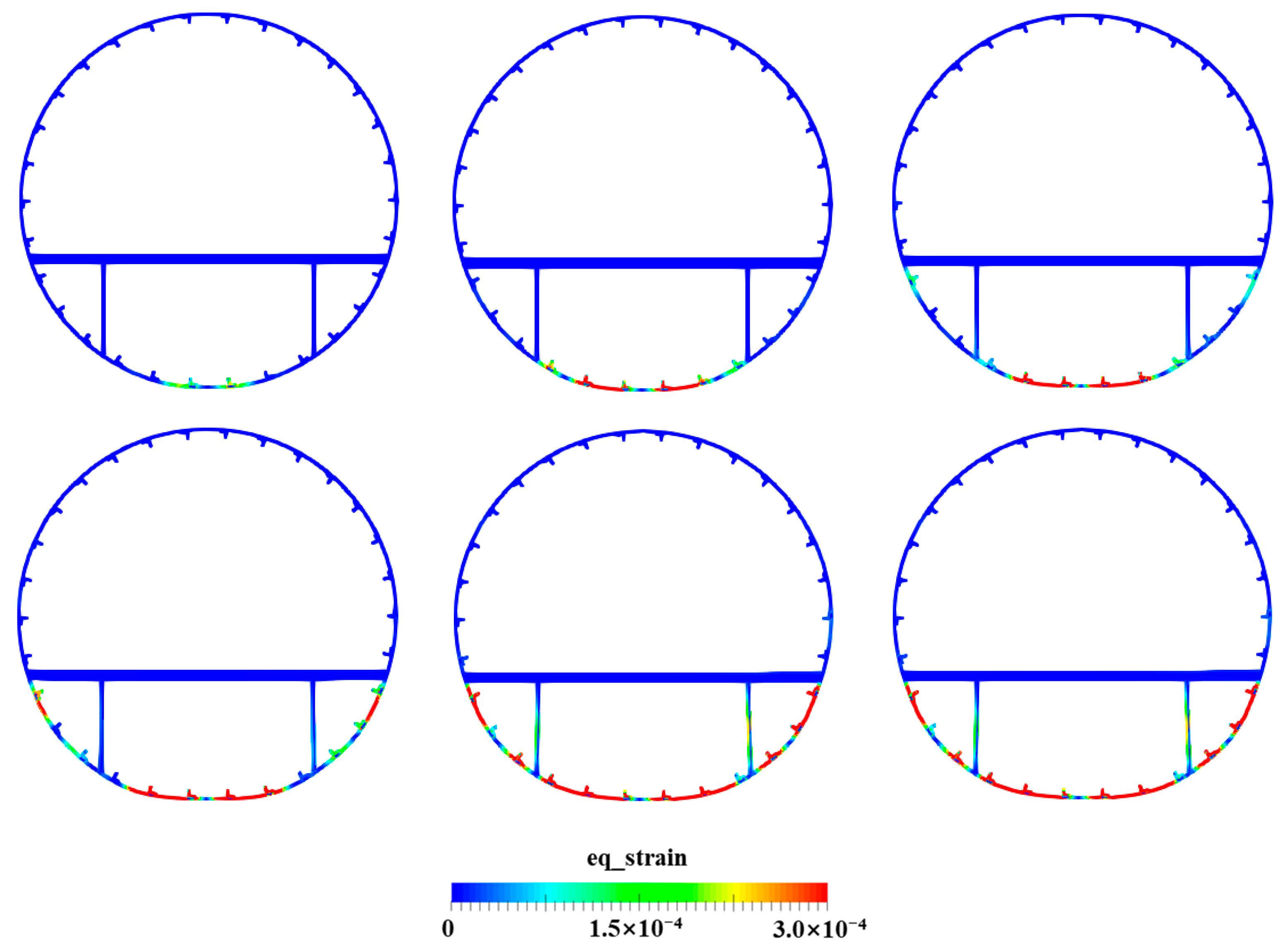
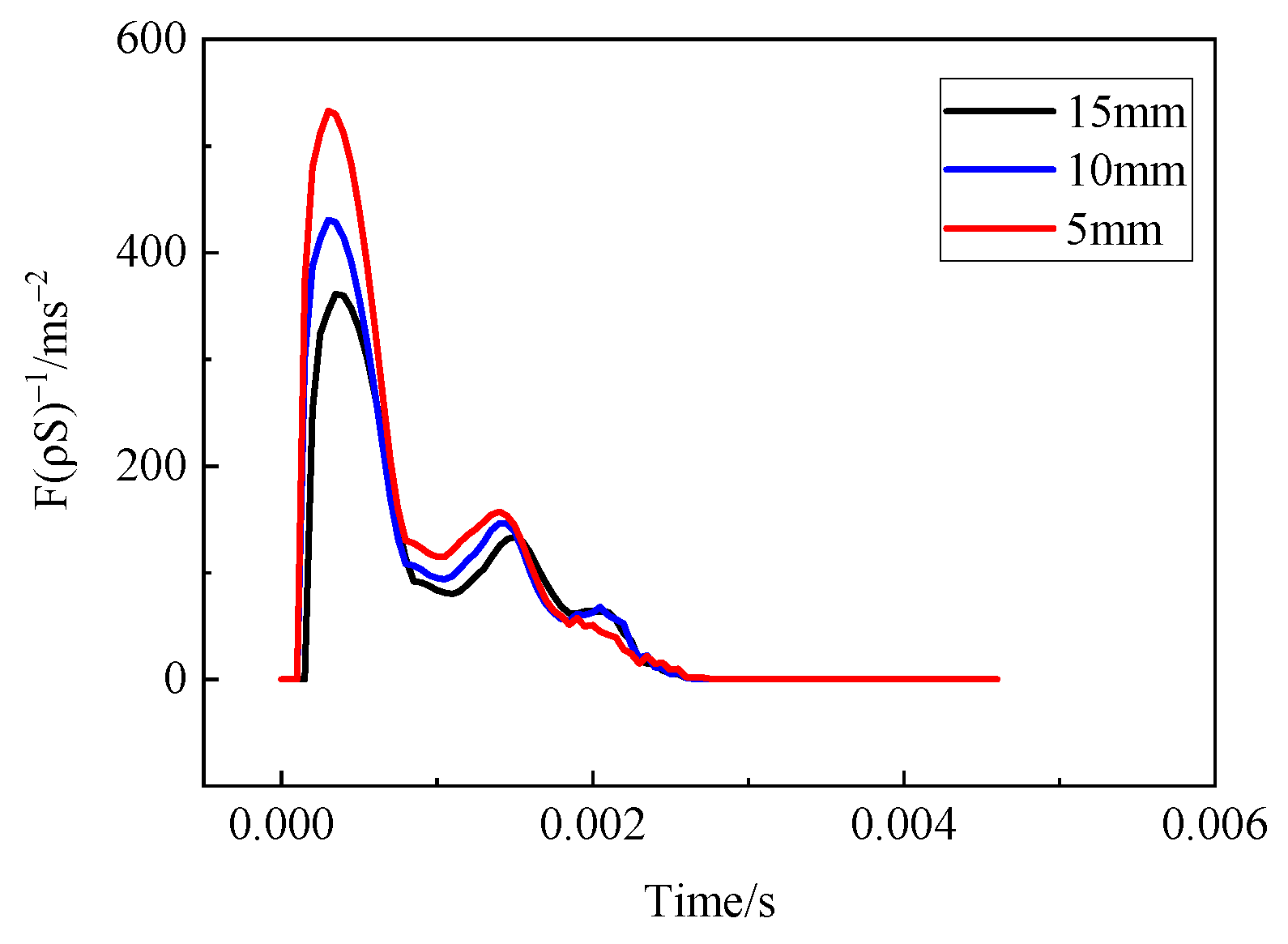
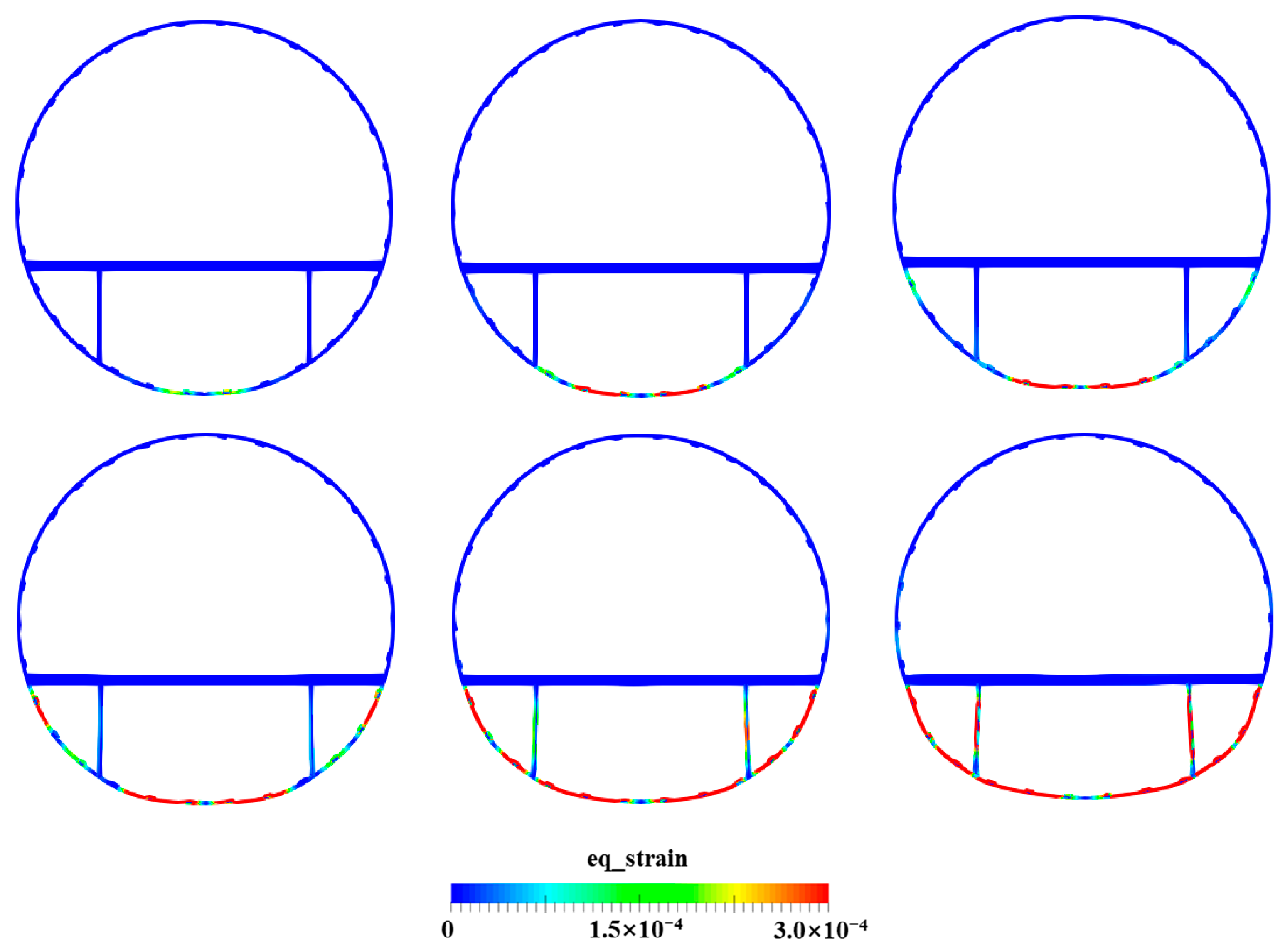
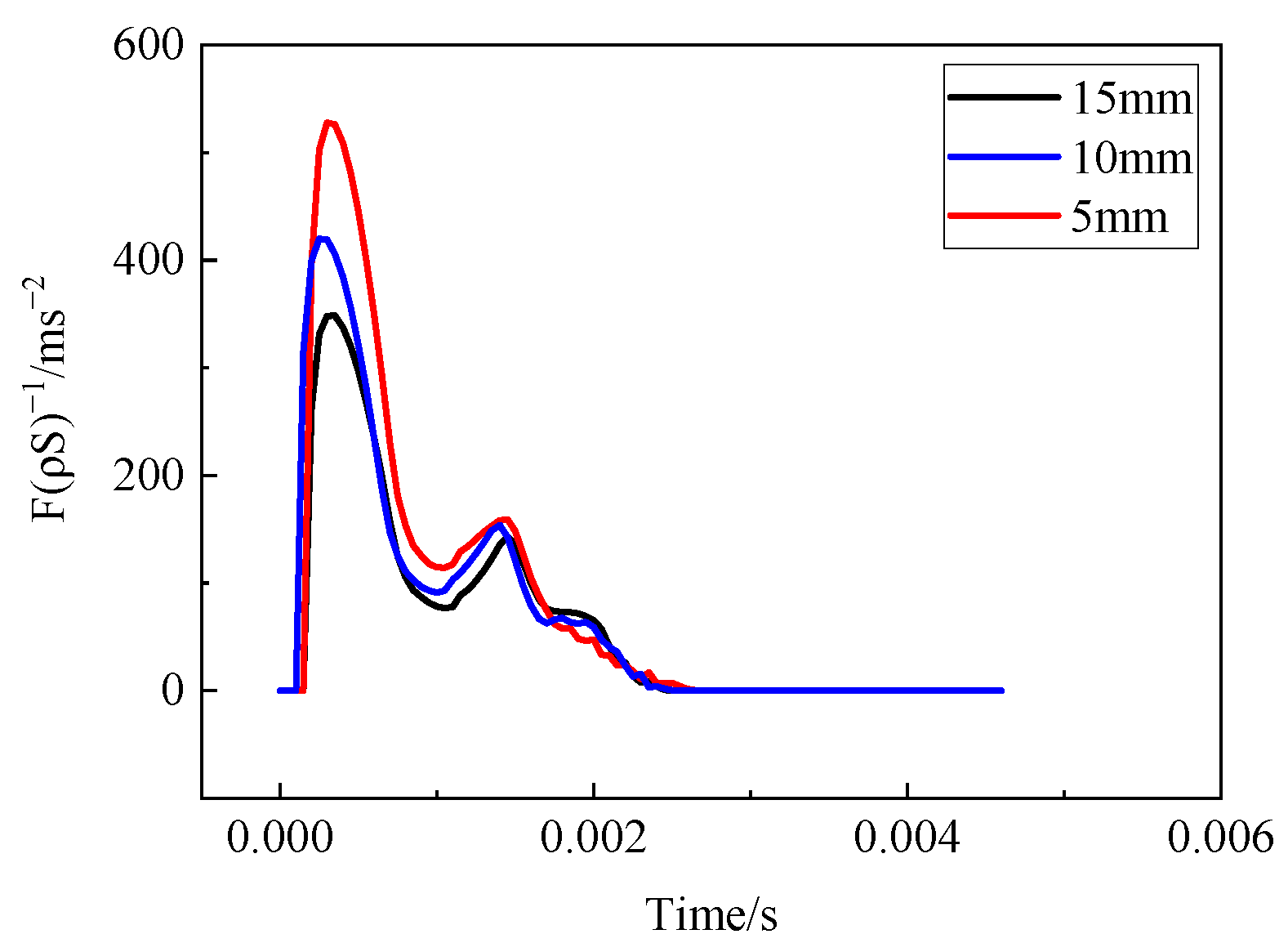
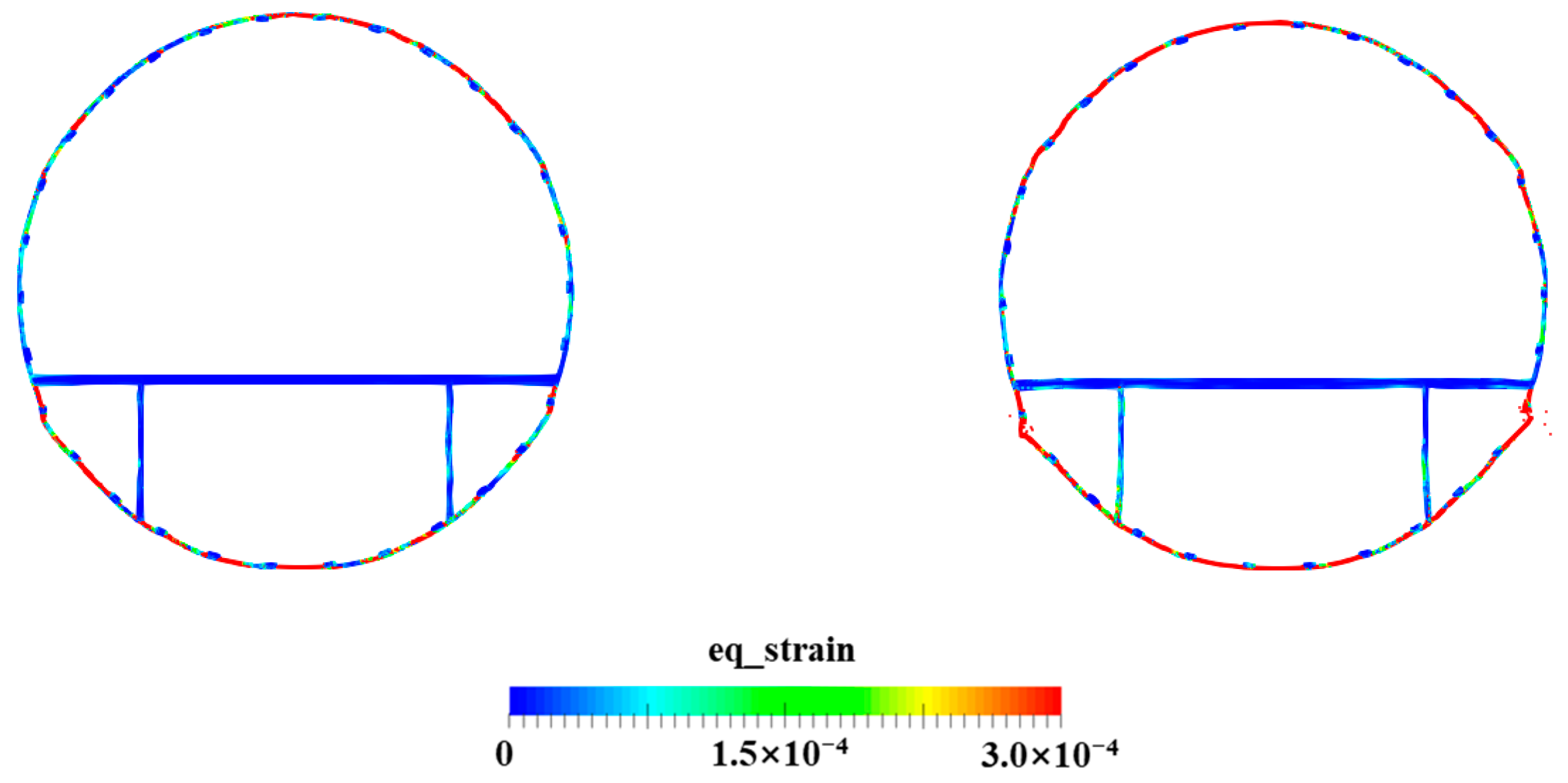
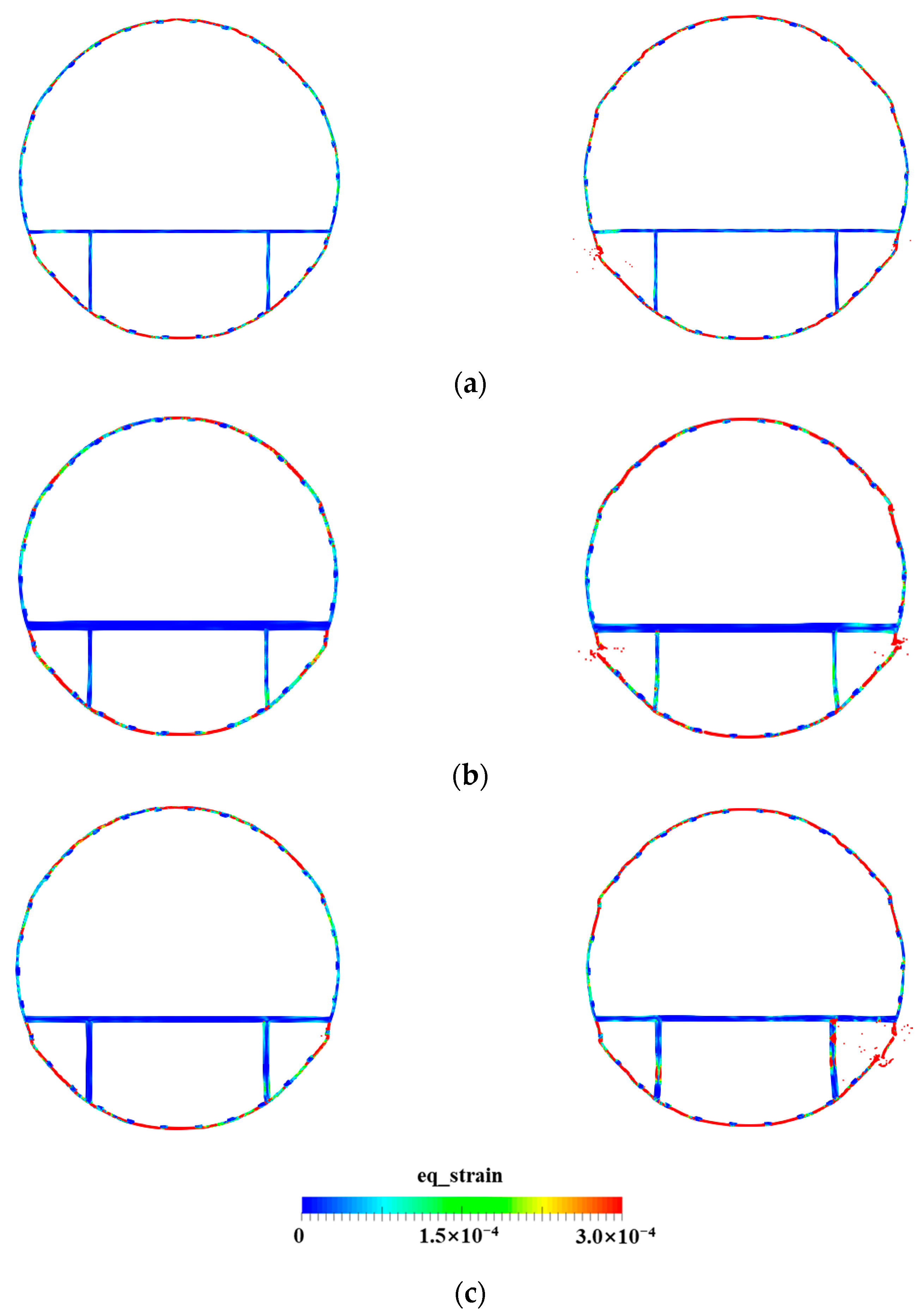
4.5. Water Entry of the Elastic–Plastic Skin–Stringer–Floor–Column Structure
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Siemann, M.H. Numerical and Experimental Investigation of the Structural Behavior during Aircraft Emergency Landing on Water. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 2016. [Google Scholar]
- Climent, H.; Benítez, L.; Rosich, F.; Rueda, F.; Pentecôte, N. Aircraft ditching numerical simulation. In Proceedings of the 25th International Congress of the Aeronautical Sciences, Hamburg, Germany, 3–8 September 2006. [Google Scholar]
- Zheng, Y.; Qu, Q.; Liu, P.; Wen, X.; Zhang, Z. Numerical analysis of the porpoising motion of a blended wing body aircraft during ditching. Aerosp. Sci. Technol. 2021, 119, 107131. [Google Scholar] [CrossRef]
- Streckwall, H.; Lindenau, O.; Bensch, L. Aircraft ditching: A free surface/free motion problem. Arch. Civ. Mech. Eng. 2007, 7, 177–190. [Google Scholar] [CrossRef]
- Seddon, C.; Moatamedi, M. Review of water entry with applications to aerospace structures. Int. J. Impact Eng. 2006, 32, 1045–1067. [Google Scholar] [CrossRef]
- Pentecote, N. Validation of the PAM-CRASH Code for the Simulation of the Impact on Water; DLR–IB 435.2003/3; Institute of Transport Research: New York, NY, USA, 2003. [Google Scholar]
- Pentecote, N.; Vigliotti, A. Crashworthiness of helicopters on water: Test and simulation of a full-scale WG30 impacting on water. Int. J. Crashworthiness 2003, 8, 559–572. [Google Scholar] [CrossRef]
- Von Karman, T.H. The Impact on Seaplane Floats During Landing, National Advisory Committee for Aeronautics; NACA-TN-321; 93R10464; National Advisory Committee for Aeronautics: Boston, MA, USA, 1929. [Google Scholar]
- Wagner, H. Phenomena Associated with Impact and Gliding on a Liquid Surface. NACA Transl. 1932, 93R10464. [Google Scholar]
- Farhat, G. Analytical method for the ditching analysis of an airborne vehicle. J. Aircr. 1989, 27, 312–319. [Google Scholar]
- Pentecôte, N.; Kohlgrüber, D. Full-scale simulation of aircraft impacting on water. In Proceedings of the International Crashworthiness Conference, San Francisco, CA, USA, 14–16 July 2004. [Google Scholar]
- Hua, C.; Fang, C.; Cheng, J. Simulation of fluid–solid interaction on water ditching of an airplane by ALE method. J. Hydrodyn. 2011, 23, 637–642. [Google Scholar] [CrossRef]
- Ortiz, R.; Portemont, G.; Charles, J.L.; Sobry, J.F. Assessment of Explicit FE Capabilities for Full Scale Coupled Fluid/Structure Aircraft Ditching Simulations. In Proceedings of the 23rd International Congress of the Aeronautical Sciences, Toronto, ON, Canada, 8–13 September 2002; pp. 8–13. [Google Scholar]
- Qu, Q.; Hu, M.; Guo, H.; Liu, P.; Agarwal, R.K. Study of ditching characteristics of transport aircraft by global moving mesh method. J. Aircr. 2015, 52, 1550–1558. [Google Scholar] [CrossRef]
- Woodgate, M.A.; Barakos, N.G.; Scrase, N.; Neville, T. Simulation of helicopter ditching using smoothed particle hydrodynamics. Aerosp. Sci. Technol. 2019, 85, 277–292. [Google Scholar] [CrossRef]
- Barreiro, A.; Crespo, A.J.C.; Dominguez, J.M.; Gomez-Gesteira, M. Smoothed particle hydrodynamics for coastal engineering problems. Comput. Struct. 2013, 120, 96–106. [Google Scholar] [CrossRef]
- Hu, X.Y.; Adams, N.A. A multi-phase SPH method for macroscopic and mesoscopic flows. J. Comput. Phys. 2006, 213, 844–861. [Google Scholar] [CrossRef]
- Gray, J.P.; Monaghan, J.J.; Swift, R.P. SPH elastic dynamics. Comput. Methods Appl. Mech. Eng. 2001, 190, 6641–6662. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, F.; Yang, Y.; Ren, X.; Wang, L.; Yang, Q.; Xu, C. An improved SPH scheme for the 3D FEI (Fluid-Elastomer Interaction) problem of aircraft tire spray. Eng. Anal. Bound. Elem. 2023, 153, 295–304. [Google Scholar]
- Zhang, T.; Li, Y.; Li, C.; Sun, S. Effect of salinity on oil production: Review on low salinity waterflooding mechanisms and exploratory study on pipeline scaling. Oil Gas Sci. Technol. Rev. IFP Energ. Nouv. 2020, 75, 50. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, T.; Sun, S. Study of the Imbibition Phenomenon in Porous Media by the Smoothed Particle Hydrodynamic (SPH) Method. Entropy 2022, 24, 1212. [Google Scholar] [CrossRef]
- Zhu, C.; Huang, Y.; Zhang, L. SPH-based simulation of flow process of a landslide at Hongao landfill in China. Nat. Hazards 2018, 93, 1113–1126. [Google Scholar] [CrossRef]
- Zheng, H.; Bin, S.; Yange, L. Numerical simulation of debris-flow behavior based on the SPH method incorporating the Herschel-Bulkley-Papanastasiou rheology model. Eng. Geol. 2019, 255, 25–36. [Google Scholar]
- Monaghan, J.J. SPH without a Tensile Instability. J. Comput. Phys. 2000, 159, 290–311. [Google Scholar] [CrossRef]
- Swegle, J.W.; Hicks, D.L.; Attaways, S.W. Smoothed Particle Hydrodynamics Stability Analysis. J. Comput. Phys. 1995, 116, 123–134. [Google Scholar] [CrossRef]
- Zhu, C.; Chen, Z.; Huang, Y. Coupled moving particle simulation–finite-element method analysis of fluid–structure interaction in geodisasters. Int. J. Geomech. 2021, 21, 6. [Google Scholar] [CrossRef]
- Huang, Y.; Zhu, C. Numerical analysis of tsunami–structure interaction using a modified MPS method. Nat. Hazards 2015, 75, 2847–2862. [Google Scholar] [CrossRef]
- Huang, Y.; Zhu, C. Simulation of flow slides in municipal solid waste dumps using a modified MPS method. Nat. Hazards 2014, 74, 491–508. [Google Scholar] [CrossRef]
- Otto, R.; Gilberto, D.; Jaime, K. Local Consistency of Smoothed Particle Hydrodynamics (SPH) in the Context of Measure Theory. Front. Appl. Math. Stat. 2022, 8, 907604. [Google Scholar]
- Evers, J.H.M.; Zisis, I.A.; van der Linden, B.J.; Duong, M.H. From continuum mechanics to SPH particle systems and back: Systematic derivation and convergence. J. Appl. Math. Mech. 2018, 98, 106–133. [Google Scholar] [CrossRef]
- Sigalotti, L.D.G.; Rendón, O.; Klapp, J.; Vargas, C.A.; Cruz, F. A new insight into the consistency of the SPH interpolation formula. Appl. Math. Comput. 2019, 356, 50–73. [Google Scholar] [CrossRef]
- Quinlan, N.; Basa, M.; Lastiwka, M. Truncation error in mesh-free particle methods. Int. J. Numer. Methods Eng. 2006, 66, 2064–2085. [Google Scholar] [CrossRef]
- Vaughan, G.L.; Healy, T.R.; Bryan, K.R.; Sneyd, A.D.; Gorman, R.M. Completeness, conservation and error in SPH for fluids. Int. J. Numer. Methods Fluids 2008, 56, 37–62. [Google Scholar] [CrossRef]
- Read, J.I.; Hayfield, T.; Agertz, O. Resolving mixing in smoothed particle hydrodynamics. Mon. Not. R. Astron. Soc. 2010, 405, 1513–1530. [Google Scholar] [CrossRef]
- Qirong, Z.; Lars, H.; Yuexing, L. Numerical Convergence in Smoothed Particle Hydrodynamics. Cosmol. Nongalactic Astrophys. 2015, 800, 6. [Google Scholar]
- Leonardo, D.G.S.; Jaime, K.; Moncho, G.G. The mathematics of smoothed particle hydrodynamics (SPH) consistency. Front. Appl. Math. Stat. 2021, 7, 797455. [Google Scholar]
- Chen, J.K.; Beraun, J.E. A generalized smoothed particle hydrodynamics method for nonlinear dynamic problem. Comput. Methods Appl. Mech. Eng. 2000, 190, 225–239. [Google Scholar] [CrossRef]
- Liu, M.B.; Liu, G.R. Restoring particle consistency in smoothed particle hydrodynamics. Appl. Numer. Math. 2006, 56, 19–36. [Google Scholar] [CrossRef]
- Monaghan, J.J.; Gingold, R.A. Shock simulation by the particle method SPH. J. Comput. Phys. 1983, 52, 374–389. [Google Scholar] [CrossRef]
- Bouscasse, B.; Colagrossi, A.; Marrone, S. Nonlinear water wave interaction with floating bodies in SPH. J. Fluids Struct. 2013, 42, 112–129. [Google Scholar] [CrossRef]
- Sun, P.N.; Colagrossi, A.; Marrone, S. The δplus-SPH model: Simple procedures for a further improvement of the SPH scheme. Comput. Methods Appl. Mech. Eng. 2017, 315, 25–49. [Google Scholar] [CrossRef]
- Zhang, C.; Hu, X.Y.; Adams, N.A. A weakly compressible SPH method based on a low-dissipation Riemann solver. J. Comput. Phys. 2017, 335, 605–620. [Google Scholar] [CrossRef]
- Leonardo, D.G.S.; Hender, L. Adaptive kernel estimation and SPH tensile instability. Comput. Math. Appl. 2008, 55, 23–50. [Google Scholar]
- Dyka, C.T.; Andles, P.W.; Ingel, R.P. Stress points for tension instability in SPH. Int. J. Numer. Methods Eng. 1997, 40, 2325–2341. [Google Scholar] [CrossRef]
- Sugiura, K.; Inutsuka, S. An extension of Godunov SPH II: Application to elastic dynamics. J. Comput. Phys. 2017, 333, 78–103. [Google Scholar] [CrossRef]
- Belytschko, T.; Xiao, S. Stability analysis of particle methods with corrected derivatives. Comput. Math. Appl. 2002, 43, 329–350. [Google Scholar] [CrossRef]
- Belytschko, T.; Guo, Y.; Liu, W.K. A unified stability analysis of meshless particle methods. Int. J. Numer. Methods Eng. 2000, 48, 1359–1400. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, A.; Chen, J. SPH simulations of water entry problems using an improved boundary treatment. Ocean Eng. 2021, 238, 109679. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed Particle Hydrodynamics and Its Diverse Applications. Annu. Rev. Fluid Mech. 2012, 44, 323–346. [Google Scholar] [CrossRef]
- Wang, L.; Xu, F.; Yang, Y. Improvement of the tensile instability in SPH scheme for the FEI (Fluid-Elastomer Interaction) problem. Eng. Anal. Bound. Elem. 2019, 106, 116–125. [Google Scholar] [CrossRef]
- Wang, L.; Xu, F.; Yang, Y. An improved total Lagrangian SPH method for modeling solid deformation and damage. Eng. Anal. Bound. Elem. 2021, 133, 286–302. [Google Scholar] [CrossRef]
- Zhang, C.; Yujie, Z.; Dong, W. Smoothed particle method for fluid-structure interaction. Sci. Sin. Physica Mech. Astron. 2022, 52, 6–26. [Google Scholar] [CrossRef]
- Wang, L.; Xu, F.; Yang, Y. Research on water entry problems of gas-structure-liquid coupling based on SPH method. Ocean Eng. 2022, 257, 111623. [Google Scholar] [CrossRef]
- Adami, S.; Hu, X.Y.; Adams, N.A. A generalized wall boundary condition for smoothed particle hydrodynamics. J. Comput. Phys. 2012, 231, 7057–7075. [Google Scholar] [CrossRef]
- Rui, Y. Research on Some Problems in Structure Impact with Water Using SPH Method. Ph.D. Thesis, Northwestern Polytechnical University, Xi’an, China, 2016. [Google Scholar]
- Mei, X.; Liu, Y.; Dick, K.P.Y. On the water impact of general two-dimensional sections. Appl. Ocean Res. 1999, 21, 1–15. [Google Scholar] [CrossRef]
- Sun, H.; Faltinsen, O.M. Water impact of horizontal circular cylinders and cylindrical shells. Appl. Ocean Res. 2006, 28, 299–311. [Google Scholar] [CrossRef]
- Chi, Z.; Xiangyu, Y.; Nikolaus, H.; Adams, A. A generalized transport-velocity formulation for smoothed particle hydrodynamics. J. Comput. Phys. 2017, 337, 216–232. [Google Scholar]







| Physical Quantity | Value | Physical Quantity | Value |
|---|---|---|---|
| Density, ρ, kg/m3 | 2700 | Hardening coefficient, B, MPa | 426 |
| Sound speed, Cs, m/s | 5000 | Strain hardening index, n | 0.34 |
| Poisson ratio, ν | 0.34 | Strain rate coefficient, C | 0.015 |
| E, GPa | 67.5 | Thermal softening coefficient, m | 1.0 |
| Static yield strength, A, MPa | 265 | Specific heat, Cv, J/kgK | 875 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Yang, Y.; Yang, Q. Research on the Water Entry of the Fuselage Cylindrical Structure Based on the Improved SPH Model. Appl. Sci. 2023, 13, 10801. https://doi.org/10.3390/app131910801
Wang L, Yang Y, Yang Q. Research on the Water Entry of the Fuselage Cylindrical Structure Based on the Improved SPH Model. Applied Sciences. 2023; 13(19):10801. https://doi.org/10.3390/app131910801
Chicago/Turabian StyleWang, Lu, Yang Yang, and Qiuzu Yang. 2023. "Research on the Water Entry of the Fuselage Cylindrical Structure Based on the Improved SPH Model" Applied Sciences 13, no. 19: 10801. https://doi.org/10.3390/app131910801
APA StyleWang, L., Yang, Y., & Yang, Q. (2023). Research on the Water Entry of the Fuselage Cylindrical Structure Based on the Improved SPH Model. Applied Sciences, 13(19), 10801. https://doi.org/10.3390/app131910801





