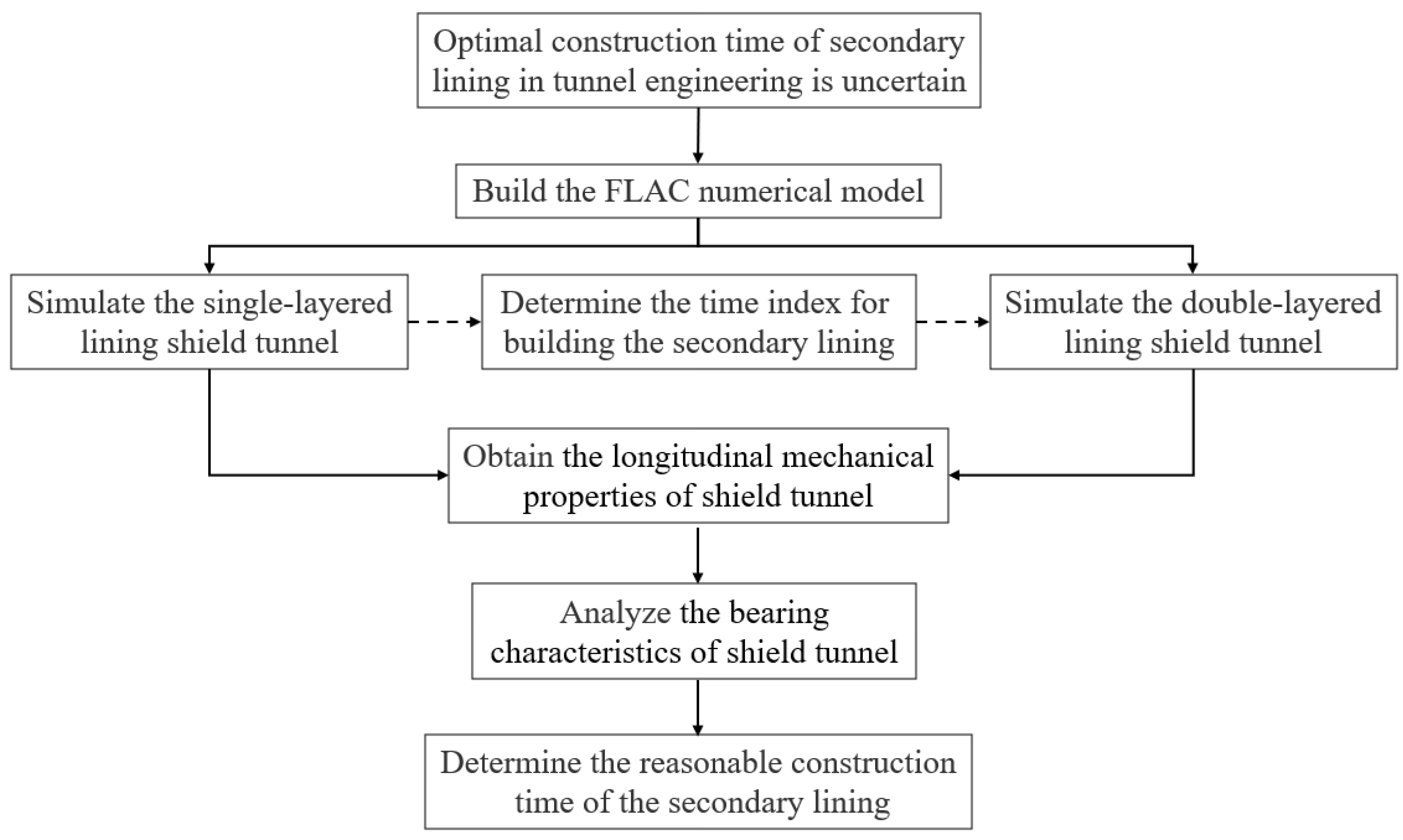
2.2. The Numerical Model
This paper utilizes FLAC
3D, which is based on the finite difference method, to perform calculations. Geotechnical engineering problems are typically expressed as differential equations, including basic equations such as the balance equation, geometric equation, and constitutive equation, as well as boundary conditions. By replacing each derivative with a finite difference approximation formula, the finite difference method transforms the problem of solving partial differential equations into the problem of solving algebraic equations. FLAC
3D takes nodes as the calculation objects and concentrates both forces and masses at each node, then solves them in the time domain using the equation of motion. The equation of node motion can be expressed as follows:
where
is the unbalance force component of node
at time
in direction
, which can be derived from the principle of virtual work.
is the concentrated mass of node
. FLAC
3D uses the velocity to calculate the strain increment of the element in a time step, as follows:
where
is the partial derivative of
with respect to the vector component
of the node position. By using the constitutive equation, the stress increment can be obtained from the strain increment. Then, by accumulating the stress increment of each time step, the total stress can be obtained.
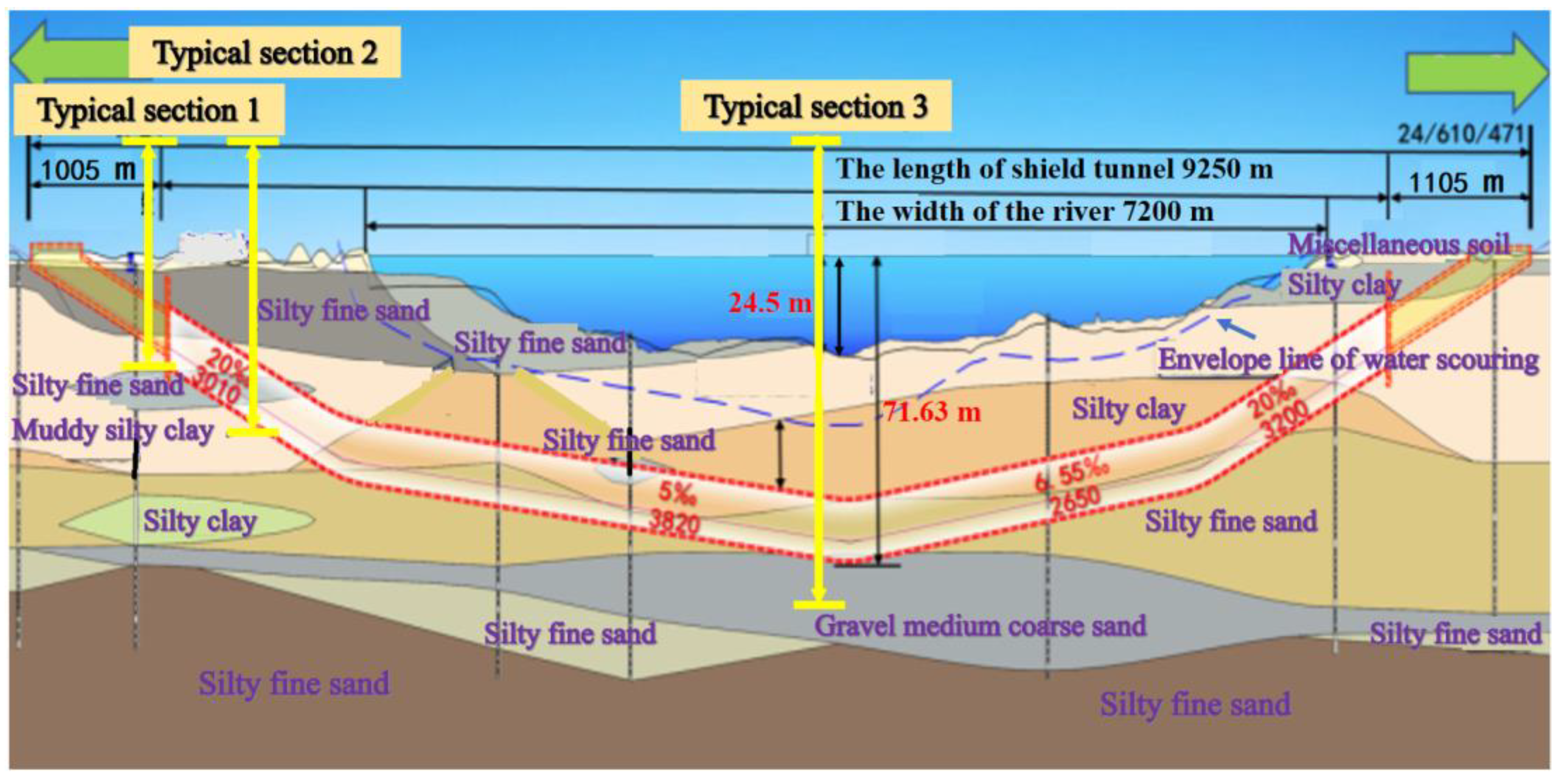
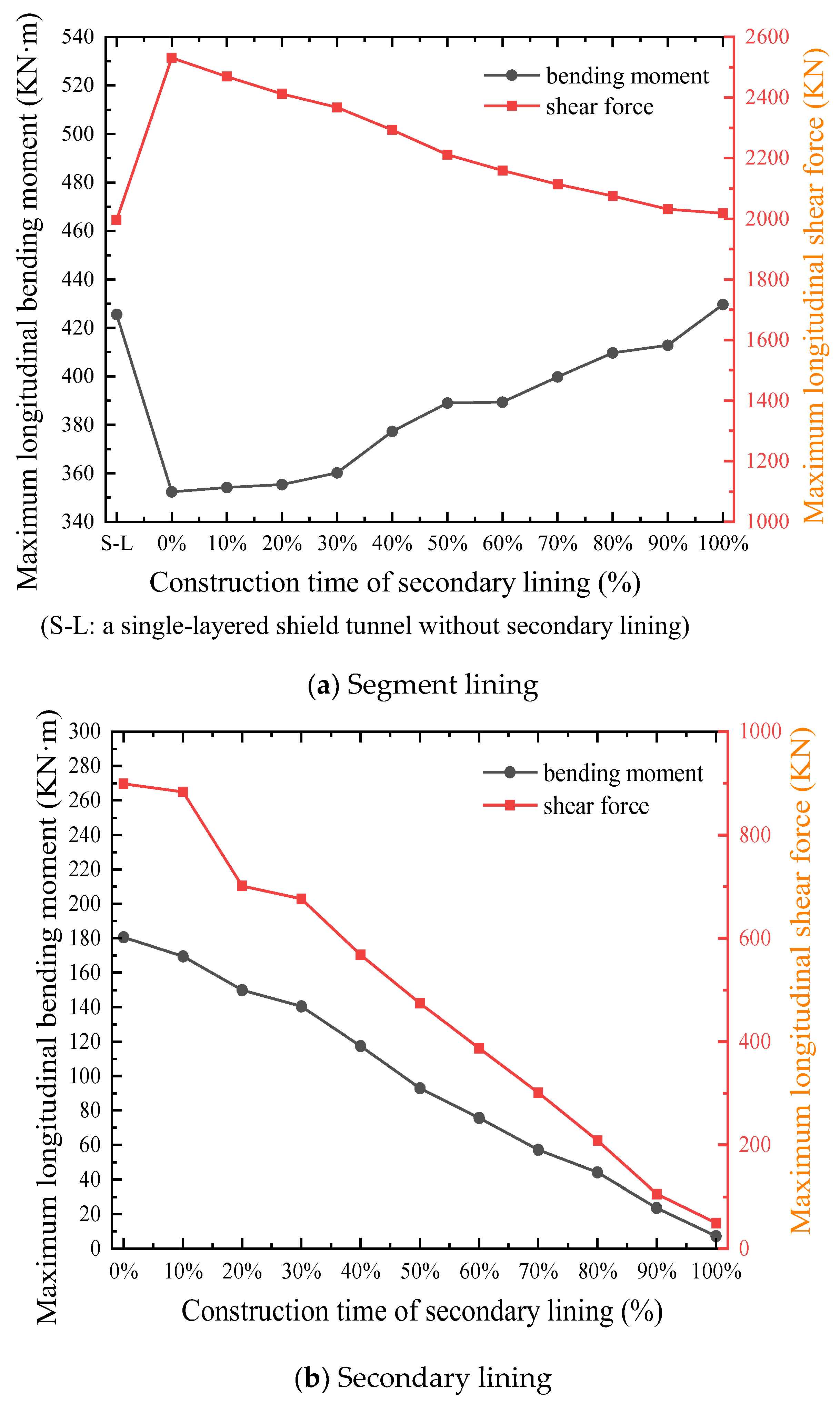
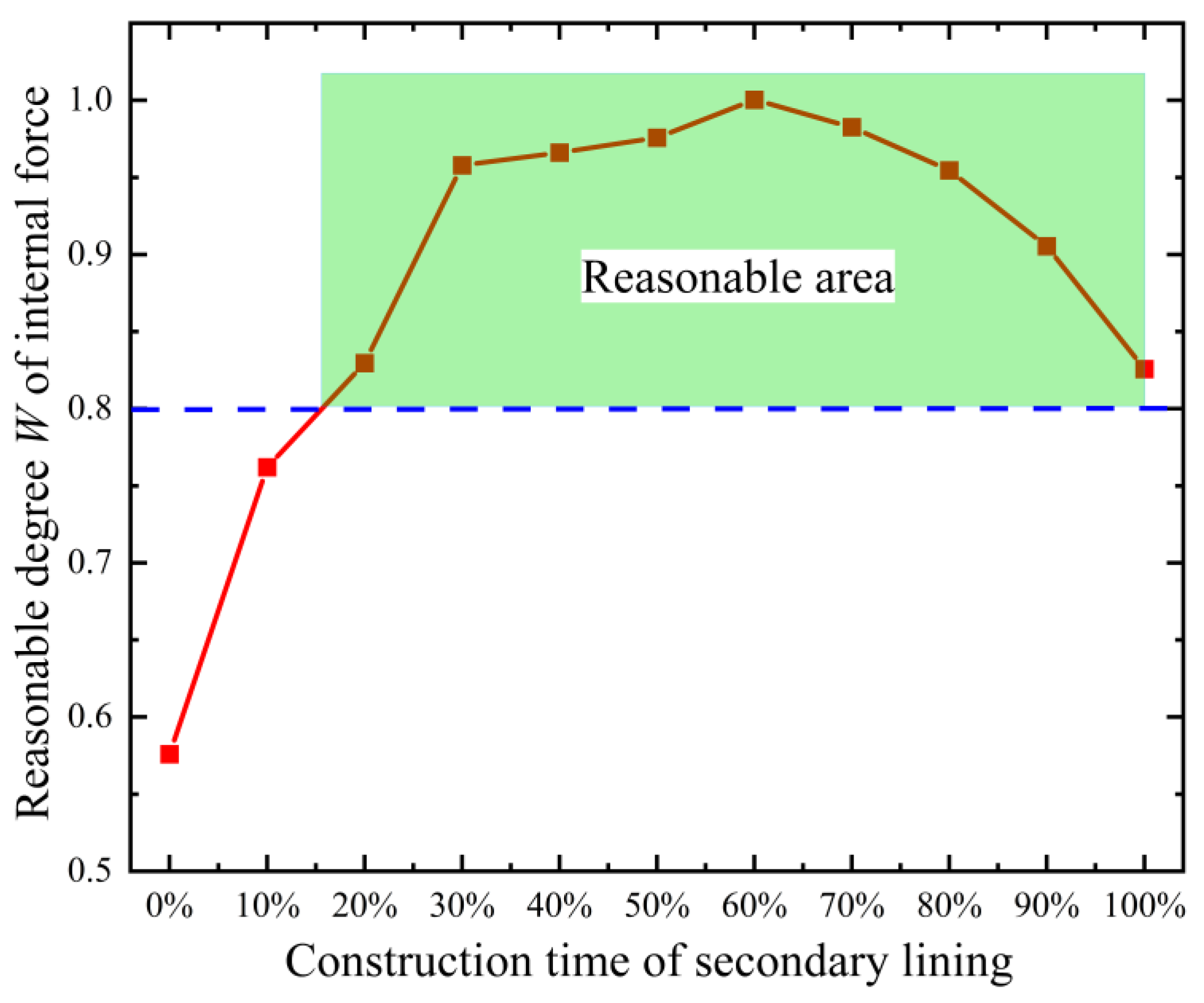
The aforementioned shield tunnel project was utilized as an exemplar for the formulation of a numerical model, depicted in
Figure 4. The model’s dimensions were 36.1 m × 100 m × 100 m (X × Y × Z). The lateral side of the model represented the boundary with a normal displacement constraint, while the bottom surface served as the fully constrained boundary. As this paper primarily focused on the mechanical properties of shield tunnel structures rather than the effect of strata deformation or strata properties, the Mohr–Coulomb constitutive model, known for its simplicity and wide applicability [
41,
42], was employed for the strata.
Table 1 presents the specific physical-mechanical parameters for the strata. The shield tunnel was located at the center of the model. Tunnel excavation was simplified to the excavation of the entire section at once. In the shield tunnel project upon which this paper relies, the soil cover near the riverbed was thicker, and the water head was higher. Consequently, the tunnel at the riverbed experienced a higher water and soil load compared to the adjacent sides. To streamline modeling and expedite model calculations, a trapezoidal stress boundary was implemented at the upper part of the model to represent the actual loading conditions. Within the model,
and
represented the soil and water load at the typical sections 1 and 3, respectively.
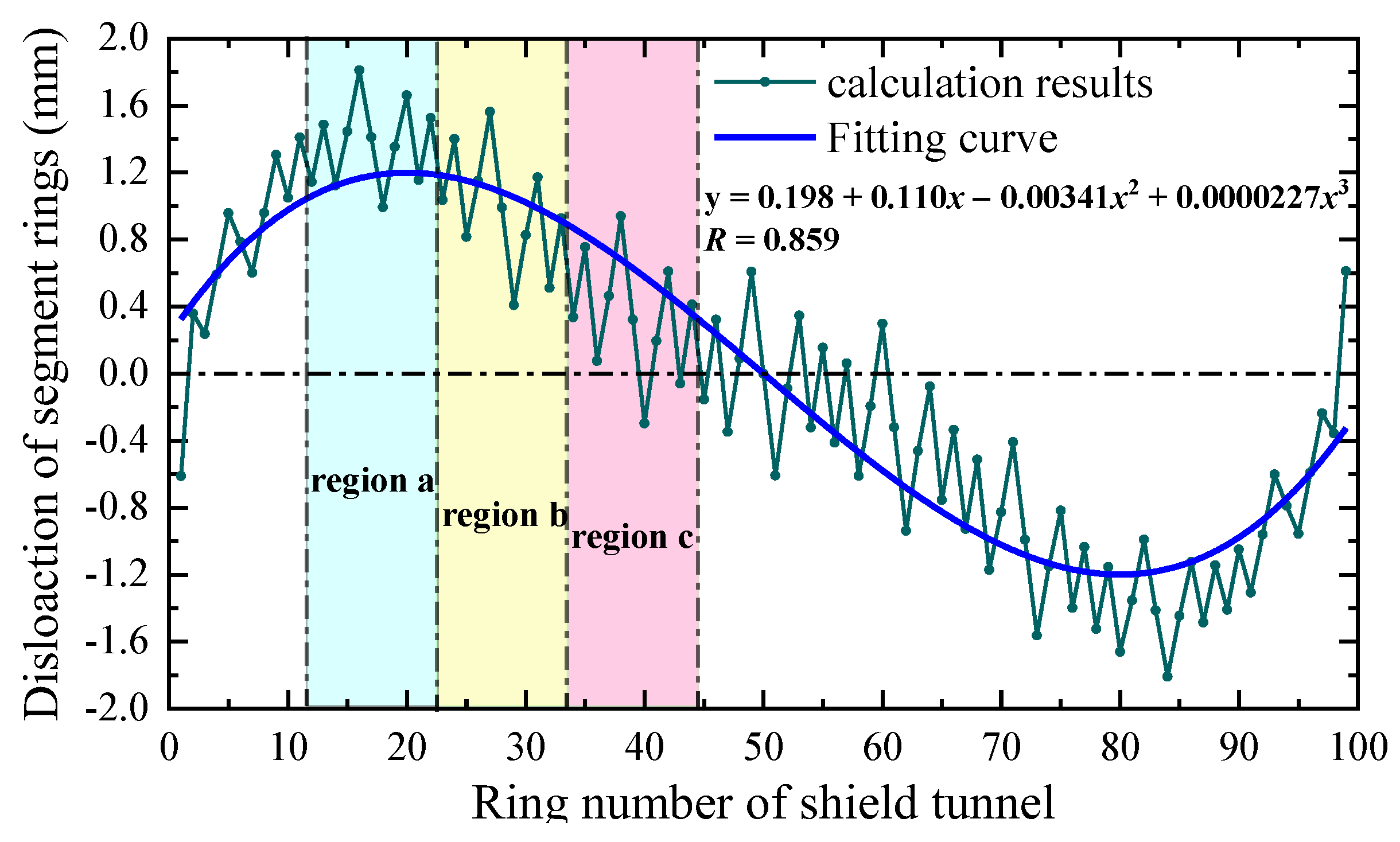
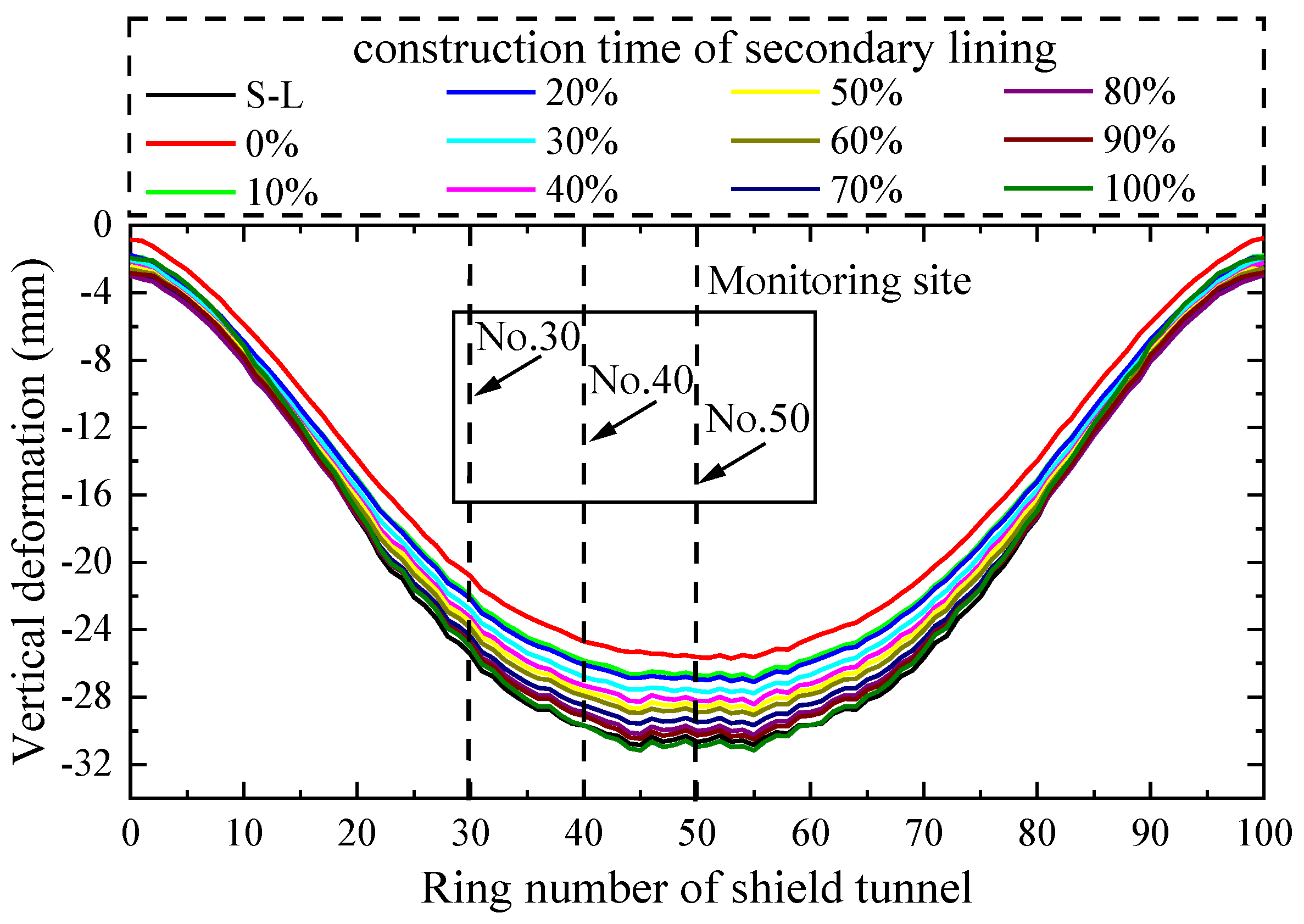
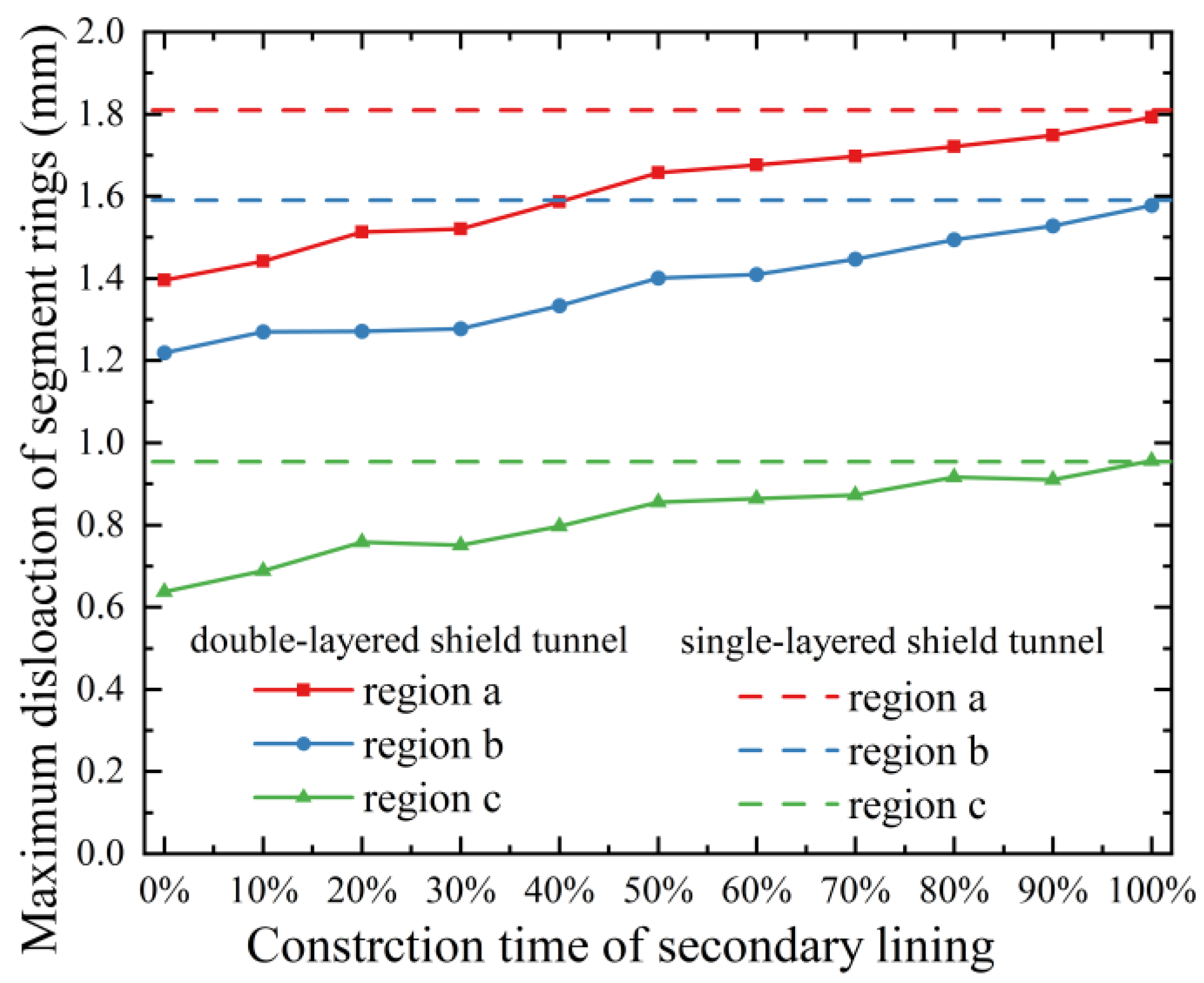
Combined with the real engineering project, a three-dimensional longitudinal refined numerical calculation model of a double-layered shield tunnel was established in the present research, and the longitudinal mechanical properties of the shield tunnel were studied. The established model was a double-layered shield tunnel with 100 rings and a total length of 100 m. A single segment ring consists of six standard blocks, two adjacent blocks, and one capping block, and the segments were assembled in a staggered manner. The secondary lining was placed inside the segment lining and composed of several homogeneous secondary lining rings (
Figure 5).
The refined numerical calculation model was calculated based on the finite difference method, and the segment lining was simulated using the Liner element (a three-node flat finite element that can resist the shear force, axial force, and bending moment, as well as simulate the effects of tangential friction and the tension and compression in the normal direction on the contact surface between the segment lining and the secondary lining). The thickness, stiffness, and strength of the secondary lining are relatively small, and the mechanical mechanism is in accordance with the characteristics of thin shell structure; therefore, the shell element was utilized to simulate the secondary lining. The parameters of segment lining and secondary lining were determined based on the engineering data shown in
Figure 2, as listed in
Table 2.
For the liner element used to simulate the segment, a reasonable method was used to divide the mesh so that the structural nodes were located exactly where the longitudinal and circumferential bolts are. This treatment allowed for the better implementation of the refined simulation of the bolts later. In addition, for shell elements used to simulate the secondary lining, the nodes of the mesh needed to coincide with the liner element. In this way, a reasonable interface element could be established between the liner element and shell element, so as to realize a reasonable simulation of the contact surface between the segment lining and the secondary lining. For convenience, the same meshing as used for the liner element was used for the shell element. The specific meshing of the model is shown in
Figure 4 and
Figure 5. The entire model comprised a total of 536,400 solid elements, 556,187 grid points, 70,400 structural elements, and 43,644 structural nodes.
The segments were assembled in a staggered manner in the refined numerical calculation model. They were joined into a segment ring using circumferential bolts, then connected into a longitudinal 3D tunnel structure using longitudinal bolts. Link elements were employed to simulate the bolts. Making the connection position and connection characteristics of the link element align with bolts used in practice helped to reflect the deformation mechanisms of the shield tunnel realistically. Each segment was uniformly divided into four pieces along the width direction, and two adjacent segments in same segment ring had five pairs of nodes with overlapping positions at the connection location of segments, numbered 1 to 5. The link element was established at nodes 2 and 4 to simulate the circumferential bolts (
Figure 6a). Then, each segment ring was uniformly divided into 50 pieces along the circumferential direction and there were 50 nodes with an overlapping position between two adjacent segment rings. The link element was established at every other node to simulate the longitudinal bolts, with a total of 25 link elements, as shown by the red dots in
Figure 6b. There were three link elements on each standard and adjacent block segment and only one link element on each capping block segment.
Each link element has six degrees of freedom in six directions, including three translational degrees of freedom (one in each axial direction) and three rotational degrees of freedom (one around each axis). Each degree of freedom has independent one-dimensional constitutive relationships and mechanical properties. Previous studies showed that the flexural stiffness
, axial stiffness
, and shear stiffness
of the link element exert a more significant influence on the mechanical properties of the shield tunnel. So, the effects of the three degrees of freedom related to the aforementioned stiffness parameters were mainly considered in the present research, which were set as elastic connections and represented by springs. The remaining three degrees of freedom were set as rigid connections. The specific connection form is shown in
Figure 7a, which is a schematic representation of the composition of three elastic springs for any link element. The linear yield ideal elastoplastic constitutive relation illustrated in
Figure 7b was adopted for springs on the three degrees of freedom [
43], and it can be expressed as:
where
and
represent the stress and the strain of the spring, respectively;
is the yield stress of spring;
is the strain corresponding to
;
is the ultimate strain of spring;
denotes the stiffness of any spring from the three degrees of freedom with elastic connection.
The spring stiffness was determined by the empirical values from the study [
44], and the yield strength was a macroscopic strength parameter in the actual project, which was determined in conjunction with the findings of the present research and previous experimental studies [
21], as shown in
Table 3.
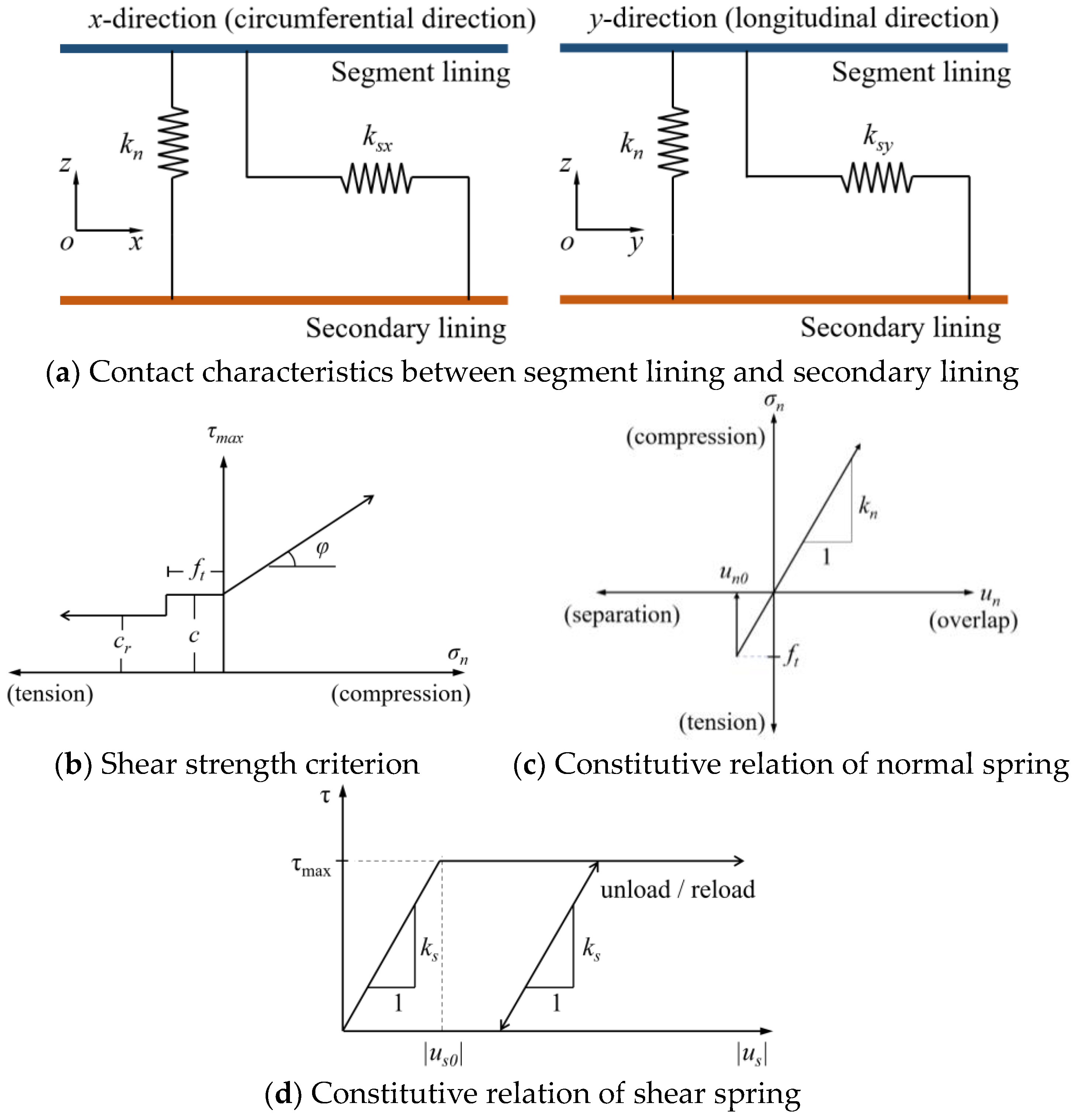
The contact characteristics of the contact surface between the segment lining and the secondary lining and their parameter value exert an important influence on the participation extent of the secondary lining in the structural bearing process. Previous studies have shown [
23] that the contact characteristics should include contact and separation in the normal direction as well as adhesion and friction in the tangential direction. Except for the tension and pressure in the normal direction, the contact surface can also transmit a certain shear force in the tangential direction. The contact characteristics in the refined numerical calculation model consist of a linear spring with tensile strength in the normal direction and two linear yield springs in the tangential direction, which were implemented using the interface element, as shown in
Figure 8a.
Figure 8b shows the shear strength criterion for the interface element, where the compressive strength of the interface element too high so its compressive failure was ignored. The maximum shear stress
changes with the normal stress
, as shown in Equation (4):
where
is the maximum stress of the shear spring of the interface element;
refers to the stress of normal spring of the interface element;
and
represent the cohesion and the residual cohesion of the interface element in the tangential direction, respectively;
is the friction angle of the interface element in the tangential direction; and
is the tensile strength of the normal spring of the interface element.
The constitutive relationship governing the behavior of the normal and shear spring is shown in
Figures 8c and
8d, respectively. When the normal spring is compressed, the maximum stress of shear spring
increases continuously with the stress on the normal spring
. When the behavior of the normal spring is tensile, the maximum stress of the shear spring
is equal to the cohesion
. If the stress reaches the tensile strength
, the normal spring of the interface element will undergo tensile failure. The cohesion
is then replaced by the residual cohesion
, and the tensile strength
is reduced to zero. The behavior of the shear spring of the interface element will return to its original state if the segment lining and secondary lining overlap and the normal spring generates pressure again. Based on these deformation properties, this refined numerical calculation model can not only reflect the shear behavior, but also realistically simulate the separation and subsequent overlap between segment lining and secondary lining. The constitutive relationship governing the behavior of the normal and shear spring can be expressed thus:
where
is the stress of the shear spring of the interface element;
is the absolute strain in the shear spring of the interface element;
is the strain in the shear spring corresponding to the maximum shear stress
;
denotes the strain in the normal spring of the interface element;
is the strain in the normal spring corresponding to the tensile strength
; and
and
represent the stiffness of the shear and normal spring of the interface element, respectively.
The stiffness of the interface element in a circular tunnel can be calculated empirically using Equation (7), as suggested in the literature [
43,
45]:
where
and
represent the bulk and shear modulus of adjoining zone, respectively;
is the smallest dimension of an adjoining zone in the normal direction. Parameters such as tensile strength
, cohesion
and
, and friction
were chosen from the empirical values given in the literature, as summarized in
Table 4.