Development of Fragility and Vulnerability Functions for Reinforced Masonry Structures in Mexico: A Case Study
Abstract
:1. Introduction
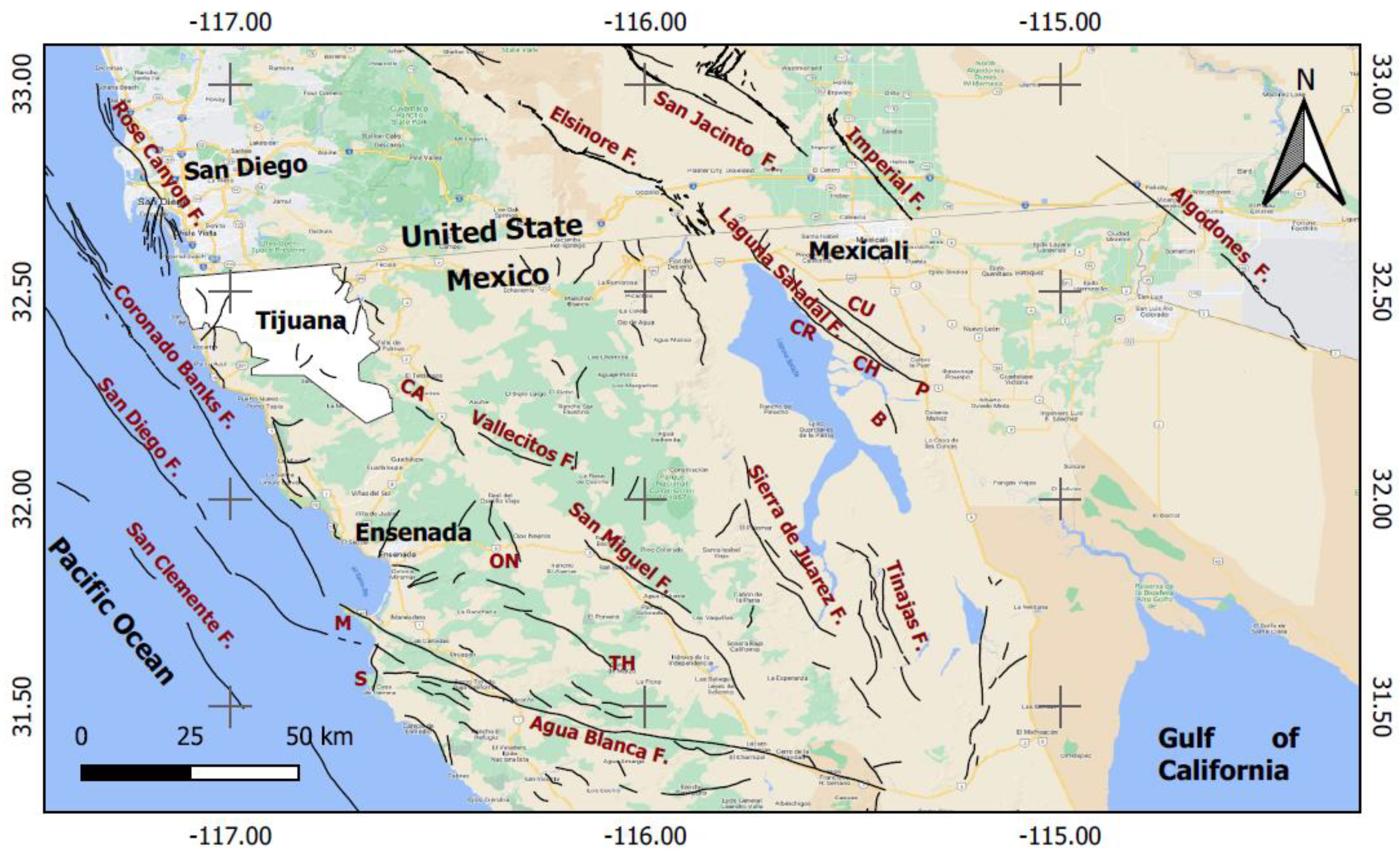
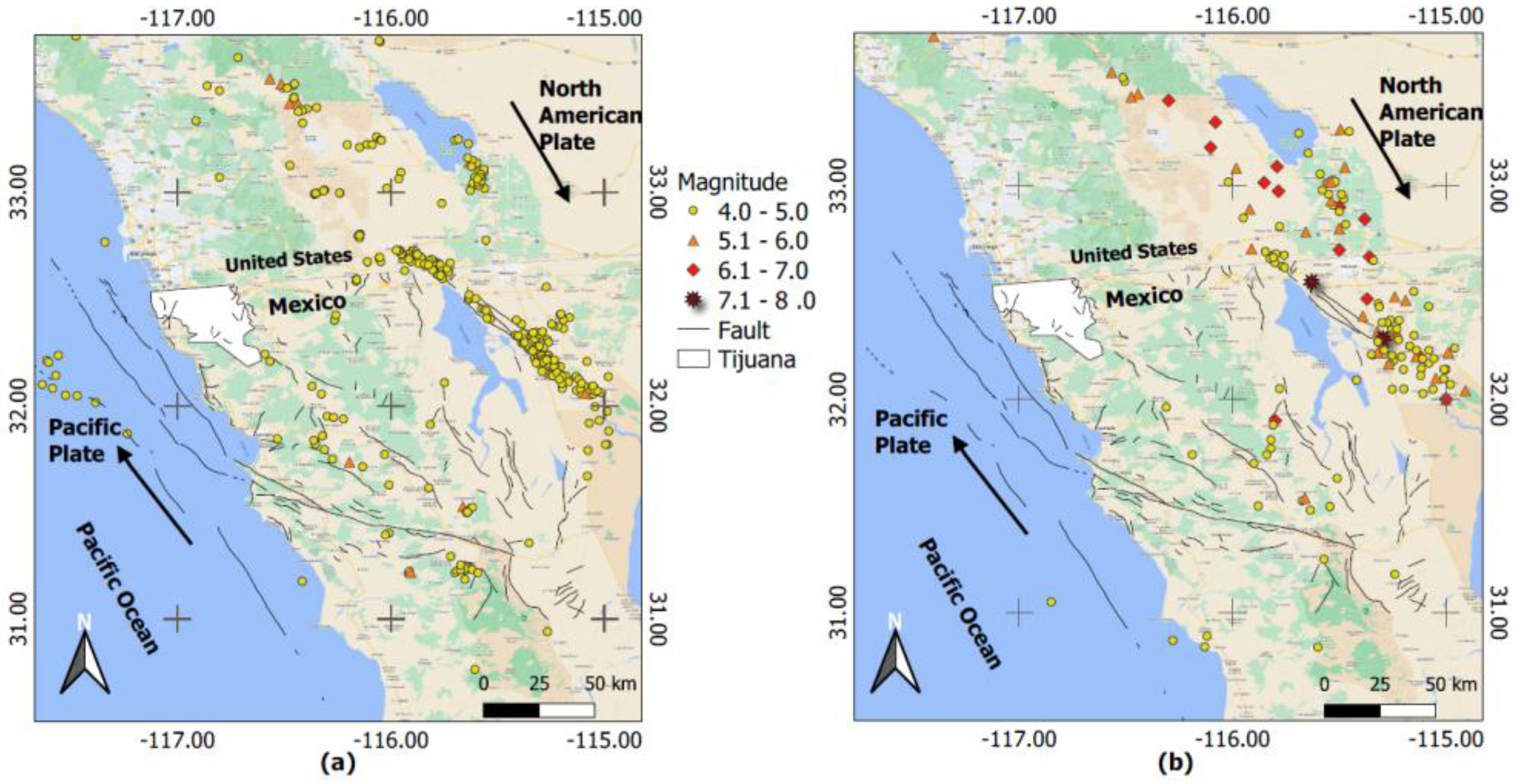
2. Seismicity of Baja California
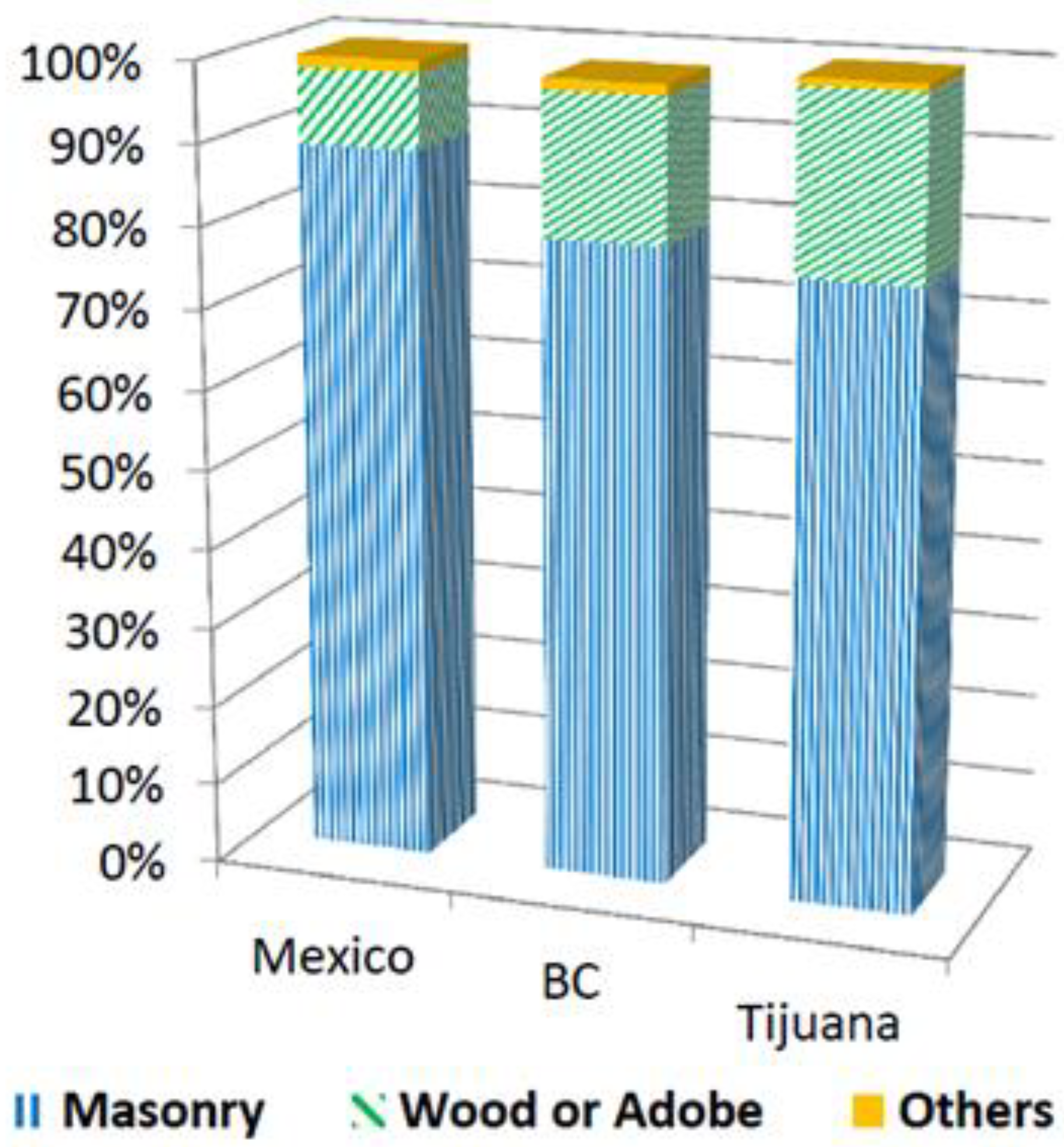
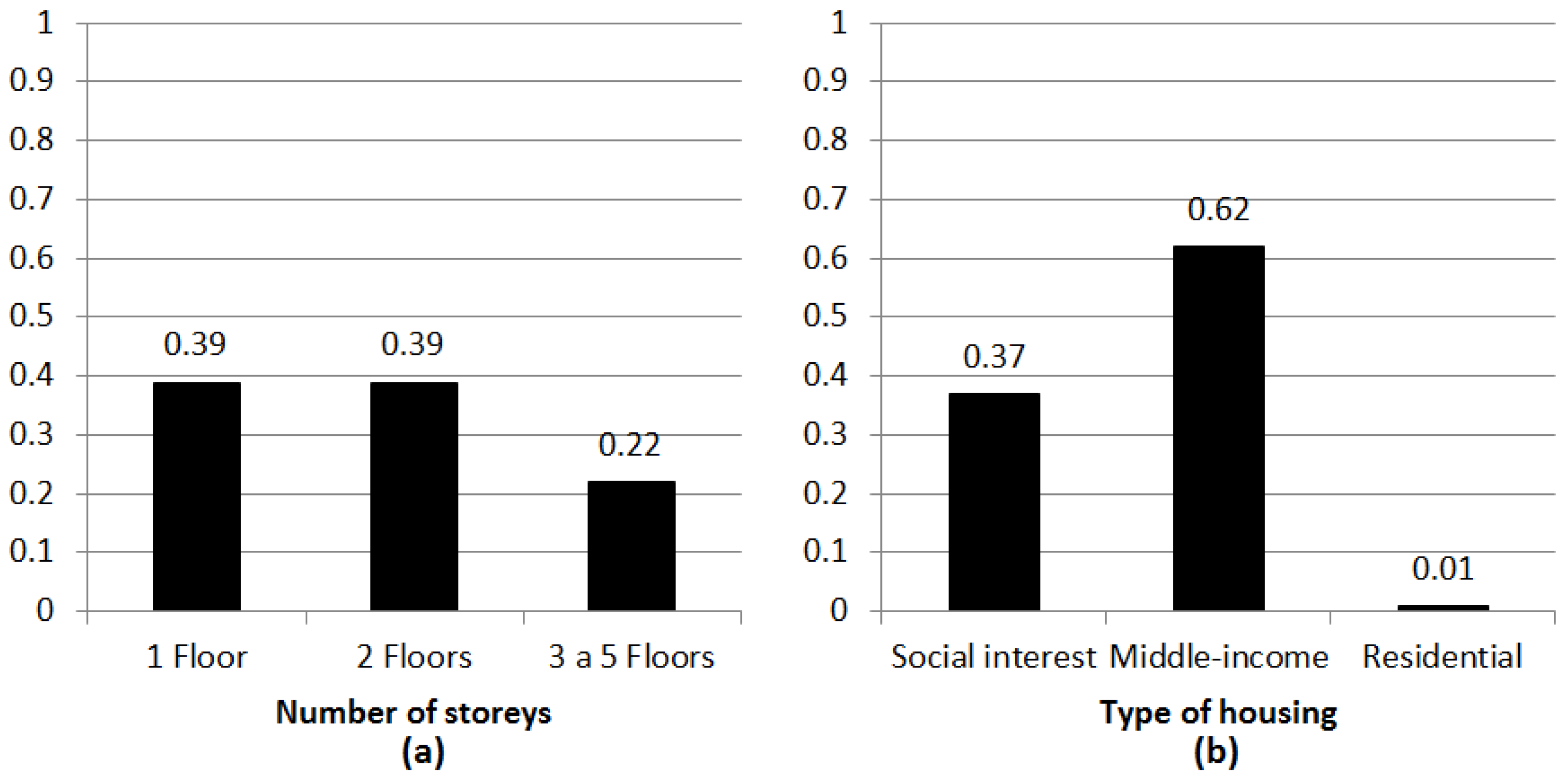
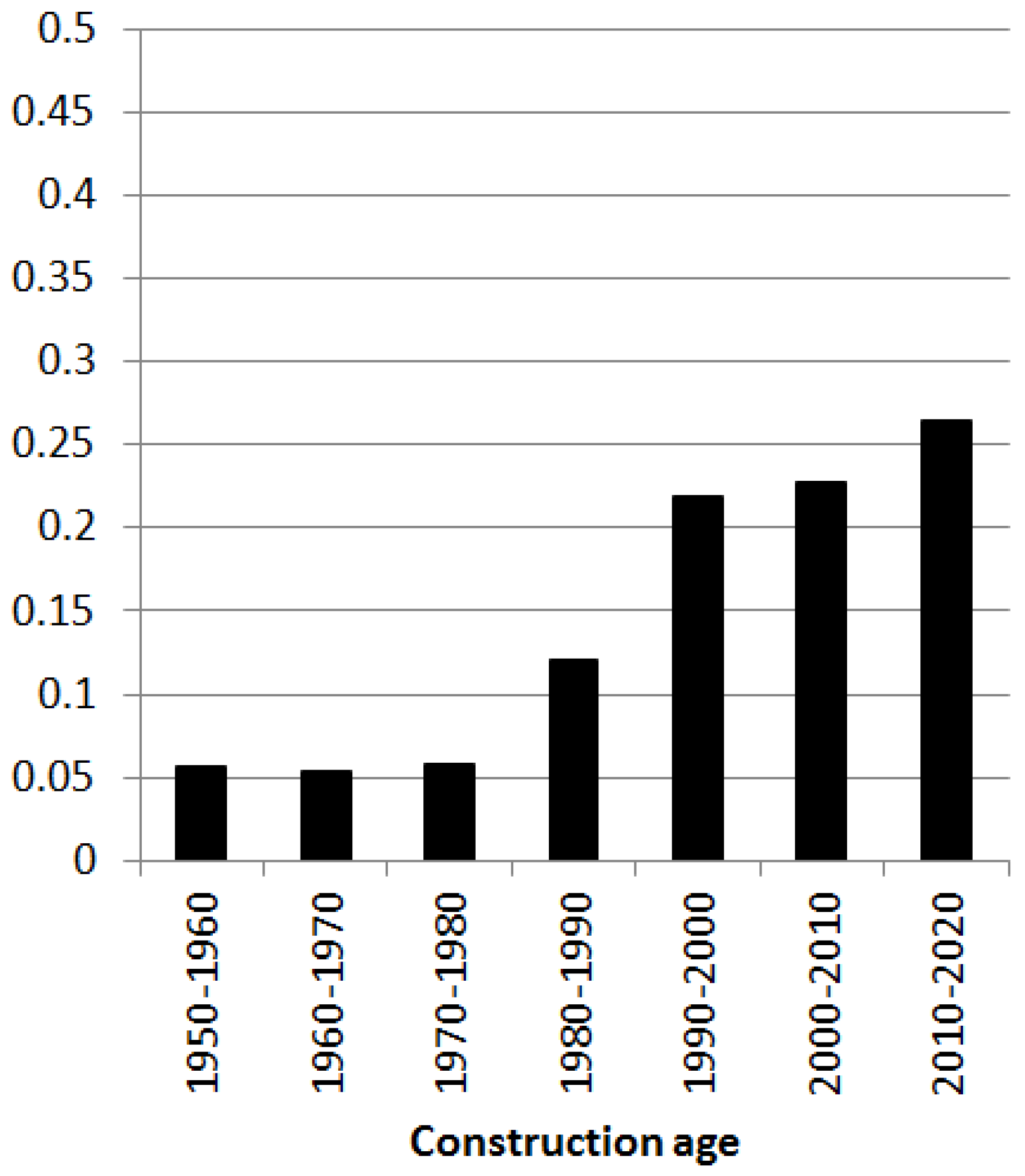
3. Identification of Common Housing Types in Tijuana
4. Vulnerability Modeller’sToolKit (VMTK)
4.1. Demand Module
4.2. Capacity Module
4.3. Structural Response Module
4.4. Fragility Module
4.5. Vulnerability Module
4.6. Comparison and Results Verification Module
5. Case Study
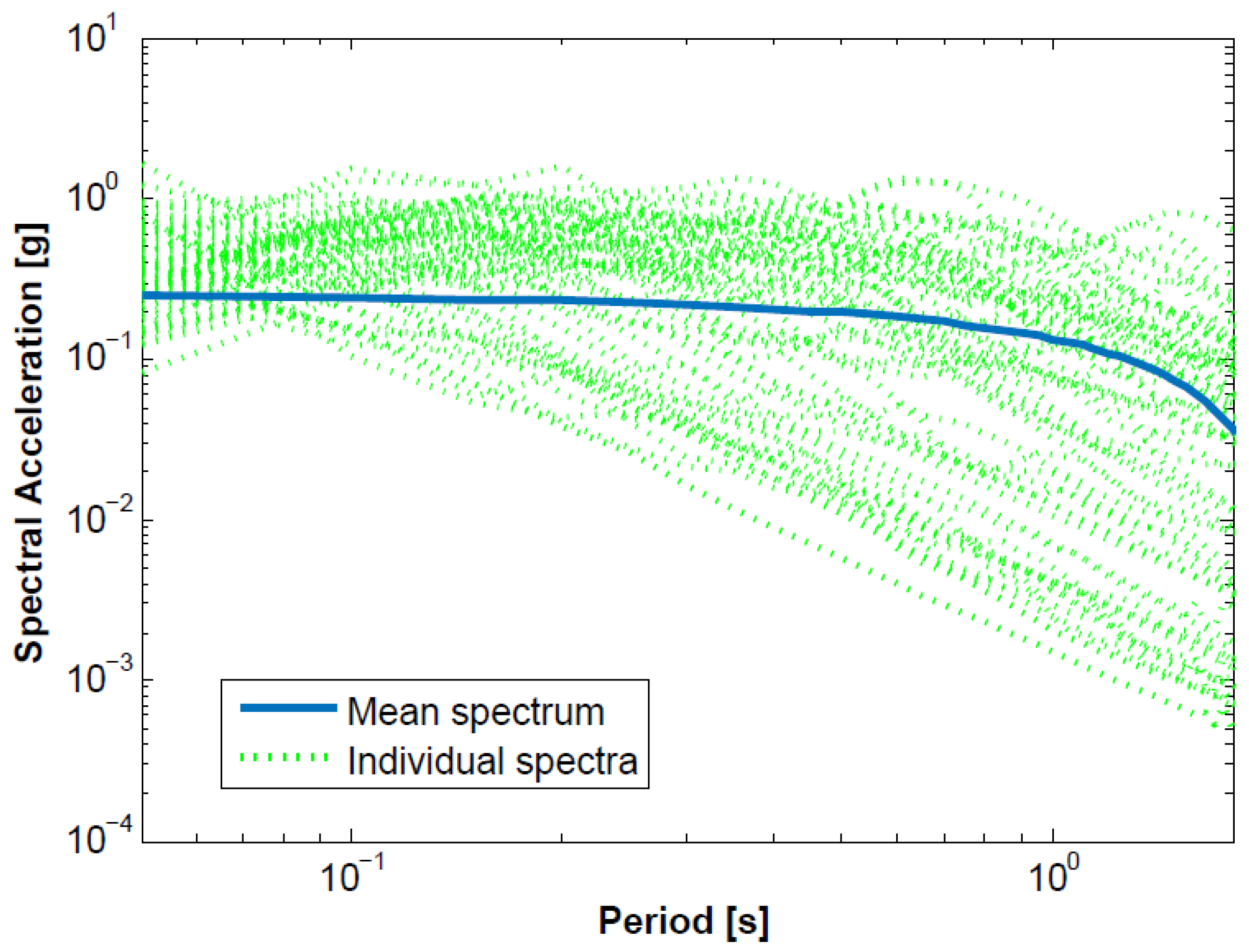
5.1. Selection of Ground Motion Records
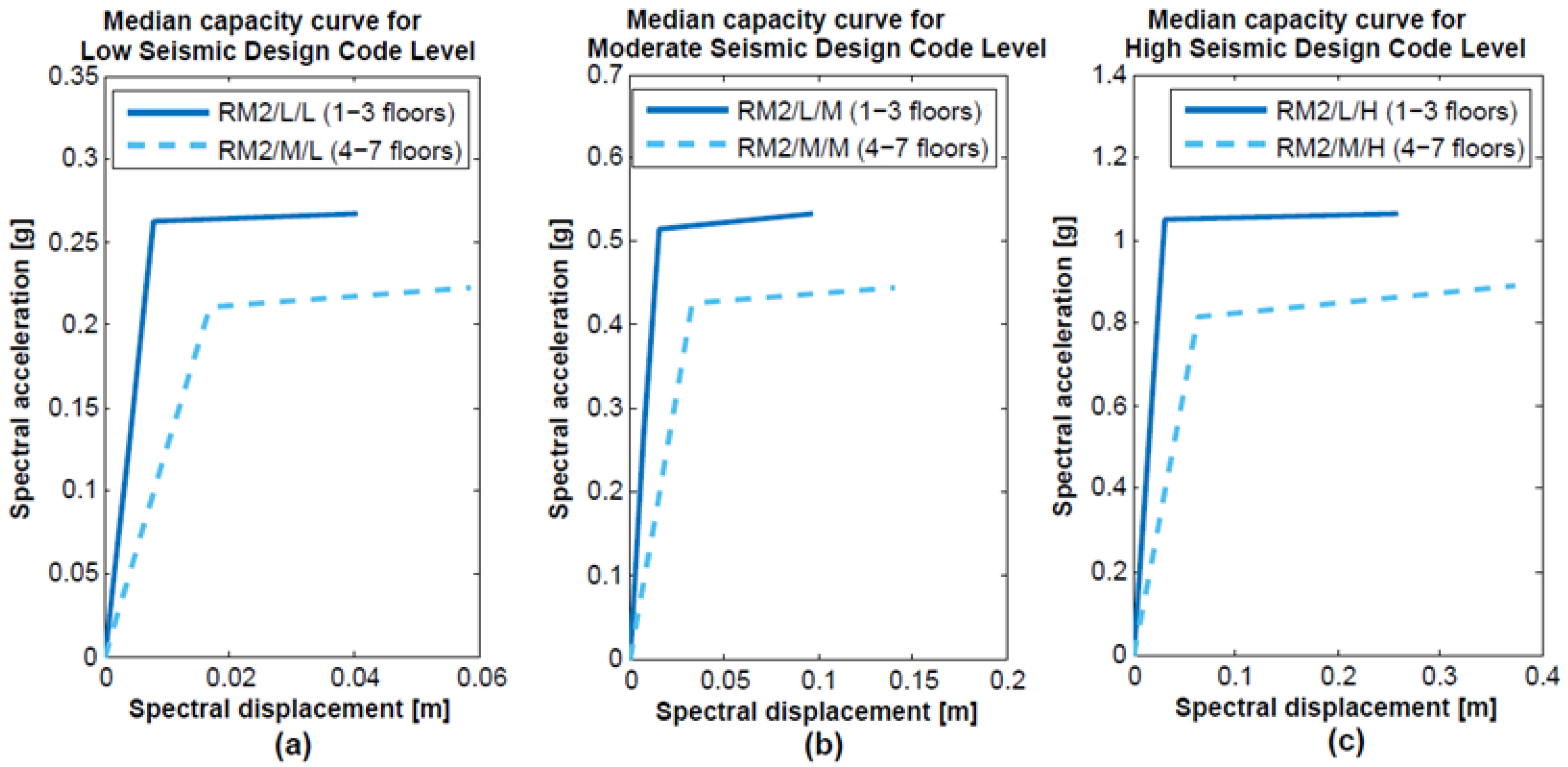
5.2. Capacity Curves
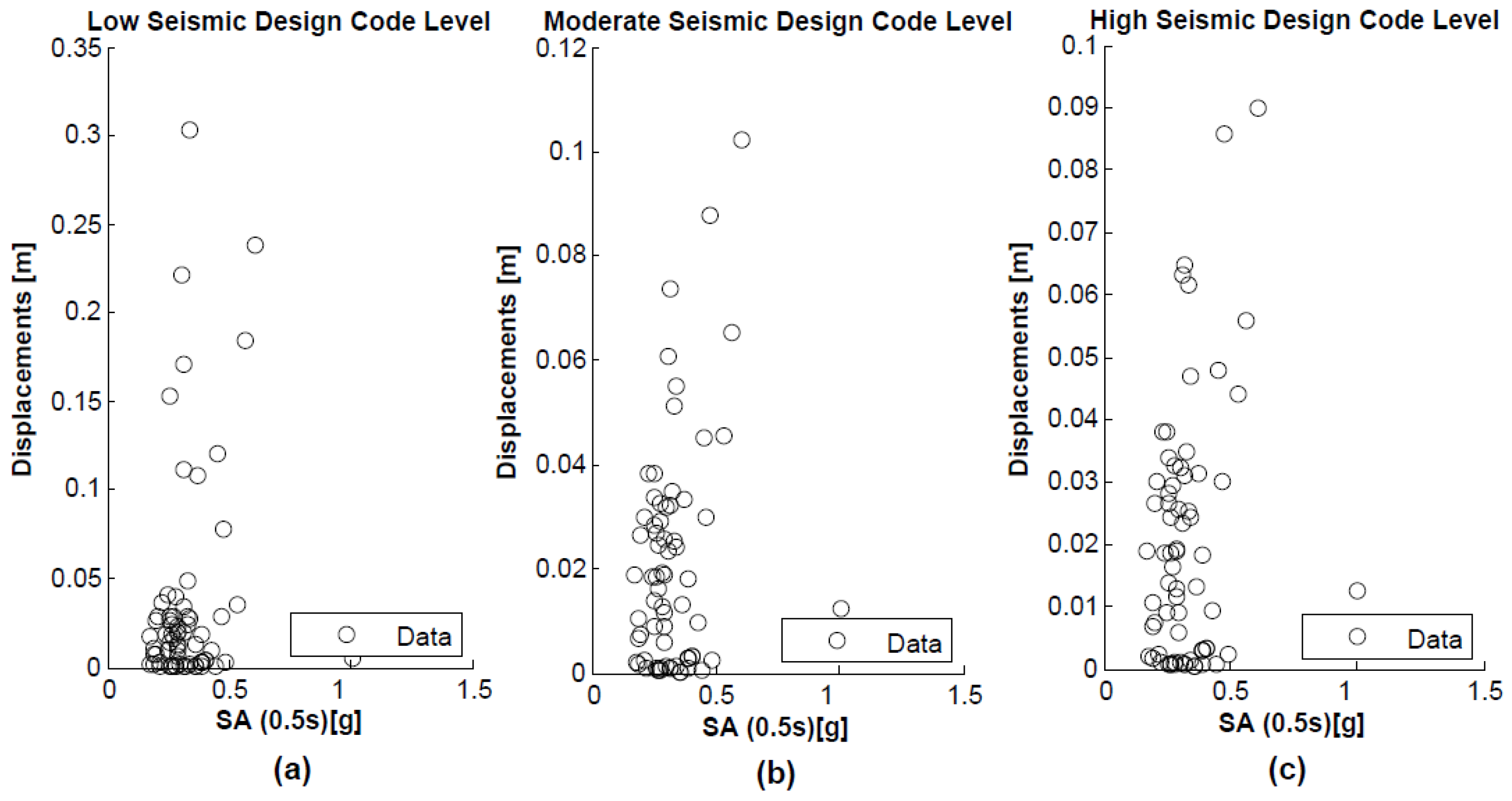
5.3. Structural Response
5.4. Definition of Damage Criterion
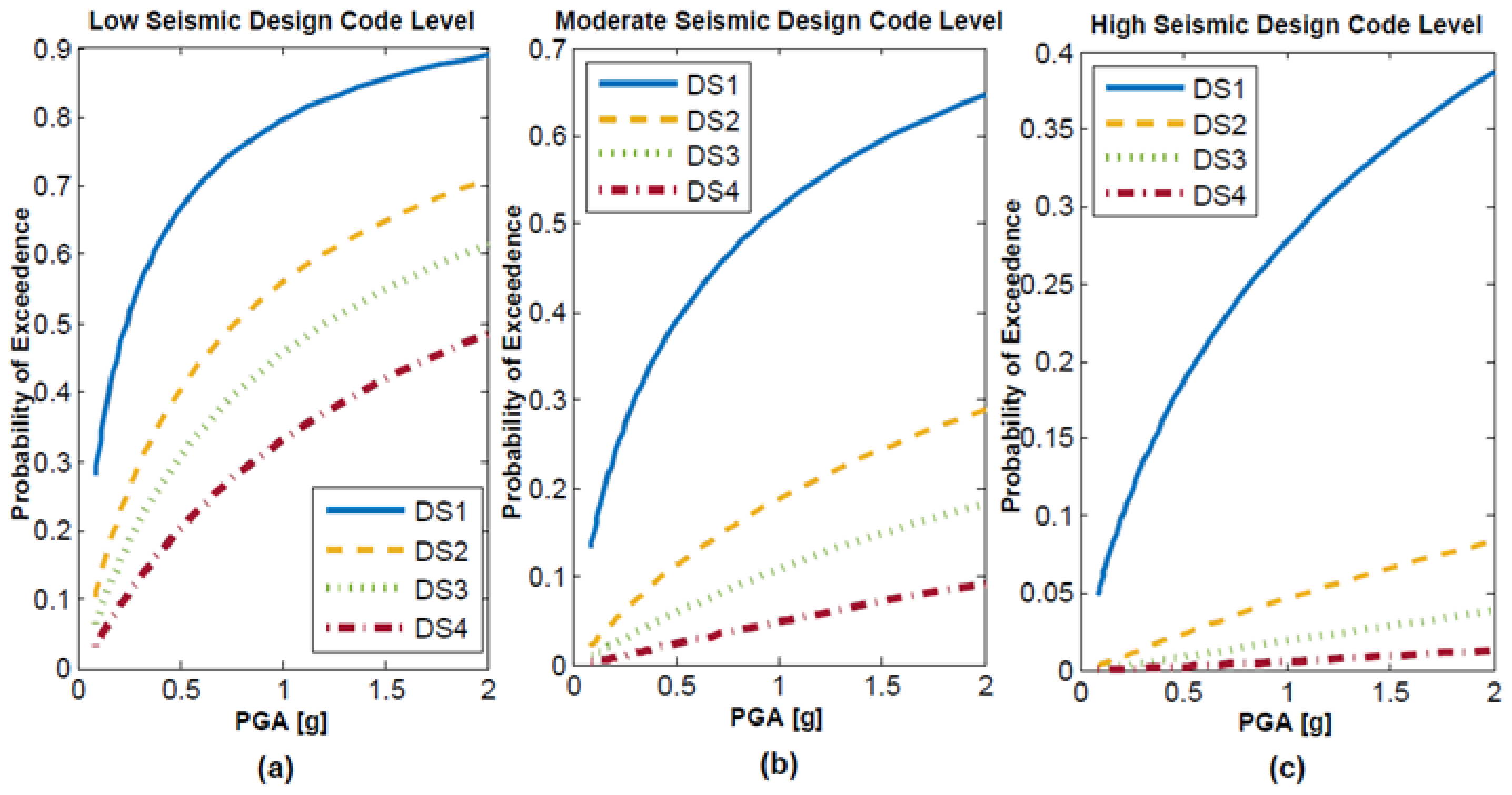
5.5. Derivation of Fragility Functions
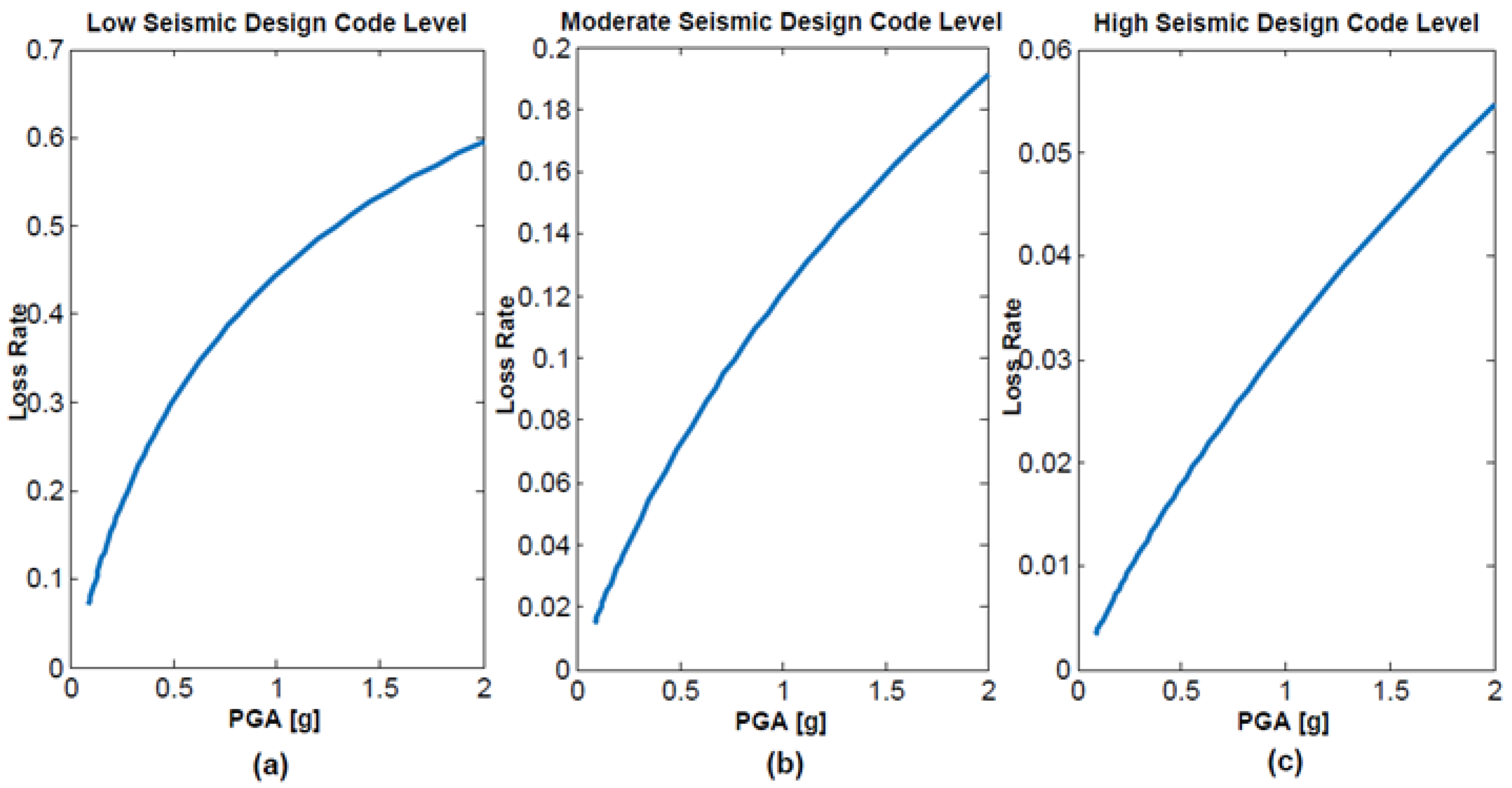
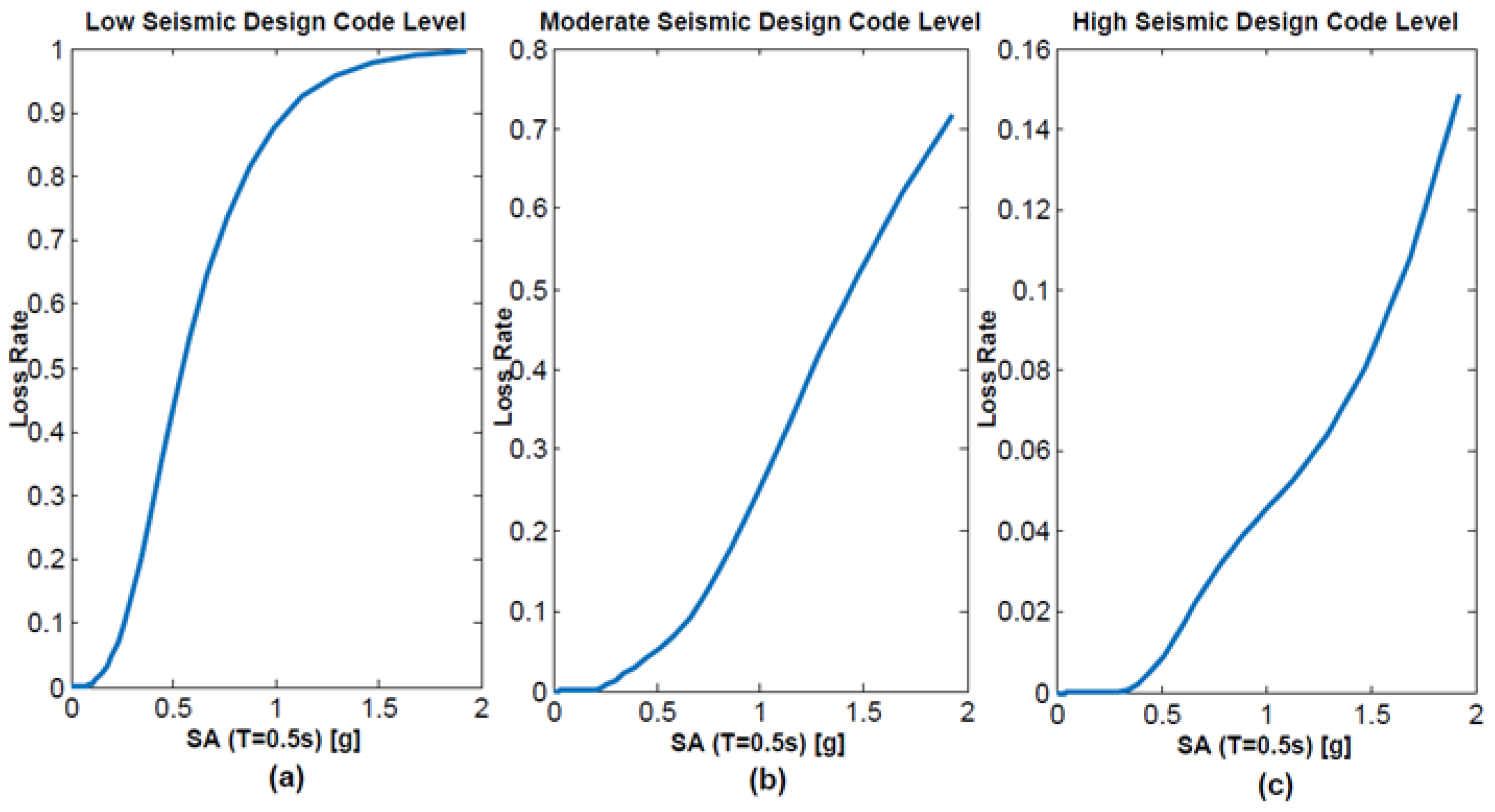
5.6. Vulnerability Functions
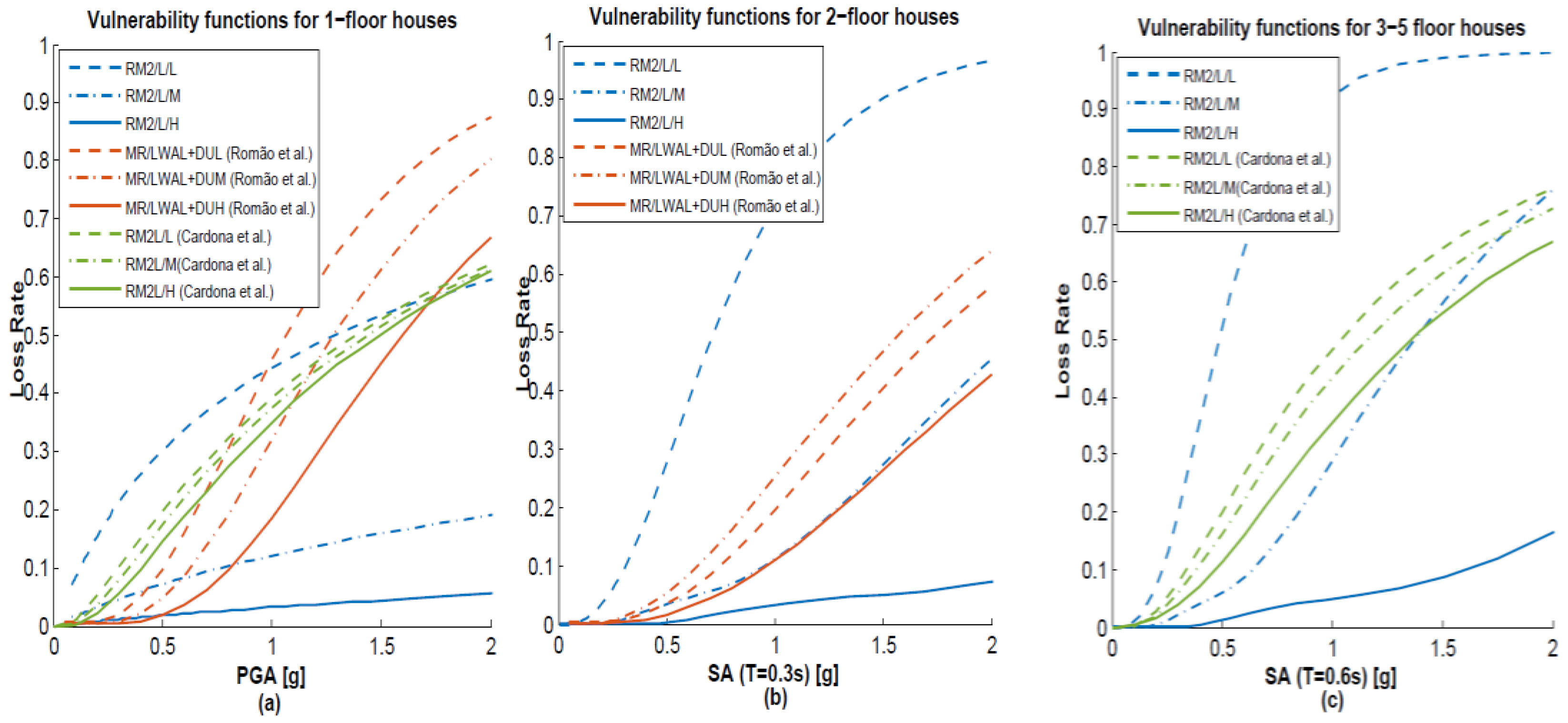
5.7. Comparison of Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Imjai, T.; Setkit, M.; Garcia, R.; Sukontasukkul, P.; Limkatanyu, S. Seismic strengthening of low strength concrete columns using high ductile metal strap confinement: A case study of kindergarten school in Northern Thailand. Walailak J. Sci. Technol. 2020, 17, 1335–1347. [Google Scholar] [CrossRef]
- Rodríguez-Valenzuela, L.M.; Mungaray-Moctezuma, A.; González-Durán, M.; Mena-Hernández, U. Structural damage to housing and effects on users due to seismic risk: A case study. Proc. Inst. Civ. Eng.-Munic. Eng. 2020, 174, 120–135. [Google Scholar] [CrossRef]
- Ruggieri, S.; Liguori, F.S.; Leggieri, V.; Bilotta, A.; Madeo, A.; Casolo, S.; Uva, G. An archetype-based automated procedure to derive global-local seismic fragility of masonry building aggregates: META-FORMA-XL. Int. J. Disaster RiskReduct. 2023, 95, 103903. [Google Scholar] [CrossRef]
- Cardinali, V.; Tanganelli, M.; Bento, R. A hybrid approach for the seismic vulnerability assessment of the modern residential masonry buildings. Int. J. Disaster Risk Reduct. 2022, 79, 103193. [Google Scholar] [CrossRef]
- Martins, L.; Silva, V. A global database of vulnerability models for seismic risk assessment. In Proceedings of the 16th European Conference on Earthquake Engineering, Thessaloniki, Greece, 18–21 June 2018. [Google Scholar]
- Silva, V.; Crowley, H.; Varum, H.; Pinho, R.; Sousa, R. Evaluation of analytical methodologies used to derive vulnerability functions. Earthq. Eng. Struct. Dyn. 2014, 43, 181–204. [Google Scholar] [CrossRef]
- Yamin, L.E.; Hurtado, A.; Rincon, R.; Dorado, J.F.; Reyes, J.C. Probabilistic seismic vulnerability assessment of buildings in terms of economic losses. Eng. Struct. 2017, 138, 308–323. [Google Scholar] [CrossRef]
- Kassem, M.; Mohamed Nazri, F.; NoroozinejadFarsangi, E. The seismic vulnerability assessment methodologies: A state-of-the-art review. Ain Shams Eng. J. 2020, 11, 849–864. [Google Scholar] [CrossRef]
- Whitman, R.; Reed, J.; Hong, S.-T. Earthquake Damage Probability Matrices. In Proceedings of the Fifth World Conference on Earthquake Engineering, Rome, Italy, 25–29 June 1974; pp. 2531–2540. [Google Scholar]
- Benedetti, D.; Benzoni, G.; Parisi, M.A. Seismic vulnerability and risk evaluation for old urban nuclei. Earthq. Eng. Struct. Dyn. 1988, 16, 183–201. [Google Scholar] [CrossRef]
- Lagomarsino, S.; Giovinazzi, S. Macroseismic and mechanical models for the vulnerability and damage assessment of current buildings. Bull. Earthq. Eng. 2006, 4, 415–443. [Google Scholar] [CrossRef]
- Baggio, C.; Bernardini, A.; Colozza, R.; Corazza, L.; Della Bella, M.; Di Pasquale, G.; Dolce, M.; Goretti, A.; Martinelli, A.; Orsini, G.; et al. Manuale per la Compilazionedellascheda di Primo Livello di Rilevamentodanno, Pronto Intervento e Agibilità per Edificiordinarinell’emergenzapost-sismica (AEDES), Italy. 2014. Available online: https://www.protezionecivile.gov.it/it/pubblicazione/manuale-la-compilazione-della-scheda-di-primo-livello-di-rilevamento-di-danno-pronto-intervento-e-agibilita-edifici-ordinari-nellemergenza-post/ (accessed on 5 September 2023).
- FEMA P-155; FEMA-155: Rapid Visual Screening of Buildings for Potential Seismic Hazards: Supporting Documentation. Federal Emergency Management Agency: Washington, DC, USA, 2015.
- Rosti, A.; Rota, M.; Penna, A. Empirical fragility curves for Italian URM buildings. Bull. Earthq. Eng. 2021, 19, 3057–3076. [Google Scholar] [CrossRef]
- D’Ayala, D. Assessing the seismic vulnerability of masonry buildings. In Handbook of Seismic Risk Analysis and Management of Civil Infrastructure Systems; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar] [CrossRef]
- D’Ayala, D.; Speranza, E. Definition of Collapse Mechanisms and Seismic Vulnerability of Historic Masonry Buildings. Earthq. Spectra. 2003, 19, 479–509. [Google Scholar] [CrossRef]
- D’Ayala, D. Force and displacement based vulnerability assessment for traditional buildings. Bull. Earthq. Eng. 2005, 3, 235–265. [Google Scholar] [CrossRef]
- Borzi, B.; Crowley, H.; Pinho, R. Simplified pushover-based earthquake loss assessment (SP-BELA) method for masonry buildings. Int. J. Archit. Herit. 2008, 2, 353–376. [Google Scholar] [CrossRef]
- Kappos, A.; Panagopoulos, G.; Penelis, G. Development of a seismic damage and loss scenario for contemporary and historical buildings in Thessaloniki, Greece. Soil Dyn. Earthq. Eng. 2008, 28, 836–850. [Google Scholar] [CrossRef]
- Molina, S.; Lang, D.; Lindholm, C. SELENA—An open-source tool for seismic risk and loss assessment using a logic tree computation procedure. Comput. Geosci. 2010, 36, 257–269. [Google Scholar] [CrossRef]
- FEMA. Hazus–MH 2.1: Technical Manual; Federal Emergency Management Agency: Washington, DC, USA, 2012. [Google Scholar]
- Silva, V.; Casotto, C.; Rao, A.; Villar, M.; Crowley, H.; Vamvatsikos, D. OpenQuake Risk Modeller’s Toolkit—User Guide. Glob. Earthq. Model (GEM) Tech. Rep. 2015, 9, 97. [Google Scholar]
- Martins, L.; Silva, V. Development of a fragility and vulnerability model for global seismic risk analyses. Bull. Earthq. Eng. 2020, 19, 6719–6745. [Google Scholar] [CrossRef]
- Martins, L.; Silva, V.; Crowley, H.; Cavalieri, F. Vulnerability modellers toolkit, an open-source platform for vulnerability analysis. Bull. Earthq. Eng. 2021, 19, 5691–5709. [Google Scholar] [CrossRef]
- NTCBC. Normas Técnicas Complementarias de la Ley de Edificaciones del Estado de Baja California, de Seguridad Estructural en Materia de “Diseño y Construccion de Mamposteria”; NTCBC: Mexico City, Mexico, 2017. [Google Scholar]
- Rosquillas, A.; Mendoza, L. Proyecto RADIUS Case Tijuana (Risk Assessment Tools for Diagnosis of Urban Areas against Seismic Disasters), 2nd ed.; CICESE and XVI District Council of Tijuana: Tijuana, Mexico, 2000; pp. 27–28. [Google Scholar]
- Garatachia, J.C.; Baró Suárez, J.E.; Huerta López, C.I. Chapter 1. Book: Aproximación a la vulnerabilidad estructural y socioeconómica en el marco de un estudio de riesgo sísmico en la zona urbana de Tijuana, Baja California. In Vulnerabilidad Territorial ante la Expansión Urbana; Universidad of Mexico: Mexico City, Mexico, 2016. [Google Scholar]
- Cardona, O.; Ordaz, M.; Reinoso, E. CAPRA–comprehensive approach to probabilistic risk assessment: International initiative for risk management effectiveness. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012; Volume 1, p. 10. Available online: http://www.iitk.ac.in/nicee/wcee/article/WCEE2012_0726.pdf (accessed on 21 August 2023).
- González, M. Impacto Socioeconómico del Daño Estructural por Sismo en Viviendas de 1 y 2 Niveles en las Ciudades de Baja California, México. Ph.D. Thesis, Universidad Autónoma de Baja California, Mexicali, Mexico, 2016. [Google Scholar]
- Romero, P. Escenario de Riesgo Sísmico en la Ciudad de Tijuana, Baja California, México. Master’s Thesis, Universidad Autónoma de Baja California, Mexicali, Mexico, 2020. [Google Scholar]
- Arce, R. Estimación de Peligro Sísmico en el Norte de BC, con Aplicación en el Cálculo de la Respuesta Dinámica de dos Edificios. Master’s Thesis, Centro de Investigación Científica y de Educación Superior de Ensenada, Ensenada, Mexico, 2016. Available online: http://cicese.repositorioinstitucional.mx/jspui/handle/1007/956 (accessed on 15 February 2022).
- Soares, J. Aplicación de la microzonación sísmica a la seguridad de estructuras críticas en la ciudad de Ensenada. Master’s Thesis, Centro de Investigación Científica y de Educación Superior de Ensenada, Ensenada, Mexico, 2003. [Google Scholar]
- Servicio Sismológico Nacional (SSN). EarthquakeCatalog. Available online: http://www.ssn.unam.mx/ (accessed on 1 March 2022).
- United States Geological Survey (USGS). Earthquake Catalog. Available online: https://www.usgs.gov/programs/earthquake-hazards/earthquakes (accessed on 1 March 2022).
- INEGI. Panorama Sociodemográfico de Baja California, Mexico, 2021, INEGI (Instituto Nacional de Estadística y Geografía). Available online: https://www.inegi.org.mx/contenidos/productos/prod_serv/contenidos/espanol/bvinegi/productos/nueva_estruc/702825197735.pdf (accessed on 15 February 2022).
- INEGI. Anuario Estadístico y Geográfico de Baja California, Mexico, 2017, INEGI (Instituto Nacional de Estadística y Geografía). Available online: https://www.inegi.org.mx/contenido/productos/prod_serv/contenidos/espanol/bvinegi/productos/nueva_estruc/anuarios_2017/702825094874.pdf (accessed on 15 February 2022).
- Cardona, O.D.; Ordaz, M.; Yamin, L.E.; Singh, S.; Barbat, A.H.; Bernal, G.A.; Salgado, M.A.; Mora, M.G.; Velásquez, C.A.; Olaya, J.C.; et al. Modelación Probabilista de Riesgos Naturales en el Nivel Global: El Modelo Global de Riesgo. Modelos Globales de Terremoto y Ciclón y Evaluación de Riesgo de Desastres de los Países para las Amenazas de Terremoto, Ciclón e Inundaciones; Consorcio CINME, INGENIAR, ITEC, EAI: Geneva, Switzerland, 2013. [Google Scholar]
- McKenna, F. OpenSees: A framework for earthquake engineering simulation. Comput. Sci. Eng. 2011, 13, 58–66. [Google Scholar] [CrossRef]
- Jalayer, F.; De Risi, R.; Manfredi, G. Bayesian Cloud Analysis: Efficient structural fragility assessment using linear regression. Bull. Earthq. Eng. 2015, 13, 1183–1203. [Google Scholar] [CrossRef]
- Silva, V. Uncertainty and correlation in seismic vulnerability functions of building classes. Earthq. Spectra. 2019, 4, 1515–1539. [Google Scholar] [CrossRef]
- Cornell, C.A. Engineering Seismic Risk Analysis. Bull. Seismol. Soc. Am. 1968, 58, 1583–1606. [Google Scholar] [CrossRef]
- Munguia, L. Result of a preliminary earthquake hazard study in north Baja California, Mexico. SSA 2014 Annual Meeting Announcement. Seismol. Res. Lett. 2014, 85, 365–558. [Google Scholar] [CrossRef]
- Anderson, J.; Rockwell, T.; Agnew, D. Past and Possible Future Earthquakes of Significance to the San Diego Region. Earthq. Spectra. 1989, 5, 299–335. [Google Scholar] [CrossRef]
- Acosta, J.; Arellano, G.; Ruiz, E.; Mendoza, L.; Reyes, R.; Rocha, E. Microzonificación Sísmica de Tijuana; National Fund for the Prevention of Natural Disasters: Tijuana, Mexico, 2009. [Google Scholar]
- CESMD. Center for Engineering Strong Motion (CESMD): U.S. Structural and Ground Response Data. Available online: http://www.strongmotioncenter.org (accessed on 15 February 2022).
- CICESE. Centro de Investigación Científica y de Educación Superior de Ensenada (CICESE): Red Sísmica del Noroeste de México. Available online: https://resnom.cicese.mx/sitio/CatalogoAceleracion?i= (accessed on 1 March 2022).
- ATC-40; ATC-40: Seismic Evaluation and Retrofit of Concrete Buildings. Applied Technology Council: Redwood City, CA, USA, 1996.
- Vargas, Y.F.; Barbat, A.H.; Pujades, L.G.; Hurtado, J.E. Probabilistic seismic risk evaluation of reinforced concrete buildings. Proc. Inst. Civ. Eng.-Struct. Build. 2014, 167, 327–336. [Google Scholar] [CrossRef]
- Acevedo, A.B.; Jaramillo, J.D.; Yepes, C.; Silva, V.; Osorio, F.A.; Villar, M. Evaluation of the seismic risk of the unreinforced masonry building stock in Antioquia, Colombia. Nat. Hazards 2017, 86, 31–54. [Google Scholar] [CrossRef]
- Villar-Vega, M.; Silva, V.; Crowley, H.; Yepes, C.; Tarque, N.; Acevedo, A.B.; Hube, M.A.; Gustavo, C.D.; Santa Maria, H. Development of a fragility model for the residential building stock in South America. Earthq. Spectra 2017, 33, 581–604. [Google Scholar] [CrossRef]
- Stafford, P.J. Conditional prediction of absolute durations. Bull. Seismol. Soc. Am. 2008, 98, 1588–1594. [Google Scholar] [CrossRef]
- Silva, V.; Crowley, H.; Pinho, R.; Varum, H. Extending displacement-based earthquake loss assessment (DBELA) for the computation of fragility curves. Eng. Struct. 2013, 56, 343–356. [Google Scholar] [CrossRef]
- FEMA. Technical and User’s Manual of Advanced Engineering Building Module (AEBM) “Hazus MH 2.1.”; Federal Emergency Management Agency: Washington, DC, USA, 2015. [Google Scholar]
- Romão, X.; Pereira, N.; Castro, M.; De Maio, F.; Crowley, H.; Silva, V.; Martins, L. European_Building_Vulnerability_Database. 2022. Available online: https://gitlab.seismo.ethz.ch/efehr/esrm20_vulnerability/-/blob/master/European_Building_Vulnerability_Database.xlsx (accessed on 5 September 2023).


| Taxonomy (1) | Description Typology |
|---|---|
| MCF/LWAL/DUC/H:1-5/L-M-H | Confined masonry, ductile, 1–5 floors |
| MCF/LWAL/DNO/H:1-5/L-M-H | Confined masonry, non-ductile, 1–5 floors |
| MR/LWAL/DUC/H:1-5/L-M-H | Reinforced masonry, ductile, 1–5 floors |
| MR/LWAL/DNO/H:1-5/L-M-H | Reinforced masonry, non-ductile, 1–5 floors |
| Site | Longitude | Latitude | Vs30 (m/s) | Settlement Site | Classification According to IBC 2006 |
|---|---|---|---|---|---|
| PR | −116.906667 | 32.445000 | 646 | Volcanic Rock | C (Very dense soil and soft rock) |
| TUN | −117.006727 | 32.480516 | 487 | Sandstone–Conglomerate | C (Very dense soil and soft rock) |
| COL | −116.878755 | 32.503136 | 368 | Sandstone–Conglomerate | C (Very dense soil and soft rock) |
| PCI | −117.054227 | 32.515075 | 348 | Conglomerate | D (Stiff soil profile) |
| CCC | −116.992590 | 32.532390 | 250 | Conglomerate | D (Stiff soil profile) |
| PLA | −117.122693 | 32.518990 | 175 | Siltstone–Sandstone | E (Soft soil profile) |
| Site | Most Contributing Fault | PGA | Probability of Exceedance in 50 Years (%) | Magnitude Range | Distance Range (km) |
|---|---|---|---|---|---|
| PR | San Miguel–Vallecitos Fault (Northern) 36 | 0.20 | 1.47 | 5.0–7.0 | 15–30 |
| TUN | Rose Canyon–Newport Inglewood Fault (multiple) 37 | 0.26 | 5.35 | 5.5–7.0 | 15–30 |
| COL | Falla San Migue–Vallecitos Fault (Northern) 36 | 0.26 | 4.08 | 5.0–6.5 | 15–30 |
| PCI | Rose Canyon Newport Inglewood Fault(multiple) 37 | 0.34 | 13.83 | 5.0–6.5 | 0–15 |
| CCC | Falla Rose Canyon–Newport Inglewood Fault (La Nación) 39 | 0.38 | 21.79 | 4.5–6.5 | 0–15 |
| PLA | Rose Canyon–Newport Inglewood Fault(multiple)37 | 0.54 | 60.87 | 4.5–6.5 | 0–30 |
| Station Name | Earthquake | Origin Date | Magnitude | Distance (km) | PGA (g) | Vs30 |
|---|---|---|---|---|---|---|
| WRC2 | SearlesValley | 5/07/2019 | 5.0 Mw | 26.2 | 0.355 | 686 |
| 13879 | La Habra | 28/03/2014 | 5.1 Mw | 8.3 | 0.307 | 283 |
| 36138 | Parkfield | 28/09/2004 | 6.0 Ml | 10.7 | 0.308 | 270 |
| 68150 (Chn 1) | South Napa | 24/08/2014 | 6.0 Mw | 6.4 | 0.339 | 300 |
| 68150 (Chn 3) | South Napa | 24/08/2014 | 6.0 Mw | 6.4 | 0.370 | 300 |
| 57191 | MorganHill84 | 24/04/1984 | 6.2 Ml | 3.9 | 0.314 | 282 |
| 24643 | Northridge | 17/01/1994 | 6.4 Ml | 20.1 | 0.320 | 258 |
| 36431 | Parkfield | 20/12/1994 | 4.9 Mw | 7.5 | 0.433 | 297 |
| WMD | Westmorland | 30/09/2020 | 4.9 Mw | 2.1 | 0.538 | 301 |
| CLC | Searles Valley | 5/07/2019 | 5.0 Mw | 10.8 | 0.511 | 1464 |
| 11369 | Westmorland | 27/04/1981 | 5.7 Mw | 6.9 | 0.480 | 194 |
| 36228 | Parkfield | 28/09/2004 | 6.0 Ml | 11.9 | 0.600 | 173 |
| 36410 | Parkfield | 28/09/2004 | 6.0 Ml | 12.3 | 0.570 | 231 |
| 24386 | Northridge | 17/01/1994 | 6.4 Ml | 6.6 | 0.450 | 284 |
| 14125 | Inglewood | 17/05/2009 | 4.7 Mw | 21.8 | 0.290 | 334 |
| 57187 | Livemore80B | 26/01/1980 | 5.8 Ml | 20.4 | 0.280 | 378 |
| 36445 | Parkfield | 28/09/2004 | 6.0 Ml | 15.2 | 0.141 | 308 |
| 24283 | Northridge | 17/01/1994 | 6.4 Ml | 32.5 | 0.290 | 342 |
| 24592 | Northridge | 17/01/1994 | 6.4 Ml | 38.2 | 0.260 | 365 |
| 13068 | Chino Hills | 29/07/2008 | 5.4 Mw | 10.4 | 0.270 | 485 |
| 13873 | Chino Hills | 29/07/2008 | 5.4 Mw | 12.4 | 0.260 | 396 |
| CCC | Searles Valley | 3/06/2020 | 5.5 Mw | 11.5 | 0.260 | 432 |
| 89101 | Petrolia | 22/06/2019 | 5.6 Mw | 5.8 | 0.300 | 422 |
| KCO | Petrolia | 22/06/2019 | 5.6 Mw | 3.8 | 0.270 | -- |
| 12204 | PalmSprings86 | 08/07/1986 | 6.0 Mw | 33.7 | 0.240 | 447 |
| 36520 (Chn 1) | Parkfield | 28/09/2004 | 6.0 Ml | 7.7 | 0.29 0 | 467 |
| 36520 (Chn 3) | Parkfield | 28/09/2004 | 6.0 Ml | 7.7 | 0.290 | 467 |
| 24464 | Northridge | 17/01/1994 | 6.4 Ml | 18.5 | 0.320 | 464 |
| 57217 | CoyoteLake | 6/08/1979 | 5.7 Ml | 2.1 | 0.250 | 561 |
| 36437 (Chn 1) | Parkfield | 28/09/2004 | 6.0 Ml | 9.5 | 0.192 | 565 |
| 36437 (Chn 3) | Parkfield | 28/09/2004 | 6.0 Ml | 9.5 | 0.199 | 565 |
| 54171 (Chn 1) | ChalfantValley | 21/07/1986 | 6.4 Ml | 21 | 0.170 | 522 |
| 54171 (Chn 3) | ChalfantValley | 21/07/1986 | 6.4 Ml | 21 | 0.250 | 522 |
| CLC | Ridgecrest | 4/07/2019 | 6.4 Mw | 14.8 | 0.192 | 1464 |
| 57562 | Loma Prieta | 17/10/1989 | 6.9 Ml | 20.5 | 0.160 | 648 |
| 57563 (Chn 1) | Loma Prieta | 17/10/1989 | 6.9 Ml | 20.3 | 0.270 | 648 |
| 57563 (Chn 3) | Loma Prieta | 17/10/1989 | 6.9 Ml | 20.3 | 0.230 | 648 |
| Station Name | Origin Date | Magnitude | Distance (km) | PGA (g) | Vs30 |
|---|---|---|---|---|---|
| Aguascalientes | 19/11/2018 | 4.9 Ml | 11.8 | 0.360 | 188 |
| Aguascalientes | 19/11/2018 | 4.9 Ml | 11.8 | 0.267 | 188 |
| Chihuahua | 9/02/2008 | 5.5 Ml | 10.3 | 0.221 | 181 |
| Chihuahua | 9/02/2008 | 5.5 Ml | 10.3 | 0.299 | 181 |
| Chihuahua | 11/02/2008 | 5.1 Ml | 11.2 | 0.389 | 181 |
| Chihuahua | 11/02/2008 | 5.1 Ml | 11.2 | 0.488 | 181 |
| Chihuahua | 4/04/2010 | 7.2 Mw | 20.32 | 0.389 | 181 |
| Chihuahua | 4/04/2010 | 7.2 Mw | 20.32 | 0.249 | 181 |
| Planta Geotérmica | 22/02/2002 | 5.8 Ml | 7.46 | 0.403 | 205 |
| Planta Geotérmica | 22/02/2002 | 5.8 Ml | 7.46 | 0.238 | 205 |
| Planta Geotérmica | 13/02/2003 | 5.2 Ml | 6.2 | 0.220 | 205 |
| Planta Geotérmica | 13/01/2003 | 5.2 Ml | 6.2 | 0.192 | 205 |
| Planta Geotérmica | 22/08/2004 | 5.1 Ml | 2.29 | 0.360 | 205 |
| Planta Geotérmica | 22/08/2004 | 5.1 Ml | 2.29 | 0.267 | 205 |
| Planta Geotérmica | 24/05/2006 | 5.4 Mw | 3.75 | 0.430 | 205 |
| Planta Geotérmica | 24/05/2006 | 5.4 Mw | 3.75 | 0.366 | 205 |
| Planta Geotérmica | 19/09/2009 | 5.3 Ml | 3.02 | 0.316 | 205 |
| Planta Geotérmica | 19/09/2009 | 5.3 Ml | 3.02 | 0.342 | 205 |
| Planta Geotérmica | 30/12/2009 | 6.0 Ml | 7.93 | 0.216 | 205 |
| Planta Geotérmica | 30/12/2009 | 6.0 Ml | 7.93 | 0.178 | 205 |
| Planta Geotérmica | 4/04/2010 | 7.2 Mw | 12.27 | 0.286 | 205 |
| Planta Geotérmica | 4/04/2010 | 7.2 Mw | 12.27 | 0.288 | 205 |
| Tamaulipas | 9/02/2008 | 5.5 Ml | 13.83 | 0.258 | 217 |
| Tamaulipas | 9/02/2008 | 5.5 Ml | 13.83 | 0.279 | 217 |
| Tamaulipas | 12/02/2008 | 5.2 Ml | 15.33 | 0.442 | 217 |
| Tamaulipas | 12/02/2008 | 5.2 Ml | 15.33 | 0.390 | 217 |
| Tamaulipas | 19/02/2008 | 5.0 Ml | 14.57 | 0.320 | 217 |
| Tamaulipas | 19/02/2008 | 5.0 Ml | 14.57 | 0.278 | 217 |
| Volcán Cerro Prieto | 22/02/2002 | 5.8 Ml | 7.81 | 1.003 | 437 |
| Volcán Cerro Prieto | 22/02/2002 | 5.8 Ml | 7.81 | 1.003 | 437 |
| Housing Classification in Tijuana | HAZUS Housing Classification | ||
|---|---|---|---|
| Taxonomy | Description Typology | Taxonomy (1) | Description Typology |
| MCF/LWAL/DUC/H:1–3 | Confined masonry, ductile, 1–3 floors | RM2/LWAL/L(H:1–3) | Reinforced brick or block masonry, 1–3 floors |
| MCF/LWAL/DNO/H:1–3 | Confined masonry, non-ductile, 1–3 floors | ||
| MR/LWAL/DUC/H:1–3 | Reinforced masonry, ductile, 1–3 floors | ||
| MR/LWAL/DNO/H:1–3 | Reinforced masonry, non-ductile, 1–3 floors | ||
| MCF/LWAL/DUC/H:4–5 | Confined masonry, ductile, 4–5 floors | RM2/LWAL/M(H:4–7) | Reinforced brick or block masonry, 4–7 floors |
| MCF/LWAL/DNO/H:4–5 | Confined masonry, non-ductile, 4–5 floors | ||
| MR/LWAL/DUC/H:4–5 | Reinforced masonry, ductile, 4–5 floors | ||
| MR/LWAL/DNO/H:4–5 | Reinforced masonry, non-ductile, 4–5 floors | ||
| Housing | Expected Value | Damage State | Probability of Exceedance for Code Seismic Design Level (%) | ||
|---|---|---|---|---|---|
| Low | Moderate | High | |||
| RM2/L (1–3 floors) | 0.5 g of PGA | DS1 | 66 | 38 | 18 |
| DS2 | 40 | 11 | 2 | ||
| DS3 | 30 | 6 | 0.8 | ||
| DS4 | 20 | 2 | 0.2 | ||
| RM2/M (4–7 floors) | 0.5 g of SA (T = 0.5 s) | DS1 | 100 | 80 | 18 |
| DS2 | 77 | 4 | 0 | ||
| DS3 | 50 | 0.3 | 0 | ||
| DS4 | 16 | 0 | 0 | ||
| Housing | Expected Value IM | Loss Rate for Code Seismic Design Level (%) | ||
|---|---|---|---|---|
| Low | Moderate | High | ||
| RM2/L (1–3 floors) | 0.5 g of PGA | 30 | 7 | 1.8 |
| RM2/M (4–7 floors) | 0.5 g of SA (T = 0.5 s) | 44 | 5 | 0.9 |
| Número de Pisos Number of Floors | Expected Value IM | Masonry House | Loss Rate (%) |
|---|---|---|---|
| 1 floor | 0.5 g of PGA | RM2/L/L | 30 |
| RM2/L/M | 7 | ||
| RM2/L/H | 1.8 | ||
| RM2L/L (Cardona et al.) [37] | 19.7 | ||
| RM2L/M (Cardona et al.) [37] | 17.4 | ||
| RM2L/H (Cardona et al.) [37] | 14.4 | ||
| MR/LWAL + DUL (Romão et al.) [54] | 9.7 | ||
| MR/LWAL + DUM (Romão et al.) [54] | 4.7 | ||
| MR/LWAL + DUH (Romão et al.) [54] | 1.8 | ||
| 2 floors | 0.5 g of SA (T = 0.30 s) | RM2/L/L | 30 |
| RM2/L/M | 3.4 | ||
| RM2/L/H | 0.3 | ||
| MR/LWAL + DUL (Romão et al.) [54] | 5.3 | ||
| MR/LWAL + DUM (Romão et al.) [54] | 3.5 | ||
| MR/LWAL + DUH (Romão et al.) [54] | 1.5 | ||
| 3–5 floors | 0.5 g of SA (T = 0.60 s) | RM2/M/L | 52 |
| RM2/M/M | 6 | ||
| RM2/M/H | 1 | ||
| RM2M/L (Cardona et al.) [37] | 20.1 | ||
| RM2M/M (Cardona et al.) [37] | 16.4 | ||
| RM2M/H (Cardona et al.) [37] | 11.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Díaz, F.-D.; González-Durán, M.; Flores, D.-L.; López-Lambraño, A.; Mena-Hernández, U.; Villada-Canela, M. Development of Fragility and Vulnerability Functions for Reinforced Masonry Structures in Mexico: A Case Study. Appl. Sci. 2023, 13, 10634. https://doi.org/10.3390/app131910634
Díaz F-D, González-Durán M, Flores D-L, López-Lambraño A, Mena-Hernández U, Villada-Canela M. Development of Fragility and Vulnerability Functions for Reinforced Masonry Structures in Mexico: A Case Study. Applied Sciences. 2023; 13(19):10634. https://doi.org/10.3390/app131910634
Chicago/Turabian StyleDíaz, Francisco-Damián, Mario González-Durán, Dora-Luz Flores, Alvaro López-Lambraño, Ulises Mena-Hernández, and Mariana Villada-Canela. 2023. "Development of Fragility and Vulnerability Functions for Reinforced Masonry Structures in Mexico: A Case Study" Applied Sciences 13, no. 19: 10634. https://doi.org/10.3390/app131910634
APA StyleDíaz, F.-D., González-Durán, M., Flores, D.-L., López-Lambraño, A., Mena-Hernández, U., & Villada-Canela, M. (2023). Development of Fragility and Vulnerability Functions for Reinforced Masonry Structures in Mexico: A Case Study. Applied Sciences, 13(19), 10634. https://doi.org/10.3390/app131910634








