Short-Term Forecasting of Ozone Concentration in Metropolitan Lima Using Hybrid Combinations of Time Series Models
Abstract
:1. Introduction
- We improve the efficiency and accuracy of one-hour-ahead ozone concentration forecasting using a proposed hybrid combination of time series models based on the seasonal trend decomposition technique and various standard time series models.
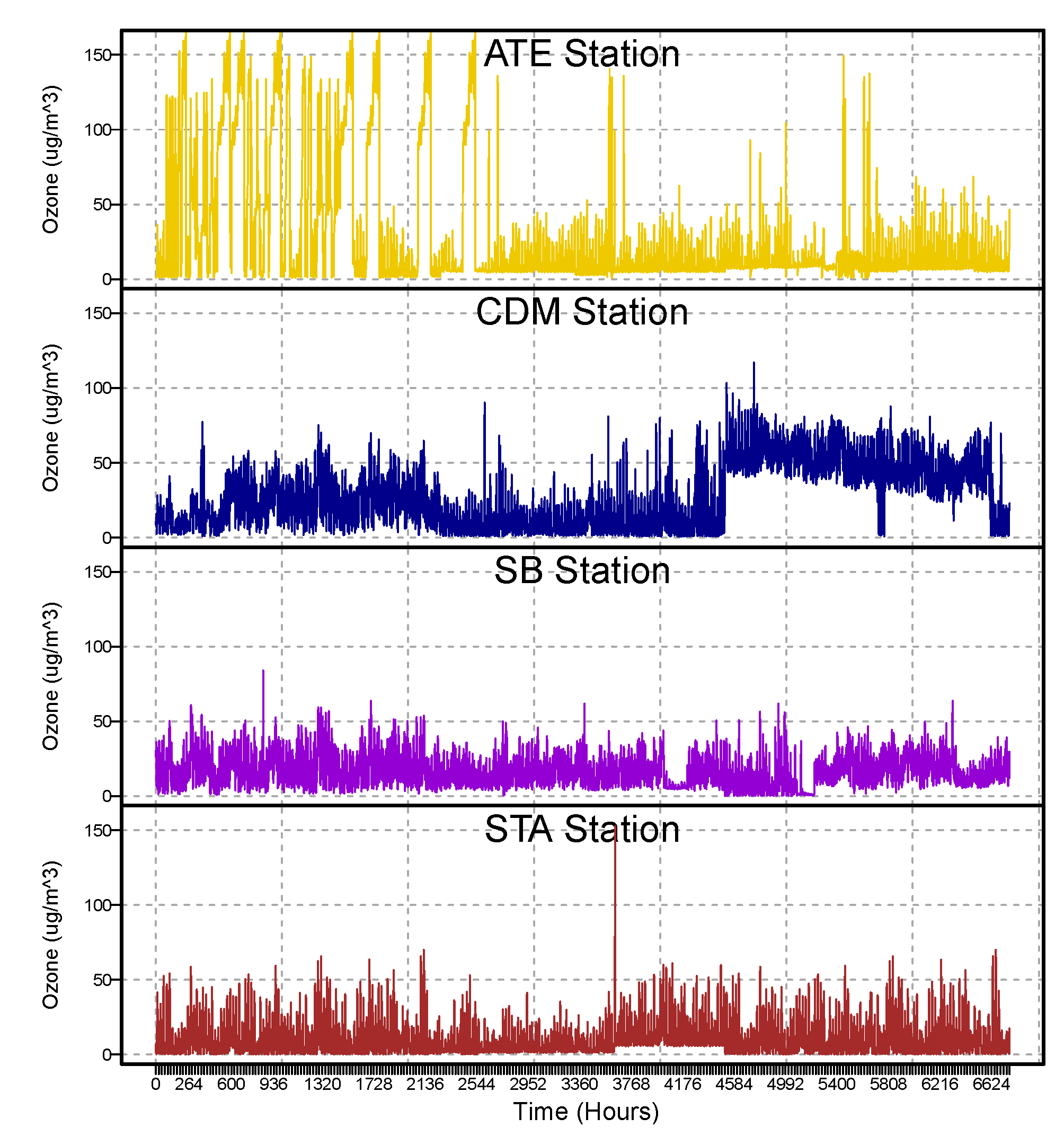
- We apply the seasonal trend decomposition method of the ozone concentration database in four districts—ATE, Campo de Marte (CDM), San Borja (SB), and Santa Anita (STA)—with severe episodes of ozone contamination between 2017 and 2019.
- We evaluate the performance of the proposed hybrid combination of time series models, by determining five different accuracy mean errors: two relative mean errors, two absolute mean errors, and one correlation measure, such as root mean square error, root mean square percentage error, mean absolute error, and mean absolute percentage error; a statistical test, the Diebold–Mariano test; and a visual evaluation.
- In this study, the results of the final best combination model are compared with the best model proposed in the literature as well as the considered baseline models and the comparative results are recorded. Based on these results, the proposed final best combination model from this work is highly accurate and efficient compared to the best models reported in the literature.
- We present a methodological proposal applicable to the environmental management system in order to mitigate ozone pollution aimed at the stakeholders of the national air quality program.
- Finally, the current work uses only the four district datasets in Lima, Peru. This can be extended to other districts of Lima, other regions of Peru, and even the world level to evaluate the performance of the proposed hybrid time series modeling and forecasting technique.
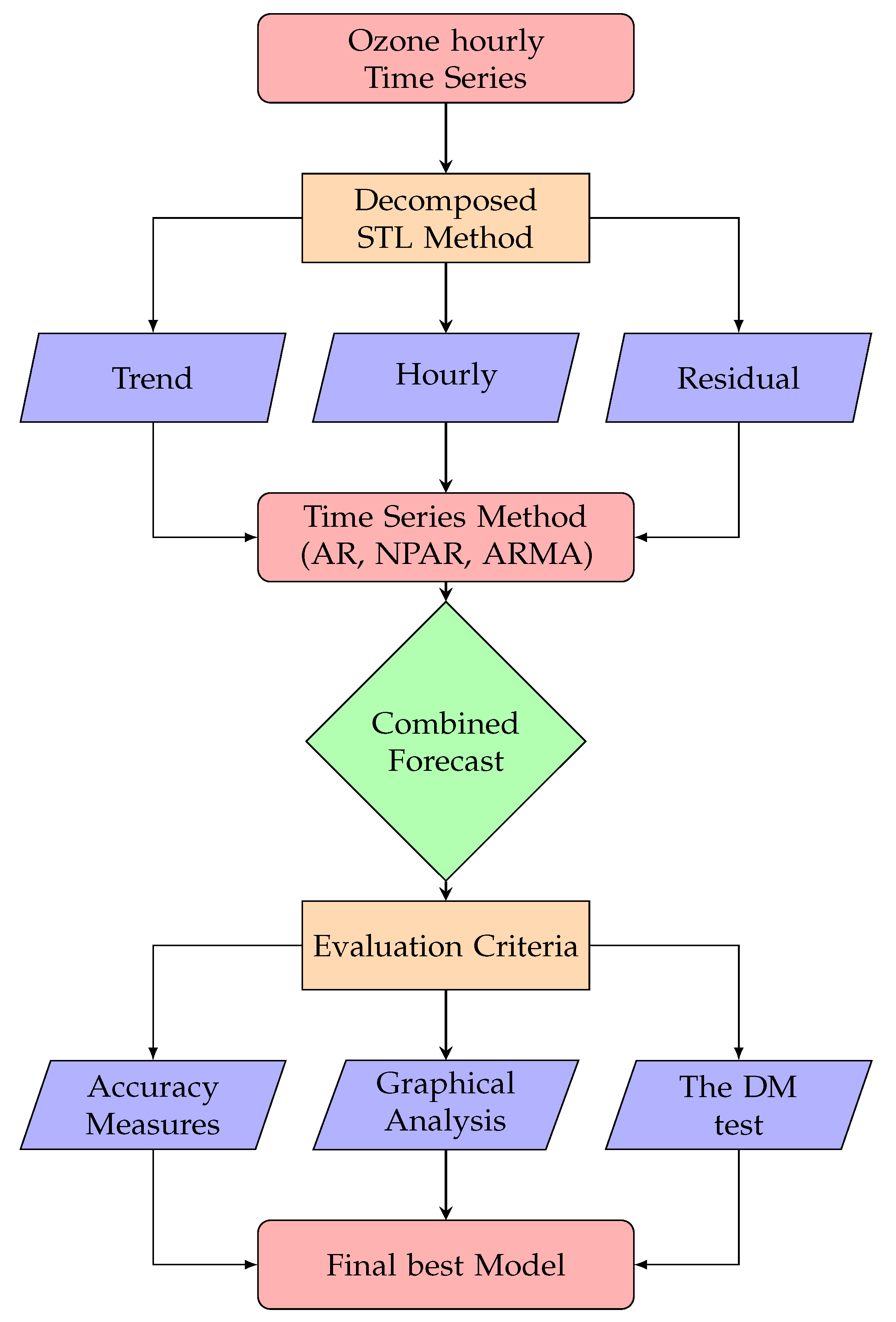
2. The Proposed Hybrid Time Series Forecasting Methodology
2.1. Seasonal Trend Decomposition Method
2.2. Modeling the Decomposed Sub-Series
2.2.1. Autoregressive Model
2.2.2. Nonlinear Autoregressive Model
2.2.3. Autoregressive Moving Average Model
2.3. Accuracy Measures
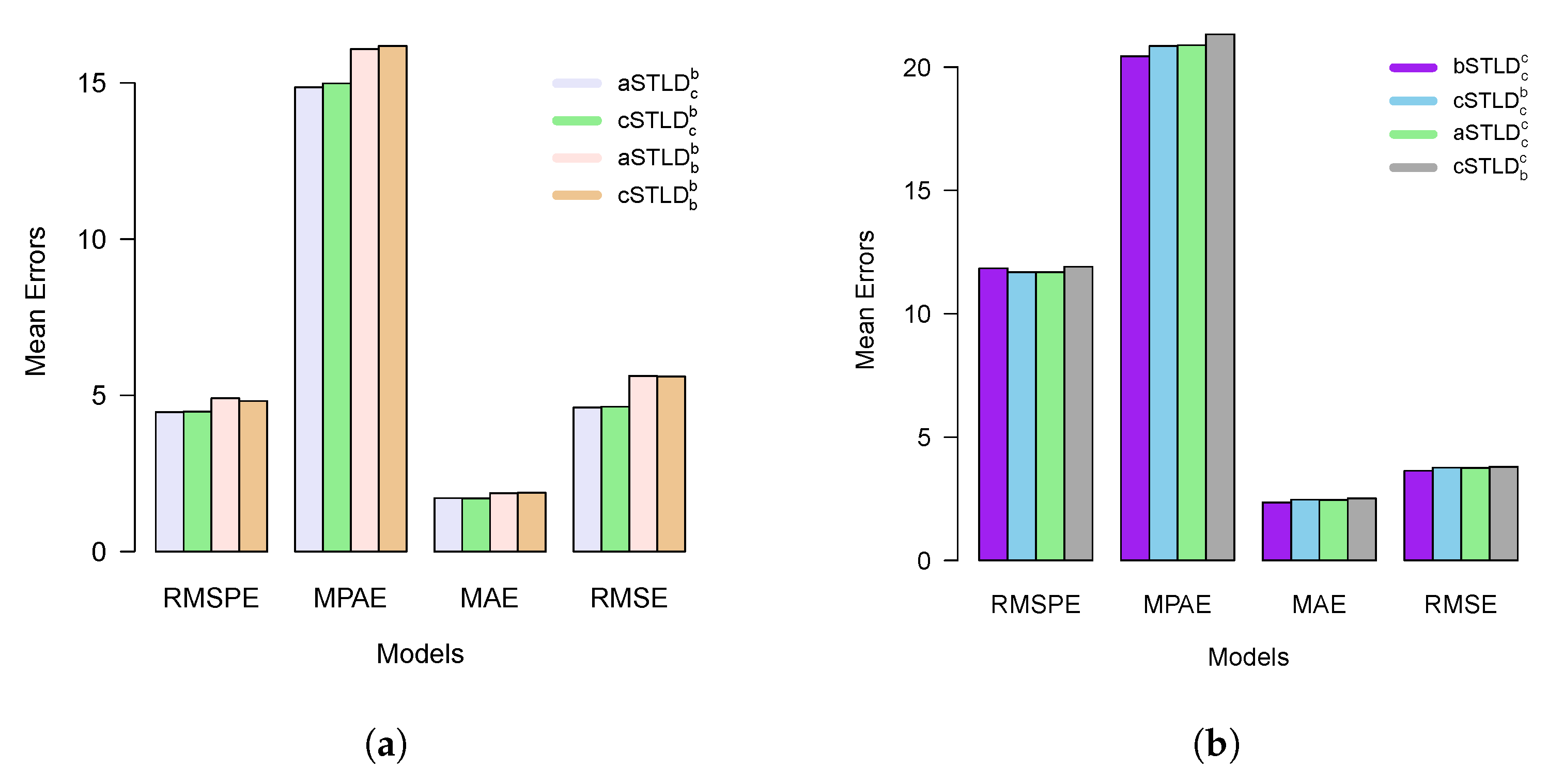
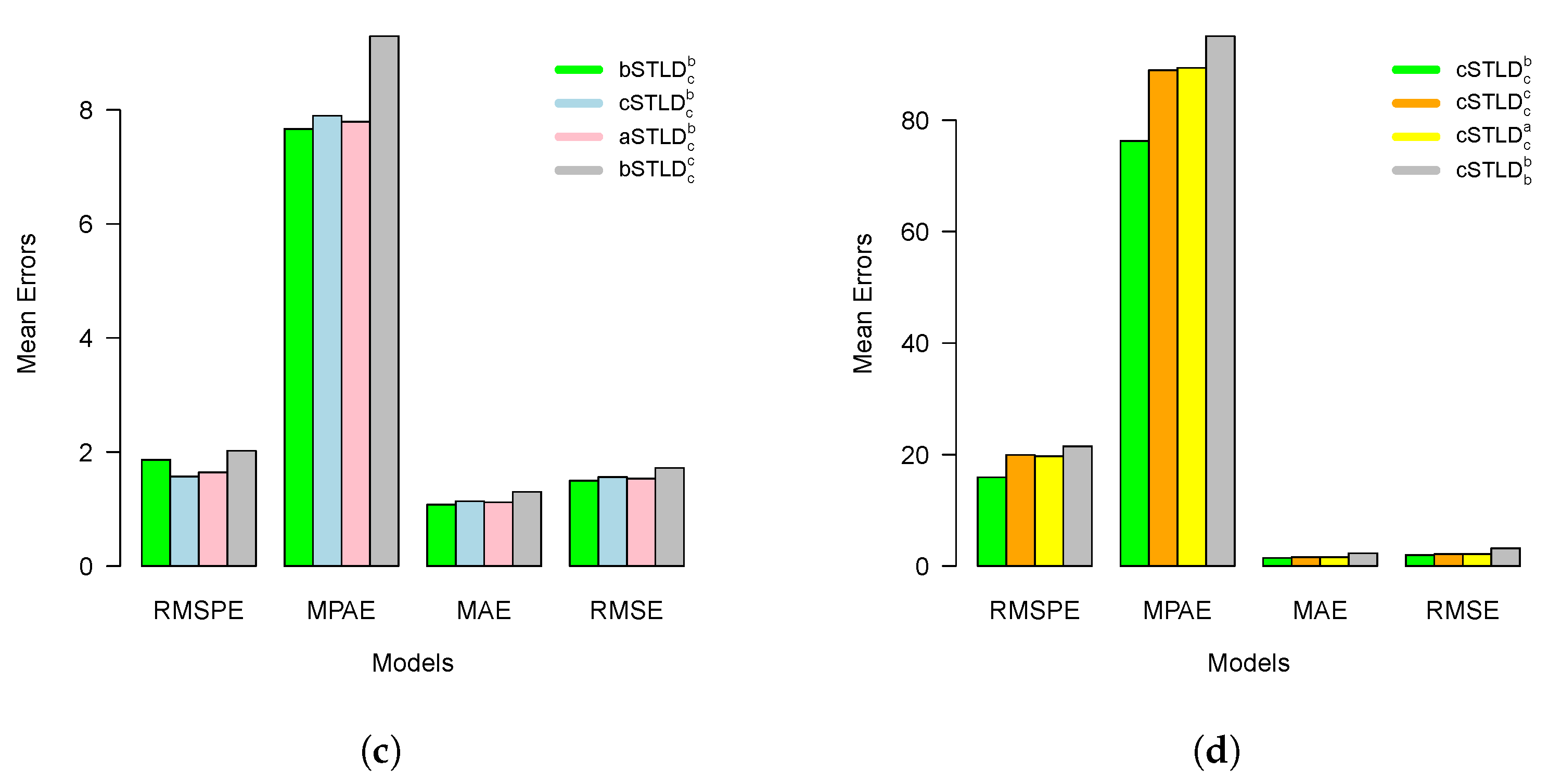
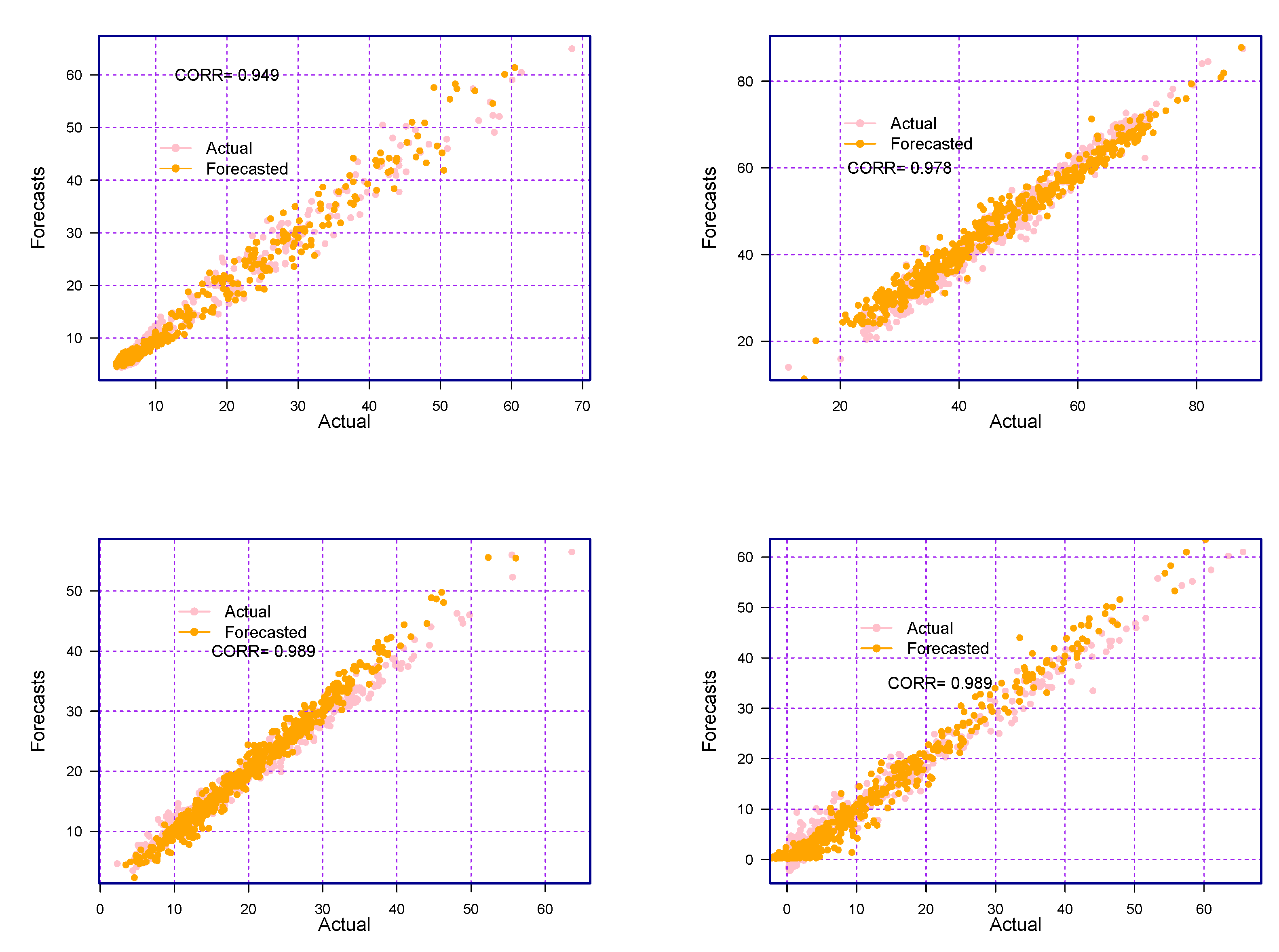
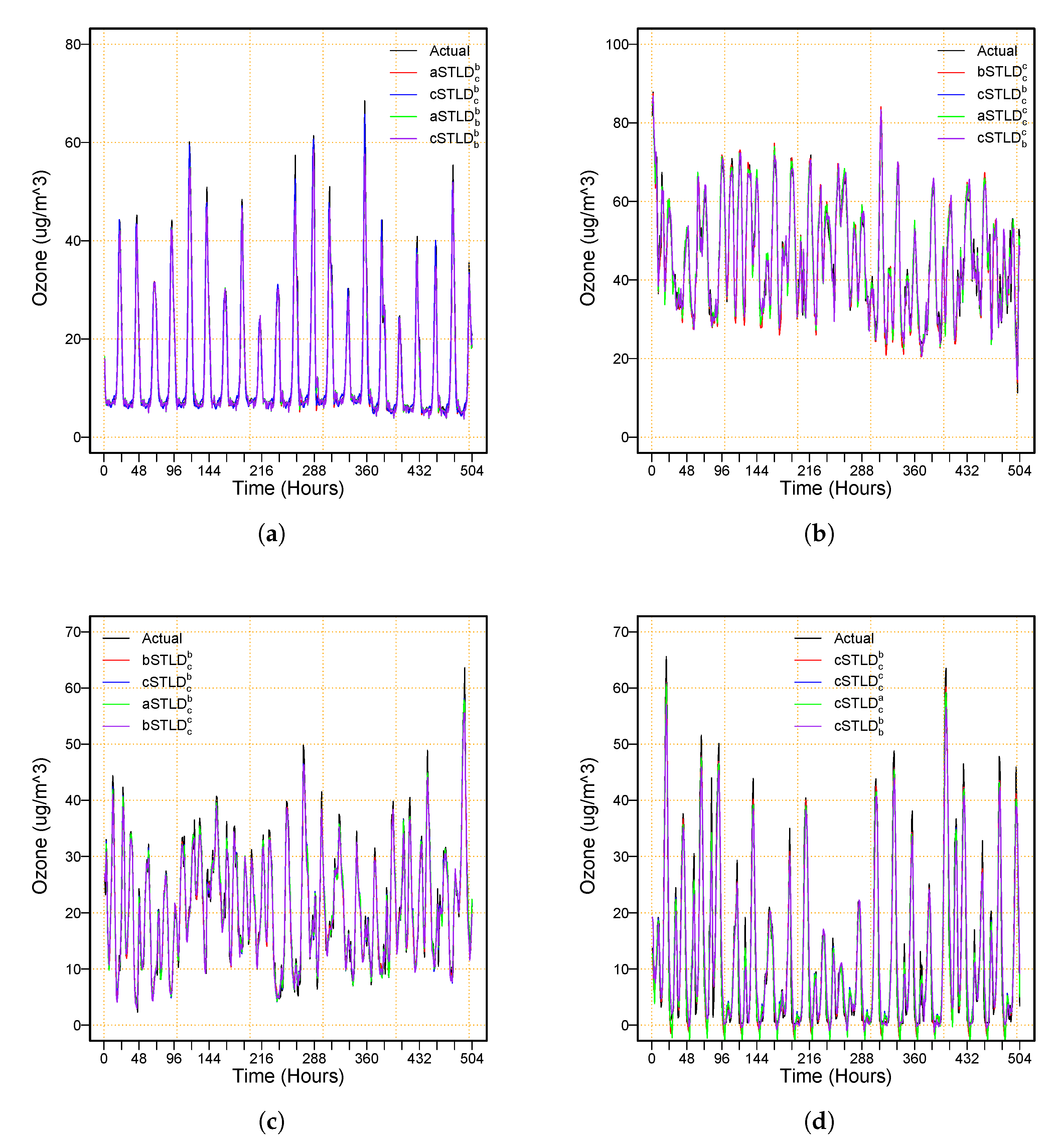
3. Case Study Results
Metropolitan Lima Stations
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, T.; Xue, L.; Feng, Z.; Dai, J.; Zhang, Y.; Tan, Y. Ground-level ozone pollution in China: A synthesis of recent findings on influencing factors and impacts. Environ. Res. Lett. 2022, 17, 063003. [Google Scholar] [CrossRef]
- Feng, Z.; Xu, Y.; Kobayashi, K.; Dai, L.; Zhang, T.; Agathokleous, E.; Calatayud, V.; Paoletti, E.; Mukherjee, A.; Agrawal, M.; et al. Ozone pollution threatens the production of major staple crops in East Asia. Nat. Food 2022, 3, 47–56. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Huang, J.; Li, G.; Wang, W.; Wang, K.; Wang, J.; Wei, C.; Li, Y.; Deng, F.; Baccarelli, A.A.; et al. Ozone pollution and hospital admissions for cardiovascular events. Eur. Heart J. 2023, 44, 1622–1632. [Google Scholar] [CrossRef]
- Lei, Y.; Yue, X.; Liao, H.; Zhang, L.; Zhou, H.; Tian, C.; Gong, C.; Ma, Y.; Cao, Y.; Seco, R.; et al. Global perspective of drought impacts on ozone pollution episodes. Environ. Sci. Technol. 2022, 56, 3932–3940. [Google Scholar] [CrossRef] [PubMed]
- Cabello-Torres, R.J.; Estela, M.A.P.; Sánchez-Ccoyllo, O.; Romero-Cabello, E.A.; Ávila, F.F.G.; Castañeda-Olivera, C.A.; Valdiviezo-Gonzales, L.; Eulogio, C.E.Q.; De La Cruz, A.R.H.; López-Gonzales, J.L. Statistical modeling approach for pm10 prediction before and during confinement by COVID-19 in South Lima, Perú. Sci. Rep. 2022, 12, 16737. [Google Scholar] [CrossRef] [PubMed]
- Ding, J.; Dai, Q.; Fan, W.; Lu, M.; Zhang, Y.; Han, S.; Feng, Y. Impacts of meteorology and precursor emission change on O3 variation in Tianjin, China from 2015 to 2021. J. Environ. Sci. 2023, 126, 506–516. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.; Lin, H. A novel optimal-hybrid model for daily air quality index prediction considering air pollutant factors. Sci. Total Environ. 2019, 683, 808–821. [Google Scholar] [CrossRef]
- Fu, H.; Zhang, Y.; Liao, C.; Mao, L.; Wang, Z.; Hong, N. Investigating PM 2.5 responses to other air pollutants and meteorological factors across multiple temporal scales. Sci. Rep. 2020, 10, 15639. [Google Scholar] [CrossRef]
- Ewusie, J.E.; Soobiah, C.; Blondal, E.; Beyene, J.; Thabane, L.; Hamid, J.S. Methods, applications and challenges in the analysis of interrupted time series data: A scoping review. J. Multidiscip. Healthc. 2020, 13, 411–423. [Google Scholar] [CrossRef]
- Li, W.; Jiang, X. Prediction of air pollutant concentrations based on TCN-BiLSTM-DMAttention with STL decomposition. Sci. Rep. 2023, 13, 4665. [Google Scholar] [CrossRef]
- Tudor, C. Ozone pollution in London and Edinburgh: Spatiotemporal characteristics, trends, transport and the impact of COVID-19 control measures. Heliyon 2022, 8, e11384. [Google Scholar] [CrossRef]
- Hong, J.; Wang, W.; Bai, Z.; Bian, J.; Tao, M.; Konopka, P.; Ploeger, F.; Müller, R.; Wang, H.; Zhang, J.; et al. The Long-Term Trends and Interannual Variability in Surface Ozone Levels in Beijing from 1995 to 2020. Remote Sens. 2022, 14, 5726. [Google Scholar] [CrossRef]
- Chang, S.W.; Chang, C.L.; Li, L.T.; Liao, S.W. Reinforcement learning for improving the accuracy of pm 2.5 pollution forecast under the neural network framework. IEEE Access 2019, 8, 9864–9874. [Google Scholar] [CrossRef]
- Gemst, M.V. Forecasting Stock Index Volatility—A Comparison of Models. Ph.D. Thesis, Universidade Nova de Lisboa, Lisbon, Portugal, 2020. [Google Scholar]
- Iftikhar, H.; Bibi, N.; Canas Rodrigues, P.; López-Gonzales, J.L. Multiple Novel Decomposition Techniques for Time Series Forecasting: Application to Monthly Forecasting of Electricity Consumption in Pakistan. Energies 2023, 16, 2579. [Google Scholar] [CrossRef]
- Iftikhar, H.; Turpo-Chaparro, J.E.; Canas Rodrigues, P.; López-Gonzales, J.L. Forecasting Day-Ahead Electricity Prices for the Italian Electricity Market Using a New Decomposition—Combination Technique. Energies 2022, 15, 3607. [Google Scholar] [CrossRef]
- Ghoneim, O.A.; Manjunatha, B.R. Forecasting of ozone concentration in smart city using deep learning. In Proceedings of the 2017 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Udupi, India, 13–16 September 2017; pp. 1320–1326. [Google Scholar]
- Juarez, E.K.; Petersen, M.R. A comparison of machine learning methods to forecast tropospheric ozone levels in Delhi. Atmosphere 2021, 13, 46. [Google Scholar] [CrossRef]
- Chaloulakou, A.; Saisana, M.; Spyrellis, N. Comparative assessment of neural networks and regression models for forecasting summertime ozone in Athens. Sci. Total Environ. 2003, 313, 1–13. [Google Scholar] [CrossRef]
- Borhani, F.; Ehsani, A.H.; Hosseini Shekarabi, H.S. Prediction and spatiotemporal analysis of atmospheric Fine Particles and their effect on temperature and vegetation cover in Iran using Exponential Smoothing approach in Python. J. Nat. Environ. 2023, 76, 325–344. [Google Scholar]
- Tang, H.; Bhatti, U.A.; Li, J.; Marjan, S.; Baryalai, M.; Assam, M.; Ghadi, Y.Y.; Mohamed, H.G. A New Hybrid Forecasting Model Based on Dual Series Decomposition with Long-Term Short-Term Memory. Int. J. Intell. Syst. 2023, 2023, 9407104. [Google Scholar] [CrossRef]
- Romero, Y.; Diaz, C.; Meldrum, I.; Velasquez, R.A.; Noel, J. Temporal and spatial analysis of traffic–Related pollutant under the influence of the seasonality and meteorological variables over an urban city in Peru. Heliyon 2020, 6, e04029. [Google Scholar] [CrossRef]
- Carbo-Bustinza, N.; Belmonte, M.; Jimenez, V.; Montalban, P.; Rivera, M.; Martínez, F.G.; Mohamed, M.M.H.; De La Cruz, A.R.H.; da Costa, K.; López-Gonzales, J.L. A machine learning approach to analyse ozone concentration in metropolitan area of Lima, Peru. Sci. Rep. 2022, 12, 22084. [Google Scholar] [CrossRef] [PubMed]
- Leon, C.A.M.; Felix, M.F.M.; Olivera, C.A.C. Influence of Social Confinement by COVID-19 on Air Quality in the District of San Juan de Lurigancho in Lima, Perù. Chem. Eng. Trans. 2022, 91, 475–480. [Google Scholar]
- Van Buuren, S.; Oudshoorn, C.G. Multivariate Imputation by Chained Equations; Netherlands Organization for Applied Scientific Research (TNO): The Hague, The Netherlands, 2000. [Google Scholar]
- Cleveland, R.B.; Cleveland, W.S.; McRae, J.E.; Terpenning, I. STL: A seasonal-trend decomposition. J. Off. Stat. 1990, 6, 3–73. [Google Scholar]
- Iftikhar, H.; Zafar, A.; Turpo-Chaparro, J.E.; Canas Rodrigues, P.; López-Gonzales, J.L. Forecasting Day-Ahead Brent Crude Oil Prices Using Hybrid Combinations of Time Series Models. Mathematics 2023, 11, 3548. [Google Scholar] [CrossRef]
- Iftikhar, H.; Turpo-Chaparro, J.E.; Canas Rodrigues, P.; López-Gonzales, J.L. Day-Ahead Electricity Demand Forecasting Using a Novel Decomposition Combination Method. Energies 2023, 16, 6675. [Google Scholar] [CrossRef]
- Davis, P.J.B.R.A. Introduction to Time Series and Forecasting; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Wasserman, L. All of Nonparametric Statistics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice; OTexts: Melbourne, Australia, 2018. [Google Scholar]
- Iftikhar, H. Modeling and Forecasting Complex Time Series: A Case of Electricity Demand. Master’s, Thesis, Quaid-i-Azam University, Islamabad, Pakistan, 2018. Available online: https://www.researchgate.net/publication/372103958_Modeling_and_Forecasting_Complex_Time_Series_A_Case_of_Electricity_Demand (accessed on 28 July 2023).
- Shah, I.; Iftikhar, H.; Ali, S.; Wang, D. Short-Term Electricity Demand Forecasting Using Components Estimation Technique. Energies 2019, 12, 2532. [Google Scholar] [CrossRef]
- Shah, I.; Iftikhar, H.; Ali, S. Modeling and Forecasting Medium-Term Electricity Consumption Using Component Estimation Technique. Forecasting 2020, 2, 9. [Google Scholar] [CrossRef]
- Shah, I.; Iftikhar, H.; Ali, S. Modeling and Forecasting Electricity Demand and Prices: A Comparison of Alternative Approaches. J. Math. 2022, 2022, 3581037. [Google Scholar] [CrossRef]
- Diebold, F.; Mariano, R. Comparing predictive accuracy. J. Bus. Econ. Stat. 1995, 13, 253–263. [Google Scholar]
- Iftikhar, H.; Khan, M.; Khan, Z.; Khan, F.; Alshanbari, H.M.; Ahmad, Z. A Comparative Analysis of Machine Learning Models: A Case Study in Predicting Chronic Kidney Disease. Sustainability 2023, 15, 2754. [Google Scholar] [CrossRef]
- Iftikhar, H.; Khan, M.; Khan, M.S.; Khan, M. Short-Term Forecasting of Monkeypox Cases Using a Novel Filtering and Combining Technique. Diagnostics 2023, 13, 1923. [Google Scholar] [CrossRef] [PubMed]
- Alshanbari, H.M.; Iftikhar, H.; Khan, F.; Rind, M.; Ahmad, Z.; El-Bagoury, A.A.A.H. On the Implementation of the Artificial Neural Network Approach for Forecasting Different Healthcare Events. Diagnostics 2023, 13, 1310. [Google Scholar] [CrossRef] [PubMed]
- Dickey, D.A.; Fuller, W.A. Distribution of the estimators for autoregressive time series with a unit root. J. Am. Stat. Assoc. 1979, 74, 427–431. [Google Scholar] [CrossRef]
- Kawano, N.; Nagashima, T.; Sugata, S. Changes in the seasonal cycle of surface ozone over Japan during 1980–2015. Atmos. Environ. 2022, 279, 119108. [Google Scholar] [CrossRef]
- Leite Coelho da Silva, F.; da Costa, K.; Canas Rodrigues, P.; Salas, R.; López-Gonzales, J.L. Statistical and artificial neural networks models for electricity consumption forecasting in the Brazilian industrial sector. Energies 2022, 15, 588. [Google Scholar] [CrossRef]
- Gonzales, J.L.L.; Calili, R.F.; Souza, R.C.; Coelho da Silva, F.L. Simulation of the energy efficiency auction prices in Brazil. Renew. Energy Power Qual. J. 2016, 1, 574–579. [Google Scholar] [CrossRef]
- López-Gonzales, J.L.; Castro Souza, R.; Leite Coelho da Silva, F.; Carbo-Bustinza, N.; Ibacache-Pulgar, G.; Calili, R.F. Simulation of the Energy Efficiency Auction Prices via the Markov Chain Monte Carlo Method. Energies 2020, 13, 4544. [Google Scholar] [CrossRef]
- da Silva, K.L.S.; López-Gonzales, J.L.; Turpo-Chaparro, J.E.; Tocto-Cano, E.; Rodrigues, P.C. Spatio-temporal visualization and forecasting of PM 10 in the Brazilian state of Minas Gerais. Sci. Rep. 2023, 13, 3269. [Google Scholar] [CrossRef]
- Jeldes, N.; Ibacache-Pulgar, G.; Marchant, C.; López-Gonzales, J.L. Modeling air pollution using partially varying coefficient models with heavy tails. Mathematics 2022, 10, 3677. [Google Scholar] [CrossRef]
- Quispe, K.; Martínez, M.; da Costa, K.; Romero Giron, H.; Via y Rada Vittes, J.F.; Mantari Mincami, L.D.; Hadi Mohamed, M.M.; Huamán De La Cruz, A.R.; López-Gonzales, J.L. Solid Waste Management in Peru’s Cities: A Clustering Approach for an Andean District. Appl. Sci. 2023, 13, 1646. [Google Scholar] [CrossRef]
- Orrego Granados, D.; Ugalde, J.; Salas, R.; Torres, R.; López-Gonzales, J.L. Visual-Predictive Data Analysis Approach for the Academic Performance of Students from a Peruvian University. Appl. Sci. 2022, 12, 11251. [Google Scholar] [CrossRef]
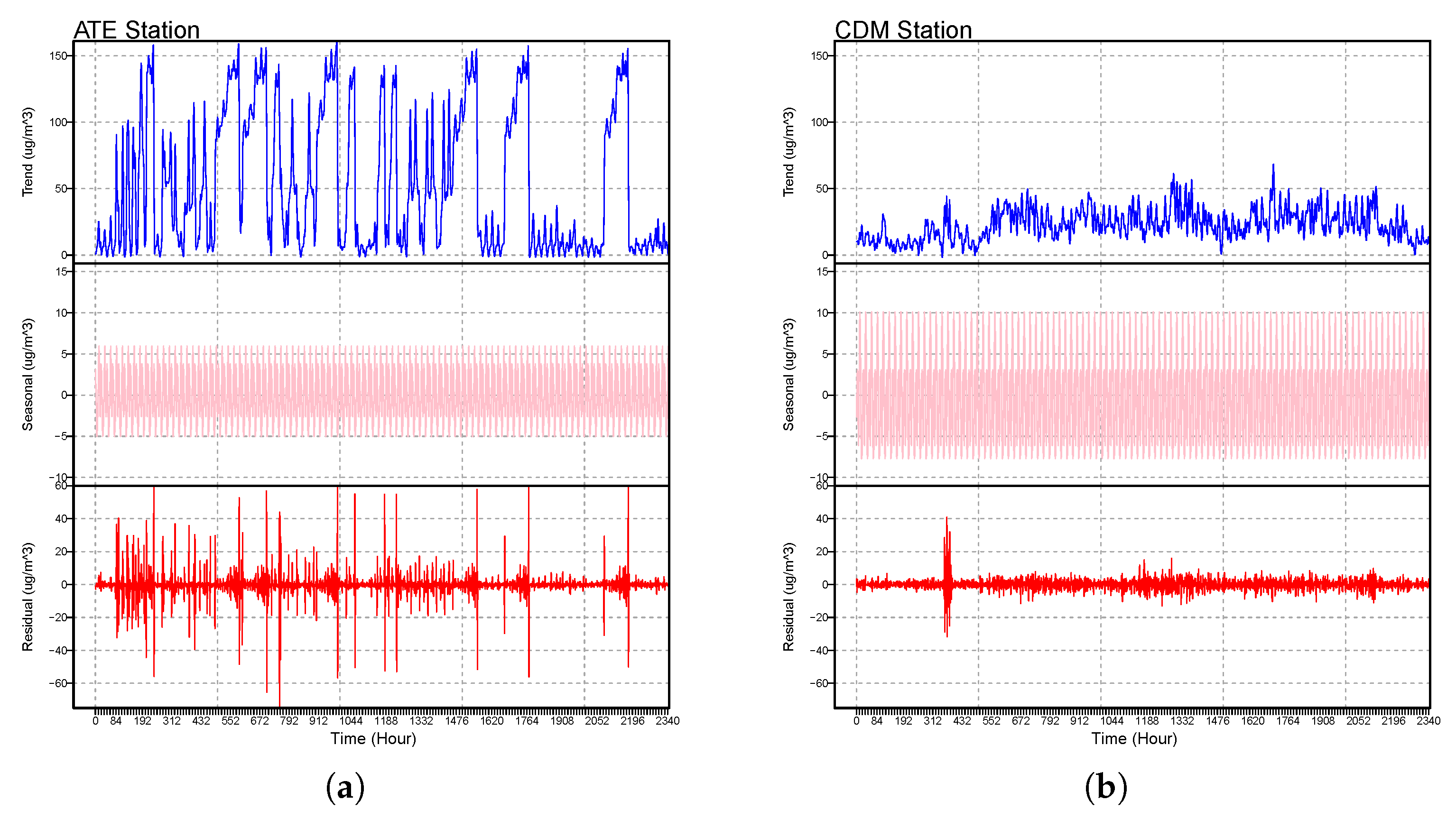
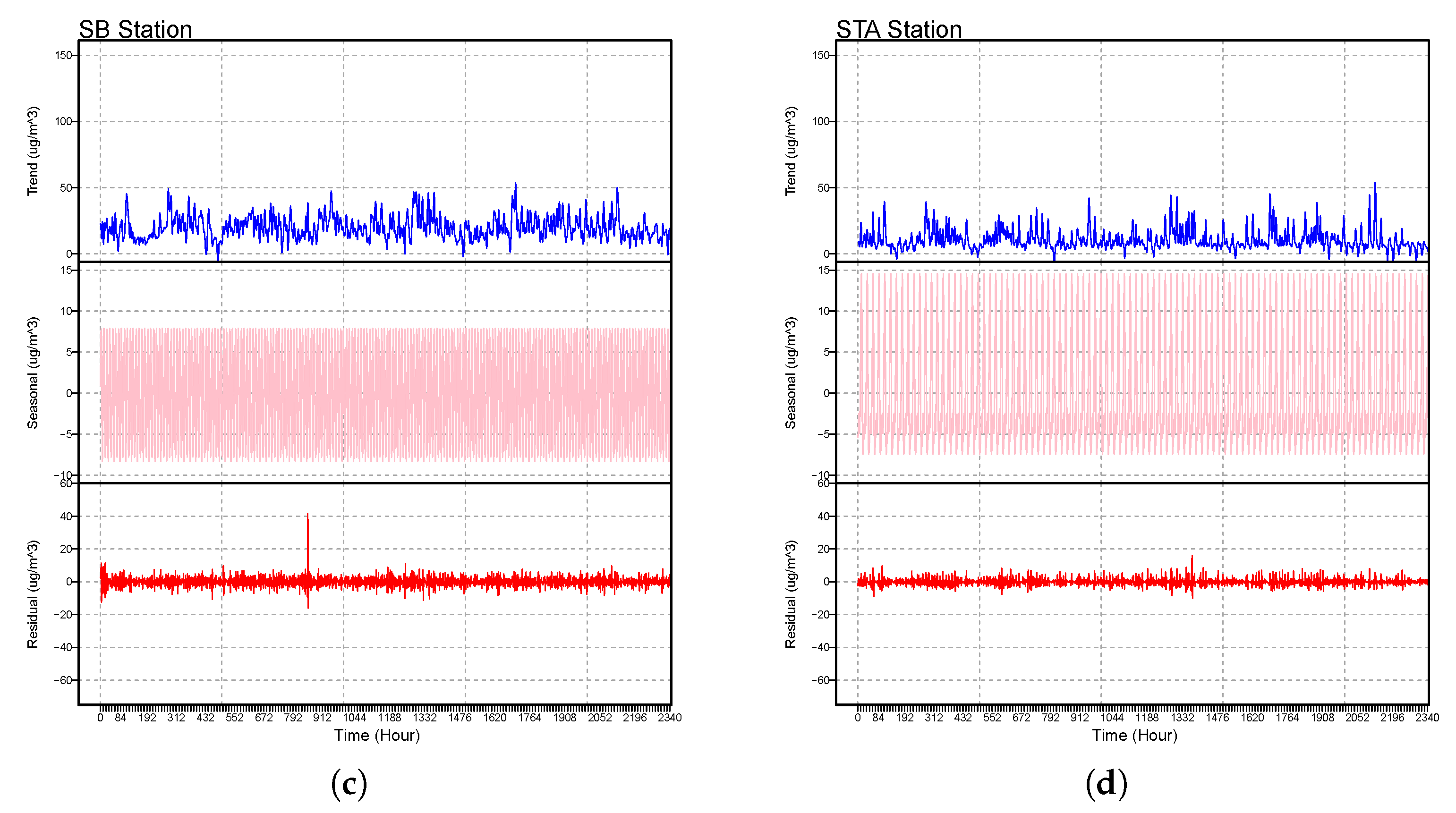

| Station | ATE | CDM | SB | STA |
|---|---|---|---|---|
| Total hours | 6768 | 6768 | 6768 | 6768 |
| Available hours | 6654 | 6634 | 6614 | 6613 |
| Imputed hours | 114 | 134 | 154 | 155 |
| Imputed% | 1.68% | 1.98% | 2.27% | 2.29% |
| Measure | Min | Q1 | Median | Mean | Mode | Var | S.D | Skewness | Kurtosis | Q3 | Max | ADF (Statistic) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ATE | 0.80 | 5.50 | 8.50 | 28.36 | 5.20 | 1606.08 | 40.08 | 1.89 | 2.30 | 29.30 | 165.80 | −8.61 |
| log(ATE) | −0.22 | 1.70 | 2.14 | 2.55 | 1.65 | 1.50 | 1.23 | 0.49 | −0.54 | 3.38 | 5.11 | −8.70 |
| CDM | 0.80 | 8.98 | 24.50 | 28.13 | 1.00 | 454.02 | 21.31 | 0.53 | −0.67 | 44.03 | 117.10 | −6.03 |
| log(CDM) | −0.22 | 2.19 | 3.20 | 2.86 | 0.00 | 1.37 | 1.17 | −0.89 | −0.19 | 3.78 | 4.76 | −6.53 |
| SB | 0.20 | 8.30 | 15.10 | 17.09 | 6.50 | 122.05 | 11.05 | 0.83 | 0.51 | 24.00 | 83.90 | −13.02 |
| log(SB) | −1.61 | 2.12 | 2.71 | 2.56 | 1.87 | 0.78 | 0.88 | −1.46 | 3.38 | 3.18 | 4.43 | −10.35 |
| STA | 0.10 | 1.80 | 6.20 | 10.56 | 0.40 | 149.09 | 12.21 | 1.94 | 5.54 | 14.80 | 152.60 | −16.17 |
| log(STA) | −2.30 | 0.59 | 1.82 | 1.59 | −0.92 | 2.02 | 1.42 | −0.44 | −0.61 | 2.69 | 5.03 | −14.38 |
| Station | ATE | Campo de Marte | San Borja | Santa Anita | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S.No | Models | RMSE | RMSPE | MAE | MAPE | CC | RMSE | RMSPE | MAE | MAPE | CC | RMSE | RMSPE | MAE | MAPE | CC | RMSE | RMSPE | MAE | MAPE | CC |
| 1 | STLD | 5.529 | 5.414 | 2.209 | 20.827 | 0.932 | 5.073 | 16.53 | 3.329 | 25.735 | 0.957 | 2.115 | 2.600 | 1.587 | 11.217 | 0.975 | 5.279 | 40.464 | 3.958 | 196.406 | 0.916 |
| 2 | STLD | 5.699 | 4.828 | 2.076 | 18.005 | 0.921 | 5.145 | 16.406 | 3.354 | 24.908 | 0.955 | 2.081 | 2.417 | 1.547 | 10.817 | 0.976 | 5.338 | 40.070 | 3.959 | 188.568 | 0.913 |
| 3 | STLD | 4.675 | 4.628 | 1.913 | 18.257 | 0.947 | 3.993 | 12.117 | 2.719 | 22.96 | 0.973 | 1.818 | 1.854 | 1.376 | 9.768 | 0.982 | 3.958 | 33.264 | 2.965 | 158.543 | 0.954 |
| 4 | STLD | 5.410 | 4.976 | 1.950 | 17.562 | 0.937 | 4.889 | 16.474 | 3.136 | 25.196 | 0.96 | 1.974 | 2.497 | 1.448 | 10.279 | 0.979 | 5.224 | 36.786 | 3.878 | 179.823 | 0.917 |
| 5 | STLD | 5.622 | 4.906 | 1.871 | 16.081 | 0.923 | 4.921 | 16.336 | 3.108 | 24.118 | 0.959 | 1.973 | 2.333 | 1.439 | 10.174 | 0.979 | 5.310 | 36.972 | 3.907 | 172.380 | 0.914 |
| 6 | STLD | 4.611 | 4.464 | 1.711 | 14.862 | 0.949 | 3.774 | 11.89 | 2.504 | 21.293 | 0.976 | 1.535 | 1.644 | 1.118 | 7.793 | 0.987 | 3.909 | 30.357 | 2.937 | 148.290 | 0.955 |
| 7 | STLD | 5.529 | 5.414 | 2.209 | 20.827 | 0.932 | 4.717 | 16.474 | 2.848 | 26.253 | 0.963 | 2.115 | 2.600 | 1.587 | 11.217 | 0.975 | 5.277 | 40.431 | 3.959 | 197.407 | 0.916 |
| 8 | STLD | 5.699 | 4.828 | 2.076 | 18.005 | 0.921 | 4.685 | 16.271 | 2.764 | 24.623 | 0.963 | 2.081 | 2.417 | 1.547 | 10.817 | 0.976 | 5.337 | 40.071 | 3.963 | 190.219 | 0.913 |
| 9 | STLD | 4.675 | 4.628 | 1.913 | 18.258 | 0.947 | 3.746 | 11.68 | 2.458 | 20.882 | 0.976 | 1.818 | 1.854 | 1.376 | 9.767 | 0.982 | 3.958 | 33.365 | 2.970 | 159.531 | 0.954 |
| 10 | STLD | 5.607 | 5.313 | 2.277 | 21.015 | 0.933 | 5.485 | 16.957 | 3.697 | 26.817 | 0.949 | 2.213 | 2.872 | 1.664 | 11.793 | 0.974 | 5.319 | 41.263 | 3.977 | 199.487 | 0.915 |
| 11 | STLD | 5.730 | 4.845 | 2.067 | 17.830 | 0.922 | 5.579 | 16.845 | 3.776 | 26.481 | 0.947 | 2.231 | 2.711 | 1.680 | 11.819 | 0.973 | 5.375 | 40.769 | 3.979 | 191.434 | 0.912 |
| 12 | STLD | 4.709 | 4.683 | 2.033 | 19.601 | 0.947 | 4.187 | 12.464 | 2.984 | 24.15 | 0.971 | 1.721 | 2.021 | 1.301 | 9.293 | 0.985 | 3.991 | 33.742 | 2.979 | 160.368 | 0.953 |
| 13 | STLD | 5.509 | 4.895 | 2.047 | 17.770 | 0.937 | 5.247 | 16.859 | 3.458 | 26.089 | 0.954 | 2.132 | 2.803 | 1.597 | 11.384 | 0.976 | 5.257 | 37.440 | 3.894 | 182.865 | 0.916 |
| 14 | STLD | 5.672 | 4.951 | 1.909 | 16.143 | 0.924 | 5.305 | 16.733 | 3.507 | 25.446 | 0.952 | 2.182 | 2.661 | 1.643 | 11.671 | 0.975 | 5.339 | 37.506 | 3.927 | 175.424 | 0.913 |
| 15 | STLD | 4.669 | 4.552 | 1.893 | 16.799 | 0.949 | 3.886 | 12.183 | 2.687 | 22.163 | 0.975 | 1.495 | 1.864 | 1.078 | 7.668 | 0.989 | 3.933 | 30.607 | 2.941 | 148.480 | 0.954 |
| 16 | STLD | 5.607 | 5.313 | 2.277 | 21.015 | 0.933 | 4.921 | 16.764 | 2.979 | 26.353 | 0.959 | 2.213 | 2.872 | 1.664 | 11.793 | 0.974 | 5.317 | 41.231 | 3.978 | 200.433 | 0.915 |
| 17 | STLD | 5.730 | 4.845 | 2.067 | 17.830 | 0.922 | 4.921 | 16.575 | 2.995 | 25.119 | 0.959 | 2.231 | 2.711 | 1.680 | 11.820 | 0.973 | 5.374 | 40.771 | 3.984 | 193.141 | 0.912 |
| 18 | STLD | 4.709 | 4.683 | 2.033 | 19.601 | 0.947 | 3.637 | 11.846 | 2.356 | 20.441 | 0.978 | 1.721 | 2.021 | 1.301 | 9.293 | 0.985 | 3.991 | 33.843 | 2.985 | 161.576 | 0.953 |
| 19 | STLD | 5.545 | 5.581 | 2.197 | 20.797 | 0.932 | 5.092 | 16.544 | 3.34 | 25.732 | 0.956 | 2.124 | 2.506 | 1.606 | 11.322 | 0.975 | 3.267 | 25.624 | 2.460 | 125.732 | 0.973 |
| 20 | STLD | 5.678 | 4.753 | 2.081 | 17.964 | 0.922 | 5.166 | 16.42 | 3.363 | 24.898 | 0.955 | 2.075 | 2.316 | 1.554 | 10.821 | 0.976 | 3.289 | 25.472 | 2.435 | 117.338 | 0.971 |
| 21 | STLD | 4.700 | 4.659 | 1.900 | 18.266 | 0.946 | 4.013 | 12.134 | 2.73 | 22.965 | 0.973 | 1.858 | 1.807 | 1.421 | 10.163 | 0.981 | 2.143 | 19.669 | 1.603 | 89.367 | 0.988 |
| 22 | STLD | 5.427 | 5.143 | 1.940 | 17.535 | 0.936 | 4.909 | 16.487 | 3.146 | 25.199 | 0.96 | 1.965 | 2.384 | 1.441 | 10.090 | 0.979 | 3.125 | 20.593 | 2.277 | 99.420 | 0.975 |
| 23 | STLD | 5.601 | 4.817 | 1.882 | 16.179 | 0.924 | 4.942 | 16.35 | 3.118 | 24.128 | 0.959 | 1.947 | 2.212 | 1.415 | 9.869 | 0.979 | 3.190 | 21.490 | 2.298 | 95.063 | 0.972 |
| 24 | STLD | 4.636 | 4.480 | 1.704 | 14.985 | 0.948 | 3.794 | 11.906 | 2.514 | 21.323 | 0.976 | 1.559 | 1.568 | 1.136 | 7.897 | 0.987 | 1.969 | 15.924 | 1.462 | 76.261 | 0.989 |
| 25 | STLD | 5.545 | 5.581 | 2.197 | 20.797 | 0.932 | 4.734 | 16.481 | 2.855 | 26.204 | 0.962 | 2.124 | 2.506 | 1.606 | 11.322 | 0.975 | 3.262 | 25.637 | 2.460 | 126.306 | 0.973 |
| 26 | STLD | 5.678 | 4.753 | 2.081 | 17.963 | 0.922 | 4.704 | 16.28 | 2.771 | 24.576 | 0.963 | 2.075 | 2.316 | 1.554 | 10.821 | 0.976 | 3.286 | 25.540 | 2.432 | 116.842 | 0.971 |
| 27 | STLD | 4.700 | 4.659 | 1.900 | 18.267 | 0.946 | 3.762 | 11.689 | 2.464 | 20.847 | 0.976 | 1.858 | 1.807 | 1.421 | 10.163 | 0.981 | 2.141 | 19.925 | 1.605 | 88.958 | 0.988 |
| ATE Station | |||||
|---|---|---|---|---|---|
| Models | RMSE | RMSPE | MAE | MAPE | CC |
| STLD | 4.611 | 4.464 | 1.711 | 14.862 | 0.949 |
| STLD | 4.636 | 4.480 | 1.704 | 14.985 | 0.948 |
| STLD | 5.601 | 4.817 | 1.882 | 16.179 | 0.924 |
| STLD | 5.622 | 4.906 | 1.871 | 16.081 | 0.923 |
| Campo de Marte Station | |||||
| Models | RMSE | RMSPE | MAE | MAPE | CC |
| STLD | 3.637 | 11.846 | 2.356 | 20.441 | 0.978 |
| STLD | 3.762 | 11.689 | 2.464 | 20.847 | 0.976 |
| STLD | 3.746 | 11.68 | 2.458 | 20.882 | 0.976 |
| STLD | 3.794 | 11.906 | 2.514 | 21.323 | 0.976 |
| San Borja Station | |||||
| Models | RMSE | RMSPE | MAE | MAPE | CC |
| STLD | 1.495 | 1.864 | 1.078 | 7.668 | 0.989 |
| STLD | 1.559 | 1.568 | 1.136 | 7.897 | 0.987 |
| STLD | 1.535 | 1.644 | 1.118 | 7.793 | 0.987 |
| STLD | 1.721 | 2.021 | 1.301 | 9.293 | 0.985 |
| Santa Anita Station | |||||
| Models | RMSE | RMSPE | MAE | MAPE | CC |
| STLD | 1.969 | 15.924 | 1.462 | 76.261 | 0.989 |
| STLD | 2.141 | 19.925 | 1.605 | 88.958 | 0.988 |
| STLD | 2.143 | 19.669 | 1.603 | 89.367 | 0.988 |
| STLD | 3.190 | 21.490 | 2.298 | 95.063 | 0.972 |
| ATE Station | ||||
|---|---|---|---|---|
| Models | STLD | STLD | STLD | STLD |
| STLD | - | 0.229 | 0.988 | 0.992 |
| STLD | 0.771 | - | 0.991 | 0.993 |
| STLD | 0.012 | 0.009 | - | 0.332 |
| STLD | 0.008 | 0.007 | 0.668 | - |
| Campo de Marte Station | ||||
| Models | STLD | STLD | STLD | STLD |
| STLD | - | 0.965 | 0.944 | 0.963 |
| STLD | 0.036 | - | 0.000 | 0.716 |
| STLD | 0.056 | 1.000 | - | 0.806 |
| STLD | 0.037 | 0.284 | 0.194 | - |
| San Borja Station | ||||
| Models | STLD | STLD | STLD | STLD |
| STLD | - | 0.989 | 0.945 | 1.000 |
| STLD | 0.011 | - | 0.005 | 1.000 |
| STLD | 0.055 | 0.996 | - | 1.000 |
| STLD | 0.000 | 0.000 | 0.000 | - |
| Santa Anita Station | ||||
| Models | STLD | STLD | STLD | STLD |
| STLD | - | 1.000 | 1.000 | 1.000 |
| STLD | 0.000 | - | 0.704 | 1.000 |
| STLD | 0.000 | 0.296 | - | 1.000 |
| STLD | 0.000 | 0.000 | 0.000 | - |
| ATE Station | |||||
|---|---|---|---|---|---|
| Models | RMSE | RMSPE | MAE | MAPE | CC |
| STLD | 4.611 | 4.464 | 1.711 | 14.862 | 0.949 |
| PAR | 5.607 | 5.313 | 2.277 | 21.015 | 0.933 |
| NPAR | 5.730 | 4.845 | 2.067 | 17.830 | 0.922 |
| ARIMA | 4.709 | 4.683 | 2.033 | 19.601 | 0.947 |
| Campo de Marte Station | |||||
| Models | RMSE | RMSPE | MAE | MAPE | CC |
| STLD | 3.637 | 11.846 | 2.356 | 20.441 | 0.978 |
| PAR | 5.485 | 16.957 | 3.697 | 26.817 | 0.949 |
| NPAR | 5.579 | 16.845 | 3.776 | 26.481 | 0.947 |
| ARIMA | 4.187 | 12.464 | 2.984 | 24.150 | 0.971 |
| San Borja Station | |||||
| Models | RMSE | RMSPE | MAE | MAPE | CC |
| STLD | 1.495 | 1.864 | 1.078 | 7.668 | 0.989 |
| PAR | 2.213 | 2.872 | 1.664 | 11.793 | 0.974 |
| NPAR | 2.231 | 2.711 | 1.680 | 11.819 | 0.973 |
| ARIMA | 1.721 | 2.021 | 1.301 | 9.293 | 0.985 |
| Santa Anita Station | |||||
| Models | RMSE | RMSPE | MAE | MAPE | CC |
| STLD | 1.969 | 15.924 | 1.462 | 76.261 | 0.989 |
| PAR | 5.319 | 41.263 | 3.977 | 199.487 | 0.915 |
| NPAR | 5.375 | 40.769 | 3.979 | 191.434 | 0.912 |
| ARIMA | 3.991 | 33.742 | 2.979 | 160.368 | 0.953 |
| ATE Station | ||||
|---|---|---|---|---|
| Models | STLD | PAR | NPAR | ARIMA |
| STLD | - | 0.999 | 0.995 | 0.927 |
| PAR | 0.001 | - | 0.662 | 0.001 |
| NPAR | 0.005 | 0.338 | - | 0.006 |
| ARIMA | 0.073 | 0.999 | 0.995 | - |
| Campo de Marte Station | ||||
| Models | STLD | PAR | NPAR | ARIMA |
| STLD | - | 1.000 | 1.000 | 1.000 |
| PAR | 0.000 | - | 0.926 | 0.000 |
| NPAR | 0.000 | 0.074 | - | 0.000 |
| ARIMA | 0.000 | 1.000 | 1.000 | - |
| San Borja Station | ||||
| Models | STLD | PAR | NPAR | ARIMA |
| STLD | - | 1.000 | 1.000 | 1.000 |
| PAR | 0.000 | - | 0.907 | 0.000 |
| NPAR | 0.000 | 0.093 | - | 0.000 |
| ARIMA | 0.000 | 1.000 | 1.000 | - |
| Santa Anita Station | ||||
| Models | STLD | PAR | NPAR | ARIMA |
| STLD | - | 1.000 | 1.000 | 1.000 |
| PAR | 0.000 | - | 0.995 | 0.000 |
| NPAR | 0.000 | 0.005 | - | 0.000 |
| ARIMA | 0.000 | 1.000 | 1.000 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carbo-Bustinza, N.; Iftikhar, H.; Belmonte, M.; Cabello-Torres, R.J.; De La Cruz, A.R.H.; López-Gonzales, J.L. Short-Term Forecasting of Ozone Concentration in Metropolitan Lima Using Hybrid Combinations of Time Series Models. Appl. Sci. 2023, 13, 10514. https://doi.org/10.3390/app131810514
Carbo-Bustinza N, Iftikhar H, Belmonte M, Cabello-Torres RJ, De La Cruz ARH, López-Gonzales JL. Short-Term Forecasting of Ozone Concentration in Metropolitan Lima Using Hybrid Combinations of Time Series Models. Applied Sciences. 2023; 13(18):10514. https://doi.org/10.3390/app131810514
Chicago/Turabian StyleCarbo-Bustinza, Natalí, Hasnain Iftikhar, Marisol Belmonte, Rita Jaqueline Cabello-Torres, Alex Rubén Huamán De La Cruz, and Javier Linkolk López-Gonzales. 2023. "Short-Term Forecasting of Ozone Concentration in Metropolitan Lima Using Hybrid Combinations of Time Series Models" Applied Sciences 13, no. 18: 10514. https://doi.org/10.3390/app131810514
APA StyleCarbo-Bustinza, N., Iftikhar, H., Belmonte, M., Cabello-Torres, R. J., De La Cruz, A. R. H., & López-Gonzales, J. L. (2023). Short-Term Forecasting of Ozone Concentration in Metropolitan Lima Using Hybrid Combinations of Time Series Models. Applied Sciences, 13(18), 10514. https://doi.org/10.3390/app131810514







