Abstract
Woodworking manipulators are applied in wood processing to promote automatic levels in the wood industry. However, traditional trajectory planning results in low operational stability and inefficiency. Therefore, we propose a method combining 3-5-3 piecewise polynomial (composed of cubic and quintic polynomials) interpolation and an improved particle swarm optimization (PSO) algorithm to study trajectory planning and time optimization of woodworking manipulators. In trajectory planning, we conducted the kinematics analysis to determine the position information of joints at path points in joint space and used 3-5-3 piecewise polynomial interpolation to fit a point-to-point trajectory and ensure the stability. For trajectory time optimization, we propose an improved PSO that adapts multiple strategies and incorporates a golden sine optimization algorithm (Gold-SA). Therefore, the proposed improved PSO can be called GoldS-PSO. Using benchmark functions, we compared GoldS-PSO to four other types of PSO algorithms and Gold-SA to verify its effectiveness. Then, using GoldS-PSO to optimize the running time of each joint, our results showed that GoldS-PSO was superior to basic PSO and Gold-SA. The shortest running time obtained by using GoldS-PSO was 47.35% shorter than before optimization, 8.99% shorter than the basic PSO, and 6.23% shorter than the Gold-SA, which improved the running efficiency. Under optimal time for GoldS-PSO, our simulation results showed that the displacement and velocity of each joint were continuous and smooth, and the acceleration was stable without sudden changes, proving the method’s feasibility and superiority. This study can serve as the basis for the motion control system of woodworking manipulators and provide reference for agricultural and forestry engineering optimization problems.
1. Introduction
Wood processing, as a follow-up industry to forest harvesting and transportation, is a key step in enhancing the synthetic utilization rate of wood in the forestry sector [1,2]. Compared to other industrial fields, the wood processing industry has a relatively late start-up and slow development, and with the increasing demand for wood products, advanced processing machinery, such as multi-axis CNC, industrial robots, and manipulators, are urgently needed to improve mechanization and automation levels in wood processing [3,4,5,6]. Manipulators are widely used in related industries such as mechanical manufacturing, electronic and electrical, food manufacturing, and aerospace manufacturing [7,8,9]. They are designed to replace workers for tasks requiring high repeatability, high execution difficulty, and low safety. With the expansion of its application scope, it will likely bring unprecedented efficiency and quality to other production and manufacturing industries. Therefore, applying manipulators to wood processing improves processing efficiency, safety, product quality, reduces labor costs and create more value. Woodworking manipulators are convenient, which can realize the free movement and rotation of four-head high-speed electric spindles in the workspace to drill and mill wooden structures. However, their unstable operation and long running times pose challenges to the wood processing process, leading to high accident rates and poor efficiency [10,11]. Appropriate trajectory interpolation algorithms can improve manipulator’s operational stability, and the use of intelligent optimization algorithms for time-optimal trajectory planning can improve the manipulator’s efficiency. Thus, trajectory planning and time optimization are crucial to improving the security of operation and shortening the running time of woodworking manipulators. These improvements will enhance the machining efficiency and quality of wood processing [12].
Trajectory planning is an important prerequisite step in manipulator’s control system, which includes kinematic modeling of the manipulator, forward and inverse kinematic analysis, trajectory interpolation algorithms, trajectory optimization, and simulation. It significantly impacts the energy consumption, service life, and production efficiency of the manipulator, which determines whether the manipulator’s terminals can accurately and fast pass through specified path points and obtain a smooth trajectory [13,14]. According to different methods of describing motion states, there are two typical types of trajectory planning, trajectory planning in joint space and trajectory planning in the Cartesian space. When trajectory planning in joint space, the joint angle is used to represent the position and pose of the manipulator end-effector, which conveniently calculates inverse kinematics and avoids singularity problems compared to the Cartesian space [15,16]. Joint angels or positions can be obtained through inverse kinematics. In addition, introducing a trajectory planning algorithm is necessary to generate a trajectory between path points.
B-spline curves and polynomial function interpolation are commonly used in trajectory planning algorithms [17,18]. B-splines have excellent smoothing performance [19], but cannot pass through all the path points due to their inherent properties, whether it is approximate fitting or interpolation fitting. When using polynomial functions in trajectory planning, continuity of velocity and acceleration can only be ensured when the polynomials’ order is at least five [18]. As the polynomials’ order increases, the trajectory becomes more accurate and smoother; however, it may cause Runge’s phenomenon [20]. Piecewise polynomial interpolation has proven to be a feasible method for guaranteeing trajectory smoothness while simplifying calculation [21,22]. The 3-5-3 piecewise polynomial [23] combines the advantages of cubic and quintic polynomials, enabling the stable operation of the manipulator and without the need for complex calculations in trajectory planning. It is suitable for the trajectory planning of the woodworking manipulator.
Efficiency is a primary factor in industrial production. Therefore, time optimization for trajectory planning has great practical significance, as it improves the operating efficiency of the woodworking manipulators. Recently, many intelligent optimization algorithms were proven effective at solving time-optimal problems of trajectory planning; for instance, the genetic algorithm (GA) [24], whale optimization algorithm (WOA) [25], sparrow search algorithm (SSA) [26], PSO [27], and ant colony optimization algorithm (ACO), etc. [28]. Due to its few parameter settings, easy implementation, and good applicability, PSO has been a popular research topic. However, the basic PSO has a slow convergence rate and is prone to fall into the local extremum, causing low precision. Accordingly, several studies have reformed the PSO algorithm and been successfully applied to engineering problems, among which integrating other algorithms is considered effective. Zhao et al. [29] proposed a hybrid improved whale optimization and PSO algorithm method that enhances the convergence rate, which was applied to the optimum time-jerk path planning of serial manipulators. Kamel et al. [30] applied a GA-PSO algorithm to a team of wheeled mobile robots’ position control, which is superior to the GA or PSO algorithm alone. Song et al. [31] improved the PSO-ACO algorithm to achieve comprehensive and global optimization of energy dispatching; the results showed the effectiveness and higher security of this algorithm.
Although the aforementioned PSO algorithms are effective optimization solutions in their application field, they require complex parameter debugging and need many iteration numbers for convergence. Meanwhile, many previous works have only adopted the single strategy, which is limited in improving algorithm performance. Therefore, to simplify the algorithm structure and improve algorithm performance, we propose a novel PSO algorithm that adapts multiple strategies and integrates Gold-SA [32]. It has a fast convergence rate and better optimization ability, which can be well applied in 3-5-3 piecewise polynomial trajectory planning of the woodworking manipulators to reduce operating time and improve the wood processing efficiency. The following studies were conducted: (1) we established the kinematics model and kinematics analysis of the manipulator by a modified D-H parameter method [33]; (2) based on inverse kinematics, we fit the trajectory between the path points by 3-5-3 piecewise polynomial interpolation; (3) we developed an improved PSO algorithm and optimized the running time of each joint; and (4) we conducted simulation experiments and analyses.
2. Materials and Methods
2.1. Mechanism of Woodworking Manipulator
2.1.1. Physical Model of Woodworking Manipulator
Figure 1 shows the woodworking manipulator’s structure. The woodworking manipulator has a T-shaped layout consisting of four motion axes components (A, B, X, and Z), and is equipped with a four-head high-speed electric spindles at the A axis. From the perspective of an industrial robot, it consists of two rectilinear motion joints and two revolute joints. The rectilinear motion joints and the revolute joints can, respectively, achieve the translational motion of the woodworking manipulator along the X, Z axis and the rotation around the A, B axis. All joints are electrically driven by servo motors, drivers, and reducers. When processing the wooden structure, the upper computer sends instructions, and the motion controller responds to the input by controlling the joint angle or displacement, achieving control of the manipulator’s velocity and position. Consequently, the end of the woodworking manipulator can run smoothly and quickly according to the predetermined trajectory, and finally reach the designated working position for processing.
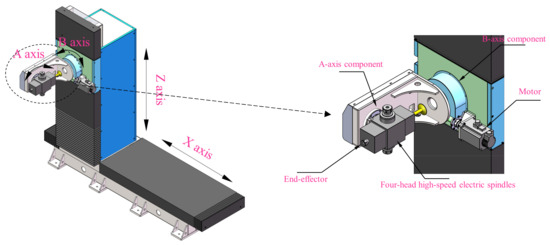
Figure 1.
Woodworking manipulator.
2.1.2. Kinematic Model of Woodworking Manipulator
The relative motion components in the woodworking manipulator are treated as rigid connecting rods represented by straight lines. The motion joints are represented as moving and rotating pairs. Thus, the woodworking manipulator can be simplified. The modified D-H parameter method is commonly used for modeling different kinds of manipulators’ connecting rod and joint. It is defined by four parameters: connecting rod torsion angle, connecting rod length, connecting rod offset, and joint angle, which can achieve coordinate system transformations through homogeneous transformation matrices and describe the pose and position of the end-effector [33]. Compared with the D-H parameter method, the modeling results are the same, but the position of the coordinate system is different. In our study, the modified D-H parameter method is more convenient. Then, the simplified manipulator’s connecting rod and joint model, established by the modified D-H method, is shown in Figure 2, and the parameters are shown in Table 1.
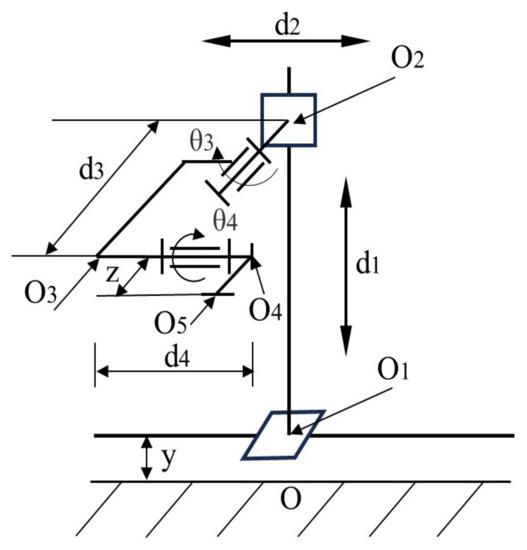
Figure 2.
Simplified woodworking manipulator.

Table 1.
Modified D-H parameters of woodworking manipulator.
The modified D-H parameter method was used for the kinematic model, obtaining a homogeneous transformation matrix [33] between adjacent connecting rod coordinate systems.
where Cθ is cosine function, and Sθ is sine function.
Then, calculate the manipulator’s forward kinematics T-matrix through the variable values of each joint in Table 1, which shown in the following equation:
where T0 is the base coordinate transformation matrix; Ttool is tool coordinate system transformation matrix and y, z are the parameters in them. rij represents the pose information of the end-effector, and px, py and pz represent the position information of the end-effector.
After the kinematics equation was obtained from the forward kinematics analysis, we assumed that the value of the T-matrix was known and used the algebraic method to reverse solve the values of θ3, θ4, d1, and d2, in the Equation (3) to obtain the inverse kinematics.
2.2. 3-5-3 Piecewise Polynomial Interpolation
By inverse kinematics, the angle of each joint when the manipulator’s end-effector passes through the path point can be obtained. Planning the trajectory between each path point is necessary to determine the joint trajectory interpolation function and calculate the joint angle, velocity, and acceleration motion parameters between the path points. Polynomial functions are commonly used as trajectory interpolation functions. However, when only a cubic polynomial is used, the angular acceleration is discontinuous, and when only using a quintic polynomial to pass through multiple path points, it leads to complex calculations. Therefore, we used the 3-5-3 piecewise polynomial interpolation [23] to conduct trajectory planning, which reduces computational complexity, effectively ensuring the manipulator’s stability while passing through multiple path points. The 3-5-3 piecewise polynomial interpolation is divided into three segments, with the first and third segments being cubic polynomial and the second segment being quintic polynomial. Taking joint 1 as an example, the joint trajectory interpolation functions of each segment are shown in the following equation:
where aij is the jth coefficient of the ith function; t is interpolation time of each segment; and θi(t) represents the ith angular displacement at time t. Thus, the angular velocity and the angular acceleration are:
To ensure the continuous and smooth trajectory of each segment during operation, the joint angular displacement, velocity, and acceleration must satisfy the constraints as per the following equation:
where , , and are the joint angular displacement, velocity, and acceleration at the beginning of the ith segment, respectively; and , and are the angular displacement, velocity, and acceleration at the end of the ith segment. When the manipulator starts and stops, the angular velocity and acceleration must be 0 to ensure safety. Then, the polynomial coefficient matrix a can be solved by Equations (16)–(18), where ti of A matrix is ith segment interoperation time and Xi is the ith path point interpolation position of joint 1.
Figure 3 shows the joint 1 trajectory planning results when the interpolation time of each section of 3-5-3 polynomial interpolation is 5 s. The results show that the joint displacement and velocity curves are smooth, and there are no abrupt changes in the acceleration curve. This indicates that the 3-5-3 piecewise polynomial interpolation can ensure the smooth operation of the woodworking manipulator.
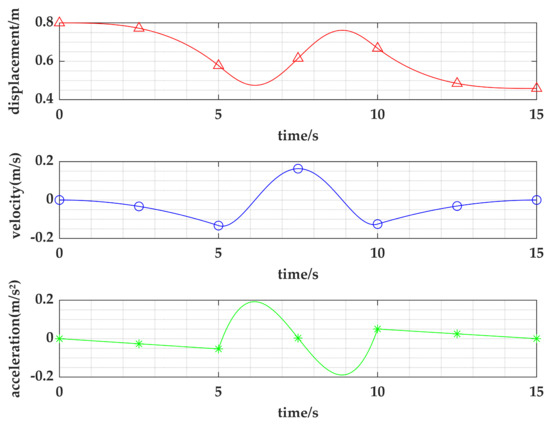
Figure 3.
Joint 1 trajectory planning results by 3-5-3 polynomial interpolation.
According to the solving process of coefficient matrix a, 3-5-3 piecewise polynomial interpolation must predetermine the ti of each polynomial, which greatly impacts the overall trajectory planning. Thus, selecting a suitable ti not only ensures the stability of each joint during operation, but also improves the efficiency of the manipulator.
2.3. The Traditional PSO Algorithm
PSO is an intelligent optimization algorithm originating from research into the behavior of birds foraging in forests. In PSO, bird swarms are abstracted into particle swarms with each bird representing a particle. The particles iteratively solving the extremum of the fitness function in the search space simulate the process of birds sharing information with each other to search for the largest food in the forest, as shown in Figure 4.
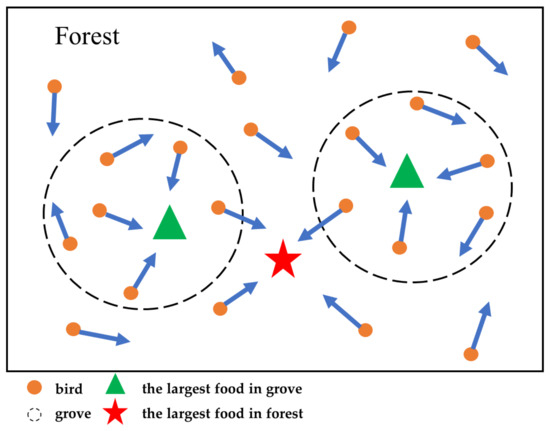
Figure 4.
The process of birds foraging.
The process of particle iterative solution is achieved by continuously updating the particles’ position and velocity information. Figure 5 shows the process of updating particle position and velocity. In the D dimension search space, we can assume that the particle number is N, Xi = [Xi1, Xi2, …, XiD], which represents the position of the ith particle, Vi = [Vi1, Vi2, …, ViD], which represents the velocity of the ith particle. Pi = [Pi1, Pi2, …, PiD] represents the current best position of ith particle and can be updated by the following equation:
where iter represents iterations; fitness () is fitness function; and are the position and current best position of the ith particle when the iteration number is iter, respectively.
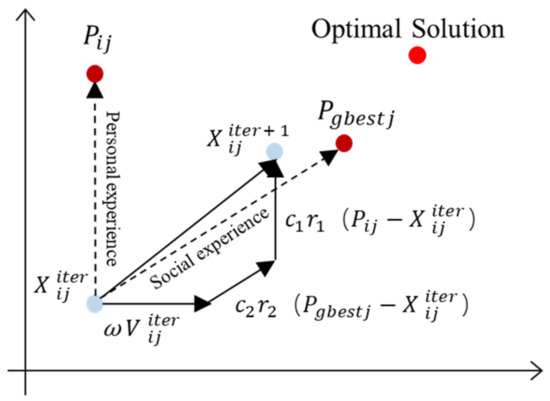
Figure 5.
The updating of particle position and velocity.
Pgbest = [Pgbest1, Pgbest2, … PgbestD] is the current global best position. Then, the formula for updating the position and velocity of particles is as follows:
where ω is inertia weight; c1 and c2 are learning factors; r1 and r2 are the random numbers in the range (0,1); and are the velocity and position of the jth dimensional component of the ith particle when the number of iterations is iter, respectively. It is called basic PSO [34] when inertia weight ω = 1.
2.4. The Improvement Strategy of PSO
From the structure of PSO, improvements can be made in terms of population initialization, inertia weights, and learning factors, as well as particle position and velocity update formulas. Hu et al. [35] analyzed the impact of PSO velocity on algorithm performance and confirmed that it was not an essential part and the presence of velocity may cause the iterative process in the wrong evolutionary direction. So, they proposed a simpler particle swarm optimization (SPSO), and the position update formula is shown in Equation (22):
Compared to PSO, SPSO removes the velocity term, simplifies the control process of particles, and avoids the velocity parameters’ impact on the algorithm’s convergence rate and accuracy.
We adopted the idea of SPSO in this paper. Firstly, the initialization of the population was based on Circle chaotic mapping. Introducing tanh function to PSO, we proposed an S-curve type inertia weight nonlinear decreasing method, which increased the algorithm’s ability to develop a large search space in the early iteration and precision search around the optimal solution in the later iteration. It also integrated Gold-SA to change the particle position update method. The convergence rate and accuracy of the improved algorithm significantly increased, and overall performance was better.
2.4.1. Initial Population by Circle Chaotic Mapping
The rand function is commonly used for population initialization to generate particle position and velocity information. Although this method has high randomness, it is difficult to ensure the uniformity of distribution in the whole search space. Consequently, population diversity reduces, leading to a slow convergence rate and affecting the convergence accuracy of the algorithm. Chaotic mapping has good ergodicity and randomness [36], providing a more uniform initial population distribution than conventional random number generators by generating chaotic sequences, and increasing the population diversity. Therefore, we used Circle chaotic mapping to initialize the population, and the generated chaotic sequence was as follows [37]:
where mod (a, b) is the remainder of a over b, and k (i) is the ith chaotic sequences number. The generation of a Circle chaotic sequence does not rely on initial values, and k (1) can be a random number between [0,1]. Figure 6 shows the distribution diagram and histogram of the 0–1 sequence values generated by the rand function and Circle chaotic map when the population size is 100. Obviously, when comparing histograms (c) and (d), there is less randomness in the Circle map, and the distribution of data points between 0.2 and 0.6 is denser. However, in comparing distributions (a) and (b), while some randomness is lost, the data points generated by the Circle map are more evenly distributed in space than the rand function. Furthermore, there are no data “clustering” or “overlapping” phenomena, which can generate high-quality initial populations in the search space, accelerate the convergence rate and enhance the ability of particles to escape from local extremum.
k(i + 1) = mod(k(i) + 0.2 − (0.5/2π)sin(2πk(i)), 1),
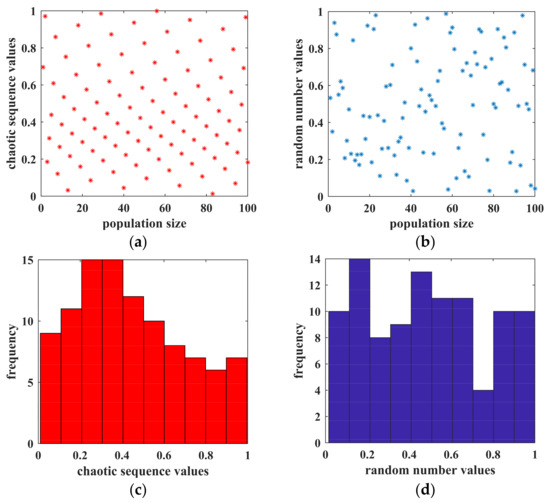
Figure 6.
Comparison between two kinds of random number generators: (a) distribution diagram of Circle mapping chaotic sequence values; (b) distribution diagram of random number values of rand function; (c) histogram of Circle mapping chaotic sequence values; (d) histogram of random number values of rand function.
2.4.2. S-curve Type Inertia Weight Nonlinear Decreasing Method
ω is a vital parameter in PSO. In the early iteration, it generally has a larger value with a strong global optimization ability to accelerate the population’s evolution toward the dominant population [38]. When the particles approach the optimal solution in the later iteration, it can seek local optima by using smaller values ω and performing fine searches to improve convergence accuracy. Thus, we propose an S-curve type inertia weight nonlinear decreasing method based on the tanh function [39]. The inertia weight updating formula is as follows, and Figure 7 shows the inertia weight curve:
where ωmin is the minimum inertia weight value; ωmax is the max inertia weight value; tanh() is hyperbolic tangent function; and itermax is the max iterations.
ω = ωmin + (ωmax − ωmin)(1 + tanh(2 − 4iter/itermax))/2,
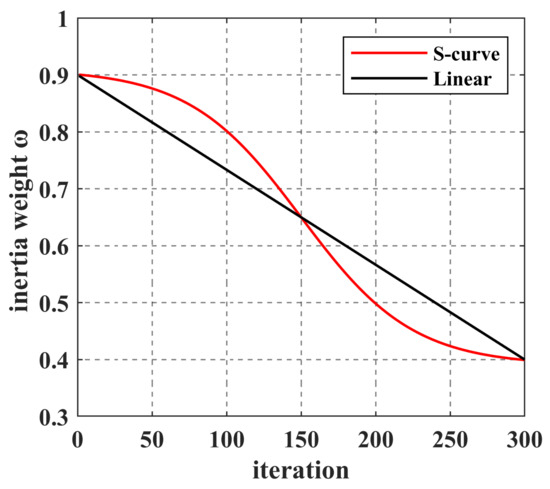
Figure 7.
Inertia weight S-curve decreasing and Linear decreasing.
Compared to Linear decreasing, the S-curve decreasing in the early and late iteration of the search is slower change. Maintaining a larger ω value in the early iteration is beneficial for global optimization, whereas maintaining a smaller ω value in the later iteration is beneficial for local optimization.
2.4.3. Position Updating Integrating the Gold-SA
Gold-SA is an optimization algorithm developed by Tanyildizi et al. in 2017 based on the sine function, which has the advantages of good convergence, strong robustness, and less parameter tuning [32]. Gold-SA, which searches the entire solution space, is simulating the process of scanning a unit circle with a radius to obtain a sine function. Therefore, it has good ergodicity, can carry out extensive searches, and has a strong local optimization ability. In addition, Gold-SA continuously reduces the search space near the optimal solution through a golden section operator, improving the algorithm’s convergence rate and accuracy. The position information of Gold-SA is updated using the following formula.
where R1 is the random numbers in the range (0, 2π), and R2 is the random numbers in the range (0, π). x1 and x2 are golden section coefficients, which are updated in the following equation:
The initial values of a and b are −π and π, respectively [32]. The golden ratio τ is approximately 0.618033. By integrating the Gold-SA position update strategy with the SPSO algorithm, a new position update formula is obtained as the following equation:
Meanwhile, to further improve search efficiency, an acceleration factor λ was introduced to improve the convergence rate [40]. Finally, the GoldS-PSO position update formula is as follows:
In conclusion, the implementation steps of the GoldS-PSO are as follows:
Step 1: Set the maximum iterations itermax, the particle number N, upper bounds Ub and lower bounds Lb of particle position and fitness function ‘s dimension D;
Step 2: Population initialization based on Circle chaotic mapping;
Step 3: Calculate the fitness of each particle and record the current historical best position Pi for each particle, the current global best position Pgbest and optimal value of fitness Gbest;
Step 4: Update the inertia weight ω, golden section coefficients x1 and x2, and position ;
Step 5: Determine whether the updated particle position is out of bounds and use the boundary value as the particle position if it is;
Step 6: Calculate particle fitness again, update the current best historical position Pi for each particle, the current global best position Pgbest, and the current optimal value of fitness Gbest;
Step 7: Repeat Step 4–6 before reaching the maximum iterations and return the optimal solution Xbest and optimal value Gbest after reaching it.
2.5. Comparative Testing Experiment
To test the performance of the GoldS-PSO algorithm, we selected eight test functions commonly used by IEEE Congress on Evolutionary Computation (IEEE CEC) and verified its effectiveness experimentally [40]. In Table 2, F1–F5 are unimodal benchmark test functions with only one optimal solution, which involves testing the algorithm’s convergence rate and accuracy. F6–F8 are multimodal benchmark testing functions with many local optima, which mainly test the algorithm’s ability to jump out of the local extremum.

Table 2.
Benchmark functions.
Figure 8 shows the F1–F8 diagram when the function dimension is 2. Then, we selected four related algorithms, basic PSO [34], SPSO [35], compression factor particle swarm optimization (CFPSO) [41] and Gold-SA [32] for comparative experiments. In the experiment, to ensure fairness, the basic parameters of different PSO and Gold-SA were set the same, with a population size of N = 30, a dimension of D = 30, and maximum iterations of itermax = 1000. Other parameters are consistent with the original literature.
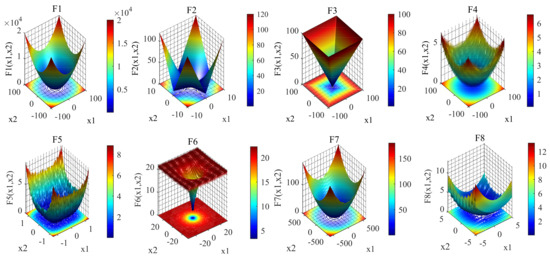
Figure 8.
F1–F8 benchmark test function three-dimensional diagram.
Each algorithm runs 30 times independently, calculating the mean value (Mean), best value (Best), and standard deviation (Std) of the optimal results as performance indicators for algorithm optimization, reflecting the algorithm’s convergence accuracy and stability. As there are no high requirements for real-time in the woodworking manipulator’s trajectory planning, we did not choose to compare and analyze the running time of each algorithm as a specific performance indicator. The results of specific performance indicators in the comparative experiment are recorded in Table 3, and the best results are highlighted in bold font.

Table 3.
The optimization results of the comparative testing experiment.
Table 3 shows that the average and standard deviation of GoldS-PSO optimization results in F1–F3 reached the theoretical optimal values. This finding indicates that the improved algorithm had good solving accuracy and stability in such unimodal optimization problems. Gold-SA and SPSO algorithms also achieved good results but did not reach the theoretical optimal values in the F2 and F3. However, there is still a significant gap in algorithm accuracy compared to GoldS-PSO. None of the algorithms reached the theoretical optimal value at F4 and F5, but GoldS-PSO had higher accuracy. For the test functions F6 and F7, GoldS-PSO and Gold-SA achieved better results with standard deviations of 0, indicating better robustness of the algorithm. In the F8 test results, although the mean and best values of GoldS-PSO are slightly lower than Gold-SA, it had higher convergence accuracy than the PSO, CFPSO, and SPSO, demonstrating that the improved algorithm has a stronger ability to jump out of local optima. In summary, GoldS-PSO has significantly improved convergence accuracy and stability compared to other PSO algorithms. It is only slightly inferior to Gold-SA in the terms of F8 results. The overall performance of the algorithm has improved.
Figure 9 shows the curve of the best fitness value for each algorithm during the iterative evolution of the F1–F8 test function, which can more intuitively compare algorithm’s convergence rate and accuracy. F1–F3 in Figure 9 shows that GoldS-PSO’s convergence rate is significantly better than other algorithms. It can fully converge to the theoretical optimal value in the first 600 generations, nearly 300 generations faster than the fastest Gold-SA on average.
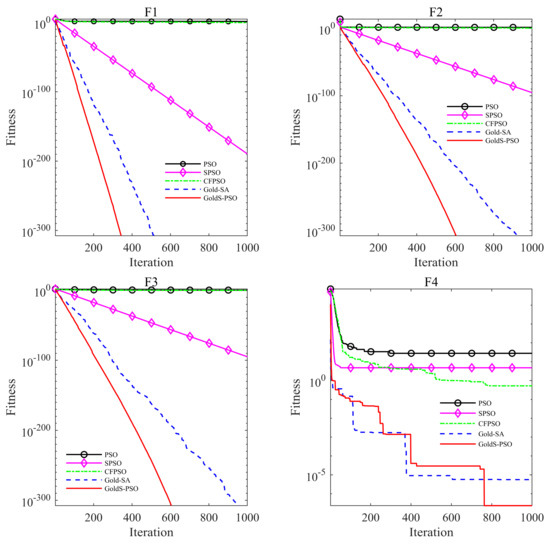
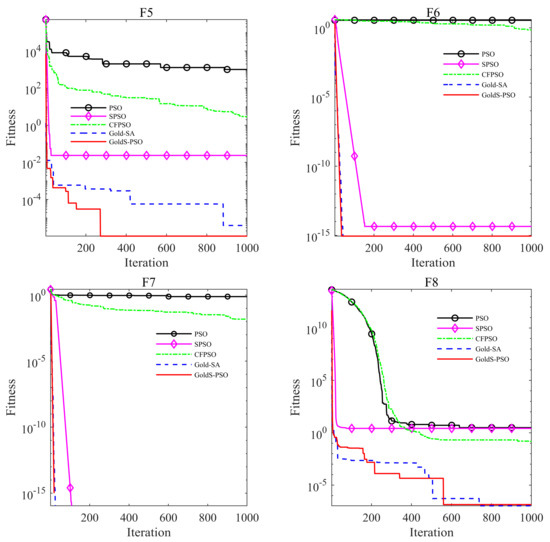
Figure 9.
The best F1–F8 fitness evolution curves by using PSO, SPSO, CFPSO, Gold-SA, and GoldS-PSO in 30 times independent runs.
Although Gold-SA and GoldS-PSO both completed convergence in the first 100 generations from the F6 and F7 in Figure 9, GoldS-PSO still used the least iterations, showing that the efficiency and rapidity of the improved algorithm was significantly enhanced. It is shown from the F4, F5 and F8 in Figure 9 that GoldS-PSO has an excellent ability to jump out of local extremum.
3. Experiments and Results
3.1. Time Optimal Trajectory Planning Process
In this section, GoldS-PSO was used to optimize the running time of woodworking manipulator within the constraints of each joint’s maximum velocity and acceleration. As described in Section 2.2, the interpolation time ti of each segment is an important parameter in 3-5-3 piecewise polynomial interpolation trajectory planning. Therefore, while ensuring a smooth and controllable trajectory, minimizing the ti of each segment is necessary to improve the efficiency of manipulation. The optimization problem for the interpolation time of the ith joint is as follows:
where tij, vij, and aij are the interpolation time, velocity, and acceleration of the jth segment of the ith joint, respectively. Vmax and Amax represent the maximum velocity and acceleration of each joint. The simultaneous movement of each joint was optimized separately to ensure that they meet the velocity and acceleration limits. The maximum value of each optimized joint in each segment was considered the optimization result. Tallying the optimization results of each segment to obtain the final optimized running time. Then, we could propose a woodworking manipulator time-optimal trajectory planning method based on 3-5-3 piecewise polynomial interpolation and the GoldS-PSO algorithm. Figure 10 shows a flowchart of the process.
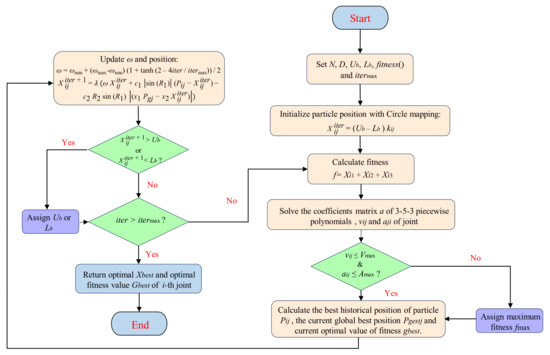
Figure 10.
Time-optimal 3-5-3 piecewise polynomial trajectory planning process based on GoldS-PSO.
3.2. Time Optimization Experiment of Woodworking Manipulator
Time Optimization experiments were conducted on the four joints of woodworking manipulator to optimize runtime. The woodworking manipulator passed through four path points A, B, C, and D. The corresponding joint position and joint angle were obtained through the inverse kinematics of Section 2.1, as shown in Table 4. The basic PSO, Gold-SA and algorithms proposed in this paper were selected for time-optimal trajectory planning. For each algorithm, the population size was set to 50, the maximum iterations were 300, the maximum velocity of joints 1 and 2 was 0.6 m/s, the maximum acceleration was 0.8 m/s2, the maximum velocity of joints 3 and 4 was 1.8 rad/s, the maximum acceleration was 2.4 rad/s2, and the particle position range was constrained at [1,5]. Under velocity and acceleration limitations, the total optimal interpolation time and the three-stage interpolation time for each joint were recorded in Table 5. The shortest Ttotal and maximum ti of each joint are highlighted in bold.

Table 4.
Four joint positions and angle of path points.

Table 5.
Interpolation time after optimizing each joint.
According to Table 5, GoldS-PSO achieved the best results compared to basic PSO and Gold-SA, with the optimized total running time Ttotal of each joint being 7.0672 s, 7.2177 s, 6.8970 s, and 6.8713 s, respectively. Moreover, the maximum interpolation time of each joint segment under GoldS-PSO optimization was also the smallest compared to basic PSO and Gold-SA. The fitness iterative evolution curve for each joint is depicted in Figure 11. It better reflects the performance of each algorithm in the optimization process.
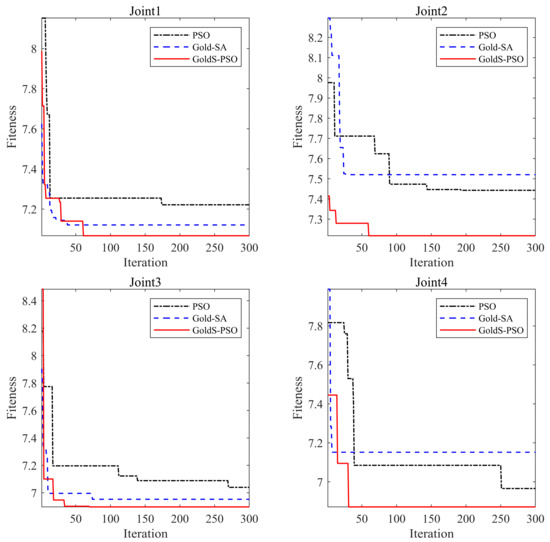
Figure 11.
Four joints’ iterative process by using PSO, Gold-SA, and GoldS-PSO.
Figure 11 shows that GoldS-PSO had a faster rate of convergence than PSO. Out of all the optimization processes, the iterations of GoldS-PSO were within the 60 generations to complete global convergence, whereas PSO required at least the 120 generations. Compared to Gold-SA, GoldS-PSO’s rate of convergence did not significantly improve; however, its ability to jump out of local extreme values was stronger and its convergence accuracy was the highest. Although Gold-SA achieved global convergence within the 50 generations, it was hard to adjust the evolutionary direction in the middle or later iteration and easily fell into the dilemma of local extremum. Even in the optimization processes of joints 2 and 4, Gold-SA’s convergence accuracy was lower than that of PSO. In a word, GoldS-PSO has a good convergence rate and is not easily trapped in local convergence. It balances the rapidity and accuracy of convergence, which indicates better performance for such engineering optimization problems.
Subsequently, we selected the maximum interpolation time of each joint segment as the final t1, t2, and t3. Then, the total interpolation time obtained after optimizing the PSO, Gold-SA, and GoldS-PSO was 9.3442 s, 8.6057 s, and 7.8776 s, respectively. The GoldS-PSO algorithm reduced time consumption by 47.483% compared to before optimization, 15.695% compared to PSO optimization, and 8.461% compared to Gold-SA optimization, demonstrating the effectiveness and superiority of the algorithm. The final planning times t1 = 2.3189 s, t2 = 2.9540 s, and t3 = 2.6047 s of each segment was substituted into the 3-5-3 piecewise polynomial interpolation function in Section 2.2 to obtain the displacement, velocity, and acceleration simulation curves of each joint.
3.3. Simulation Results
According to the simulation curve in Figure 12, the displacement and velocity curves of each joint are smooth and continuous, and there is no sudden change in the acceleration, and none exceeds the limit range. In the velocity and acceleration curves, the maximum velocity and acceleration of the joint tend toward the maximum limit value, indicating improved joint operation efficiency. In conclusion, the above results proved the successful of the time optimal trajectory planning method proposed in this paper. It not only improved the operational efficiency but also effectively ensured the continuity and stability of the manipulator.
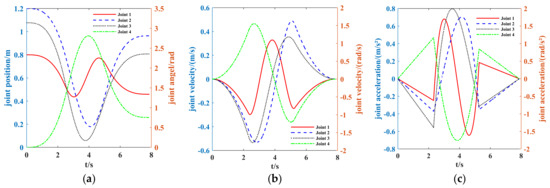
Figure 12.
Woodworking manipulator displacement, velocity, and acceleration of each joint (a) Joint displacement running curve; (b) joint velocity running curve; (c) joint acceleration running curve.
Figure 13 depicts three trajectories from starting point A to ending point D of the woodworking manipulator end-effector under optimal time and a simulation model of the woodworking manipulator by simplifying the woodworking manipulator into a series of connecting rods in the MATLAB Robotics Toolbox [42]. As shown in the following figure, the connecting rod can stretch and rotate to simulate the movement and rotation of the four joints of the woodworking manipulator. The red curve represents the end-effector trajectory of the woodworking manipulator and the four black dots marked represent the four path points A, B, C, and D in the Cartesian space. Figure 13a–d shows the entire operation process in detail. The trajectory of the end-effector passes through all paths point stably without interruption. Our results proved that the proposed algorithm achieved the time-optimal trajectory planning of the woodworking manipulator while ensuring stability and operational accuracy. In other words, we demonstrated that the proposed method is feasible.
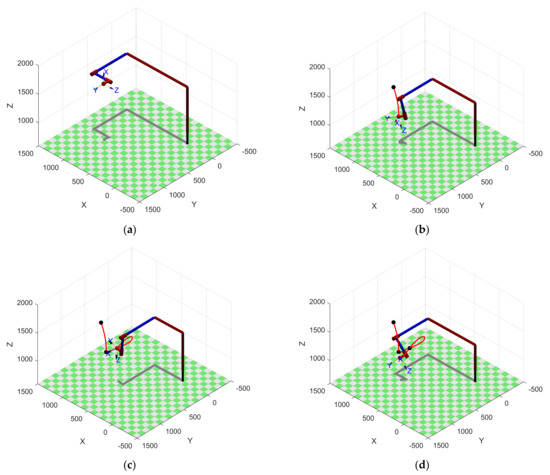
Figure 13.
The woodworking manipulator end-effector trajectory under optimal time (a) The end-effector at starting point A; (b) the end-effector at point B and the trajectory from A to B; (c) the end-effector at point C and the trajectory from A to C; (d) the end-effector at end point D and the trajectory from A to D.
4. Discussion
For the woodworking manipulator, joints 1 and 2 are rectilinear motion joints, while joints 3 and 4 are revolute joints. Therefore, the limitations of joint velocity and acceleration are different. In the experiment of optimizing joint running time, joints 1 and 2 can be divided into one group experiment, and joints 3 and 4 are another group. From Table 5, the difference in total running time of joints 1 and 2 optimized by GoldS-PSO is 0.1505 s, and the difference in total running time of joints 3 and 4 is 0.0257 s, which is smaller than the 0.2262 s and 0.0681 s of basic PSO and the 0.3993 s and 0.1992 s of Gold-SA, indicating that GoldS-PSO has better stability. The simulation results in Section 3.3 show that the displacement and velocity curves of the manipulator maintain good operational smoothness. However, due to the trajectory being divided into three segments, there is a clear convergence in the operation patterns of the first and third segments, which may not be conducive to meeting the special needs of some machining tasks. Additionally, because of the different interpolation functions used, the acceleration curve can maintain continuity at the connection of two trajectories, but it is not smooth enough and can result in non-differentiable points. But in summary, the simulation results meet the working requirements of the woodworking manipulator.
The method proposed in this paper achieved satisfactory results in time-optimal trajectory planning of woodworking manipulator. However, some areas must be considered for future research. Firstly, from the perspective of the proposed GoldS-PSO algorithm, further testing is needed to evaluate the effectiveness of different parameter combinations that may need strict mathematical derivations [43]. Moreover, currently we only applied GoldS-PSO to time-optimal trajectory planning of woodworking manipulators. More experiments are needed to assess the effectiveness of other optimization problems in agricultural and forestry engineering, which may require adjustments to the algorithm structure again. Then, after completing the time-optimal trajectory planning, it is necessary to comprehensively consider the effect of energy consumption, impact, and other factors on the operation and carry out multi-objective optimization [44,45] of the trajectory to enhance the general performance of manipulator. The design of the manipulator control system and trajectory tracking control is also the focus of subsequent studies.
Recently, some advanced technologies, such as machine vision, image processing, artificial intelligence algorithms, etc., have been integrated into automated manipulator and robot systems, which has provided unprecedented opportunities for traditional agriculture and forestry industries to achieve an automate decision-making processes and improve efficiency [46,47]. In this process, the GoldS-PSO algorithm proposed in this paper can be used for the training of neural networks and optimization of control model structure in the intelligent control system [48,49], as well as for the optimization of target recognition, positioning, and tracking technology in visual detection systems [50,51]. Meanwhile, some relevant studies indicate that it has great potential in optimizing forestry management structure [52].
5. Conclusions
In this paper, we proposed a time-optimal trajectory planning method based on a 3-5-3 piecewise polynomial interpolation combined with GoldS-PSO algorithm. Aiming to optimize the trajectory of woodworking manipulator in joint space and improve processing efficiency. Firstly, a brief introduction was provided to the structure and operating principles of the woodworking manipulator. Then, we used a modified D-H parameter method to establish a kinematic model of the manipulator for forward and inverse kinematic analysis and used a 3-5-3 piecewise polynomial interpolation to fit three segment trajectories between four path points in joint space. By introducing a Circle chaotic map for population initialization, proposing an S-curve type nonlinear decreasing method to update inertia weight, and integrating the Gold-SA for improving the particle position update formula to obtain the GoldS-PSO, we utilized the commonly used benchmark functions to test the performance of GoldS-PSO, and compared it to basic PSO, SPSO, CFPSO and Gold-SA. Afterward, under the limitations of joints’ displacement, velocity, and acceleration, the GoldS-PSO was used to optimize the trajectory interpolation time of each joint, with the target of obtaining the minimum total running time. The experimental results demonstrated that GoldS-PSO decreased each segment’s maximum time of 5 s by 2.6811 s, 2.046 s, and 2.3953 s, respectively. Therefore, the total running time obtained via GoldS-PSO optimization was 7.8876 s, which had reduced by 47.483%, 15.695%, and 8.461% form 15 s before optimization, the 9.3442 s for PSO optimization, and the 8.6057 s for Gold-SA optimization, respectively. These findings indicate that GoldS-PSO converges faster and more accurately. The optimized trajectory displacement and velocity curves are smooth and stable, and the acceleration curve is continuous without sudden changes. Our results demonstrate the feasibility and superiority of the proposed method by continuously passing through all the given path points in the Cartesian space in optimal time. In future work, the structure of GoldS-PSO needs further adjustment to improve algorithm performance, and we will carry out multi-objective trajectory optimization for the woodworking manipulator in terms of energy consumption, time, and impact. The GoldS-PSO algorithm proposed in this paper can provide guidance for relative agricultural and forestry engineering optimization problems.
Author Contributions
Conceptualization, S.C. and C.Z.; funding acquisition, C.Z.; methodology, S.C.; resources, C.Z.; software, S.C.; supervision, C.Z.; validation, S.C. and J.Y.; visualization, S.C.; writing—original draft, S.C.; writing—review and editing, S.C. and J.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Fundamental Research Funds of CAF, grant number CAFYBB2020SY043.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, J.; Yang, L.; Liu, H. Green and efficient processing of wood with supercritical CO2: A Review. Appl. Sci. 2021, 11, 3929. [Google Scholar] [CrossRef]
- Medvedev, S.; Mokhirev, A.; Rjabova, T. Methodical approach to increase efficiency of use of wood resource potential of the region. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Saint Petersburg, Russia, 22–24 May 2019. [Google Scholar]
- Pantscharowitsch, M.; Kromoser, B. Influence of machining parameters on subtractive manufacturing of elementary geometries in glued-laminated timber using an industrial robot. Wood Mater. Sci. Eng. 2023, 18, 472–490. [Google Scholar] [CrossRef]
- Ji, M.; Zhang, W.; Diao, X.; Wang, G.; Miao, H. Intelligent automation manufacturing for Betula solid timber based on machine Vision detection and optimization grading system applied to building materials. Forests 2023, 14, 1510. [Google Scholar] [CrossRef]
- Cunha, J.; Ferreira, R.; Lau, N. Computer vision and robotic manipulation for automated feeding of cork drillers. Mater. Des. 2015, 82, 290–296. [Google Scholar] [CrossRef]
- Rossander, M.; Lideskog, H. Design and implementation of a control system for an autonomous reforestation machine using finite state machines. Forests 2023, 14, 1340. [Google Scholar] [CrossRef]
- Zhu, Y.; Qiao, J.; Guo, L. Adaptive sliding mode disturbance observer-based composite control with prescribed performance of space manipulators for target capturing. IEEE Trans. Ind. Electron. 2018, 66, 1973–1983. [Google Scholar] [CrossRef]
- Junge, K.; Hughes, J.; Thuruthel, T.G.; Iida, F. Improving robotic cooking using batch Bayesian optimization. IEEE Robot. Autom. Lett. 2020, 5, 760–765. [Google Scholar] [CrossRef]
- Kim, Y.J.; Cheng, S.; Kim, S.; Iagnemma, K. A stiffness-adjustable hyper redundant manipulator using a variable neutral-line mechanism for minimally invasive surgery. IEEE Trans. Robot. 2014, 30, 382–395. [Google Scholar] [CrossRef]
- Abdelsalam, A.; Happonen, A.; Kärhä, K.; Kapitonov, A.; Porras, J. Toward autonomous vehicles and machinery in mill yards of the forest industry: Technologies and proposals for autonomous vehicle operations. IEEE Access 2020, 10, 88234–88250. [Google Scholar] [CrossRef]
- Qiao, W.; Wang, Z.; Wang, D.; Zhang, L. A new mortise and tenon timber structure and its automatic construction system. J. Build. Eng. 2021, 44, 103369. [Google Scholar] [CrossRef]
- Gao, R.; Zhang, W.; Wang, G.; Wang, X. Experimental research on motion analysis model and trajectory planning of GLT palletizing robot. Buildings 2023, 13, 966. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, S.; Jiang, A.; Xiao, J.; Wang, B. Trajectory planning of 6-dof manipulator based on gaussian process regression method. Int. J. Robot. Autom. 2020, 35, 209–220. [Google Scholar] [CrossRef]
- Huang, J.; Hu, P.; Wu, K.; Zeng, M. Optimal time-jerk trajectory planning for industrial robots. Mech. Mach. Theory 2018, 121, 530–544. [Google Scholar] [CrossRef]
- Stilman, M. Global manipulation planning in robot joint space with task constraints. IEEE Trans. Robot. 2010, 26, 576–584. [Google Scholar] [CrossRef]
- Xu, W.; Li, C.; Wang, X.; Liu, Y.; Liang, B.; Xu, Y. Study on non-holonomic cartesian path planning of a free-floating space robotic system. Adv. Robot. 2009, 23, 113–143. [Google Scholar] [CrossRef]
- Thompson, S.E.; Patel, R.V. Formulation of joint trajectories for industrial robots using B-splines. IEEE Trans. Ind. Electron. 1987, 2, 192–199. [Google Scholar] [CrossRef]
- Gasparetto, A.; Boscariol, P.; Lanzutti, A.; Vidoni, R. Path planning and trajectory planning algorithms: A general overview. Mech. Mach. Sci. 2015, 29, 3–27. [Google Scholar]
- Gasparetto, A.; Zanotto, V. A new method for smooth trajectory planning of robot manipulators. Mech. Mach Theory 2007, 42, 455–471. [Google Scholar] [CrossRef]
- Zhang, X.; Xiao, F.; Tong, X.; Yun, J.; Liu, Y.; Sun, Y.; Tao, B.; Kong, J.; Xu, M.; Chen, B. Time optimal trajectory planning based on improved sparrow search algorithm. Front. Bioeng. Biotech 2022, 10, 852408. [Google Scholar]
- Wu, Y.; You, Y.; Jiang, J. New predictor-corrector methods based on piecewise polynomial interpolation for milling stability prediction. Mach. Sci. Technol. 2020, 24, 688–718. [Google Scholar] [CrossRef]
- Sun, J.; Han, X.; Zuo, Y.; Tian, S.; Song, J.; Li, S. Trajectory planning in joint space for a pointing mechanism based on a novel hybrid interpolation algorithm and NSGA-II algorithm. IEEE Access 2020, 8, 228628–228638. [Google Scholar] [CrossRef]
- Hu, X.; Wu, H.; Sun, Q.; Liu, J. Robot Time Optimal Trajectory Planning Based on Improved Simplified Particle Swarm Optimization Algorithm. IEEE Access 2023, 11, 44496–44508. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools. Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef] [PubMed]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Mazhoud, I.; Hadj-Hamou, K.; Bigeon, J.; Joyeux, P. Particle swarm optimization for solving engineering problems: A new constraint-handling mechanism. Eng. Appl. Artif. Intell. 2013, 26, 1263–1273. [Google Scholar] [CrossRef]
- Fang, S.; Ru, Y.; Liu, Y.; Hu, C.; Chen, X.; Liu, B. Route planning of helicopters spraying operations in multiple forest areas. Forests 2021, 12, 1658. [Google Scholar] [CrossRef]
- Zhao, J.; Zhu, X.; Song, T. Serial manipulator time-jerk optimal trajectory planning based on hybrid IWOA-PSO algorithm. IEEE Access 2022, 10, 6592–6604. [Google Scholar] [CrossRef]
- Kamel, M.A.; Yu, X.; Zhang, Y. Real-time fault-tolerant formation control of multiple WMRs based on hybrid GA–PSO algorithm. IEEE Trans. Autom. Sci. Eng. 2020, 18, 1263–1276. [Google Scholar] [CrossRef]
- Song, Q.; Yu, L.; Li, S.; Hanajima, N.; Zhang, X.; Pu, R. Energy dispatching based on an improved PSO-ACO algorithm. Int. J. Intell. Syst. 2023, 2023, 3160184. [Google Scholar] [CrossRef]
- Tanyildizi, E.; Demir, G. Golden sine algorithm: A novel math-inspired algorithm. Adv. Electr. Comput. Eng. 2017, 17, 71–78. [Google Scholar] [CrossRef]
- Singh, A.; Singla, A.; Soni, S. Extension of DH parameter method to hybrid manipulators used in robot-assisted surgery. Proc. Inst. Mech. Eng. Part H 2015, 229, 703–712. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the IEEE 6th International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Hu, W.; Li, S. A simpler and more effective particle swarm optimization algorithm. J. Softw. 2007, 18, 861–868. (In Chinese) [Google Scholar] [CrossRef]
- Varol Altay, E.; Alatas, B. Bird swarm algorithms with chaotic mapping. Artif. Intell. Rev. 2020, 53, 1373–1414. [Google Scholar] [CrossRef]
- Hu, S.; Liu, H.; Feng, Y.; Cui, C.; Ma, Y.; Zhang, G.; Huang, X. Tool Wear Prediction in Glass Fiber Reinforced Polymer Small-Hole Drilling Based on an improved circle chaotic mapping grey wolf algorithm for bp neural network. Appl. Sci. 2023, 13, 2811. [Google Scholar] [CrossRef]
- Chauhan, P.; Deep, K.; Pant, M. Novel inertia weight strategies for particle swarm optimization. Memet. Comput. 2013, 5, 229–251. [Google Scholar] [CrossRef]
- Fan, E. Extended tanh-function method and its applications to nonlinear equations. Phys. Lett. A 2000, 277, 212–218. [Google Scholar] [CrossRef]
- Clerc, M.; Kennedy, J. The particle swarm-explosion, stability, and convergence in a multidimensional complex space. IEEE Trans. Evol. Comput. 2002, 6, 58–73. [Google Scholar] [CrossRef]
- Jin, Y. Surrogate-assisted evolutionary computation: Recent advances and future challenges. Swarm Evol. Comput. 2011, 1, 61–70. [Google Scholar] [CrossRef]
- Corke, P.I. A robotics toolbox for MATLAB. IEEE Robot. Autom. Mag. 1996, 3, 24–32. [Google Scholar] [CrossRef]
- Xu, J.; Ren, C.; Chang, X. Robot time-optimal trajectory planning based on quintic polynomial interpolation and improved Harris Hawks algorithm. Axioms 2023, 12, 245. [Google Scholar] [CrossRef]
- Yang, J.; Liu, R.; Tong, Q.; Yang, X.; Liu, Q.; Yao, A. Multi-objective optimization of LCC-S-compensated IPT system for improving misalignment tolerance. Appl. Sci. 2023, 13, 3666. [Google Scholar] [CrossRef]
- Jin, R.; Rocco, P.; Geng, Y. Cartesian trajectory planning of space robots using a multi-objective optimization. Aerosp. Sci. Technol. 2021, 108, 106360. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Peer, A. Wood products manufacturing optimization: A survey. IEEE Access 2022, 10, 121653–121683. [Google Scholar] [CrossRef]
- Kunic, A.; Naboni, R.; Kramberger, A.; Schlette, C. Design and assembly automation of the robotic reversible timber beam. Autom. Constr. 2021, 123, 103531. [Google Scholar] [CrossRef]
- Dong, W.; Xiong, X.; Ma, Y.; Yue, X. Woodworking tool wear condition monitoring during milling based on power signals and a particle swarm optimization-back propagation neural network. Appl. Sci. 2021, 11, 9026. [Google Scholar] [CrossRef]
- Mukherjee, S.; Kumar, R.; Borah, S. An intelligent fast controller for autonomous wheeled robot path navigation in challenging environments. Ind. Robot 2022, 50, 107–121. [Google Scholar] [CrossRef]
- Wang, F.; Xie, B.; Lü, E.; Zeng, Z.; Mei, S.; Ma, C.; Guo, J. Design of a Moisture content detection system for yinghong no. 9 tea leaves based on machine vision. Appl. Sci. 2023, 13, 1806. [Google Scholar] [CrossRef]
- Ji, W.; Chen, G.; Xu, B.; Meng, X.; Zhao, D. Recognition method of green pepper in greenhouse based on least-squares support vector machine optimized by the improved particle swarm optimization. IEEE Access 2019, 7, 119742–119754. [Google Scholar] [CrossRef]
- Qiu, H.; Zhang, H.; Lei, K.; Hu, X.; Yang, T.; Jiang, X. A New Tree-Level Multi-Objective Forest Harvest Model (MO-PSO): Integrating Neighborhood Indices and PSO algorithm to improve the optimization effect of spatial structure. Forests 2023, 14, 441. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).