Insights into Bending Stiffness Modeling of Elementary Flexure Hinges
Abstract
:1. Introduction
2. Nonlinear Bending of a Straight Beam
2.1. Large Displacement Model of a Planar Beam
2.2. Dimensionless Model of a Planar Beam
3. Analytical Solution of the Flexure Joint Bending Stiffness Model
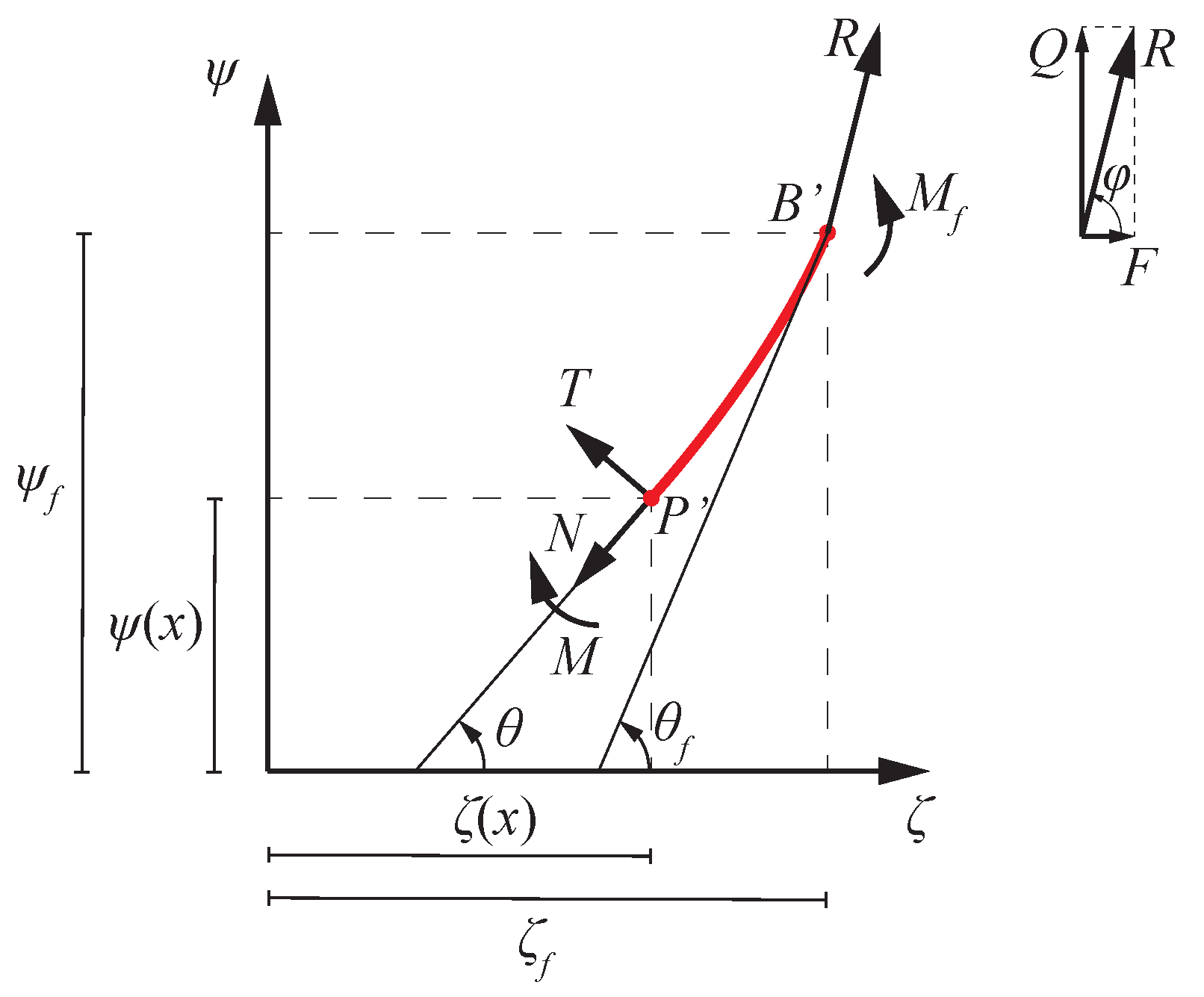
3.1. Nonlinear Model Simplification and Analytical Solution
3.2. Boundary Conditions
4. Bending Stiffness Model of a Flexure Hinge
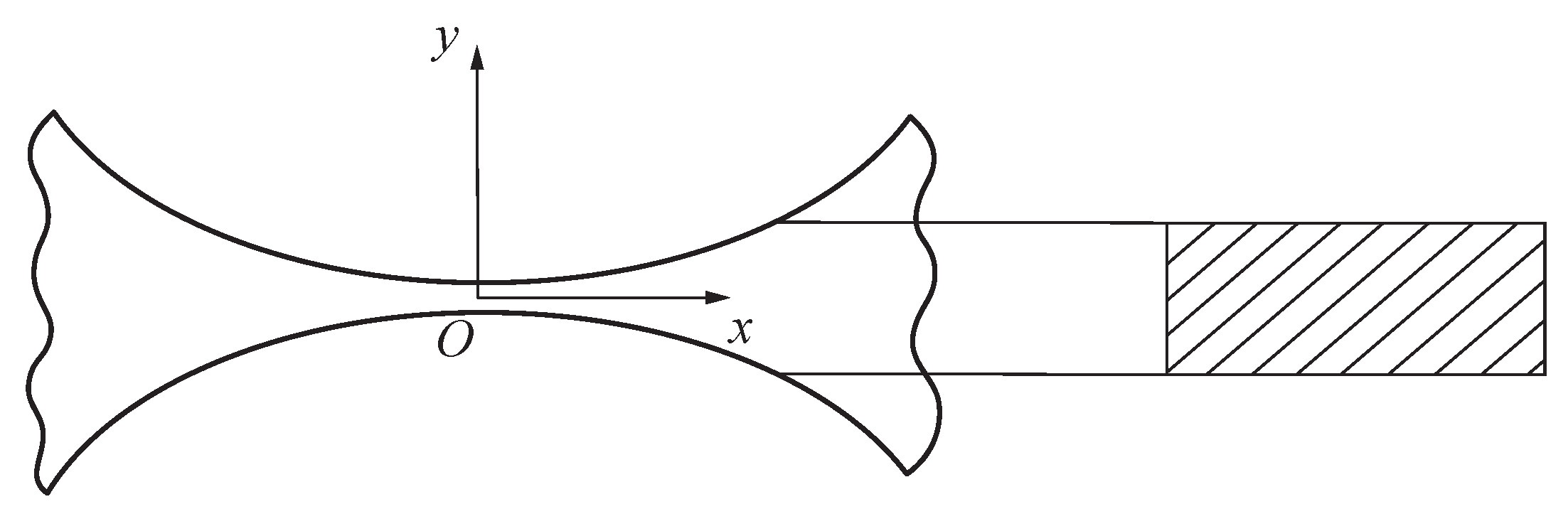
4.1. Case Study: An Elliptical Flexure Hinge
4.2. Conditions of Applicability of the Linear Model
4.3. Solution of the Model for an Elliptical Flexure Hinge
5. Domain of Application of the Linear Model
6. Comparison of Analytical and Numerical Solutions
6.1. Case I
6.2. Case II
6.3. Case III
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Howell, L.L. Compliant Mechanisms; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Wang, P.Y.; Xu, Q.S. Design and Modeling of Constant-Force Mechanisms: A Survey. Mech. Mach. Theory 2018, 119, 1–21. [Google Scholar] [CrossRef]
- Oh, Y.S.; Kota, S. Synthesis of Multistable Equilibrium Compliant Mechanisms Using Combinations of Bistable Mechanisms. ASME J. Mech. Des. 2009, 131, 021002. [Google Scholar] [CrossRef]
- Kota, S.J.; Joo, Z.L.; Rodgers, S.M.; Sniegowski, J. Design of Compliant Mechanisms: Applications to MEMS. Analog Integr. Circuits Signal Process. 2001, 29, 7–15. [Google Scholar] [CrossRef]
- Qin, Y.D.; Shirinzadeh, B.; Tian, Y.L.; Zhang, D.W.; Bhagat, U. Design and Computational Optimization of a Decoupled 2-DOF Monolithic Mechanism. IEEE/ASME Trans. Mechatron. 2014, 19, 874–883. [Google Scholar] [CrossRef]
- Fleming, A.J.; Yong, Y.K. An Ultrathin Monolithic XY Nanopositioning Stage Constructed From a Single Sheet of Piezoelectric Material. IEEE/ASME Trans. Mechatron. 2017, 22, 2611–2618. [Google Scholar] [CrossRef]
- Xu, Q.S. Design and Development of a Novel Compliant Gripper With Integrated Position and Grasping/Interaction Force Sensing. IEEE Trans. Autom. Sci. Eng. 2017, 14, 1415–1428. [Google Scholar] [CrossRef]
- Tanikawa, T.; Arai, T. Development of a Micro-Manipulation System Having a Two-Fingered Micro-Hand. IEEE Trans. Robot. Autom. 1999, 15, 152–162. [Google Scholar] [CrossRef]
- Rakuff, S.; Cuttino, J.F. Design and Testing of a Long-Range, Precision Fast Tool Servo System for Diamond Turning. Precis. Eng. 2009, 33, 18–25. [Google Scholar] [CrossRef]
- Han, Y.M.; Han, C.; Kim, W.H.; Seong, H.Y.; Choi, S.B. Control Performances of a Piezoactuator Direct Drive Valve System at High Temperatures With Thermal Insulation. Smart Mater. Struct. 2016, 25, 097003. [Google Scholar] [CrossRef]
- Granstrom, J.; Feenstra, J.; Sodano, H.A.; Farinholt, K. Energy Harvesting From a Backpack Instrumented With Piezoelectric Shoulder Straps. Smart Mater. Struct. 2007, 16, 1810. [Google Scholar] [CrossRef]
- Sun, X.Q.; Yang, B.T. A New Methodology for Developing Flexure-Hinged Displacement Amplifiers With Micro-Vibration Suppression for a Giant Magnetostrictive Micro Drive System. Sens. Actuators A 2017, 263, 30–43. [Google Scholar] [CrossRef]
- Odhner, L.U.; Dollar, A.M. The Smooth Curvature Model: An Efficient Representation of Euler–Bernoulli Flexures as Robot Joints. IEEE Trans. Robot. 2012, 28, 761–772. [Google Scholar] [CrossRef]
- Paros, J.; Weisbord, L. How to design flexure hinge. Mach. Des. 1965, 37, 151–156. [Google Scholar]
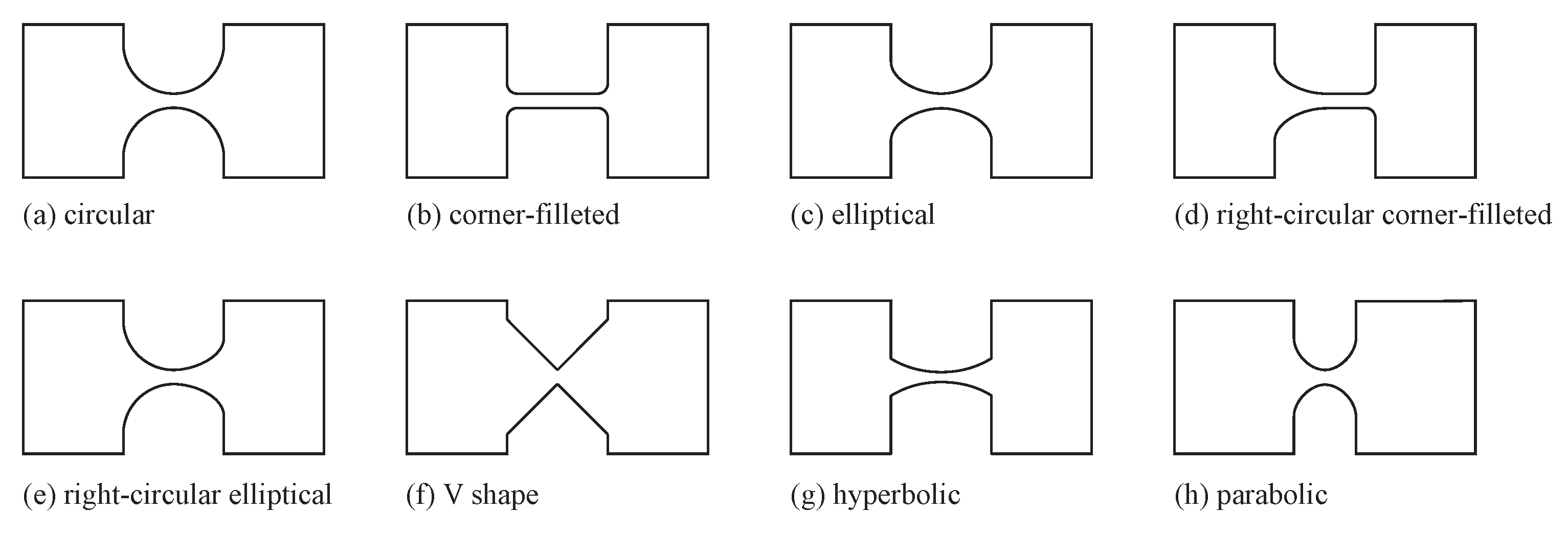
- Smith, S.; Badami, V.; Dale, J.; Xu, Y. Elliptical flexure hinges. Rev. Sci. Instrum. 1997, 68, 1474–1483. [Google Scholar] [CrossRef]
- Lobontiu, N.; Paine, J.; Garcia, E.; Goldfarb, M. Corner-filleted flexure hinges. J. Mech. Des. 2001, 123, 346–352. [Google Scholar] [CrossRef]
- Lobontiu, N.; Paine, J.S.N.; O’Malley, E.; Samuelson, M. Parabolic and hyperbolic flexure hinges: Flexibility, motion precision and stress characterization based on compliance closed-form equations. Precis. Eng. 2002, 26, 183–192. [Google Scholar] [CrossRef]
- Tian, Y.; Shirinzadeh, B.; Zhang, D.; Zhong, Y. Three flexure hinges for compliant mechanism designs based on dimensionless graph analysis. Precis. Eng. 2010, 34, 92–100. [Google Scholar] [CrossRef]
- Tian, Y.; Shirinzadeh, B.; Zhang, D. Closed-form equations of the filleted V-shaped flexure hinges for compliant mechanism designs. Precis. Eng. 2010, 34, 408–418. [Google Scholar] [CrossRef]
- Chen, G.; Liu, X.; Gao, H.; Jia, J. A Generalized Model for Conic Flexure Hinges. Rev. Sci. Instrum. 2009, 80, 055106. [Google Scholar] [CrossRef]
- Lobontiu, N.; Cullin, M.; Ali, M.; Brock, J. A generalized analytical compliance model for transversely symmetric three-segment flexure hinges. Rev. Sci. Instrum. 2011, 82, 105116-1–105116-9. [Google Scholar] [CrossRef]
- Chen, G.M.; Jia, J.Y.; Li, Z.W. On Hybrid Flexure Hinges. In Proceedings of the 2005 IEEE Networking, Sensing and Control, Tucson, AZ, USA, 19–22 March 2005; pp. 700–704. [Google Scholar]
- Lin, R.; Zhang, X.; Long, X.; Fatikow, S. Hybrid flexure hinges. Rev. Sci. Instrum. 2013, 84, 085004. [Google Scholar] [CrossRef] [PubMed]
- Qi, K.Q.; Xiang, Y.; Fang, C.; Zhang, Y.; Yu, C.S. Analysis of the Displacement Amplification Ratio of Bridge-Type Mechanism. Mech. Mach. Theory 2015, 87, 45–56. [Google Scholar] [CrossRef]
- Ling, M.X.; Cao, J.Y.; Zeng, M.H.; Lin, J.; Inman, D.J. Enhanced Mathematical Modeling of the Displacement Amplification Ratio for Piezoelectric Compliant Mechanisms. Smart Mater. Struct. 2016, 25, 75022–75032. [Google Scholar] [CrossRef]
- Clark, L.; Shirinzadeh, B.; Pinskier, J.; Tian, Y.; Zhang, D. Topology Optimization of Bridge Input Structures With Maximal Amplification for Design of Flexure Mechanisms. Mech. Mach. Theory 2018, 122, 113–131. [Google Scholar] [CrossRef]
- Yong, Y.K.; Leang, K.K. Mechanical Design of High-Speed Nanopositioning Systems. In Nanopositioning Technologies; Springer: Cham, Switzerland, 2016; pp. 61–121. [Google Scholar]
- Lobontiu, N.; Paine, J.S.N.; Garcia, E.; Goldfarb, M.A. Design of Symmetric Conic-Section Flexure Hinges Based on Closed-Form Compliance Equations. Mech. Mach. Theory 2002, 37, 477–498. [Google Scholar] [CrossRef]
- Lyon, S.M.; Howell, L.L. A Simplified Pseudo-Rigid-Body Model for Fixed-Fixed Flexible Segments. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Montreal, QC, Canada, 29 September–2 October 2002; ASME: New York, NY, USA, 2002; Volume 36533, pp. 23–33. [Google Scholar]
- Zhang, A.M.; Chen, G.M. A Comprehensive Elliptic Integral Solution to the Large Deflection Problems of Thin Beams in Compliant Mechanisms. ASME J. Mech. Robot. 2013, 5, 021006. [Google Scholar] [CrossRef]
- Wang, P.; Xu, Q.S. Design and Testing of a Flexure-Based Constant-Force Stage for Biological Cell Micromanipulation. IEEE Trans. Autom. Sci. Eng. 2018, 15, 1114–1126. [Google Scholar] [CrossRef]
- Ling, M.; Howell, L.; Cao, J.; Chen, G. Kinetostatic and dynamic modeling of flexure-based compliant mechanisms: A survey. Appl. Mech. Rev. 2020, 72, 030802. [Google Scholar] [CrossRef]
- Boyle, C.; Howell, L.L.; Magleby, S.P.; Evans, M.S. Dynamic Modeling of Compliant Constant-Force Compression Mechanisms. Mech. Mach. Theory 2003, 38, 1469–1487. [Google Scholar] [CrossRef]
- Li, Y.M.; Wu, Z.G. Design, Analysis and Simulation of a Novel 3-DOF Translational Micromanipulator Based on the PRB Model. Mech. Mach. Theory 2016, 100, 235–258. [Google Scholar] [CrossRef]
- Zhu, W.L.; Zhu, Z.; Guo, P.; Ju, B.F. A Novel Hybrid Actuation Mechanism Based XY Nanopositioning Stage With Totally Decoupled Kinematics. Mech. Syst. Signal Process. 2018, 99, 747–759. [Google Scholar] [CrossRef]
- Awtar, S.; Slocum, A.H. Closed-form nonlinear analysis of beam-based flexure modules. In Proceedings of the ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Long Beach, CA, USA, 24–28 September 2005; pp. 101–110. [Google Scholar]
- Awtar, S.; Sen, S. A Generalized Constraint Model for Two-Dimensional Beam Flexures: Nonlinear Load-Displacement Formulation. ASME J. Mech. Des. 2010, 132, 081008. [Google Scholar] [CrossRef]
- Teo, T.; Chen, I.; Yang, G.; Lin, W. A generic approximation model for analyzing large nonlinear deflection of beam-based flexure joints. Precis. Eng. 2010, 34, 607–618. [Google Scholar] [CrossRef]
- Sen, S.; Awtar, S. A Closed-Form Nonlinear Model for the Constraint Characteristics of Symmetric Spatial Beams. ASME J. Mech. Des. 2013, 135, 031003. [Google Scholar] [CrossRef]
- Friedrich, R.; Lammering, R.; Heurich, T. Nonlinear modeling of compliant mechanisms incorporating circular flexure hinges with finite beam Elements. Precis. Eng. 2015, 42, 73–79. [Google Scholar] [CrossRef]
- Coffman, C.V. The Nonhomogeneous Classical Elastica; Technical Report; Department of Mathematics, Carnegie-Mellon University: Pittsburgh, PA, USA, 1976. [Google Scholar]
- Moschini, S.; Palpacelli, M.C. Practical range of applicability of a linear stiffness model of an elliptical flexure hinge. In Proceedings of the 2022 18th IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications (MESA), Taipei, Taiwan, 28–30 November 2022; pp. 1–6. [Google Scholar]
- Lenci, S.; Clementi, F.; Rega, G. Comparing nonlinear free vibrations of Timoshenko beams with mechanical or geometric curvature definition. Procedia IUTAM 2017, 20, 34–41. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Pai, P.F. Linear and Nonlinear Structural Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Luongo, A.; Zulli, D. Mathematical Models of Beams and Cables; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Gerstmayr, J.; Irschik, H. On the correct representation of bending and axial deformation in the absolute nodal coordinate formulation with an elastic line approach. J. Sound Vib. 2008, 318, 461–487. [Google Scholar] [CrossRef]
- Lenci, S.; Rega, G. Nonlinear free vibrations of planar elastic beams: A unified treatment of geometrical and mechanical effects. Procedia IUTAM 2016, 19, 35–42. [Google Scholar] [CrossRef]
- Lenci, S.; Clementi, F.; Rega, G. A comprehensive analysis of hardening/softening behaviour of shearable planar beams with whatever axial boundary constraint. Meccanica 2016, 51, 2589–2606. [Google Scholar] [CrossRef]
- Babilio, E. Dynamics of an axially functionally graded beam under axial load. Eur. Phys. J. Spec. Top. 2013, 222, 1519–1539. [Google Scholar] [CrossRef]
- Chen, G.; Shao, X.; Huang, X. A new generalized model for elliptical arc flexure hinges. Rev. Sci. Instrum. 2008, 79, 095103. [Google Scholar] [CrossRef] [PubMed]
- Villaggio, P. Mathematical Models for Elastic Structures; Cambridge Univeristy Press: Cambridge, UK, 1997. [Google Scholar]
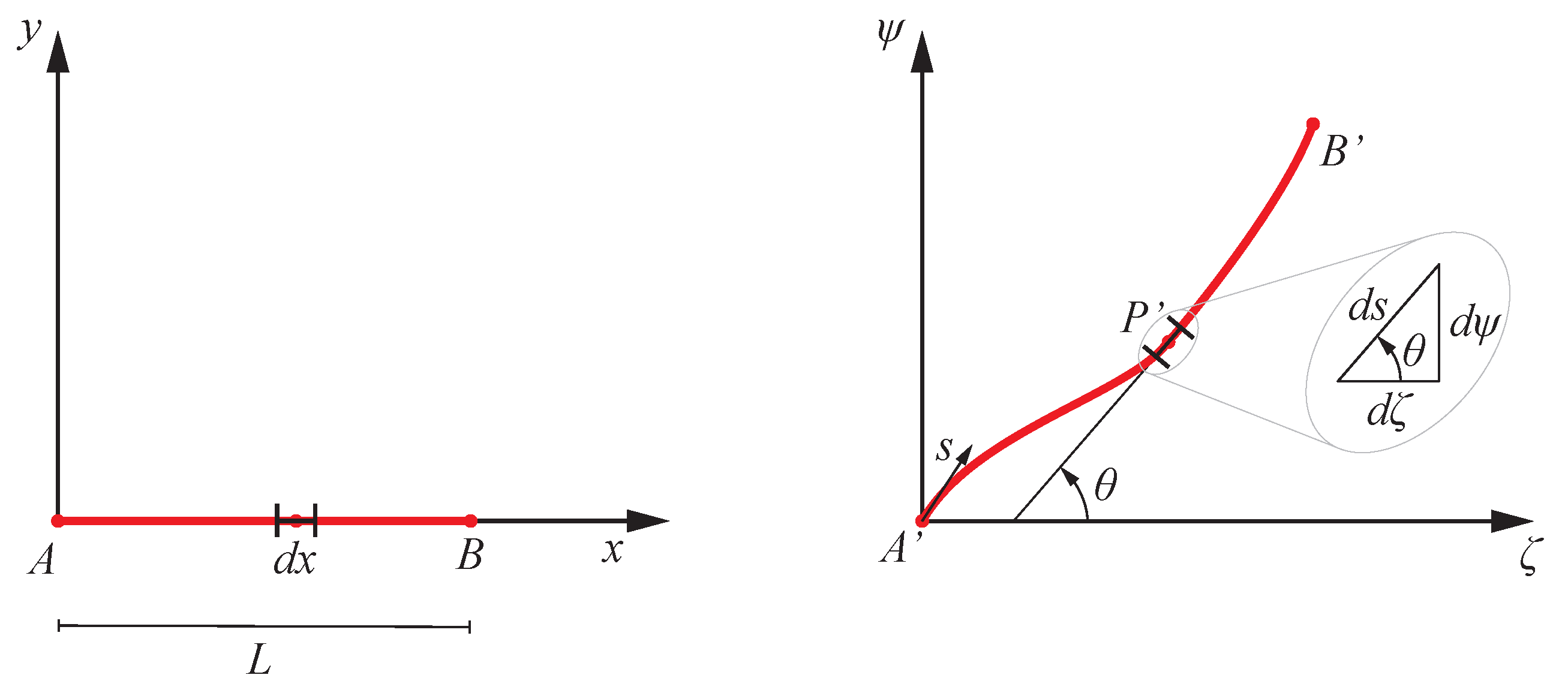


| 5 | |||||||
| 5 | |||||||
| 5 | |||||||
| 10 | |||||||
| 10 | |||||||
| 10 | |||||||
| 15 | |||||||
| 15 | |||||||
| 15 | |||||||
| 5 | |||||||
| 5 | |||||||
| 5 | |||||||
| 10 | |||||||
| 10 | |||||||
| 10 | |||||||
| 15 | |||||||
| 15 | |||||||
| 15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moschini, S.; Palpacelli, M. Insights into Bending Stiffness Modeling of Elementary Flexure Hinges. Appl. Sci. 2023, 13, 9785. https://doi.org/10.3390/app13179785
Moschini S, Palpacelli M. Insights into Bending Stiffness Modeling of Elementary Flexure Hinges. Applied Sciences. 2023; 13(17):9785. https://doi.org/10.3390/app13179785
Chicago/Turabian StyleMoschini, Simir, and Matteo Palpacelli. 2023. "Insights into Bending Stiffness Modeling of Elementary Flexure Hinges" Applied Sciences 13, no. 17: 9785. https://doi.org/10.3390/app13179785
APA StyleMoschini, S., & Palpacelli, M. (2023). Insights into Bending Stiffness Modeling of Elementary Flexure Hinges. Applied Sciences, 13(17), 9785. https://doi.org/10.3390/app13179785







