Abstract
This paper presents a screw dynamics method for multi-rigid-body systems. It establishes the relationship between velocity screw (twist) and force screw (wrench) in the theorem of momentum screw. Then, the structure of a 2UPS + 2UPU parallel manipulator is introduced as an example of application. By analyzing the constraint wrench of each limb and the twist of the moving platform in the theorem of momentum screw, the dynamics equation for solving the driving force makes the method very convenient for computer programming. The dynamics equation can be reorganized into a non-homogeneous linear equation and establishes the relationship between the constraint wrench of each limb and the twist of the moving platform in screw coordinate. The outstanding advantage of the algorithm proposed in this paper is that the average calculation time is only 83.21% of that of the Newton–Euler method for the 2UPS + 2UPU parallel manipulator on the same computer. This methodology provides a convenient canonical form for the dynamics analysis of multi-rigid-body systems.
1. Introduction
At present, parallel manipulators are widely used in machine tools because of their high stiffness and loading capacity, fewer driving branches, and easy control. With the application of parallel robots in machine tools, the dynamics analysis of a parallel manipulator becomes increasingly important. The mobility characteristics of the Schoenflies motion include three independent translations and one rotation around a fixed axis. The parallel mechanism that performs the Schoenflies motion can be used in special manipulation. For example, it can be used for product grabbing, assembly, and the processing production line. However, a Schoenflies parallel manipulator has a structure of multiple closed loops, which leads to a very complicated dynamics model. Inverse dynamics is utilized to calculate the driving force as an input to control the motion required by the end effector. Compared with their series counterparts with perfect dynamics modeling methods, the dynamics of parallel mechanisms is still a problem []. Therefore, this paper aims to propose an effective dynamics method for such multi-rigid-body systems.
In the field of robot dynamics, research on the dynamics modeling of parallel robots has made significant progress. The main method includes the Newton–Euler equation, the Euler–Lagrange equation, the Kane method, and the virtual work principle []. The Newton–Euler equation is widely used to establish the dynamics model of a robot. Considering the inertial force and moment, the Newton equations and Euler equations of all rigid bodies can be obtained to solve the closed-loop dynamics of systems such as the Stewart platform [], a self-reconfiguring chain [], and multilink cable-driven hyper-redundant robots []. The Newton–Euler equations take all joint forces, including the torques and forces, and input and output into account, which is one major advantage of this method. However, a large number of algebraic and differential equations increase the calculation cost for the Newton–Euler method. From the perspective of analytical mechanics, some scholars utilized the Lagrange method to investigate the dynamics of manipulators [,,]. The Lagrange equation of the first type takes the Lagrange multiplier and treats the constraint as an additional equation []. The Lagrange equation of the second type allows one to establish the ordinary differential equations of a mechanical system and obtain the solution of the equation by using a numerical algorithm []. For example, the inverse dynamics of the Stewart platform were derived by using the Lagrange method [,]. Kumar et al. [] proposed a modular analysis method for the dynamics of hybrid robots and demonstrated its application under a software framework. The Kane method takes the generalized rate as an independent variable and can eliminate constrained forces/moments []. Enferadi et al. [] derived a closed-form dynamics formula for a spherical parallel manipulator by using the Kane method. The virtual work principle provides a universal method for solving the dynamics problems of complex mechanical systems []. In the dynamic simulation and control of robots, these methods have higher computational efficiency [,]. However, when conducting inverse dynamics and structure design, constraints need to be easily calculated. When analyzing the inverse dynamics of robots, these methods all have their individual limitations. In addition, the natural orthogonal complement method [,], the particle dynamics and a recursive approach [], a parallel Hamiltonian formulation [], and a symbolic–numerical method [] are adopted to establish the dynamics models of closed-loop systems. The existing methods for the dynamics of complicated multi-closed-loop systems often face severe difficulties [,,]. In the aforementioned research, seldom were the dynamics discussed in the coordinates of a momentum screw.
This paper aims at the dynamics of a multi-rigid-body system with the example of the Schoenflies parallel manipulator from the aspect of a momentum screw. It derives the dynamics equation of the momentum screw in one coordinate frame to solve the multi-rigid-body system. The theorem of the momentum screw proposed in this paper provides a vector dynamics algorithm and reveals the relationship between the velocity screw and the force screw. It brings a new idea for the research of wrench and twist. The real-time calculation of the Schoenflies parallel manipulator is performed by programming the algorithm on a computer. When solving the input force(s), we eliminate the redundant internal force and joint constraint force/torque, which effectively reduces the calculation load. This paper proposes an inverse dynamics algorithm based on the theorem of the momentum screw. Compared with the traditional methods, our algorithm has higher computation efficiency and lower computation cost.
2. Momentum Screw
Screw theory is a useful mathematical tool used to represent motion and force of rigid bodies. In this paper, the concept of a momentum screw to connect the force screw (wrench) and velocity screw (twist) provides a new theoretical basis for the dynamics analysis of a multi-rigid-body system.
Suppose that the velocity of a differential mass on the rigid body is , then its momentum is
where represents the differential of momentum.
In the coordinate frame shown in Figure 1, the differential moment of the momentum of the differential mass is indicated by where represents the moment of momentum of the particle about the origin of the coordinate frame:
where represents the position vector of the differential mass .
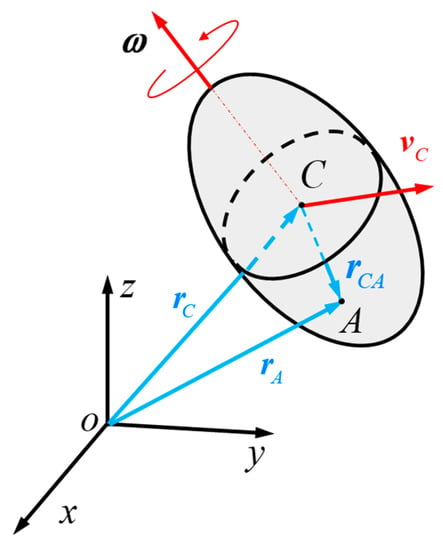
Figure 1.
Momentum and moment of momentum of a rigid body.
Define the differential momentum screw as
where represents the momentum screw.
Therefore, the momentum screw of a rigid body is
where represents the whole space of the rigid body. Because
where represents the center of mass, is the linear velocity of the mass center. At the same time,
where is the angular velocity of the rigid body, is the vector from point to point , and . So, we obtain that
As a result, the momentum screw can be defined as
where , which is the momentum of a rigid body; , which represents the moment of momentum of the rigid body; and the left subscript represents the quantity in the coordinate frame .
Let the resultant force screw acting on the rigid body be
where represents the position vector of an arbitrary point on the action line of the force in the coordinate frame. According to Newton’s second law, there is
Therefore, separating the variables of differential Equation (10) and integrating both sides of the equation yields
When , it can be obtained from Equation (11) that
Equation (12) shows the conservation of momentum and the conservation of the moment of momentum of a rigid body when the resultant wrench of the external forces acting on the rigid body is zero.
For a system composed of rigid bodies, the theorem of momentum screw is expressed as
where represents the total number of the external forces.
When , the rigid-body system is in equilibrium. Otherwise,
where represents that the momentum screw is about the rigid body, represents the total number of rigid bodies, and represents the resultant external force screw on the rigid body.
Equation (14) jointly states the theorem of momentum and the theorem of moment of momentum of a multi-rigid-body system in screw coordinate. In this paper, we call Equation (14) the theorem of momentum screw.
3. Screw Kinematics and Dynamics of a Limb of a Schoenflies Manipulator
3.1. Description of the Schoenflies Manipulator
A spatial Schoenflies parallel manipulator is made up of two UPU kinematic chains and two UPS kinematic chains as shown in Figure 2. Here U represents a universal joint, P represents a prismatic joint, and S represents a spherical joint.
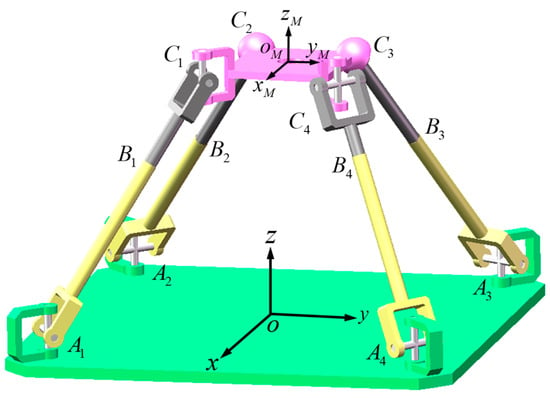
Figure 2.
A Schoenflies parallel manipulator.
In the absolute coordinate frame , the z-axis is perpendicular to the plane , the origin is located at the geometric center of , the x-axis is perpendicular to , and the y-axis is determined by the right-hand rule. The local coordinate frame is established on the end effector . The origin of the coordinate frame, , is seated at the geometric center of the plane . The -axis is perpendicular to the plane , the -axis is perpendicular to line , and the -axis is determined in accordance to the right-hand rule.
3.2. Kinematic Analysis of a Limb
According to the theory of degree of freedom analysis [,], in a nonsingular space, the end effector of the 2UPS + 2UPU mechanism has four DoFs, which allows it to perform Schoenflies motion. In this section, the kinematics of each limb will be analyzed. The displacement analysis of the UPS limb of the parallel mechanism is shown in Figure 3.
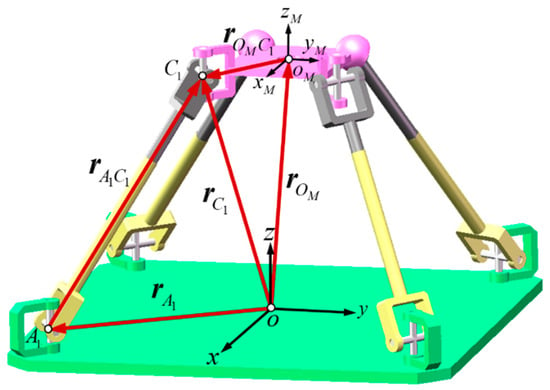
Figure 3.
Displacement analysis of an UPU limb.
The connection point in the platform coordinate frame can be transformed to the base frame:
where and are the position vectors in the absolute coordinate frame and platform coordinate frame. We obtain that
or
which is the inverse displacement equation for the Schoenflies parallel manipulator. Supposing that the length of limb is , and its unit direction vector is , we have
and
The time derivative of the limb vector gives the velocity of the connection point of the limb and platform:
where is the angular velocity of the moving platform around the z-axis, and is the linear velocity of the moving platform.
The linear velocity between two connecting parts of the limb is specified by the component of this velocity along the limb:
The linear velocity perpendicular to the limb is related to the angular velocity of the limb:
where is the angular velocity of the first UPS limb perpendicular to the second limb, and
which is shown in Figure 4.
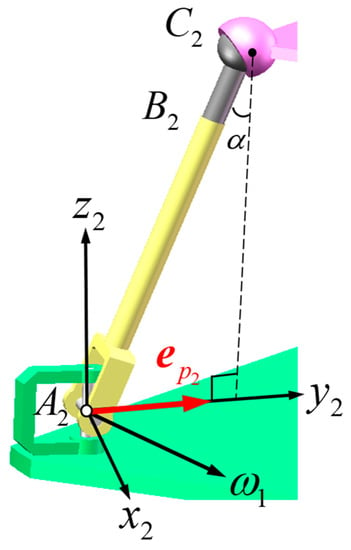
Figure 4.
Angular velocity analysis of a single kinematic chain.
Hence, the twist of each limb may be uniformly expressed by:
3.3. Screw Dynamics Analysis of a Limb
The momentum screw of the lower limb is
where is the position vector of the center of mass of the lower limb in the absolute coordinate frame. is the mass moment of inertia matrix of the lower limb relative to in the absolute coordinate frame. It is worth noting that the given is the mass moment of inertia matrix of the lower limb relative to its center, , in the local coordinate frame, and they meet that . For a kinematic chain, is a transformation matrix from its local coordinate frame to the absolute coordinate frame.
The momentum screw of the upper limb is
where is the position vector of the center of mass of the upper limb in the absolute coordinate frame. is the mass moment of inertia matrix of the upper limb relative to in the absolute coordinate frame. Similarly, meets .
The force screw acting on the single limb is
Substituting Equations (25)–(27) into Equation (14) yields
or
where is the sum of the external force screw, including the constraints of joints and . is the force screw of gravity.
Here, the viscous friction between the prismatic joint belongs to the internal force and therefore does not appear on the right side of the momentum screw Equation (14).
Suppose , we obtain that
Next, the dynamics equations of the UPU and UPS kinematic chains will be discussed separately.
- UPU kinematic chains
According to the physical meaning of a reciprocal screw, stands for the constraint torque around as shown in Figure 5 for . The terminal constraint of the UPU limbs is a torque parallel to the vector . Therefore, the constraint torques of the UPU limbs can be expressed by .
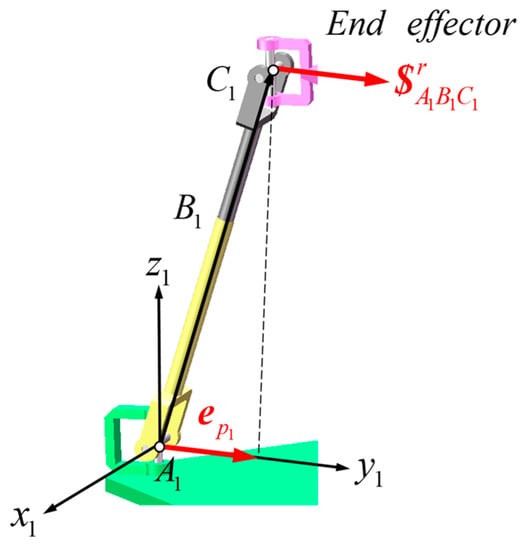
Figure 5.
Constraint torque of the UPU kinematic chain.
The constraint torques can be eliminated from Equation (30) by taking the cross products on both sides of the equation with as
Therefore, the constraint force is obtained from Equation (31):
where is the component of the force at the universal joint along the limb.
- 2.
- UPS kinematic chain
For the UPS kinematic chain, the constraint torques and are equal to zero at the spherical joint. can be obtained as
Similarly, the force can be obtained by the cross products on both sides of Equation (33). Therefore, the force can be expressed as follows:
where is the component of the force at the spherical joint or universal joint along the limb , and .
The spherical joints at and only contain constraint forces. The constraint forces are and . For the universal joints at and , there are both constraint forces and torques. The constraint forces are and . The constraint torques and can be expressed by and , where and are the magnitudes of two constraint torques. It is worth noting that is not the magnitude of force , while and are the magnitudes of moments and . is the component of constraint force along the limb direction.
3.4. Screw Dynamics Analysis of the Moving Platform
The constraint force screws from the four joints to the end actuator are demonstrated in Figure 6.
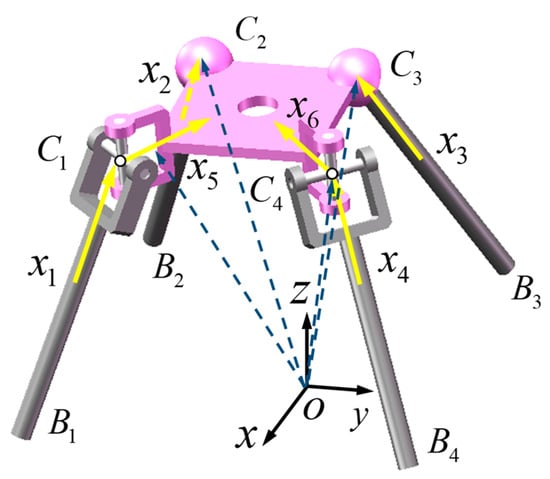
Figure 6.
The constraints force screws applied to the moving platform.
It can be seen from Equation (14) that the momentum screw of the moving platform is
The sum of the external force screws acting on the moving platform is
Substituting Equations (38) and (39) into Equation (14) presents
The constraint force can be transformed by Equations (32) and (34). Therefore, Equation (37) contains six scalar equations in the unknowns denoted by a vector . From Equations (32), (34), and (37), we obtain that
Rearranging Equation (38) yields
Thus, Equation (39) can be expressed in matrix multiplication form,
where is the coefficient matrix, and is a column vector: and .
From Figure 5, we know that and are located in the plane. Therefore, only need to be calculated because they are required in the calculation of driving forces.
3.5. Solution of the Driving Forces
For manipulator control, the driving forces in the limbs need to be fully determined. After obtaining , the driving force, , of each limb can be found by
where is the momentum of the upper limb. We can resort to Equation (41) to solve the driving force of each limb.
4. Simulation and Discussion
The Schoenflies parallel mechanism can be used in machine tools to fabricate complex workpieces. To verify the dynamics equations of the 2UPS + 2UPU parallel manipulator, the desired trajectory function that changes over time is given as follows:
The trajectory changes over time, and the reason for choosing this trajectory is that it represents reciprocating motion. It should be noted that the trajectory at the left and right sides of the intersection point are identical, and the diagram displays their periodic motion.
The geometry parameters of the structure and dynamics parameters of the Schoenflies parallel manipulator are listed in Table 1.

Table 1.
The structure parameters of the Schoenflies parallel manipulator.
The first step in solving the inverse dynamics is to solve the joint motion based on the motion equation of the end effector. According to the inverse kinematics algorithm, we obtained the velocity of the actuators and plotted them in Figure 7.
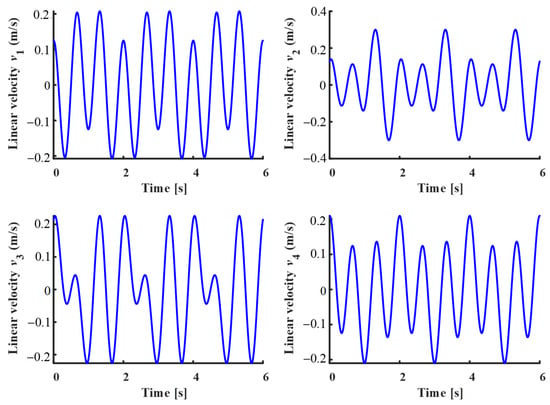
Figure 7.
Input velocity of the actuator.
To evaluate the computation efficiency of this method, the computation cost is evaluated by programming the algorithm on a computer. The computation cost of the rigid-body dynamics algorithm means the number of operations of the algorithm []. The computation cost of an algorithm can be quantified by the calculation time. The momentum screw method only eliminates unnecessary constraints, which is similar to but different from the Newton–Euler equation.
To compare the momentum screw method with the existing methods, we also used the Newton–Euler method to obtain the dynamics equations of the same Schoenflies manipulator. Figure 8 illustrates the simulation results obtained by the momentum screw method and the Newton–Euler method. From Figure 8, it can be seen that the final dynamics results obtained using these two methods are the same. Next, we will discuss three aspects: Computational results discussion, the real-time computing power, and a comparison of the computational advantages.
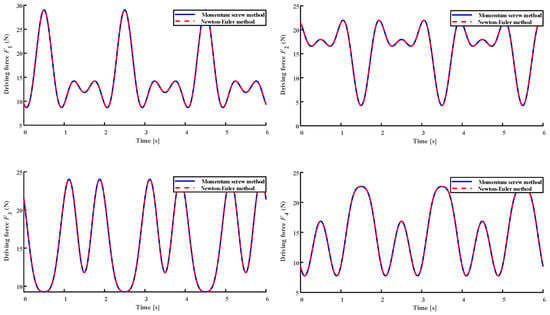
Figure 8.
Input forces of the actuators on these 4 limbs.
- (1)
- Computational results discussion
From Figure 8, it can be seen that the amplitude of the force calculated using our method show good consistency with the results carried out through Newton-Euler method. The results validate our method.
Next, we will discuss the difference in calculation costs when using the Newton–Euler method and the momentum screw method proposed in this paper for calculation. A comparison of the Newton–Euler method and the proposed momentum screw method in terms of the elapsed time in computation is listed in Table 2.

Table 2.
Comparison of elapsed time by utilizing the momentum screw method versus the Newton–Euler method.
- (2)
- The real-time capabilities
To demonstrate the real-time capabilities of the codes, the runtime of the codes is calculated using the tic/toc method in MATLAB. The dynamics modeling algorithms for these two methods were implemented via programming on MATLAB. These programs are executed on Windows 11 computers equipped with Intel Core i7-12700H CPUs. The calculation time for solving dynamics equations utilizing the momentum screw method is 0.767529 s, while the calculation time for the Newton–Euler method is 0.923187 s. The codes run within 6 s. Thus, the real-time advantage of the momentum screw method for the Schoenflies parallel manipulator is validated.
- (3)
- Comparison of computational advantages
Using the Newton–Euler method, there are three constraint forces and one constraint torque at a universal joint. Therefore, when using the Newton–Euler equation, each UPS limb will provide 13 unknowns: 3 constraint forces and 3 constraint torques at the prismatic joint, 3 constraint forces and 1 constraint torque at the universal joint, and 3 pure constraint forces at the spherical joint. Similarly, each UPU limb will provide 14 unknowns. The difference between the UPU limb and the UPS limb is that the universal joint connecting the leg and the end effector will provide an additional constraint torque. A large number of second-order differential equations and calculations for the Newton–Euler method are inevitable. Appendix A provides the calculation process of the Newton–Euler method.
Unlike the traditional Newton–Euler method, the screw formulation avoids second-order differential equations, which leads to lower computation cost. It is worth noting that there are two unknowns in the equations of the UPU limb and one unknown in the equation of the UPS limb for the true effective constraint of the end effector. Therefore, there are six unknowns provided by the four limbs to the moving platform with a definite direction. The six unknowns can be solved by adopting the momentum screw equation for the moving platform. Compared with the Newton–Euler method, we only need to analyze the constraint forces of the end effector and convert the joint forces to be four unknowns (Equation (40)), which greatly reduces the computation cost. Therefore, the algorithm proposed in this paper is effective, has lower computation cost, and is therefore more convenient in on-time control.
5. Conclusions
This paper presents a momentum screw method to study the dynamics of multi-rigid-body systems through an example of a Schoenflies unsymmetrical parallel manipulator. The momentum screw theorem provides a new perspective between the velocity screw and force screw. Therefore, a set of momentum screw equations of the multi-rigid-body system are derived in the screw coordinate. The kinematics model of each limb is established by vectors, and the velocity screw of each limb is obtained. By linearizing the constraint force of each joint, the momentum screw equation of a rigid body is established. The dynamics equation can be reorganized into a non-homogeneous linear equation. By analyzing the relationship between the constraint wrench of each leg and its twist in the theorem of the momentum screw, the dynamics for solving the driving force makes the method very suitable for computer programming. The dynamics equation in the theorem of the moment of momentum of the screw establishes the relationship between the wrench of each limb and the twist of the moving platform in the screw coordinate. Using a Schoenflies parallel manipulator as a case for dynamics modeling, we validate the merit of efficiency of the screw dynamics of multibody systems. Compared with the traditional methods, this algorithm has a lower cost of computation.
Author Contributions
Conceptualization, J.-S.Z.; methodology, J.-S.Z. and H.-L.S.; formal analysis, J.-S.Z., H.-L.S., H.-Y.L. and D.-J.Z.; writing—original draft preparation, J.-S.Z. and H.-L.S.; H.-L.S., H.-Y.L. and D.-J.Z. performed the programming in MATLAB and plotted all the diagrams. All authors discussed and revised the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Basic Research Project Group of China (No. 514010305-301-3).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This work was supported in part by the Basic Research Project Group of China under Grant 514010305-301-3; in part by 2020GQI1003 from the Guoqiang Research Institute of Tsinghua University; and in part by the State Key Laboratory of Tribology, Tsinghua University.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Notation | Meanings of the Notation |
| Velocity of the differential mass | |
| Position vector of the differential mass in the absolute coordinate | |
| Momentum screw | |
| Velocity screw (twist) | |
| Coordinate space of the rigid body | |
| Linear velocity of the center of mass | |
| Force screw (wrench) | |
| Mass moment of inertia of a rigid body relative to its center of mass | |
| Density of a rigid body | |
| Momentum | |
| Moment of momentum | |
| Unit axial vector | |
| Reciprocal screws of the limb | |
| Position vector of the point in the absolute coordinate frame | |
| Rotation transformation matrix | |
| Angular velocity of the limb | |
| Linear velocity of point in the absolute coordinate frame | |
| Unit direction vector of the limb | |
| plane | |
| Constraint torque of joint | |
| Mass of the lower part | |
| Mass of the upper part | |
| Angular velocity of the moving platform around the z-axis | |
| Gravity acceleration |
Appendix A
The Newton–Euler method is the basic method of dynamics modeling in robot dynamics. Reference [] provided the dynamics modeling process of the parallel mechanism. The Schoenflies parallel manipulator consists of four legs, a moving platform, and a base. For the kinematic and dynamics modeling of four legs, we use the method in reference []. The difference between the two methods is in the processing of acceleration. When using the Newton–Euler method, the acceleration at the connection point is the time derivative of velocity:
This acceleration can be expressed as the linear acceleration of the prismatic pair and the angular acceleration of the leg:
Simplify and obtain
The linear accelerations of the center of gravity of two parts of a leg are
where is the linear accelerations of the center of gravity of the lower part, and is the linear accelerations of the center of gravity of the upper part. Based on the acceleration, we can obtain the dynamics equations of a leg. For the upper part of the leg, its Newton equation is
and its Euler equation is
Similarly, we can obtain the Newton–Euler equations for all rigid bodies and ultimately organize them into a linear system of equations []. This requires solving a linear equation. The Newton–Euler equation can obtain all joint forces, including driving and constraint forces and torques. This is the advantage of the method.
References
- Xin, G.; Deng, H.; Zhong, G. Closed-form dynamics of a 3-DOF spatial parallel manipulator by combining the Lagrangian formulation with the virtual work principle. Nonlinear Dyn. 2016, 86, 1329–1347. [Google Scholar] [CrossRef]
- Tsai, L.W. Robot Analysis and Design: The Mechanics of Serial and Parallel Manipulators; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Dasgupta, B.; Mruthyunjaya, T.S. A Newton-Euler formulation for the inverse dynamics of the Stewart platform manipulator. Mech. Mach. Theory 1998, 33, 1135–1152. [Google Scholar] [CrossRef]
- Fass, T.H.; Hao, G.; Cantillon-Murphy, P. Vectorized Formulation of Newton-Euler Dynamics for Efficiently Computing Three-Dimensional Folding Chains. ASME J. Mech. Robot. 2022, 14, 060911. [Google Scholar] [CrossRef]
- Peng, J.; Wu, H.; Lau, D. Operational Space Iterative Learning Control of Coupled Active/Passive Multilink Cable-Driven Hyper-Redundant Robots. ASME J. Mech. Robot. 2022, 15, 011013. [Google Scholar] [CrossRef]
- Tafrishi, S.A.; Svinin, M.; Yamamoto, M. Inverse dynamics of underactuated planar manipulators without inertial coupling singularities. Multibody Syst. Dyn. 2021, 52, 407–429. [Google Scholar] [CrossRef]
- Dopico Dopico, D.; López Varela, Á.; Luaces Fernández, A. Augmented Lagrangian index-3 semi-recursive formulations with projections. Multibody Syst. Dyn. 2021, 52, 377–405. [Google Scholar] [CrossRef]
- Quental, C.; Simões, F.; Sequeira, M.; Ambrósio, J.; Vilas-Boas, J.P.; Nakashima, M. A multibody methodological approach to the biomechanics of swimmers including hydrodynamic forces. Multibody Syst. Dyn. 2022, 57, 413–426. [Google Scholar] [CrossRef]
- Nguyen, C.C.; Pooran, F.J. Dynamic analysis of a 6 DOF CKCM robot end-effector for dual-arm telerobot systems. Robot. Auton. Syst. 1989, 5, 377–394. [Google Scholar] [CrossRef]
- Calogero, J.; Frecker, M.; Hasnain, Z.; Hubbard, J.E., Jr. Tuning of a Rigid-Body Dynamics Model of a Flapping Wing Structure With Compliant Joints. ASME J. Mech. Robot. 2017, 10, 011007. [Google Scholar] [CrossRef]
- Geng, Z.; Haynes, L.S.; Lee, J.D.; Carroll, R.L. On the dynamic model and kinematic analysis of a class of Stewart platforms. Robot. Auton. Syst. 1992, 9, 237–254. [Google Scholar] [CrossRef]
- Guo, H.B.; Li, H.R. Dynamic analysis and simulation of a six degree of freedom Stewart platform manipulator. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2006, 220, 61–72. [Google Scholar]
- Kumar, S.; Szadkowski, K.A.v.; Mueller, A.; Kirchner, F. An Analytical and Modular Software Workbench for Solving Kinematics and Dynamics of Series-Parallel Hybrid Robots. ASME J. Mech. Robot. 2020, 12, 021114. [Google Scholar] [CrossRef]
- Kane, T.R.; Levinson, D.A. The Use of Kane’s Dynamical Equations in Robotics. Int. J. Robot. Res. 1983, 2, 1–21. [Google Scholar] [CrossRef]
- Enferadi, J.; Jafari, K. A Kane’s based algorithm for closed-form dynamic analysis of a new design of a 3RSS-S spherical parallel manipulator. Multibody Syst. Dyn. 2020, 49, 377–394. [Google Scholar] [CrossRef]
- Liu, S.; Huang, T.; Mei, J.; Zhao, X.; Wang, P.; Chetwynd, D.G. Optimal Design of a 4-DOF SCARA Type Parallel Robot Using Dynamic Performance Indices and Angular Constraints. ASME J. Mech. Robot. 2012, 4, 031005. [Google Scholar] [CrossRef]
- Lafi, W.; Djemal, F.; Akrout, A.; Walha, L.; Haddar, M. Effects of the interval geometric deviation and crowning parameters on the automotive differential dynamics. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2021, 235, 602–625. [Google Scholar] [CrossRef]
- Li, K.; Liu, M.; Yu, Z.; Lan, P.; Lu, N. Multibody system dynamic analysis and payload swing control of tower crane. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2022, 236, 407–421. [Google Scholar] [CrossRef]
- Chen, G.; Yu, W.; Li, Q.; Wang, H. Dynamic modeling and performance analysis of the 3-PRRU 1T2R parallel manipulator without parasitic motion. Nonlinear Dyn. 2017, 90, 339–353. [Google Scholar]
- Kamman, J.W.; Huston, R.L. Dynamics of Constrained Multibody Systems. ASME J. Appl. Mech. 1984, 51, 899–903. [Google Scholar] [CrossRef]
- Giacaglia, G.E.O.; de Queiroz Lamas, W. Notes on Newton–Euler formulation of robotic manipulators. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2011, 226, 61–71. [Google Scholar] [CrossRef]
- Chadaj, K.; Malczyk, P.; Frączek, J. A parallel Hamiltonian formulation for forward dynamics of closed-loop multibody systems. Multibody Syst. Dyn. 2017, 39, 51–77. [Google Scholar] [CrossRef]
- Plöchl, M.; Heinzl, P.; Mack, W.; Lugner, P. Dynamic analysis of an articulated interurban train by means of a symbolic-numerical method for closed-loop mechanisms. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2000, 214, 243–252. [Google Scholar] [CrossRef]
- Craig, J.J. Introduction to Robotics: Mechanics and Control, 4th ed.; Pearson Education, Inc.: London, UK, 2017. [Google Scholar]
- Milica, L.; Năstase, A.; Andrei, G. A novel algorithm for the absorbed power estimation of HEXA parallel mechanism using an extended inverse dynamic model. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2019, 234, 185–197. [Google Scholar] [CrossRef]
- Zhao, J.S.; Zhou, K.; Mao, D.Z.; Gao, Y.F.; Fang, Y.F. A new method to study the degree of freedom of spatial parallel mechanisms. Int. J. Adv. Manuf. Technol. 2004, 23, 288–294. [Google Scholar] [CrossRef]
- Zhao, J.S.; Fu, Y.Z.; Zhou, K.; Feng, Z.J. Mobility properties of a Schoenflies-type parallel manipulator. Robot. Comput. Integr. Manuf. 2006, 22, 124–133. [Google Scholar] [CrossRef]
- Featherstone, R. Rigid Body Dynamics Algorithms; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Zhao, J.-S.; Wei, S.-T.; Sun, X.-C. Computational Dynamics of Multi-Rigid-Body System in Screw Coordinate. Appl. Sci. 2023, 13, 6341. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).