Abstract
This study focuses on the structural design analysis of a cura baglama, a traditional Turkish string instrument that does not have in place a regulated set of manufacturing standards to follow. The aim therefore is to introduce a structural deformation analysis for a sample cura baglama in three different string tensions via a numerical method-based engineering analysis technique. The three-dimensional solid model of a sample cura baglama was created using a 3D scanner and parametric 3D solid modelling software. Based on experimental frequency analysis, structural deformation analyses of the instrument were conducted using finite element method-based engineering simulation techniques. The simulation results revealed useful visual and numerical outputs related to the deformation behaviour of the instrument under pre-defined boundary conditions. A maximum deformation of 0.223 mm on the soundboard (at the D3 tune) and a maximum equivalent stress of 18.325 MPa on the bridge (at the D3 tune) were calculated. The outputs of this research contribute to further research into the usage of numerical method-based deformation simulation studies related to the standardisation, development, and preservation of such traditional string instruments.
1. Introduction
Music is an integral part of human culture and has been for centuries. From classical to contemporary, music continues to evolve and reach new heights, but the importance of traditional music should not be underestimated. Traditional music is the embodiment of cultural heritage, reflecting the history, values, and beliefs of a society. Turkish folk music is one such example that has roots deeply embedded in the Anatolian culture and the Turkic geography.
Musical instruments are part of the historical heritage of humanity, and they must be preserved and used for performances [1]. The baglama is a traditional Turkish musical instrument that plays an important role in Turkish folk music, and is one of the symbols of Turkish culture. The baglama, also known as the saz, is a stringed musical instrument that has been played in the Turkic geography for centuries. Studies carried out to date reveal that the ‘baglama’ comes from the Asian ‘kopuz’. The kopuz is a traditional stringed instrument from Central Asia, specifically from the Turkic-speaking regions of Kazakhstan, Kyrgyzstan, and Turkmenistan. However, it is important to note that some studies suggest that kopuz may not be the original source of the baglama. The baglama is believed to be a variation of the long-necked lutes known as tanburs, which were first mentioned in literary and iconographic sources during the Sasanian era (AD 224-651). These instruments spread across various musical traditions along the Silk Road, giving rise to a range of closely or distantly related tanburs, featuring two or more courses, occasionally doubled or tripled, a varying number of frets, and distinctive sounds, techniques, and repertoires. Similar instruments, known by different names, such as the saz or bağlama, dotâr or dutâr, setâr, dömbra, and damburâ, can also be found [2,3,4,5]. In any case, it is safe to say that the baglama has a long history that dates back to at least the 10th century. The baglama is a fretted long-necked stringed instrument that is played with a plectrum. It has a pear-shaped body made of wood and typically has seven strings (in three groups), although some variations may have more or fewer strings. The baglama has evolved over time and has undergone several changes in its design and construction. The original baglama was made of a single piece of wood and had two strings. Today, the instrument is played in a variety of styles, including classical, folk, and popular music [6,7]. The baglama has continued to evolve from the past to the present day. The number of strings increased to seven, and the instrument is made with various versions such as a larger body and a shorter neck. This new design allows for even more complex and expressive playing, and is used in a wide range of musical styles [8].
Traditionally, depending on what parts of the baglama are being handled, different wood types are used. Mulberry and chestnut are typically preferred tree species if the soundbox is carved; if the soundbox is made of ribs by a pattern, then maple, juniper, and mahogany are often used. For the soundboard, the component that has the greatest influence on the baglama’s tone, softwoods are preferred. Spruce wood is typically utilised, although fir, beech, and cedar may also be utilised. For the neck, medium-hard woods like hornbeam and occasionally maple are utilised. The bridge is entirely made of maple, while nuts and pegs (tuning keys) are best constructed from hardwoods. They may also be made of ebony, boxwood, or rosewood [7].
The baglama family includes a variety of stringed instruments that are traditionally used in Turkish music. Some of the most common members of the baglama family from larger to smaller sizes include the “Meydan Sazı”, “Divan Sazı”, “Cogur”, “Bozuk”, “Asik/Dede Sazı (Short neck baglama)”, “Tanbura”, and “Cura” [8]. The cura baglama is the smallest size of the baglama family; it is a traditional Turkish stringed instrument often used as an accompanying instrument in traditional Turkish folk music. In the early days, due to its ergonomics, the cura baglama was primarily played by itinerant musicians, who would travel from village to village to entertain people. The cura baglama can be played with a plectrum, also known as a mizrap or tezene, which is used to pluck the strings. The players can also use their fingers to strum or pick the strings, creating different sounds and styles of playing. The tuning of the strings and the style of playing determine the specific sound and style of the instrument. In the 20th century, the cura baglama became increasingly popular in Turkey and other parts of the Middle East. The cura baglama also became popular in other parts of the world and is now played in many countries around the globe. Today, the cura baglama is considered an important part of Turkish culture and heritage. Many young people in Turkey are learning to play the instrument, and it continues to be an important part of Turkish music and culture. Many musicians have begun to experiment with the instrument, incorporating new techniques and styles into their playing [9,10].
Studying the organology of the cura baglama entails a comprehensive exploration of various facets in order to attain a thorough comprehension of the instrument and its significance within Turkish musical culture. The organology of the cura baglama necessitates an understanding of its diverse components, the materials used in its construction, the techniques involved in playing it, and its cultural context. Instruments characterised by a body and keyboard, featuring strings stretched between two fixed points, are generally categorised as part of the lute family. The baglama family conforms to this definition, particularly in terms of its structure. The cura baglama typically comprises a wooden body adorned with a rounded or pear-shaped soundboard. Its extended neck is equipped with frets, the number of which can vary depending on the specific cura type. Made from steel, the strings, numbered from three to seven, are pivotal components, and their quantity may be changed depending on the instrument’s size. Sound is generated via finger plucking or the use of a plectrum. The resultant string vibrations are transmitted to the soundboard, thereby causing resonance and sound amplification. A truss rod is not employed to provide support to the soundboard, as is commonly seen in guitar-like instruments. Some variations include a sound hole on the soundbox. The precise tuning can diverge based on the musician’s preference and the executed musical style. Players employ a blend of fingerpicking and strumming techniques, manipulating them to create diverse rhythms and melodies. The positioning of fingers on the frets governs the pitch of the notes produced.
The standardisation of string instruments like the baglama involves establishing consistent specifications for factors such as size, shape, strings, and tuning. This ensures a uniform sound and playability, aiding musicians and manufacturers. Despite the historical development of many instruments, the baglama lacks standardisation due to its traditional production methods. Challenges in standardising string instruments include variations in production and materials, subjective sound perception, historical design differences, difficulty in measuring subjective sound qualities, complex instrument design, lack of standardised testing methods, player technique influence, and resistance to change from traditional designs among musicians. These complexities hinder the establishment of universal dimensions for a string instrument such as the cura baglama.
In studies on musical instruments in Turkey, it is stated that there are unexplained points about the origin, naming, morphology, development, standardisation, and classification of instruments, and in order to elucidate these issues, it is necessary to conduct research that approaches organology and its main problems analytically [11]. Additionally, although stringed instruments are widely used in Turkish music, their sound formation processes and their structural features affecting this process have not been studied in detail. As a result, the production method used in the field of instrument making was based on trial and error, and the production processes of these instruments were devoid of scientific basis [12].
In this context, it is an important point to research and present new ideas about the development of such instruments. Especially in the durability perspective that also affects sustainable sound production, it is important to understand the deformation behaviour of a stringed instrument’s structure under string tension in static and dynamic conditions. Structural deformation analysis is important for string music instruments because it helps ensure that the instrument can withstand the stresses and strains of playing and tuning. This type of analysis can reveal potential weak points in the instrument’s design, such as areas of high stress or areas where the wood may be prone to cracking. By identifying these issues early on, instrument makers can take steps to prevent or mitigate them, ensuring that the instrument is durable and able to produce high-quality sound for a long time. Additionally, analysing structural deformation can help instrument makers optimise the design of the instrument for improved sound quality and playability. In this regard, the utilisation of advanced computer-aided engineering (CAE) analysis techniques such as finite element analysis (FEA) may be useful [13].
FEA is a valuable tool for understanding the behaviour of string music instruments and optimising their design and construction. This leads to better instruments and a better experience for musicians. The utilisation of FEA in product design analysis, including string music instruments, holds significance for various reasons. Firstly, FEA facilitates the simulation and analysis of diverse materials and designs, aiding in optimising the instrument’s structure and acoustics. This optimisation can lead to enhancements in sound quality, durability, and playability. Secondly, FEA serves as a tool for quality control by ensuring instruments adhere to design specifications and identifying potential issues prior to construction, thereby guaranteeing high-quality instruments that meet musicians’ expectations. Additionally, FEA enables the customisation of instruments tailored to individual musicians’ needs, accommodating factors like ergonomic requirements and sound preferences. Lastly, FEA contributes to the preservation of cultural heritage by analysing and conserving historic instruments, thereby offering insights into their design, construction, and cultural significance [14,15,16,17,18,19].
Traditional musical instruments constitute an integral part of humanity’s historical heritage. In order to preserve their legacy for future generations, it is imperative to ensure that their structural design specifications are adequately documented for future research and cultural purposes. In this focus, the structural behaviour of a stringed instrument can be studied under three main categories: first, the behaviour of the stretched string manipulated by the player; second, the reaction of the wooden soundbox of the instrument and the surrounding air to the string’s movement; and third, the radiation of sound, which primarily originates from the soundbox and displays a complex directional dependence [20]. As a part of the structural design analysis of a traditional string instrument, this study aims to analyse the structural deformation of a sample cura baglama with different string tension forces using FEA. In the study, a three-dimensional (3D) solid model of the cura baglama was created using a reverse engineering approach. Different string tensions, which were analytically calculated via experimental frequency data measurements that correspond to three different tunings, were applied to the instrument model, and the structural deformation behaviour of the instrument was simulated.
2. Materials and Methods
2.1. Cura Baglama and Three-Dimensional Modelling Procedure
The sample “cura baglama” used in this study was made by an instrument maker (Mr. Dundar ALTUN) in Ankara, Turkey, in 2019. The instrument has various parts made of different wood-based materials, three string groups, and six cold-drawn steel strings (ASTM A228) [21] coded from S1 to S6, from the lower to the upper group. The soundbox was made using a handcrafted carving. The major components, such as the soundbox, soundboard, and neck, were joined using a hot-melt adhesive (bone glue). The reverse engineering approach and advanced solid modelling techniques were applied in the solid modelling process to generate accurate three-dimensional (3D) computer-aided design (CAD) data of the cura baglama. The 3D scanning and digitisation of the physical sample were performed using a NextEngine-2020i desktop 3D laser scanner and Scan-StudioHD (v 2.02) software. The final surface refinement and additional modelling operations were carried out using SolidWorks (v 2022) 3D parametric solid modelling software. Figure 1 shows the digitisation procedure from physical objects to 3D CAD data and highlights the key geometrical features and component material list of the scanned sample.
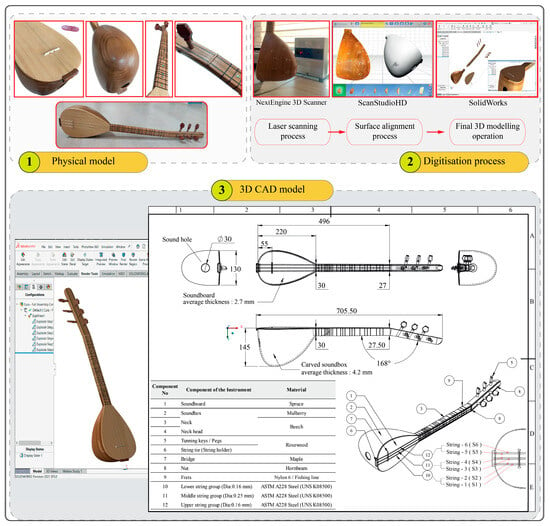
Figure 1.
Illustration of the sample cura baglama and the 3D modelling process.
2.2. Frequency Measurement and Calculations for String Tension Force
In stringed instruments, taut strings exert significant stress on the neck and soundboard of the instrument. Estimating the deformations that may be encountered due to the tension forces applied by the string is very important in terms of determining the design and material properties of the instrument [12]. The sound input to the body of a stringed instrument is provided when the string is plucked. The frequencies of the component modes of a string supported at both ends can be related to the length, tension, and mass per unit length of the string. Here, the tension forces can be calculated using the frequency and related material and geometrical features of the string. Frequency analysis (or spectral analysis) in string instruments refers to the process of determining the distribution of energy in the sound produced by the instrument across different frequency bands. This analysis provides a visual representation of the frequencies present in the sound and the strength or amplitude of each frequency. The frequency content of a sound can provide information about its timbre or tone colour and help in identifying and analysing different harmonic components. The spectral analysis can be performed using various techniques such as Fourier transforms or wavelet transforms, and the results can be displayed in a spectrogram. This information can be used to study the acoustics of string instruments, understand how different playing techniques affect the sound, and even in the development of new instruments or the improvement of existing ones [22,23,24].
In this study, the cura baglama was tuned with a digital tuner and frequency analysis was carried out for each string of the instrument with single plucking sound records via Adobe Audition (v 2022) audio processor software. Sound recording was realised with a 44,100 Hz sample rate, 16-bit bit depth, and mono channel recording using a Logic Pro X digital audio workstation system, including an SE Electronics Z3300A Multi-pattern Microphone and an Apollo Twin Duo MKII soundcard. A professional baglama performer (Dr. Sevilay GOK) generated identical single-plucking actions. A thermoplastic plectrum was used in plucking. The Shore-A scale (ASTM D2240 ISO/868) was utilised in the hardness measurements of the plectrum. The hardness measurement was repeated five times and the average scale was obtained as 83 ± 2. Three repetitions of the plucking action were recorded for each of the strings, and then average values were calculated. The instrument adjusted to the tunings (end tune) of B2 (Si), C3 (Do), and D3 (Re) referenced to the tune of A4 (La) at 440 Hz, respectively. “Playing end note or playing tuning or end tune” is defined as the concluding note of a melody/musical phrase/composition or its modal progression, and within Turkish Folk Music, it encompasses various forms of determining tonality and their corresponding sound characteristics. Turkish terminology refers to this particular definition as the “karar”, “eksen”, or “durak” sound [25,26].
These tunings were set up since they force the limits of the string materials and are the preferred tones played by most performers in specific regional melodies. Subsequently, Equation (1) was employed for the string tension force calculations [27]. Additionally, cross-sectional stress magnitudes of the corresponding strings were calculated by using Equation (2) [28]:
where n = 1, 2, 3, …; L: Length of the string (m); T: Tension force of the string (N); μ: mass per unit length of the string (kg m−1); and f: Frequency of the string (Hz).
When n = 1, Equation (1) provides the frequency of the lowest mode. This is the f0 of the string, which is also known as the “first harmonic”. Thus, the first mode (f1) in Equation (1) is the f0 of string vibration. Equation (1) shows that the frequencies of the higher modes are harmonically related to f0.
where Si: String number = 1, 2, 3, 4, 5, 6; T: Tension force of the string (N); A: Cross-sectional area of the string (mm2) and σSi: Cross-sectional stress of the corresponding string (MPa).
Sound recording, sample frequency measurement and calculations related to string tension force are given in Figure 2 and Table 1, respectively.
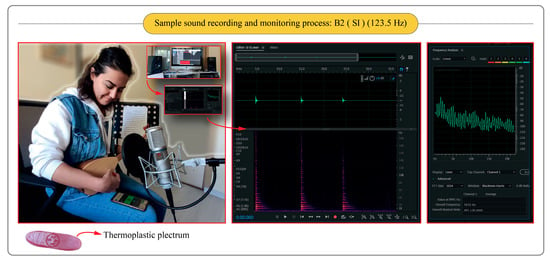
Figure 2.
Illustrative example of the experimental process for sound recording and monitoring.

Table 1.
Frequency measurements and calculations pertaining to string tension force.
2.3. Finite Element Analysis Procedure
The CAD model of the instrument was prepared for the FEA procedure and imported into the FEA code. The mechanical module of the ANSYS Workbench (v 2022R2) commercial FEA code was utilised for the deformation analysis. The original geometrical details of each component were included in the analysis to simulate realistic deformation behaviour under pre-defined boundary conditions. Three different playing tunes (B2 (Si) (123.5 Hz); C3 (Do) (130.8 Hz); and D3 (Re) (146.8 Hz)) corresponding to different string tension forces were set up in the simulation study.
The boundary condition was set up by considering the real-life environment. In the context of the musical instrument, the strings are fastened between a string holder (string tie) on the soundbox and the pegs. These pegs apply tension to their corresponding strings during the tuning process. To replicate this scenario, the instrument was fixed from the string holder (string tie) and the nut. Subsequently, the pre-calculated string tension forces for each string bearing on the bridge were separately applied, including the standard earth gravity effect (9.81 m s−2). Realistic contact conditions were also considered between the parts. Frictional contact definitions were assigned between the bridge and the soundboard, and the friction coefficient between these components was assigned as 0.25 [29]. The contacts between the other components were defined as bonded contact, as it was utilised in the instrument making. The literature on non-linear FEM-based analyses explores non-linearity in three main categories: boundary conditions (contact) nonlinearity, material nonlinearity, and geometry non-linearity. This FEA study focuses on boundary conditions, specifically the non-linearities arising from geometry and contact [30,31].
The FE model (mesh structure) was constructed using the FEA code’s meshing functions. To ensure accurate results, curvature-based meshing approaches were employed, and smaller element sizes were assigned to specific components such as the string holder, bridge, and head nut. The appropriate element size for the FE model was determined via pre-trials. To assess the accuracy of the FE model and to make internal verification, a skewness metric was employed, which measures the deviation of the elements from equilateral cells. A skewness value of 0 indicates perfect cell quality, while a value of 1 indicates fully degenerated cells (0: equilateral; >0–0.25: excellent; 0.25–0.50: good; 0.50–0.75: fair; 0.75–0.9: poor; 0.9–<1: bad; 1: degenerate) [32,33]. The FE model had an average skewness metric value of 0.241, which is considered excellent cell quality.
The instrument consists of various components made from different materials. The materials utilised for the instrument components were separately assigned. Most importantly, wood-based materials exhibit anisotropic material behaviour because of the nature of their inner structure, and this may result in some limitations such as converging problems, increasing solving time, etc., in engineering simulation studies. Therefore, some assumptions are inevitable. In this regard, the critical components, such as the soundboard and neck, were defined using a homogeneous linear orthotropic material model, which takes into account their susceptibility to deformation. The remaining components were assumed to be made of homogeneous linear isotropic material [34,35,36,37,38,39,40,41]. The material properties assigned to the instrument’s components in the analysis setup are given in Table 2. The description of the boundary conditions, including forces acting on the bridge, and visual and numerical details of the FE model are given in Figure 3, Table 3, and Figure 4, respectively.

Table 2.
Components and corresponding material properties assigned in the FEA study.
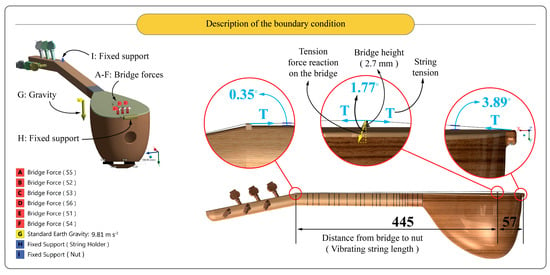
Figure 3.
Boundary condition.

Table 3.
Calculated string forces acting on the bridge.

Figure 4.
Details of the finite element model (mesh structure).
3. Results and Discussion
A realistic full-scale 3D model of the sample cura baglama was successfully created and the geometrical dimensions of the instrument was revealed. The 3D model was utilised for the deformation simulation in this study. After the simulation-solving process, numerical and visual outputs were obtained, and the results were recorded. The simulation visually demonstrated the deformation behaviour of the instrument under pre-defined string tension forces, and numerical results of the stress and deformation distribution, contact details, and reaction forces for related components were extracted. The string tension forces were seen to increase from the B2 (Si) tune to the D3 (Re) tune. Maximum string tension force was seen in the D3 (Re) tune setting (S3 = S4: 46.765 N). Corresponding resultant string forces affecting the bridge component were calculated as 12.89 N, 14.52 N, and 18.29 N for the adjusted end tunes of B2 (Si), D3 (Re), and C3 (Do), respectively (Figure 3). In a linear perspective, increases in the instrument deformation and related stress values on the components from the B2 (Si) tune to the D3 (Re) tune settling would be expected. This situation was confirmed and clearly exhibited by the simulation results. Accordingly, maximum equivalent stress magnitudes of 12.883 MPa, 14.545 Mpa, and 18.325 MPa were calculated on the bridge component for the adjusted end tunes of B2 (Si), D3 (Re), and C3 (Do), respectively. The maximum deformation values were calculated on the soundboard component as 0.159 mm, 0.178 mm, and 0.223 mm for the adjusted end tunes of B2 (Si), D3 (Re), and C3 (Do), respectively. The maximum equivalent stress value on the soundboard was 3.111 MPa. Visual outputs of the simulation are given in Figure 5.
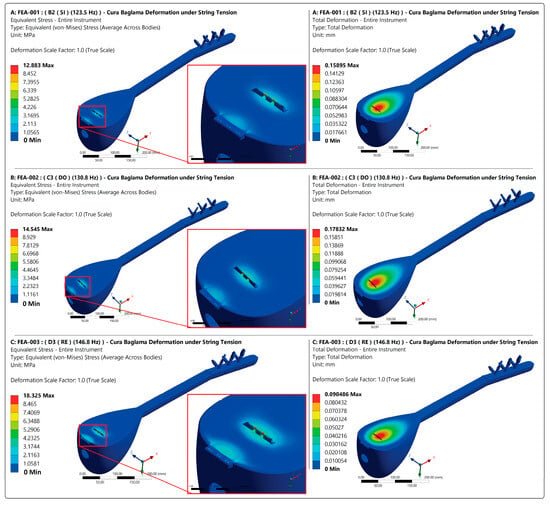
Figure 5.
Simulation visual outputs of the deformation and stress distribution.
In string instruments, most especially, soundboard deformation under string tension affects the sound occurrence and quality. Structural deformation can disrupt the instrument’s inherent resonance and vibrational patterns and it can lead to unintended buzzing, rattling, or other undesirable noises when playing. This can occur when the strings come into contact with frets, bridges, or other parts of the instrument due to changes in the instrument’s geometry; however, specific to this study, it was interpreted that the deformation magnitudes on the soundboard did not negatively affect the sound quality and tune regulations, which was confirmed by frequency outputs and performer feedback. The contact results revealed the frictional stress (0.251 MPa at the D3 tune) and contact pressure (1.208 MPa at the D3 tune) between the bridge and soundboard and the outputs related to contact results were seen to increase from the B2 (Si) tune to the D3 (Re) tune. Lateral sliding (in the Z direction) of the bridge on the soundboard was also observed (0.022 mm at the D3 tune). It was interpreted that the contact results did not disturb the sound occurrence. Numerical data supported the graphical expressions of the simulation outputs, and soundboard deformation by settled tunes and contact results between the bridge and soundboard are given in Figure 6 and Figure 7, respectively.
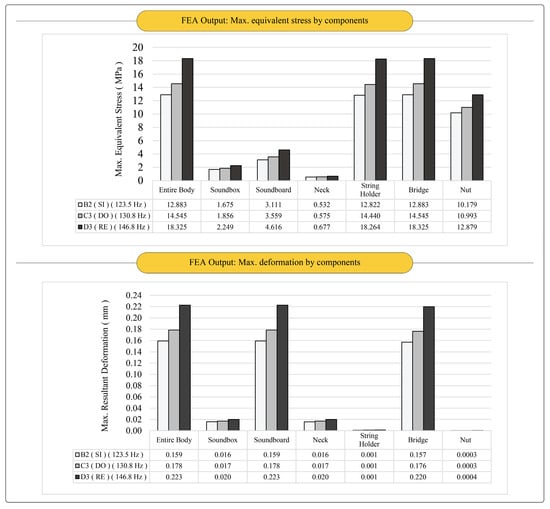
Figure 6.
Simulation numerical outputs of the maximum deformation and stress values.
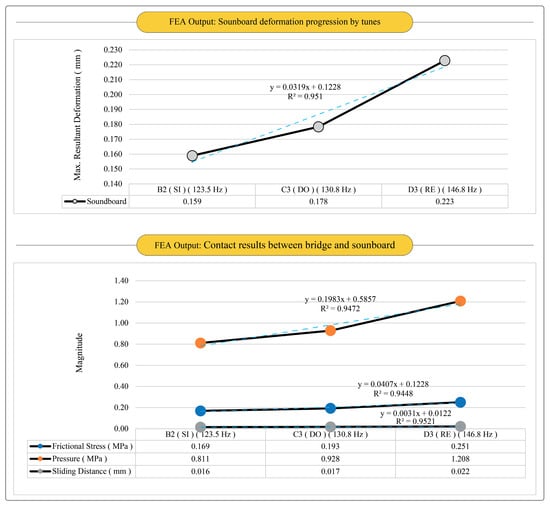
Figure 7.
Simulation numerical outputs of the contact results between bridge and soundboard.
In a stress analysis, calculating the factor of safety (FoS) is crucial for ensuring the structural integrity and safety of a component or structure under expected loading conditions. In this regard, the FoS of the components and the strings were calculated. The results indicated that there was no evidence of failure on the components and the strings in consideration of the failure threshold of the related materials. A minimum FoS of 2.95 and 1.34 for the bridge (at the D3 tune) and lower string group (at the D3 tune) were calculated, respectively. Additionally, reaction forces acting on the components where string tension has a major effect were extracted from the simulation results. FoS calculations and reaction forces of the components are given in Table 4 and Table 5, respectively.

Table 4.
Factor of safety (FoS) calculations by components.

Table 5.
Corresponding reaction forces at related components.
Another concern is the choice of material for the instrument. Past experiences have shown that the texture of the wood used in constructing string instruments plays an important role in determining the sound quality, in addition to the instrument’s shape. The study discussed in this paper assumes a linear material model in the simulation, and therefore does not take into account how changes in the acoustic features are affected by the texture of the material. However, this aspect could be explored in future studies. Using FEA is a valuable way to understand how materials behave in structural analyses. However, it is important to note that simulations based on numerical methods only offer an approximate representation of real-world phenomena. As such, it is crucial to carefully assess how well the results of simulation studies reflect actual physical conditions. The most reliable way to validate these simulation results is to correlate them via experimental testing.
Regarding the final evaluation of outputs obtained from the simulation study, several factors were taken into account. These included unexpected and unpredictable dynamic conditions that can occur during actual operating conditions, limitations in simulating these conditions, a solution approach that is specific to numerical methods, necessary assumptions made to overcome these limitations, and the consideration of the capacity of the simulation solver platform to eliminate any anomalies in the results obtained. Despite these challenges, it was concluded that the FEM-based analysis performed to simulate the deformation conditions of the cura baglama was conducted accurately and could satisfactorily represent real deformation behaviours. As such, the simulation results could be utilised in the production and standardisation studies of this string instrument.
4. Conclusions
The traditional string instrument fabrication process involves a complex set of skills and knowledge that has been passed down from generation to generation. The deformation behaviour of musical string instruments is an important research area, as it plays a significant role in determining the quality of the sound produced. Understanding the complex mechanics involved in the deformation of such instruments can provide valuable insights into their design and performance. In particular, the deformation behaviour of traditional string instruments such as the cura baglama is of great interest, as it is deeply rooted in cultural and historical contexts.
The design and standardisation of the cura baglama is another important area of research. By defining a set of design principles and specifications, researchers can ensure that instruments are consistent in terms of quality, durability, and performance. This can help preserve the cultural significance of the instrument and ensure that it continues to be used and enjoyed by future generations. By standardising the design and manufacturing process, instrument makers can produce consistent instruments that meet the desired quality and strength standards. This study can help instrument makers improve their processes and create higher-quality instruments that are more durable and have better tonal quality.
Understanding the deformation of a string instrument is also crucial for instrument makers to produce high-quality instruments that can withstand the stress of playing without losing their tonal quality. FEA can be used to analyse the deformation of string instruments, and the standardisation of design and manufacturing processes can help ensure consistent quality. In this study, FEA was used to investigate the deformation behaviour of the cura baglama under varying string tensions. The numerical findings revealed that the deformation behaviour is influenced by a range of factors, including the instrument geometry, material properties, and the tension of the strings. It was also found that the deformation behaviour varied clearly between different parts of the instrument, highlighting the importance of considering the instrument as a whole when designing and analysing it.
This study has important implications for instrument makers, as it provides a detailed understanding of the deformation behaviour of the cura baglama under pre-defined boundary conditions. By incorporating these findings into their designs, makers can ensure that their instruments perform to the highest standards, delivering high-quality sound and preserving the cultural significance of the instrument. Furthermore, this study contributes to the broader scientific understanding of the mechanics of string instruments, providing valuable insights into the deformation behaviour of this important class of musical instruments. The knowledge gained from this study can help instrument makers create higher-quality instruments that are durable, have better tonal quality, and meet the desired strength standards.
Author Contributions
H.K.C.: Project administration, Investigation, Visualization, Formal analysis, Writing—original draft; S.G.: Conceptualization, Methodology, Resources; N.C.: Data curation, methodology, Writing—original draft; A.E.W.R.: Supervision, Writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This article was partially supported financially by The Scientific Research Projects Coordination Unit of Akdeniz University (Turkey).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available in this article.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Winternitz, E. Musical Instruments and Their Symbolism in Western Art, 2nd ed.; Yale University Press: New Haven, CT, USA, 1979; ISBN 9780300023244. [Google Scholar]
- de Zeeuw, H. The Turkish Long-Necked Lute Saz or Bağlama; Archaeopress Publishing Ltd.: Oxford, UK, 2020; ISBN 9781789694338. [Google Scholar]
- de Zeeuw, H. Tanbûr Long-Necked Lutes along the Silk Road and Beyond; Archaeopress Publishing Ltd.: Oxford, UK, 2019; ISBN 9781789691702. [Google Scholar]
- de Zeeuw, H. The Ottoman Tanbûr: The Long-Necked Lute of Ottoman Art Music; Archaeopress Publishing Ltd.: Oxford, UK, 2022; ISBN 9781803271064. [Google Scholar]
- Saz Kopuz’dan Türemiş Olamaz. Yildiray Erdener. Available online: https://www.sanattanyansimalar.com/yazarlar/yildiray-erdener/saz-kopuzdan-turemis-olamaz/1395/ (accessed on 25 April 2023). (In Turkish).
- Ekim, G. Historical Progression of Baglama; Ege University: İzmir, Turkey, 2002. (In Turkish) [Google Scholar]
- Mert, B. “Baglama” with New Expression Opportunities from the Past to the Present; Mimar Sinan Fine Arts University: Istanbul, Turkey, 2018. (In Turkish) [Google Scholar]
- Yilmaz, A. Current Changes in Professional Baglama Performance; Halic University: Istanbul, Turkey, 2011. (In Turkish) [Google Scholar]
- Demirbas, T. Stringed and Bowed Turkish Folk Music Instruments in Terms of Instrumentation; Istanbul Technical University: Istanbul, Turkey, 2020. (In Turkish) [Google Scholar]
- Erbil, K. An Investigation of the Usability of Burdur Three Strings (Üçtelli) Bağlama in Music Teaching Programs in the Line of Expert Opinions; Necmettin Erbakan University: Konya, Turkey, 2021. (In Turkish) [Google Scholar]
- Tetik Isik, S. Organology Studies in Turkey. Mukaddime 2015, 6, 197–220. (In Turkish) [Google Scholar] [CrossRef]
- Degirmenli, E. An Investigation of the Sound Production in the Turkish Musical Instrument Oud and a Proposal for Determining the Design of Stringed Instruments from the Aspect of Their Sound Characteristics; Gazi University: Ankara, Turkey, 2018. (In Turkish) [Google Scholar]
- Carlson, M. Application of Finite Element Analysis for an Improved Musical Instrument Design; Fender Musical Instruments Corporation, Guitar Products Research & Development Department: Corona, CA, USA, 2011. [Google Scholar]
- Narasaiah, G.L. Finite Element Analysis; B.S. Publications: Hyderabad, India, 2008; ISBN 9788178001401. [Google Scholar]
- Kuna, M. Finite Elements in Fracture Mechanics; Gladwell, G.M.L., Ed.; Springer: London, UK, 2004; ISBN 9789400766792. [Google Scholar]
- Chakrabarty, B.K. Integrated CAD by Optimization; Springer International Publishing: Cham, Switzerland, 2022; ISBN 978-3-030-99305-4. [Google Scholar]
- Szabó, B.; Babuška, I. Finite Element Analysis: Method, Verification and Validation, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2021; ISBN 9781119426479. [Google Scholar]
- Cook, R.D.; Robert, D. Finite Element Modeling for Stress Analysis; Wiley: Hoboken, NJ, USA, 1995; Volume 32, ISBN 978-0-471-10774-3. [Google Scholar]
- Kim, N.-H.; Sankar, B.V.; Kumar, A.V. Introduction to Finite Element Analysis and Design, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2018; p. 552. [Google Scholar]
- McIntyre, M.E.; Woodhouse, J. The Acoustics of Stringed Musical Instruments. Interdiscip. Sci. Rev. 1978, 3, 157–173. [Google Scholar] [CrossRef]
- Bülbül, F. Microscopic Examination of Play-Worn Steel Music Strings. Frict. Wear Res. 2015, 3, 1. [Google Scholar] [CrossRef]
- Alm, J.F.; Walker, J.S. Time-Frequency Analysis of Musical Instruments. SIAM Rev. 2002, 44, 457–476. [Google Scholar] [CrossRef]
- Brahmi, M.; Banerjee, S.D.A.; Banerjee, S. Frequency Analysis of Plucked Musical Instruments. In The Surprising Case of Suppressed Fundamental; Indian Institute of Science Education and Research Kolkata: Mohanpur, India, 2017. [Google Scholar]
- Meyer, J. Acoustics and the Performance of Music, 5th ed.; Springer: New York, NY, USA, 2009; ISBN 978-0-387-09516-5. [Google Scholar]
- Ozbek, M. Turkish Folk Music Handbook-I: Glossary of Terms; Ataturk Culture Center: Ankara, Turkey, 1998. (In Turkish) [Google Scholar]
- Say, A. Music Encyclopedia; Music Encyclopedia Publisher: Ankara, Turkey, 2002; ISBN 975-7436-29-1. (In Turkish) [Google Scholar]
- Howard, D.M.; Angus, J.A. Acoustics and Psychoacoustics, 4th ed.; Routledge: London, UK, 2009; ISBN 9780240521756. [Google Scholar]
- Ugural, A.C.; Fenster, S.K. Advanced Strength and Applied Elasticity; Prentice Hall: Hoboken, NJ, USA, 2003; Volume 1, ISBN 9780130473929. [Google Scholar]
- Deta, U.A.; Suprapto, N.; Mubarok, H.; Adam, A.S.; Kholiq, A. The Comparison of Static Friction Coefficient on Wood between the Combination of Wood-Metal Load System and Wood-Sand Load System. In International Conference on Science and Technology (ICST 2018); Atlantis Press: Amsterdam, The Netherlands, 2018; Volume 1, pp. 887–890. [Google Scholar] [CrossRef]
- SolidWorks Doc. SolidWorks Simulation Premium: Nonlinearity Training Manual Document No. 22658021044-ENG0001; Dassault Systemes SolidWorks Corporation: Waltham, MA, USA, 2010. [Google Scholar]
- Wakabayashi, N.; Ona, M.; Suzuki, T.; Igarashi, Y. Nonlinear Finite Element Analyses: Advances and Challenges in Dental Applications. J. Dent. 2008, 36, 463–471. [Google Scholar] [CrossRef] [PubMed]
- ANSYS Product Doc. ANSYS Meshing User’s Guide: Skewness (Release 2019 R2); ANSYS Inc.: Canonsburg, PA, USA, 2019. [Google Scholar]
- Brys, G.; Hubert, M.; Struyf, A. A Robust Measure of Skewness. J. Comput. Graph. Stat. 2004, 13, 996–1017. [Google Scholar] [CrossRef]
- Obara, P. Verification of Orthotropic Model of Wood. Arch. Civ. Eng. 2018, 64, 31–44. [Google Scholar] [CrossRef]
- Pedrammehr, S.; Aghdam, N.J.; Pakzad, S.; Ettefagh, M.M.; Sadeghi, M.H. A Study on Vibration of Setar: Stringed Persian Musical Instrument. J. Vibroengineering 2018, 20, 2680–2689. [Google Scholar] [CrossRef]
- Ross, R.J. Wood Handbook: Wood as an Engineering Material; U.S. Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2010.
- Higuchi, K.; Takai, H. Stress-Strain Diagram, Young’s Modulus and Poisson’s Ratio of Textile Fibers. J. Text. Mach. Soc. Jpn. 1961, 7, 4–12. [Google Scholar] [CrossRef]
- Fu, Y.; Fang, H.; Dai, F. Study on the Properties of the Recombinant Bamboo by Finite Element Method. Compos. Part B Eng. 2017, 115, 151–159. [Google Scholar] [CrossRef]
- Gao, Z.; Zhang, X.; Wang, Y.; Yang, R.; Wang, G.; Wang, Z. Measurement of the Poisson’s Ratio of Materials Based on the Bending Mode of the Cantilever Plate. BioResources 2016, 11, 5703–5721. [Google Scholar] [CrossRef]
- Meier, E. WOOD! Identifying and Using Hundreds of Woods Worldwide. The Wood Database. 2015. Available online: https://www.wood-database.com/book/ (accessed on 25 January 2023).
- MatWeb. MatWeb: Online Materials Information Resource. Available online: https://www.matweb.com/ (accessed on 3 March 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).