Abstract
This work presents research concerning the numerical assessment of two previously measured temperatures due to firebrand accumulation on surfaces, which was determined in former thermal experimental campaigns. A 3D numerical model using thermal transient non-linear analysis is used to validate the thermal outputs of these two previous experimental campaigns, and therefore, corroborating the previous temperature vs. time curves created with a prescribed flux in the firebrand accumulation area. The firebrand thermal heat transfer to the plane surface is simulated using convection and radiation film conditions, in which a 3D non-linear, time-dependent finite element simulation is used. Then, the previous proposed standard firebrand accumulation curve, ISO 834, and external fire curve are numerically compared with the results from previous firebrand accumulation curves in a wood corner wall. Finally, the merit assessment of the proposed standard firebrand accumulation curve shows a visible improvement, which has low values and is in accordance with the experimental results in the temperature field distribution of firebrand accumulation onto a contact surface. It is fair to argue that it constitutes a point to search for an efficient design for structures at elevated temperatures due to firebrand accumulation.
1. Introduction
Over the past few years there has been a tremendous increase in the number of devastating wildland–urban interface (WUI) fires because of climate change, fuel management practices, and increased human development in WUI areas [1,2]. A couple of recent examples in Asia and North America are the WUI fires that occurred in South Korea in 2019 [3] and those in California in the United States in 2018 [4,5,6]. Portugal experienced two major wildfires in 2017, resulting in 117 deaths and 204 injuries, according to reports released by the Portuguese government [7,8]. Recently, standard wildfire curves that can be used in the protection design of dwellings located in the WUI against wildfires were reported [9]. Firebrands are a dominant mechanism for the spread of fires [10], as they are transported by wind and can ignite secondary fires far away from the fire start point [11].
The formation of firebrands is a part of the fire generation process and an indirect action of wildfire in dwellings. Trees and bushes, being combustible materials in a forest fire, become so warm that they break into small pieces that are carried out by the wind and create spot fires. The firebrand accumulation heats up the contact surface, resulting in the formation of flammable fuel mixtures above the contact surface, and the continuation of heat leads to ignition, which commonly happens in wooden structural components [12,13]. A better understanding of thermal properties and transportation for firebrands can help to slow down the fire spread in WUI communities. Structures ignite in a WUI fire through three different pathways: direct flame contact, radiation heat transfer, and the transport of firebrands [1], as shown in Figure 1.
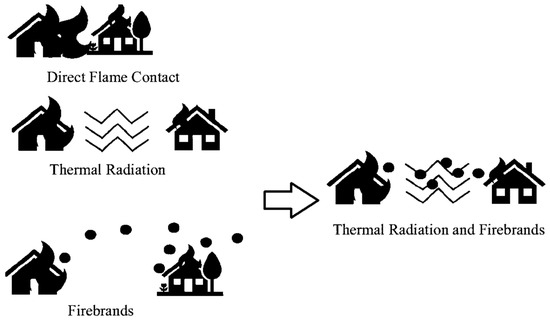
Figure 1.
Fire spread mechanisms [14].
Investigations of past fires [7,8,15,16] have found that firebrands play the main role in structure losses due WUI fires. Firebrands travel from 2 km to 9 km ahead of the fire start point to the dwellings due to the strong action of the wind [7,16] and remain incandescent for several hours. The safety of dwellings must take into account all of these potential sources of ignition, therefore, the exposure from firebrands (indirect exposure) deserves special attention because the international literature indicates that at least half of ignition is due to them [17]. Firebrand transportation has been studied in recent decades [14,18,19,20,21,22,23], but only recently, several experimental investigations of ignition properties [11], thermal properties, firebrand amount–size exposure [24,25,26,27], and wood structure vulnerability due to firebrands have been addressed [12,28,29,30,31,32,33,34,35,36]. An experimental study is presented that investigates the heat flux from firebrand accumulations to a substrate [37]. The findings show that high-temperature firebrands may not represent the most dangerous condition as these particles do not retain high temperatures for long periods of time. The accumulation is capable of sustaining smouldering compared to fully charred particle accumulations, thus, these may be considered more hazardous to solid combustible structural material [37]. An experimental campaign was conducted, where different types and geometries of firebrands were burned in controlled conditions until they reached the thermal pyrolysis state [38]. The temperature of the firebrands and the transfer temperature to the surfaces were measured using a test setup with metal plates and thermocouples, in order to develop a firebrand accumulation curve to be used in the future design for the protection of dwellings against the indirect action of a wildland fire [38].
Theoretical models and analytical expressions were developed to investigate the interaction of the firebrand with a target fuel bed (contact surface), using the “hot spot” theory, which was validated by experiments that consisted in heating the samples in a basket and identifying critical conditions for ignition [39,40,41,42,43,44]. Grishin et al. [45] used numerical models to examine a porous condensed phase, simulating natural vegetation. Their research involved theoretical and experimental investigations into the ignition of forest combustible materials with different moisture contents, heights, and densities. Through their findings, they determined the time of ignition and critical ignition energy. Recently, the flux transmission via radiation and convection of firebrands in contact with a plane surface was investigated [46].
1.1. Research Significance
At the moment, there is no procedure to numerically simulate the thermal effect of firebrand accumulation on surfaces. This work aims to fill in this knowledge gap. Although the California fire code [47] already has the firebrand test to assess the fireproof efficiency of construction materials against the thermal action of firebrand accumulation, there is no standard to numerically simulate its effect on plane surfaces. With this new knowledge, it will be possible in the future, to fireproof the design of dwellings against the actions of wildfires avoiding demands for experimental tests.
1.2. Objectives
Finally, the main objective of this paper is to numerically assess the efficiency of a firebrand flux transmission model using radiation and convection film conditions. These thermal numerical models are then compared in terms of temperature distribution, with the data acquired from two experimental campaigns [37,38]. This paper begins with an overview of the previously experimental campaign about firebrand accumulation, then addresses a previously proposed firebrand accumulation curve [38]. The validation of the finite element model using two experimental campaigns is then presented. Furthermore, a case study using fire design curves is discussed. This paper can be understood as an extension of the ongoing investigation about wildfire fireproof protection [9,38,48].
2. Previous Experimental Campaign for Firebrand Accumulation
All experiments described here were conducted at the laboratory of the research institute CERIS-IST in Portugal [38]. The experimental setup, the wood specimens analysed, and the measured temperatures are described below.
In order to simulate the firebrands, five different types of wood were characterised, which are the most common in Portugal: Eucalyptus, Pine, Branches, Wood Pallets, and Charcoal. All specimens were kept in a low-humidity room during the summer to achieve a low moisture content. In this context, the spot fire formation due to heat transfer by firebrand accumulation is a complex process that depends on several factors. These factors include the size of the firebrands, their state (temperature, smoldering, glowing, or flaming), the properties of the contact surface (temperature, density, porosity, and moisture content), as well as environmental conditions (temperature, humidity, and wind velocity). A standard firebrand geometry of 30 mm × 30 mm × 5 mm was chosen, with the exception of branches that were assigned a diameter of 6 mm and length of 30 mm (Figure 2). It is crucial to clearly characterise the firebrand because their geometry defines the behaviour of the heat transfer distribution on the contact surface. Similarly, it specifies the amount of energy available in the build-up [49]. Additionally, cases where wood types were mixed with charcoal were considered because, in a wildfire, the vegetation layer is composed of different fuel elements, so it is necessary to understand the thermal behaviour of unburned wood with already-burned wood (charcoal).

Figure 2.
Standard geometry for specimens [38].
The experimental procedure was followed according to [37], using 200 g of wood in each test. For the sake of correctly collecting the temperature of the contact surface, the first step was to keep all wood specimens in a grill until they reached the pyrolysis state and then carefully transfer them into the metal plates, in which thermocouples were installed. A 150 mm diameter basket was used to control the deposition area because other diameters had already been experimented with [37], and this diameter better quantified the accumulation shape. Regarding the steel plates, three layers of 5 mm each were used, whose properties at elevated temperatures are well-known. Each plate was instrumented with three thermocouples welded (RS PRO Type K Thermocouple, 2 m length and 1/0.3 mm diameter) in order to record the heat flux due to firebrand accumulation on the surface (direct contact with the firebrands) and its transmission to the bottom plates. The parameters adopted for temperature data acquisition were a frequency of 1 Hz and 90 min of test duration. The thermocouples were placed in the centre of the steel plate, with a small distance between them. The experimental setup is displayed in Figure 3.
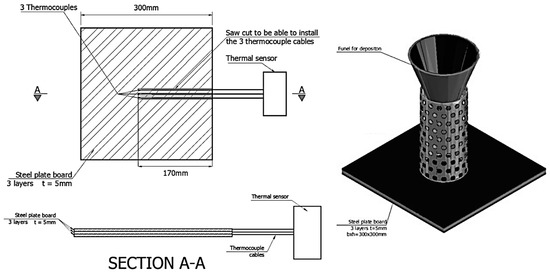
Figure 3.
Schematic of the experimental setup [38].
Figure 4 presents the maximum temperature over time for all types of wood used, including a combination of woods as it occurs in a real wildfire, and it also displays the average maximum temperature of all specimens for thermocouples on the top side of the top steel plate, which was in direct contact with the firebrands.
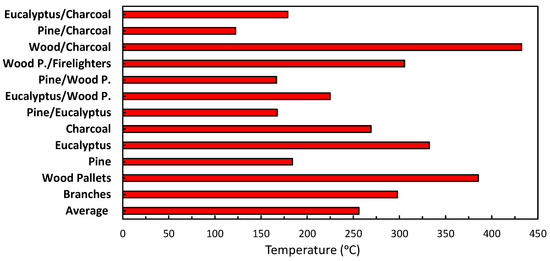
Figure 4.
Maximum temperatures for the specimens.
The maximum temperature was in the range from 123 °C to 432 °C. The average temperature is not admissible to design a fireproof structure because there is variability in the experimental values correlated with the wood utilised (see Figure 4). The authors did an extensive review of firebrands, gathering information about the firebrand’s internal temperature, surface temperature, firebrand radius, firebrand weight, heat flux, and duration, which can be consulted in [38]. In the literature, it was found that the minimum surface temperature was 200 °C, measured in the contact surface with an individual isolated firebrand, and it was used in a numerical model to estimate the resistance between the thermal contacts of the firebrand and the target fuel bed [13]. Similarly, the maximum surface temperature was 477 °C [27], which was measured from a wood–wood surface in contact with firebrand accumulation. In this context, the average maximum temperature of all firebrand specimens presented a lower value than expected (477 °C). The firebrand weight, after the test was measured, observed a mass reduction in above 72%, consequently promoting a high possibility of wind transportation, which is in accordance with the values reported by the scientific community. Finally, all wood types analysed can be consulted in [38] as temperature vs. time graphs.
3. Standard Firebrand Accumulation Temperature Curve
In this section, the firebrand accumulation temperature curve proposed by [38] is reviewed, using the previous measured temperatures of the firebrand experimental campaign. It is worth noting that this standard design curve is used to simulate the effect of firebrand accumulation on a plane surface, showing the fire growth and cooling phase.
In order to develop a standard design curve, the 95% characteristic value () in Annex D “Design Assisted by Testing” of Eurocode 0 [50] for the maximum temperature was used, given using
using the average peak temperature of all experiments (). The values of , which depend on the size of the sample, can be consulted in Annex D of [50], and the value of 1.72 is used. The standard deviation coefficient () adopted is 96.68, in which this value is almost 1/3 of the average peak temperature of all experiments (see Figure 4), showing that the variability of the results is high. This observation depends mainly on the type of wood analysed, and for this reason, a conservative value of is used in this work ().
The experimental campaign showed that if there is an influence of wind, the firebrand temperature tended to stabilize at a maximum temperature between 15 to 30 min after the test started. This fact guides the idea that the proposed design standard firebrand curve must maintain its maximum temperature after a few minutes. In a wildfire situation, the engineer must always take into account the worst possible scenario, which is with wind exposure, and the design curve should show endurances for 60 min without cooling. The proposed standard firebrand accumulation curve (Figure 5) is divided in two phases, heating and cooling. The heating phase has a duration of 60 min (simple function based in exponential growth until it reaches the maximum temperature ()), and the cooling phase admits a linear variation for another 60 min until it reaches the ambient temperature () (see Equation (2)). The value of 0.003685 was determined for —a parameter that impacts the flashover of the curve. More information about how to calculate this parameter can be consulted in [38]. The ambient temperature in the presence of a nearby fire must be taken as a higher value, therefore the value of 50 °C was adopted [9]. As mention before, with the and , the maximum temperature () due to firebrand accumulation stabilizes at 480 , which is in accordance with the observed maximum values provided by [27].
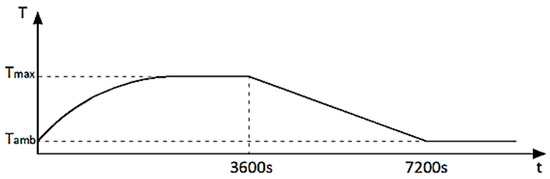
Figure 5.
Proposed standard firebrand accumulation curve [38].
4. Validation of the Numerical Model
In this section, the validation methodology used in this work is presented, in which the experimental campaign was numerically simulated and was then compared with the thermocouple values measured in the surfaces. The finite element analyses were realized using ABAQUS [51], and all the parameters adopted are addressed below. For all examples, surface convection and radiation were admitted, with the upper bond parameters provided by the standard [52], resulting in coefficients of convection of and for the firebrand exposed surface and unexposed side of separating members, respectively. For the emissivity coefficient, due to firebrands being black at the flashover, it was admitted . For the Stefan–Boltzmann constant, was adopted, and for all examples, the numerical thermal analysis was performed considering Kelvin as the unit for temperature; therefore, the admitted absolute temperature was zero. Since all thermal properties vary with temperature, a nonlinear transient thermal analysis was performed using the incremental Newton–Raphson iterative method. In all analyses, in order to regulate the flux transfer between nodes, the maximum allowed temperature change per increment was 10 K. This precaution indicates that reducing the time step increment because of the maximum allowed temperature can result in a more reliable numerical solution for nonlinear thermal analyses [53].
4.1. Previous Experimental Campaign by Cantor et al. [38]
4.1.1. Geometry and Type of Analysis
The geometry of the experimental setup used to study the firebrand accumulation, from burning different types of wood, is shown in Figure 6, where the numerical model used and the schematic of the experiment can be seen. The experimental setup explained in Section 2 was numerically modelled. In order to reduce the computational cost, taking advantage of symmetry, only 1/8 of the experiment size was considered in the numerical model.
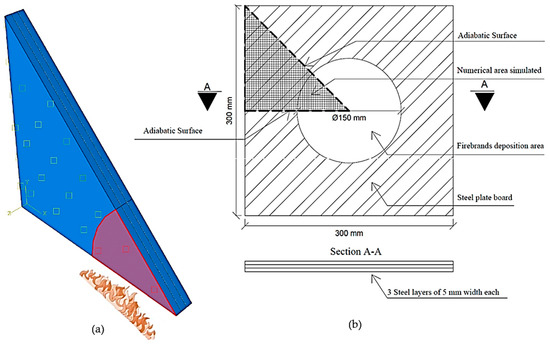
Figure 6.
Geometry used in (a) the numerical model and (b) the experimental schematic setup.
4.1.2. Materials and Methods
All effective thermal properties (without change transformation) used in the model was taken from Eurocode 4:1-2 [54], which is the one used for steel material and can be consulted in Figure 7. For the steel density (ρ), a constant value of 7850 kg/m3; was used, since the maximum contact surface temperature of the firebrands is below 750 °C. All models used, as ambient temperature, the value measured in the experimental campaign before they got in contact with the firebrands, in which the three plates started with the same temperature. But the value is different for the different types of wood tested. The methodology consisted of replicating the experiments using the temperature vs. time curve measured experimentally on the top steel plate and comparing the temperature distribution from the top plate (TP) to the middle plate (MP).
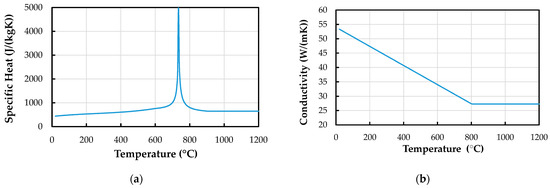
Figure 7.
(a) Specific heat () and (b) thermal conductivity () used [54].
4.1.3. Boundary Conditions
It was demonstrated that firebrand can transmit heat flux via radiation and convection on plane surfaces [46], therefore a surface convection and radiation boundary condition were used to simulate the flux transfer between the firebrands and the steel plates. This procedure is in accordance with standard fire safety design in structural codes [52], when a structure is subjected to the action of a nominal or performance base fire. Hence, the prescribed heat flux is given using
where is the heat flux in the n direction given using , and is a heat flux in the normal direction. The heat flux can assume a positive (supplied heat) or negative (subtracted heat) value. On the surface, on which the firebrands were accumulated, a sink temperature equal to the top thermocouple in the top steel plate was adopted (Figure 8). All other surfaces were simulated with convection and radiation at an ambient temperature (, using Equation (3), but two sides had adiabatic surfaces due to the symmetrical axes (Figure 9). The interaction between the steel plates was simulated using gap radiation ()—functionality in ABAQUS for modelling radiation between surfaces across a narrow gap—because there is a small gap between the steel plates that must be taken into account. Hence, the heat flux per unit surface area crossing the gap between steel plates is given using
where F is the effective viewfactor, which corresponds to viewing the A surface (master) from the B surface (slave). The viewfactor should have a value between 0 and 1, where 0 means that there is no radiative heat transfer and 1 means that there is no gap between surfaces. The viewfactor was calculated considering that the gap is less than 1 mm, so the value 0.99 was used [55].
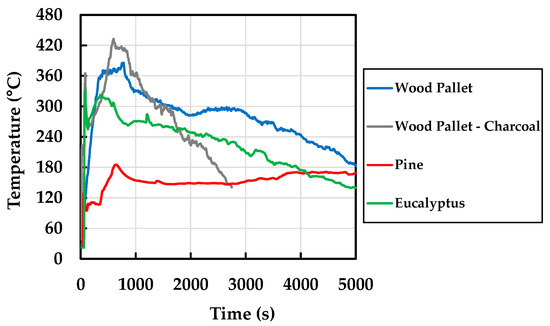
Figure 8.
Firebrand data inputted.
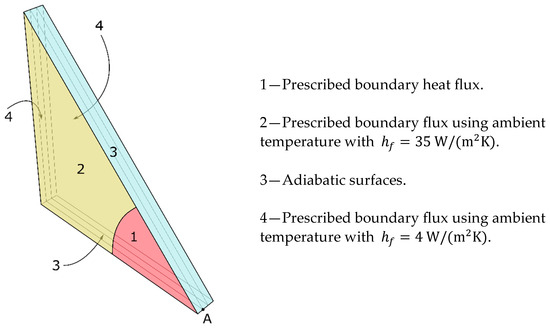
Figure 9.
Boundary conditions adopted for the simulation of the previous experimental campaign by Cantor et al. [38].
Finally, the temperature distribution in a medium is obtained through conduction thermal analysis, and the heat transfer equation is formulated by applying the principle of conservation of the energy to a three-dimensional differential control volume. The heat transfer equation in this problem, for isotropic material, is given by
where is the temperature gradient in the x-direction, same for the y- and z-direction, and is the time rate of change of the thermal energy of the medium per unit volume. It is worth pointing out that for all models analysed in this paper, internal heat generation was not considered, and the material is not experiencing a change in phase.
4.1.4. Adopted Mesh
Figure 10 shows the mesh used in the finite element analysis. It was also tested with a more refined mesh for the whole model but did not present any significant differences in the temperature distribution. The type of element used was a DC3D8 (8-node linear heat transfer brick) with full integration that is part of the heat transfer family from ABAQUS to correctly acquire the temperature field distribution due to a strong flux gradient (Figure 11). It was used as a solver in the ABAQUS/Standard implicit method [51], and the maximum allowable nodal temperature change per increment was 10, thus ABAQUS restricts the time increments to ensure that this value is not exceeded at any node during any increment of the analysis. This approach is used in all numerical models of this paper.
Figure 10.
Adopted mesh in the numerical model.
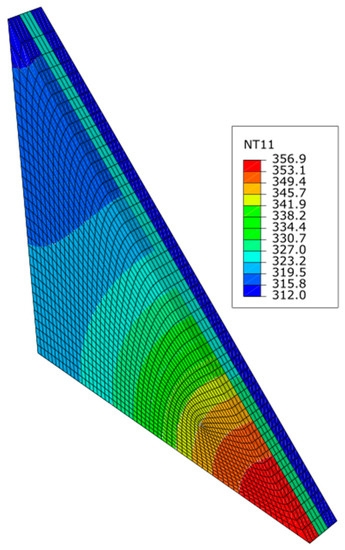
Figure 11.
Temperature field distribution for wood pallets at 5000 s in Kelvin.
4.1.5. Results
In order to validate the finite element model used to determine the temperature field distribution, a fraction of the experimental campaign [38] is first replicated—consisting of wood pallets, wood pallets mixing with charcoal, eucalyptus, and pine—all data tested can be seen in [38]. Figure 3 provides an overall view of the experimental setup that was specially designed and built at the Structures and Strength of Materials Laboratory of the Instituto Superior Técnico—University of Lisbon in Portugal. The temperature measured in the top plate from the experimental campaign was from the firebrands () and was from the steel plate in the numerical models, so these values cannot be compared between them, therefore the goal in this validation was to compare the temperature distribution for the middle plate.
The dashed lines represent the experimental values, and the solid lines, which are the same colours as the experimental ones, represent the numerical values. The first gap is the gap between the bottom side (BS) of the top plate and the top side (TS) of the middle plate. Due to the gap between the steel plates, it is not expected that both the experimental and numerical values are directly comparable, for this reason, to directly compare the experimental values of the thermocouples, an average numerical value of the first gap is used. This means, that it is expected that the temperature field distribution may present some discontinuities between steel plates (Figure 11). Figure 12 shows the numerical results with the experimental values for comparison purposes for the first gap, it is worth noting that the experimental data from the wood pallet had a drop in 800–2000 s due to a malfunction, but it is still possible to compare them with the numerical model. The temperature values were measured at the closest integration Gauss point to the fire contact surface, which is point A in Figure 9.
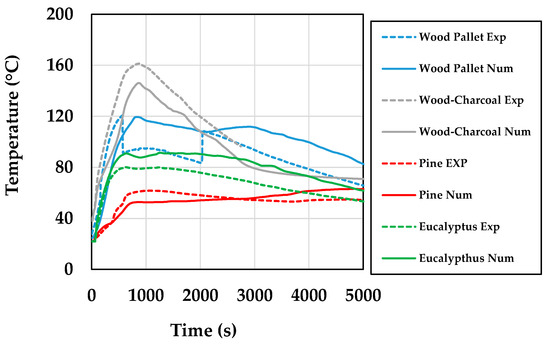
Figure 12.
Comparison between experimental and numerical values for the first gap.
Figure 13 presents the experimental average of the four types of wood used, with the numerical average of the same woods. This approach is used because there are relevant differences between temperatures that depends on the type of wood used, as can be seen in Figure 12, especially for Wood Pallet–Charcoal and Pine.
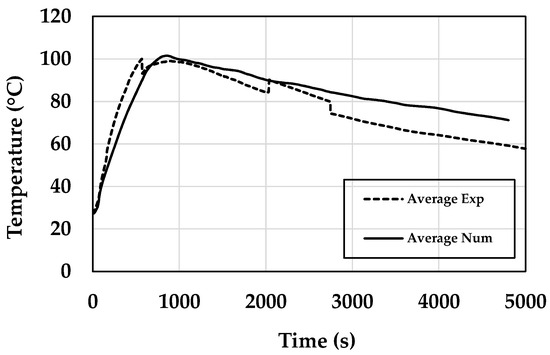
Figure 13.
Average of the types of wood used.
The observation of these results prompts the following remarks: (i) in any case for the first gap, the numerical temperature value provides a good comparison with the experimental ones, but there are significant differences between different types of woods; (ii) using an average for all numerical and experimental values of the temperature over time shows a good fit, then it can be stated that the proposed heat flux for firebrand accumulation model can simulate the temperature field distribution in plane surfaces; (iii) the average approach is acceptable because in a wildfire there are lots of woods types to be burn, thus it is close to the real life situation.
4.2. Previous Experimental Campaign by Mueller et al. [37]
4.2.1. Geometry and Type of Analysis
The experimental setup is shown in Figure 14, where the geometry of the numerical model adopted can also be seen. In order to reduce computational cost, only 1/4 of the specimen was considered in the numerical model. The basket had 75 mm of diameter. Instead of steel plates, the authors in [37] chose to use a calcium silicate substrate base, since it provides higher insulation properties, and therefore, may increase the localized temperature in the top surfaces, due to firebrand accumulation.
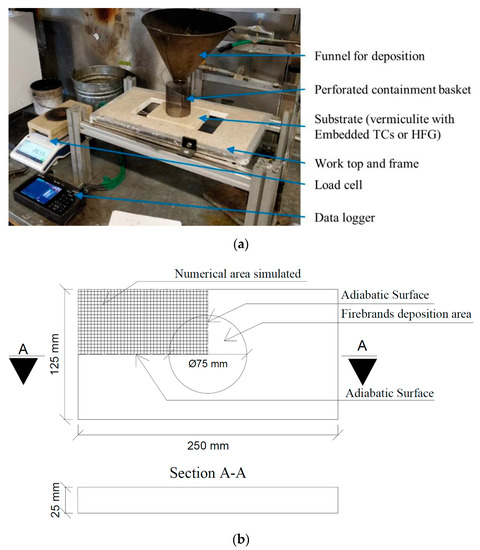
Figure 14.
(a) Experimental setup [37] and (b) geometry used in the numerical model.
4.2.2. Materials and Methods
The substrate applied was a 125 mm × 62.5 mm × 25 mm vermiculite insulation board (calcium silicate), which has similar thermal properties to wood at ambient temperature . Figure 15 shows the temperature dependence of the ratio factor applicable to the density (, thermal conductivity , and specific heat [56,57]. Furthermore, these two sets of ratios at elevated temperature were adopted in this validation. These different thermal properties variations were used since the authors did not know the real variation of thermal properties, as these are not provided by the commercial company. Therefore, similar substrate properties were used to inquire about possible variation in thermal output, due to uncertainties in material properties.
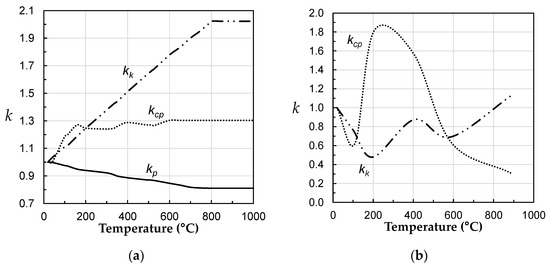
Figure 15.
Variation of the ratio factors , , and with temperature for (a) [56] and (b) [57].
The model employed the ambient temperature measured during the experimental campaign, prior to coming into contact with the firebrands. Four thermocouples were located nominally 5, 10, 15, and 20 mm deep from the firebrand contact surface to collect the temperature over time in the experiment. Therefore, the methodology consisted of replicating the experiment using the temperature vs. time curve measured in the contact surface and then compared the temperature field distribution from the surface to the 5, 10, 15, and 20 mm layers.
4.2.3. Boundary Conditions and Adopted Mesh
The same boundary conditions adopted in Section 4.1 are used in this example, including the local values of the sink temperature for the firebrand accumulation surface (Figure 16b) and ambient temperature surfaces. For the adopted mesh, it was used an 8-node linear heat transfer brick DC3D8 with full integration, using an advancing front algorithm to generate the mesh and admitting an element maximum size of 2.5 mm (Figure 16a). Figure 17 also shows the prescribed boundary condition adopted.
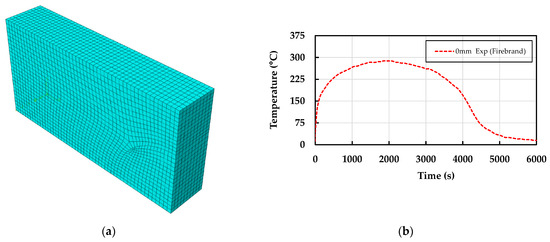
Figure 16.
(a) Adopted mesh and (b) inputted firebrand data [37].
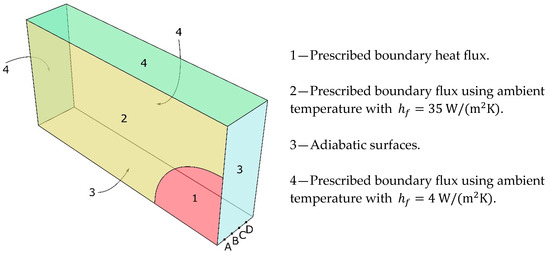
Figure 17.
Boundary conditions adopted for the simulation of the previous experimental campaign by Mueller et al. [38].
4.2.4. Results
In this subsection, the results from the thermal nonlinear analysis of a calcium silicate substrate are presented, in which temperature values were measured at the closest integration Gauss point to the fire contact surface, which are points A, B, C, and D in Figure 17. Figure 18 provides the numerical results with the experimental values using three different approaches for the modelling of thermal properties: (i) constant at ambient temperature; (ii) temperature dependence with density ratio factors according to [56] and specific heat and thermal conductivity ratio factors according to [57]; (iii) temperature dependence with all ratio factors according to [56]. Figure 19 shows the temperature distribution that does not present discontinuities between layers as in the first validation model since in this case the substrate is completely continuous.
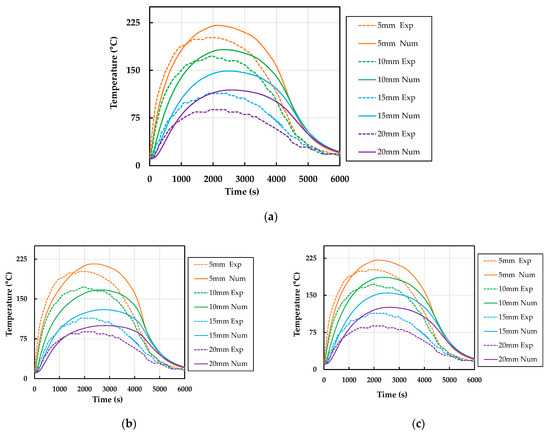
Figure 18.
Comparison between experimental and numerical values in-depth for (a) constant thermal properties at ambient temperature, (b) thermal properties with temperature dependence [56,57], and (c) thermal properties with temperature dependence [56].
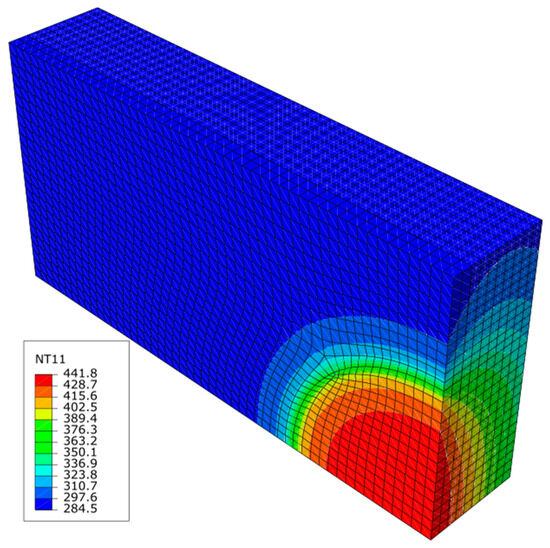
Figure 19.
Temperature field distribution at 4000 s in Kelvin.
Upon observing these results, the following observations can be made: (i) it was observed that in-depth temperature distribution over time follow the same patterns as the firebrand temperature during the analysed period for all cases; (ii) for the constant thermal properties (Figure 18a), it showed a good fit between results at the beginning of heating phase and then the values started to differ; (iii) the case with thermal properties with temperature dependence according to the reduction factors from [56,57] exhibited the best behaviour, demonstrating a good agreement for the maximum temperature across all depths (Figure 18b); (iv) the case with thermal properties with temperature dependence according to the reduction factors from [56] (Figure 18c) showed similar results as using constant thermal properties at ambient temperature. This similarity can be attributed to the low variation in the ratio factors ( and ), at the maximum measured temperature of 200 °C. In contrast, when utilising the thermal properties based on [54], these ratio factors were higher ( and ), which can account for the significant difference in the obtained results; (v) in all cases the beginning of the heating phase is well modelled, but for lower temperatures the differences are higher; and (vi) finally, the cooling phase (>2500 s) could not have been accurately validated because the thermal properties are different from the heating phase. During the heat transfer, the material suffers internal damage, and the properties values change—the thermal property values from 20 °C to 200 °C are different from 200 °C to 20 °C—and these values could not be found in the literature.
In view of this quite good correlation of both validation studies, it seems fair to argue that the finite element model employed in this work may be deemed satisfactorily validated.
5. Case Study of Firebrand Accumulation
In this section, a different approach is addressed to evaluate the firebrands action, in which a wood corner wall that has its surface in contact with firebrands is used (Figure 20). In this case, the standard fire design curves are also used [52], namely, ISO 834, external fire curve (EFC) [52], and a standard firebrand accumulation curve (FAC) [38].
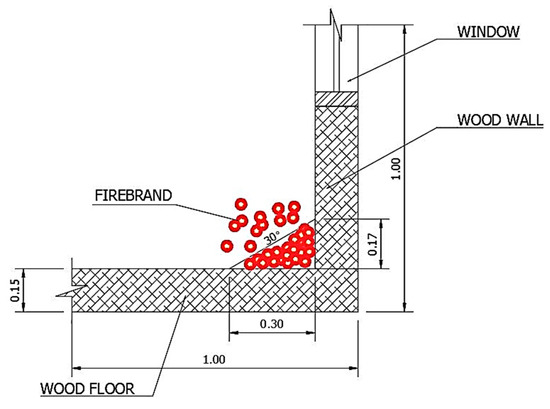
Figure 20.
Example of a wood dwelling porch with firebrand accumulation, units in m.
The numerical model is a 2D wall with dimension of 100 cm × 100 cm with 15 cm of thickness, using the properties with temperature dependence (thermal conductivity, specific heat, and density) from Eurocode 5:1-2 [58]. The “jump” in the specific heat from 99–120 °C was replaced into a linear variation (Figure 21) and introduced the latent heat , using the heat of vaporization (ΔHvap) of 2.260 kJ/kg with different percentages (0%, 3%, 6%, 12%, and 20%) of moisture content (u) in order to make sure that the heat from water vaporization is taken into account during the non-linear finite element analysis [59,60]. It is worth noting that for 0% of initial moisture content the specific heat used was presented in Figure 21a, which is the default values of Eurocode 5:1-2 [58], and no latent heat was used, but this does not mean that there is no moisture content because the Eurocode has already taken this into account with the peak “jump” in the specific heat. In addition, the latent heat with different moisture content helps to understand the thermal behaviour for different scenarios, and all percentages addressed are related to structural design (service classes 1 and 2). While employing modified specific heat to account for phase changes during the heating of a material is a valid approach, it can potentially give rise to numerical challenges, especially when dealing with scenarios characterised by a narrow phase change temperature range and high moisture content [60]. The ABAQUS [51] software tackles this issue by using latent heat property, instead of relying solely on modified specific heat. In cases where substantial latent heat effects are present, a significant disparity in the tangent terms of the internal energy arises between the interior and exterior of the phase change temperature range. To counteract this, in the initial iterations of the solution for a given time step, the tangent term is transformed from its original form to a secant approximation [51]. In light of these considerations, the decision was made to adopt the more robust latent heat approach.
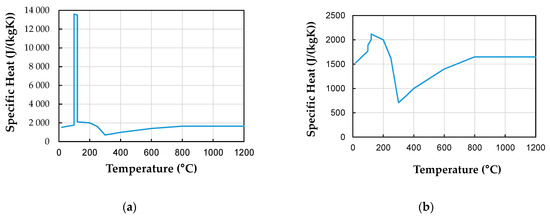
Figure 21.
Specific heat from (a) Eurocode 5:1-2 [58] and (b) Eurocode 5:1-2 adapted.
The density adopted for the timber is 510 kg/m3 [61], a reference value for softwoods (fir and pine). The temperature/dependence ratio, which considers the moisture content, is presented in Figure 22a based on Eurocode 5:1-2 [58]. This ratio takes into account the moisture content, thus for each moisture content the initial density changes. Finally, Figure 22b shows the thermal conductivity used in the model [58].
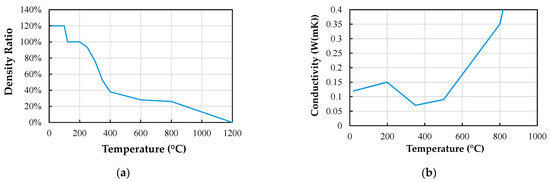
Figure 22.
(a) Density ratio with an initial moisture content of 20% and (b) thermal conductivity.
The thermal surface convection and radiation parameters are the same as the ones used in Section 4.1 and follow the recommendations in [52]. Equation (3) is used for the prescribed heat flux due to firebrand accumulation and ambient temperature. For the sink temperature, the measured firebrand contact surface temperature (Figure 8) and fire design curves (Figure 23) were used. For the adopted mesh, it was used a 4-node linear heat transfer brick DC2D4 with full integration and the maximum element size was 3 cm (Figure 24a).
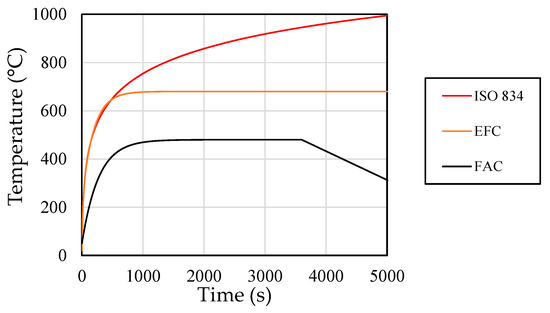
Figure 23.
Fire design curves.
Figure 24.
(a) Mesh adopted, (b) prescribed boundary heat flux for the firebrands, (c) prescribed boundary flux using ambient temperature with , (d) prescribed boundary flux using ambient temperature with , and (e) adiabatic surfaces.
Results
The goal of this case study is to understand the temperature distribution from firebrands into the contact surface. It is worth noting that the results were measured at the closest integration Gauss point to the prescribed heat flux–fire contact surface. Firstly, Figure 25 shows the temperature field distribution considering wood pallet firebrands at the last step time accounted, in which the maximum temperature can be seen in the unexposed side of the wall that is 24 °C. The temperature field was similar to all firebrand wood types studied. Figure 26, Figure 27 and Figure 28 display the numerical outputs using different initial moisture contents for the four types of firebrand wood and the three fire design curves analysed.

Figure 25.
Temperature distribution in the model for wood pallet at 5000 s (in Kelvin).
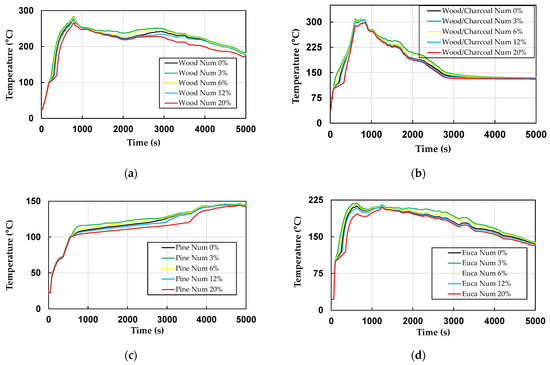
Figure 26.
Numerical maximum surface temperatures using (a) Wood Pallet, (b) Wood Pallet/Charcoal, (c) Pine, and (d) Eucalyptus with different moisture contents.
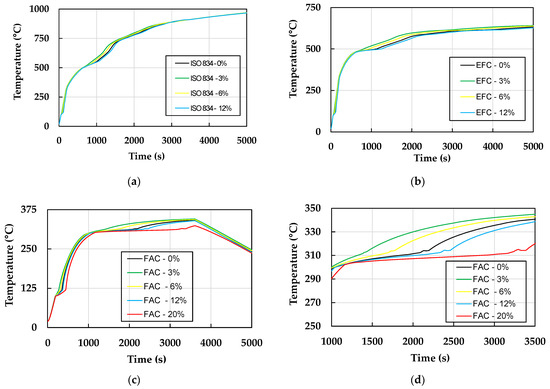
Figure 27.
Numerical maximum surface temperatures using (a) ISO 834, (b) external fire curve, (c) firebrand accumulation curve, and (d) zoom in of firebrand curve.
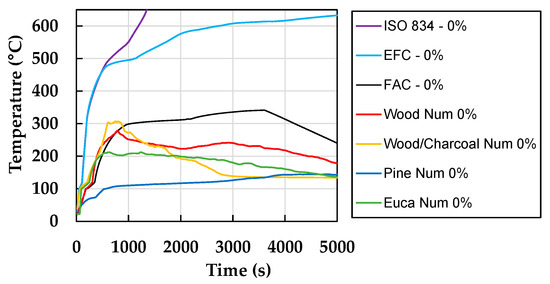
Figure 28.
Numerical maximum surface temperature for all 0% initial moisture content results.
The joint observation of these plots leads to the following comments: (i) the firebrand maximum temperature measured was from the wood pallet firebrands, and wood pallet/charcoal firebrands reached around 300 °C for all results at approximately 1000 s; (ii) the initial moisture content affects considerable the maximum temperature and behaviour, which using , shows that the temperature distribution stays almost in the middle of the results from 6% and 12% (see Figure 27d), meaning that the specific heat in Eurocode admits an initial moisture content around 9% [58]. Similar results were expected since the specific heat from Eurocode already taking into account the water latent heat using a peak “jump” in the values (Figure 21a); (iii) all fire design curves analysed showed maximum temperature values above those of firebrands (Figure 28), which means that all the curves are in accordance with the safety indicator. The results also presented that for 1000 s, the ISO 834 and External Fire curve provides temperature values of 500 °C and continues on the heating phase, which is higher than the firebrand values, showing that for an indirect action of a wildfire, the current fire design curves are conservative because they were developed for a different fire scenario; (iv) on the other hand, for the firebrand accumulation curve, the maximum temperature was around 350 °C at 3500 s, showing a good match with the values from the four types of firebrands (see Figure 28) and taking into account the cooling phase.
6. Final Remarks
In this work, the use of heat flux transmission via convection and radiation was proposed to simulate the thermal effect of firebrand accumulation on plane surfaces, using thermal non-linear transient analysis with a classical finite element method, in which all thermal properties were temperature-dependent and one case with constant thermal properties at ambient temperature. The numerical temperatures due to prescribed heat flux were compared with experimental temperature values, obtained in test setup with thermocouples and firebrand accumulation. It was shown in the validation studies that the prescribed heat flux due to firebrands can simulate the temperature field distribution on plane surfaces. This work also presented a comparison of results between fire design curves and firebrand contact in order to investigate whether the proposed standard firebrand accumulation curve leads to higher temperatures in real structures compared to direct firebrand contact. Additionally, the suitability of current fire design curves for indirect actions caused by wildfires was evaluated. It was concluded that the fire design curves [52], namely, ISO 834 and External Fire curve, provide conservative values when compared to the proposed firebrand curve. These findings demonstrate that there is potential for thermal optimization in the design of structures exposed to wildfire, and this work contributes to the researching of an efficient design for structures at elevated temperatures due to a wildfire.
Finally, the initial moisture content using the latent heat approach showed this behaviour until 20%, which is the final value of moisture content for structural purpose and has a significant impact in the temperature field distribution.
6.1. Future Developments
The next step in this ongoing investigation is to address a different approach to evaluate firebrand accumulation, studying the temperature distribution into the thickness with different materials to analyse what percentage of firebrand accumulation curve transfers flux via convection and radiation.
By considering the effects of temperature resulting from direct contact with wildfire flames [9], as well as the indirect impact of wildfire through firebrand accumulation [38], it becomes feasible to propose a forthcoming standard for fire-resistant dwelling design against the hazards of wildfires.
6.2. Limitations of the Study
It is crucial to point out that the proposed standard firebrand curve is only intended to simulate the thermal behaviour of firebrand accumulation on a plane surface, which is the most severe scenario when designing fireproof dwellings against wildfire indirect impact. It does not intend to simulate the thermal effect of an isolated single firebrand on a plane surface, which has a lower thermal effect when in contact with the plane surface. In addition, it does not simulate the internal temperature of an isolated firebrand since its thermal energy transfer is reduced when in contact with a surface. Also it is important to point out that it does not simulate the direct wildfire contact with a dwelling, and those types of standard performances based on wildfire curves can be found in [9].
Author Contributions
Conceptualization, M.R.A. and C.T.; methodology, M.R.A. and C.T.; software, A.R.B.; validation, A.R.B. and P.C.; formal analysis, A.R.B., M.R.A. and C.T.; investigation, A.R.B., P.C. and E.B.d.A.; resources, A.R.B., P.C. and E.B.d.A.; data curation, A.R.B., P.C. and E.B.d.A.; writing—original draft preparation, A.R.B.; writing—review and editing, A.R.B., P.C., M.R.A., C.T., E.B.d.A. and F.B.; visualization, M.R.A. and C.T.; supervision, M.R.A., C.T. and F.B.; project administration, M.R.A. and F.B.; funding acquisition, M.R.A. and F.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the FCT, National Funding Agency for Science, Research and Technology, Portugal (Research Project “New Fireproof Dwellings for Wildfire” PTDC/ECI-CON/2240/2020). This study was also financed in part by CERIS (Project UIDB/04625/2020) and the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior—Brasil (CAPES)—Finance Code 001.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Caton, S.E.; Hakes, R.S.; Gorham, D.J.; Zhou, A.; Gollner, M.J. Review of Pathways for Building Fire Spread in the Wildland Urban Interface Part I: Exposure Conditions. Fire Technol. 2017, 53, 429–473. [Google Scholar] [CrossRef]
- Hakes, R.S.; Caton, S.E.; Gorham, D.J.; Gollner, M.J. A Review of Pathways for Building Fire Spread in the Wildland Urban Interface Part II: Response of Components and Systems and Mitigation Strategies in the United States. Fire Technol. 2017, 53, 475–515. [Google Scholar] [CrossRef]
- Firefighter, W. Thousands Flee South Korea Wildfire. Available online: https://www.wildlandfirefighter.com/2019/04/05/thousands-flee-south-korea-wildfire/#gref (accessed on 19 October 2022).
- Marlon, J.R.; Bartlein, P.J.; Gavin, D.G.; Long, C.J.; Anderson, R.S.; Briles, C.E.; Brown, K.J.; Colombaroli, D.; Hallett, D.J.; Power, M.J.; et al. Long-term perspective on wildfires in the western USA. Proc. Natl. Acad. Sci. USA 2012, 109, E535–E543. [Google Scholar] [CrossRef]
- Calfire. 2018 Incident Archive. Available online: https://www.fire.ca.gov/incidents/2018/ (accessed on 19 October 2022).
- Syifa, M.; Panahi, M.; Lee, C.-W. Mapping of Post-Wildfire Burned Area Using a Hybrid Algorithm and Satellite Data: The Case of the Camp Fire Wildfire in California, USA. Remote Sens. 2020, 12, 623. [Google Scholar] [CrossRef]
- Guerreiro, J.; Fonseca, C.; Salgueiro, A.; Fernandes, P.; Lopez, I.E.; de Neufville, R.; Mateus, F.; Castellnou, R.M.; Sande, S.J.; Moura, J.M.; et al. Avaliação dos Incêndios Ocorridos Entre 14 e 16 de Outubro de 2017 em Portugal Continental. 2018. Available online: https://www.portugal.gov.pt/pt/gc21/comunicacao/documento?i=avaliacao-dos-incendios-ocorridos-entre-14-e-16-de-outubro-de-2017-em-portugal-continental (accessed on 19 July 2023).
- Viegas, D.X.; Almeida, M.F.; Ribeiro, L.M.; Raposo, J.M.T.V.; Oliveira, R.; Alves, D.; Pinto, C.; Jorge, A.R.H.; Lucas, D.; Lopes, S.; et al. O Complexo de Incêndios de Pedrógão Grande e Concelhos Limítrofes, Iniciado a 17 de Junho de 2017. 2017. Available online: https://www.portugal.gov.pt/pt/gc21/comunicacao/documento?i=o-complexo-de-incendios-de-pedrogao-grande-e-concelhos-limitrofes-iniciado-a-17-de-junho-de-2017 (accessed on 19 July 2023).
- Cantor, P.; Arruda, M.R.T.; Firmo, J.; Branco, F. Proposal of Standard Wildfire Curves for the Design Protection of Dwellings against Wildland Fire. J. Hazard. Toxic Radioact. Waste 2022, 26, 04022021. [Google Scholar] [CrossRef]
- Manzello, S.L.; Suzuki, S. Experimental investigation of wood decking assemblies exposed to firebrand showers. Fire Saf. J. 2017, 92, 122–131. [Google Scholar] [CrossRef]
- Manzello, S.L.; Cleary, T.G.; Shields, J.R.; Maranghides, A.; Mell, W.; Yang, J.C. Experimental investigation of firebrands: Generation and ignition of fuel beds. Fire Saf. J. 2008, 43, 226–233. [Google Scholar] [CrossRef]
- Manzello, S.L.; Park, S.-H.; Cleary, T.G. Investigation on the ability of glowing firebrands deposited within crevices to ignite common building materials. Fire Saf. J. 2009, 44, 894–900. [Google Scholar] [CrossRef]
- Warey, A. Influence of thermal contact on heat transfer from glowing firebrands. Case Stud. Therm. Eng. 2018, 12, 301–311. [Google Scholar] [CrossRef]
- Suzuki, S.; Manzello, S.L. Investigating Coupled Effect of Radiative Heat Flux and Firebrand Showers on Ignition of Fuel Beds. Fire Technol. 2021, 57, 683–697. [Google Scholar] [CrossRef]
- Jack, D.; Cohen, R.D.S. Home Destruction Examination: Grass Valley Fire; United State Department of Agriculture: Lake Arrowhead, CA, USA, 2008; p. 26.
- Maranghides, D.M.A.; Vihnanek, R.; Restaino, J.; Leland, C. A Case Study of a Community Affected by the Waldo Fire Event Timeline and Defensive Actions; National Institute of Standards and Technology: Gaithersburg, MA, USA, 2015.
- Mell, W.E.; Manzello, S.L.; Maranghides, A.; Butry, D.; Rehm, R.G. The wildlandurban interface fire problem current approaches and research needs. Int. J. Wildland Fire 2010, 19, 238–251. [Google Scholar] [CrossRef]
- Tarifa, C.S.; Del Notario, P.P.; Moreno, F.G. On the flight paths and lifetimes of burning particles of wood. Symp. Int. Combust. 1965, 10, 1021–1037. [Google Scholar] [CrossRef]
- Woycheese, J.P.; Pagni, P.J.; Liepmann, D. Brand Propagation from Large-Scale Fires. J. Fire Prot. Eng. 1999, 10, 32–44. [Google Scholar] [CrossRef]
- Wadhwani, R.; Sullivan, C.; Wickramasinghe, A.; Kyng, M.; Khan, N.; Moinuddin, K. A review of firebrand studies on generation and transport. Fire Saf. J. 2022, 134, 103674. [Google Scholar] [CrossRef]
- Usda, F.A.A. Transport of Firebrands by Line Thermals. Combust. Sci. Technol. 1983, 32, 277–288. [Google Scholar] [CrossRef]
- Matvienko, O.V.; Fil’kov, A.I.; Grishin, A.M. Computational Investigation of the Transport of Burning Particles. J. Eng. Phys. Thermophys. 2016, 89, 1315–1324. [Google Scholar] [CrossRef]
- Wang, H.-H. Analysis on Downwind Distribution of Firebrands Sourced from a Wildland Fire. Fire Technol. 2011, 47, 321–340. [Google Scholar] [CrossRef]
- Suzuki, S.; Manzello, S.L. Characteristics of Firebrands Collected from Actual Urban Fires. Fire Technol. 2018, 54, 1533–1546. [Google Scholar] [CrossRef]
- Suzuki, S.; Manzello, S.L.; Lage, M.; Laing, G. Firebrand generation data obtained from a full-scale structure burn. Int. J. Wildland Fire 2012, 21, 961–968. [Google Scholar] [CrossRef]
- Manzello, S.L.; Maranghides, A.; Mell, W.E. Firebrand generation from burning vegetation. Int. J. Wildland Fire 2007, 16, 458–462. [Google Scholar] [CrossRef]
- Hakes, R.S.P.; Salehizadeh, H.; Weston-Dawkes, M.J.; Gollner, M.J. Thermal characterization of firebrand piles. Fire Saf. J. 2019, 104, 34–42. [Google Scholar] [CrossRef]
- Manzello, S.L.; Suzuki, S. Experimentally Simulating Wind Driven Firebrand Showers in Wildland-urban Interface (WUI) Fires: Overview of the NIST Firebrand Generator (NIST Dragon) Technology. Procedia Eng. 2013, 62, 91–102. [Google Scholar] [CrossRef]
- Suzuki, S.; Manzello, S.L. Initial study on thatched roofing assembly ignition vulnerabilities to firebrand showers. Fire Saf. J. 2019, 103, 34–37. [Google Scholar] [CrossRef]
- Kasymov, D.; Paletsky, A. Effect of a fire retardant on the ignition of pine wood exposed to smoldering particles of pine bark. EPJ Web Conf. 2017, 159, 00026. [Google Scholar] [CrossRef][Green Version]
- Suzuki, S.; Manzello, S.L. Firebrand production from building components fitted with siding treatments. Fire Saf. J. 2016, 80, 64–70. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, S.; Manzello, S.L. Garnering understanding into complex firebrand generation processes from large outdoor fires using simplistic laboratory-scale experimental methodologies. Fuel 2020, 267, 117154. [Google Scholar] [CrossRef]
- Suzuki, S.; Manzello, S.L.; Hayashi, Y. The size and mass distribution of firebrands collected from ignited building components exposed to wind. Proc. Combust. Inst. 2013, 34, 2479–2485. [Google Scholar] [CrossRef]
- Kasymov, D.P.; Tarakanova, V.A.; Martynov, P.S.; Agafontsev, M.V. Studying firebrands interaction with flat surface of various wood construction materials in laboratory conditions. J. Phys. Conf. Ser. 2019, 1359, 012092. [Google Scholar] [CrossRef]
- Salehizadeh, H.; Hakes, R.S.P.; Gollner, M.J. Critical Ignition Conditions of Wood by Cylindrical Firebrands. Front. Mech. Eng. 2021, 7, 17. [Google Scholar] [CrossRef]
- Manzello, S.L.; Suzuki, S.; Naruse, T. Quantifying wind-driven firebrand production from roofing assembly combustion. Fire Mater. 2019, 43, 3–7. [Google Scholar] [CrossRef]
- Thomas, J.C.; Mueller, E.; Hadden, R.M. Estimating net heat flux from surrogate firebrand accumulations using an inverse heat transfer approach. In Advances in Forest Fire Research; University of Coimbra: Coimbra, Portugal, 2018; pp. 769–779. [Google Scholar] [CrossRef]
- Cantor, P.; Arruda, M.R.T.; Firmo, J.; Branco, F. Development of a standard firebrand accumulation temperature curve for residential wildfire protection system. Results Eng. 2023, 17, 100935. [Google Scholar] [CrossRef]
- Jones, J.C.; Raj, S.C. The self-heating and ignition of vegetation debris. Fuel 1988, 67, 1208–1210. [Google Scholar] [CrossRef]
- Jones, J.C.; Rahmati, H. The self-heating and ignition of vegetation debris. 2. Authentic litter samples. Fuel 1990, 69, 253–255. [Google Scholar] [CrossRef]
- Jones, J.C.; Ramahti, H.; Fowler, D.; Vorasurayakarnt, J.; Bridges, R.G. The Self-Heating and Thermal Ignition Propensity of Forest Floor Litter. J. Fire Sci. 1990, 8, 207–223. [Google Scholar] [CrossRef]
- Jones, J.C. Predictive Calculations of the Effect of an Accidental Heat Source on a Bed of Forest Litter. J. Fire Sci. 1993, 11, 80–86. [Google Scholar] [CrossRef]
- Jones, J.C. Further Calculations Regarding the Accidental Supply of Heat to a Bed of Forest Material. J. Fire Sci. 1994, 12, 502–505. [Google Scholar] [CrossRef]
- Jones, J.C. Improved Calculations Concerning the Ignition of Forest Litter by Hot Particle Ingress. J. Fire Sci. 1995, 13, 350–356. [Google Scholar] [CrossRef]
- Grishin, A.M.; Dolgov, A.A.; Zima, V.P.; Kryuchkov, D.A.; Reino, V.V.; Subbotin, A.N.; Tsvyk, R.S. Ignition of a layer of combustible forest materials. Combust. Explos. Shock. Waves 1998, 34, 613–620. [Google Scholar] [CrossRef]
- Bearinger, E.D.; Hodges, J.L.; Yang, F.; Rippe, C.M.; Lattimer, B.Y. Localized heat transfer from firebrands to surfaces. Fire Saf. J. 2021, 120, 103037. [Google Scholar] [CrossRef]
- California Building Code. Chapter 7A [SFM] Materials and Construction Methods for Exterior Wildfire Exposure. 2010. Available online: https://up.codes/viewer/california/ca-building-code-2016/chapter/7A/sfm-materials-and-construction-methods-for-exterior-wildfire-exposure#7A (accessed on 19 July 2023).
- Arruda, M.R.T.; Tenreiro, T.; Branco, F. Rethinking How to Protect Dwellings against Wildfires. J. Perform. Constr. Facil. 2021, 35, 06021004. [Google Scholar] [CrossRef]
- El Houssami, M.; Mueller, E.; Filkov, A.; Thomas, J.C.; Skowronski, N.; Gallagher, M.R.; Clark, K.; Kremens, R.; Simeoni, A. Experimental Procedures Characterising Firebrand Generation in Wildland Fires. Fire Technol. 2016, 52, 731–751. [Google Scholar] [CrossRef]
- EN 1990:2002; Eurocode 0—Basis of Structural Design. Comité Européen de Normalisation: Brussels, Belgium, 2002.
- Dassault Systemes Simulia Corporation. ABAQUS v.2018; Dassault Systèmes: Johnston, RI, USA, 2018; Available online: https://www.3ds.com/products-services/simulia/products/abaqus/ (accessed on 19 July 2023).
- EN 1991-1-2:2002; Eurocode 1: Actions on Structures—Part 1–2: General Actions—Actions on Structures Exposed to Fire. Comité Européen de Normalisation: Brussels, Belgium, 2002.
- Thomas, H.R.; Zhou, Z. Minimum time-step size for diffusion problem in FEM analysis. Int. J. Numer. Methods Eng. 1997, 40, 3865–3880. [Google Scholar] [CrossRef]
- EN 1994-1-2:2005; Eurocode 4: Design of Composite Steel and Concrete Structures—Part 1–2: General Rules—Structural Fire Design. Comité Européen de Normalisation: Brussels, Belgium, 2005.
- Hottel, H.C. Radiant Heat Transmission Between Surfaces Separated by Non-Absorbing Media. Trans. Am. Soc. Mech. Eng. 2023, 53, 265–271. [Google Scholar] [CrossRef]
- Morgado, T.M.R. Thermal and Structural Response of Pultruded GFRP Profiles under Fire Exposure. Ph.D. Thesis, Universidade de Lisboa, Lisboa, Portugal, 2018. [Google Scholar]
- Mazzuca, P. Fire Behaviour of GFRP Sandwich Panels for the Rehabilitation of Building Floors. Ph.D. Thesis, Universita’ Della Calabria, Rende, Italy, 2022. [Google Scholar]
- EN 1995-1-2:2004; Eurocode 5: Design of Timber Structures—Part 1–2: General—Structural Fire Design. Comité Européen de Normalisation: Brussels, Belgium, 2004.
- Assis, E.B.; Neto, J.M. Analysis of heat transfer mechanisms on hollow concrete masonry units under standardized fire conditions. Proceedings of XLI Ibero-Latin-American Congress on Computational Methods in Engineering, Foz do Iguaçu, Brazil, 16–19 November 2020; Available online: https://cilamce.com.br/anais/arearestrita/apresentacoes/194/7822.pdf (accessed on 19 July 2023).
- Wickström, U. Temperature Calculation in Fire Safety Engineering, 1st ed.; Springer: Cham, Switzerland, 2016; 243p. [Google Scholar] [CrossRef]
- Bergman, T.; Lavine, A.; Incropera, F.; Dewitt, D. Fundamentals of Heat and Mass Transfer, 7th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).