Multi-Objective Optimization of Micro-Milling Parameters—The Trade-Offs between Machining Quality, Efficiency, and Sustainability in the Fabrication of Thin-Walled Microstructures
Abstract
:1. Introduction
2. Materials and Methods
2.1. Power Consumption Modeling
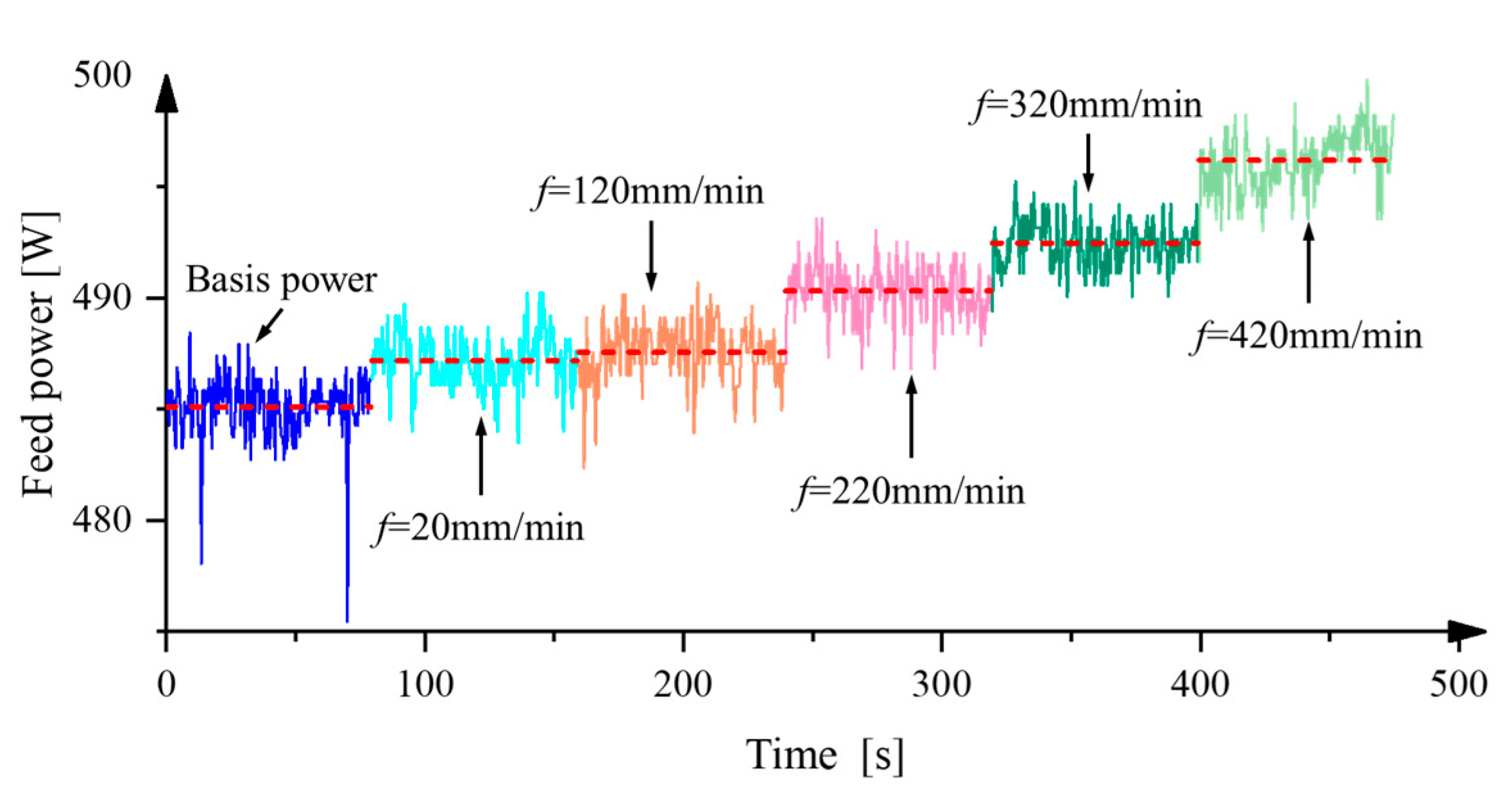
2.1.1. Power Consumption Modeling in Feed and Spindle Subsystems
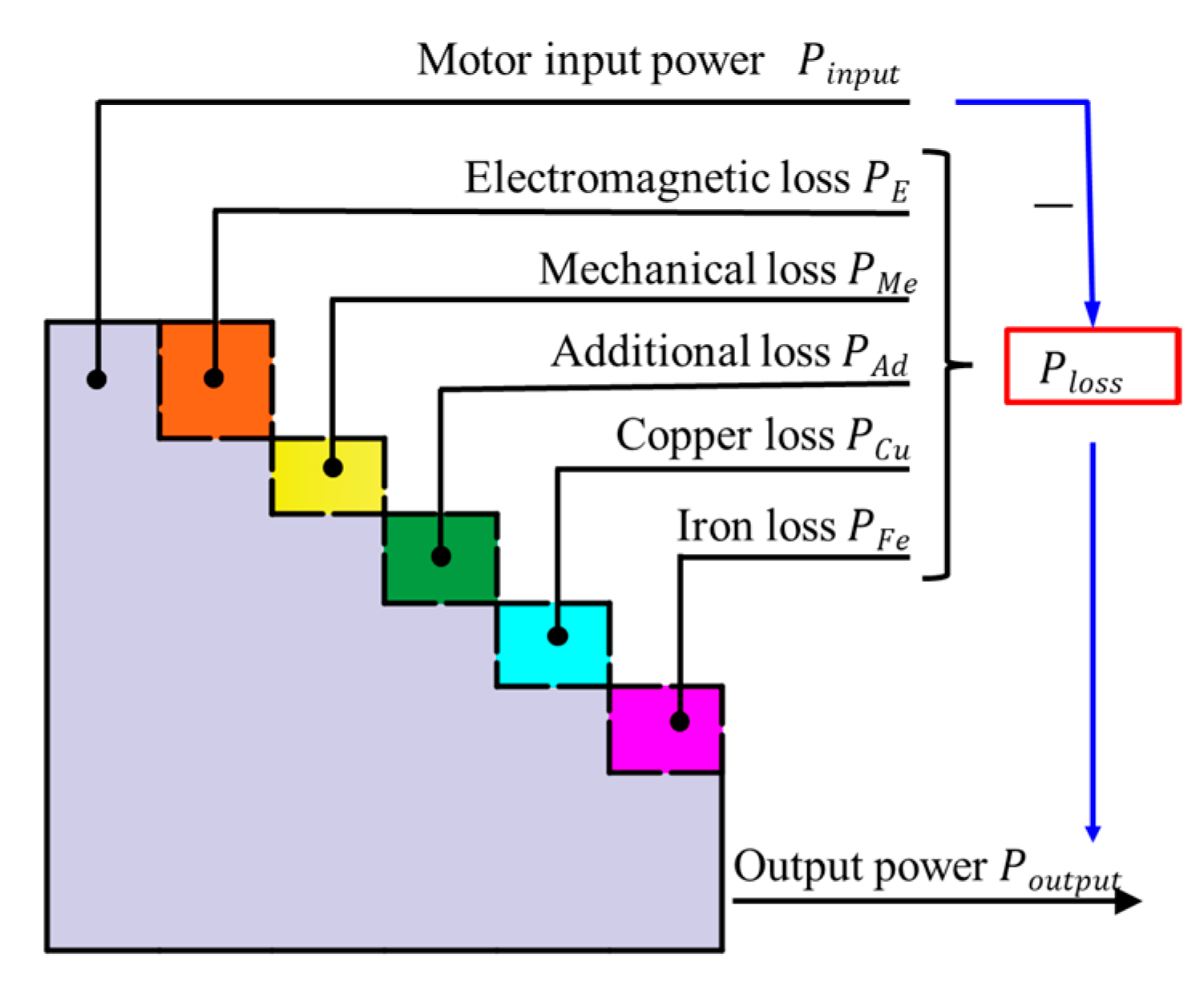
2.1.2. Material Removal Power Modeling
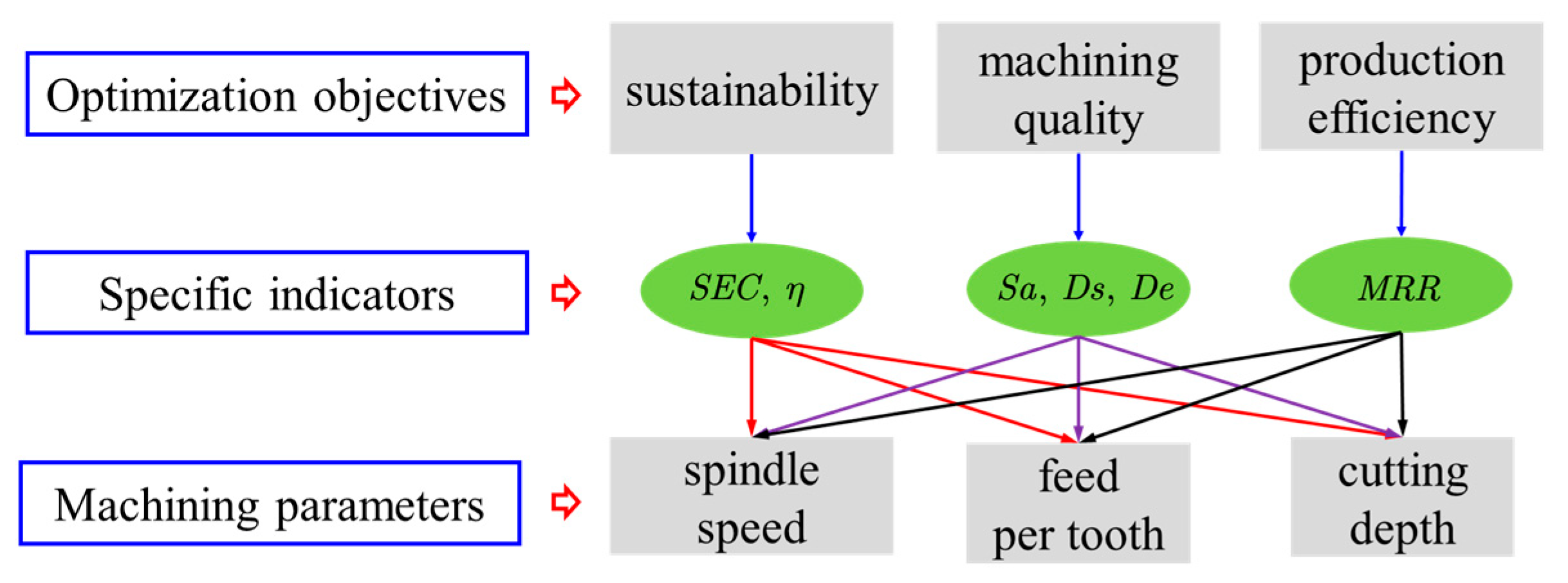
2.2. Description of the Multi-Objective Optimization Problem
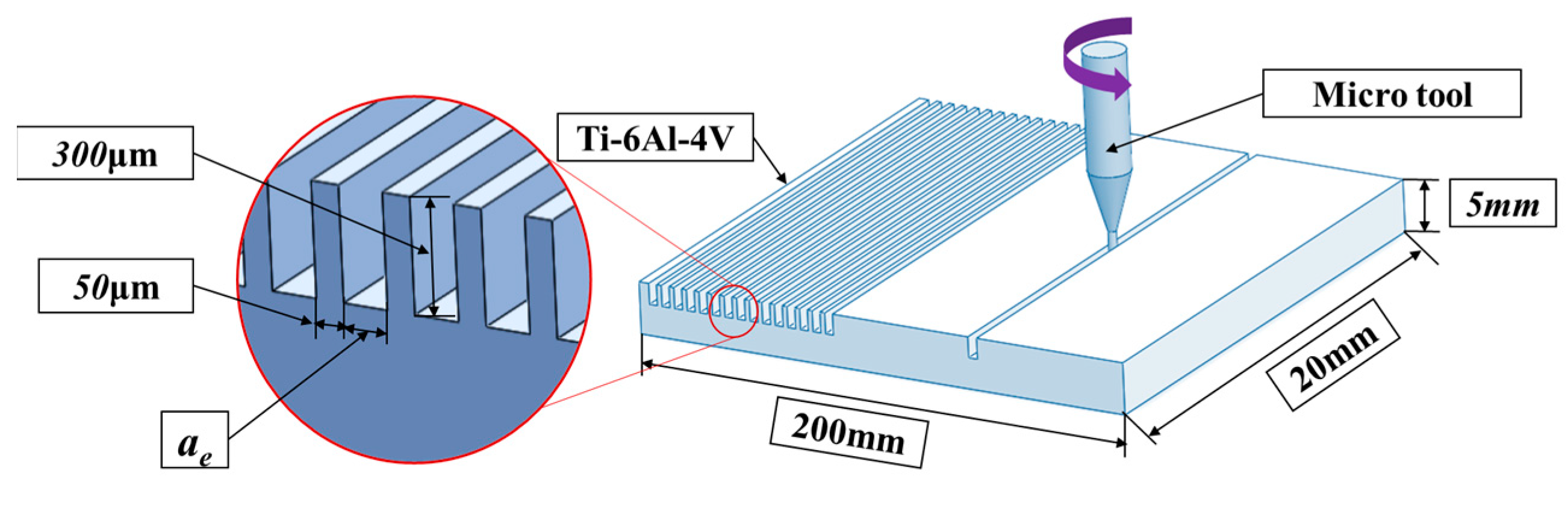
2.3. Experimental Design
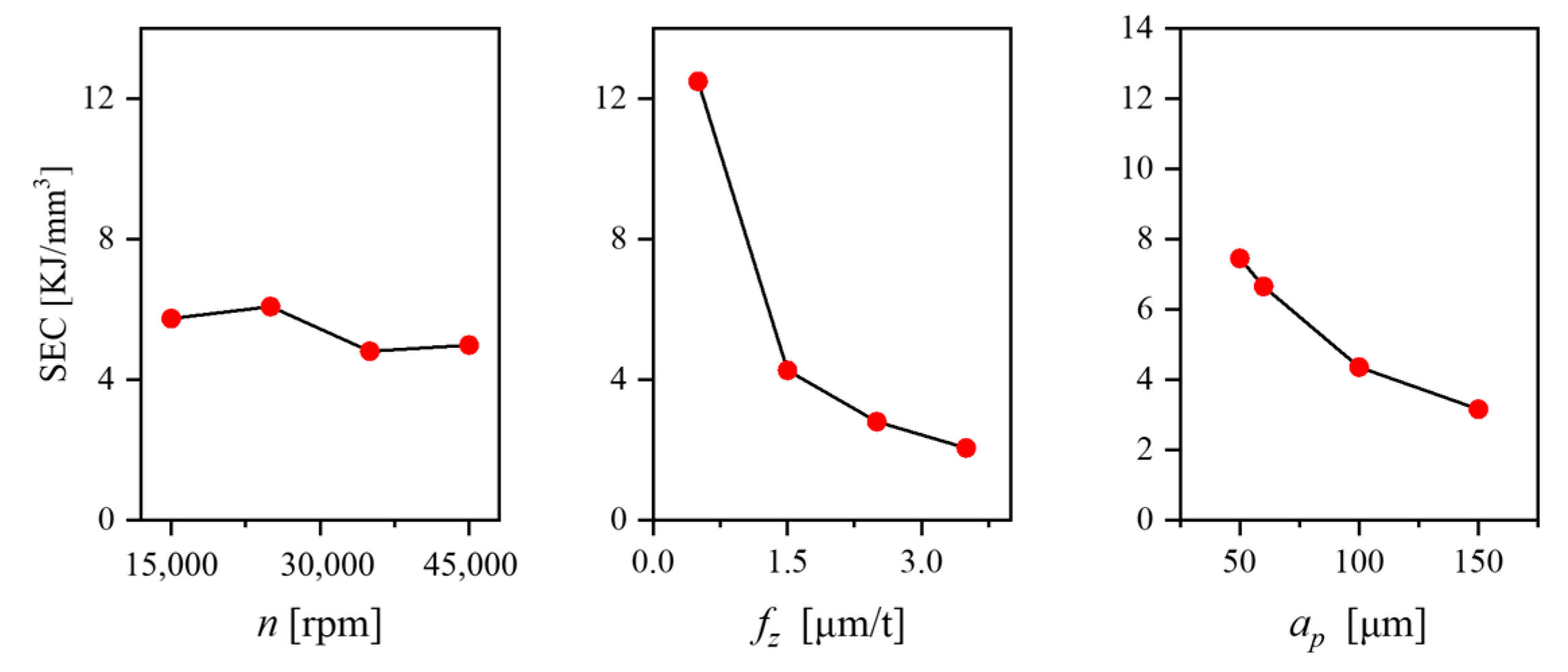
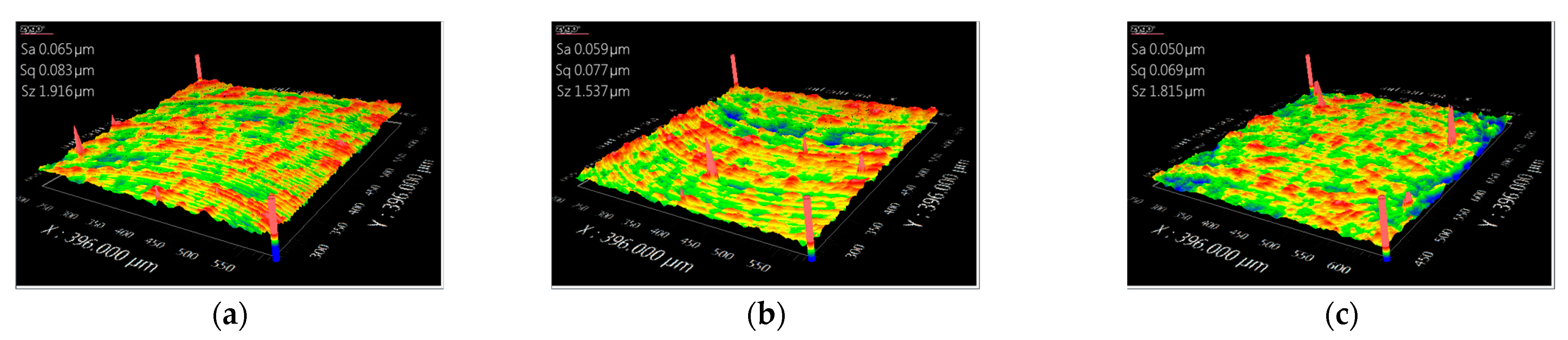
3. Results and Discussions
4. Conclusions
- (1)
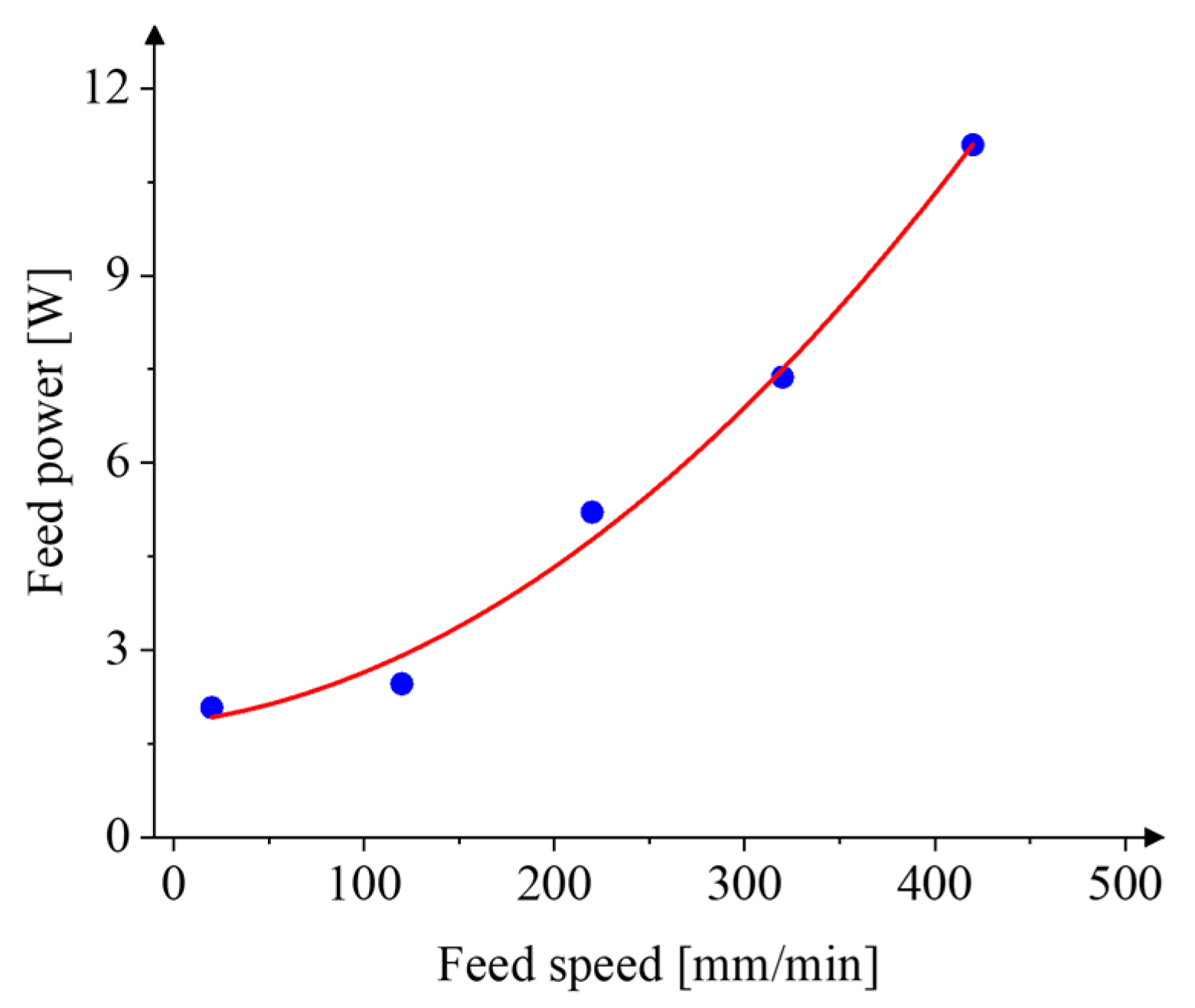
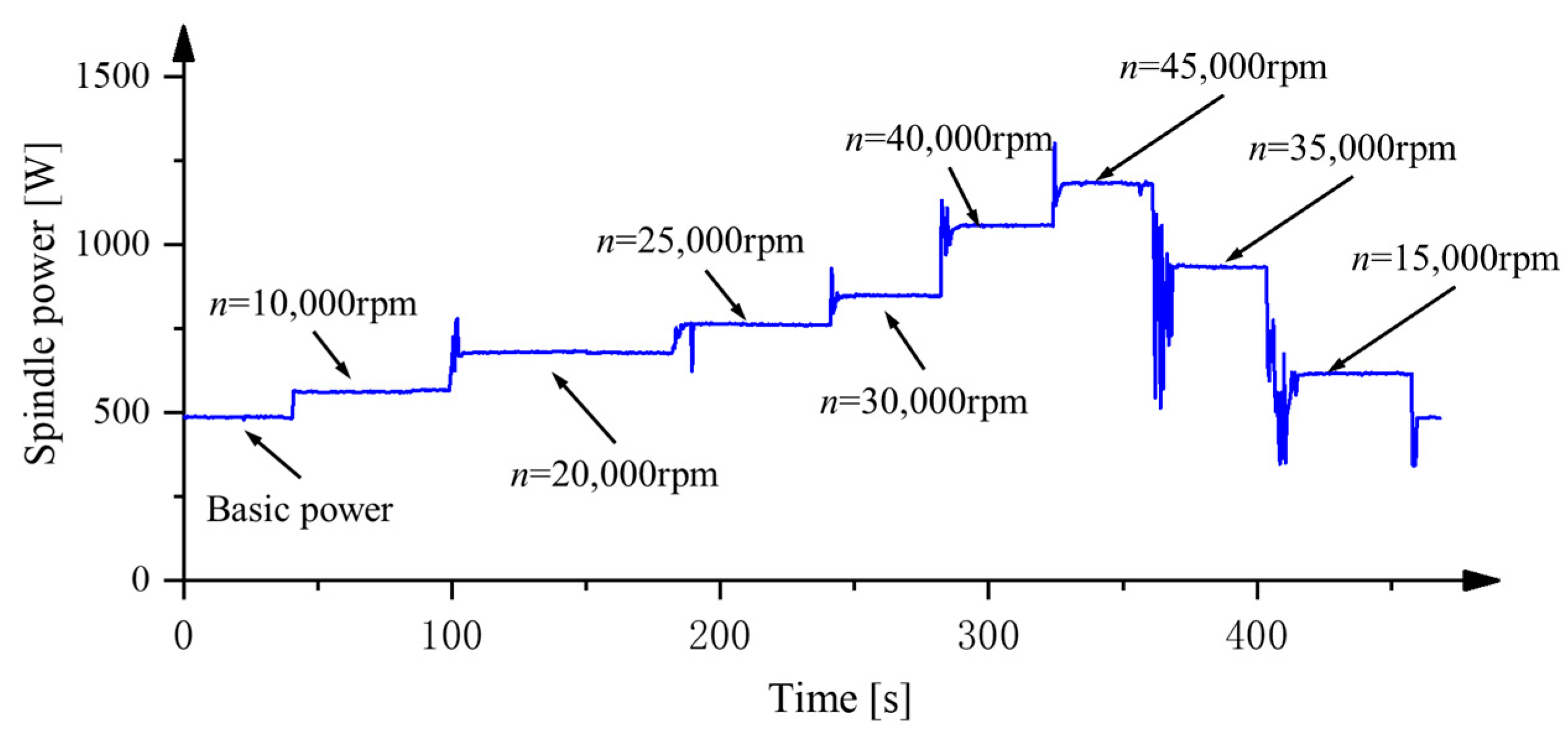
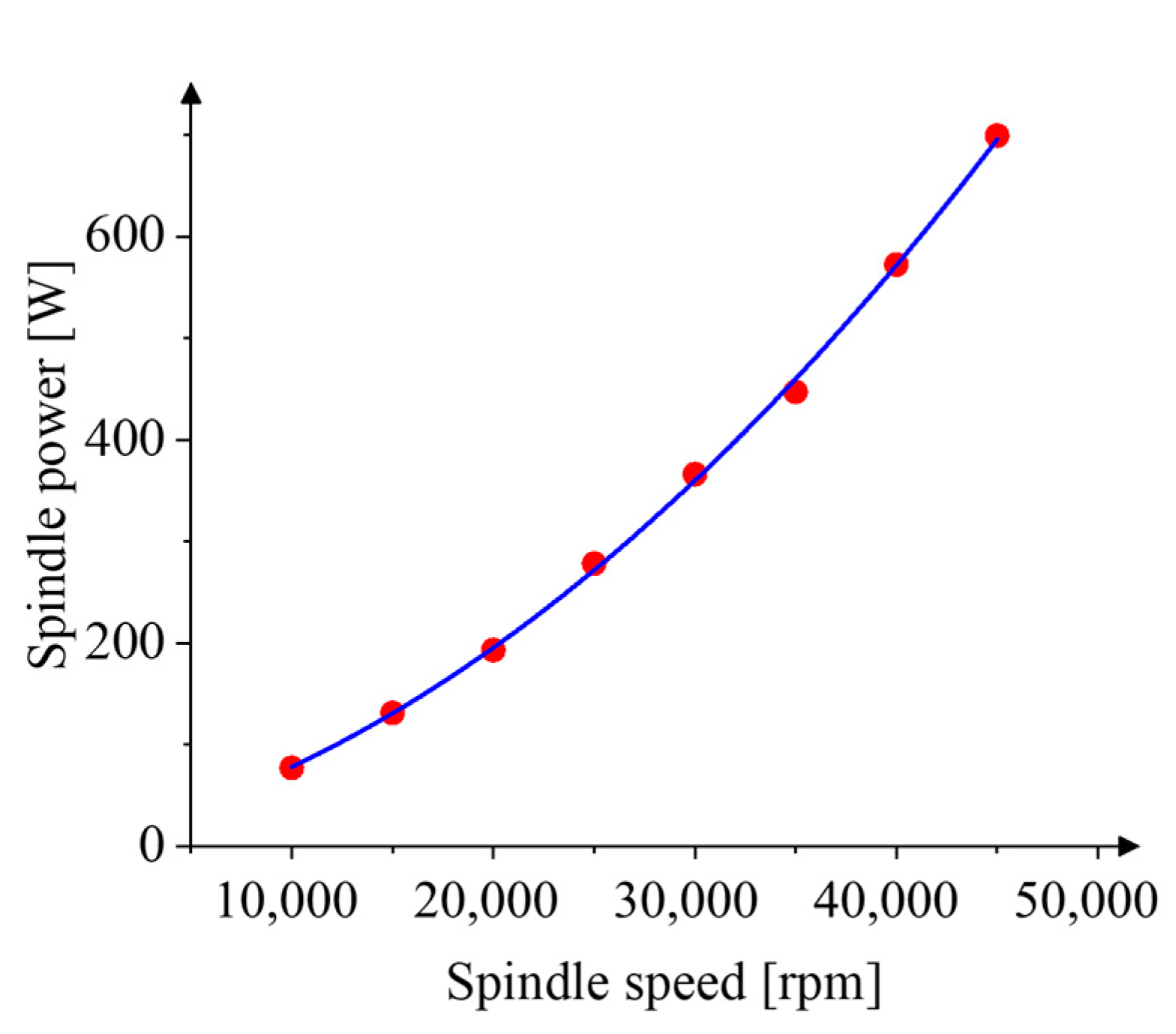
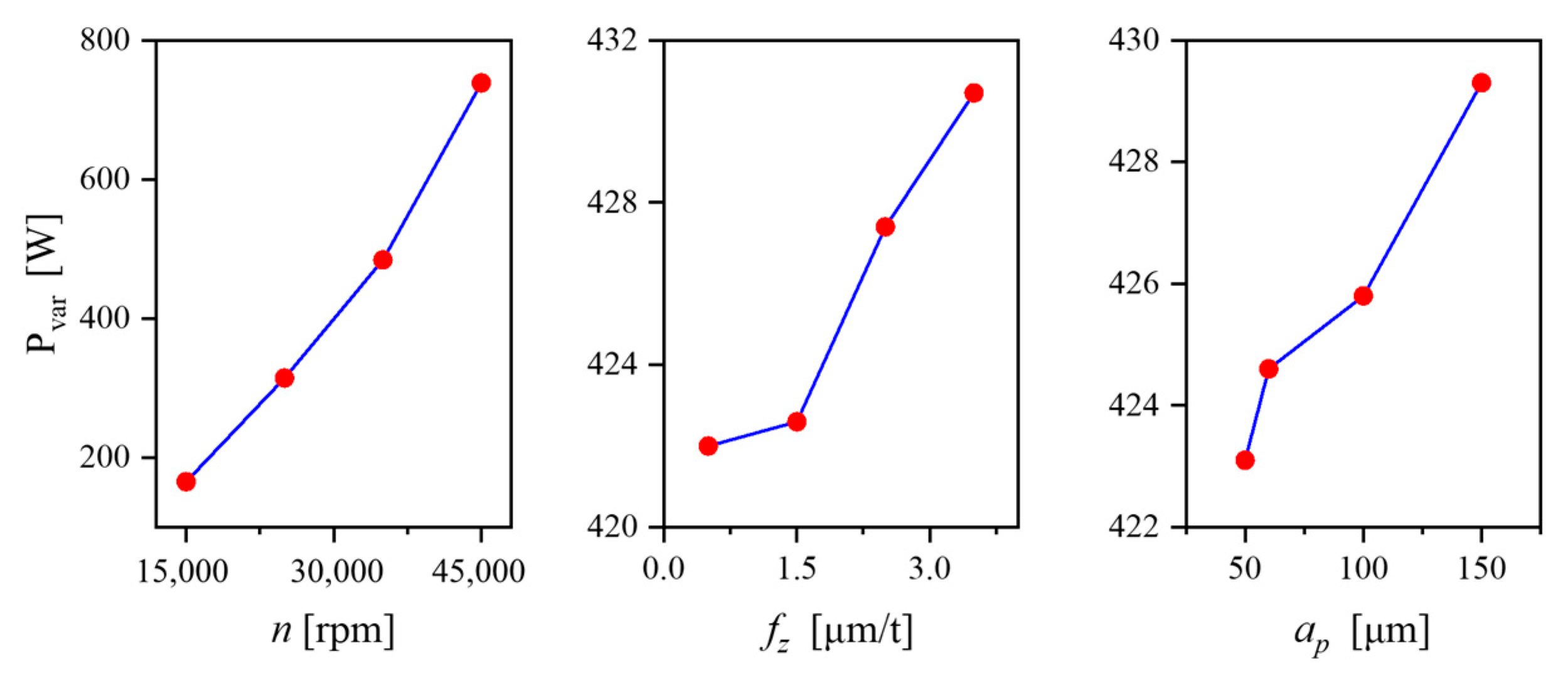
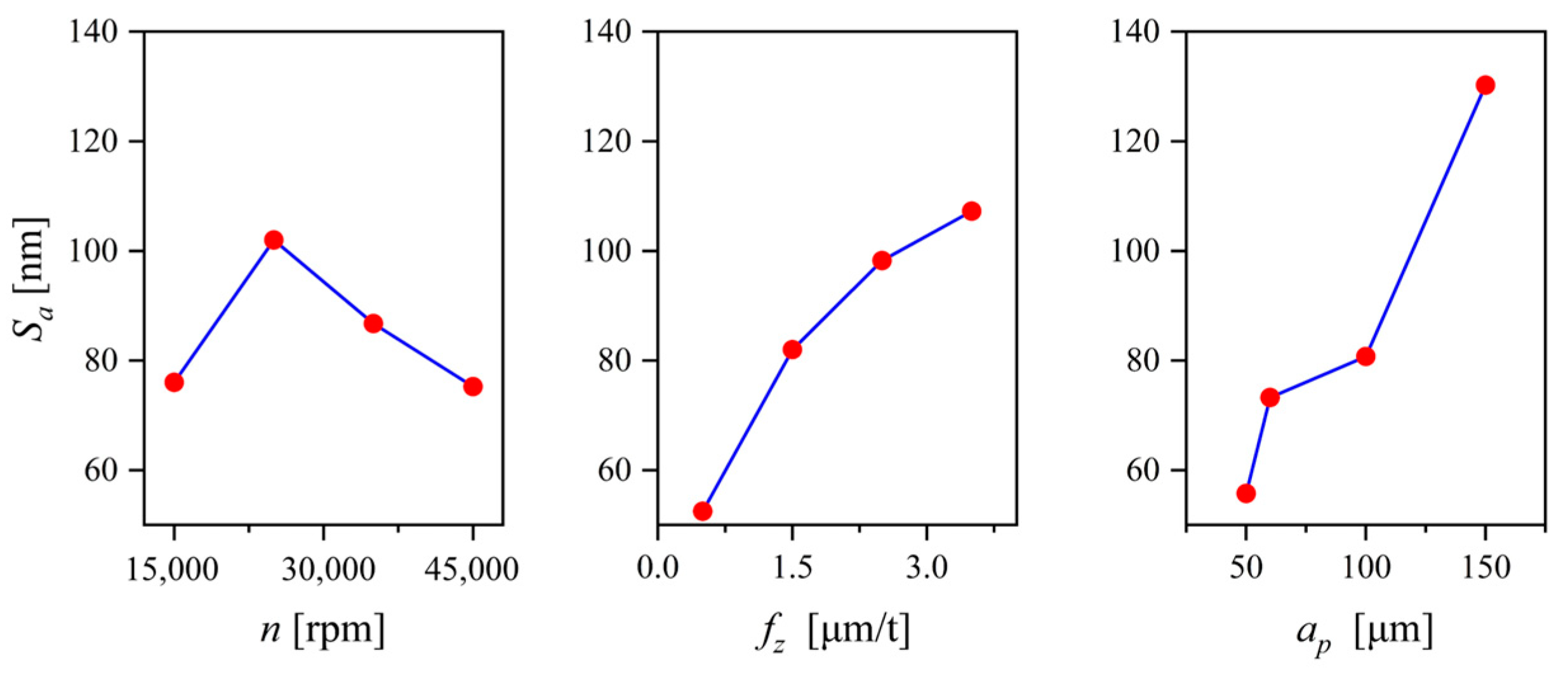
- The power consumption characteristics of the micro-milling process were analyzed, and a process-parameter-based power consumption model was established. The analysis revealed that the power consumption of non-machining feed motion exhibits a quadratic relationship with the feed rate, while the non-machining spindle power consumption shows a quadratic relationship with the spindle speed. The spindle speed exerts the greatest influence on the variable power consumption.
- (2)
- The coefficient between SCE and MRR was −0.793, which indicates that enhancing machining efficiency can simultaneously improve machining sustainability.
- (3)
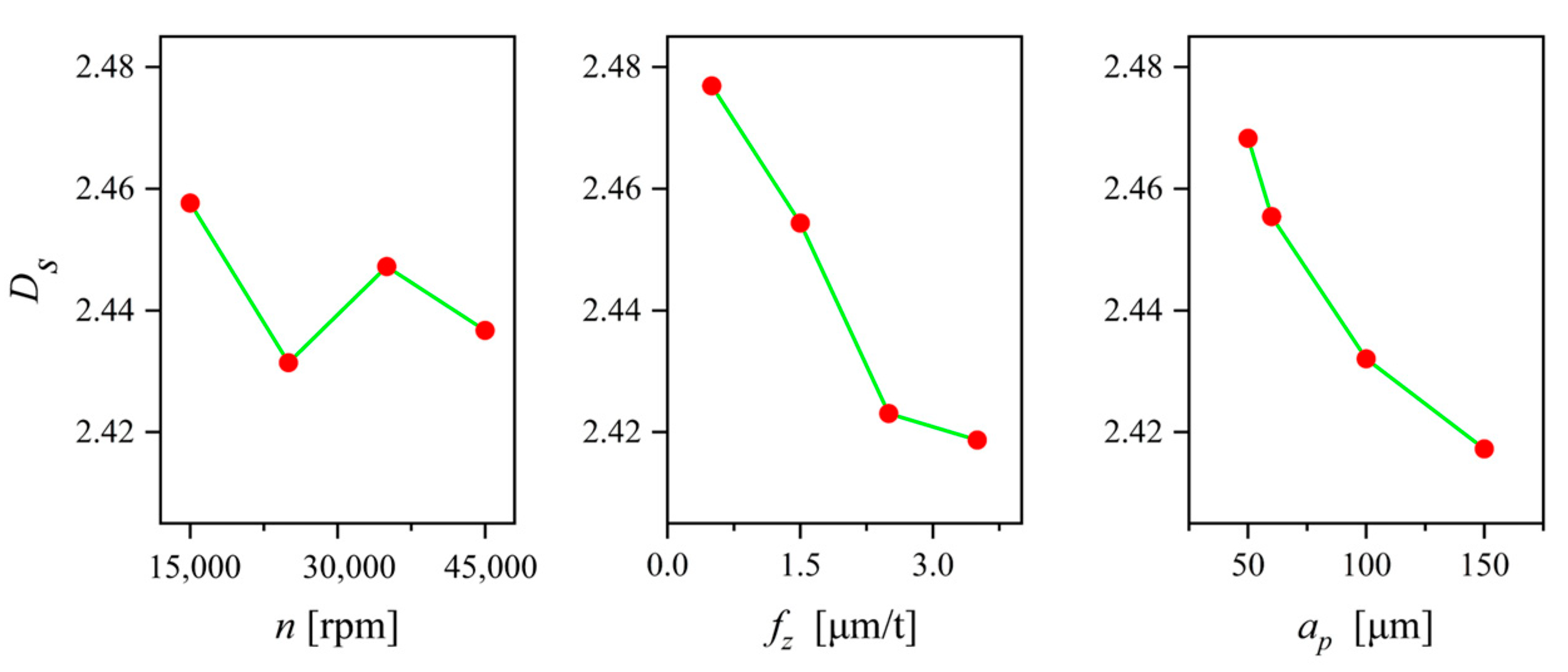
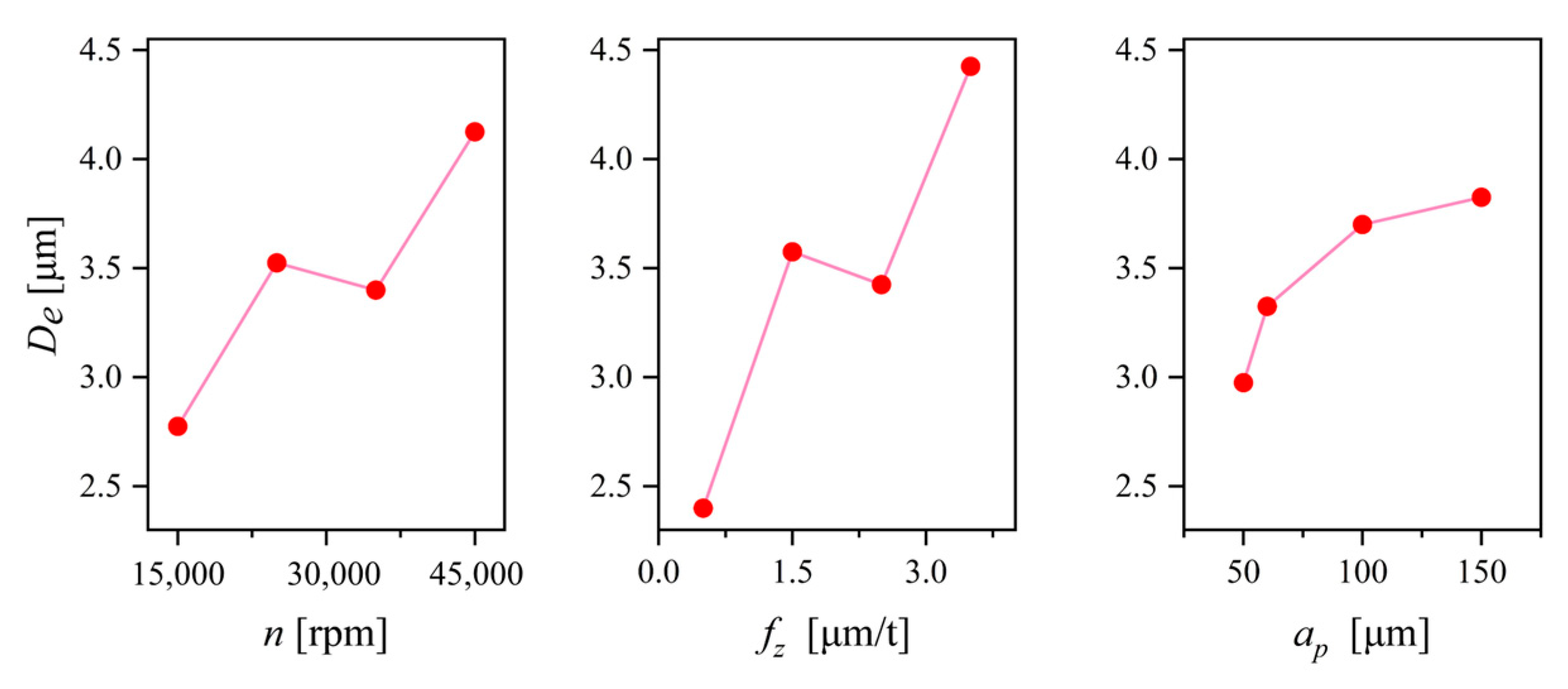
- Among the three indicators characterizing machining quality, surface roughness and surface fractal dimension exhibited a significant negative correlation (with a correlation coefficient of −0.832). However, their correlations with dimensional error were relatively small, being 0.57 and −0.628, respectively. After performing PCA, the variance extraction percentages for Sa, Ds, and De all exceeded 50%, indicating a good level of information condensation.
- (4)
- The optimization results of the process parameters demonstrate that the NSGA-III-based optimization method yields a better trade-off between machinability and sustainability, indicating that NSGA-III exhibits superior performance in handling multi-objective optimization problems and can obtain globally optimal parameters. The optimal combination of micro-milling parameters was n = 28,800 rpm, fz = 2.6 μm/t, and ap = 62 μm.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shang, Z.; Gao, D.; Jiang, Z.; Lu, Y. Towards less energy intensive heavy-duty machine tools: Power consumption characteristics and energy-saving strategies. Energy 2019, 178, 263–274. [Google Scholar] [CrossRef]
- Li, C.; Li, L.; Tang, Y.; Zhu, Y.; Li, L. A comprehensive approach to parameters optimization of energy-aware CNC milling. J. Intell. Manuf. 2019, 30, 123–138. [Google Scholar] [CrossRef]
- Hu, L.; Tang, R.; Cai, W.; Feng, Y.; Ma, X. Optimisation of cutting parameters for improving energy efficiency in machining process. Robot. Comp. Int. Manuf. 2019, 59, 406–416. [Google Scholar] [CrossRef]
- Feng, C.; Chen, X.; Zhang, J.; Huang, Y.; Qu, Z. Minimizing the energy consumption of hole machining integrating the optimization of tool path and cutting parameters on CNC machines. Int. J. Adv. Manuf. Technol. 2022, 121, 215–228. [Google Scholar] [CrossRef]
- Yan, J.; Li, L. Multi-objective optimization of milling parameters—The trade-offs between energy, production rate and cutting quality. J. Clean. Prod. 2013, 52, 462–471. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, T.; Dai, Y.; Qu, S.; Zhao, J. Energy consumption considering tool wear and optimization of cutting parameters in micro milling process. Int. J Mech. Sci. 2020, 178, 105628. [Google Scholar] [CrossRef]
- Wang, W.; Tian, G.; Chen, M.; Tao, F.; Zhang, C.; AI-Ahmari, A.; Li, Z.; Jiang, Z. Dual-objective program and improved artificial bee colony for the optimization of energy-conscious milling parameters subject to multiple constraints. J. Clean. Prod. 2020, 245, 118714. [Google Scholar] [CrossRef]
- Zhong, Q.; Tang, R.; Peng, T. Decision rules for energy consumption minimization during material removal process in turning. J. Clean. Prod. 2017, 140, 1819–1827. [Google Scholar] [CrossRef]
- Li, L.; Yan, J.; Xing, Z. Energy requirements evaluation of milling machines based on thermal equilibrium and empirical modelling. J. Clean. Prod. 2013, 52, 113–121. [Google Scholar] [CrossRef]
- Velchev, S.; Kolev, I.; Ivanov, K.; Gechevski, S. Empirical models for specific energy consumption and optimization of cutting parameters for minimizing energy consumption during turning. J. Clean. Prod. 2014, 80, 139–149. [Google Scholar] [CrossRef]
- Gutowski, T.G.; Branham, M.S.; Dahmus, J.B.; Jones, A.J.; Thiriez, A. Thermodynamic analysis of resources used in manufacturing processes. Environ. Sci. Technol. 2009, 43, 1584–1590. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Z.; Gao, D.; Lu, Y.; Liu, X. Optimization of Cutting Parameters for Trade-off Among Carbon Emissions, Surface Roughness, and Processing Time. Chin. J. Mech. Eng 2019, 32, 94. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Sealy, M.P.; Guo, Y.B.; Liu, Z.Q. Energy Consumption Characteristics in Finish Hard Milling of Tool Steels. Procedia Manuf. 2015, 1, 477–486. [Google Scholar] [CrossRef]
- Deng, Z.; Zhang, H.; Fu, Y.; Wan, L.; Liu, W. Optimization of process parameters for minimum energy consumption based on cutting specific energy consumption. J. Clean. Prod. 2017, 166, 1407–1414. [Google Scholar] [CrossRef]
- Lv, J.; Tang, R.; Jia, S.; Liu, Y. Experimental study on energy consumption of computer numerical control machine tools. J. Clean. Prod. 2016, 122, 3864–3874. [Google Scholar] [CrossRef]
- Lv, L.; Deng, Z.; Yan, C.; Liu, T.; Wan, L.; Gu, Q. Modelling and analysis for processing energy consumption of mechanism and data integrated machine tool. Int. J. Prod. Res. 2020, 58, 7078–7093. [Google Scholar] [CrossRef]
- de Carvalho, H.M.B.; de Gomes Oliveira, J.; Schmidt, M.A.; Brandão, V.L.C. Vibration Analysis and Energy Efficiency in Interrupted Face Milling Processes. Procedia CIRP 2015, 29, 245–250. [Google Scholar] [CrossRef]
- Pervaiz, S.; Deiab, I.; Rashid, A.; Nicolescu, M. Prediction of energy consumption and environmental implications for turning operation using finite element analysis. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2015, 229, 1925–1932. [Google Scholar] [CrossRef]
- Shi, K.N.; Zhang, D.H.; Liu, N.; Wang, S.B.; Ren, J.X.; Wang, S.L. A novel energy consumption model for milling process considering tool wear progression. J. Clean. Prod. 2018, 184, 152–159. [Google Scholar] [CrossRef]
- Li, C.; Tang, Y.; Cui, L.; Li, P. A quantitative approach to analyze carbon emissions of CNC-based machining systems. J. Intell. Manuf. 2015, 26, 911–922. [Google Scholar] [CrossRef]
- Tian, C.; Zhou, G.; Lu, F.; Chen, Z.; Zou, L. An integrated multi-objective optimization approach to determine the optimal feature processing sequence and cutting parameters for carbon emissions savings of CNC machining. Int. J. Comput. Integr. Manuf. 2020, 33, 609–625. [Google Scholar] [CrossRef]
- Zhou, L.; Li, J.; Li, F.; Meng, Q.; Li, J.; Xu, X. Energy consumption model and energy efficiency of machine tools: A comprehensive literature review. J. Clean. Prod. 2016, 112, 3721–3734. [Google Scholar] [CrossRef]
- Jamil, M.; Zhao, W.; He, N.; Gupta, M.K.; Sarikaya, M.; Khan, A.M.; Sanjay, M.R.; Siengchin, S.; Pimenov, Y.D. Sustainable milling of Ti–6Al–4V: A trade-off between energy efficiency, carbon emissions and machining characteristics under MQL and cryogenic environment. J. Clean. Prod. 2021, 281, 125374. [Google Scholar] [CrossRef]
- Singh, R.; Dureja, J.S.; Dogra, M.; Gupta, M.K.; Jamil, M.; Mia, M. Evaluating the sustainability pillars of energy and environment considering carbon emissions under machining ofTi-3Al-2.5 V. Sustain. Energy Technol. Assess. 2020, 42, 100806. [Google Scholar] [CrossRef]
- Turhan, M.H.; Tseng, G.W.G.; Erkorkmaz, K.; Fidan, B. Dynamic model identification for CNC machine tool feed drives from in-process signals for virtual process planning. Mechatronics 2020, 72, 102445. [Google Scholar] [CrossRef]
- Zheng, W.; Zhou, M.; Zhou, L. Influence of process parameters on surface topography in ultrasonic vibration- assisted end grinding of SiCp/Al composites. Int. J. Adv. Manuf. Technol. 2017, 91, 2347–2358. [Google Scholar] [CrossRef]
- Liu, J. Research on Material Removal and Parameter Optimization in Micro Milling SICp/AL Composites. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2018; pp. 75–77. (In Chinese). [Google Scholar]
- Chaudhari, P.; Thakur, K.A.; Kumar, R.; Banerjee, N.; Kumar, A. Comparison of NSGA-III with NSGA-II for multi objective optimization of adiabatic styrene reactor. Mater. Today Proc. 2022, 57, 1509–1514. [Google Scholar] [CrossRef]
- Tavana, M.; Li, Z.; Mobin, M.; Komaki, M.; Teymourian, E. Multi-objective control chart design optimization using NSGA-III and MOPSO enhanced with DEA and TOPSIS. Expert Syst. Appl. 2016, 50, 17–39. [Google Scholar] [CrossRef]
- Selvakumar, S.; Arulshri, K.P.; Padmanaban, K.P.; Sasikumar, K.S.K. Design and optimization of machining fixture layout using ANN and DOE. Int. J. Adv. Manuf. Technol. 2013, 65, 1573–1586. [Google Scholar] [CrossRef]
- Wang, P.; Bai, Q.; Cheng, K.; Zhao, L.; Ding, H.; Zhang, Y. Machinability analysis of micro-milling thin-walled Ti-6Al-4V micro parts under dry, lubrication, and chatter mitigation conditions. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2023, 1–12. [Google Scholar] [CrossRef]







| f (mm/min) | n (rpm) | ap (μm) |
|---|---|---|
| 20, 120, 220, 320, and 420 | 0 | 0 |
| 0 | 10,000, 15,000, 20,000, 25,000, 30,000, 35,000, 40,000, and 45,000 | 0 |
| Symbol | Process Parameters | Units | Level | |||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| A | Spindle speed (n) | r/min | 15,000 | 25,000 | 35,000 | 45,000 |
| B | Axial depth of cut (ap) | μm | 50 | 60 | 100 | 150 |
| C | Feed per tooth (fz) | μm/tooth | 0.5 | 1.5 | 2.5 | 3.5 |
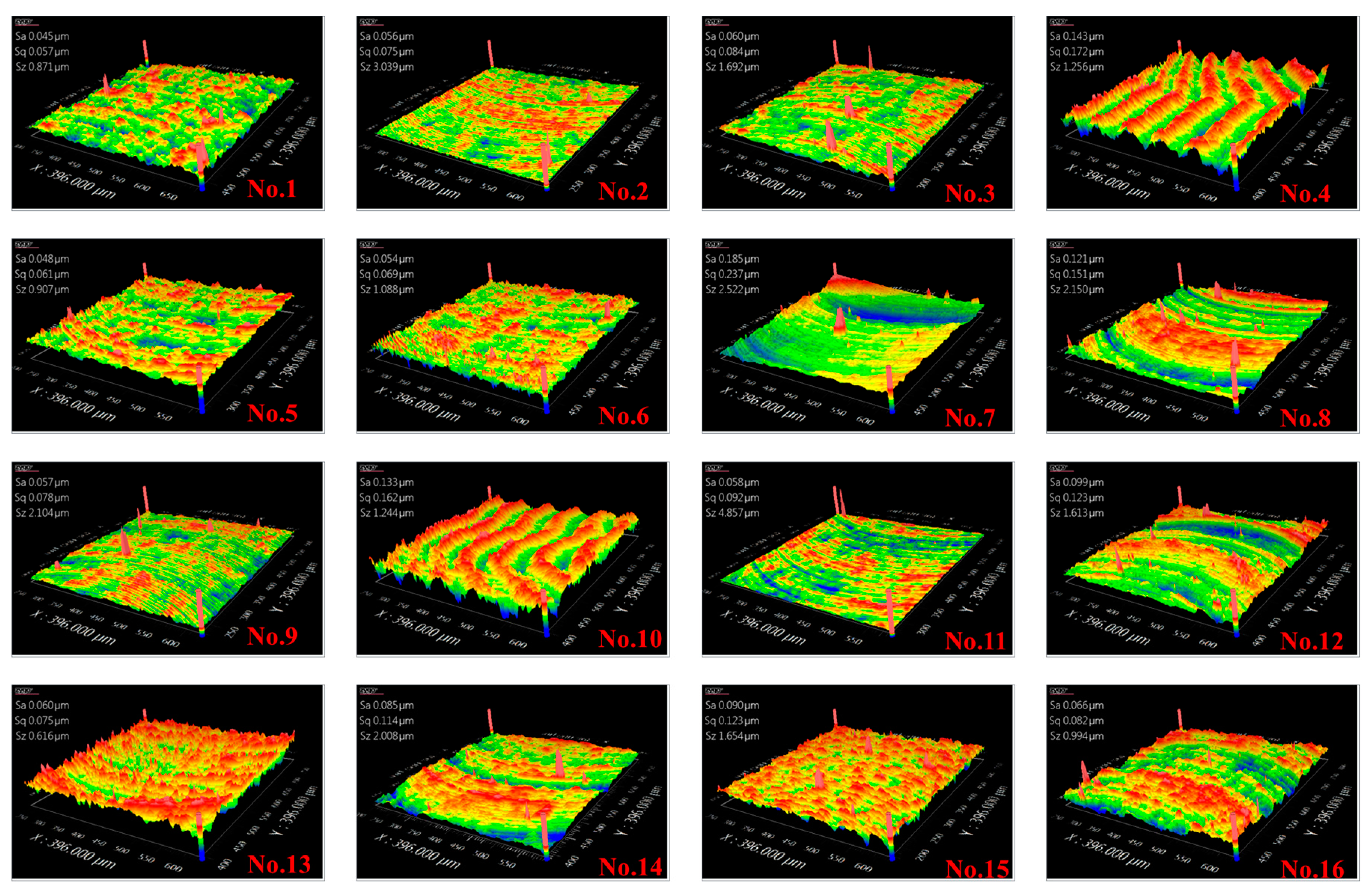
| No. | Symbol | Sa (nm) | De (μm) | Ds | SCE (kJ/mm3) | MRR (mm3/min) | Level | ||
|---|---|---|---|---|---|---|---|---|---|
| A | B | C | |||||||
| 1 | A1B1C1 | 45 | 1.3 | 2.5110 | 15.94 | 0.60 | 15,000 | 50 | 0.5 |
| 2 | A1B2C2 | 56 | 2.8 | 2.4620 | 4.50 | 2.16 | 15,000 | 60 | 1.5 |
| 3 | A1B3C3 | 60 | 2.9 | 2.4468 | 1.67 | 6.00 | 15,000 | 100 | 2.5 |
| 4 | A1B4C4 | 143 | 4.1 | 2.4108 | 0.82 | 12.60 | 15,000 | 150 | 3.5 |
| 5 | A2B1C2 | 48 | 3.2 | 2.4960 | 15.50 | 1.20 | 20,000 | 60 | 0.5 |
| 6 | A2B2C1 | 54 | 2.2 | 2.4730 | 6.15 | 3.00 | 20,000 | 50 | 1.5 |
| 7 | A2B3C4 | 185 | 4.3 | 2.3663 | 1.28 | 15.00 | 20,000 | 150 | 2.5 |
| 8 | A2B4C3 | 121 | 4.4 | 2.3903 | 1.38 | 14.00 | 20,000 | 100 | 3.5 |
| 9 | A3B1C3 | 57 | 2.8 | 2.4565 | 10.27 | 2.80 | 25,000 | 100 | 0.5 |
| 10 | A3B2C4 | 133 | 4.6 | 2.4478 | 2.31 | 12.60 | 25,000 | 150 | 1.5 |
| 11 | A3B3C1 | 58 | 2.7 | 2.4500 | 4.15 | 7.00 | 25,000 | 50 | 2.5 |
| 12 | A3B4C2 | 99 | 3.5 | 2.4346 | 2.49 | 11.76 | 25,000 | 60 | 3.5 |
| 13 | A4B1C4 | 60 | 2.3 | 2.4441 | 8.22 | 5.40 | 30,000 | 150 | 0.5 |
| 14 | A4B2C3 | 85 | 4.7 | 2.4346 | 4.09 | 10.80 | 30,000 | 100 | 1.5 |
| 15 | A4B3C2 | 90 | 3.8 | 2.4291 | 4.10 | 10.80 | 30,000 | 60 | 2.5 |
| 16 | A4B4C1 | 66 | 5.7 | 2.4391 | 3.52 | 12.60 | 30,000 | 50 | 3.5 |
| Feed Unit | Spindle Unit | ||||
|---|---|---|---|---|---|
| R2 | R2-pre | R2-adj | R2 | R2-pre | R2-adj |
| 99.21% | 94.42% | 98.43% | 99.92% | 99.82% | 98.89% |
| No. | Ptatal (W) | Pb (W) | Ps (W) | Pf (W) | Pm (W) |
|---|---|---|---|---|---|
| (Measured) | (Measured) | (Calculated) | (Calculated) | (Calculated) | |
| 1 | 645.4 | 486 | 127 | 1.9 | 33.5 |
| 2 | 648.1 | 2.1 | 36.0 | ||
| 3 | 653.3 | 2.4 | 40.9 | ||
| 4 | 659.3 | 2.7 | 46.6 | ||
| 5 | 793.9 | 271 | 2.4 | 36.5 | |
| 6 | 795.7 | 2.0 | 34.7 | ||
| 7 | 802.5 | 3.8 | 44.7 | ||
| 8 | 806.9 | 3.0 | 46.9 | ||
| 9 | 965.2 | 440 | 3.8 | 35.4 | |
| 10 | 969.0 | 5.4 | 39.6 | ||
| 11 | 970.7 | 2.1 | 42.6 | ||
| 12 | 976.2 | 2.7 | 45.5 | ||
| 13 | 1221.4 | 692 | 7.4 | 40.0 | |
| 14 | 1202.3 | 4. 9 | 38.7 | ||
| 15 | 1224.0 | 3.1 | 42.9 | ||
| 16 | 1228.5 | 2.1 | 46.4 |
| R2 | R2-adj | R2-pre | AIC | BIC | |
|---|---|---|---|---|---|
| Exponential model | 0.8589 | 0.8236 | 0.7300 | −34.32 | −36.46 |
| Polynomial model | 0.9185 | 0.8641 | 0.6755 | 89.53 | 75.14 |
| n (rpm) | fz (μm/t) | ap (μm) | |
|---|---|---|---|
| Rj | 572.9 | 8.7 | 6.2 |
| Ranking | 1 | 2 | 3 |
| Sa | Ds | De | |||
|---|---|---|---|---|---|
| R2 | R2-adj | R2 | R2-adj | R2 | R2-adj |
| 77.71% | 72.14% | 81.27% | 76.59% | 67.47% | 59.33% |
| Sa | Ds | De | |
|---|---|---|---|
| Sa | 1 | −0.832 | 0.579 |
| Ds | −0.832 | 1 | −0.628 |
| De | 0.579 | −0.628 | 1 |
| Sampling Adequacy KMO Measure | 0.681 | |
|---|---|---|
| Bartlett’s test of sphericity | Approximate chi-square | 22.351 |
| df | 3 | |
| Sig. | 0.000 | |
| Initial Variance | Extracted Variance | |
|---|---|---|
| Sa | 1.000 | 0.834 |
| Ds | 1.000 | 0.867 |
| De | 1.000 | 0.665 |
| No. | Initial Eigenvalue | Extract Loading Sum of Squares | ||||
|---|---|---|---|---|---|---|
| Eigenvalue | Initial Variance % | Cumulative Variance % | Eigenvalue | Initial Variance % | Cumulative Variance % | |
| 1 | 2.366 | 78.851 | 78.851 | 2.366 | 78.851 | 78.851 |
| 2 | 0.470 | 15.654 | 94.505 | |||
| 3 | 0.165 | 5.495 | 100.000 | |||
| Sa | Ds | De |
|---|---|---|
| 0.386 | −0.394 | 0.345 |
| n | fz | ap | Sa | Ds | De | MRR | SCE | |
|---|---|---|---|---|---|---|---|---|
| NSGA-II | 17,760 | 3.3 | 98 | 65 | 2.4860 | 3.5 | 9.37 | 0.960 |
| MOPSO | 21,000 | 3.2 | 88 | 59 | 2.4980 | 3.6 | 9.46 | 1.110 |
| NSGA-III | 28,800 | 2.6 | 62 | 50 | 2.5010 | 2.0 | 9.36 | 1.126 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.; Bai, Q.; Cheng, K.; Zhao, L.; Zhang, Y. Multi-Objective Optimization of Micro-Milling Parameters—The Trade-Offs between Machining Quality, Efficiency, and Sustainability in the Fabrication of Thin-Walled Microstructures. Appl. Sci. 2023, 13, 9392. https://doi.org/10.3390/app13169392
Wang P, Bai Q, Cheng K, Zhao L, Zhang Y. Multi-Objective Optimization of Micro-Milling Parameters—The Trade-Offs between Machining Quality, Efficiency, and Sustainability in the Fabrication of Thin-Walled Microstructures. Applied Sciences. 2023; 13(16):9392. https://doi.org/10.3390/app13169392
Chicago/Turabian StyleWang, Peng, Qingshun Bai, Kai Cheng, Liang Zhao, and Yabo Zhang. 2023. "Multi-Objective Optimization of Micro-Milling Parameters—The Trade-Offs between Machining Quality, Efficiency, and Sustainability in the Fabrication of Thin-Walled Microstructures" Applied Sciences 13, no. 16: 9392. https://doi.org/10.3390/app13169392
APA StyleWang, P., Bai, Q., Cheng, K., Zhao, L., & Zhang, Y. (2023). Multi-Objective Optimization of Micro-Milling Parameters—The Trade-Offs between Machining Quality, Efficiency, and Sustainability in the Fabrication of Thin-Walled Microstructures. Applied Sciences, 13(16), 9392. https://doi.org/10.3390/app13169392







