Parameter Optimization for Low-Rank Matrix Recovery in Hyperspectral Imaging
Abstract
1. Introduction
2. Methods and Materials
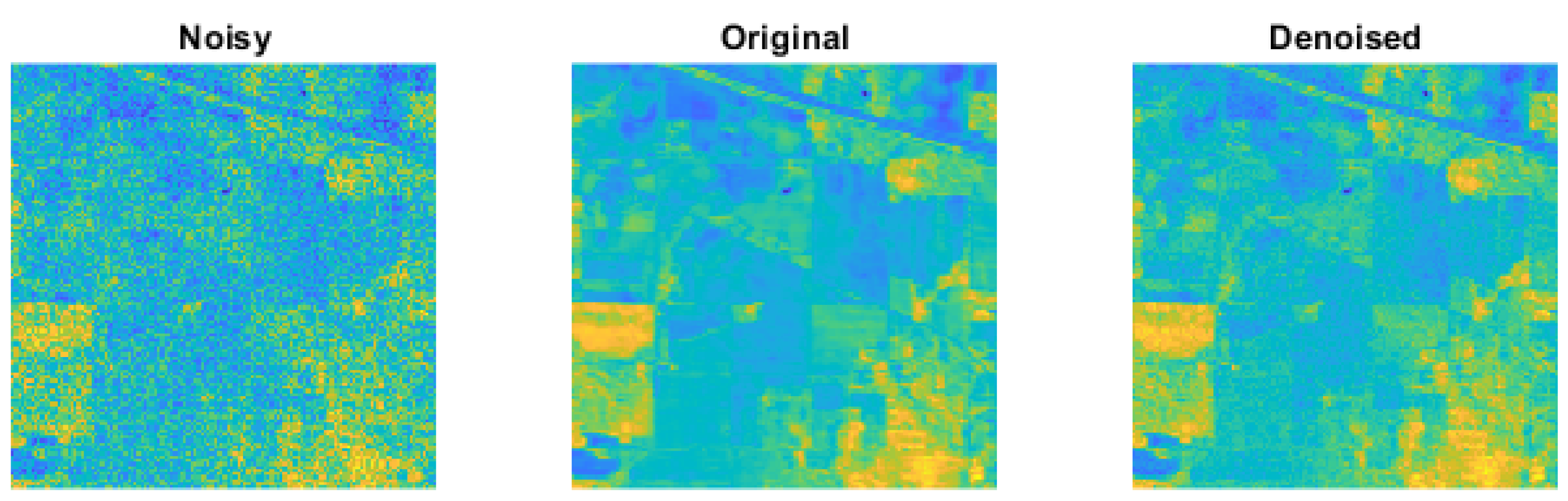
2.1. Methods
2.2. Materials
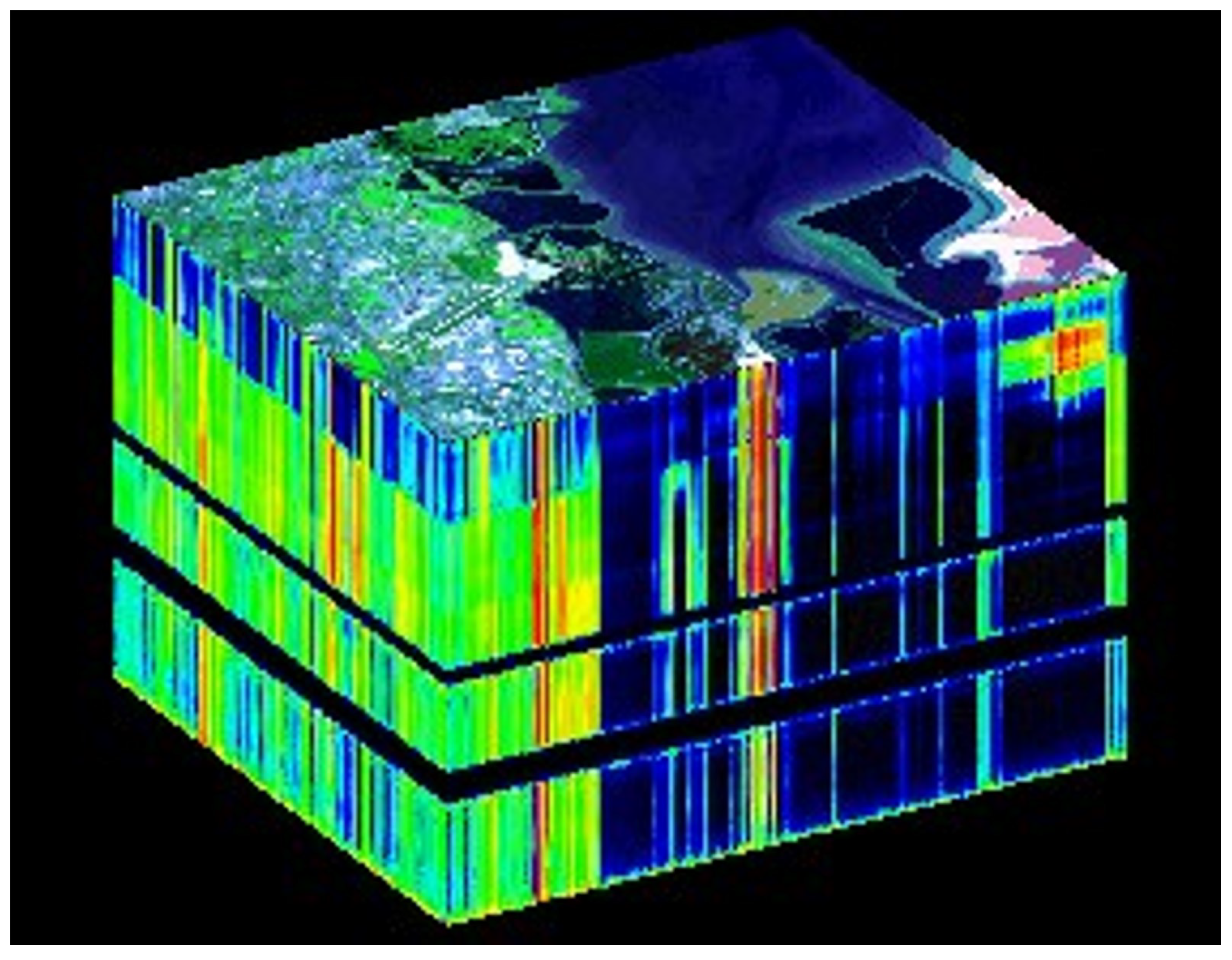
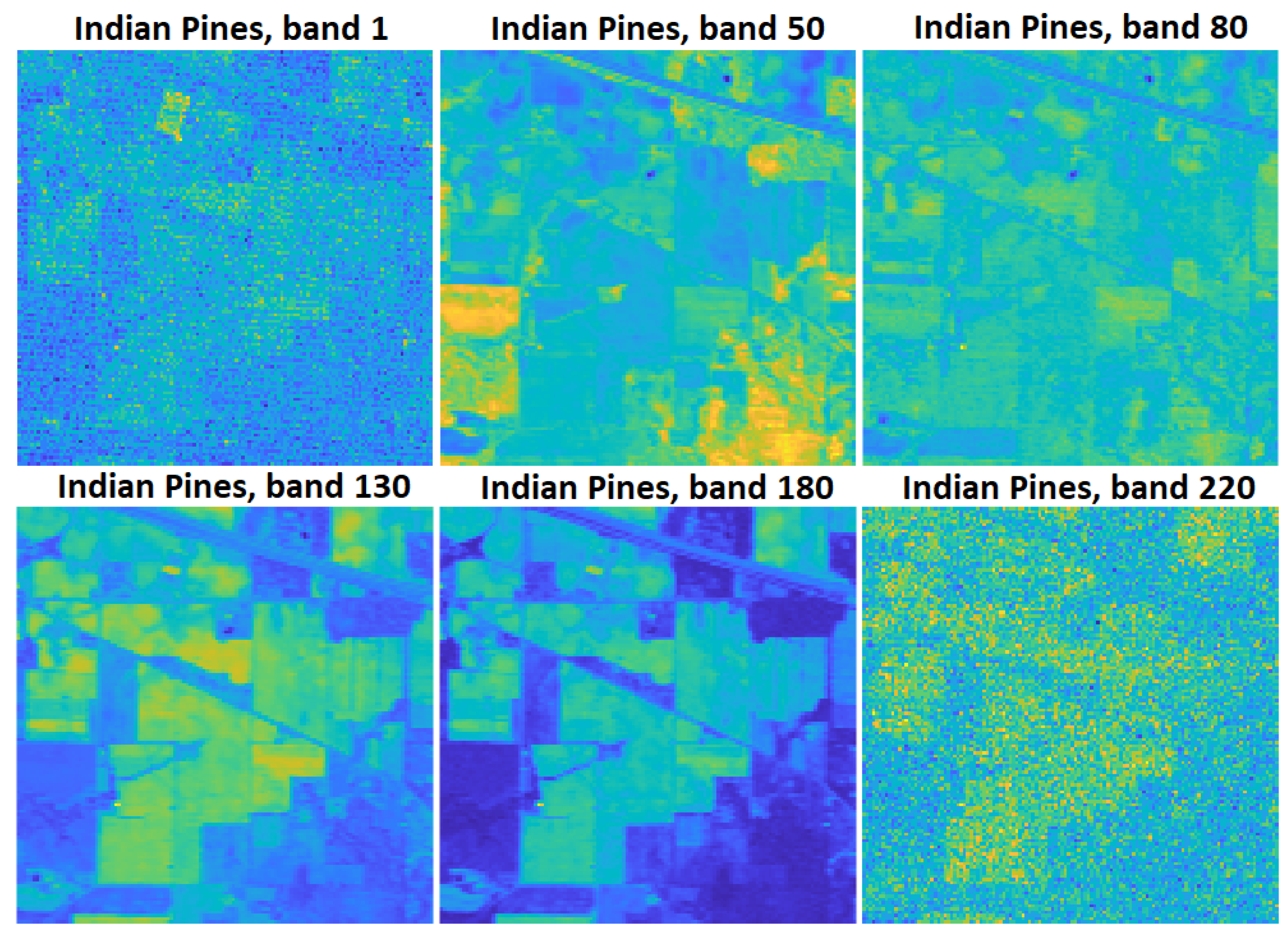
2.2.1. Indian Pines Data Set
2.2.2. Pavia Centre Data Set
2.2.3. Pavia University Data Set
3. Results
3.1. Parameter Analysis for r
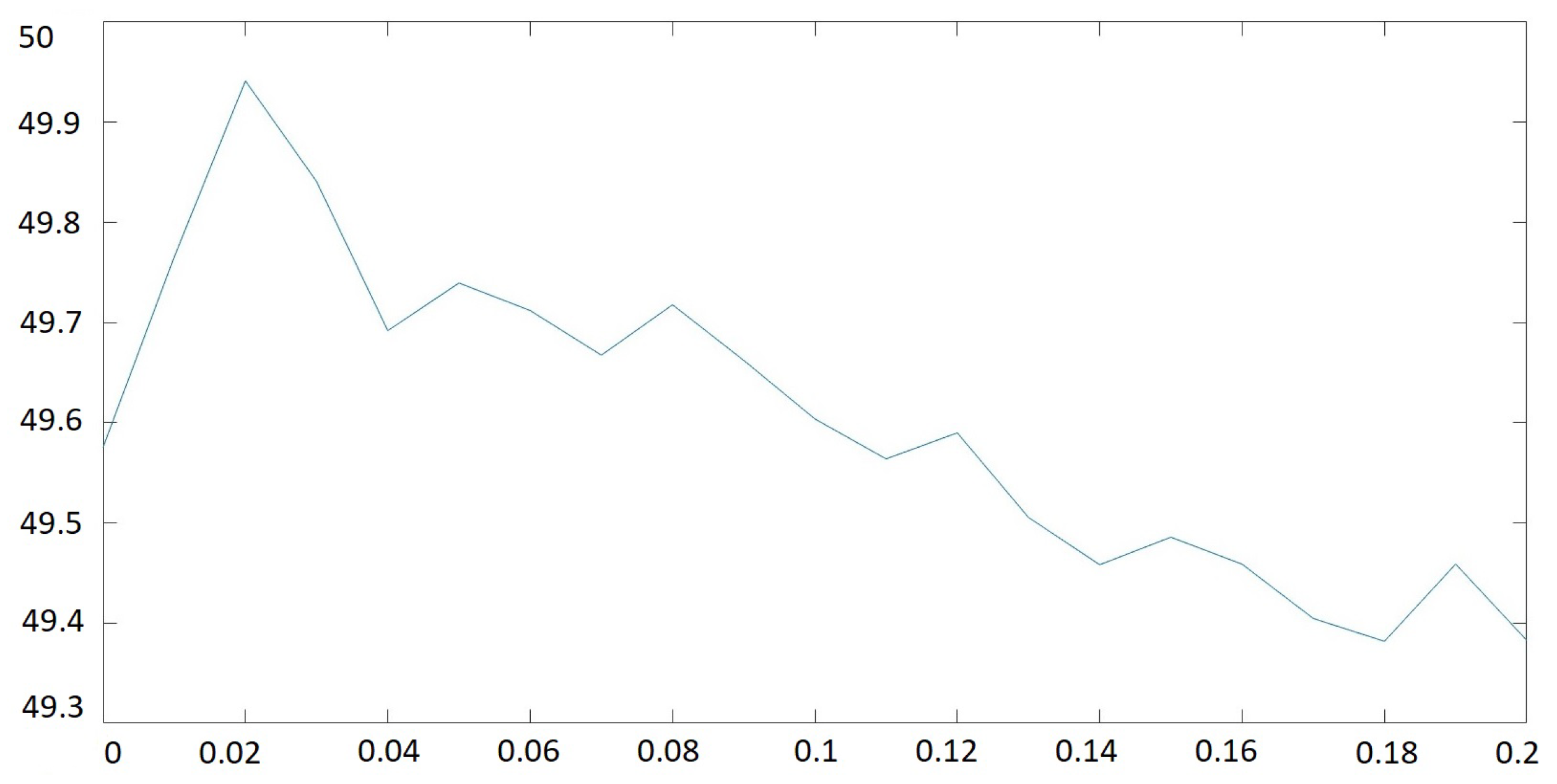
3.2. Parameter Analysis for s
3.3. Parameter Analysis for r and s
3.4. Parameter Analysis for b
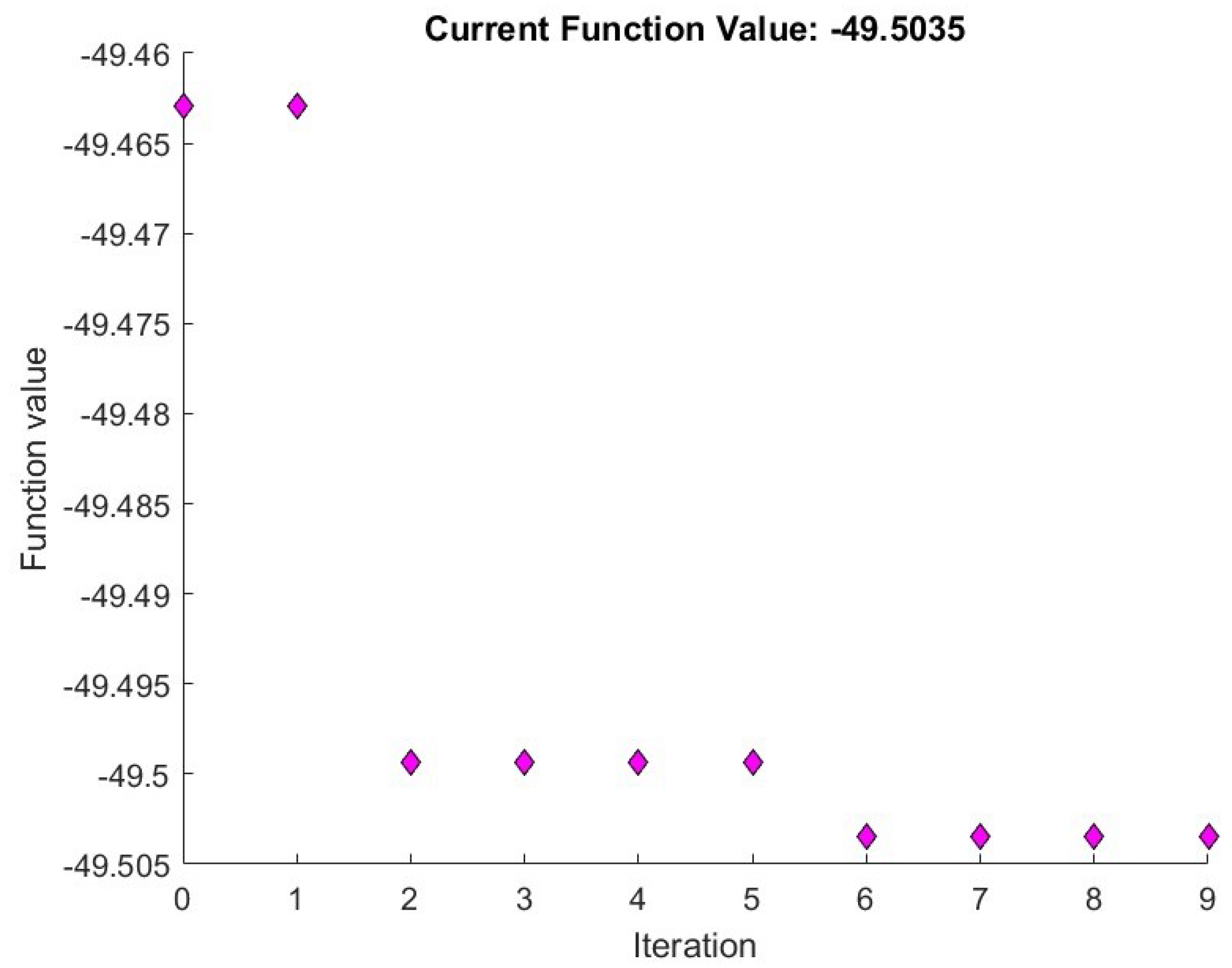
3.5. Parameter Analysis for p
3.6. Optimized Parameter Choice
3.6.1. Indian Pines Data Set
3.6.2. Pavia Centre Data Set
3.6.3. Pavia University Data Set
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| HSI | hyperspectral imaging |
| LRMR | low-rank matrix recovery |
| GoDec | Go Decomposition |
| PSNR | peak signal-to-noise ratio |
| BFGS | Broyden–Fletcher–Goldfarb–Shanno |
References
- Mandelbrot, B.B. A fast fractional Gaussian noise generator. Water Resour. Res. 1971, 7, 543–553. [Google Scholar] [CrossRef]
- Majumdar, A.; Ansari, N.; Aggarwal, H.; Biyani, P. Impulse denoising for hyper-spectral images: A blind compressed sensing approach. Signal Process. 2016, 119, 136–141. [Google Scholar] [CrossRef][Green Version]
- Shen, H.; Zhang, L. A MAP-based algorithm for destriping and inpainting of remotely sensed images. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1492–1502. [Google Scholar] [CrossRef]
- Rogass, C.; Mielke, C.; Scheffler, D.; Boesche, N.K.; Lausch, A.; Lubitz, C.; Guanter, L. Reduction of uncorrelated striping noise—Applications for hyperspectral pushbroom acquisitions. Remote Sens. 2014, 6, 11082–11106. [Google Scholar] [CrossRef]
- Sun, L.; Cao, Q.; YChen, Y.; Zheng, Y.; Wu, Z. Mixed Noise Removal for Hyperspectral Images Based on Global Tensor Low-Rankness and Nonlocal SVD-Aided Group Sparsity. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–17. [Google Scholar] [CrossRef]
- Ghamisi, P.; Yokoya, N.; Li, J.; Liao, W.; Liu, S.; Plaza, J.; Rasti, B.; Plaza, A. Advances in hyperspectral image and signal processing: A comprehensive overview of the state of the art. IEEE Geosci. Remote Sens. Mag. 2017, 5, 37–78. [Google Scholar] [CrossRef]
- Rasti, B.; Scheunders, P.; Ghamisi, P.; Licciardi, G.; Chanussot, J. Noise reduction in hyperspectral imagery: Overview and application. Remote Sens. 2018, 10, 482. [Google Scholar] [CrossRef]
- Singh, S.; Suresh, B. Role of hyperspectral imaging for precision agriculture monitoring. ADBU J. Eng. Technol. 2022, 11, 1–5. [Google Scholar]
- Calin, M.A.; Calin, A.C.; Nicolae, D.N. Application of airborne and spaceborne hyperspectral imaging techniques for atmospheric research: Past, present, and future. Appl. Spectrosc. Rev. 2021, 56, 289–323. [Google Scholar] [CrossRef]
- Peyghambari, S.; Zhang, Y. Hyperspectral remote sensing in lithological mapping, mineral exploration, and environmental geology: An updated review. J. Appl. Remote Sens. 2021, 15, 031501. [Google Scholar] [CrossRef]
- Qian, S.E. Hyperspectral satellites, evolution, and development history. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 7032–7056. [Google Scholar] [CrossRef]
- Wolfmayr, M.; Pölönen, I.; Lind, L.; Kašpárek, T.; Penttilä, A.; Kohout, T. Noise reduction in asteroid imaging using a miniaturized spectral imager. SPIE Sensors Syst. Next-Gener. Satell. XXV 2021, 11858, 121–133. [Google Scholar]
- Zhang, H.; He, W.; Zhang, L.; Shen, H.; Yuan, Q. Hyperspectral image restoration using low-rank matrix recovery. IEEE Trans. Geosci. Remote Sens. 2013, 52, 4729–4743. [Google Scholar] [CrossRef]
- Zhou, T.; Tao, D. Godec: Randomized low-rank & sparse matrix decomposition in noisy case. In Proceedings of the 28th International Conference on Machine Learning, ICML 2011, Bellevue, WA, USA, 28 June–2 July 2011; pp. 33–40. [Google Scholar]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence Properties of the Nelder-Mead Simplex Method in Low Dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]
- Purdue University Research Repository. Indian Pines Data Set. Available online: https://purr.purdue.edu/publications/1947/1 (accessed on 12 December 2022).
- Pavia Centre and University Data Sets; Gamba, P. Telecommunications and Remote Sensing Laboratory, Pavia University. Available online: https://www.ehu.eus/ccwintco/index.php/Hyperspectral_Remote_Sensing_Scenes#Pavia_Centre_and_University (accessed on 12 December 2022).
- Wright, J.; Ganesh, A.; Rao, S.; Peng, Y.; Ma, Y. Robust principal component analysis: Exact recovery of corrupted low-rank matrices via convex optimization. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 7–10 December 2009; p. 22. [Google Scholar]
- Broyden, C.G. The Convergence of a Class of Double-Rank Minimization Algorithms. IMA J. Appl. Math. 1970, 6, 76–90. [Google Scholar] [CrossRef]
- Fletcher, R. A New Approach to Variable Metric Algorithms. Comput. J. 1970, 13, 317–322. [Google Scholar] [CrossRef]
- Goldfarb, D. A Family of Variable Metric Updates Derived by Variational Means. Math. Comput. 1970, 24, 23–26. [Google Scholar] [CrossRef]
- Shanno, D.F. Conditioning of Quasi-Newton Methods for Function Minimization. Math. Comput. 1970, 24, 647–656. [Google Scholar] [CrossRef]


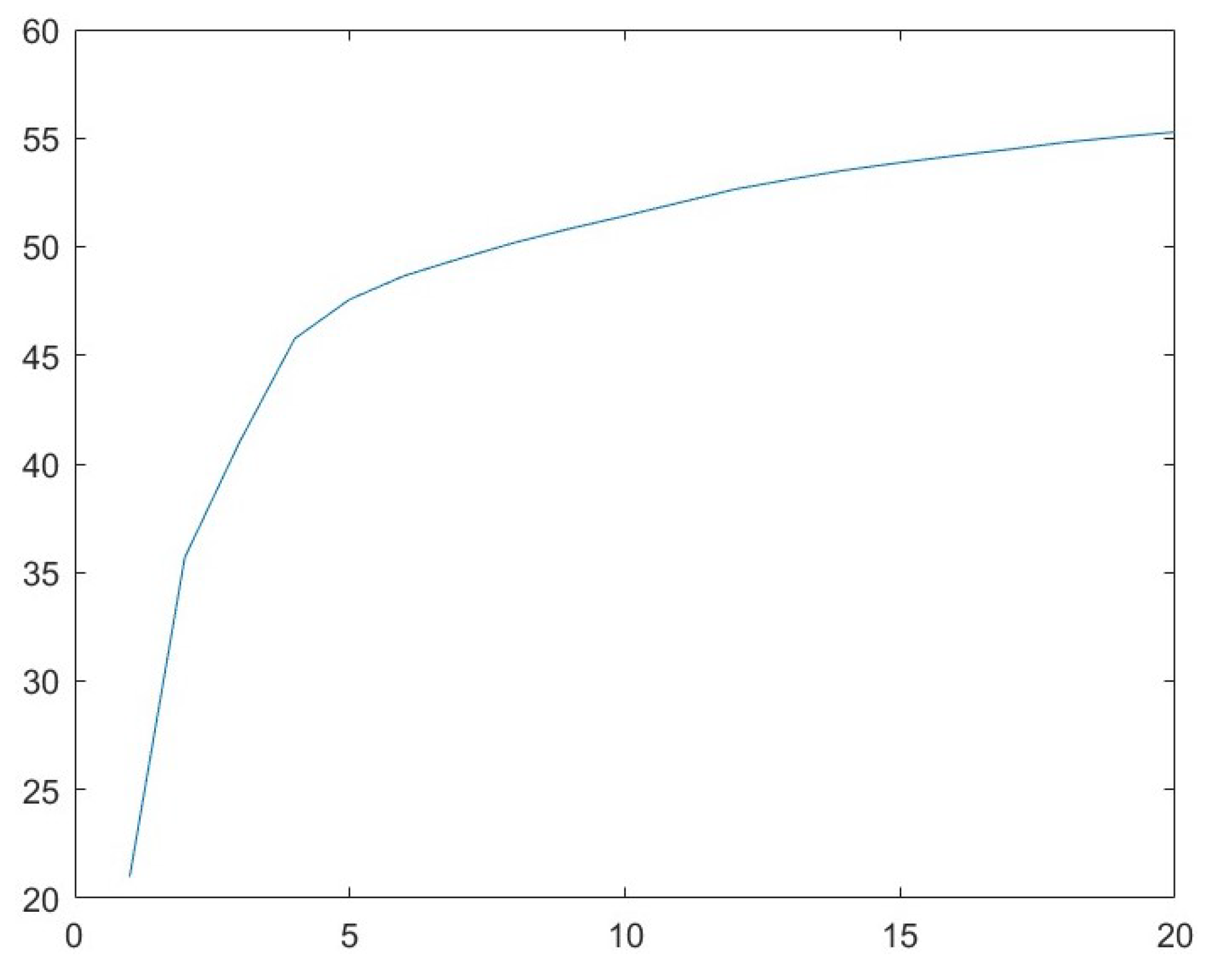
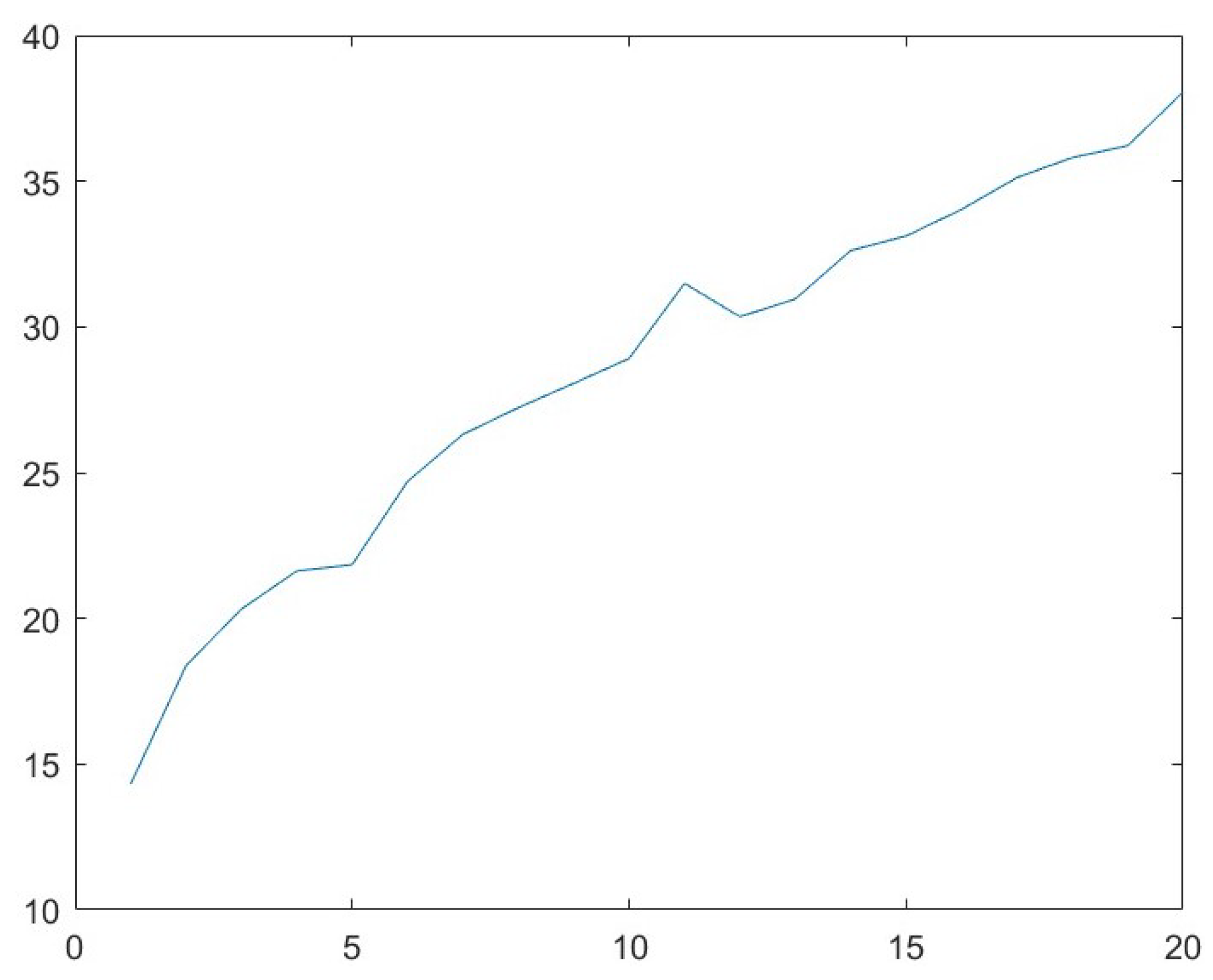
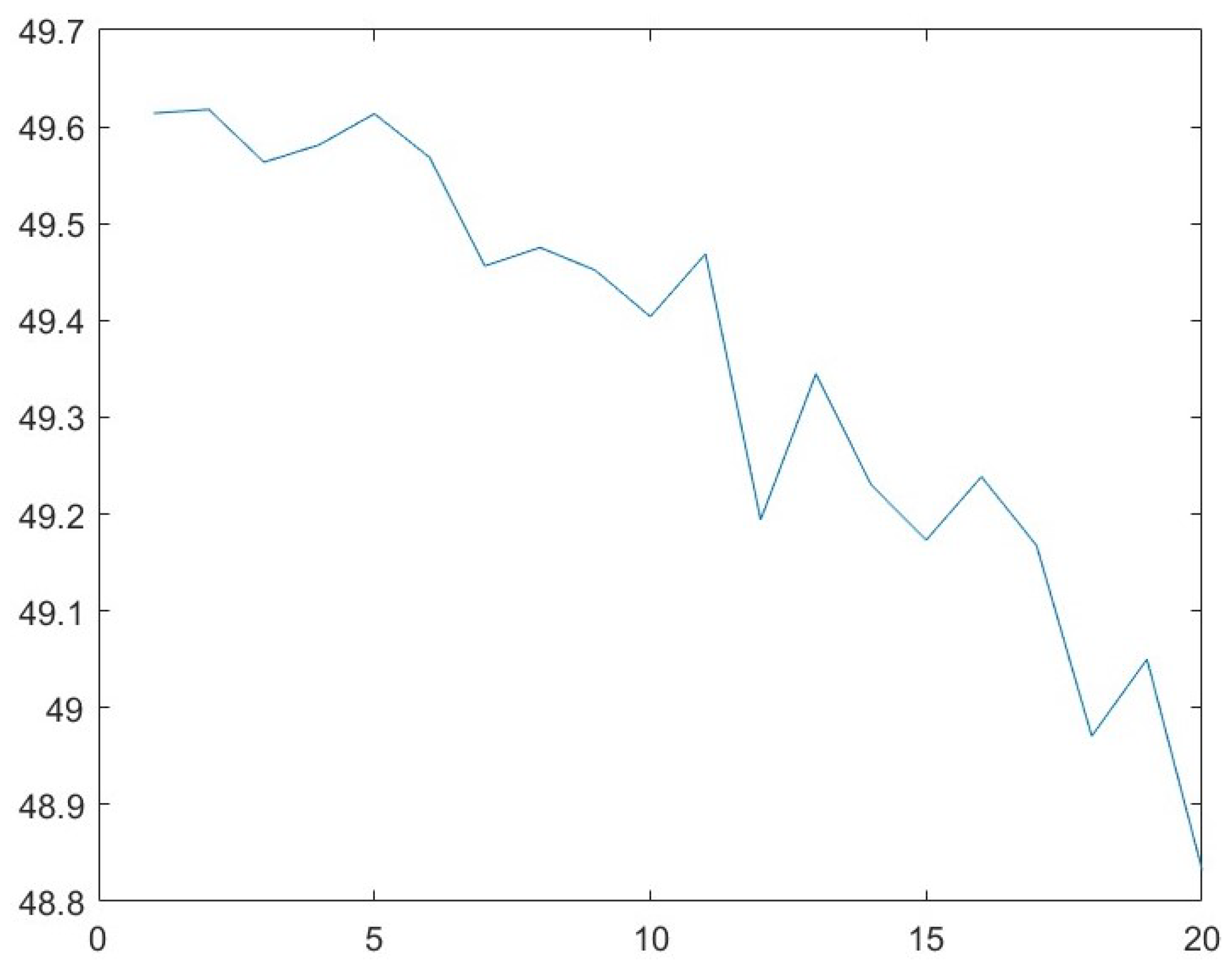

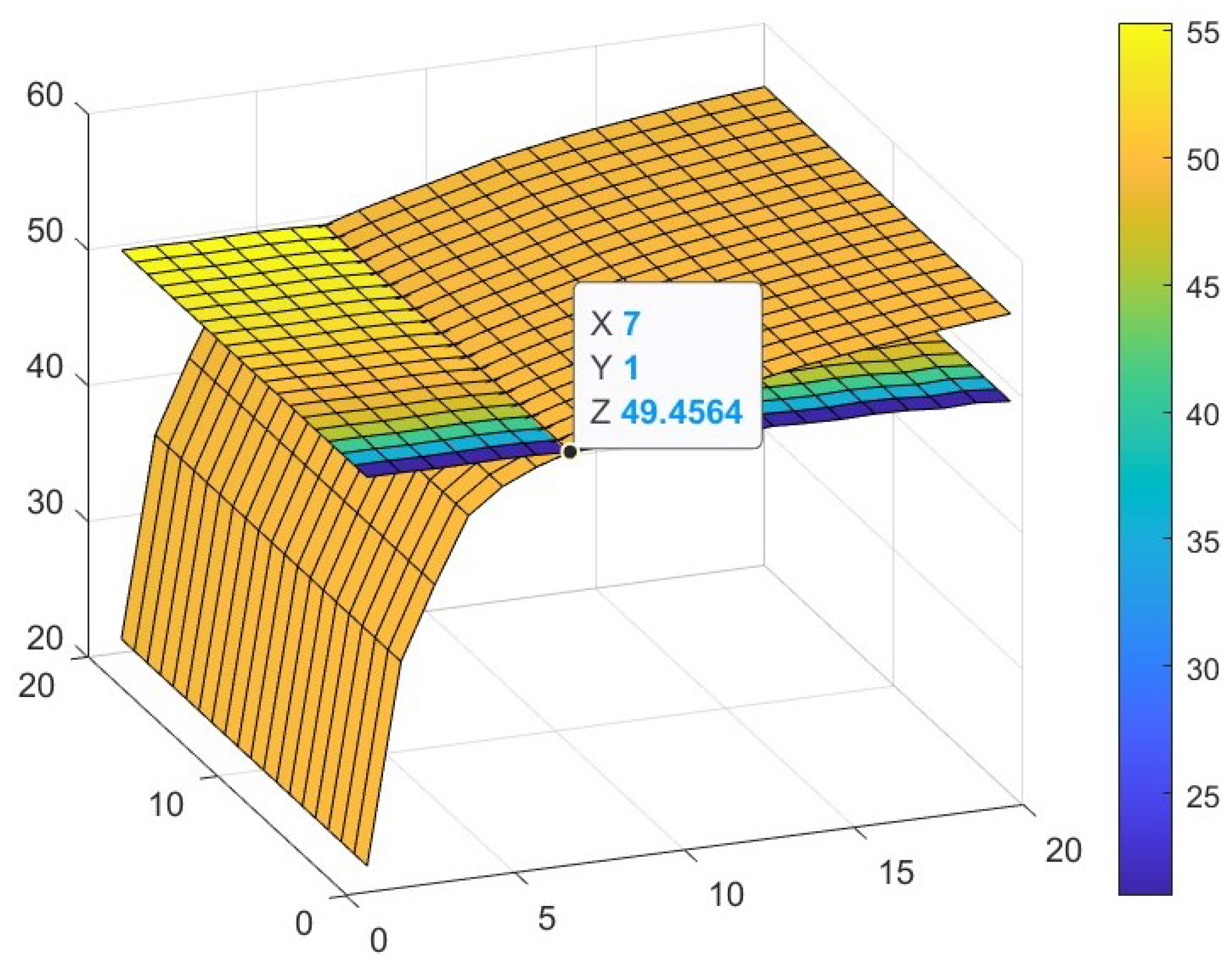

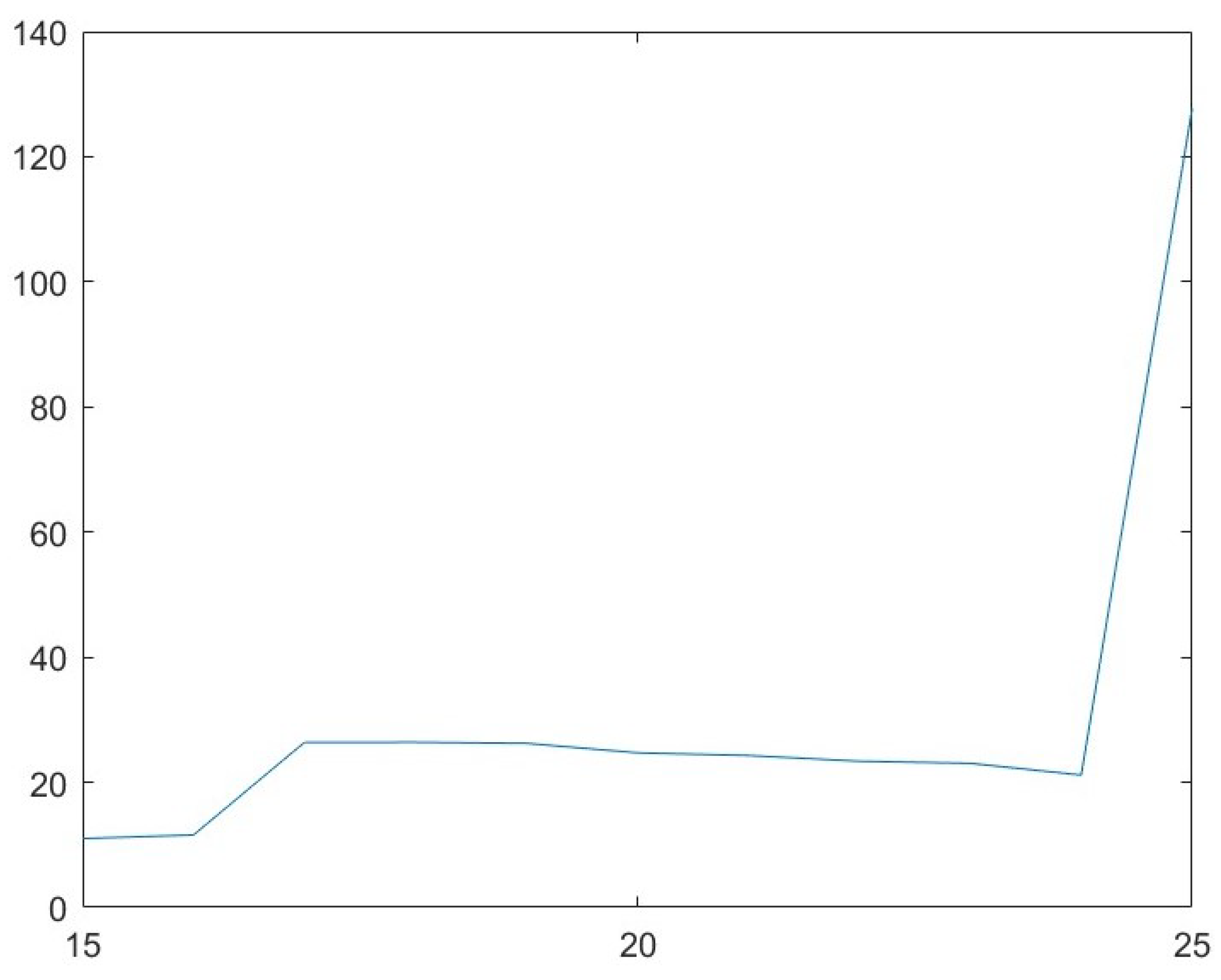
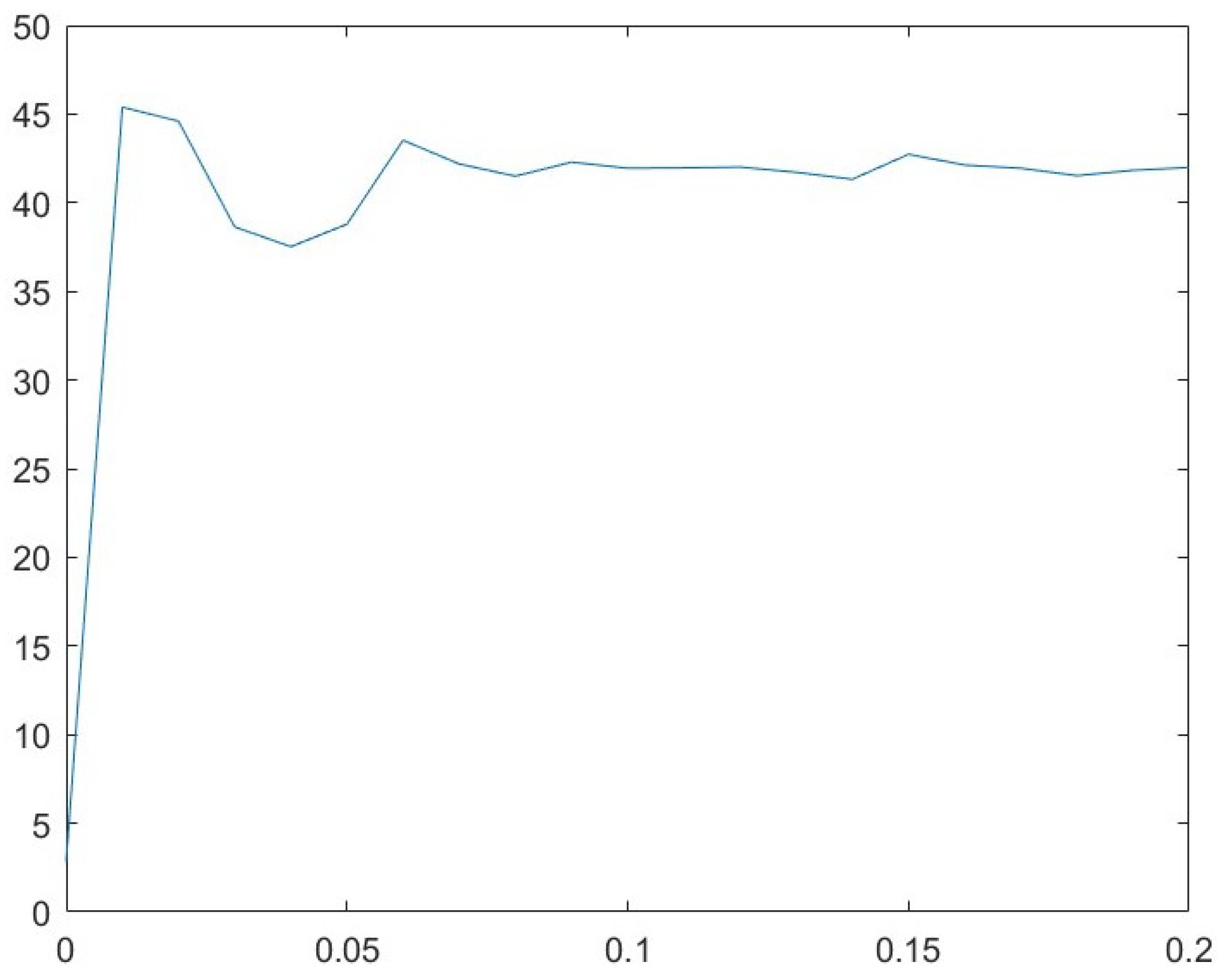



| r | PSNR | ∇PSNR | ||
|---|---|---|---|---|
| 1 | 20.99 | 14.70 | 14.31 | 95.15 |
| 2 | 35.69 | 10.02 | 18.37 | 85.57 |
| 3 | 41.02 | 5.04 | 20.32 | 108.98 |
| 4 | 45.77 | 3.28 | 21.63 | 107.42 |
| 5 | 47.58 | 1.45 | 21.84 | 109.01 |
| 6 | 48.67 | 0.94 | 24.70 | 108.22 |
| 7 | 49.45 | 0.76 | 26.32 | 115.23 |
| 8 | 50.19 | 0.69 | 27.23 | 112.48 |
| 9 | 50.83 | 0.61 | 28.06 | 114.21 |
| 10 | 51.42 | 0.60 | 28.92 | 116.79 |
| 11 | 52.03 | 0.61 | 31.49 | 117.49 |
| 12 | 52.65 | 0.53 | 30.35 | 99.18 |
| 13 | 53.10 | 0.44 | 30.96 | 100.97 |
| 14 | 53.52 | 0.38 | 32.62 | 103.88 |
| 15 | 53.87 | 0.33 | 33.12 | 97.06 |
| 16 | 54.19 | 0.31 | 34.03 | 111.33 |
| 17 | 54.49 | 0.31 | 35.12 | 113.62 |
| 18 | 54.81 | 0.28 | 35.81 | 104.27 |
| 19 | 55.06 | 0.24 | 36.22 | 121.06 |
| 20 | 55.28 | 0.22 | 38.06 | 125.18 |
| s | PSNR | |||
|---|---|---|---|---|
| 1 | 49.61 | 951.11 | −706.38 | 3793.27 |
| 2 | 49.62 | 244.72 | −420.41 | 1007.87 |
| 3 | 49.56 | 110.29 | −90.82 | 481.01 |
| 4 | 49.58 | 63.09 | −30.02 | 301.01 |
| 5 | 49.61 | 50.24 | −16.93 | 193.88 |
| 6 | 49.57 | 29.22 | −10.62 | 178.32 |
| 7 | 49.46 | 29.00 | −1.63 | 114.31 |
| 8 | 49.48 | 25.96 | −7.63 | 100.41 |
| 9 | 49.45 | 13.74 | 1.54 | 139.66 |
| 10 | 49.40 | 29.04 | 7.71 | 112.07 |
| 11 | 49.47 | 29.16 | −10.48 | 111.66 |
| 12 | 49.19 | 8.08 | −7.71 | 137.42 |
| 13 | 49.34 | 13.74 | 9.01 | 53.73 |
| 14 | 49.23 | 26.11 | −1.90 | 100.47 |
| 15 | 49.17 | 9.94 | 1.53 | 38.31 |
| 16 | 49.24 | 29.18 | 1.85 | 111.84 |
| 17 | 49.17 | 13.63 | −12.60 | 52.35 |
| 18 | 48.97 | 3.98 | 7.81 | 178.98 |
| 19 | 49.05 | 29.25 | 5.95 | 114.47 |
| 20 | 48.83 | 15.88 | −13.36 | 60.94 |
| b | PSNR | ||
|---|---|---|---|
| 15 | 50.14 | 11.01 | 48.13 |
| 16 | 49.96 | 11.58 | 83.56 |
| 17 | 49.87 | 26.39 | 102.33 |
| 18 | 49.73 | 26.41 | 124.62 |
| 19 | 49.62 | 26.23 | 122.86 |
| 20 | 49.42 | 24.71 | 127.33 |
| 21 | 49.36 | 24.29 | 97.29 |
| 22 | 49.23 | 23.37 | 92.63 |
| 23 | 49.16 | 23.04 | 102.33 |
| 24 | 49.07 | 21.16 | 179.84 |
| 25 | 48.88 | 127.72 | 257.69 |
| −PSNR | ||
|---|---|---|
| 0.015 | −49.990256 | 0.014977 |
| 0.05 | −49.887782 | 0.047813 |
| 0.15 | −49.503483 | 0.143438 |
| 0.5 | −49.476512 | 0.596875 |
| 1. | −49.616882 | 0.975000 |
| 1.5 | −49.750781 | 1.818750 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wolfmayr, M. Parameter Optimization for Low-Rank Matrix Recovery in Hyperspectral Imaging. Appl. Sci. 2023, 13, 9373. https://doi.org/10.3390/app13169373
Wolfmayr M. Parameter Optimization for Low-Rank Matrix Recovery in Hyperspectral Imaging. Applied Sciences. 2023; 13(16):9373. https://doi.org/10.3390/app13169373
Chicago/Turabian StyleWolfmayr, Monika. 2023. "Parameter Optimization for Low-Rank Matrix Recovery in Hyperspectral Imaging" Applied Sciences 13, no. 16: 9373. https://doi.org/10.3390/app13169373
APA StyleWolfmayr, M. (2023). Parameter Optimization for Low-Rank Matrix Recovery in Hyperspectral Imaging. Applied Sciences, 13(16), 9373. https://doi.org/10.3390/app13169373







