Hyperspectral Image Dimensionality Reduction Algorithm Based on Spatial–Spectral Adaptive Multiple Manifolds
Abstract
1. Introduction
2. Related Work
2.1. Super-Pixel Segmentation Algorithm
2.2. Dimensionality Reduction Algorithm Based on Manifold Learning
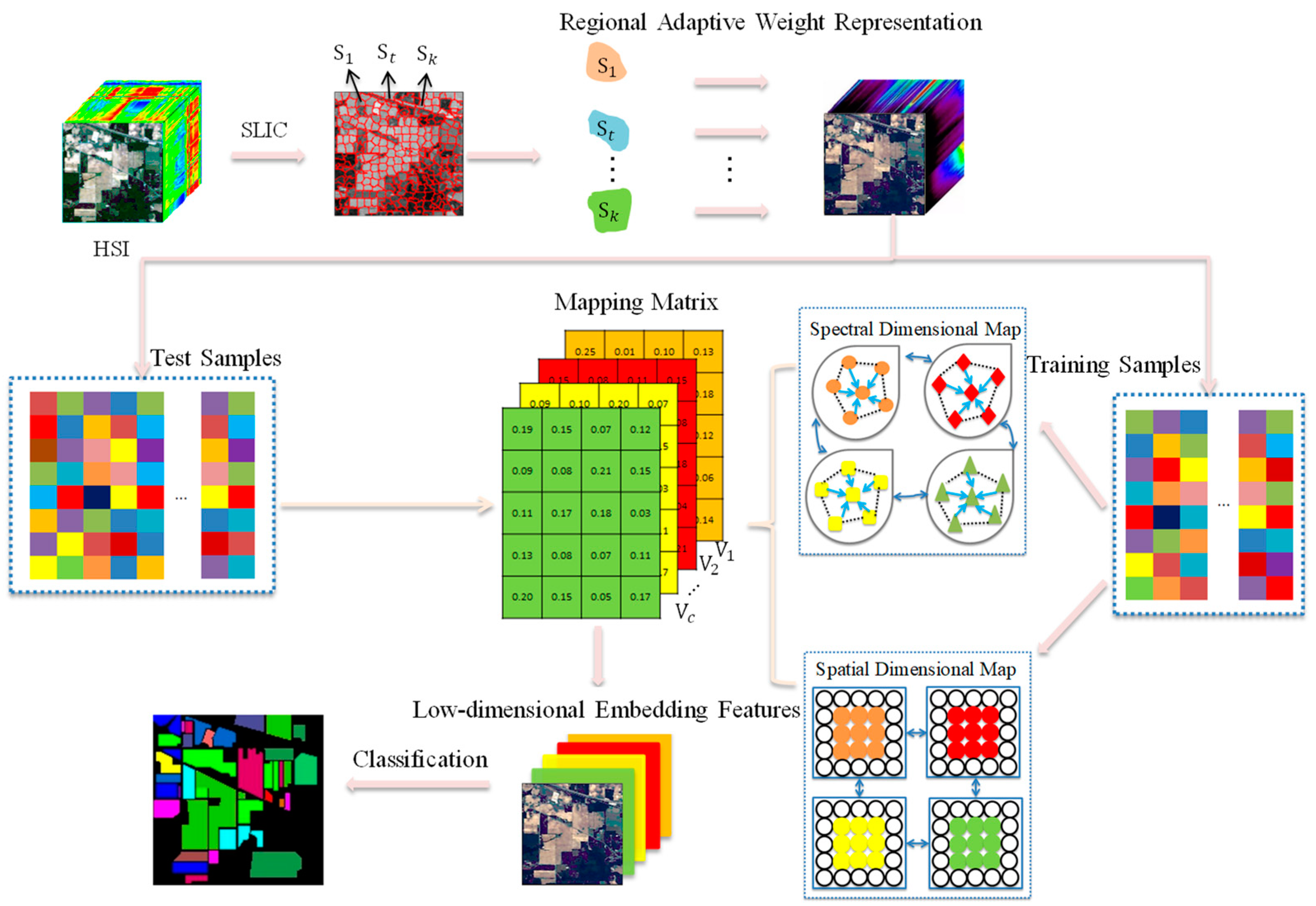
3. Proposed Method
3.1. Regional Adaptive Weight Representation
3.2. Space–Spectrum Adaptive Multi-Manifold Analysis
4. Experimental Results and Analysis
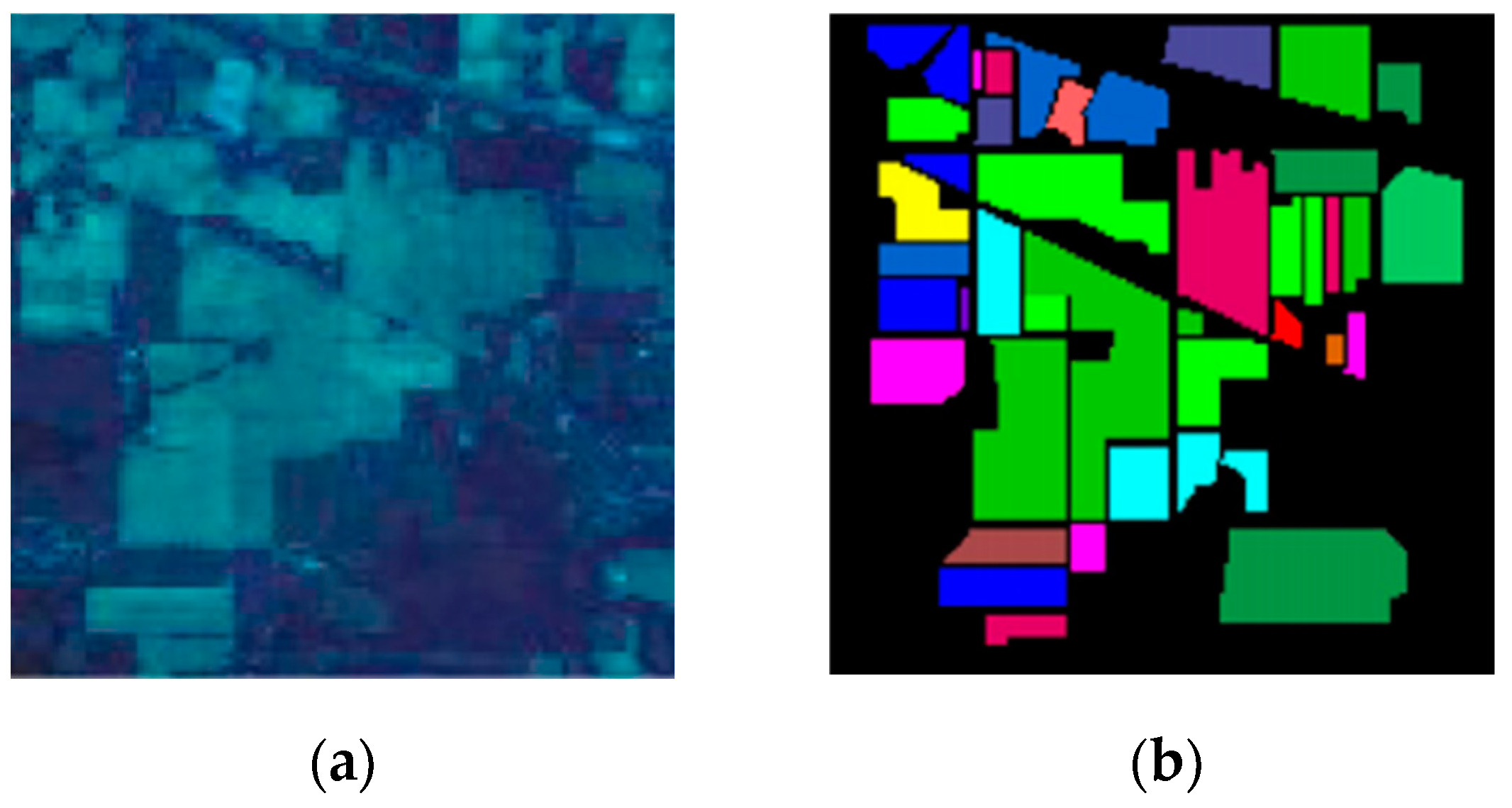
4.1. Datasets
4.2. Implementation Details
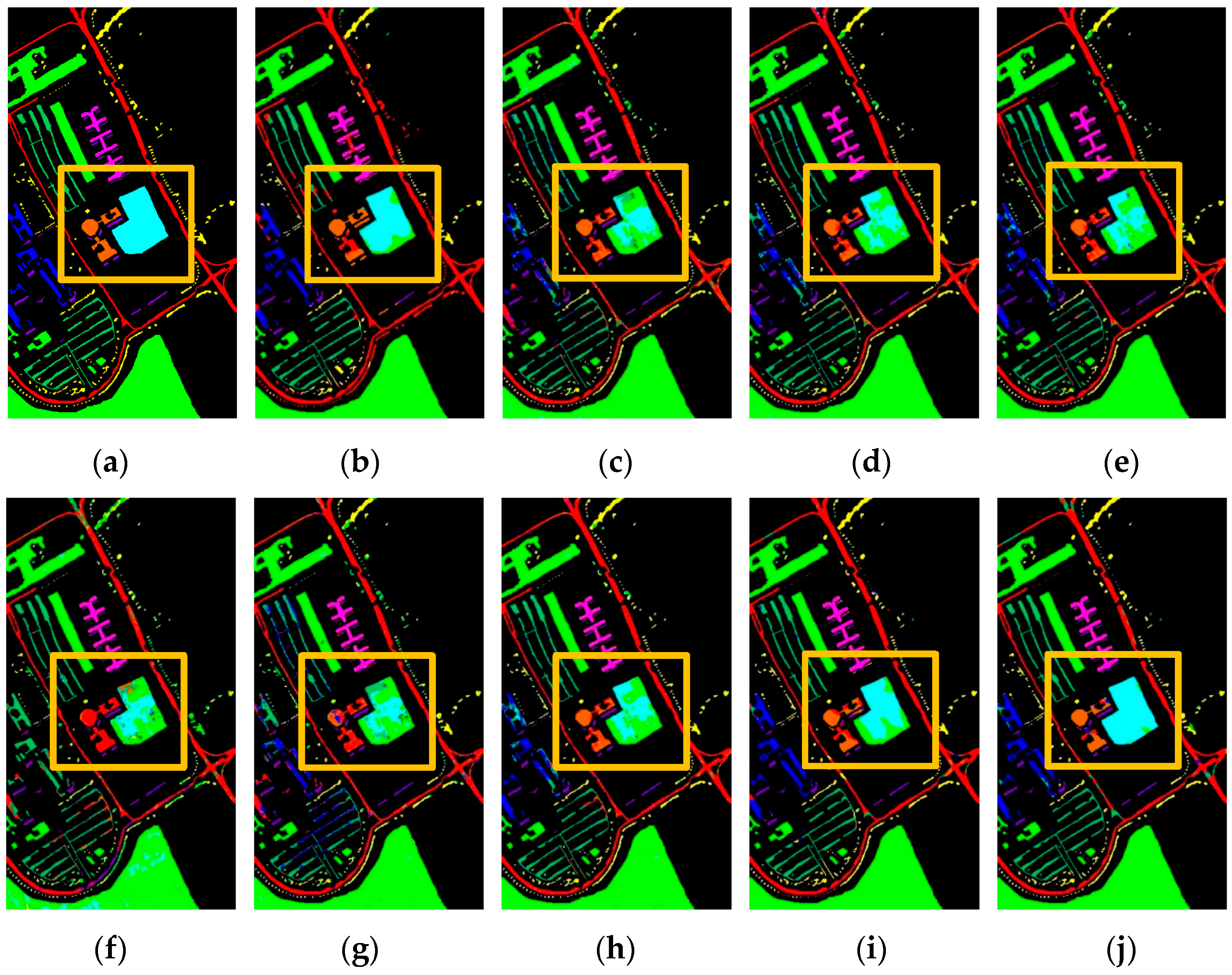
4.3. Comparison with Existing Methods
4.3.1. Classification Results on the IP Dataset
4.3.2. Classification Results on the UP Dataset
4.4. Parameter Analysis
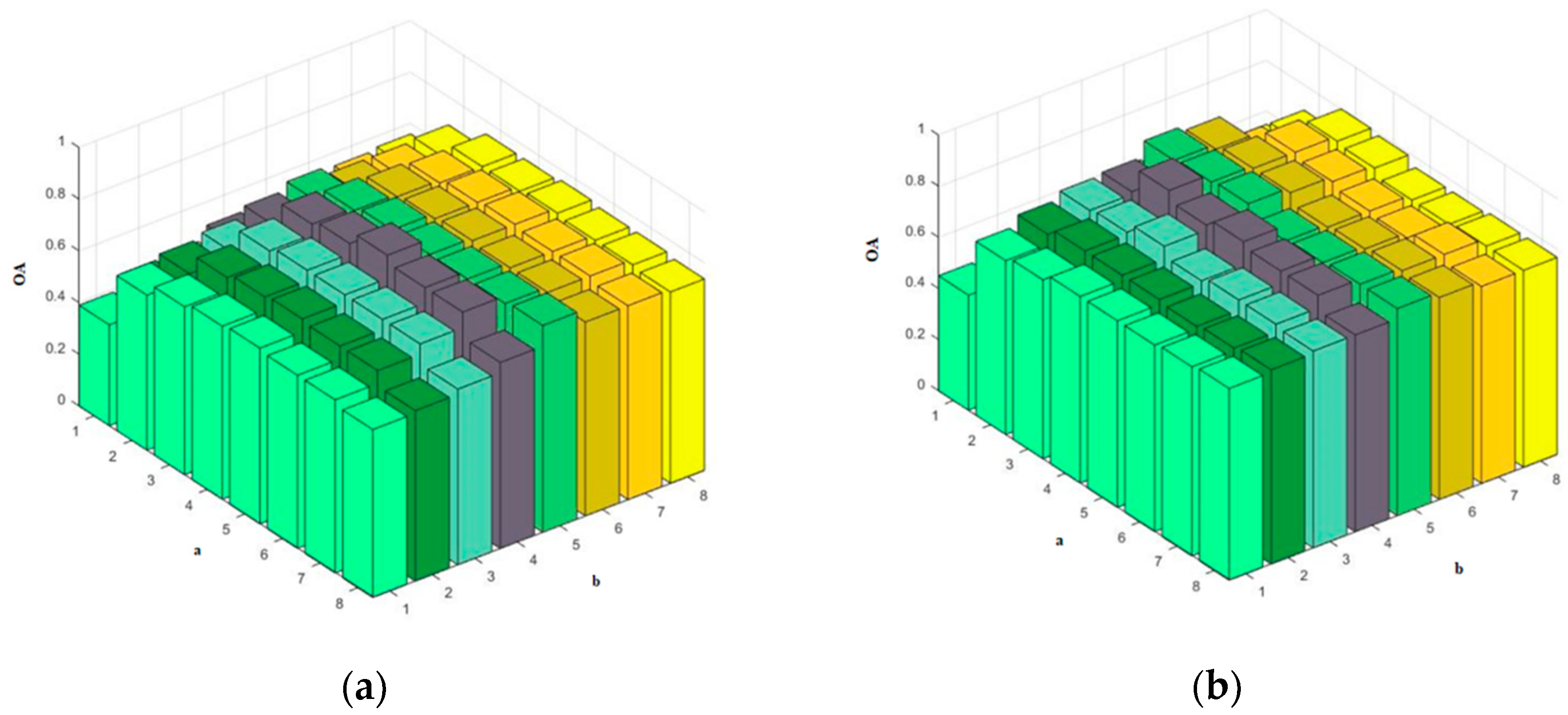
4.4.1. Inter-Manifold and Intra-Manifold near Neighbors a and b
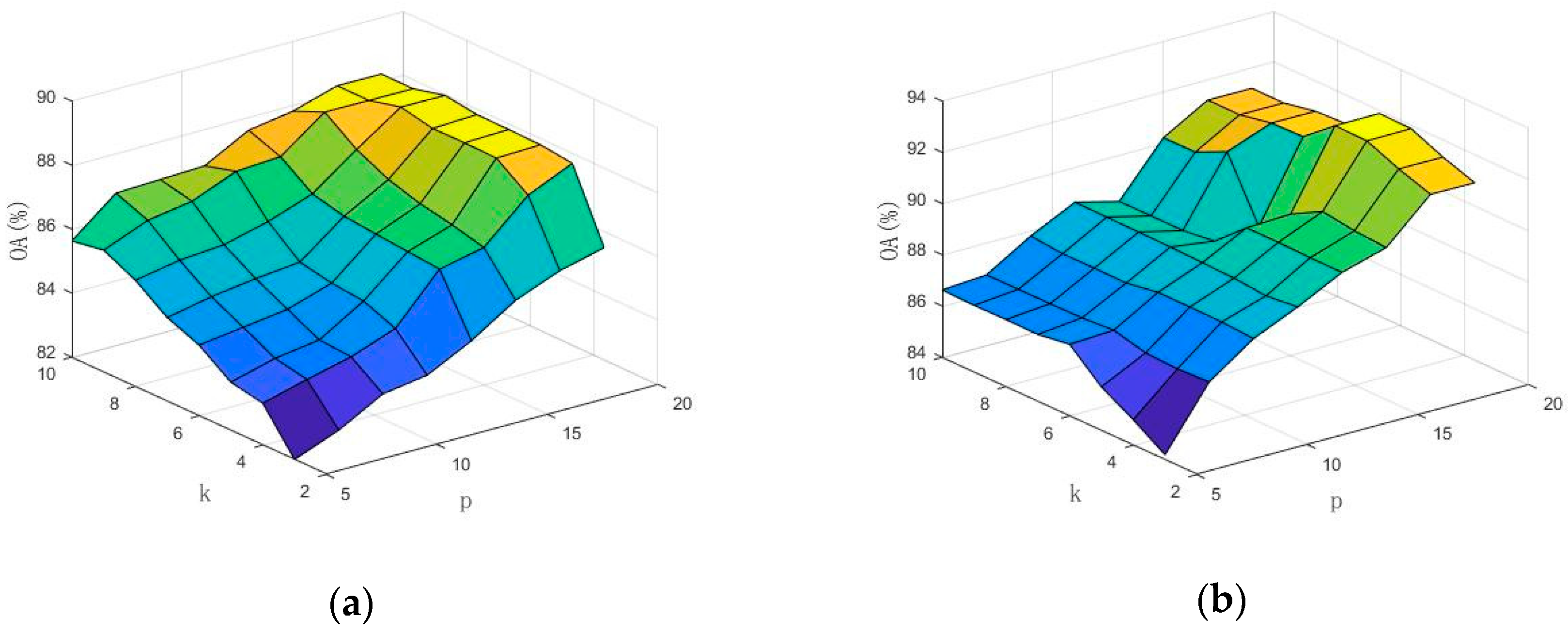
4.4.2. Spatial Window Size p and the Number of Near Neighbors k
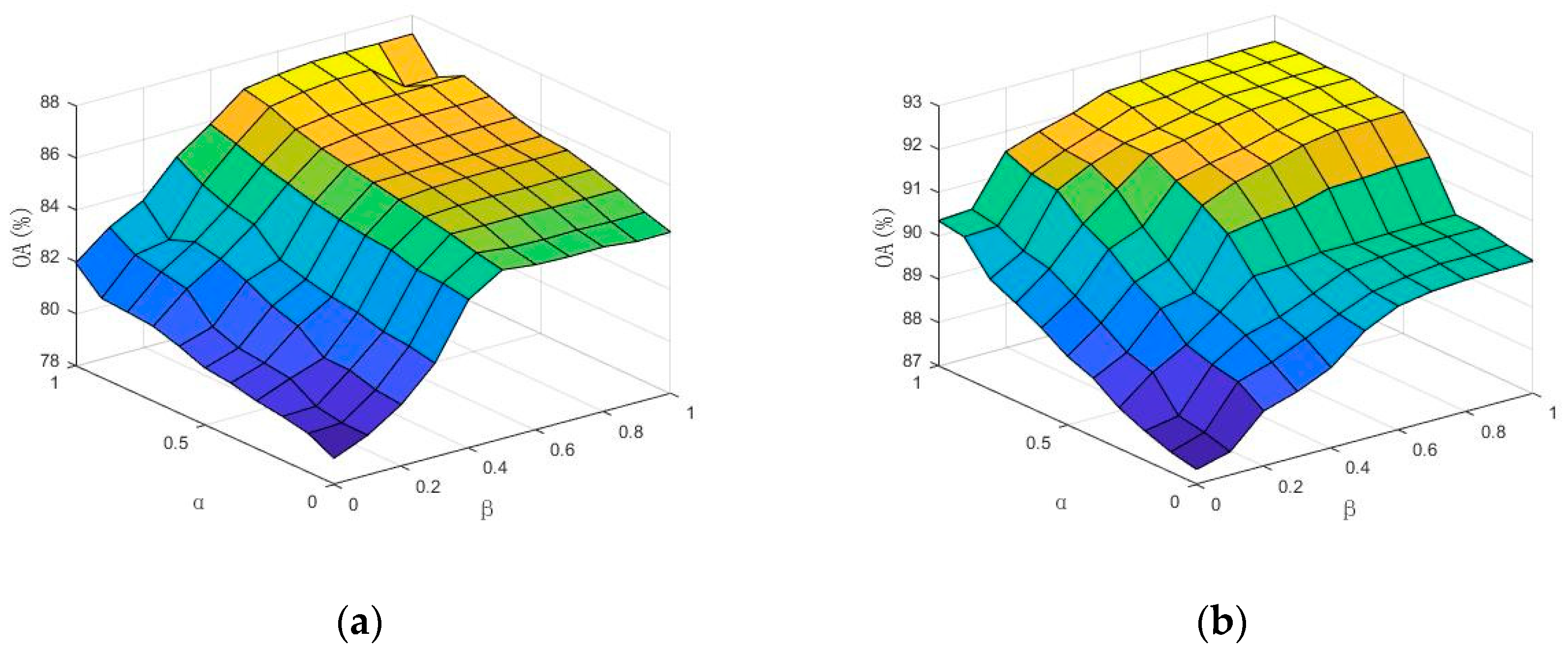
4.4.3. Balancing Spectral Information Parameters α and Spatial Information Parameters β
4.4.4. The Dimension of the Subspace d after Dimensionality Reduction
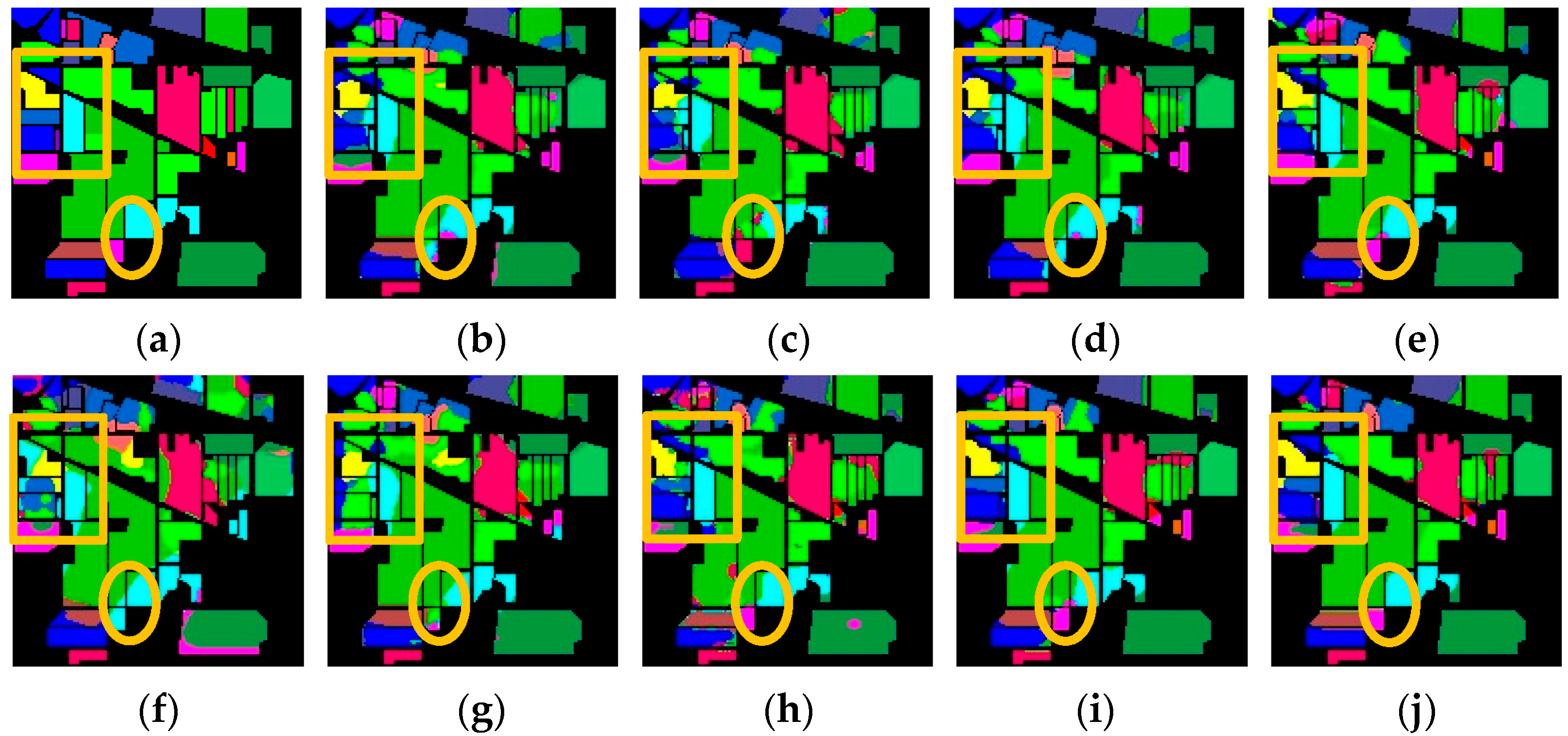
4.5. Ablation Experiments
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Landgrebe, D. Hyperspectral image data analysis. IEEE Signal Process. Mag. 2002, 1, 17–28. [Google Scholar] [CrossRef]
- Gao, H.; Chen, Z.; Li, C. Hierarchical shrinkage multiscale network for hyperspectral image classification with hierarchical feature fusion. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2021, 14, 5760–5772. [Google Scholar] [CrossRef]
- Gao, H.; Chen, Z.; Li, C. Shallow network based on depthwise overparameterized convolution for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2022, 19, 6005205. [Google Scholar] [CrossRef]
- Hong, D.; Gao, L.; Yao, J.; Zhang, B.; Plaza, A.; Chanussot, J. Graph convolutional networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2021, 7, 5966–5978. [Google Scholar] [CrossRef]
- Lv, Z.; Liu, T.; Benediktsson, J.A.; Falco, N. Land cover change detection techniques: Very-high-resolution optical images: A review. IEEE Geosci. Remote Sens. Mag. 2022, 1, 44–63. [Google Scholar] [CrossRef]
- Lv, Z.; Wang, F.; Cui, G.; Benediktsson, J.A.; Lei, T.; Sun, W. Spatial–spectral attention network guided with change magnitude image for land cover change detection using remote sensing images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4412712. [Google Scholar] [CrossRef]
- Chang, C.I. Hyperspectral anomaly detection: A dual theory of hyperspectral target detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5511720. [Google Scholar] [CrossRef]
- Feng, S.; Tang, S.; Zhao, C.; Cui, Y. A hyperspectral anomaly detection method based on low-rank and sparse decomposition with density peak guided collaborative representation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5501513. [Google Scholar] [CrossRef]
- Zhao, C.; Li, C.; Feng, S.; Li, W. Spectral–spatial anomaly detection via collaborative representation constraint stacked autoencoders for hyperspectral images. IEEE Geosci. Remote Sens. Lett. 2022, 19, 5503105. [Google Scholar] [CrossRef]
- Wu, X.; Hong, D.; Chanussot, J. UIU-Net: U-Net in U-Net for infrared small object detection. IEEE Trans. Image Process. 2023, 32, 364–376. [Google Scholar] [CrossRef]
- Yao, J.; Hong, D.; Xu, L.; Meng, D.; Chanussot, J.; Xu, Z. Sparsityenhanced convolutional decomposition: A novel tensor-based paradigm for blind hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5505014. [Google Scholar] [CrossRef]
- Chang, C.I.; Kuo, Y.M.; Chen, S.; Liang, C.C.; Ma, K.Y.; Hu, P.F. Self-Mutual Information-Based Band Selection for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2020, 59, 5979–5997. [Google Scholar] [CrossRef]
- Shang, X.; Song, M.; Wang, Y.; Yu, H.; Chang, C.I. Hyperspectral target detection based on target-constrained interference-minimized band selection. In Proceedings of the IGARSS 2020–2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 2033–2036. [Google Scholar]
- Shaw, G.; Manolakis, D. Signal processing for hyperspectral image exploitation. IEEE Signal Process. Mag. 2002, 1, 12–16. [Google Scholar] [CrossRef]
- Kuo, B.C.; Landgrebe, D.A. Nonparametric weighted feature extraction for classification. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1096–1105. [Google Scholar]
- Valle, S.; Li, W.; Qin, S.J. Selection of the number of principal components: The variance of the reconstruction error criterion with a comparison to other methods. Ind. Eng. Chem. Res. 1999, 38, 4389–4401. [Google Scholar] [CrossRef]
- Abbas, A.M. Image encryption based on independent component analysis and arnold’cCat map. Egypt. Inform. J. 2016, 17, 139–146. [Google Scholar] [CrossRef]
- Struc, V.; Paveic, N. Gabor-based kernel partial-least-squares discrimination features for face recognition. Informatica 2019, 20, 115–138. [Google Scholar] [CrossRef]
- Pang, Y.; Ji, Z.; Jiang, P. Ranking graph embedding for learning to rerank. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 1292–1303. [Google Scholar] [CrossRef]
- Luo, F.; Huang, H.; Duan, Y. Local geometric structure feature for dimensionality reduction of hyperspectral imagery. Remote Sens. 2017, 9, 790. [Google Scholar] [CrossRef]
- He, X.; Deng, C.; Yan, S. Neighborhood preserving embedding. In Proceedings of the Tenth IEEE International Conference on Computer Vision, Beijing, China, 17–21 October 2005. [Google Scholar]
- Pu, H.; Chen, Z.; Wang, B. A novel spatial–spectral similarity measure for dimensionality reduction and classification of hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7008–7022. [Google Scholar]
- Deng, Y.; Li, H.; Pan, L. Modified tensor locality preserving projection for dimensionality reduction of hyperspectral images. IEEE Geosci. Remote Sens. Lett. 2018, 15, 77–281. [Google Scholar] [CrossRef]
- Cheng, B.; Yang, J.; Yan, S. Learning with l1-graph for image analysis. IEEE Trans. Image Process. 2010, 19, 58–66. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.Z.; Huang, H.; Feng, H.L. Application of Multilinear Local and Global Preserving Embedding in Hyperspectral Remote Sensing Image Classification. J. Comput.-Aided Des. Comput. Graph. 2012, 24, 780–786. [Google Scholar]
- Huang, H.; Li, Z.; Pan, Y. Multi-feature manifold discriminant analysis for hyperspectral image classification. Remote Sens. 2019, 11, 651. [Google Scholar] [CrossRef]
- Li, J.; Zhang, H.; Zhang, L. Joint collaborative representation with multitask learning for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5923–5936. [Google Scholar] [CrossRef]
- Kang, X.; Li, S.; Benediktsson, J.A. Spectral-spatial hyperspectral image classification with edge-preserving filtering. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2666–2677. [Google Scholar] [CrossRef]
- Zhang, S.; Li, S.; Fu, W. Multiscale superpixel-based sparse representation for hyperspectral image classification. Remote Sens. 2017, 9, 139. [Google Scholar] [CrossRef]
- Liu, H.; Li, W.; Xia, X. Superpixelwise collaborative-representation graph embedding for unsupervised dimension reduction in hyperspectral imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 4684–4698. [Google Scholar] [CrossRef]
- Dong, Y.; Jin, Y.; Cheng, S. Clustered multiple manifold metric learning for hyperspectral image dimensionality reduction and classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5516813. [Google Scholar] [CrossRef]
- Achanta, R.; Shaji, A.; Smith, K.; Lucchi, A.; Fua, P.; Süsstrunk, S. SLIC superpixels compared to state-of-the-art superpixel methods. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2274–2281. [Google Scholar] [CrossRef]
- Wu, D.Y.; Ma, L. Multi-manifold LE algorithm for dimension reduction and classification of multitemporal hyperspectral image. Remote Sens. Land Resour. 2018, 30, 80–86. [Google Scholar]
- Li, D.Q. Spatial-Spectral Graph Embedding for Dimensionality Reduction of Hyperspectral Data. Ph.D. Thesis, China University of Mining and Technology, Beijing, China, 2019. [Google Scholar]
- Lu, J.; Tan, Y.P.; Wang, G. Discriminative multi-manifold analysis for face recognition from a single training sample per person. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 35, 39–51. [Google Scholar] [CrossRef] [PubMed]
- Wong, W.K. Discover latent discriminant information for dimensionality reduction: Non-negative sparseness preserving embedding. Pattern Recognit. 2012, 45, 511–1523. [Google Scholar] [CrossRef]
- Liu, B.; Zhou, Y.; Xia, Z.G. Spectral regression based marginal fisher analysis dimensionality reduction algorithm. Neurocomputing 2018, 277, 101–107. [Google Scholar] [CrossRef]
- Wu, D.Y.; Ma, L. Application of Multi-manifold LE Algorithm in Dimensionality Reduction and Classification of Hyperspectral Images. Remote Sens. Land Resour. 2018, 30, 7. [Google Scholar]
- Jiang, J.; Ma, J.; Chen, C.; Wang, Z.; Cai, Z.; Wang, L. Superpca: A superpixelwise pca approach for unsupervised feature extraction of hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4581–4593. [Google Scholar] [CrossRef]
- Huang, H.; Shi, G.; He, H. Dimensionality reduction of hyperspectral imagery based on spatial–spectral manifold learning. IEEE Trans. Cybern. 2020, 50, 2604–2616. [Google Scholar] [CrossRef]


| Category Number | Category Name | Sample Number | Color |
|---|---|---|---|
| 1 | Alfalfa | 46 |  |
| 2 | Corn-notill | 1428 |  |
| 3 | Corn-mintill | 830 |  |
| 4 | Corn | 237 |  |
| 5 | Grass-pasture | 483 |  |
| 6 | Grass-trees | 730 |  |
| 7 | Grass-pasture-mowed | 28 |  |
| 8 | Hay-windrowed | 478 |  |
| 9 | Oats | 20 |  |
| 10 | Soybean-notill | 972 |  |
| 11 | Soybean-mintill | 2455 |  |
| 12 | Soybean-clean | 593 |  |
| 13 | Wheat | 205 |  |
| 14 | Woods | 1265 |  |
| 15 | Buildings-grass-trees-drives | 386 |  |
| 16 | Stone-steel-towers | 93 |  |
| Total | 10,249 |
| Category Number | Category Name | Sample Number | Color |
|---|---|---|---|
| 1 | Asphalt | 6631 |  |
| 2 | Meadows | 18,649 |  |
| 3 | Gravel | 2099 |  |
| 4 | Trees | 3064 |  |
| 5 | Painted metal sheets | 1345 |  |
| 6 | Bare Soil | 5029 |  |
| 7 | Bitumen | 1330 |  |
| 8 | Self-blocking bricks | 3682 |  |
| 9 | Shadows | 947 |  |
| Total | 42,776 |
| No. | PCA | LPP | MFA | NSPE | MLE | MMDA | SSMRPE | SPCA | SSAMMA |
|---|---|---|---|---|---|---|---|---|---|
| C1 | 73.67 | 84.97 | 86.38 | 72.07 | 68.85 | 85.08 | 81.23 | 98.87 | 96.23 |
| C2 | 92.56 | 79.96 | 89.29 | 66.85 | 72.06 | 80.74 | 80.58 | 90.54 | 90.87 |
| C3 | 82.05 | 58.99 | 85.60 | 63.20 | 70.67 | 65.03 | 74.09 | 91.27 | 93.96 |
| C4 | 60.39 | 32.02 | 58.92 | 67.28 | 48.82 | 68.25 | 71.20 | 93.82 | 92.38 |
| C5 | 95.43 | 94.07 | 95.47 | 72.81 | 79.58 | 93.28 | 93.28 | 97.28 | 96.97 |
| C6 | 97.22 | 97.23 | 97.56 | 76.58 | 89.25 | 98.53 | 97.56 | 97.01 | 99.78 |
| C7 | 80.11 | 45.06 | 84.68 | 66.50 | 68.91 | 84.31 | 91.65 | 91.52 | 95.86 |
| C8 | 96.58 | 97.89 | 98.78 | 79.21 | 93.63 | 98.60 | 97.28 | 98.07 | 99.69 |
| C9 | 85.70 | 68.00 | 87.82 | 66.00 | 57.98 | 68.87 | 69.87 | 98.64 | 94.22 |
| C10 | 73.35 | 62.25 | 75.65 | 67.25 | 68.46 | 73.38 | 78.99 | 76.49 | 78.87 |
| C11 | 85.68 | 85.62 | 84.87 | 88.16 | 75.72 | 83.64 | 85.31 | 90.72 | 92.34 |
| C12 | 68.97 | 71.06 | 68.36 | 71.02 | 62.39 | 81.25 | 75.82 | 85.25 | 89.70 |
| C13 | 95.02 | 99.30 | 95.13 | 80.03 | 88.24 | 99.01 | 98.86 | 99.52 | 100 |
| C14 | 93.65 | 97.61 | 94.65 | 95.16 | 83.18 | 97.12 | 97.58 | 97.34 | 98.53 |
| C15 | 65.22 | 62.35 | 68.30 | 57.55 | 50.03 | 72.45 | 97.36 | 90.65 | 88.38 |
| C16 | 95.83 | 86.51 | 96.56 | 76.85 | 71.34 | 88.24 | 68.45 | 91.36 | 92.66 |
| OA | 82.65 | 83.02 | 86.25 | 72.35 | 78.23 | 85.86 | 88.75 | 91.34 | 91.59 |
| AA | 80.28 | 67.33 | 83.06 | 70.47 | 75.62 | 83.06 | 86.37 | 92.60 | 92.76 |
| K | 81.26 | 76.87 | 84.87 | 71.56 | 76.44 | 84.57 | 87.60 | 90.67 | 90.48 |
| T(s) | 0.17 | 4.26 | 7.93 | 8.57 | 20.15 | 30.54 | 42.82 | 0.48 | 46.52 |
| No. | PCA | LPP | MFA | NSPE | MLE | MMDA | SSMRPE | SPCA | SSAMMA |
|---|---|---|---|---|---|---|---|---|---|
| C1 | 83.20 | 85.86 | 87.38 | 85.96 | 82.09 | 92.45 | 92.64 | 79.64 | 95.61 |
| C2 | 90.05 | 91.50 | 95.26 | 91.63 | 89.47 | 94.65 | 97.89 | 93.08 | 97.85 |
| C3 | 63.68 | 64.22 | 75.03 | 56.06 | 60.56 | 68.73 | 76.21 | 97.54 | 92.03 |
| C4 | 78.14 | 81.03 | 82.17 | 79.90 | 72.38 | 90.76 | 81.23 | 85.33 | 88.38 |
| C5 | 97.38 | 97.48 | 98.25 | 92.74 | 95.65 | 88.23 | 99.58 | 96.88 | 99.85 |
| C6 | 86.56 | 62.47 | 67.28 | 59.42 | 79.26 | 79.15 | 95.66 | 94.80 | 97.21 |
| C7 | 81.87 | 83.88 | 88.24 | 65.50 | 75.60 | 73.24 | 87.45 | 92.38 | 98.43 |
| C8 | 75.12 | 78.86 | 78.81 | 67.24 | 71.83 | 85.43 | 81.18 | 92.55 | 89.07 |
| C9 | 98.50 | 98.51 | 98.52 | 69.88 | 94.57 | 95.32 | 99.76 | 95.53 | 99.38 |
| OA | 85.93 | 86.04 | 87.38 | 74.26 | 79.82 | 87.58 | 92.35 | 90.96 | 96.53 |
| AA | 82.65 | 85.35 | 86.50 | 70.45 | 76.67 | 86.83 | 91.19 | 91.97 | 94.12 |
| K | 82.76 | 82.76 | 83.57 | 72.12 | 73.78 | 86.72 | 91.32 | 88.16 | 95.38 |
| T(s) | 0.68 | 96.22 | 9.64 | 106.54 | 24.62 | 41.28 | 44.64 | 0.51 | 10.71 |
| Dataset | Model | Module | Metrics | |||
|---|---|---|---|---|---|---|
| SAWRM | SSMMM | OA | AA | K | ||
| IP | M1 | × | × | 82.65 | 80.72 | 79.68 |
| M2 | × | 88.04 | 87.13 | 86.19 | ||
| M3 | × | 88.27 | 87.36 | 86.50 | ||
| M4 | 90.56 | 89.71 | 88.02 | |||
| PU | M1 | × | × | 92.87 | 91.48 | 90.16 |
| M2 | × | 95.11 | 94.00 | 93.14 | ||
| M3 | × | 95.34 | 94.29 | 94.05 | ||
| M4 | 97.86 | 97.06 | 96.22 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, S.; Geng, S.; Yang, Q.; Gao, H. Hyperspectral Image Dimensionality Reduction Algorithm Based on Spatial–Spectral Adaptive Multiple Manifolds. Appl. Sci. 2023, 13, 9180. https://doi.org/10.3390/app13169180
Xu S, Geng S, Yang Q, Gao H. Hyperspectral Image Dimensionality Reduction Algorithm Based on Spatial–Spectral Adaptive Multiple Manifolds. Applied Sciences. 2023; 13(16):9180. https://doi.org/10.3390/app13169180
Chicago/Turabian StyleXu, Shufang, Sijie Geng, Qi Yang, and Hongmin Gao. 2023. "Hyperspectral Image Dimensionality Reduction Algorithm Based on Spatial–Spectral Adaptive Multiple Manifolds" Applied Sciences 13, no. 16: 9180. https://doi.org/10.3390/app13169180
APA StyleXu, S., Geng, S., Yang, Q., & Gao, H. (2023). Hyperspectral Image Dimensionality Reduction Algorithm Based on Spatial–Spectral Adaptive Multiple Manifolds. Applied Sciences, 13(16), 9180. https://doi.org/10.3390/app13169180






