Fractional Calculus-Based Statistical Damage Model of Unsaturated Soil under the Coupling Effect of Moistening and Stress Fields
Abstract
:1. Introduction
2. Principle and Intensity of Effective Stress of Unsaturated Soil
2.1. Principle of Effective Stress in Unsaturated Soil
2.2. The Shear Strength Theory of Unsaturated Soil
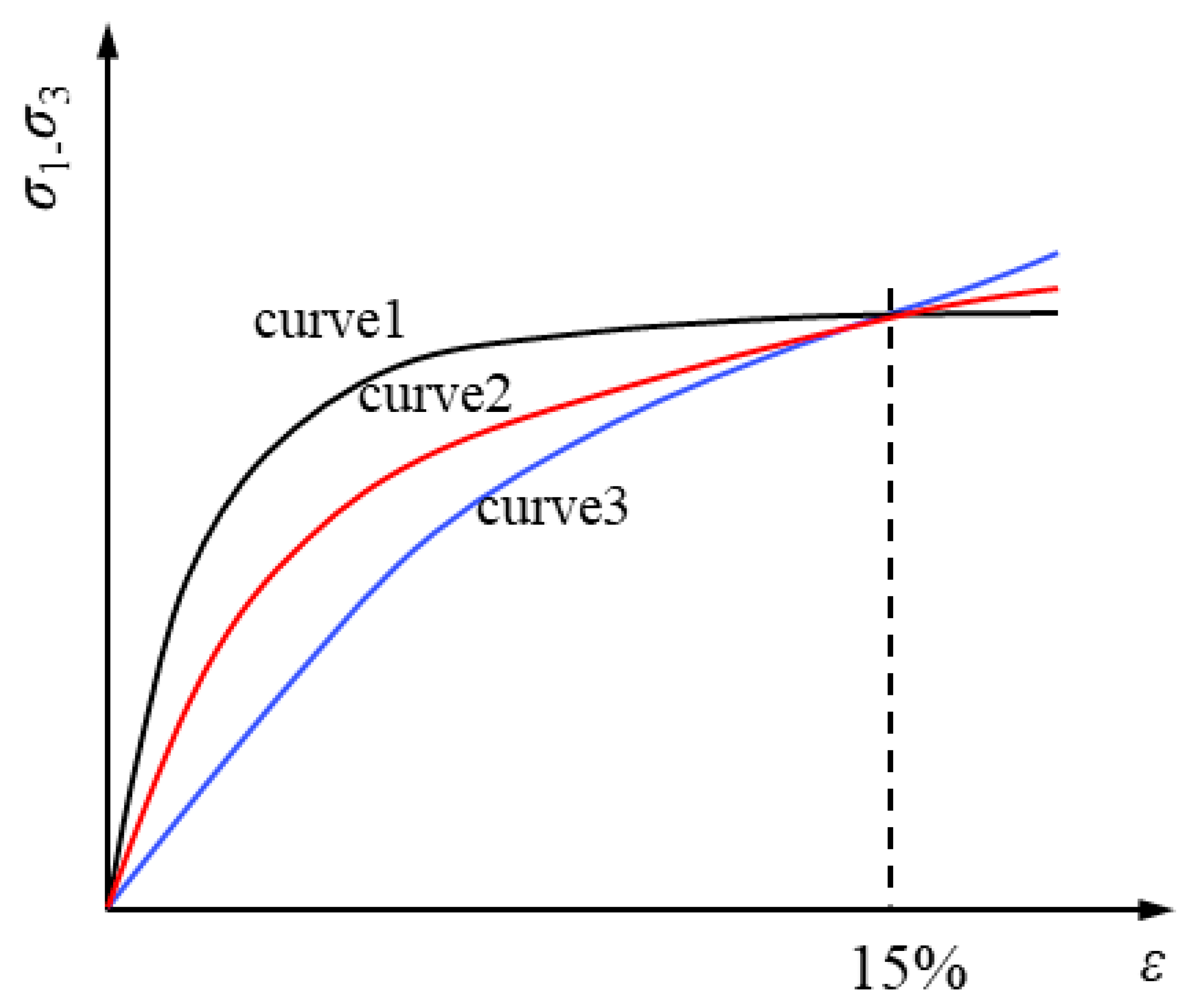
2.3. Strain Characteristics of Unsaturated Soil in the Stress Field
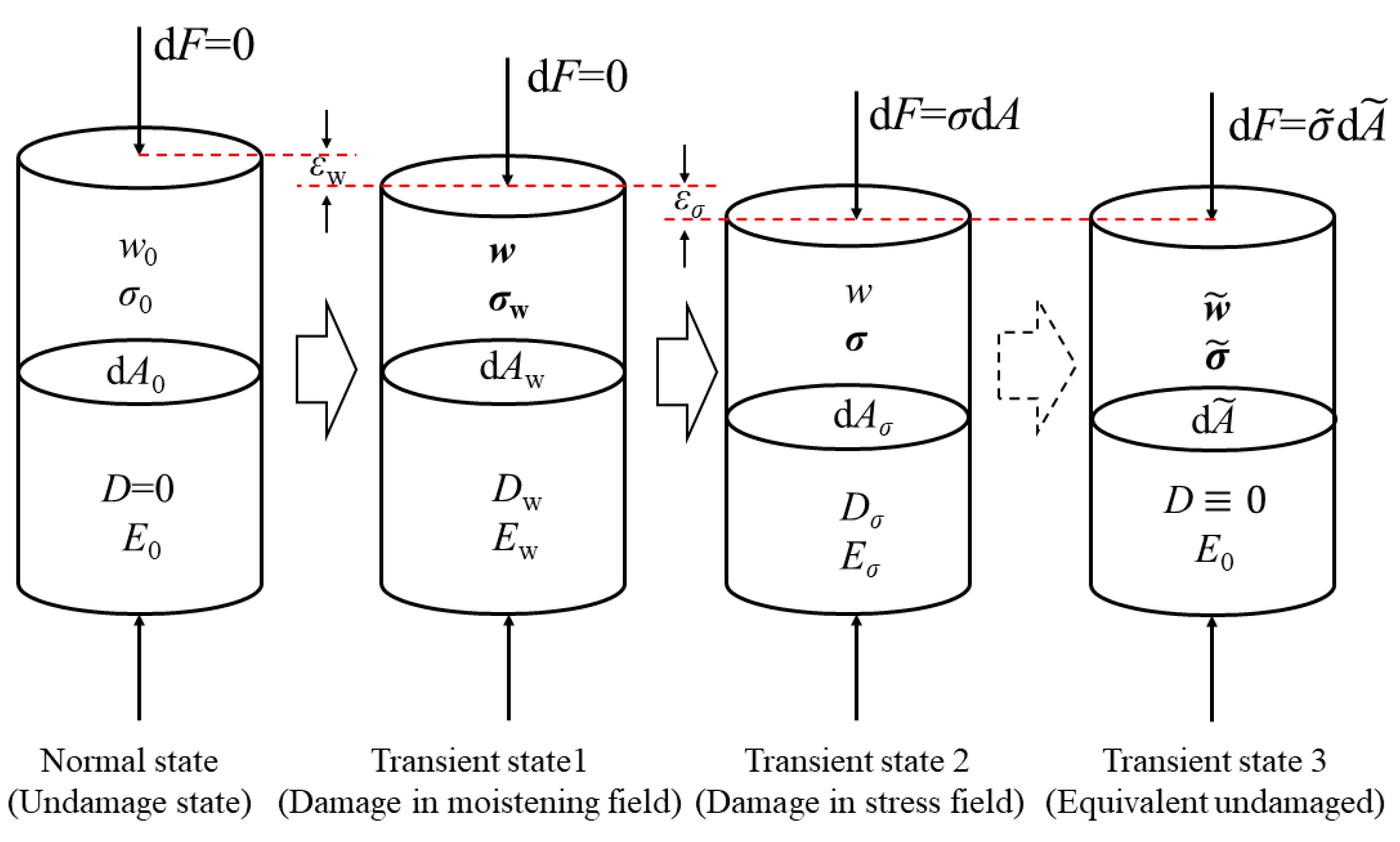
2.4. The Damage Evolution Law of Unsaturated Soil
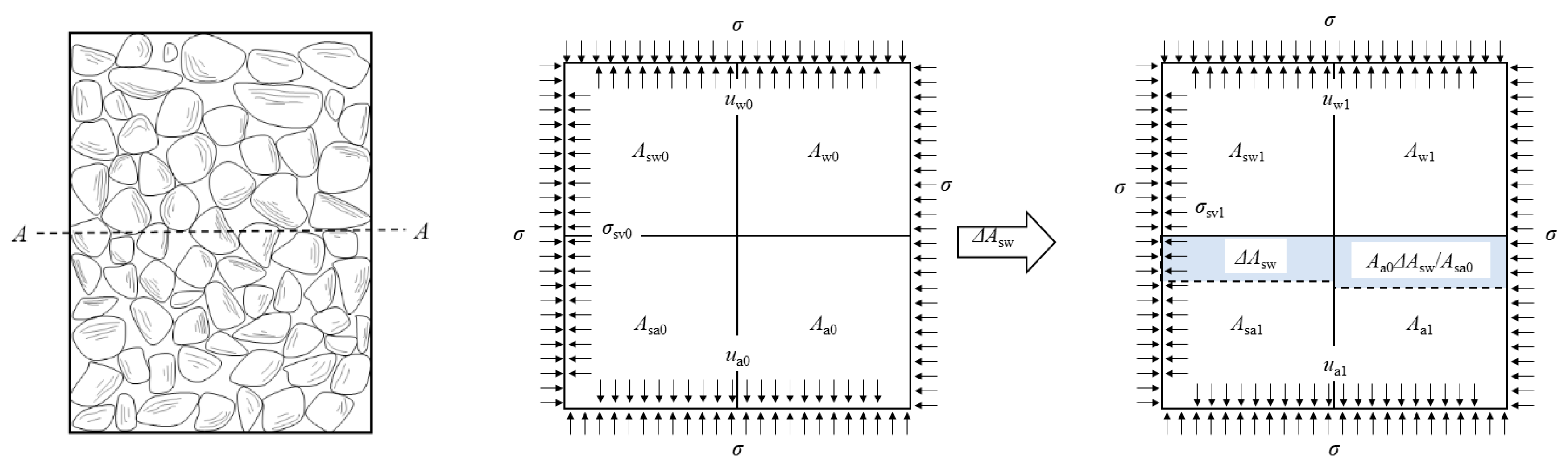
2.4.1. Micro-Unit Damage Variables
2.4.2. Evolution of Damage Variables
2.5. The Micro-Unit Strength of Unsaturated Soil
3. Model Parameter Solving
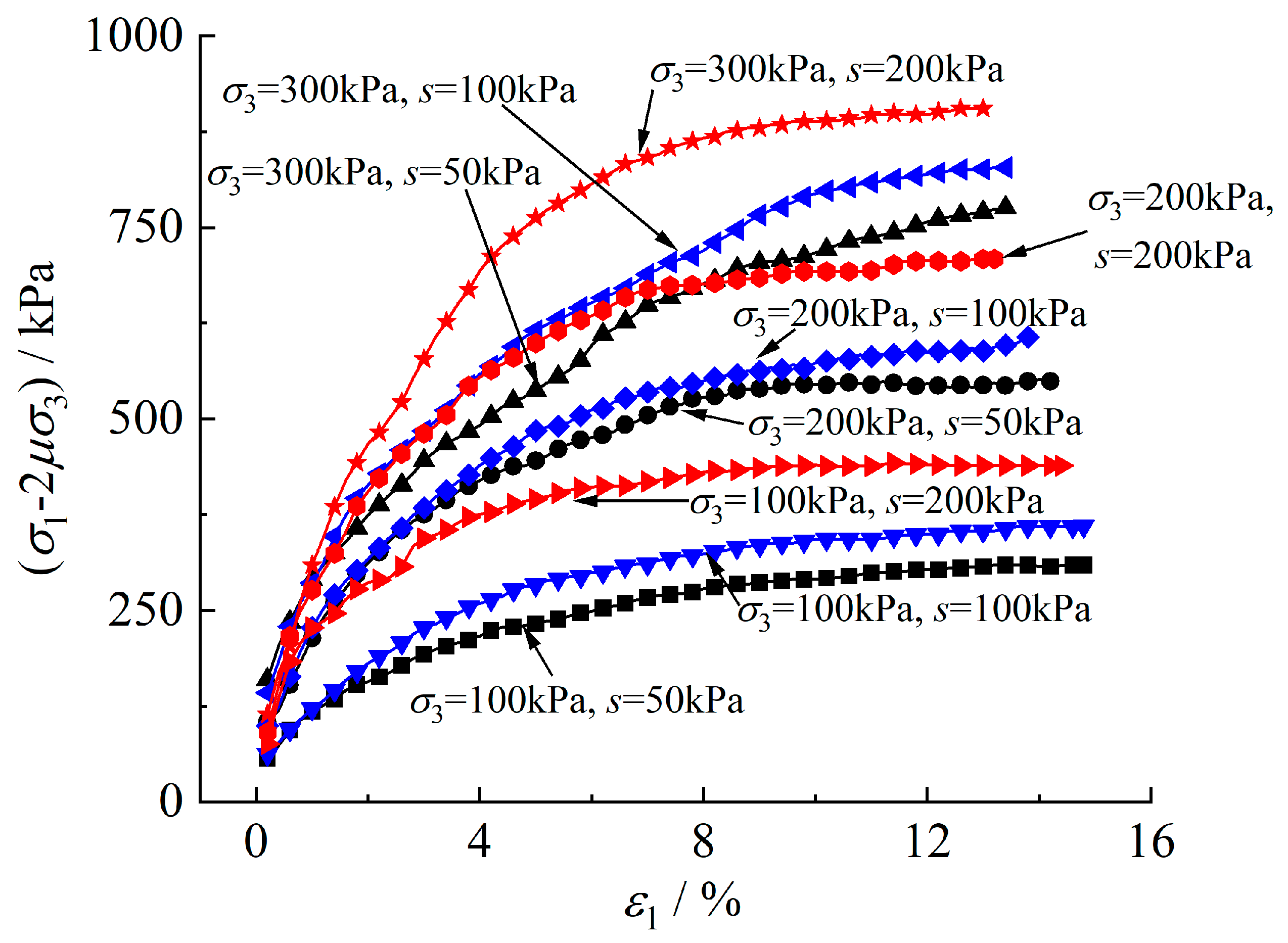
4. Model Validation and Discussion
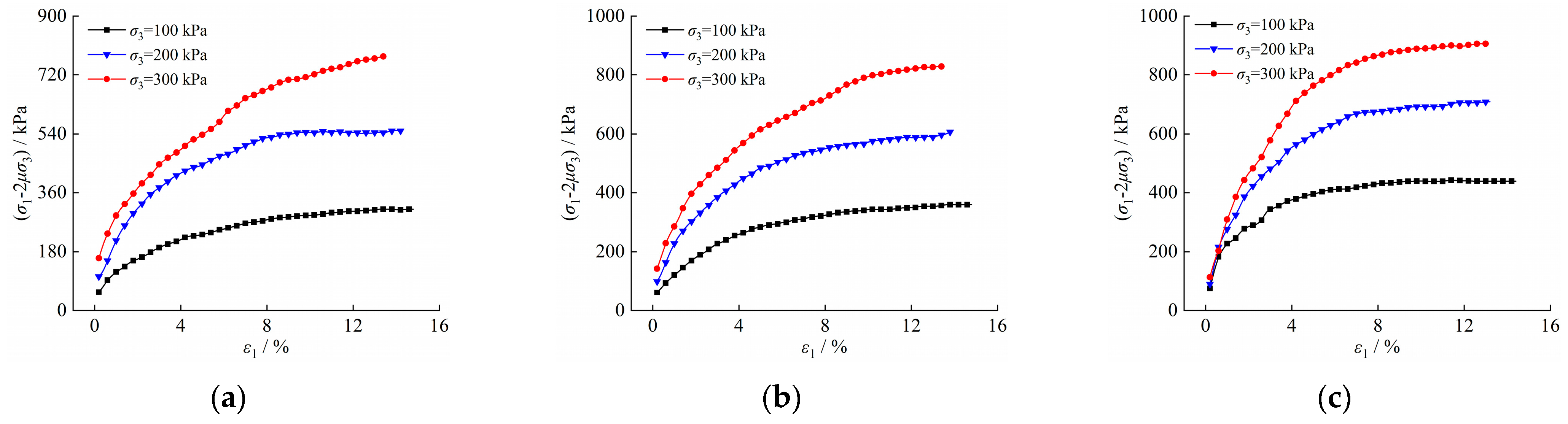
4.1. Model Parameters and Validation
4.2. Discussion
- (1)
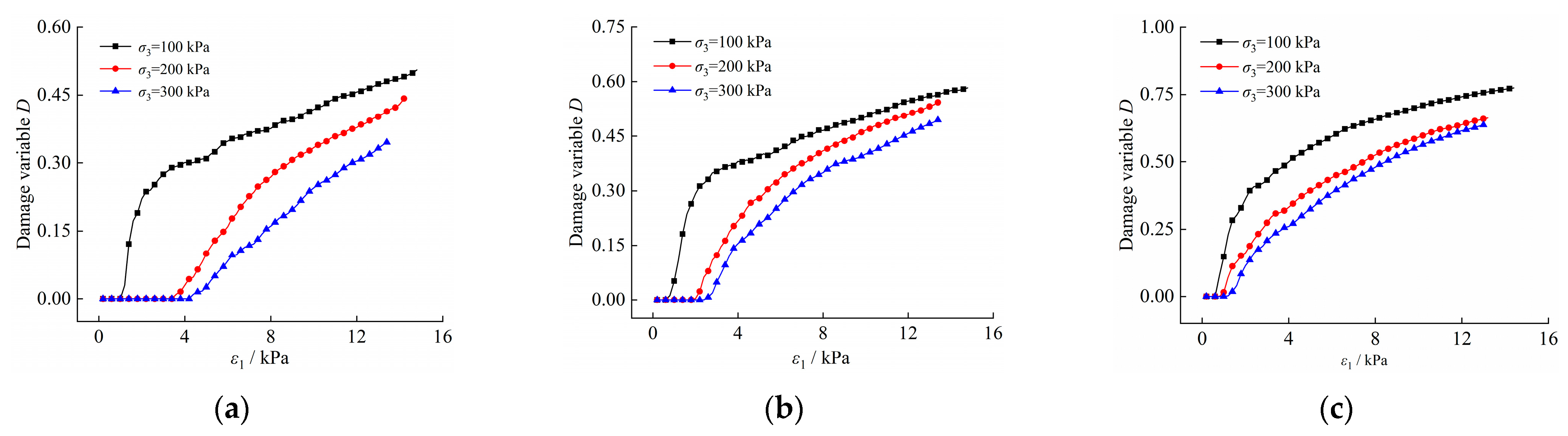
- Damage variable D
- (2)
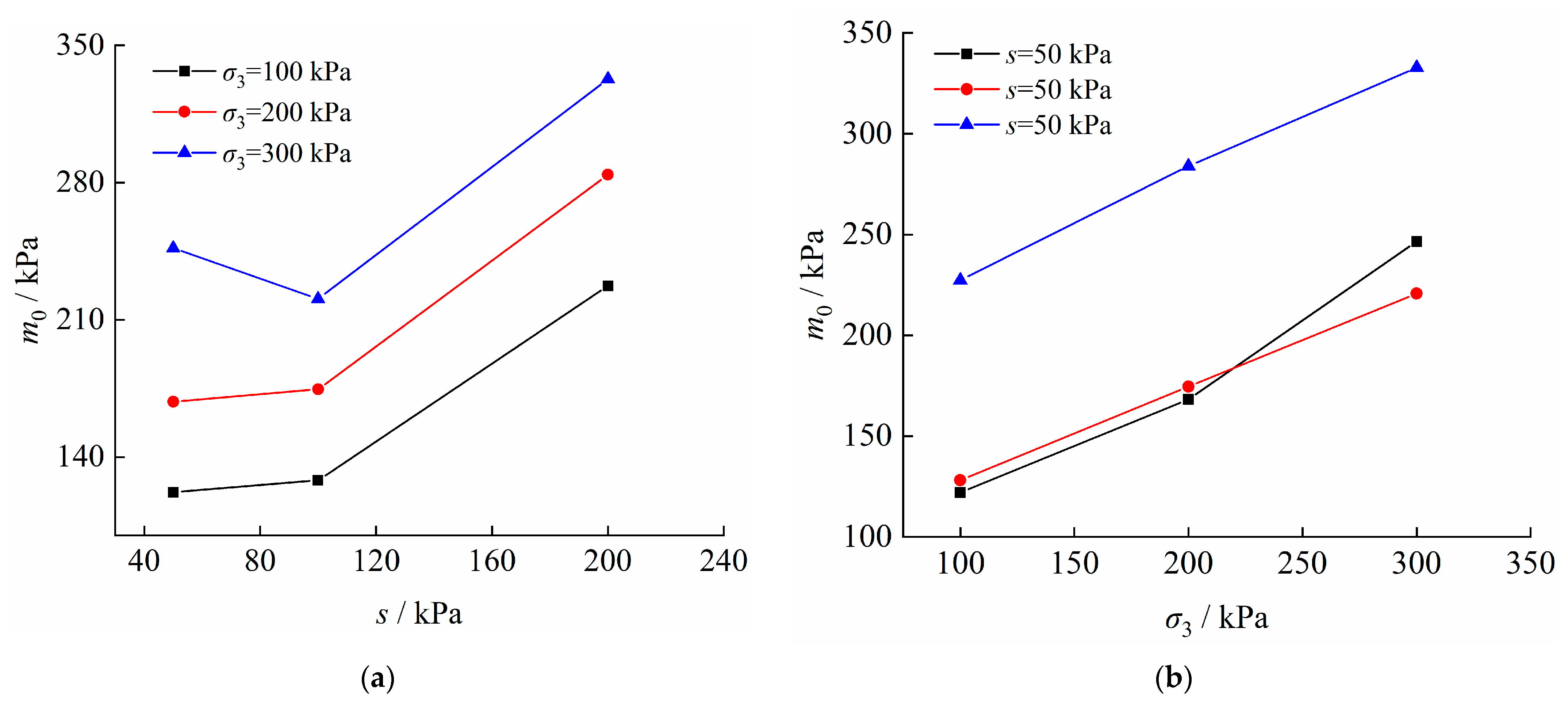
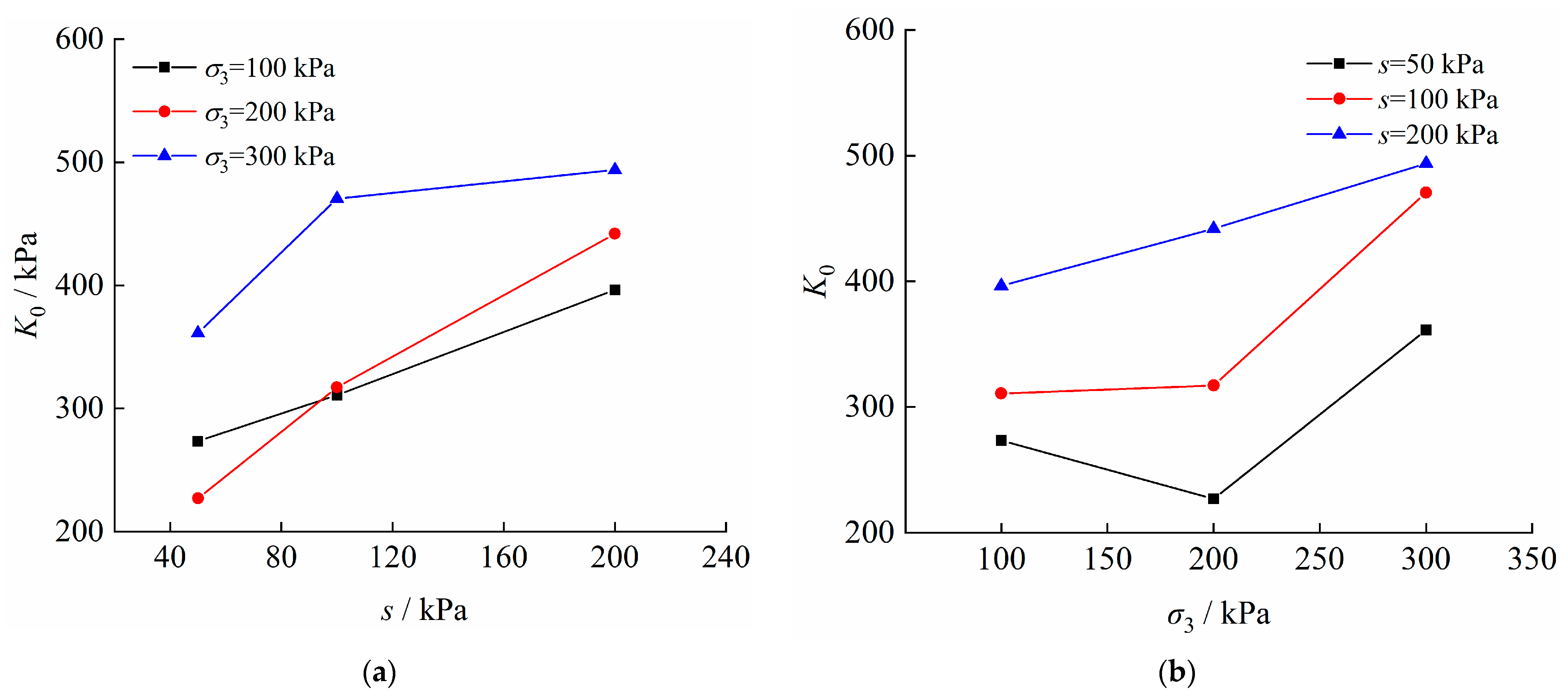
- Laplace distribution parameters m0 and K0
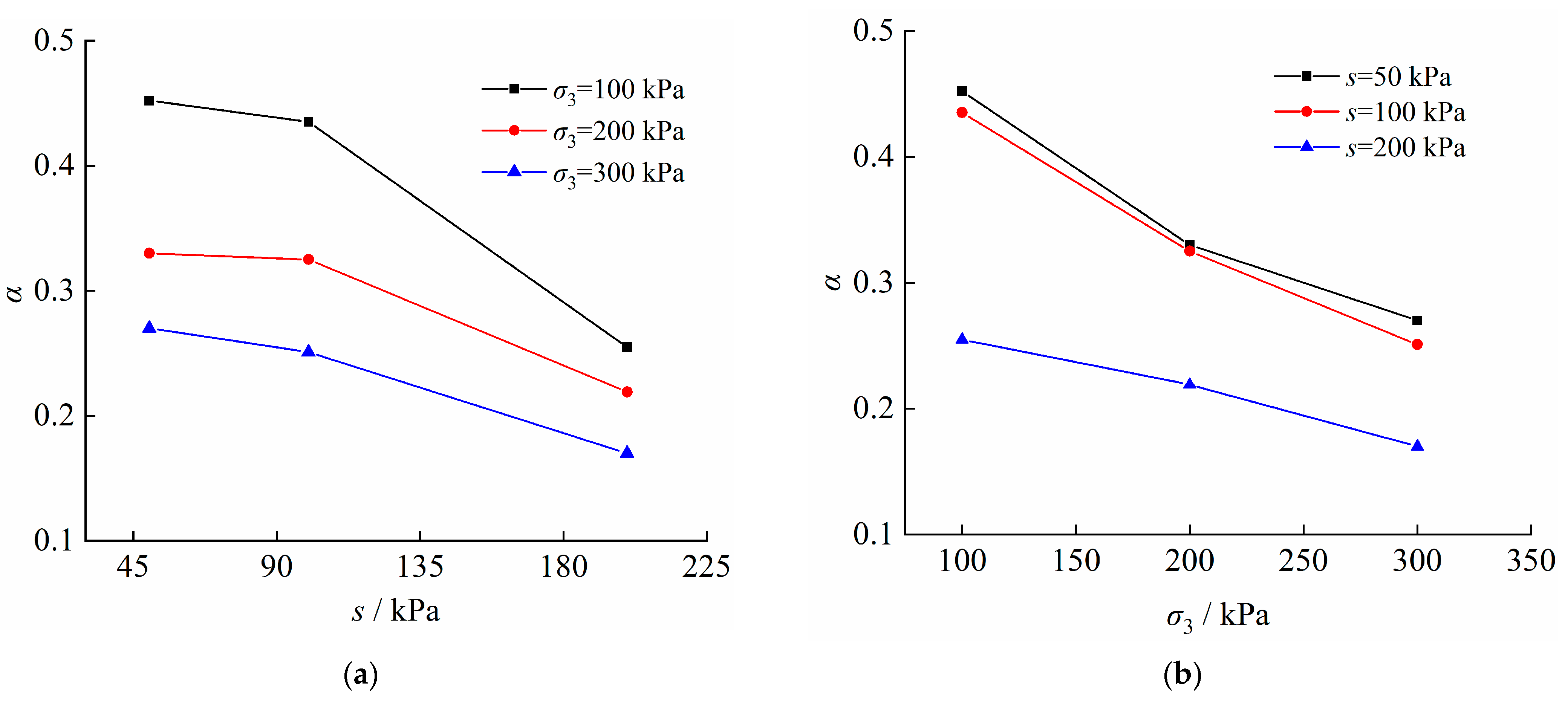
- (3)
- Strain hardening parameter α
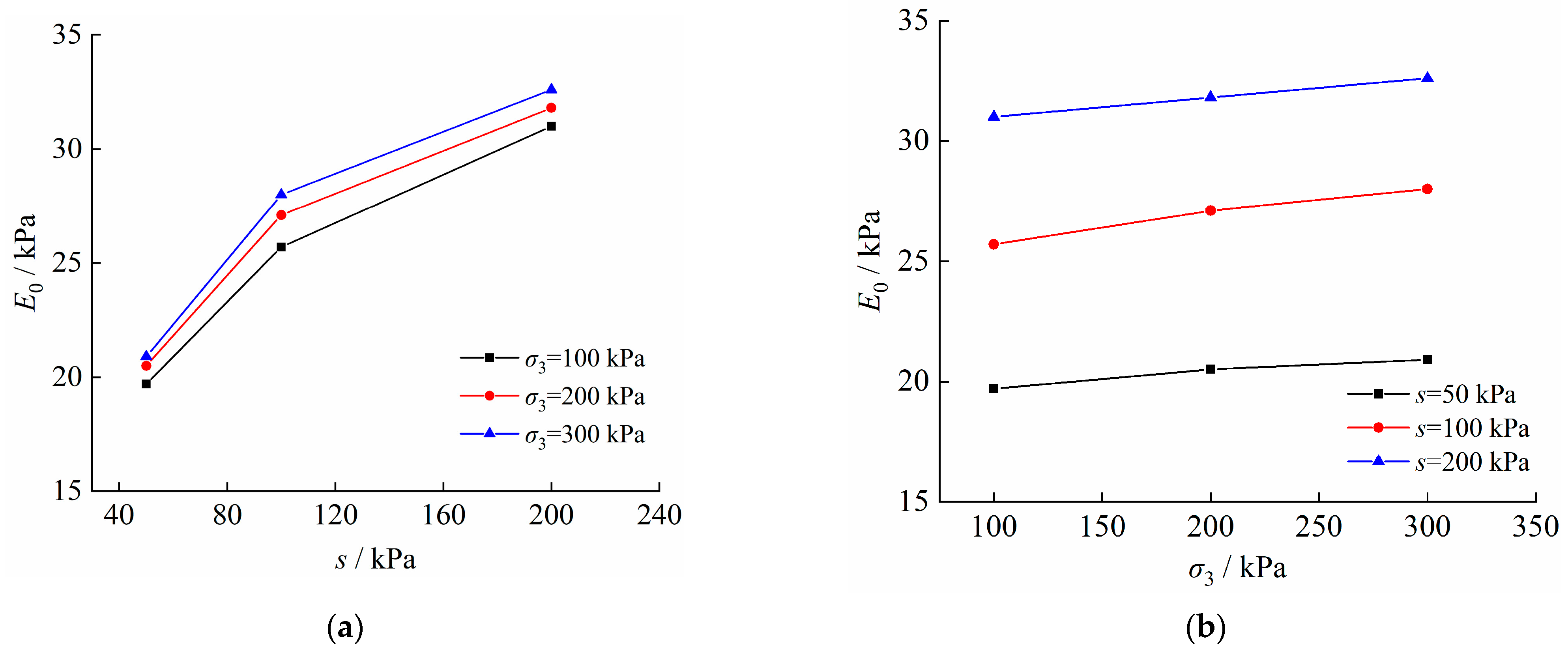
- (4)
- Elastic modulus E0
5. Conclusions
- (1)
- Based on the classical soil mechanics principle, unsaturated soil mechanics and VG model, the mathematical formula for effective stress of unsaturated soil expressed by saturation is established in this paper. On this basis, the mathematical formula of mechanical shear strength of unsaturated soil, considering the coupling of moistening and stress fields, is established by Schrefler’s shear strength formula.
- (2)
- A fractional-order strain-hardening model based on a conventional unsaturated triaxial shear test is established by using fractional-order calculus theory. Based on the principle of damage mechanics, the coupling damage variable of unsaturated soil under the influence of stress and water content is established. Finally, a fractional-order strain-hardening model of unsaturated soil under the coupling of stress and moistening fields is established.
- (3)
- The experimental data of unsaturated loess with strain-hardening characteristics are used to verify the proposed model. Results show that the model can describe the whole process of strain-hardening of unsaturated soil under the coupling of stress and moistening fields.
- (4)
- Through discussions on parameters of the proposed model, it is found that there is an initial threshold as unsaturated soil being damaged in coupling of the stress and moistening fields. The initial threshold value increases with the increase in confining pressure and decreases with the increase in matric suction. The hardening ability of unsaturated soil increases with the increase in matric suction or confining pressure. The overall mechanical properties of unsaturated soils improve nonlinearly with the increase of matric suction or confining pressure.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yao, C.; Yang, X.-L. Limit Analysis of Unsaturated Soil Slope Stability Considering Intermediate Principal Stress and Strength Nonlinearity. Geotech. Geol. Eng. 2017, 35, 2053–2063. [Google Scholar] [CrossRef]
- Liu, J.-X.; Liu, W.; Liu, P.; Yang, C.-H.; Xie, Q.; Liu, Y.-T. Preliminary research on the theory and application of unsaturated Red-layers embankment settlement based on rheology and consolidation theory. Environ. Earth Sci. 2016, 75, 503. [Google Scholar]
- Xu, X.; Cai, G.-Q.; Song, Z.-Y.; Li, J.; Xu, C.-B.; Wang, H.-L.; Zhao, C.-G. Dilatancy Characteristics and Constitutive Modelling of the Unsaturated Soil Based on Changes in the Mass Water Content. Appl. Sci. 2021, 11, 4859. [Google Scholar] [CrossRef]
- Cai, G.-Q.; Han, B.-W.; Li, M.-Z.; Di, K.-N.; Liu, Y.; Li, J.; Wu, T.-C. Numerical Implementation of a HydroMechanical Coupling Constitutive Model for Unsaturated Soil Considering the Effect of Micro-Pore Structure. Appl. Sci. 2021, 11, 5368. [Google Scholar] [CrossRef]
- Ofoegbu, G.I.; Dasgupta, B.; Manepally, C.; Stothoff, S.A.; Fedors, R. Modeling the mechanical behavior of unsaturated expansive soils based on Bishop principle of effective stress. Environ. Earth Sci. 2017, 76, 555. [Google Scholar] [CrossRef]
- Samui, P.; Jagan, J. Determination of effective stress parameter of unsaturated soils: A Gaussian process regression approach. Front. Struct. Civ. Eng. 2013, 7, 133–136. [Google Scholar]
- Li, H.; Li, T.-L.; Li, P.; Zhang, Y.-G. Prediction of loess soil-water characteristic curve by mercury intrusion porosimetry. J. Mt. Sci. 2020, 17, 2203–2213. [Google Scholar] [CrossRef]
- Satyanaga, A.; Rahardjo, H.; Koh, Z.H.; Mohamed, H. Measurement of a soil-water characteristic curve and unsaturated permeability using the evaporation method and the chilled-mirror method. J. Zhejiang Univ. Sci. A 2019, 20, 368–374. [Google Scholar] [CrossRef]
- Alves, R.D.; Gitirana, G.d.F.N., Jr.; Vanapalli, S.K. Advances in the Modeling of the Soil-Water Characteristic Curve Using Pore-Scale Analysis. Comput. Geotech. 2020, 127, 103766. [Google Scholar] [CrossRef]
- Sillers, W.S.; Fredlund, D.G.; Zakerzaheh, N. Mathematical attributes of some soil–water characteristic curve models. Geotech. Geol. Eng. 2001, 19, 243–283. [Google Scholar] [CrossRef]
- Jiang, Y.; Chen, W.-W.; Wang, G.-H.; Sun, G.-P.; Zhang, F.-Y. Influence of initial dry density and water content on the soil–water characteristic curve and suction stress of a reconstituted loess soil. Bull. Eng. Geol. Environ. 2017, 76, 1085–1095. [Google Scholar] [CrossRef]
- Bishop, A.W.; Blight, G.E. Some Aspects of Effective Stress in Saturated and Partly Saturated Soils. Geotechnique 1963, 13, 177–197. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Xing, A. Equations for the soil-water characteristic curve. Can. Geotech. J. 1994, 31, 521–532. [Google Scholar] [CrossRef]
- Vanapalli, S.K.; Fredlund, D.G.; Pufahl, D.E. Model for the prediction of shear strength with respect to soil suction. Can. Geotech. J. 1996, 33, 379–392. [Google Scholar] [CrossRef]
- Schrefler, B.A. The Finite Element Method in Soil Consolidation: With Applications to Surface Subsidence. Ph.D. Thesis, University College of Swansea, Swansea, UK, 1984. [Google Scholar]
- Chen, J.Y.; Hai, Y. A φb Model for Predicting Shear Strength of Unsaturated Soils. Adv. Mater Res. 2012, 594–597, 425–429. [Google Scholar]
- Lloret-Cabot, M.; Wheeler, S.J.; Sánchez, M. A unified mechanical and retention model for saturated and unsaturated soil behaviour. Acta Geotech. 2017, 12, 1–21. [Google Scholar] [CrossRef]
- Zhai, Q.; Rahardjo, H.; Satyanaga, A.; Dai, G.-L. Estimation of tensile strength of sandy soil from soil-water characteristic curve. Acta Geotech. 2020, 15, 3371–3381. [Google Scholar] [CrossRef]
- Zhai, Q.; Rahardjo, H.; Satyanaga, A.; Dai, G.-L. Estimation of unsaturated shear strength from soil-water characteristic curve. Acta Geotech. 2019, 14, 1977–1990. [Google Scholar] [CrossRef]
- Kamoun, J.; Bouassida, M. Creep behavior of unsaturated cohesive soils subjected to various stress levels. Arab. J. Geosci. 2018, 11, 77. [Google Scholar] [CrossRef]
- Li, J.-Z.; Yang, Y.-l. Creep behavior of unsaturated reticulate red clay under matric suction. KSCE J. Civ. Eng. 2018, 22, 582–587. [Google Scholar] [CrossRef]
- Swain, S.; Swain, A.; Sahoo, S. Inter-conversion of Modulus and Compliance for Viscoelastic Soil. Indian Geotech. J. 2021, 51, 1145–1150. [Google Scholar] [CrossRef]
- Sheng, D.-C.; Pedroso, D.M.; Abbo, A.J. Non-convexity and stress-path dependency of unsaturated soil models. Comput. Mech. 2008, 42, 695. [Google Scholar] [CrossRef]
- Li, W.-G.; Yang, Q.; Xue, Z.-J.; Liu, W.-H.; Hua, Y. Experimental study and constitutive modeling of volume change behavior in unsaturated soils. Bull. Eng. Geol. Environ. 2021, 80, 679–689. [Google Scholar] [CrossRef]
- Shao, S.-J.; Yu, Q.-G.; Long, J.-Y. Stress-strain relationship with soil structural parameter of collapse loess. Front. Arch. Civ. Eng. China 2008, 2, 151–160. [Google Scholar] [CrossRef]
- Shi, S.; Zhang, F.; Feng, D.-C.; Tang, K.-W. Creep Constitutive Model for Frozen Soils Based on Hardening and Damage Effects. KSCE J. Civ. Eng. 2020, 24, 1146–1158. [Google Scholar] [CrossRef]
- Xu, L.-F.; Wong, H.; Fabbri, A.; Champire, F.; Branque, D. Modelling the poroplastic damageable behaviour of earthen materials. Mater Struct. 2018, 51, 112. [Google Scholar] [CrossRef]
- Yao, Z.-H.; Chen, Z.-H.; Fang, X.-W.; Wang, W.-G.; Li, W.; Su, L.-H. Elastoplastic damage seepage–consolidation coupled model of unsaturated undisturbed loess and its application. Acta Geotech. 2020, 15, 1637–1653. [Google Scholar] [CrossRef]
- Luo, W.-B.; Li, B.; Zhang, Y.-J.; Yin, B.-Y.; Dai, J.-L. A Creep Model of Asphalt Mixture Based on Variable Order Fractional Derivative. Appl. Sci. 2020, 10, 3862. [Google Scholar] [CrossRef]
- Zhang, B.-L.; Chen, K.-S.; Hu, X.; Zhang, K. A Variable-Order Dynamic Constitutive Model for Clay Based on the Fractional Calculus. Appl. Sci. 2022, 12, 6416. [Google Scholar] [CrossRef]
- Yin, D.-S.; Zhang, W.; Cheng, C.; Li, Y.-Q. Fractional time dependent Bingham model for muddy clay. J. Non-Newton. Fluid Mech. 2012, 187–188, 32–35. [Google Scholar] [CrossRef]
- Zhou, H.-W.; Wang, C.-P.; Han, B.-B.; Duan, Z.-Q. A creep constitutive model for salt rock based on fractional derivatives. Int. J. Rock Mech. Min. Sci. 2011, 48, 116–121. [Google Scholar] [CrossRef]
- Di Mino, G.; Airey, G.; Di Paola, M.; Pinnola, F.-P.; D’Angelo, G.; Lo Presti, D. Linear and nonlinear fractional hereditary constitutive laws of asphalt mixtures. J. Civ. Eng. Manag. 2016, 22, 882–889. [Google Scholar] [CrossRef] [Green Version]
- Ng, C.W.W.; Zhou, C.; Chiu, C.F. Constitutive modelling of state-dependent behaviour of unsaturated soils: An overview. Acta Geotech. 2020, 15, 2705–2725. [Google Scholar]
- Gao, D.-H.; Chen, Z.-H.; Guo, N.; Zhu, Y.-P.; Hu, S.-X.; Yao, Z.-H. The influence of dry density and matric suction on the deformation and the strength characteristics of the remolded unsaturated loess soils. Chin. J. Rock Mech. Eng. 2017, 36, 736–744. [Google Scholar]

| Dry Density ρd/g·cm−3 | Relative Density ds | Plastic Limit wp/% | Liquid Limit wL/% |
|---|---|---|---|
| 1.51 | 2.71 | 17.3 | 31.1 |
| s /kPa | σ3 /kPa | Basic Physical Parameters | Saturated Soil Strength Parameters | Laplace Distribution Parameters | Strain Hardening Parameters | ||||
|---|---|---|---|---|---|---|---|---|---|
| E0 /kPa | μ | v0 /mm·h−1 | /kPa | /° | m0 | K0 | α | ||
| 50 | 100 | 19.7 | 0.38 | 0.432 | 12.26 | 30.65 | 122.03 | 273.50 | 0.452 |
| 200 | 20.5 | 168.20 | 227.05 | 0.330 | |||||
| 300 | 20.9 | 246.61 | 361.40 | 0.270 | |||||
| 100 | 100 | 25.7 | 128.11 | 310.78 | 0.435 | ||||
| 200 | 27.1 | 174.51 | 317.17 | 0.325 | |||||
| 300 | 28.0 | 220.66 | 470.55 | 0.251 | |||||
| 200 | 100 | 31.0 | 227.36 | 396.41 | 0.255 | ||||
| 200 | 31.8 | 283.92 | 441.97 | 0.219 | |||||
| 300 | 32.6 | 332.64 | 493.81 | 0.170 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Wang, P. Fractional Calculus-Based Statistical Damage Model of Unsaturated Soil under the Coupling Effect of Moistening and Stress Fields. Appl. Sci. 2023, 13, 9156. https://doi.org/10.3390/app13169156
Zhang H, Wang P. Fractional Calculus-Based Statistical Damage Model of Unsaturated Soil under the Coupling Effect of Moistening and Stress Fields. Applied Sciences. 2023; 13(16):9156. https://doi.org/10.3390/app13169156
Chicago/Turabian StyleZhang, Hua, and Peng Wang. 2023. "Fractional Calculus-Based Statistical Damage Model of Unsaturated Soil under the Coupling Effect of Moistening and Stress Fields" Applied Sciences 13, no. 16: 9156. https://doi.org/10.3390/app13169156
APA StyleZhang, H., & Wang, P. (2023). Fractional Calculus-Based Statistical Damage Model of Unsaturated Soil under the Coupling Effect of Moistening and Stress Fields. Applied Sciences, 13(16), 9156. https://doi.org/10.3390/app13169156






