Post-Earthquake Dynamic Performance of Intact Masonry Building Based on Finite Element Model Updating
Abstract
1. Introduction
2. Dynamic Properties’ Changes Due to the Seismic Action
3. Experimental Investigation
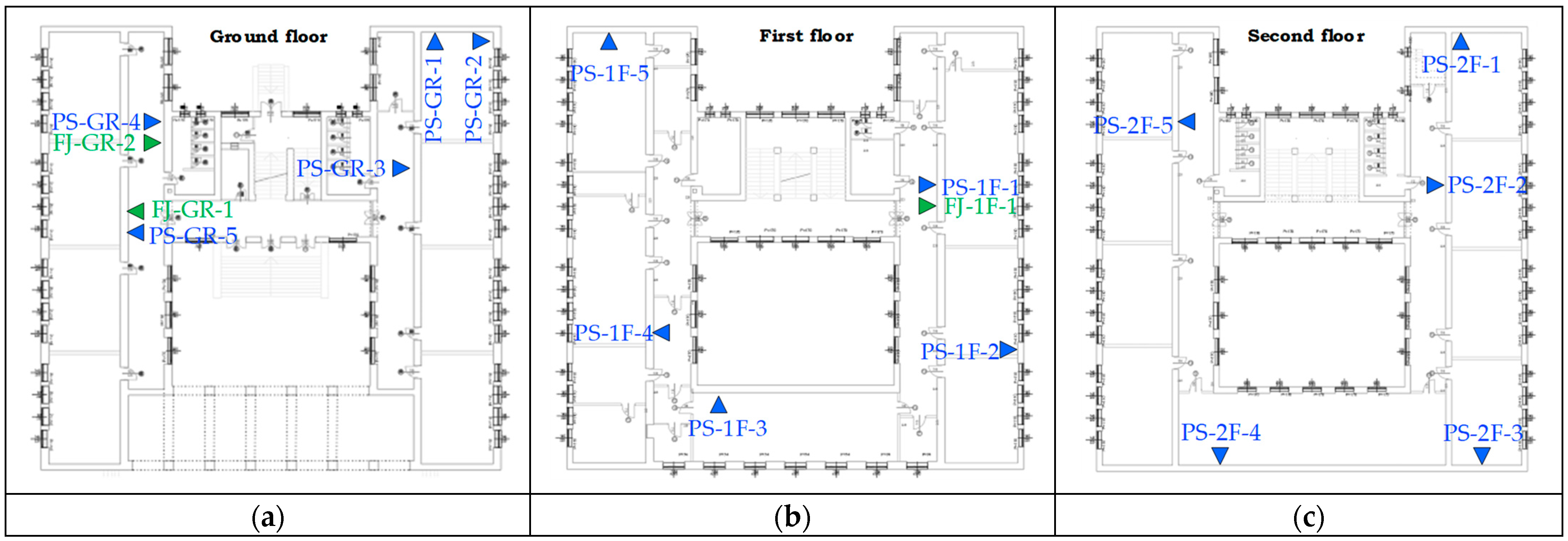
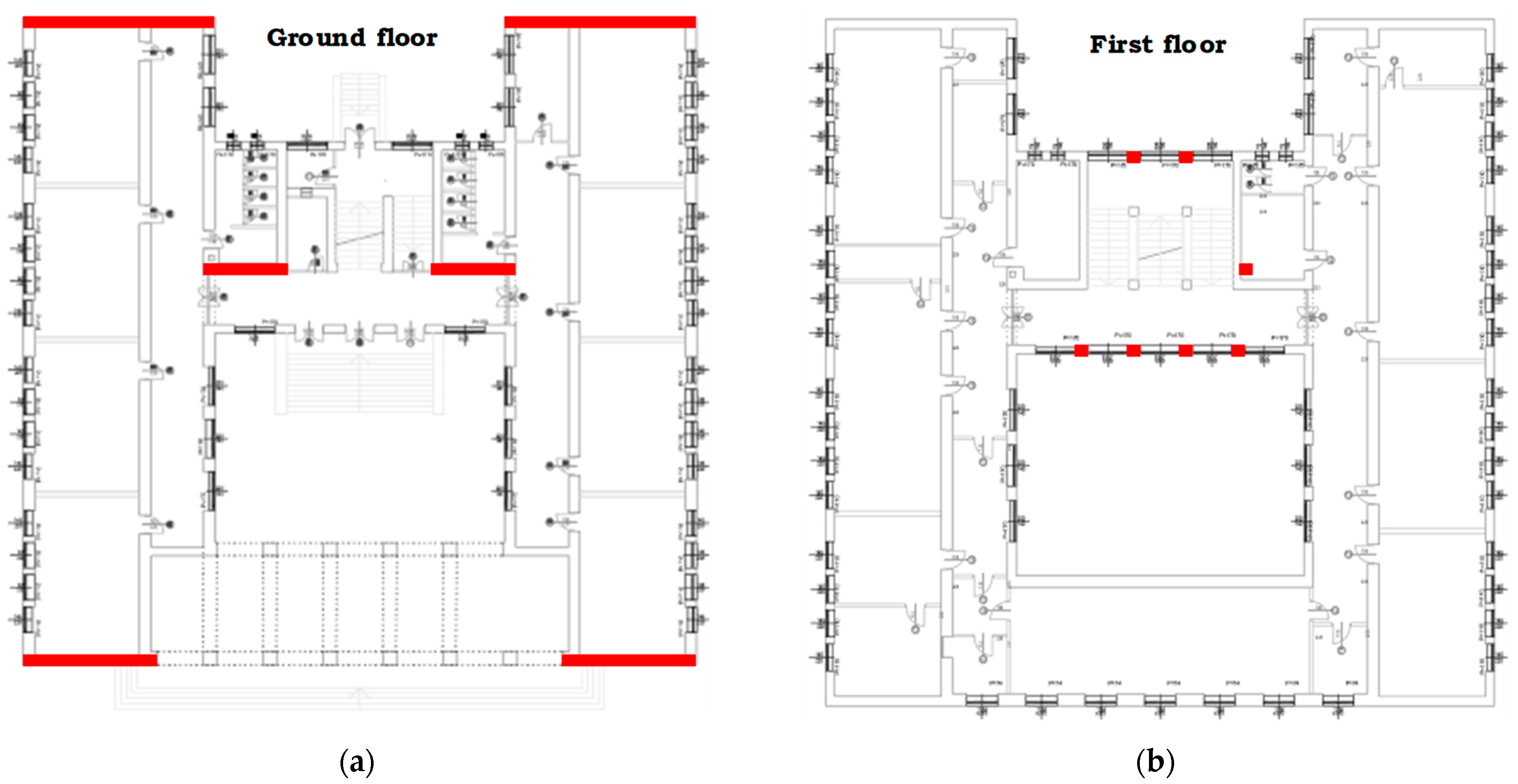
3.1. Visual Inspection
3.2. Determination of the Mechanical Properties of Masonry Walls
3.3. Dynamic Properties
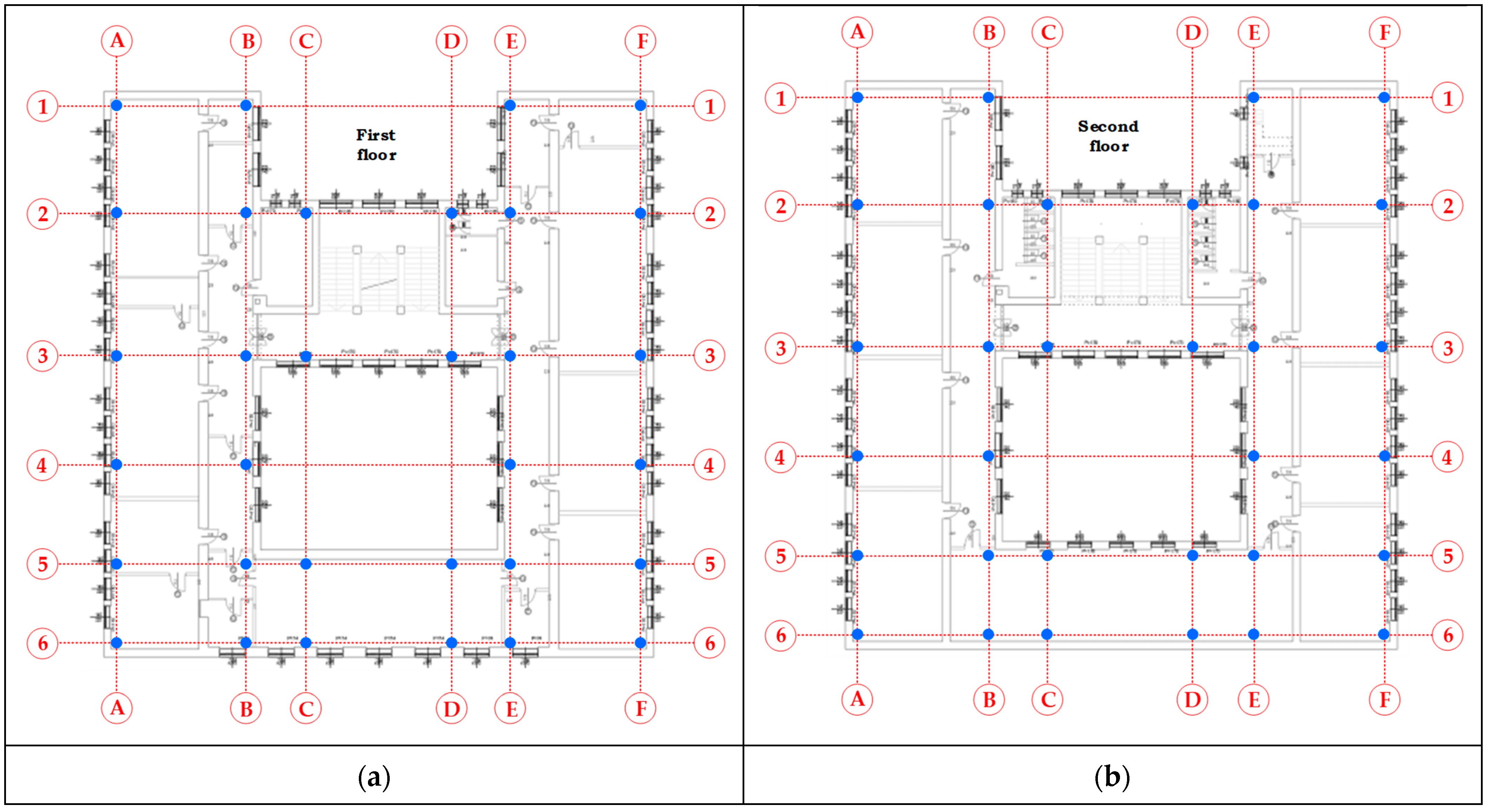
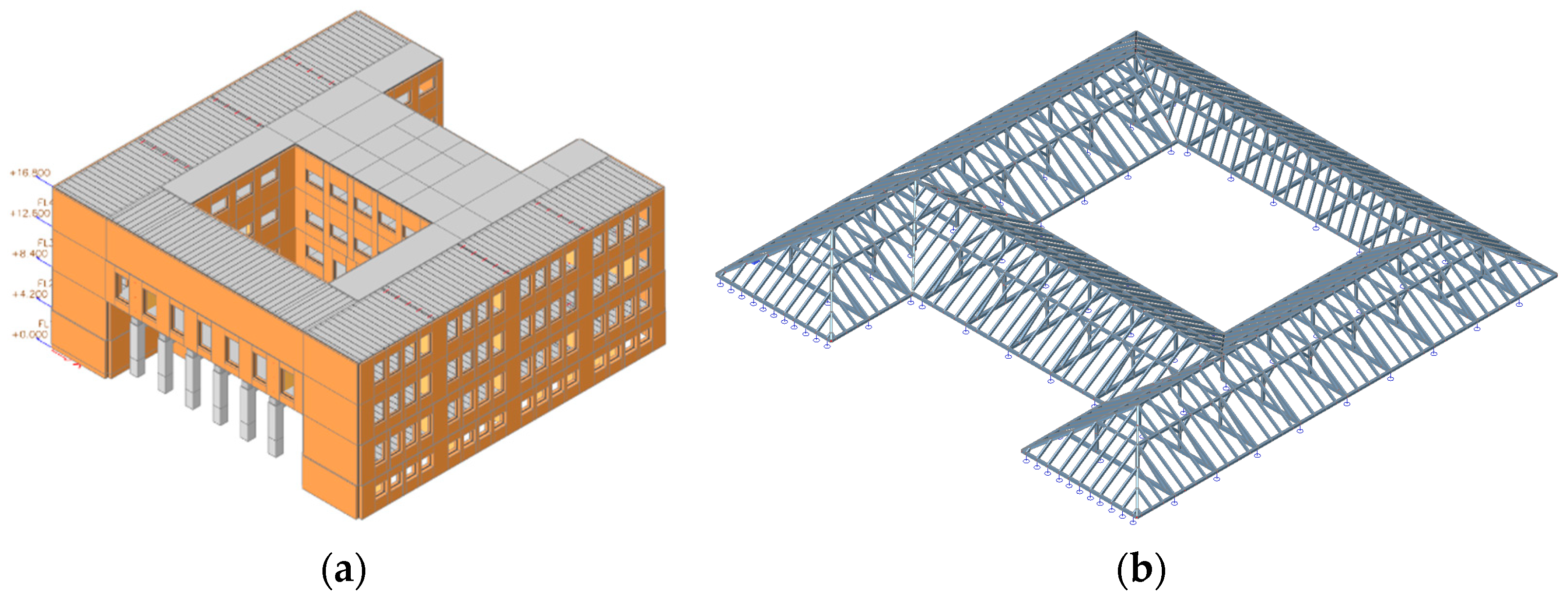
4. Numerical Analysis
4.1. Evaluation of the Initial Numerical Model
4.1.1. Evaluation of the Vertical Compression Stress
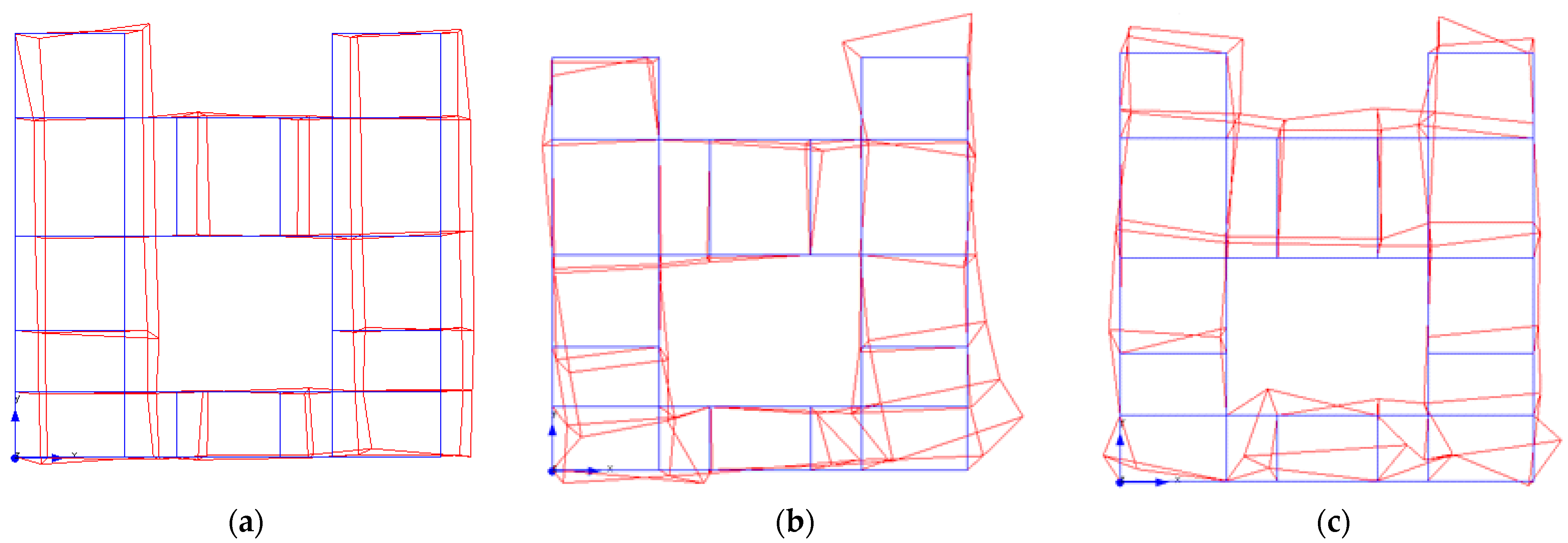
4.1.2. Evaluation Based on the Structural Dynamic Properties
5. Finite Element Model Updating
5.1. Analysis of the Influence of the Boundary Conditions—Model 1
5.2. Analysis of the Influence of the Partition Walls Modelling Method—Model 2
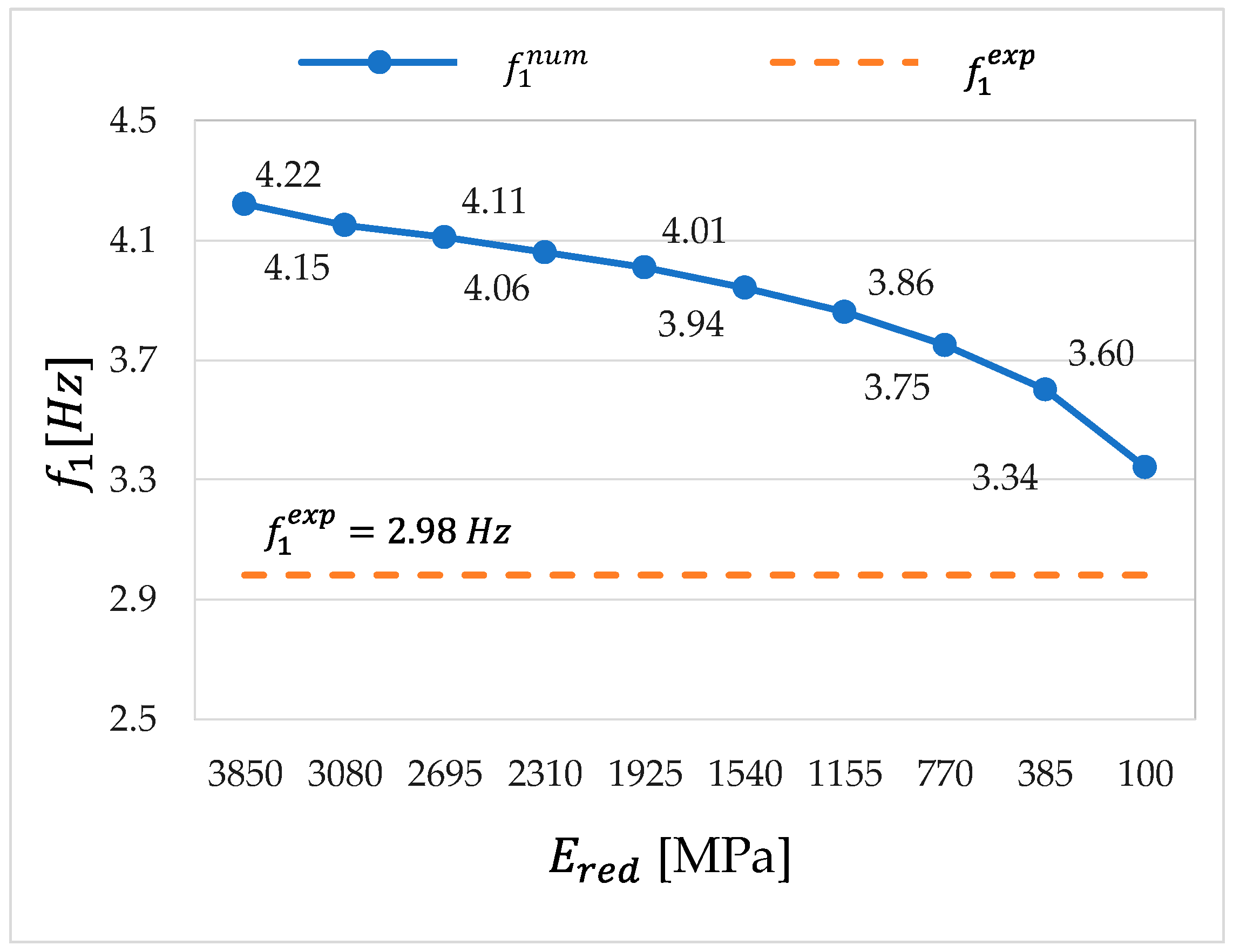
5.3. Analysis of the Influence of Damaged Load Bearing Walls with Reduced Elasticity Modulus—Model 3
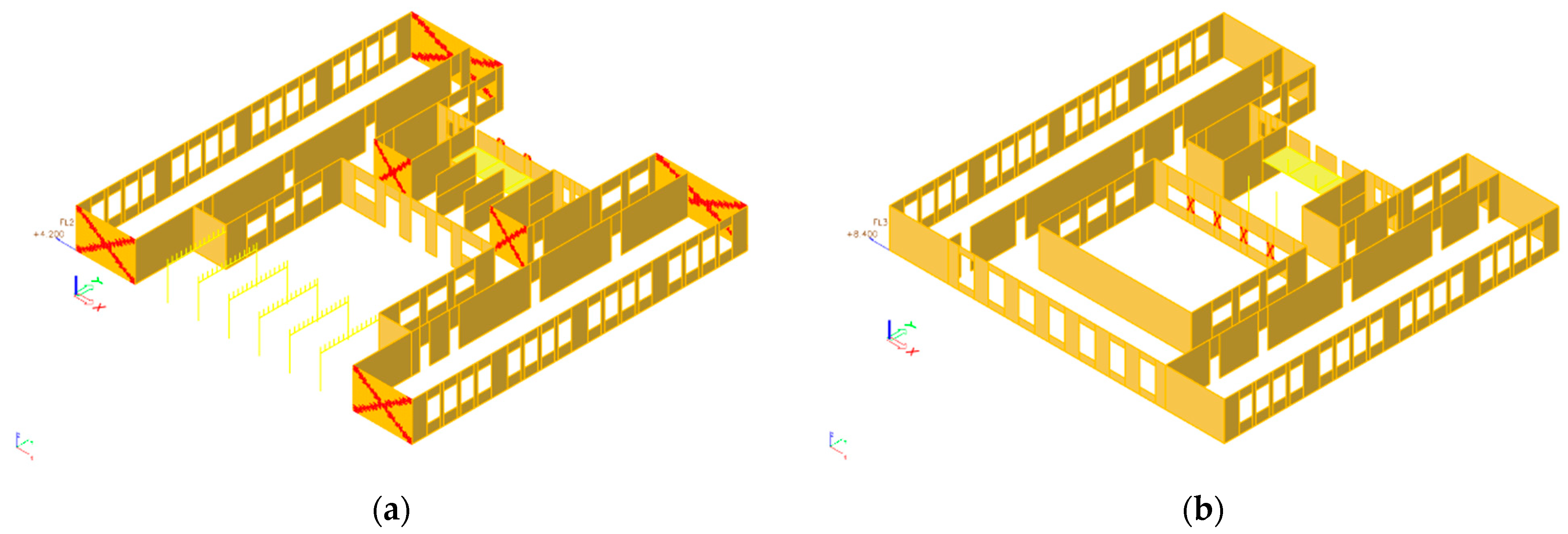
5.4. Analysis of Influence of Introducing the Diagonal Cracks in Damaged Load Bearing Walls—Model 4
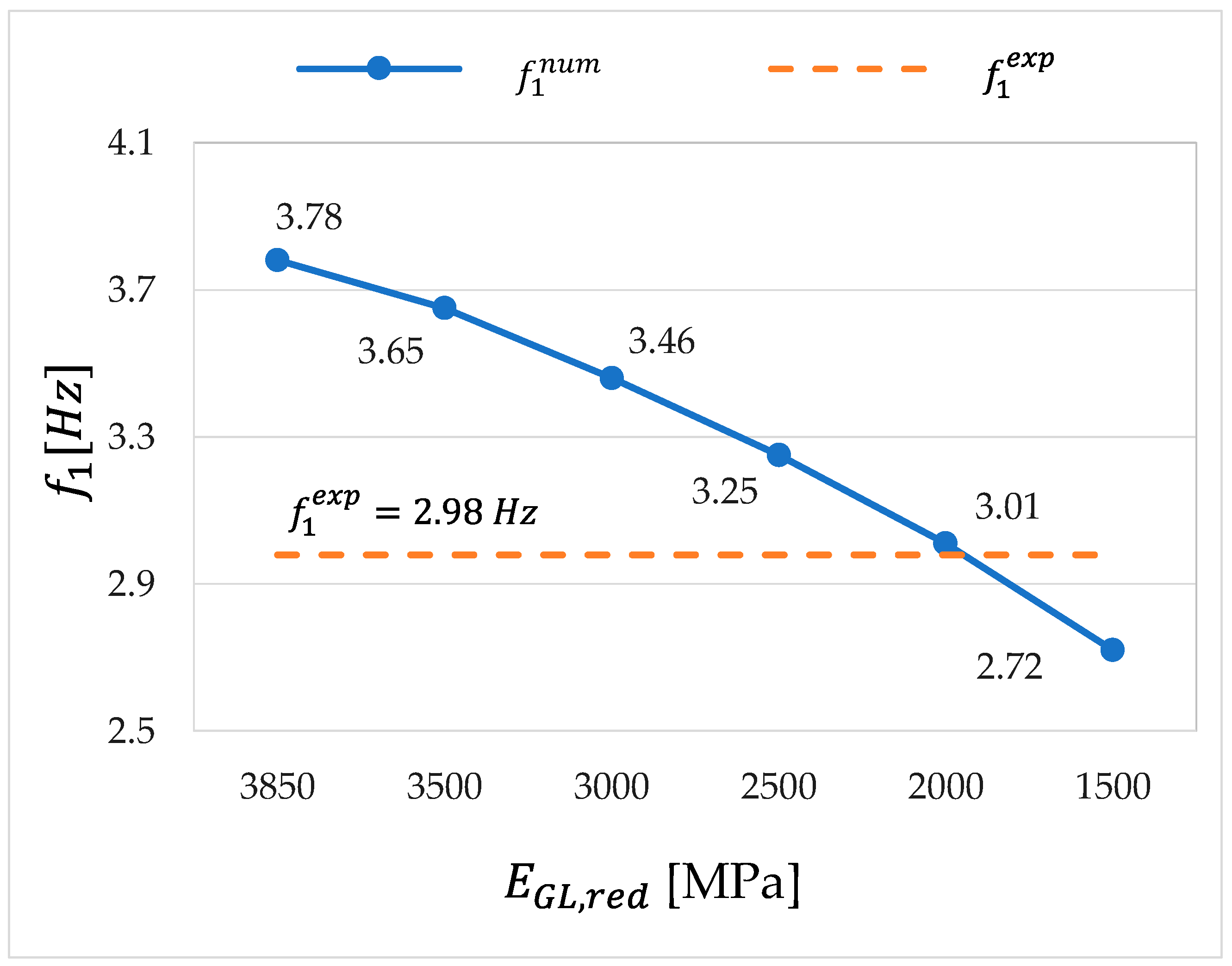
5.5. Analysis of the Influence of Global Elasticity Modulus’ Reduction—Model 5
6. Assessment of the Structural Condition before the Earthquake
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lulić, L.; Ožić, K.; Kišiček, T.; Hafner, I.; Stepinac, M. Post-earthquake damage assessment-case study of the educational building after the zagreb earthquake. Sustainability 2021, 13, 6353. [Google Scholar] [CrossRef]
- Simoen, E.; De Roeck, G.; Lombaert, G. Dealing with uncertainty in model updating for damage assessment: A review. Mech. Syst. Signal Process. 2015, 56, 123–149. [Google Scholar] [CrossRef]
- Catbas, F.N.; Brown, D.L.; Aktan, A.E. Use of Modal Flexibility for Damage Detection and Condition Assessment: Case Studies and Demonstrations on Large Structures. J. Struct. Eng. 2006, 132, 1699–1712. [Google Scholar] [CrossRef]
- Law, S.S.; Yong, D. Substructure methods for structural condition assessment. J. Sound Vib. 2011, 330, 3606–3619. [Google Scholar] [CrossRef]
- Lyu, M.; Zhu, X.; Yang, Q. Condition assessment of heritage timber buildings in operational environments. J. Civ. Struct. Health Monit. 2017, 7, 505–516. [Google Scholar] [CrossRef]
- Valente, M. Seismic behavior and damage assessment of two historical fortified masonry palaces with corner towers. Eng. Fail. Anal. 2022, 134, 106003. [Google Scholar] [CrossRef]
- Valente, M. Earthquake response and damage patterns assessment of two historical masonry churches with bell tower. Eng. Fail. Anal. 2023, 151, 107418. [Google Scholar] [CrossRef]
- Krolo, J.; Damjanović, D.; Duvnjak, I.; Smrkić-Frančić, M.; Bartolac, M.; Košćak, J. Methods for determining mechanical properties of walls. J. Croat. Assoc. Civ. Eng. 2021, 73, 127–140. [Google Scholar] [CrossRef]
- Ramos, L.F.; Marques, L.; Lourenço, P.B.; De Roeck, G.; Campos-Costa, A.; Roque, J. Monitoring historical masonry structures with operational modal analysis: Two case studies. Mech. Syst. Signal Process. 2010, 24, 1291–1305. [Google Scholar] [CrossRef]
- Ereiz, S.; Duvnjak, I.; Damjanović, D.; Bartolac, M. Analysis of seismic action on the tie rod system in historic buildings using finite element model updating. Buildings 2021, 11, 453. [Google Scholar] [CrossRef]
- Ereiz, S.; Duvnjak, I.; Fernando Jiménez-Alonso, J. Review of finite element model updating methods for structural applications. Structures 2022, 41, 684–723. [Google Scholar] [CrossRef]
- Marwala, T. Finite-Element-Model Updating Using Computional Intelligence Techniques: Applications to Structural Dynamics, 1st ed.; Springer: London, UK, 2010; ISBN 9781849963220. [Google Scholar]
- Chen, H.-P. Structural Health Monitoring of Large Civil Engineering Structures, 1st ed.; John Wiley and Sons Inc.: Oxford, UK, 2018; ISBN 9781119166627. [Google Scholar]
- Jarosińska, M.; Berczyński, S. Changes in Frequency and Mode Shapes Due to Damage in Steel–Concrete Composite Beam. Materials 2021, 14, 6232. [Google Scholar] [CrossRef] [PubMed]
- Borri, A.; Castori, G.; Corradi, M. Determination of Shear Strength of Masonry Panels Through Different Tests. Int. J. Archit. Herit. 2015, 9, 913–927. [Google Scholar] [CrossRef]
- Celano, T.; Argiento, L.U.; Ceroni, F.; Casapulla, C. Literature Review of the In-Plane Behavior of Masonry Walls: Theoretical vs. Experimental Results. Materials 2021, 14, 3063. [Google Scholar] [CrossRef] [PubMed]
- Lulić, L.; Stepinac, M.; Bartolac, M.; Lourenço, P.B. Review of the flat-jack method and lessons from extensive post-earthquake research campaign in Croatia. Constr. Build. Mater. 2023, 384, 131407. [Google Scholar] [CrossRef]
- Altunişik, A.C.; Adanur, S.; Genç, A.F.; Günaydin, M.; Okur, F.Y. Non-destructive testing of an ancient Masonry Bastion. J. Cult. Herit. 2016, 22, 1049–1054. [Google Scholar] [CrossRef]
- Cavalagli, N.; Comanducci, G.; Gentile, C.; Guidobaldi, M.; Saisi, A.; Ubertini, F. Detecting earthquake-induced damage in historic masonry towers using continuously monitored dynamic response-only data. Procedia Eng. 2017, 199, 3416–3421. [Google Scholar] [CrossRef]
- Gaile, L.; Ratnika, L.; Pakrastins, L. RC Medium-Rise Building Damage Sensitivity with SSI Effect. Materials 2022, 15, 1653. [Google Scholar] [CrossRef]
- Ji, X.; Fenves, G.L.; Kajiwara, K.; Nakashima, M. Seismic Damage Detection of a Full-Scale Shaking Table Test Structure. J. Struct. Eng. 2011, 137, 14–21. [Google Scholar] [CrossRef]
- Sivori, D.; Cattari, S.; Lepidi, M. A methodological framework to relate the earthquake-induced frequency reduction to structural damage in masonry buildings. Bull. Earthq. Eng. 2022, 20, 4603–4638. [Google Scholar] [CrossRef]
- Mendes, N.; Lourenço, P.B.; Campos-Costa, A. Shaking table testing of an existing masonry building: Assessment and improvement of the seismic performance. Earthq. Eng. Struct. Dyn. 2014, 43, 247–266. [Google Scholar] [CrossRef]
- Kaya, A.; Adanur, S.; Bello, R.A.; Genç, A.F.; Okur, F.Y.; Sunca, F.; Günaydin, M.; Altunişik, A.C.; Sevim, B. Post-earthquake damage assessments of unreinforced masonry (URM) buildings by shake table test and numerical visualization. Eng. Fail. Anal. 2023, 143, 106858. [Google Scholar] [CrossRef]
- Ohba, S.; Fukuda, T. Chnages in natural frequency of apartment buildings before and after the Hyogoken-Nanbu earthquake. In Proceedings of the 12th World Conference of Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000; pp. 1679–1687. [Google Scholar]
- Williams, E.F.; Heaton, T.H.; Zhan, Z.; Lambert, V.R. Variability in the Natural Frequencies of a Nine-Story Concrete Building from Seconds to Decades. Seism. Rec. 2022, 2, 237–247. [Google Scholar] [CrossRef]
- Pepi, C.; Cavalagli, N.; Gusella, V.; Gioffrè, M. Damage detection via modal analysis of masonry structures using shaking table tests. Earthq. Eng. Struct. Dyn. 2021, 50, 2077–2097. [Google Scholar] [CrossRef]
- Ramos, L.F.; Laurenco, P.B.; De Roeck, G.; Campos-Costa, A. Structural Analysis of Historic Construction: Preserving Safety and Significance; Two Volume Set; D’Ayala, D., Fodde, E., Eds.; CRC Press: Boca Raton, FL, USA, 2008; ISBN 9780429151965. [Google Scholar]
- Cunha, Á.; Caetano, E. Experimental Modal Analysis of Civil Engineering Structures. Sound Vib. 2006, 6, 12–20. [Google Scholar]
- Genç, A.F.; Ertürk, E.; Altunişik, A.C.; Günaydin, M.; Okur, F.Y. Effect of Damping Ratios on the Seismic Behavior of a Historical Masonry Guesthouse Building. Recep Tayyip Erdogan Univ. J. Sci. Eng. 2021, 2, 60–71. [Google Scholar] [CrossRef]
- Cruz, C.; Miranda, E. Damping Ratios of the First Mode for the Seismic Analysis of Buildings. J. Struct. Eng. 2021, 147, 04020300. [Google Scholar] [CrossRef]
- Işık, E.; Avcil, F.; Büyüksaraç, A.; İzol, R.; Hakan Arslan, M.; Aksoylu, C.; Harirchian, E.; Eyisüren, O.; Arkan, E.; Şakir Güngür, M.; et al. Structural damages in masonry buildings in Adıyaman during the Kahramanmaraş (Turkiye) earthquakes (Mw 7.7 and Mw 7.6) on 6 February 2023. Eng. Fail. Anal. 2023, 151, 107405. [Google Scholar] [CrossRef]
- Furukawa, A.; Kiyono, J.; Parajuli, R.R.; Parajuli, H.R.; Toki, K. Evaluation of Damage to a Historic Masonry Building in Nepal through Comparison of Dynamic Characteristics before and after the 2015 Gorkha Earthquake. Front. Built Environ. 2017, 3, 62. [Google Scholar] [CrossRef]
- Murty, C.V.R.; Goswami, R.; Vijayanarayanan, A.R.; Mehta, V. Some Concepts in Earthquake Behaviour of Buildings; Gujarat State Disaster Management Authority: Gujarat, India, 2012. [Google Scholar]
- Keshmiry, A.; Hassani, S.; Mousavi, M.; Dackermann, U. Effects of Environmental and Operational Conditions on Structural Health Monitoring and Non-Destructive Testing: A Systematic Review. Buildings 2023, 13, 918. [Google Scholar] [CrossRef]
- Kassem, M.M.; Beddu, S.; Ooi, J.H.; Tan, C.G.; Mohamad El-Maissi, A.; Mohamed Nazri, F. Assessment of Seismic Building Vulnerability Using Rapid Visual Screening Method through Web-Based Application for Malaysia. Buildings 2021, 11, 485. [Google Scholar] [CrossRef]
- Wang, G.; Li, Y.; Zheng, N.; Ingham, J.M. Testing and modelling the in-plane seismic response of clay brick masonry walls with boundary columns made of precast concrete interlocking blocks. Eng. Struct. 2017, 131, 513–529. [Google Scholar] [CrossRef]







| Floor, m | Measurement Location | |||||
|---|---|---|---|---|---|---|
| PS-m-1 | PS-m-2 | PS-m-3 | PS-m-4 | PS-m-5 | ||
| GR | 0.747 | 0.667 | 0.717 | 0.968 | 0.985 | 0.817 ± 0.149 |
| 1F | 0.860 | 0.743 | 0.340 | 0.731 | 0.588 | 0.652 ± 0.199 |
| 2F | 0.521 | 0.492 | 0.577 | 0.449 | 0.536 | 0.515 ± 0.048 |
[MPa] | [MPa] | [MPa] | ||||
|---|---|---|---|---|---|---|
| Floor, m | Measurement Point | Measurement Point | Measurement Point | |||
| FJ-m-1 | FJ-m-2 | FJ-m-1 | FJ-m-2 | FJ-m-1 | FJ-m-2 | |
| GR | 0.54 | 0.43 | 4020 | 4122 | 0.171 | 0.825 |
| 1F | 0.59 | - | 3470 | - | 0.134 | |
| Mean value | 3850 | 0.377 | ||||
| Mode i | |
|---|---|
| 1 | 2.972 ± 0.10 |
| 2 | 3.742 ± 0.09 |
| 3 | 4.275 ± 0.27 |
| Elements | Value |
|---|---|
| Load bearing masonry walls (LBMW) | |
| * Unit mass, [kN/m3] | 18 |
| ** Modulus of elasticity, [MPa] | 3850 |
| ** Poisson coefficient, [-] | 0.25 |
| ** Shear modulus, [MPa] | 1540 |
| ** Characteristic compressive strength [MPa] | 2.66 |
| ** Partition masonry walls (PMW) | |
| Unit mass, [kN/m3] | 13 |
| Modulus of elasticity, [MPa] | 4600 |
| Poisson coefficient, [-] | 0.05 |
| Shear modulus, [MPa] | 2190 |
| Characteristic compressive strength [MPa] | 1.70 |
| * Beams, Staircases, Rigid Elements (S) | |
| Unit mass, [kN/m3] | 25 |
| Modulus of elasticity, [MPa] | 33,000 |
| Poisson coefficient, [-] | 0.2 |
| Shear modulus, [Mpa] | 13,750 |
| * Stone columns (SC) | |
| Unit mass, [kN/m3] | 25 |
| Modulus of elasticity, [Mpa] | 31,000 |
| Poisson coefficient, [-] | 0.2 |
| Shear modulus, [Mpa] | 12,917 |
| Floor, m | Measurement Point | [MPa] | [MPa] | [MPa] |
|---|---|---|---|---|
| GR | FJ-GR-1 | 0.54 | 0.55 | 0.01 |
| GR | FJ-GR-2 | 0.43 | 0.35 | 0.08 |
| 1F | FJ-1F-1 | 0.59 | 0.38 | 0.21 |
| Mode, i | [Hz] | [Hz] | [%] |
|---|---|---|---|
| 1 | 2.98 | 4.22 | −41.6 |
| 2 | 3.96 | 5.75 | −45.2 |
| 3 | 4.45 | 6.42 | −44.3 |
| Mode, i | [Hz] | [Hz] | [%] |
|---|---|---|---|
| 1 | 2.98 | 3.78 | −26.8 |
| 2 | 3.96 | 5.29 | −33.6 |
| 3 | 4.45 | 6.29 | −41.3 |
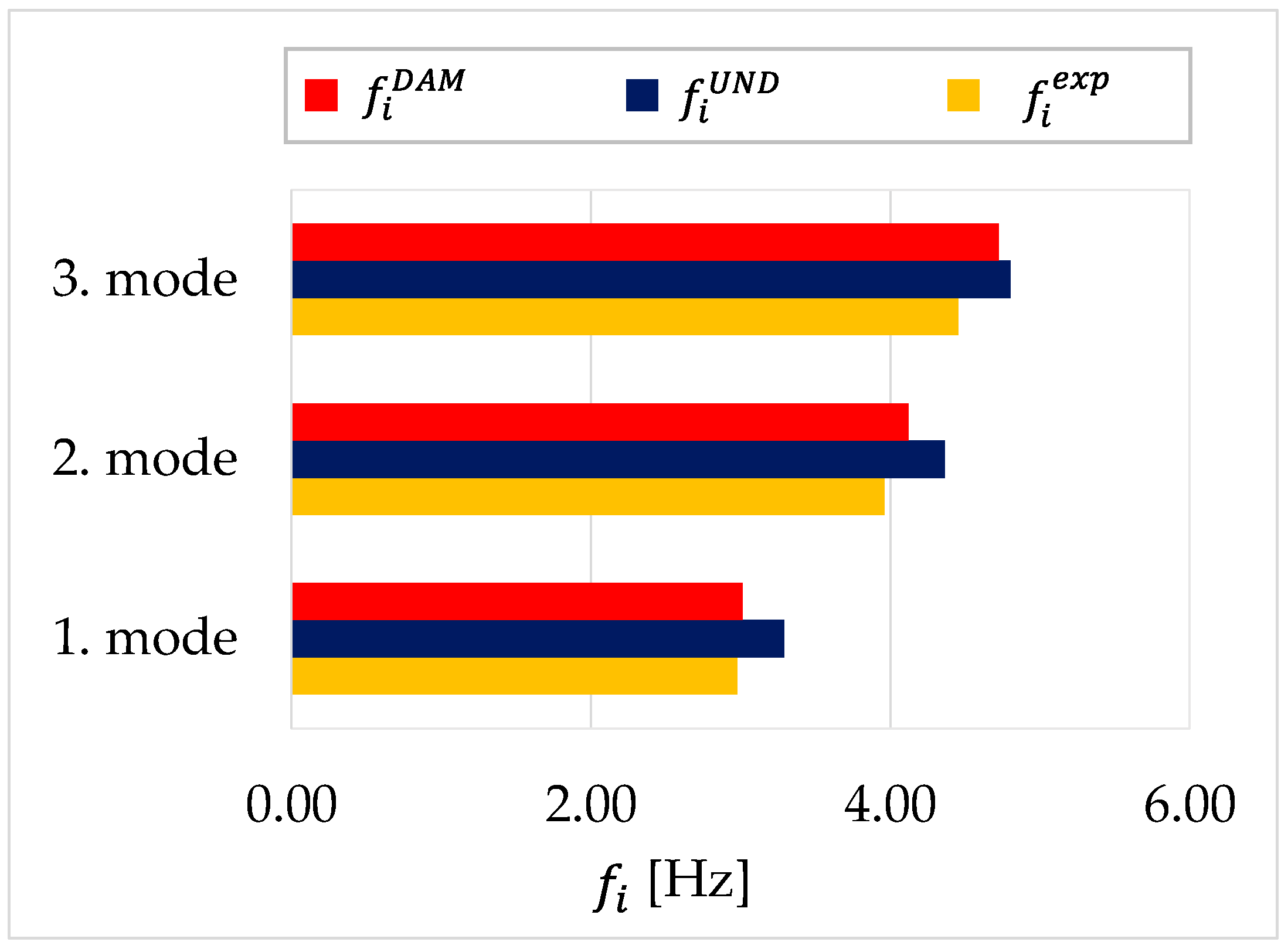
| Mode, i | [Hz] | [Hz] | [%] |
|---|---|---|---|
| 1 | 2.98 | 3.01 | −0.97 |
| 2 | 3.96 | 4.12 | −4.04 |
| 3 | 4.45 | 4.72 | −6.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duvnjak, I.; Ereiz, S.; Smrkić, M.F.; Damjanović, D. Post-Earthquake Dynamic Performance of Intact Masonry Building Based on Finite Element Model Updating. Appl. Sci. 2023, 13, 9042. https://doi.org/10.3390/app13159042
Duvnjak I, Ereiz S, Smrkić MF, Damjanović D. Post-Earthquake Dynamic Performance of Intact Masonry Building Based on Finite Element Model Updating. Applied Sciences. 2023; 13(15):9042. https://doi.org/10.3390/app13159042
Chicago/Turabian StyleDuvnjak, Ivan, Suzana Ereiz, Marina Frančić Smrkić, and Domagoj Damjanović. 2023. "Post-Earthquake Dynamic Performance of Intact Masonry Building Based on Finite Element Model Updating" Applied Sciences 13, no. 15: 9042. https://doi.org/10.3390/app13159042
APA StyleDuvnjak, I., Ereiz, S., Smrkić, M. F., & Damjanović, D. (2023). Post-Earthquake Dynamic Performance of Intact Masonry Building Based on Finite Element Model Updating. Applied Sciences, 13(15), 9042. https://doi.org/10.3390/app13159042








