Identical Parallel Machine Scheduling Considering Workload Smoothness Index
Abstract
1. Introduction
- (1)
- We introduce smoothness index to identical parallel machine scheduling and prove the NP-hardness of the considered problem.
- (2)
- A mathematical model with a minimizing smoothness index is established, and both upper and lower bounds are provided.
- (3)
- To quickly find high-quality feasible solutions, an efficient genetic algorithm and an improved list scheduling algorithm are proposed. Numerical experiments show that the proposed genetic algorithm can output high-quality feasible solutions for small-scale instances. For large-scale instances, the proposed improved list scheduling algorithm outperforms the list scheduling algorithm based on LPT, SPT, and RPT rules. Please refer to Section 6 for specific details.
2. Literature Review
2.1. Parallel Machine Workload Balancing Problem
2.2. Smoothness Index in the Assembly Line Environment
3. Problem Statement and Mathematical Model
3.1. Problem Statement
- (1)
- Each machine can only process one job at a time;
- (2)
- The setup time of processing any job on each machine is negligible;
- (3)
- All the machines are available for processing jobs from time 0.
3.1.1. Input Parameters
- : set of machines indexed by i, i.e., ;
- : set of jobs indexed by j, i.e., ;
- : the processing time of job ;
- : the given maximum workload limitation of machines.
3.1.2. Decision Variables
- : a binary variable equal to 1 if job is processed on machine and 0 otherwise;
- : a binary variable equal to 1 if jobs and are processed on machine and 0 otherwise;
- : the workload of machine .
3.2. Mathematical Model
3.3. Objective Function Linearization
4. Theoretical Analysis
4.1. NP-Hardness
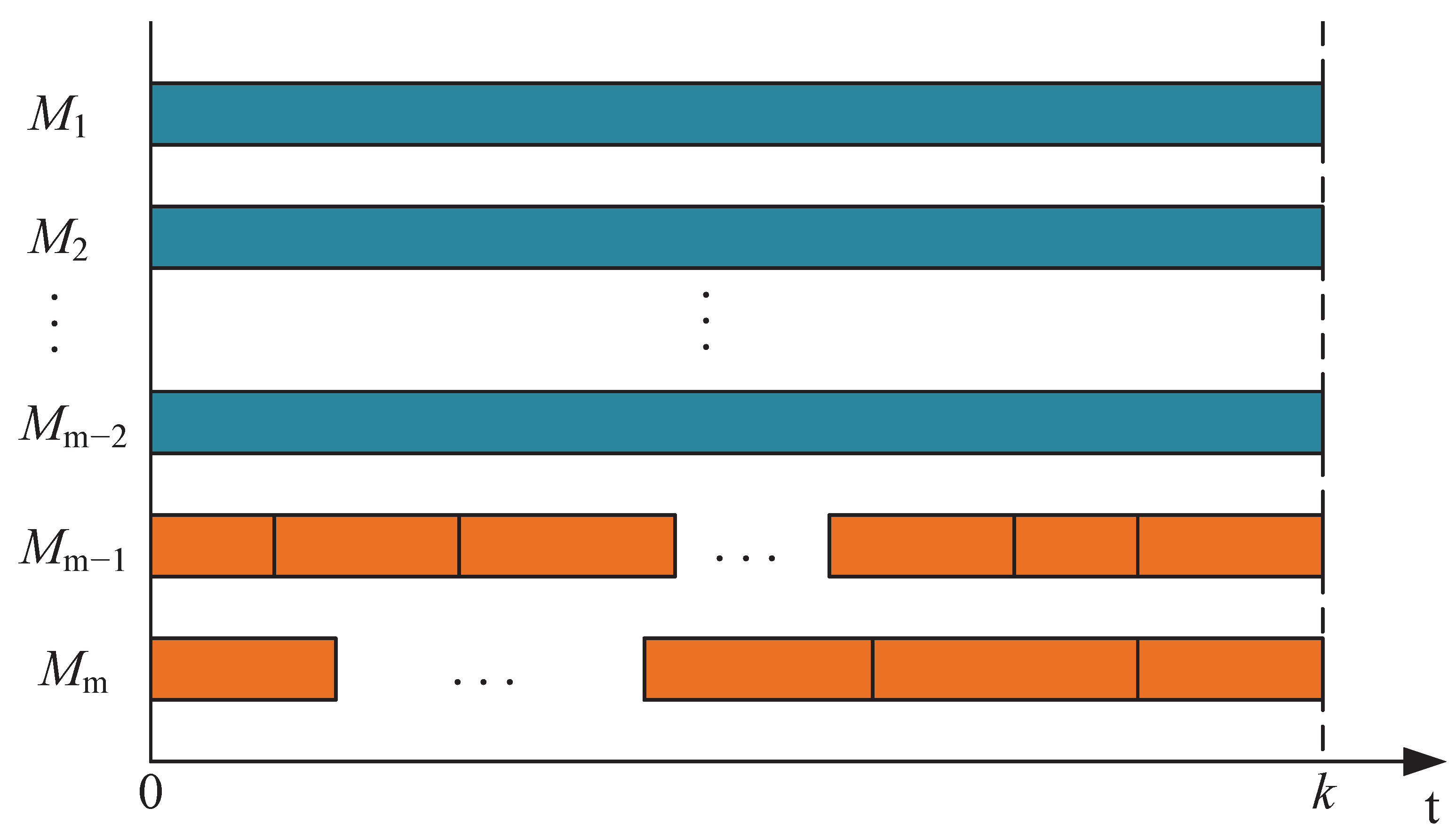
4.2. Upper and Lower Bounds
5. Heuristic Algorithms
5.1. Genetic Algorithm Based on Bounding Mechanisms
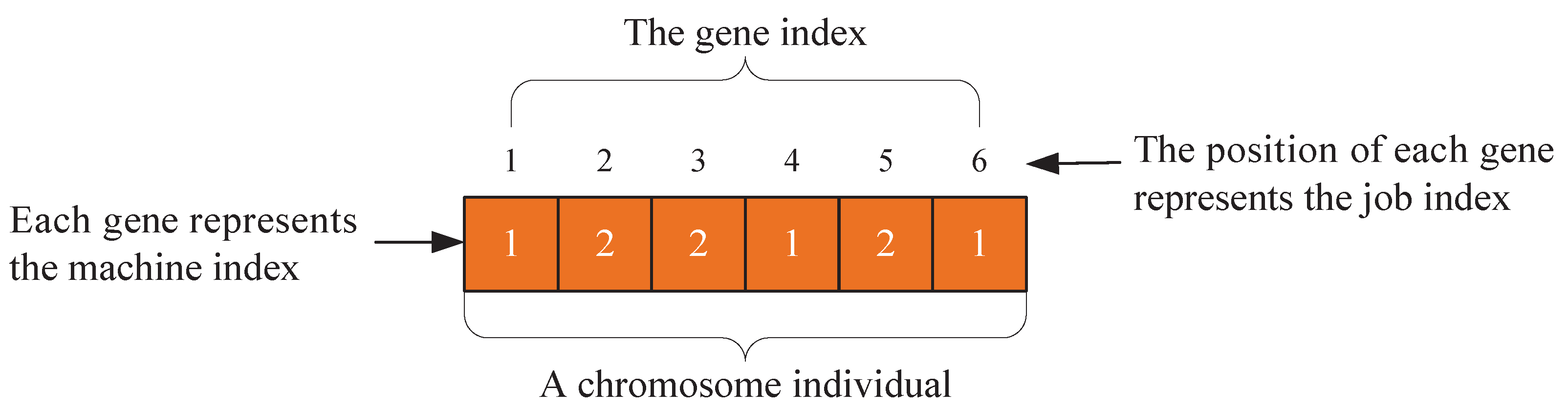
5.1.1. Chromosome Representation
5.1.2. Fitness Function
5.1.3. Initialization of Chromosomes
5.1.4. Crossover and Mutation
| Algorithm 1 algorithm |
| Require: |
|
| %Define a machine set κ in which the current workload of all jobs plus is less than or equal to ω |
|
| %A machine is randomly selected in set κ to process job |
|
| %If the objective value of the corresponding chromosome is larger than the given upper bound, a new chromosome is generated to replace it |
|
| %If the corresponding objective value of the chromosome is equal to the given lower bound, copies of that chromosome will be used as the initial population |
|
5.2. List Scheduling Algorithms
| Algorithm 2 List scheduling algorithms (LSAs) |
| Require: , |
|
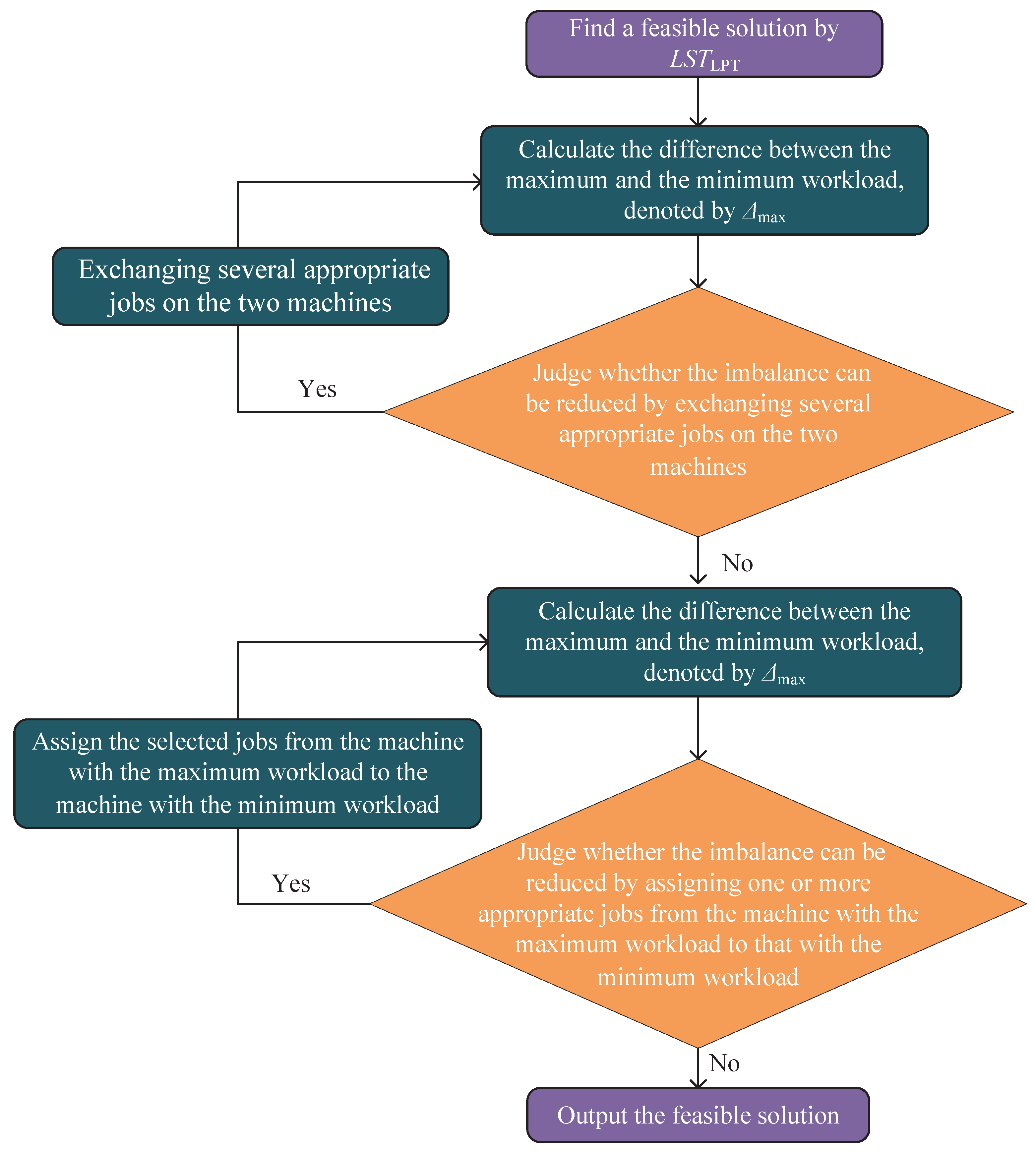
5.3. An Improved List Scheduling Algorithm
| Algorithm 3 algorithm |
| Require: |
|
6. Numerical Experiments
- The number of the population size and iterations are 200 and 100, respectively;
- The probability of crossover and mutation are 0.6 and 0.4, respectively.
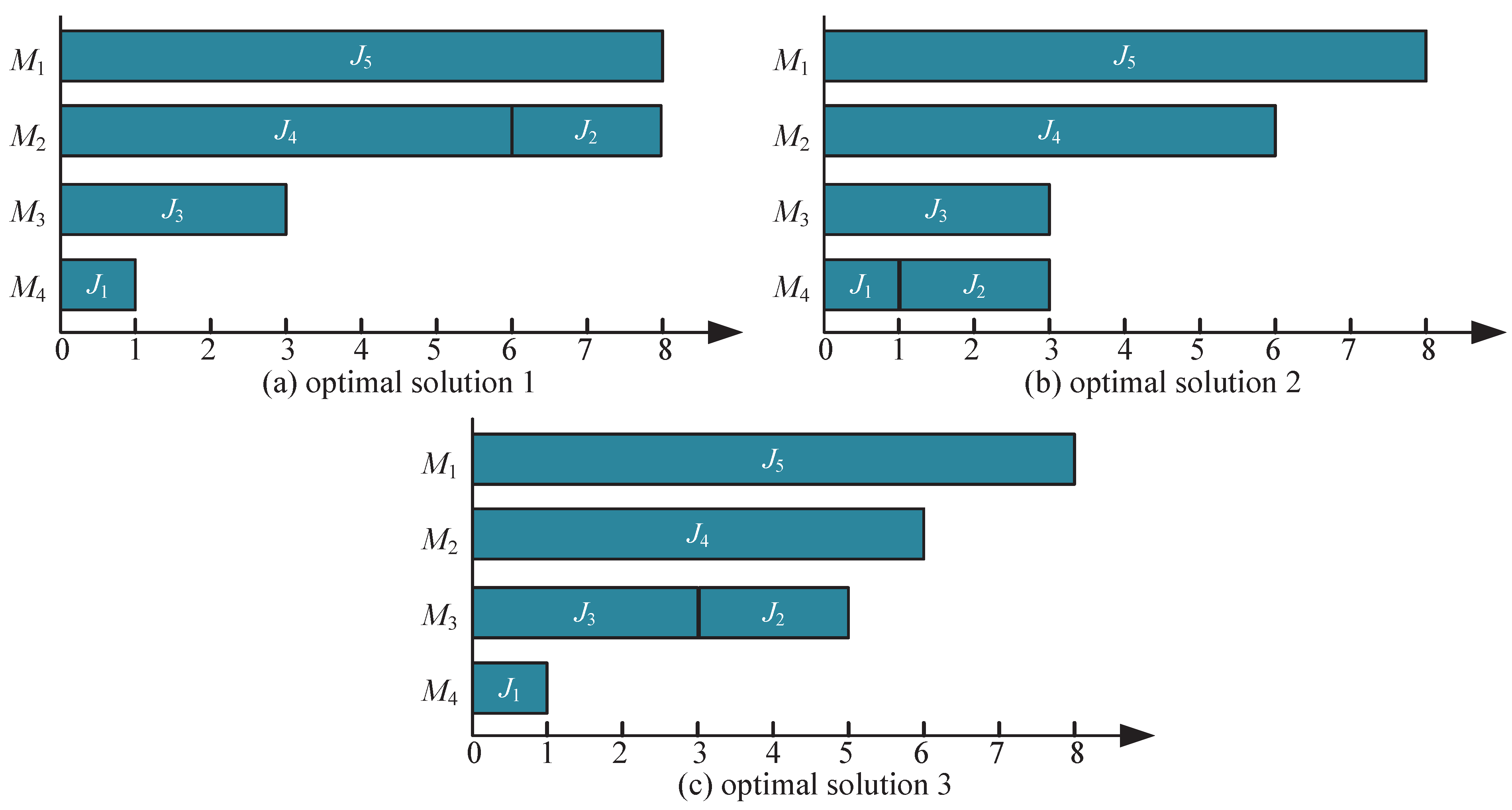
6.1. Small Job Instances ()
6.2. Large Job Instances ()
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, X.; Chu, F.; Zheng, F.; Chu, C.; Liu, M. Parallel machine scheduling with stochastic release times and processing times. Int. J. Prod. Res. 2020, 59, 6327–6346. [Google Scholar] [CrossRef]
- Kim, J.; Kim, H.J. Parallel machine scheduling with multiple processing alternatives and sequence-dependent setup times. Int. J. Prod. Res. 2020, 59, 5438–5453. [Google Scholar] [CrossRef]
- Mokotoff, E. Parallel machine scheduling problems: A survey. Asia-Pac. J. Oper. Res. 2001, 18, 193–242. [Google Scholar]
- Muter, I. Exact algorithms to minimize makespan on single and parallel batch processing machines. Eur. J. Oper. Res. 2020, 285, 470–483. [Google Scholar] [CrossRef]
- Rakrouki, M.A.; Kooli, A.; Chalghoumi, S.; Ladhari, T. A branch-and-bound algorithm for the two-machine total completion time flowshop problem subject to release dates. Oper. Res. 2020, 20, 21–35. [Google Scholar] [CrossRef]
- Strusevich, V.A. Approximation algorithms for makespan minimization on identical parallel machines under resource constraints. J. Oper. Res. Soc. 2020, 72, 2135–2146. [Google Scholar] [CrossRef]
- Yin, Y.; Chen, Y.; Qin, K.; Wang, D. Two-agent scheduling on unrelated parallel machines with total completion time and weighted number of tardy jobs criteria. J. Sched. 2019, 22, 315–333. [Google Scholar] [CrossRef]
- Christ, Q.; Dauzère-Pxexrxexs, S.; Lepelletier, G. An iterated min-max procedure for practical workload balancing on non-Identical parallel machines in manufacturing systems. Eur. J. Oper. Res. 2019, 279, 419–428. [Google Scholar] [CrossRef]
- Ouazene, Y.; Nguyen, N.Q.; Yalaoui, F. Workload balancing on identical parallel machines: Theoretical and computational analysis. Appl. Sci. 2021, 11, 3677. [Google Scholar] [CrossRef]
- Xu, G.Y.; Guan, Z.L.; Yue, L.; Mumtaz, J.; Liang, J. Modeling and optimization for multi-objective nonidentical parallel machining line scheduling with a jumping process operation constraint. Symmetry 2021, 13, 1521. [Google Scholar] [CrossRef]
- Rajakumar, S.; Arunachalam, V.P.; Selladurai, V. Workflow balancing strategies in parallel machine scheduling. Int. J. Adv. Manuf. Technol. 2004, 23, 366–374. [Google Scholar] [CrossRef]
- Keskinturk, T.; Yildirim, M.B.; Barut, M. An ant colony optimization algorithm for load balancing in parallel machines with sequence-dependent setup times. Comput. Oper. Res. 2012, 39, 1225–1235. [Google Scholar] [CrossRef]
- Moon, D.H.; Kim, D.K.; Jung, J.Y. An operator load-balancing problem in a semi-automatic parallel machine shop. Comput. Ind. Eng. 2004, 46, 355–362. [Google Scholar] [CrossRef]
- Wang, H.; Alidaee, B. Unrelated parallel machine selection and job scheduling with the objective of minimizing total workload and machine fixed costs. IEEE Trans. Autom. Sci. Eng. 2018, 15, 1955–1963. [Google Scholar] [CrossRef]
- Moodie, C.L.; Young, H.H. A heuristic method of assembly line balancing for assumptions of constant or variable work element times. J. Ind. Eng. 1965, XVI, 23–29. [Google Scholar]
- Ouazene, Y.; Yalaoui, F.; Chehade, H.; Yalaoui, A. Workload balancing in identical parallel machine scheduling using a mathematical programming method. Int. J. Comput. Intell. Syst. 2013, 7 (Suppl. S1), 58–67. [Google Scholar] [CrossRef]
- Yildirim, M.; Duman, E.; Krishna, K.; Senniappan, K. Parallel machine scheduling with load balancing and sequence dependent setups. Int. J. Oper. Res. 2007, 1, 42–49. [Google Scholar]
- Ho, J.C.; Tseng, T.L.; Ruiz-Torres, A.J.; Lopez, F.J. Minimizing the normalized sum of square for workload deviations on m parallel processors. Comput. Ind. Eng. 2009, 51, 186–192. [Google Scholar] [CrossRef]
- Walter, R.; Lawrinenko, A. A note on minimizing the normalized sum of squared workload deviations on m parallel processors. Comput. Ind. Eng. 2014, 75, 257–259. [Google Scholar] [CrossRef]
- Schwerdfeger, S.; Walter, R. A fast and effective subset sum based improvement procedure for workload balancing on identical parallel machines. Comput. Oper. Res. 2016, 73, 84–91. [Google Scholar] [CrossRef]
- Akturk, M.S.; Ilhan, T. Single CNC machine scheduling with controllable processing times to minimize total weighted tardiness. Comput. Oper. Res. 2011, 38, 771–781. [Google Scholar] [CrossRef]
- Foumani, M.; Razeghi, A.; Smith-Miles, K. Stochastic optimization of two-machine flow shop robotic cells with controllable inspection times: From theory toward practice. Robot. Comput.-Integr. Manuf. 2020, 61, 101822. [Google Scholar] [CrossRef]
- Kim, Y.J.; Kim, Y.K.; Cho, Y. A heuristic-based genetic algorithm for workload smoothing in assembly lines. Comput. Oper. Res. 1998, 25, 99–111. [Google Scholar] [CrossRef]
- Scholl, A. Balancing and sequencing of assembly lines contributions to management science. Physica 1999, 2, 23–25. [Google Scholar]
- Emde, S.; Boysen, N.; Scholl, A. Balancing mixed-model assembly lines: A computational evaluation of objectives to smoothen workload. Int. J. Prod. Res. 2009, 48, 3173–3191. [Google Scholar] [CrossRef]
- Nearchou, A.C. Maximizing production rate and workload smoothing in assembly lines using particle swarm optimization. Int. J. Prod. Econ. 2011, 129, 242–250. [Google Scholar] [CrossRef]
- Azizoǧlu, M.; İmat, S. Workload smoothing in simple assembly line balancing. Comput. Oper. Res. 2018, 89, 51–57. [Google Scholar] [CrossRef]
- Finco, S.; Battini, D.; Delorme, X.; Persona, A.; Sgarbossa, F. Workers’ rest allowance and smoothing of the workload in assembly lines. Int. J. Prod. Res. 2019, 58, 1255–1270. [Google Scholar] [CrossRef]
- Defersha, F.M.; Rooyani, D. An efficient two-stage genetic algorithm for a flexible job-shop scheduling problem with sequence dependent attached/detached setup, machine release date and lag-time. Comput. Ind. Eng. 2020, 147, 106605. [Google Scholar] [CrossRef]
- Dunbar, M.; Belieres, S.; Shukla, N.; Amirghasemi, M.; Perez, P.; Mishra, N. A genetic column generation algorithm for sustainable spare part delivery: Application to the Sydney DropPoint network. Ann. Oper. Res. 2020, 290, 923–941. [Google Scholar] [CrossRef]
- Zheng, F.; Man, X.; Chu, F.; Liu, M.; Chu, C. Two yard crane scheduling with dynamic processing time and interference. IEEE Trans. Intell. Transp. Syst. 2018, 19, 3775–3784. [Google Scholar] [CrossRef]
- Rajakumar, S.; Arunachalam, V.P.; Selladurai, V. Workflow balancing in parallel machines through genetic algorithm. Int. J. Adv. Manuf. Technol. 2007, 33, 1212–1221. [Google Scholar] [CrossRef]
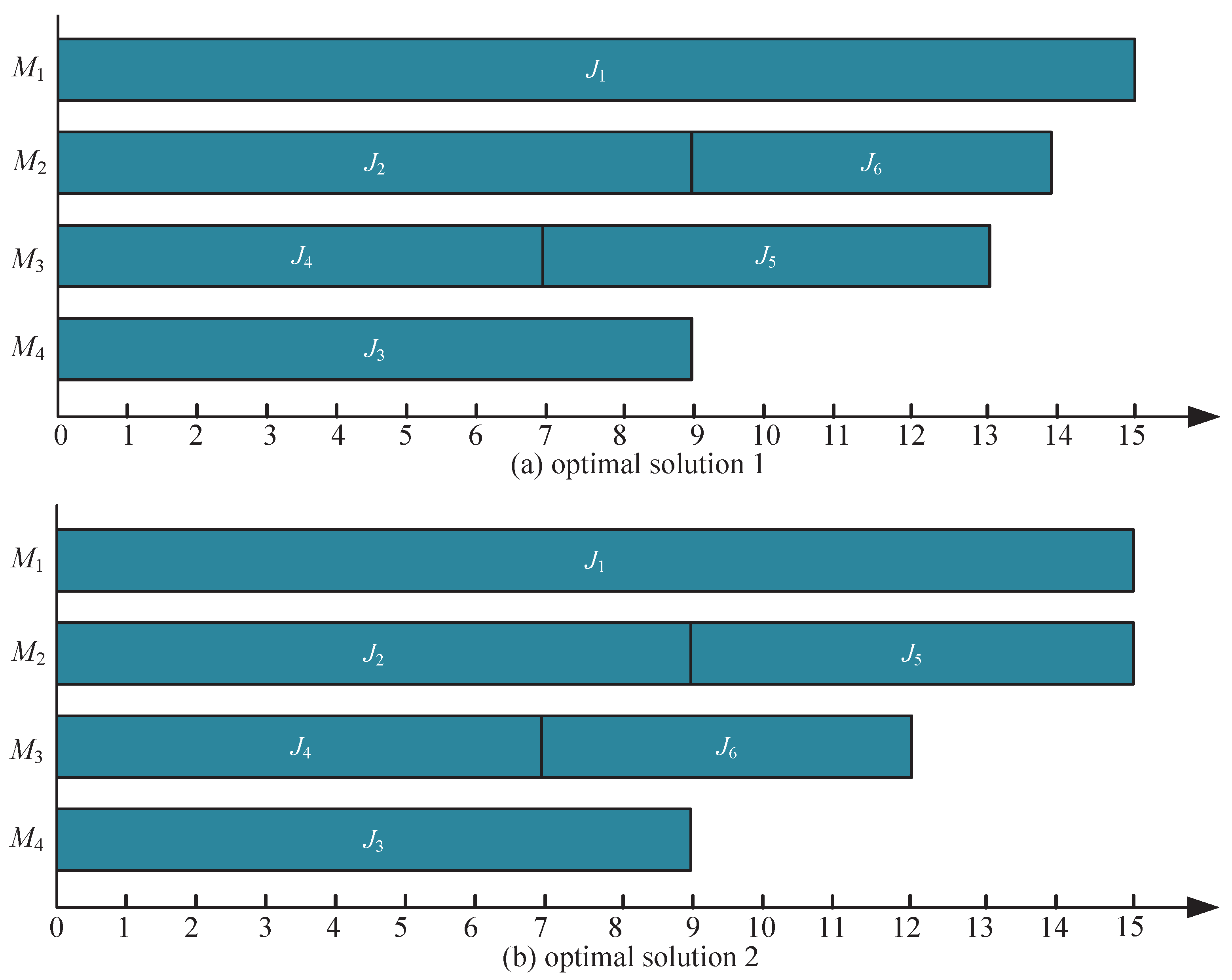

| (m, n) | CPLEX | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Average | |||||||||||
| (m, n) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Time (s) | Time (s) | Time (s) | Time (s) | Time (s) | ||||||||||
| <1 | <1 | <1 | 1 | <1 | ||||||||||
| <1 | <1 | <1 | 1 | <1 | ||||||||||
| <1 | <1 | <1 | 3 | <1 | ||||||||||
| <1 | <1 | <1 | 5 | <1 | ||||||||||
| <1 | <1 | <1 | 2 | <1 | ||||||||||
| <1 | <1 | <1 | 2 | <1 | ||||||||||
| <1 | <1 | <1 | 4 | <1 | ||||||||||
| <1 | <1 | <1 | 6 | <1 | ||||||||||
| <1 | <1 | <1 | 5 | <1 | ||||||||||
| <1 | <1 | <1 | 4 | <1 | ||||||||||
| <1 | <1 | <1 | 7 | <1 | ||||||||||
| <1 | <1 | <1 | 9 | <1 | ||||||||||
| <1 | <1 | <1 | 5 | <1 | ||||||||||
| <1 | <1 | <1 | 6 | <1 | ||||||||||
| <1 | <1 | <1 | 8 | <1 | ||||||||||
| <1 | <1 | <1 | 11 | <1 | ||||||||||
| Average | <1 | <1 | <1 | 5 | <1 | |||||||||
| (m, n) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Time (s) | Time (s) | Time (s) | Time (s) | Time (s) | ||||||||||
| 1 | ||||||||||||||
| 1 | ||||||||||||||
| 3 | ||||||||||||||
| 5 | ||||||||||||||
| 2 | ||||||||||||||
| 2 | ||||||||||||||
| 4 | ||||||||||||||
| 6 | ||||||||||||||
| 4 | ||||||||||||||
| 4 | ||||||||||||||
| 6 | ||||||||||||||
| 10 | ||||||||||||||
| 5 | ||||||||||||||
| 6 | ||||||||||||||
| 8 | ||||||||||||||
| 11 | ||||||||||||||
| Average | 5 | |||||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Zheng, F.; Liu, M. Identical Parallel Machine Scheduling Considering Workload Smoothness Index. Appl. Sci. 2023, 13, 8720. https://doi.org/10.3390/app13158720
Wang Z, Zheng F, Liu M. Identical Parallel Machine Scheduling Considering Workload Smoothness Index. Applied Sciences. 2023; 13(15):8720. https://doi.org/10.3390/app13158720
Chicago/Turabian StyleWang, Zhaojie, Feifeng Zheng, and Ming Liu. 2023. "Identical Parallel Machine Scheduling Considering Workload Smoothness Index" Applied Sciences 13, no. 15: 8720. https://doi.org/10.3390/app13158720
APA StyleWang, Z., Zheng, F., & Liu, M. (2023). Identical Parallel Machine Scheduling Considering Workload Smoothness Index. Applied Sciences, 13(15), 8720. https://doi.org/10.3390/app13158720






