High Reliable Uplink Transmission Methods in GEO–LEO Heterogeneous Satellite Network
Abstract
1. Introduction
1.1. Introduction of The Satellite Communication Network
1.2. Literature Review
1.3. Contributions of This Work
- By fully studying the characters of a heterogeneous satellite network, we find out that the beam-edge user and beam-center user still have channel gain difference, although the same equipment sets are assumed to be used by both users. Then, we propose uplink NOMA and derive analytical expressions of the outage probability with respect to NOMA and GEO–LEO cooperative OMA.
- Considering the realistic transmission condition of the beam-edge and beam-center users, the outage probability is also analyzed with channel gain ordering. Further, the diversity order is derived, which can help to assess the outage probability performance intuitively.
- Through the expressions of outage probability and adequate simulation results, we provide practical instructions on designing high reliable uplink transmission methods in heterogeneous GEO–LEO satellite networks.
2. System Model
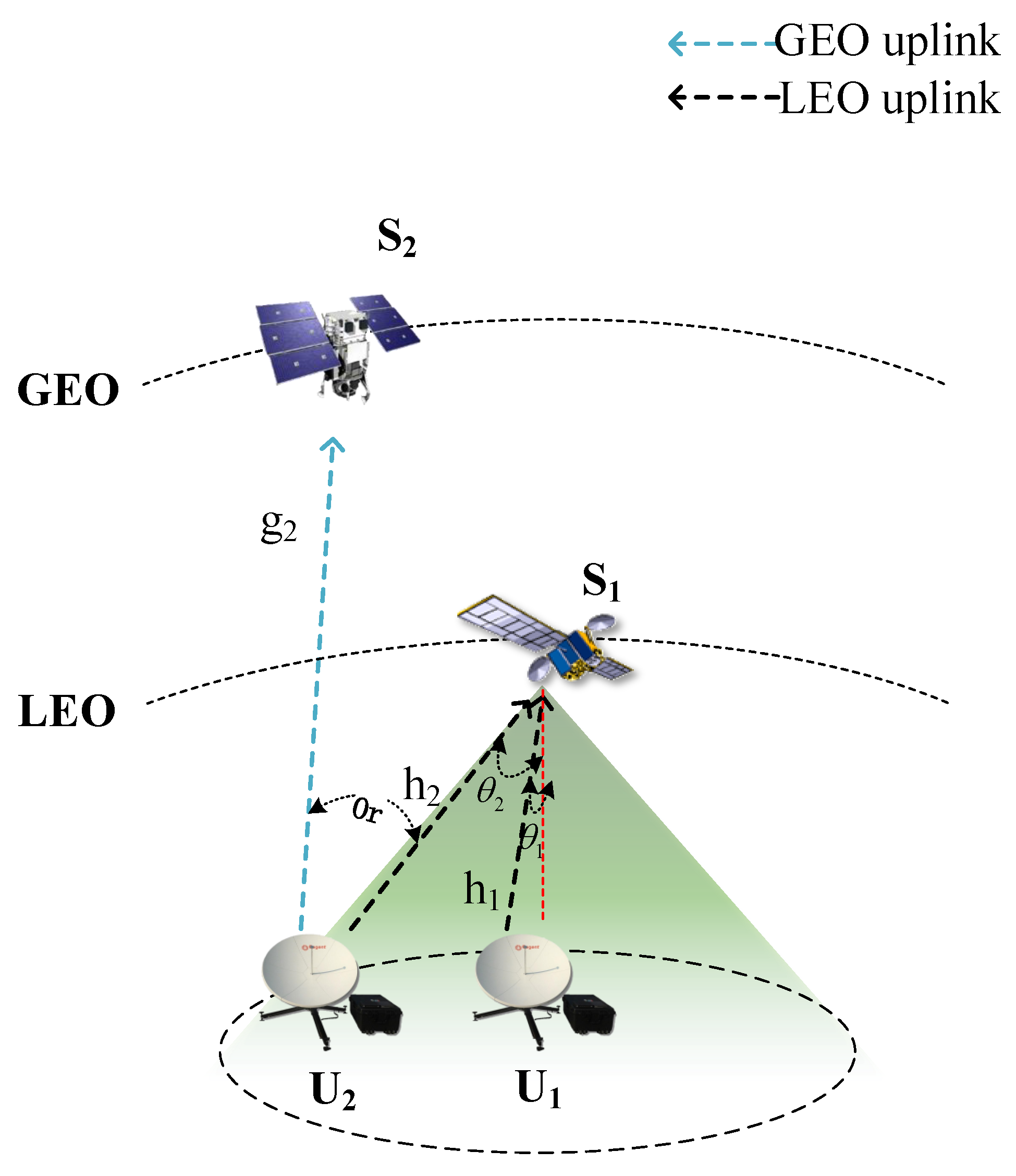
2.1. Descriptions of The Heterogeneous Satellite Network
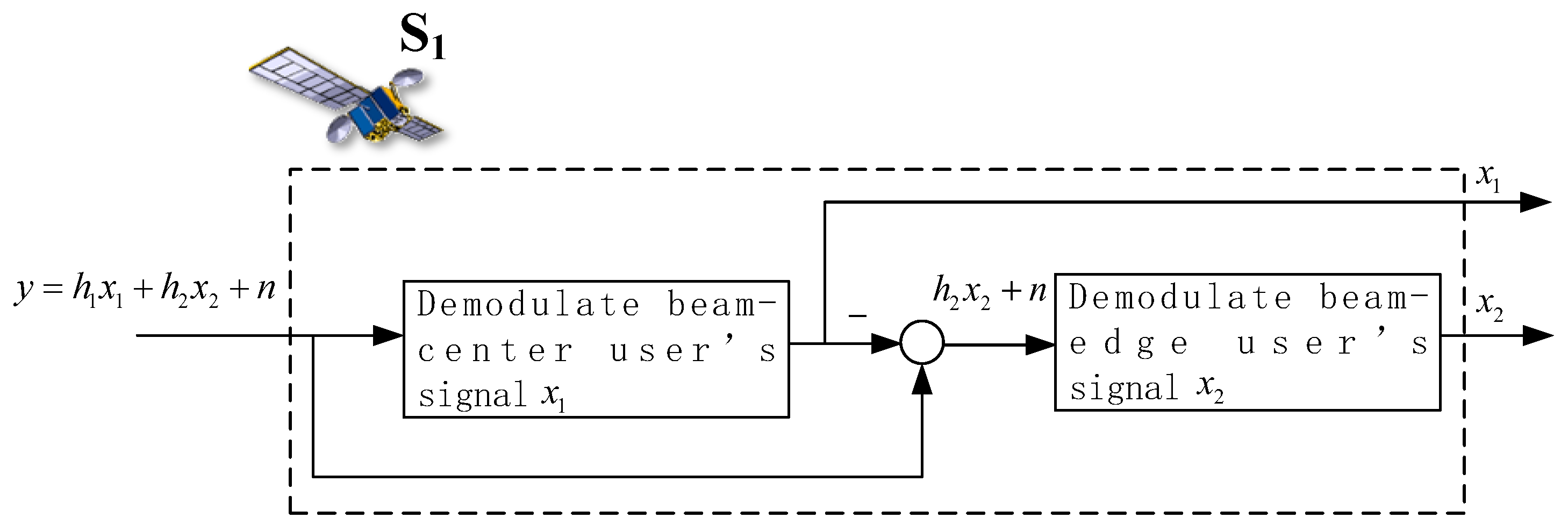
2.2. Uplink Transmission Model of NOMA Scheme
2.3. Uplink Transmission Model of Cooperative OMA Scheme
3. Performance Evaluation
3.1. Outage Probability of NOMA Method
3.2. Outage Probability of Cooperative OMA
3.3. Performance with Ordered Channel Gain
4. Diversity Order Analysis
5. Simulation Results
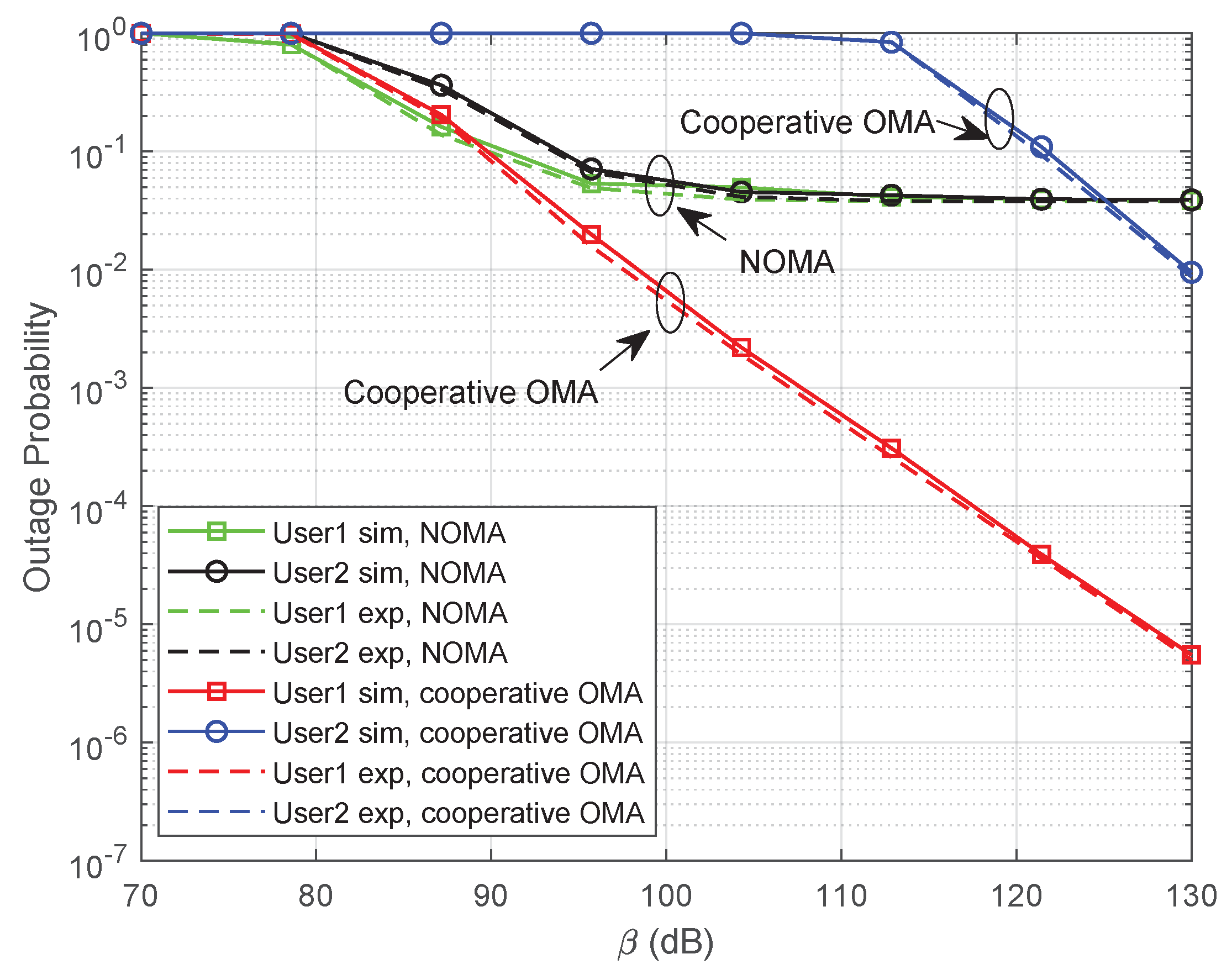
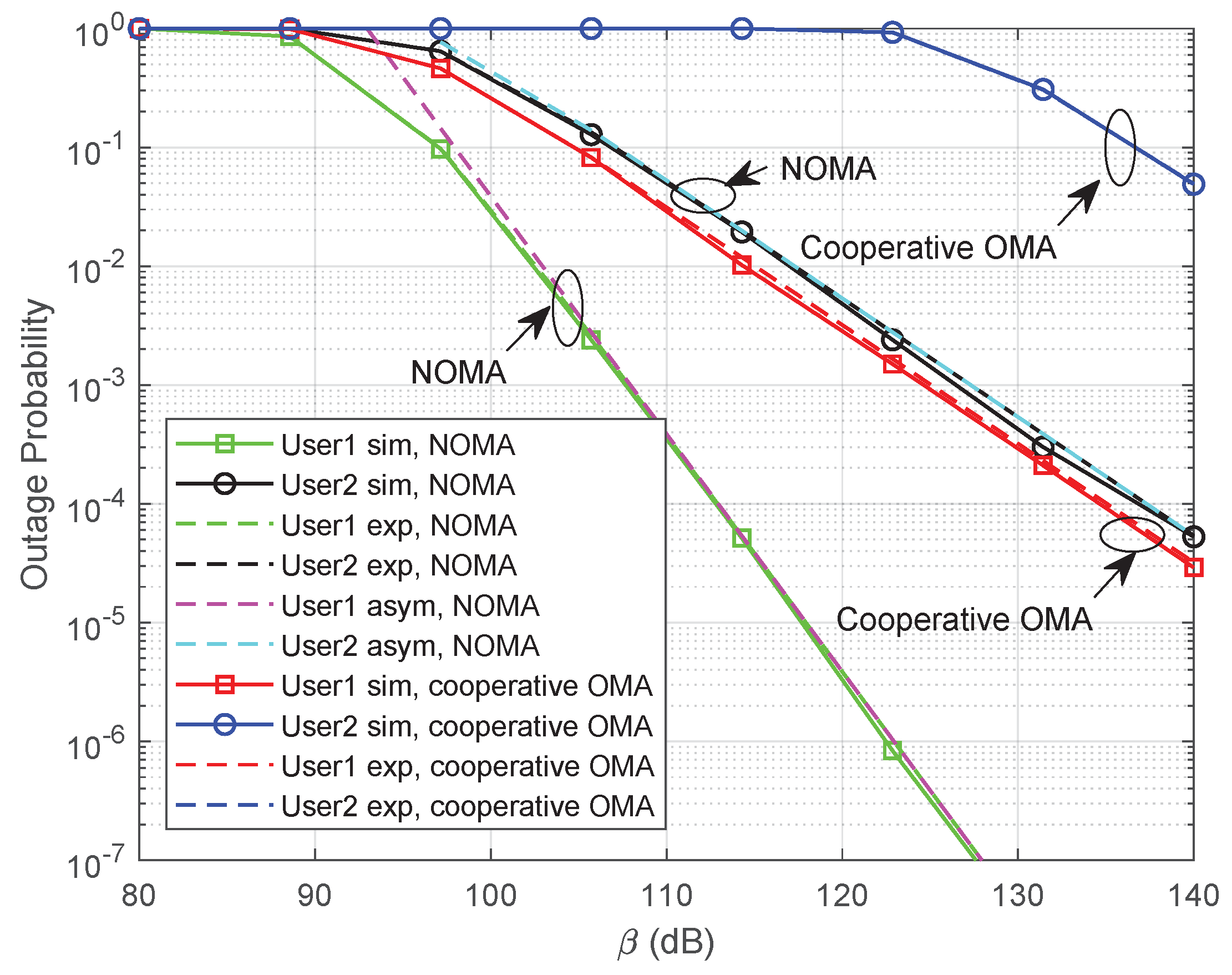
5.1. Outage Probability Without Channel Ordering
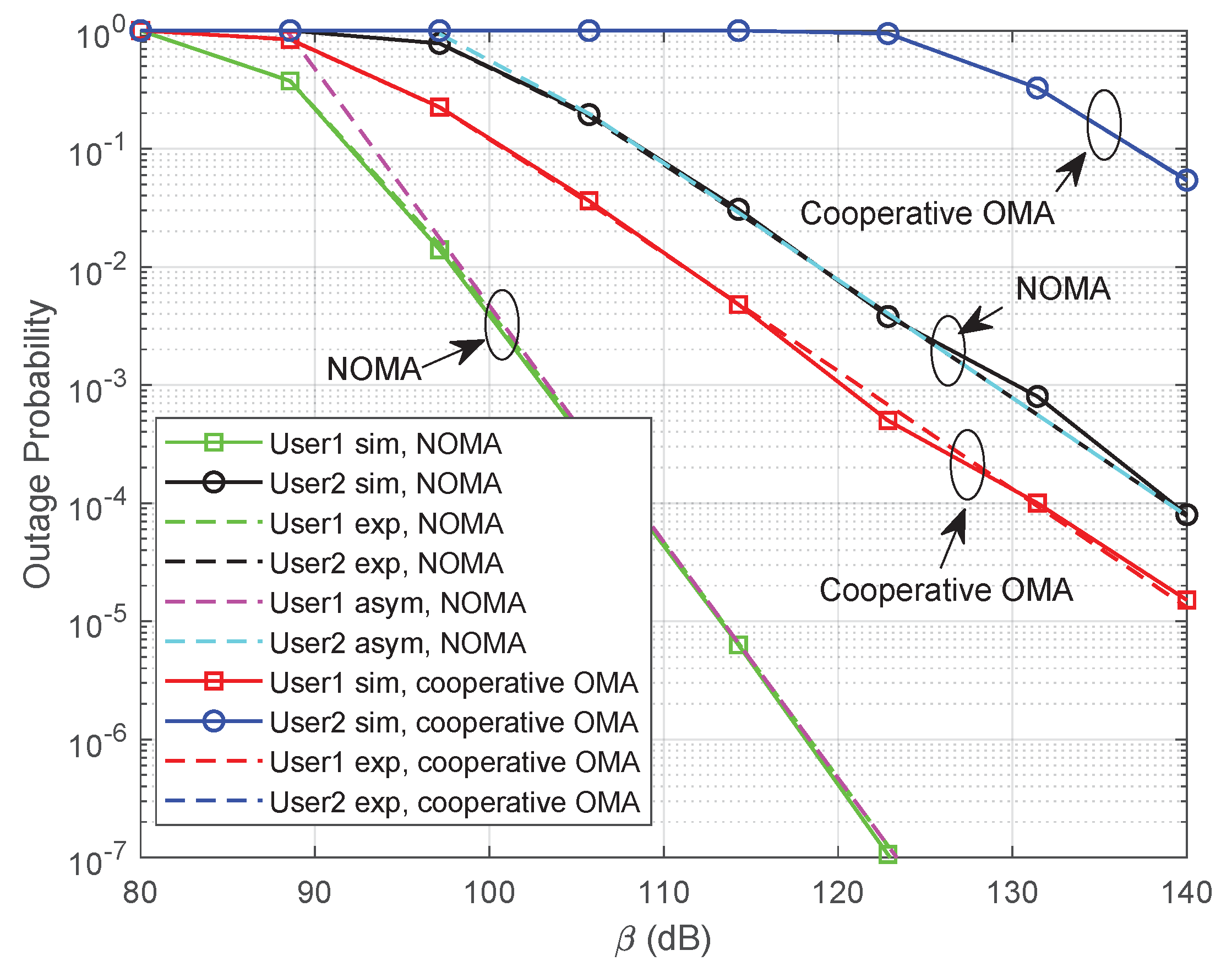
5.2. Outage Probability With Ordered Channel Gain
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Symbols and Acronyms
| 6G | Sixth Generation |
| AS | Average Shadowing |
| BER | Bit Error Rate |
| BS | Base Station |
| CSCG | Circularly Symmetric Complex Gaussian |
| FDMA | Frequency Division Multiple Access |
| FHS | Frequent Heavy Shadowing |
| GEO | Geostationary Earth Orbit |
| ILS | Infrequent Light Shadowing |
| IP | Internet Protocol |
| LEO | Low Earth Orbit |
| LoS | Line of Sight |
| Mbps | Megabits per Second |
| MEO | Medium Earth Orbit |
| NOMA | Non-Orthogonal Multiple Access |
| NTN | Non-Terrestrial Network |
| OMA | Orthogonal Multiple Access |
| Probability Density Function | |
| SATCOM | Satellite Communication |
| SIC | Successive Interference Cancellation |
| SINR | Signal-to-Interference-Noise Ratio |
| SNR | Signal-to-Noise Ratio |
| TDMA | Time Division Multiple Access |
References
- Al-Hraishawi, H.; Chougrani, H.; Kisseleff, S.; Lagunas, E.; Chatzinotas, S. A Survey on nongeostationary satellite systems: The communication perspective. IEEE Commun. Surv. Tutor. 2023, 25, 101–132. [Google Scholar] [CrossRef]
- 3GPP. Study on Integration of Satellite Components in the 5G Architecture: TR 23.700-28 v0.3.0. 2022. Available online: https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=4012 (accessed on 1 July 2023).
- Zhang, X.; Zhu, L.; Li, T.; Xia, Y.; Zhuang, W. Multiple-User transmission in space information networks: Architecture and key techniques. IEEE Wirel. Commun. 2019, 26, 17–23. [Google Scholar] [CrossRef]
- Sun, C. Research status and problems for space-based transmission network and space-ground integrated information network. Radio Eng. 2017, 47, 1–6. [Google Scholar]
- Chen, S.; Sun, S.; Kang, S. System integration of terrestrial mobile communication and satellite communication-the trends, challenges and key technologies in B5G and 6G. China Commun. 2020, 17, 156–171. [Google Scholar] [CrossRef]
- Neinavaie, M.; Khalife, J.; Kassas, Z.M. Acquisition, doppler tracking, and positioning with starlink LEO satellites: First results. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 2606–2610. [Google Scholar] [CrossRef]
- Ren, S.; Yang, X.; Wang, R.; Liu, S.; Sun, X. The interaction between the LEO satellite constellation and the space debris environment. Appl. Sci. 2021, 11, 9490. [Google Scholar] [CrossRef]
- Lyu, X.; Hristov, S.; Gashinova, M.; Stove, A.; Cherniakov, M. Ambiguity function analysis of the Inmarsat I-4 and Iridium signals. In Proceedings of the International Conference on Radar Systems (Radar 2017), Belfast, Northern Ireland, 23–26 October 2017. [Google Scholar]
- Mota, S.; Rocha, A.; Cupido, L.; Oliveira, M.; Costa, J. Challenges and achievements setting up a propagation campaign with MEO satellites. In Proceedings of the 17th European Conference on Antennas and Propagation (EuCAP), Florence, Italy, 26–31 March 2023. [Google Scholar]
- Kassas, Z.M.; Kozhaya, S.; Kanj, H.; Saroufim, J.; Hayek, S.W.; Neinavaie, M.; Khairallah, N.; Khalife, J. Navigation with multi-constellation LEO satellite signals of opportunity: Starlink, OneWeb, Orbcomm, and Iridium. In Proceedings of the 2023 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 24–27 April 2023. [Google Scholar]
- Liang, Y.C.; Tan, J.; Jia, H.; Zhang, J.; Zhao, L. Realizing intelligent spectrum management for integrated satellite and terrestrial networks. J. Commun. Inf. Netw. 2021, 6, 32–43. [Google Scholar] [CrossRef]
- Yan, X.; Xiao, H.; An, K.; Zheng, G.; Tao, W. Hybrid satellite terrestrial relay networks with cooperative non-orthogonal multiple access. IEEE Commun. Lett. 2018, 22, 978–981. [Google Scholar] [CrossRef]
- Zhu, X.; Jiang, C.; Yin, L.; Kuang, L.; Ge, N.; Lu, J. Non-orthogonal multiple access based integrated terrestrial-satellite networks. IEEE J. Sel. Areas Commun. 2017, 35, 2253–2267. [Google Scholar] [CrossRef]
- Elhalawany, B.M.; Gamal, C.; Elsayed, A.; Elsherbini, M.M.; Fouda, M.M.; Ali, N. Outage analysis of coordinated NOMA transmission for LEO satellite constellations. IEEE Open J. Commun. Soc. 2022, 3, 2195–2202. [Google Scholar] [CrossRef]
- Li, T.; Hao, X.; Yue, X. A power domain multiplexing based co-carrier transmission method in hybrid satellite communication networks. IEEE Access 2020, 8, 120036–120043. [Google Scholar] [CrossRef]
- Li, T.; Hao, X.; Yue, X. A spectrum-saving transmission method in multi-antenna satellite communication star networks: Sharing the frequency with terminals. Entropy 2023, 25, 113. [Google Scholar] [CrossRef]
- Tegos, S.A.; Diamantoulakis, P.D.; Xia, J.; Fan, L.; Karagiannidis, G.K. Outage performance of uplink NOMA in land mobile satellite communications. IEEE Wirel. Commun. Lett. 2020, 9, 1710–1714. [Google Scholar] [CrossRef]
- Yan, X.; Xiao, H.; An, K.; Zheng, G.; Chatzinotas, S. Ergodic capacity of NOMA-based uplink satellite networks with randomly deployed users. IEEE Syst. J. 2020, 14, 3343–3350. [Google Scholar] [CrossRef]
- Lee, J.H.; Joo, J.S.; Kim, P.; Ryu, J.-G. Random beam-based non-orthogonal multiple access for massive MIMO low earth orbit satellite networks. IEEE Access 2023. early access. [Google Scholar] [CrossRef]
- Ge, R.; Cheng, J.; An, K.; Zheng, G. Non-orthogonal multiple access enabled two-layer GEO/LEO satellite network. In Proceedings of the 29th European Signal Processing Conference (EUSIPCO), Dublin, Ireland, 23–27 August 2021; pp. 890–894. [Google Scholar]
- Ge, R.; Bian, D.; Cheng, J.; An, K.; Hu, J.; Li, G. Joint user pairing and power allocation for NOMA-Based GEO and LEO satellite network. IEEE Access 2021, 9, 93255–93266. [Google Scholar] [CrossRef]
- Liu, R.; Guo, K.; An, K.; Zhou, F.; Wu, Y.; Huang, Y.; Zheng, G. Resource allocation for NOMA-enabled cognitive satellite-UAV-terrestrial networks with imperfect CSI. IEEE Trans. Cogn. Commun. Netw. 2023. early access. [Google Scholar] [CrossRef]
- Yan, X.; Xiao, H.; Wang, C.; An, K. Outage performance of NOMA-based hybrid satellite-terrestrial relay networks. IEEE Wirel. Commun. Lett. 2018, 7, 538–541. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series and Products, 7th ed.; Academic Press: New York, NY, USA, 2007; pp. 1005–1006. [Google Scholar]
- Hildebrand, F.B. Introduction to Numerical Analysis, 2nd ed.; Dover publications: New York, NY, USA, 1987; pp. 392–393. [Google Scholar]
- David, H.A.; Nagaraja, H.N. Order Statistics, 3rd ed.; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; American Journal of Physics: Washington, DC, USA, 1988. [Google Scholar]
- Ding, Z.; Yang, Z.; Fan, P.; Poor, H.V. On the performance of non-orthogonal multiple access in 5G systems with randomly deployed users. IEEE Signal Process. Lett. 2014, 21, 1501–1505. [Google Scholar] [CrossRef]
- Ashraf, S.; Ahmed, T.; Aslam, Z.; Muhammad, D.; Yahya, A.; Shuaeeb, M. Depuration based efficient coverage mechanism for wireless sensor network. J. Electr. Comput. Eng. Innov. 2020, 8, 145–160. [Google Scholar]
- Abdi, A.; Lau, W.C.; Alouini, M.-S.; Kaveh, M. A new simple model for landmobile satellite channels: First- and second-order statistics. IEEE Trans. Wirel. Commun. 2003, 2, 519–528. [Google Scholar] [CrossRef]


| System Parameter | Value |
|---|---|
| Orbit height of GEO satellite | 36,000 km |
| Orbit height of LEO satellite | 700 km |
| Carrier frequency | 28 GHz |
| Angle of 3 dB beam width at the LEO satellite | |
| Beam gain of the GEO receive antenna | 54 dB |
| Normal-direction beam gain of LEO receive antenna | 50 dB |
| Transmit beam gain of user terminals | 45 dB |
| Shadowing | b | m | |
|---|---|---|---|
| Frequent heavy shadowing (FHS) | |||
| Average shadowing (AS) | |||
| Infrequent light shadowing (ILS) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Li, T.; Yue, X.; Hou, T.; Dai, B. High Reliable Uplink Transmission Methods in GEO–LEO Heterogeneous Satellite Network. Appl. Sci. 2023, 13, 8611. https://doi.org/10.3390/app13158611
Li G, Li T, Yue X, Hou T, Dai B. High Reliable Uplink Transmission Methods in GEO–LEO Heterogeneous Satellite Network. Applied Sciences. 2023; 13(15):8611. https://doi.org/10.3390/app13158611
Chicago/Turabian StyleLi, Guoyan, Tian Li, Xinwei Yue, Tianwei Hou, and Bin Dai. 2023. "High Reliable Uplink Transmission Methods in GEO–LEO Heterogeneous Satellite Network" Applied Sciences 13, no. 15: 8611. https://doi.org/10.3390/app13158611
APA StyleLi, G., Li, T., Yue, X., Hou, T., & Dai, B. (2023). High Reliable Uplink Transmission Methods in GEO–LEO Heterogeneous Satellite Network. Applied Sciences, 13(15), 8611. https://doi.org/10.3390/app13158611






