A Method for Correcting Endoscopic Images to Measure the Size of Defects on the Inner Surface of a Hole
Abstract
1. Introduction
2. Endoscope Imaging and Correction Principle
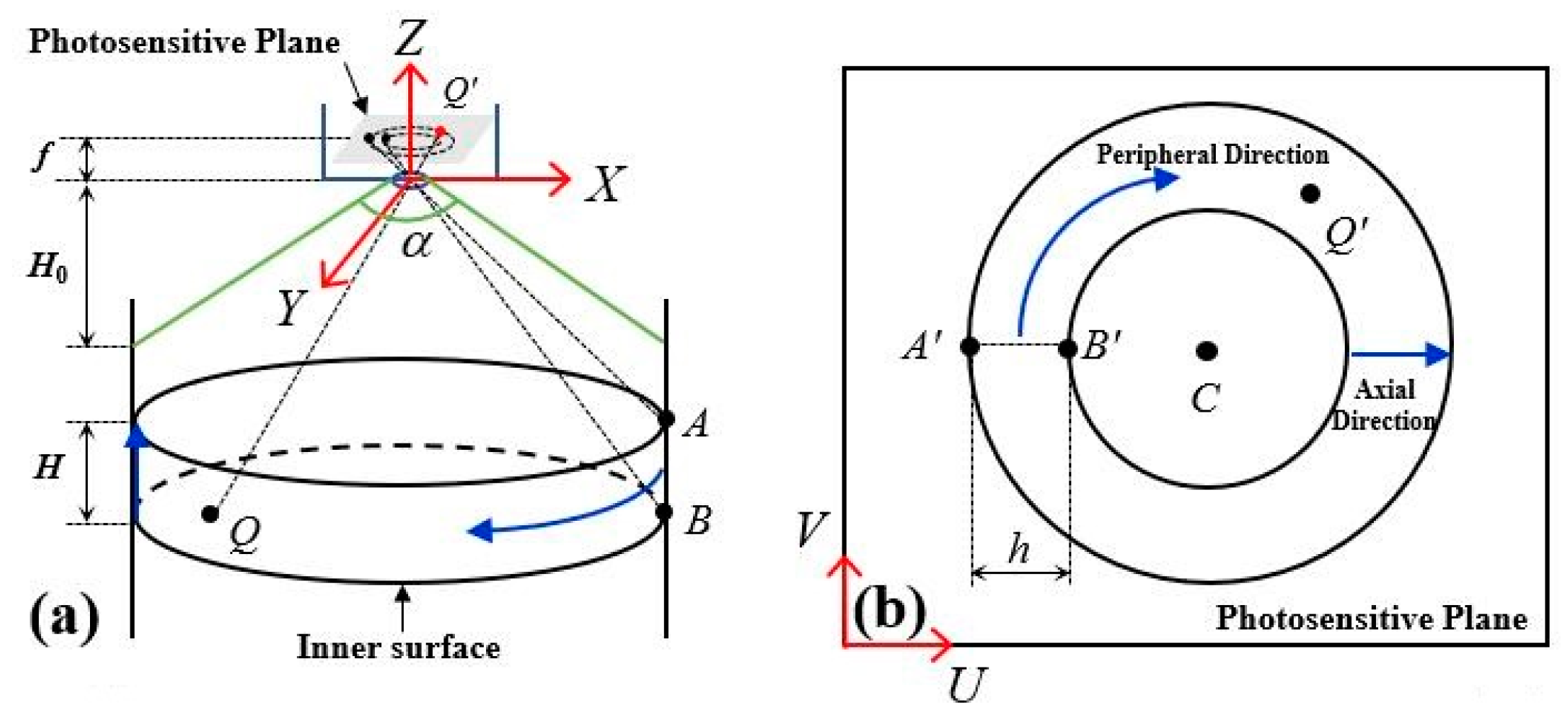
2.1. Endoscope Imaging Principle
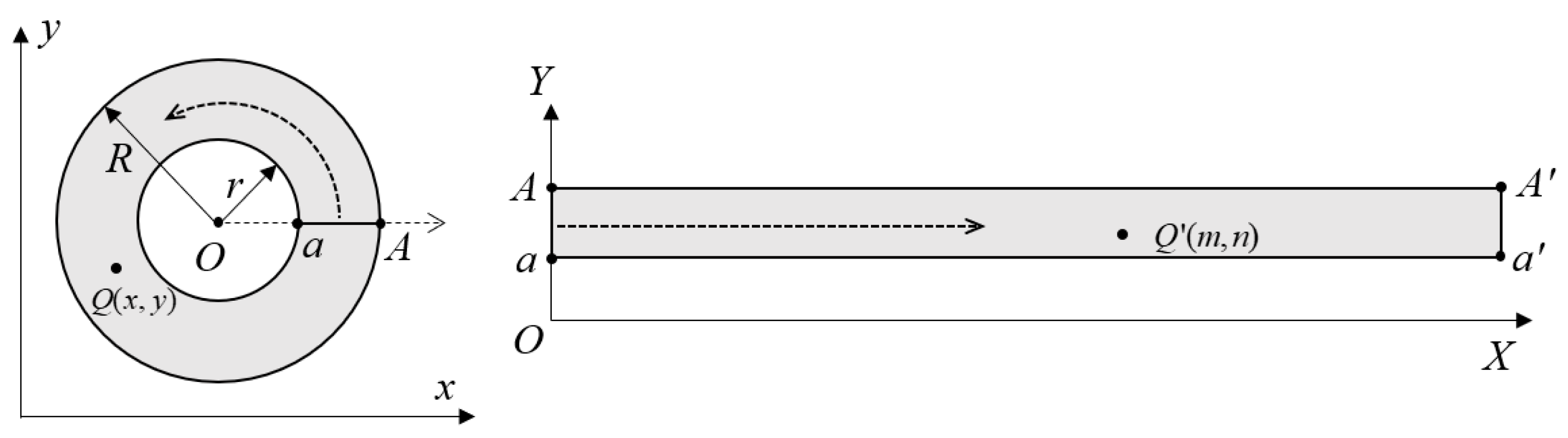
2.2. Image Correction Principle
3. Image Acquisition and Distortion Correction
3.1. Image Acquisition Scheme
3.2. Circumferential Distortion Correction
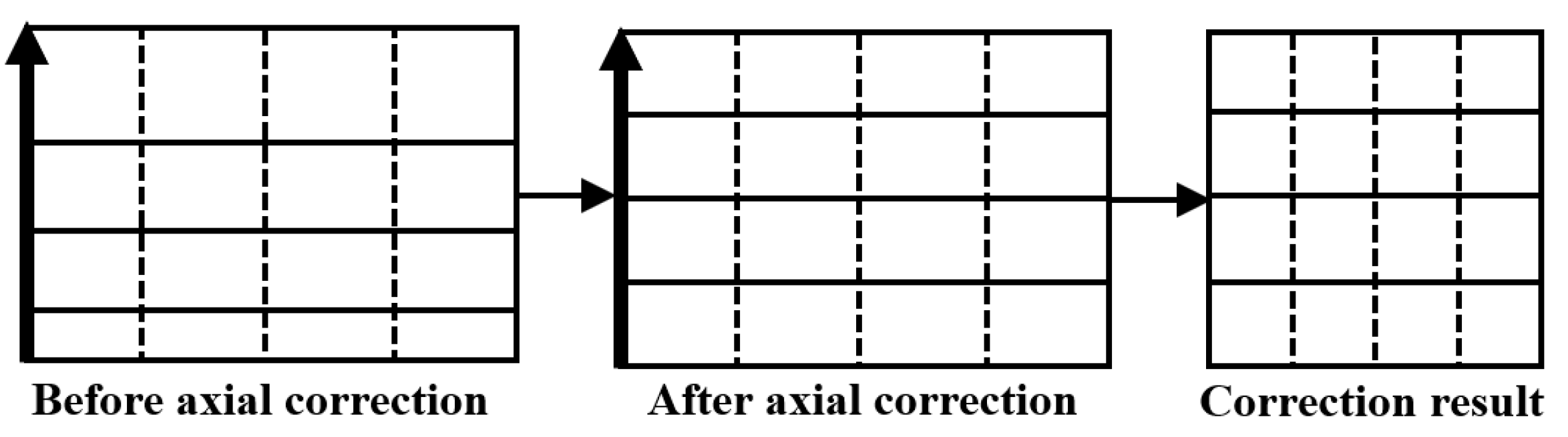
3.3. Axial Distortion Correction
4. Influencing Factors and Error Analysis
4.1. Effect of Aperture on Correction Error
4.2. Effect of Image Center on Correction Error
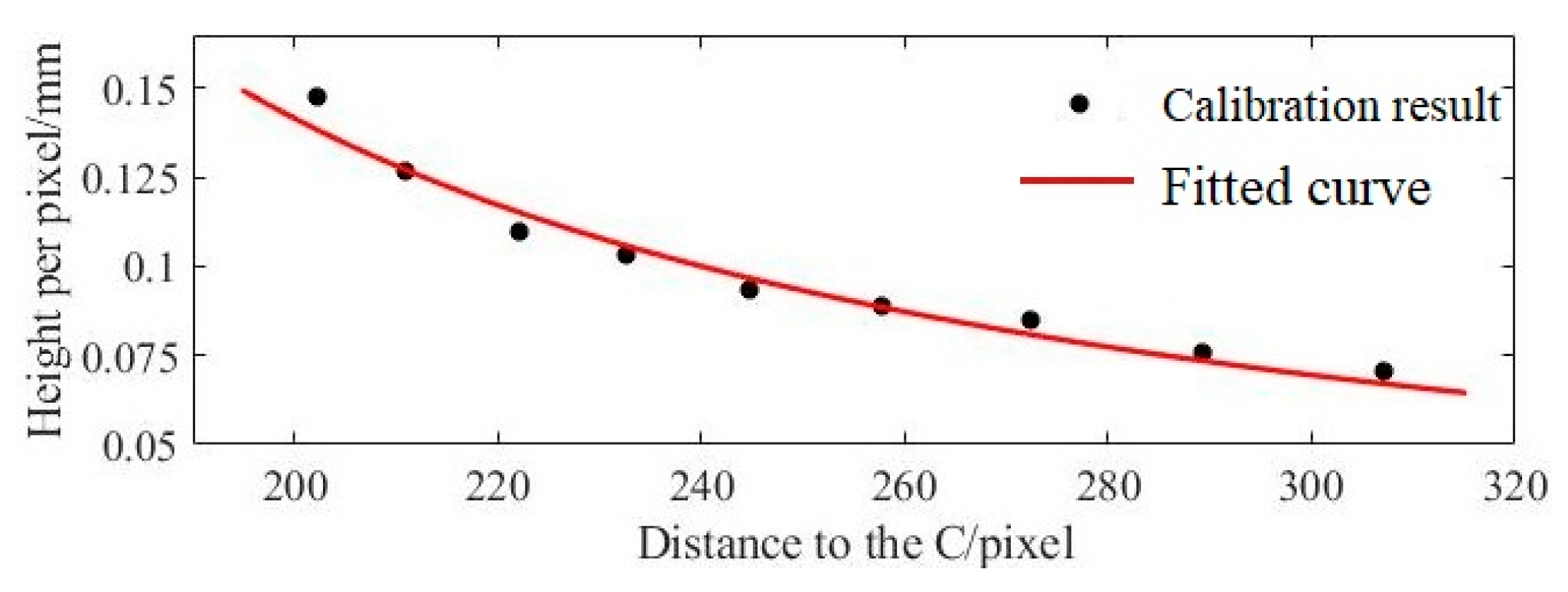
4.3. Effect of Unit Pixel Size on Measurement Error
5. Experimental Verification and Result Analysis
5.1. Experimental Scheme
5.2. Experimental Results and Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shang, H.; Gao, J. Theories and industrial applications of optical interferometric NDT techniques: A review. Insight 2009, 51, 240–251. [Google Scholar] [CrossRef]
- Erwin, P.; Michael, B.; Lutz, D. Slender Tactile Sensor for Contour and Roughness Measurements within Deep and Narrow Holes. IEEE Sens. J. 2008, 8, 1960–1967. [Google Scholar]
- Lebrasseur, E.; Pourciel, J.P.; Bourouina, T.; Masuzawa, T.; Fujita, H. A new characterization tool for vertical profile measurement of high-aspect-ratio microstructures. J. Micromech. Microeng. 2002, 12, 280–285. [Google Scholar] [CrossRef]
- Prager, J.; Kitze, J.; Acheroy, C.; Brackrock, D.; Brekow, G.; Kreutzbruck, M. SAFT and TOFD-A Comparative Study of Two Defect Sizing Techniques on a Reactor Pressure Vessel Mock-up. J. Nondestruct. Eval. 2013, 32, 1–13. [Google Scholar] [CrossRef]
- Marcio, B.S.; Nienhaysen, P.; Haboe, D.; Flesch, R.C.C. Quality Assessment and Deviation Analysis of Three-dimensional Geometrical Characterization of a Metal Pipeline by Pulse-echo Ultrasonic and Laser Scanning Techniques. Measurement 2019, 145, 30–37. [Google Scholar] [CrossRef]
- Xie, S.J.; Duan, Z.R.; Li, J.; Tong, Z.; Tian, M.; Chen, Z. A novel magnetic force transmission eddy current array probe and its application for nondestructive testing of defects in pipeline structures. Sens. Actuators A Phys. 2020, 309, 112030. [Google Scholar] [CrossRef]
- Yu, S.; Chung, W.W.S.; Lau, T.C.W.; Lai, W.W.L.; Sham, J.F.C.; Ho, C.Y. Laboratory validation of in-pipe pulsed thermography in the rapid assessment of external pipe wall thinning in buried metallic utilities. NDT E Int. 2023, 135, 102791. [Google Scholar] [CrossRef]
- Chesnokova, A.A.; Kalayeva, S.Z.; Ivanova, V.A. Development of a flaw detection material for the magnetic particle method. J. Phys. Conf. Ser. 2017, 881, 012022. [Google Scholar] [CrossRef]
- Safar, S.; Shoorehdeli, M.A. Detection and Isolation of Interior Defects Based on Image Processing and Neural Networks: HDPE Pipeline Case Study. J. Pipeline Syst. Eng. Pract. 2018, 9, 05018001. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, X.; Liu, S.I.; Jia, Z. A Roughness Measurement Method based on Genetic Algorithm and Neural Network for Micro Heterogeneous Surface in Deep-hole part. J. Circuits Syst. Comput. 2012, 21, 1250005. [Google Scholar] [CrossRef]
- Bergen, T.; Wittenberg, T. Stitching and Surface Reconstruction from Endoscopic Image Sequences: A Review of Applications and Methods. IEEE J. Biomed. Health Inform. 2016, 20, 304–321. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.Y. A Flexible New Technique for Camera Calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 22, 1330–1334. [Google Scholar] [CrossRef]
- Hartley, R.; Kang, S.B. Parameter-free radial distortion correction with center of distortion estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 1309–1321. [Google Scholar] [CrossRef]
- Horn, B.K.P. Robot Vision; Wang, L., Jiang, X.L., Eds.; China Youth Press: Beijing, China, 1986; pp. 424–427. [Google Scholar]
- Smith, W.E.; Vakil, N.; Maislin, S.A. Correction of distortion in endoscope images. IEEE Trans. Med. Imaging 1992, 11, 117–122. [Google Scholar] [CrossRef] [PubMed]
- Vijayan, A.K.; Kumar, S.; Radhakrishnan, D. A new approach for nonlinear distortion correction in endoscopic images based on least squares estimation. IEEE Trans. Med. Imaging 1999, 18, 345–354. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, M.; Farag, A. Nonmetric calibration of camera lens distortion: Differential methods and robust estimation. IEEE Trans. Image Process. 2005, 14, 1215–1230. [Google Scholar] [CrossRef] [PubMed]
- Mundhenk, T.N.; Rivett, M.J.; Liao, X.; Hall, E.L. Techniques for fisheye lens calibration using a minimal number of measurements. In Intelligent Robots and Computer Vision XIX: Algorithms, Techniques, and Active Vision; SPIE: Bellingham, WA, USA, 2000; Volume 4197, pp. 181–190. [Google Scholar]
- Wang, J.H.; Shi, F.H.; Zhang, J.; Liu, Y. A new calibration model of camera lens distortion. Pattern Recognit. 2008, 41, 607–615. [Google Scholar] [CrossRef]
- Sheng, Q.; Zheng, J.M.; Shi, W.C.; Zhao, R.F.; Liu, J.S.; Li, H.T. Measurement and modeling of reflection characteristics of hole inner surface based on endoscopic image. Measurement 2022, 190, 110742. [Google Scholar] [CrossRef]
- Liedlgruber, M.; Uhl, A. Endoscopic image processing—An overview. In Proceedings of the 6th International Symposium on Image and Signal Processing and Analysis, Salzburg, Austria, 16–18 September 2009; pp. 707–712. [Google Scholar]
- Sun, F.R.; Liu, J.R. Fast Hough transform algorithm. Chin. J. Comput. 2001, 24, 1102–1109. [Google Scholar]

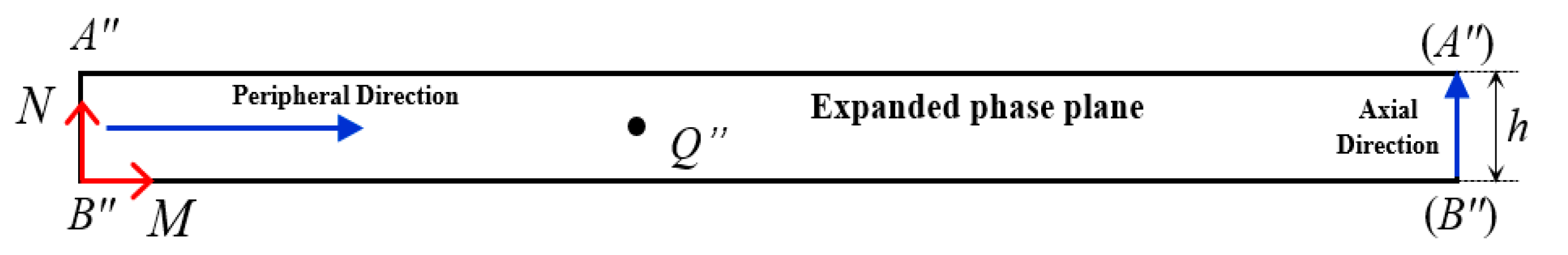









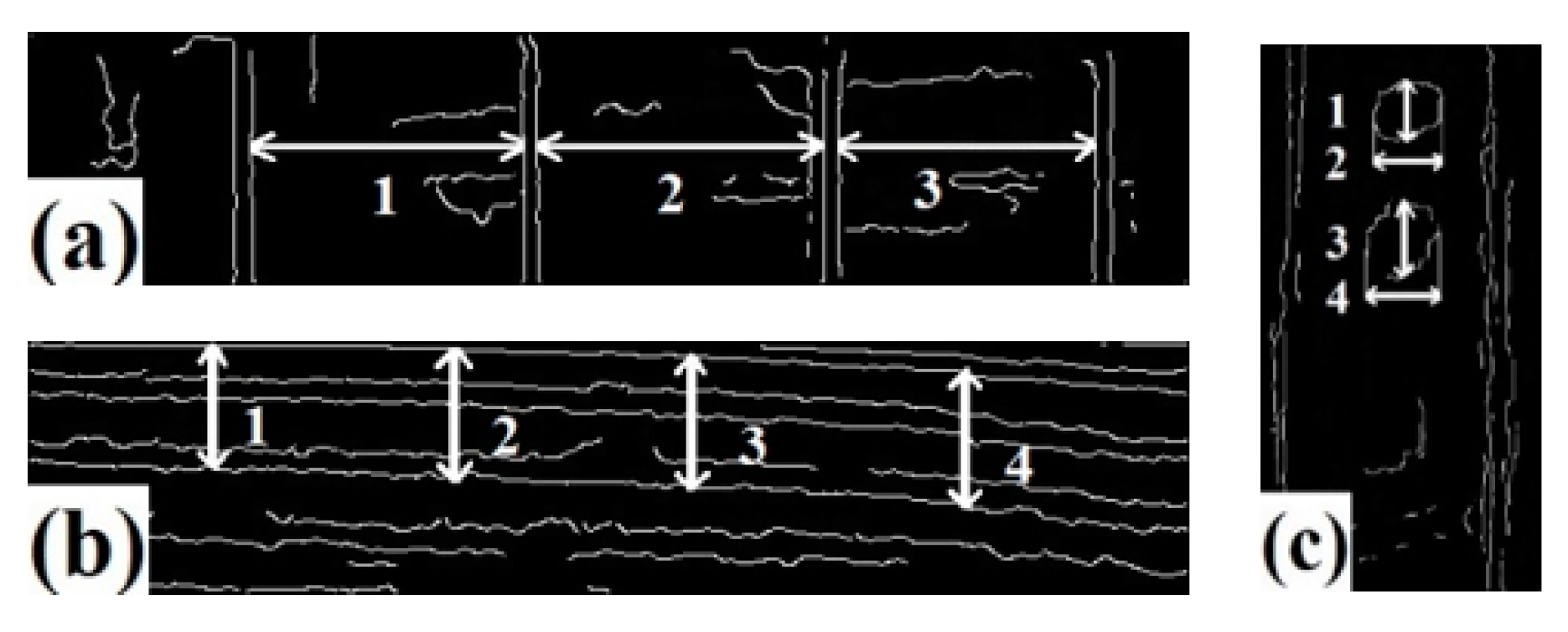
| Column Number | Mean Value | Standard Deviation | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||||
| Row Number | 1 | 138 | 139 | 137 | 132 | 130 | 122 | 133.00 | 6.450 |
| 2 | 116 | 119 | 119 | 116 | 112 | 109 | 115.20 | 3.971 | |
| 3 | 100 | 102 | 100 | 99 | 97 | 92 | 98.33 | 3.502 | |
| 4 | 83 | 85 | 86 | 84 | 84 | 81 | 83.83 | 1.722 | |
| 5 | 71 | 72 | 72 | 72 | 70 | 67 | 70.67 | 1.966 | |
| 6 | 56 | 58 | 59 | 60 | 60 | 59 | 58.67 | 1.506 | |
| 7 | 46 | 47 | 49 | 50 | 49 | 47 | 48.00 | 1.549 | |
| 8 | 34 | 35 | 36 | 38 | 39 | 39 | 36.83 | 2.137 | |
| 9 | 24 | 26 | 28 | 30 | 31 | 30 | 28.17 | 2.714 | |
| Column Number | Mean Value | Standard Deviation | Total Deviation | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |||||
| Row Number | 1 | 11 | 12 | 12 | 12 | 11 | 11 | 11.50 | 0.548 | −11.66% |
| 2 | 11 | 12 | 13 | 12 | 10 | 12 | 11.67 | 1.033 | −10.38% | |
| 3 | 14 | 14 | 12 | 13 | 13 | 13 | 13.17 | 0.753 | 1.14% | |
| 4 | 13 | 15 | 14 | 13 | 12 | 14 | 13.50 | 1.049 | 3.70% | |
| 5 | 14 | 16 | 14 | 13 | 13 | 13 | 13.83 | 1.169 | 6.26% | |
| 6 | 14 | 16 | 15 | 14 | 13 | 13 | 14.17 | 1.169 | 8.82% | |
| 7 | 14 | 15 | 14 | 13 | 13 | 12 | 13.50 | 1.049 | 3.70% | |
| 8 | 12 | 15 | 13 | 13 | 13 | 13 | 13.17 | 0.983 | 1.14% | |
| 9 | 12 | 13 | 12 | 13 | 14 | 12 | 12.67 | 0.816 | −2.70% | |
| Pixel Distance /Pixel | Mean /Pixel | Standard Deviation | Unit Pixel Size/mm2 | Maximum Positive Deviation | Maximum Negative Deviation | Deviation Range | |
|---|---|---|---|---|---|---|---|
| φ12 | 494.96; 513.58; 496.19; 502.56; 499.14 | 501.29 | 6.69 | 0.0233 × 0.0233 | 2.45% | 1.26% | 3.71% |
| φ28 | 471.88; 490.67; 487.20; 492.49; 490.03 | 482.45 | 8.46 | 0.0513 × 0.0513 | 2.08% | 2.19% | 4.27% |
| Image Center | Mean/Pixel | Standard Deviation | Maximum Positive Deviation | Maximum Negative Deviation | Deviation Range | |
|---|---|---|---|---|---|---|
| φ12 | (295, 386) | 503.68 | 12.75 | 4.10% | 3.11% | 7.21% |
| (305, 386) | 501.29 | 6.69 | 2.45% | 1.26% | 3.71% | |
| (315, 386) | 505.29 | 10.56 | 3.59% | 2.46% | 6.05% | |
| φ28 | (318, 368) | 468.17 | 28.87 | 7.94% | 8.50% | 16.44% |
| (318, 378) | 482.45 | 8.46 | 2.08% | 2.19% | 4.27% | |
| (318, 388) | 467.11 | 18.60 | 5.09% | 5.93% | 11.02% |
| rmax | Pixel Distance /Pixel | Mean/Pixel | Standard Deviation | Unit Pixel Size/mm2 | Maximum Positive Deviation | Maximum Negative Deviation | Deviation Range |
|---|---|---|---|---|---|---|---|
| 253 | 469.22; 493.71; 479.55; 472.97; 483.12 | 479.72 | 8.52 | 0.0237 × 0.0237 | 2.92% | 2.19% | 5.11% |
| 258 | 494.86; 513.59; 496.19; 502.56; 499.14 | 501.29 | 6.69 | 0.0233 × 0.0233 | 2.45% | 1.26% | 3.71% |
| 263 | 520.20; 513.95; 505.94; 517.42;508.10 | 513.12 | 5.41 | 0.0228 × 0.0228 | 0.84% | 1.40% | 2.24% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, P.; Tian, Z.; Sheng, Q.; Liu, P. A Method for Correcting Endoscopic Images to Measure the Size of Defects on the Inner Surface of a Hole. Appl. Sci. 2023, 13, 8597. https://doi.org/10.3390/app13158597
Shi P, Tian Z, Sheng Q, Liu P. A Method for Correcting Endoscopic Images to Measure the Size of Defects on the Inner Surface of a Hole. Applied Sciences. 2023; 13(15):8597. https://doi.org/10.3390/app13158597
Chicago/Turabian StyleShi, Pengtao, Zhengwei Tian, Qiang Sheng, and Peng Liu. 2023. "A Method for Correcting Endoscopic Images to Measure the Size of Defects on the Inner Surface of a Hole" Applied Sciences 13, no. 15: 8597. https://doi.org/10.3390/app13158597
APA StyleShi, P., Tian, Z., Sheng, Q., & Liu, P. (2023). A Method for Correcting Endoscopic Images to Measure the Size of Defects on the Inner Surface of a Hole. Applied Sciences, 13(15), 8597. https://doi.org/10.3390/app13158597





