Spiking Neural P Systems for Basic Arithmetic Operations

Abstract

As a novel biological computing device, the Spiking Neural P system (SNPS) has powerful computing potential. The application of SNPS in the field of arithmetic operation has been a hot research topic in recent years. Researchers have proposed methods and systems for implementing basic arithmetic operations using SNPS. This paper studies four basic arithmetic operations, improves the parallelization of addition and multiplication methods, and designs more effective natural number addition and multiplication SNPS, as well as SNPS for subtraction and for division of natural numbers based on multiple subtractions. The effectiveness of the proposed SNPS is verified by example. Compared with the same kind of SNPS, for the addition operation the number of neurons used in our system is reduced by 50% and the time overhead is reduced by 33%, while for the multiplication operation the number of neurons is reduced by 40%.

1. Introduction

Membrane computing [1] is a branch of natural computing inspired by the structure and functionality of living cells. In a research report in 1998, Gh. Păun, a member of the Romanian Academy, proposed the P system, a distributed and parallel computing model. Each membrane of a biological cell can be regarded as a separate computing unit to perform the corresponding calculation. With the incredible number of cells in living organisms and the low energy requirements for biochemical reactions, one of the greatest advantages of membrane computing is that it enables corresponding computations with maximum parallelism. The literature [2] shows that membrane computing is equivalent to Turing machines, and its powerful parallel computing capability can effectively solve the computing bottlenecks faced by current electronic computers. Research on arithmetic operations based on membrane computing has been performed in cell-like P systems, tissue-like P systems, and neural-like P systems.

In [3], the authors implemented arithmetic operations based on a membrane P System; However, its membrane system structure was complex and did not make full use of the maximum parallelism of membrane computation; In [4], the authors designed a natural coding-based arithmetic P System to implement arithmetic operations, which greatly simplified the membrane system structure; In [5], the authors designed a multi-layer membrane P System to implement unsigned quadratic operations, which reduced the computational complexity, while the authors of [6] designed a single-layer membrane P System to implement arithmetic operations, further simplifying the membrane structure and improving computational efficiency. The authors of [7] designed a multi-layer membrane P System to implement arithmetic operations with signed numbers, improving the application range and execution efficiency of basic operations, while in [8,9,10] the authors designed a single-layer membrane P System to implement expression evaluation in the domain of integers. Reference [11] implemented basic arithmetic operations by the P System in the domain of rational numbers, expanding the scope of application of arithmetic operations in P System to further enhance the computing power of biological computers, while [12] investigated the computational power of tissue P systems where each rule was assigned either a label chosen from the alphabet or an empty label. The sequence of labels of rules applied during halting of computation was defined as the result of the computation, and the set of all results computed by a given tissue P system was called the control language. The results indicated that the rule complexity is crucial in order for tissue P systems to achieve the desired computational power. In [13], the authors constructed a novel computational model called a homeostasis tissue-like P system. Based on the model, it solved the three-coloring problem in linear time within the standard timeframe. Additionally, it addressed the SAT problem using communication rules and multiset rewriting rules with a maximum length of 3 in time-free mode.

In 2006, Dr. M. Ionescu et al. proposed the Spiking Neural P system [14], which utilizes the phenomenon of neurons sending spikes to connected neurons through synapses. The SNPS is composed of a set of neurons and their connections, which are typically abstracted as a directed graph. Neurons are viewed as nodes in the graph, and the connections between neurons are considered as directed edges. Under the control of the system clock and the internal excitation rules of neurons, spike signals propagate along the synapses (represented as directed arcs in the graph) to connected neurons. The execution of the forgetting rules inside neurons simply consumes spikes. In the basic SNPS [14,15], all spikes are indistinguishable and denoted by the same symbol “a”. The operation of the system is synchronous and parallel, which means that all neurons with applicable rules should be executed [16] at each time slice. This distributed and parallel computing model has been shown to be computationally complete [15,17,18].

SNPS research in theory and application has achieved significant results, including generating numbers and languages, simulating logic circuits, system universality, and variants of spiking neural P systems. In [15], the authors showed that the basic SNPS as a device for generating sets of numbers is computationally complete in both generation mode and acceptance mode. In [16], the authors studied the language-generating capacity of SNPS; the recursively enumerable languages are the inverse image projection of the languages generated by SNPS. In [19], the authors investigated the minimum universality of SNPS as a device for computing functions and generating numbers and provided the minimum number of neurons to produce a universal SNPS using extension rules and standard rules. A restricted-rule universal system requires 76 neurons, while a universal system with extension rules only requires 50 neurons. In [20], the authors introduced a variant of SNP where neurons only contain spikes and the rules are on synapses. When the number of spikes in a given neuron matches the rule on the synapse, the rule is triggered. Compared with the SNPS in [19], a number generator constructed based on this variant SNPS requires only 39 neurons to achieve universality under standard rules, and only 30 neurons are needed when using extension rules. Many variants of SNPS have been proven to be Turing universal, such as the asynchronous spiking neural P system with local synchronization introduced in [21] and the SNPS with weights introduced in [22], where the applicability of the spike rules is controlled by a given discharge threshold. When integers are used to represent the weight, potential, and threshold parameters, this SNPS is universal. When natural numbers are used for these parameters, the characteristic of natural semilinear sets can be obtained. In [23], the aim was to address the limitations of current SNP systems in handling specific real-world data technology. Neural network structures and data processing methods were considered as a reference to improve upon these limitations. By integrating these concepts with membrane computing, spiking neural membrane computing models (SNMC models) were proposed. The paper successfully demonstrated the Turing universality of the SNMC model as a number generator and acceptor. The authors of [24] introduced neuron division and neuron budding into the framework of the spiking neural P system. A neuron can be divided into two and every budding can only produce one new neuron, proving that SNPS with neuron division and neuron budding can solve NP-complete problems in polynomial time. The Directed Hamiltonian Path (DHP) problem is an NP-hard problem, and the algorithm based on SNPS proposed by [25] effectively reduces the time complexity through massive parallelism. In [26], the authors introduced fuzzy reasoning in SNPS to establish a connection between P systems and fault diagnosis applications for the automatic implementation of complex power system fault diagnosis. Reference [27] introduced a Spiking Neural P System with spikes and anti-spikes. Biologically, spikes represent neural excitation while anti-spikes represent neural inhibition. When a spike meets an anti-spike, they cancel each other out and disappear. Based on this rule, the proof of Turing completeness of SNPS and the required rules are simplified: all rules have a singleton regular expression that precisely indicates the number of spikes or anti-spikes to be consumed.

Implementing addition, subtraction, multiplication and division on SNPS is the basis for designing a biological CPU based on the SNP system. By encoding the number as the time interval between two spikes, the literature [28] constructed four SNP systems for calculating addition, subtraction, multiplication, and division, respectively. In [29], the author encoded the number as spike sequences and designed an operation model based on SNPS to realize the addition and subtraction of two natural numbers, the multiplication of a fixed multiplicand, an arbitrary multiplier, and judging whether two numbers are equal. The SNPS operation model designed in [30] can solve the product of any two natural numbers with a binary bit length of k bits, and can solve the summation problem of n natural numbers. In [31], simple arithmetic problems were addressed using the spiking neural p system, including binary complement conversion, addition and subtraction of signed integers, and multiplication of any two natural numbers.

The motivation of the present study is to design arithmetic SNPS that are fast and contain fewer neurons and rule types. We encoded numbers as spike sequences and utilized a single input neuron and a single output neuron to design a complete set of addition, subtraction, multiplication, and division operations in SNPS based on extended rules. We analyzed the number of neurons, types of rules, and required time slices for each system. The main contributions of this paper include:

(1) Designing the SNPS Π_BASNP for k-bit binary addition. The system can complete the addition of two k-bit binary numbers in 2k + 4 time slices using k + 8 neurons, three types of instantaneous firing rules, and three types of forgetting rules.

(2) Designing the SNPS Π_BSSNP for k-bit binary subtraction. The system can complete the subtraction of two k-bit binary numbers in 2k + 3 time slices using k + 13 neurons, seven types of instantaneous firing rules, and four types of forgetting rules.

(3) Designing the SNPS Π_BMSNP for k-bit binary multiplication. The system can complete the multiplication of two k-bit binary numbers in 3k + 5 time slices using 3k + 8 neurons, five types of instantaneous firing rules, and four types of forgetting rules.

(4) Designing the SNPS Π_BDSNP for k-bit binary division. The system can complete the division of two k-bit binary numbers in 2k + quotient + 4 time slices using 5k + 12 neurons, sixteen types of instantaneous firing rules, and thirteen types of forgetting rules.

Based on instance-based analysis, the effectiveness of the four SNPS designed in this paper is verified. The rest of the paper is organized as follows. Section 2 briefly introduces the basic knowledge and related research on SNPS, Section 3 presents the designed addition, subtraction, multiplication, and division SNPS and instance analysis, and Section 4 summarizes and analyzes various known arithmetic SNPS from multiple dimensions. Finally, Section 5 summarizes the whole work.

The SNP operation model proposed in this paper uniformly uses a single input and output neuron, and a new way of input data construction was constructed. In the addition and multiplication computational models we constructed, we reduce the number of neurons used compared to the addition and multiplication proposed in [30]. Based on multiple subtraction operations, in this we paper achieve the division of any two natural numbers, and the running time of this division model is positively correlated with the size of the quotient.

2. Related Research

Spiking neural P (SN P) systems are a class of discrete neuron-inspired computation models where information is encoded by the numbers of spikes in neurons and the timing of spikes. In a spiking neural P system a spike refers to an object in a neuron, which represents the substance in a neuronal cell. In a spiking neural P system only one object is allowed in each neuron; the number of objects (spikes) is used to encode (represent) the corresponding information, such as the summand and addend in addition.

2.1. Spiking Neural P Systems

A Spiking Neural P system of degree m (m ≥ 1) is formally defined as Formula (1) [14,17,29,30,31,32]:

Π = (O, σ₁, σ₂, …, σ_m, syn, in, out)

(1)

where:

(1)

O = {a} is a singleton alphabet, where a is called a spike;

σ₁, σ₂, …, σ_m are neurons of the form σ_i = (n_i, R_i) in the Π system, with 1 ≤ i ≤ m.

Where n_i ≥ 0 is the number of spikes in neuron σ_i in the initial configuration, R_i is a finite set of rules of the following two forms:

(i)

spiking rule: E/a^c→a^p; d, where E is a regular expression over O, and c ≥ 1, d ≥ 0, p ≥ 1, c ≥ p;

(ii)

forgetting rule: E′/a^s→λ, where E′ is a regular expression over O, s ≥ 1, furthermore, for each rule E/a^c→a^p; d in the rule set R_i of type (i), it holds that$\mathrm{L}\left(\mathrm{E}\right){\displaystyle \cap }\mathrm{L}\left({\mathrm{E}}^{\prime }\right)=Ø$, where L(E) is the language generated by E.

(2)

$syn\subseteq \left\{{\mathsf{\sigma }}_1,{\mathsf{\sigma }}_2,\dots ,{\sigma }_m\right\}\times \left\{{\mathsf{\sigma }}_1,{\mathsf{\sigma }}_2,\dots ,{\sigma }_m\right\}$ is a finite set of synapses between neurons. (σ_i, σ_j) ∈ syn means that there is a synaptic connection from σ_i to neuron σ_j. For any i, 1 ≤ i ≤ m, (σ_i, σ_i)$\notin$syn;

(3)

$in,\mathrm{out}\in \left\{{\mathsf{\sigma }}_1,{\mathsf{\sigma }}_2,\dots ,{\sigma }_m\right\}$ indicate the input and output neurons, respectively. In particular, we use σ₀ to denote the environment of the system.

The explanation of the rules is as follows: if a firing rule E/a^c→a^p; d satisfies p = 1 and a forgetting rule E′/a^s→λ satisfies E′ = a^s, they are respectively called a standard firing rule and standard forgetting rule. If the firing rule E/a^c→a^p; d satisfies E = a^c, it is usually written as a^c→a^p; d. If the firing rule E/a^c→a^p; d satisfies d = 0, it is called a no-delay firing rule and written as E/a^c→a^p. If the firing rule E/a^c→a^p; d satisfies both E = a^c and d = 0, it is abbreviated as a^c→a^p. Similarly, if the forgetting rule E′/a^s→λ satisfies E′ = a^s, it can be abbreviated as a^s→λ.

The usage of a spiking rule is as follows: at a certain moment, if the neuron σ_i contains spikes and there exists a^k$\in$L(E) and k ≥ c, then the neuron σ_i can activate the spiking rule E/a^c→a^p; d, consuming c spikes (leaving k − c spikes), and after d time slices, emit p spikes to all the neurons it is connected to. Additionally, during the period of sending d spikes after using this rule, the neuron σ_i is in a closed state, which means it cannot use any rules or receive spikes from other neurons. Only after σ_i becomes open (after d time slices) can it use rules and receive spikes. If a neuron sends spikes to a closed neuron, these spikes will naturally disappear. For an output neuron, it can send spikes to the environment.

The usage of the forgetting rule is as follows: at a certain moment, if the neuron σ_i contains k’ spikes and satisfies a^k′$\in$L(E′) and k’ ≥ s, this neuron can use the forgetting rule E′/a^s→λ, which consumes s spikes and does not generate new spikes.

If multiple spiking rules are satisfied in a single neuron, it will randomly choose one of them to execute. For example, if there are two spiking rules in neuron σ_i, E₁/a^c→a^p1; d₁ and E₂/a^c2→a^p2; d₂, with $\mathrm{L}\left(\mathrm{E}1\right){\displaystyle \cap }\mathrm{L}\left(\mathrm{E}2\right)\ne Ø$, σ_i can only randomly choose one of them to use. This is the uncertainty of rule usage. While the usage of rules in a single neuron is serial, all neurons in the entire system work in parallel.

To describe the temporal evolution of each neuron in the SNP system, it is assumed that there is a unified clock in the system and timing is done using time slice. Its pattern at time slice k can be defined as C_k = (r₁^(k)/t₁^(k), r₂^(k)/t₂^(k), …, r_m^(k)/t_m^(k)). Here, r_i^(k) (1 ≤ i ≤ m) denotes the number of spikes contained in neuron σ_i at time k and t_i^(k) represents the number of time slices needed for σ_i to reach an open state starting from time slice k. In particular, the initial pattern of the system can be represented as C₀ = {r₁⁽⁰⁾/0, r₂⁽⁰⁾/0, …, r_m⁽⁰⁾/0}. Through the execution of rules, the transformation of the pattern of the Π system is called computation. A pattern in which all neurons in the system are in an open state and no rules can be used is called a termination pattern, and a computation that can reach a termination pattern is called a terminable computation.

In terminating computations, there are two encoding methods for representing the computation result [32,33]. The first method represents an operandas the number of time slices between two spikes (one binary “1” is represented as one spike). The second method represents the generated spike sequence as the computation result (one spike represents the binary digit 1, and no spike represents the binary digit 0), thereby obtaining a binary string. These results can be stored in the neurons of the SNPS or output to the environment.

2.2. Research on Arithmetic Operation of SNP

Arithmetic operations are the basis for solving other complex problems and have always been a focus of SNPS research. In [28], the authors encoded the number as the time interval between two spikes to construct four SNP systems for calculating addition, subtraction, multiplication, and division. The number of neurons used was 10, 12, 22, and 24, respectively, and there were 4, 4, 12, and 15 rule types, respectively. In [29], numbers were coded into spike sequences and realized in three parts: the addition and subtraction of two natural numbers, the multiplication of fixed multiplicands and arbitrary multipliers, and the judgment of whether two numbers were equal. In this operation model, the addition of two natural numbers used three neurons and three rule types, subtraction used 1ten neurons and six rule types, and multiplication used thirteen neurons and three rule types. In particular, the multiplier was fixed at 26 and used three neurons and two rule types to judge whether two numbers are equal. This article raised the open problem of how to design SNPS to solve the multiplication of two arbitrary natural numbers. In [30], the authors better answered the question about multiplication proposed by [29]. The designed operation model can solve the product of any two natural numbers of k-bit length binary digits (using k² + 5k + 3 neurons and ten rule types while taking 4k + 2 time slices) and designed an operation model that can solve the sum of n natural numbers (using 3k + 5 neurons and nine rule types). In [31], simple arithmetic problems were addressed using SNPS, including binary complement conversion (using six neurons and four rule types), addition and subtraction of signed integers (using seven neurons and six rule types), and the multiplication of any two natural numbers (using k²/2 + 15k/2 + 4 neurons and six rule types). The operation of signed numbers in [31] was realized based on the sign bit and complement, and the subtraction operation was realized by adding the opposite number of the addend. In [28,29,31], the system had multiple input neurons, while in [30] there was only a single input neuron. In the SNP system mentioned above, the rules in neurons are all executed within one time slice. However, the time required for different biological operations is different as well. In [34], the authors introduced an SNP system with no time limit. This system’s rule execution is time-independent and always produces the same result, and it was proven that a time-free SNP system with extended rules is Turing-complete. In [35], the authors studied and designed an adder, subtractor, multiplier, and divider based on the non-time-limited SNP system proposed in [34] using 2, 2, 11, and 10 neurons and 2, 6, 15, and 16 rule types, respectively. In [36], the authors designed the adder and multiplier of the SNPS with rules and weights using 2k + 4, 5k neurons and 13, k + 14 rule types, respectively. Based on the SNPS with anti-spikes introduced in [27], the authors of [37] considered the design of general-purpose AND gates, OR gates, and NOT gates for symmetric ternary systems. The three states correspond well to the 1, 0, and −1 of the symmetric ternary system, which could effectively solve the representation and operation of negative integers. In [37], the authors realized the addition and subtraction of signed integers with an anti-spike neural p system.

In this paper, we only deal with arithmetical operations between natural numbers. For example, when a natural number n is represented in Formula (2), we obtain the corresponding binary string b_k−1……b₁b₀, where b₀ is the least significant bit, b_k−1 is the most significant bit, and 2ⁱ is the order of 2ⁱ, with 0 ≤ i ≤ k − 1.

n = b_k−12^k−1 + …… + b₁2¹ + b₀2⁰, 0 ≤ b_i ≤ 1, 0 ≤ i ≤ k − 1

(2)

3. Arithmetic Operation in Spiking Neural P Systems

This part discusses in detail the four arithmetic SNPS designed in this paper. To perform arithmetical operations on SNPS, we input the natural numbers into the system which to be computed and output the computation results. In this paper, we use binary strings to represent natural numbers, and we make the following assumptions:

(1)

A unified clock is used to manage and maintain the operation process, with the unit of time being the time slice. The execution of each rule in the SNPS only requires one time slice.

(2)

The binary strings involved in the operations have k digits. If a string has less than k digits, it is padded with leading zeros to reach k digits.

(3)

The SNPS can accept one binary digit per time slice. When a binary digit of 1 is received, this means the system has received a spike; otherwise, no spike is received. The system receives the input binary string from the least significant bit to the most significant bit.

(4)

In the addition, subtraction, and multiplication SNPS the system operation result is outputted by the output neurons from low to high bits in the form of a binary string. In the division SNPS the operation result is stored in a set of result neurons.

(5)

In our designed SNPS we set parameter d in the rule description of Formula (1) to 0. This means that both the spiking rule and the forgetting rule will be executed immediately once the conditions are satisfied.

The four SNP operational models proposed in this paper have all been proven to function correctly. Our proof strategy involves tracking the changes in the number of spikes in key neurons over time slices and providing spike count diagrams for the critical patterns of neurons when necessary. For example, Section 3.1 illustrates the pattern of the adder at t = k + 2, where the augend has already been input into the augend cache neuron group. Finally, the system provides the computation result for each digit over the time slice.

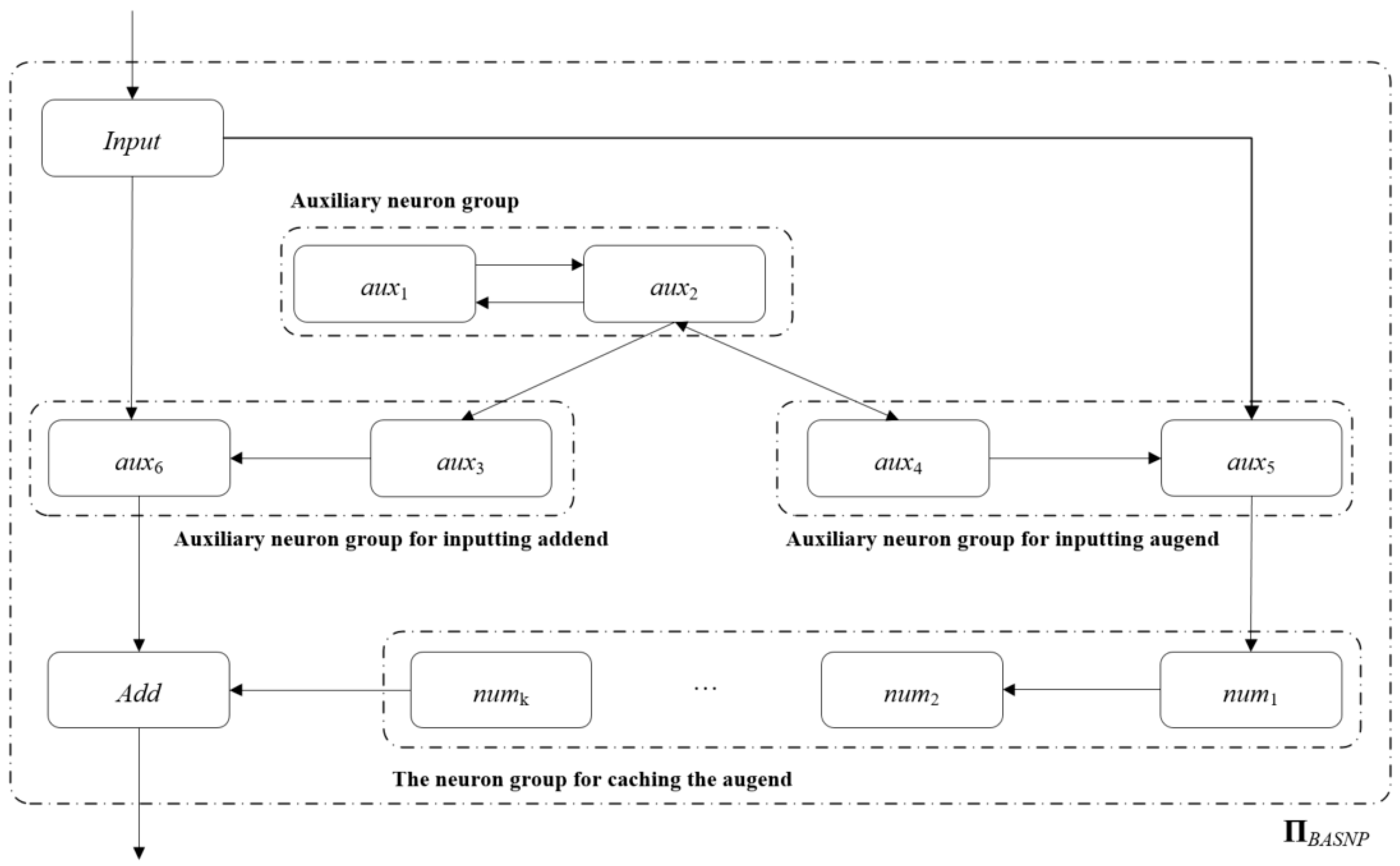
3.1. Binary Addition in SNP Systems

The addition operation is the foundation of arithmetic operations. It involves adding two binary numbers with the same order while considering the possibility of a carry from the lower order. The basic idea of our designed binary addition SNPS is:

(1)

By inputting the binary string of the addend from the lowest bit to the highest bit using the input neuron σ_input, if the i-th bit (0 ≤ i ≤ k − 1) in the input string is 1, the neuron σ_input generates one spike; otherwise, it generates no spike.

(2)

After each bit of the augend is input, it is buffered in the system and waits for the input of the addend. When the highest bit of the augend is input, the addend is immediately input.

(3)

When the i-th bit (0 ≤ i ≤ k − 1) of the augend reaches the addition neuron σ_Add, the i-th bit of the addend is taken out from the buffer and input to σ_Add. The addition operation is performed by the rules in σ_Add.

Therefore, the spike neural p system Π_BASNP for the k-bit binary number addition designed in this paper includes an input neuron, addition neuron, auxiliary neuron group, augend input auxiliary neuron group, addend input auxiliary neuron group, and augend cache group of neurons. Π_BASNP is defined as in Formula (3), and the membrane structure is shown in Figure 1.

In particular, in order to simplify the complex connections between neurons, the following conventions are used in the SNPS structure diagram in this paper:

• Neuron-to-neuron connections are indicated by thin arrows, for example, the connection between σ_aux1 and σ_aux2 in Figure 1.
• Connections of neurons to groups of neurons are indicated by thick arrows. Specifically, if the front end of the thick arrow is a single neuron σ₀, and the end is a neuron group σ_x = {σ₁, σ₂, …, σ_n}, this means that each neuron σ_i (1 ≤ i ≤ n) in neuron σ₀ is connected to neuron group σ_x; on the contrary, if the front end of the thick arrow is a neuron group σ_x, and the end is a single neuron σ₀, this means that each neuron in the neuron group σ_x has a connection to neuron σ₀.
• Group-to-neuron connections are indicated by thick arrows. If the front end of the thick arrow is a neuron group σ_x = {σ₁, σ₂, …, σ_n} and the end is a neuron group σ_x′ = {σ_1′, σ_2′, …, σ_n′}, then two neurons in the same order from the group σ_x to the neuron group σ_x′ are connected, that is, there is a connection from σ_i to σ_i′, 1 ≤ i ≤ n.

Π_BASNP = (O, σ_aux1, σ_aux2, …, σ_aux6, σ_num1, σ_num2, …, σ_numk, syn, in, out)

(3)

where:

(1)

O = {a};

(2)

σ_Input = (0,R_Input), R_Input = {a→a};

(3)

σ_aux1 = (1,R_aux1), R_aux1 = {a→a};

(4)

σ_aux2 = (1,R_aux2), R_aux2 = {a→a};

(5)

σ_aux3 = (0,R_aux3), R_aux3 = {a^k→a²};

(6)

σ_aux4 = (0,R_aux4), R_aux4 = {a^k→a²};

(7)

σ_aux5 = (0,R_aux5), R_aux5 = {a→a; a³/a→λ};

(8)

σ_aux6 = (0,R_aux6), R_aux6 = {a→λ; a³/a→a};

(9)

σ_numi = (0,R_numi), R_numi= {a→a},$i\in \left\{1,2,\cdots ,k\right\}$;

(10)

σ_Add = (0,R_Add), R_Add = {a→a; a²/a→λ; a³/a²→a};

(11)

syn = {(Input,aux_i)|$i\in \left\{5,6\right\}$}∪{(aux₁,aux₂)}∪{(aux₂,aux_i)|$i\in \left\{1,3,4\right\}$}∪{(aux₃,aux₆)}∪{(aux₄,aux_i)|$i\in \left\{2,5\right\}$}∪{(aux₅,num₁)}∪{(num_i,num_i+1)|$i\in \left\{1,2,\dots ,k-1\right\}$}}∪{(num_k,Add)};

(12)

in = σ_input;

(13)

out = σ₀ (indicates that the system outputs the calculation results to the environment)

In Π_BASNP, we divide the neurons except σ_Input and σ_Add into several groups (see the dashed box in Figure 1), and their functions are as follows:

• Neuron Input. The Input neuron receives binary strings from the environment and converts them to spikes in Π_BASNP.
• Neuron Add. The bit-by-bit addition of binary strings is realized by spiking rules and forgetting rules.
• Auxiliary neuron groups (aux₁, aux₂). Continuously send one spike to neurons aux₃ and aux₄ at each time slice.
• The augend is input to the auxiliary neuron group. Accurately input the spike train representing the augend into the augend cache neuron group, and shield the interference when the augend spike train is input.
• Addend input to auxiliary neuron group. Shield the input of the addend spike train, and accurately input the spike train representing the addend to the neuron Add.
• The augend cache neuron group. Buffer the augend spike train, and send the augend spike train to the neuron Add for operation in due course.

For Π_BASNP, Theorem 1 can be obtained.

Theorem 1. 

Input two natural numbers of length k (k ≥ 2) to the input neuron σ_Input of Π_BASNP sequentially from low to high in binary form; this system can correctly calculate the sum of these two natural numbers.

Proof of Theorem 1. 

Let t represent the system time and the unit be a time slice, that is, the value of t increases by one every time a time slice is passed. Here, X and Y are any two binary natural numbers with no more than k digits, and $\mathrm{X}={\displaystyle \sum }_{\dot{i}=0}^{k-1}{x}_i{2}^i$, $\mathrm{Y}={\displaystyle \sum }_{\dot{i}=0}^{k-1}{y}_i{2}^i$. We provide input to Π_BASNP sequentially from low bit to high bit in binary form. When the binary number received by Π_BASNP is 1, a spike a appears in σ_Input; otherwise, no spike appears in σ_Input. From t = 1 to t = 2k, Π_BASNP receives spikes corresponding to x₀ to x_k−1 and y₀ to y_k−1 in sequence. When t > 2k + 1, Π_BASNP will not accept input. We use sp-x_i to represent the spike corresponding to the binary number x_i, that is, when x_i = 1, sp-x_i = {a}; otherwise, sp-x_i = {λ}. Similarly, sp-y_i is used to represent the spike corresponding to the binary number y_i, which will be used in the following proofs. The execution process of Π_BASNP is as follows.

(1)

t = 0, start sending the corresponding spike sp-x₀ of the lowest bit x₀ of X to σ_Input.

(2)

From t = 1 to t = k, the regular execution of Π_BASNP and the change of spikes in each neuron include:

(i)

σ_Input accepts sp-x_i (0 ≤ i ≤ k − 1) and applies the corresponding rules to send sp-x_i to σ_aux5. During this period, σ_aux5 can only receive the spikes sent by σ_Input, and apply the rules to send the received spikes to σ_num1 in turn. Similarly, σ_numj (1 ≤ j ≤ k − 2) sends the received spikes to σ_numj+1 in sequence.

(ii)

σ_aux6 accepts the spikes sent by σ_Input, if sp-x_i (0 ≤ i ≤ k − 2) = {a}, use the rule a→λ to forget this spike.

(iii)

σ_aux1 and σ_aux2 (starting to work at t = 1) each maintain one spike, and σ_aux3 and σ_aux4 each maintain k − 1 spikes at t = k.

(iv)

There is no spike in σ_Add.

(3)

At time t = k + 1, the rule execution of Π_BASNP and the change of spikes in each neuron include:

(i)

σ_aux6 accepts sp-x_k−1 and forgets sp-x_k−2.

(ii)

σ_aux1 and σ_aux2 keep one spike each, σ_aux3 and σ_aux4 keep k spikes and apply the rule a^k→a² to send two spikes to σ_aux5 and σ_aux6 respectively.

(iii)

There is no spike in σ_Add.

(4)

At time t = k + 2, the rule execution of Π_BASNP and the change of spikes in each neuron include:

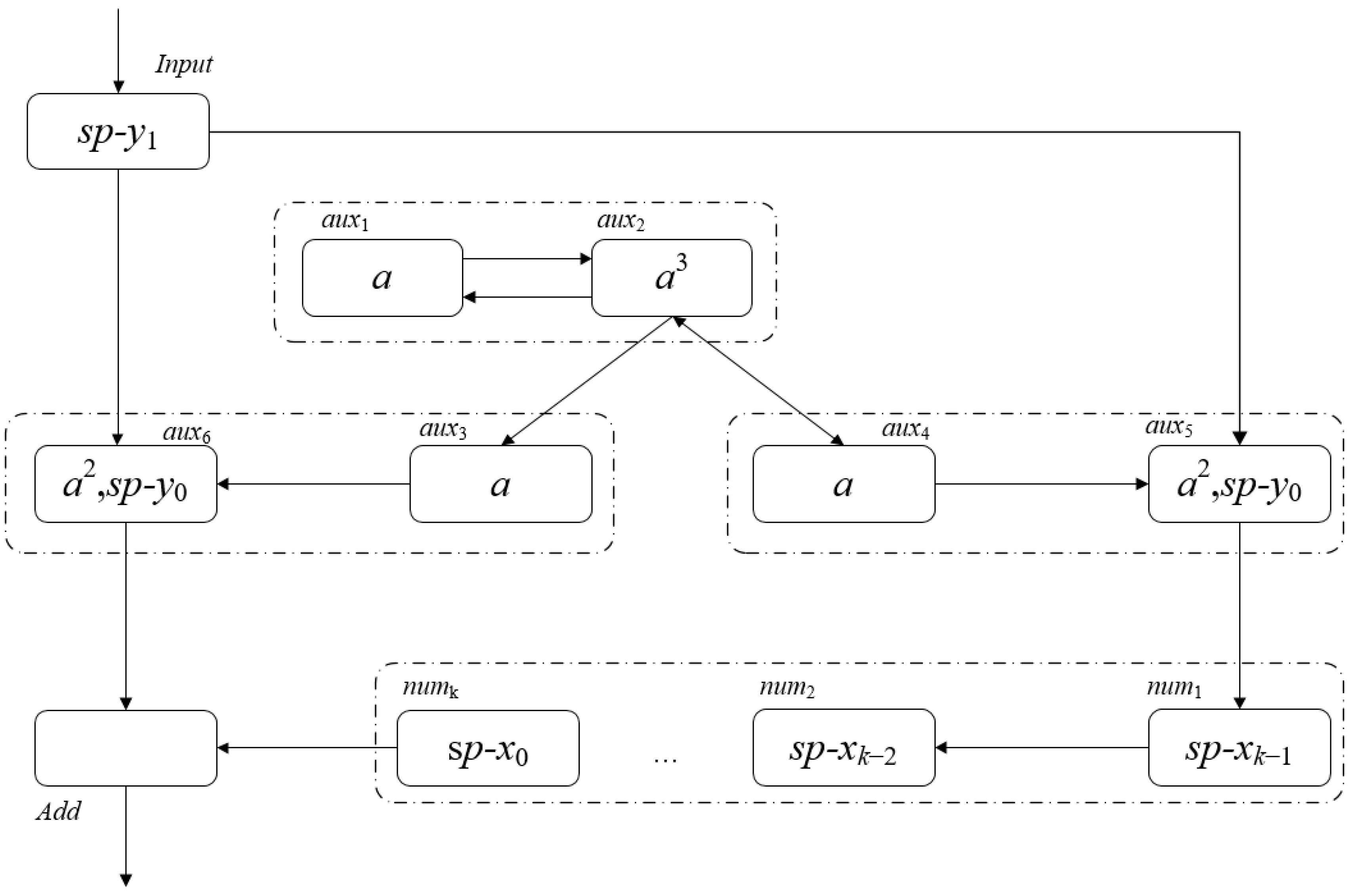
(i)

σ_Input accepts sp-y₁ and sends sp-y₀ to σ_aux5. σ_aux5 sends sp-x_k−1 to σ_num1 while receiving sp-y₀ and {a²} from σ_aux4. σ_numj (1 ≤ j ≤ k − 1) accepts sp-x_k-j and sends sp-x_k-j−1, and σ_numk accepts sp-x₀.

(ii)

σ_aux6 forgets sp-x_k−1 accepts both sp-y₀ (from σ_Input) and {a²} (from σ_aux3).

(iii)

σ_aux1 holds one spike, σ_aux2 gets three spikes (one spike from σ_aux1 and two spikes from σ_aux4), σ_aux3 and σ_aux4 hold one spike.

(iv)

There is no spike in σ_Add.

At this point, the augend has been input into the augend cache neuron group and we can obtain Figure 2, which shows the spikes contained in each neuron in the configuration C_k+2.

(5)

From t = k + 3 to t = 2k + 2, the rule execution of Π_BASNP and the change of spikes in each neuron include:

(i)

σ_Input sequentially accepts sp-y_j (2 ≤ j ≤ k − 1) and simultaneously applies the rules to send sp−y_j−1 to σ_aux5 and σ_aux6. When the number of spikes in σ_aux5 is three, the rule a³/a→λ is activated and consumes one spike, so there will always be two spikes in σ_aux5 and no spikes will be sent.

(ii)

Since σ_aux6 keeps two spikes, when it receives a spike from σ_Input, it will apply the rule a³/a→a to consume one spike and send one spike to σ_Add, and make σ_aux6 keep two spikes.

(iii)

σ_aux1 sends 1 spike to σ_aux2, σ_aux2 receives one spike, σ_aux3 and σ_aux4 keep one spike.

(iv)

Starting from time t = k + 3, σ_Add receives sp-x_i and sp-y_i (0 ≤ i ≤ k − 1) at the same time. Readers can refer to [29] for details of the addition operation in σ_Add.

(v)

From time t = k + 4, the environment starts to receive calculation results in sequence.

(vi)

From t = 2k + 1 time slice, σ_Input no longer accepts the input of the environment, and only sends the spikes it contains to σ_aux5 and σ_aux6 by using the rules.

(vii)

At t = 2k + 2, the highest bit x_k−1 of X and y_k−1 of Y reach the neuron σ_Add, if X + Y < 2^k+1, the system will reach the termination pattern at t = 2k + 3; If X + Y ≥ 2^k+1, the system will eventually reach the termination pattern at t = 2k + 4.

Based on the above description, readers can verify that for k ≥ 2, the SNPS Π_BASNP for addition constructed above can correctly solve the sum of two natural numbers with a binary length of k, and the proof is complete. □

Figure 3 shows a Π_BASNP structure for three-bit binary addition. Based on this Π_BASNP, the addition process of the natural numbers 7 and 5 is listed in

Table 1. Π_BASNP calculation process of the instance 111₂ + 101₂ = 1100₂.

Step t	Input	aux1	aux2	aux3	aux4	aux5	aux6	num1	num2	num3	Add	Output
0	-	1	1	0	0	0	0	0	0	0	0	-
1	1	1	1	0	0	0	0	0	0	0	0	-
2	1	1	1	1	1	1	1	0	0	0	0	-
3	1	1	1	2	2	1	1	1	0	0	0	-
4	1	1	1	3	3	1	1	1	1	0	0	-
5	0	1	3	1	1	3	3	1	1	1	0	-
6	1	0	4	1	1	2	2	0	1	1	2	-
7	-	0	4	1	1	3	3	0	0	1	2	0
8	-	0	4	1	1	2	2	0	0	0	3	0
9	-	0	4	1	1	2	2	0	0	0	1	1
10	-	0	4	1	1	2	2	0	0	0	0	1

, which shows the number of spikes contained in each neuron in Π_BASNP(7,5). The two natural numbers expressed in binary form are 111₂, 101₂, and 111₂ + 101₂ = 1100₂. In Figure 3, the augend and the addend are input through the neuron Input, the auxiliary neuron group (aux₁, aux₂) continuously sends a spike to the neuron aux₃, aux₄ respectively, the auxiliary neuron group (aux₄, aux₅) controls the input of the augend 7 (111) to the augend cache neuron group (num₁, num₂, num₃), and the auxiliary neuron group (aux₃, aux₆) controls the input of the addend 5 (111) to the neuron Add. Finally, the addition operation is performed in the neuron Add.

In Table 1, the first column represents the system moment, and the second to the last column represent each neuron in the system. Each row of Table 1 represents the number of spikes in each neuron in the system at the corresponding moment. For example, the number in the first column of the sixth row (step t = 5) is 0, indicating that the binary bit currently input to the neuron Input is 0. The number from the eighth column to the tenth column is 1, which successively indicates that the binary bit of the augend buffer neuron group (num₁, num₂, num₃) is 1 and the input of the augend 7 has been completed.

The Π_BASNP designed in this section can complete the addition of two k-bit binary numbers within 2k + 4 time slices, and the number of neurons used is k + 8. The neurons in Π_BASNP use three types of non-delay spiking rules and three types of forgetting rules.

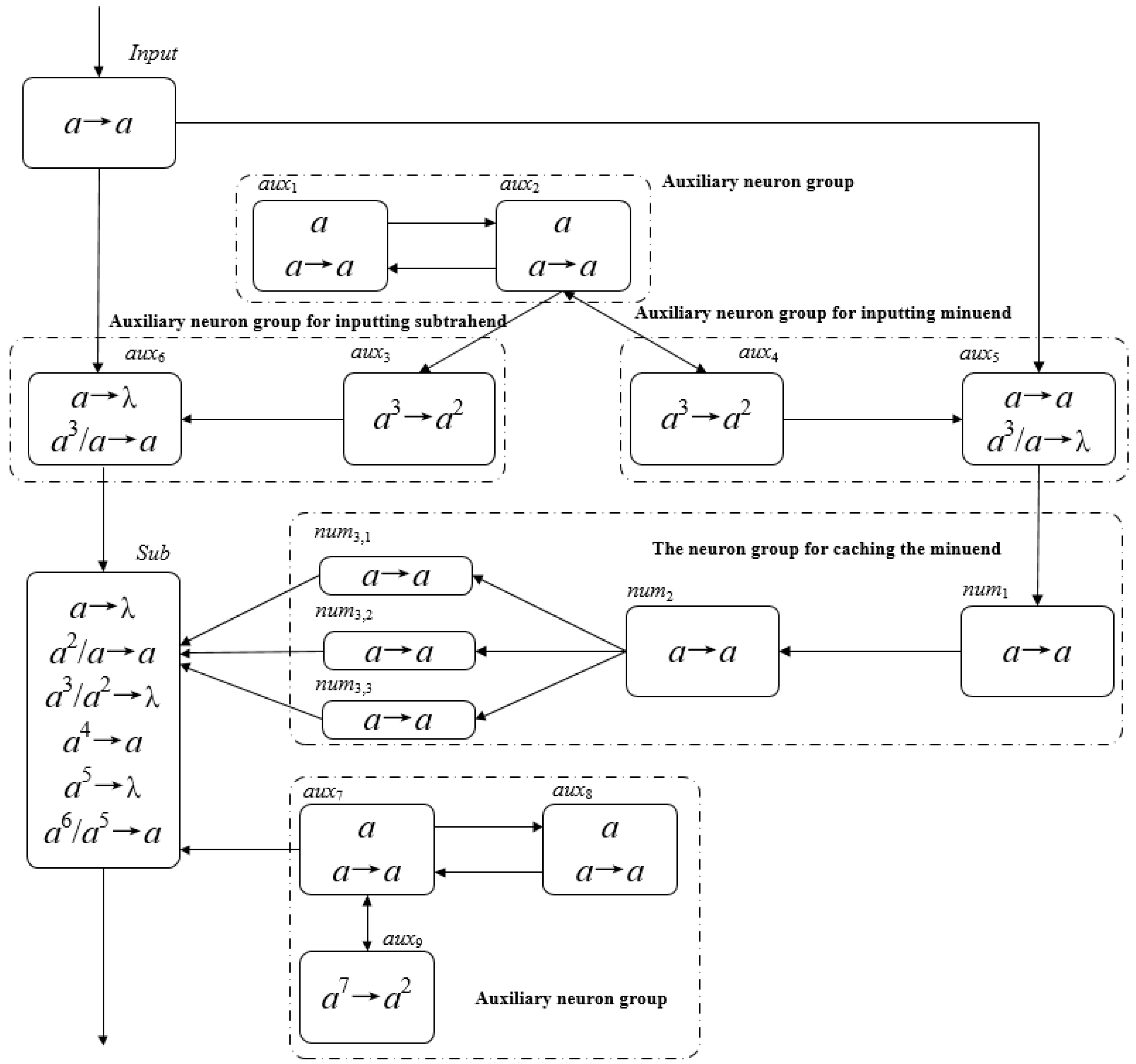
3.2. Binary Subtraction in SNP Systems

Subtraction is another basic binary arithmetic operation. The idea is to subtract the subtrahend from the minuend. Considering whether there is a borrow in the lower bit, we subtract the values of the same order from two binary numbers. The idea of our designed binary subtraction SNPS is:

(1)

Through the input neuron Input, input the binary string of the minuend from the lowest bit to the highest bit. When the i-th bit (0 ≤ i ≤ k − 1) in the input string is 1, the neuron Input gets one spike, otherwise it does not get a spike.

(2)

After each digit of the subtrahend is input, it will be cached in the system, waiting for the input of the subtrahend. Input the subtrahend immediately after the highest bit of the minuend is input.

(3)

When the i-th bit of the subtrahend (0 ≤ i ≤ k − 1) reaches the subtraction neuron Sub, the i-th bit of the minuend in the cache is taken out and put into the Sub, and the subtraction operation is performed according to the rules in the Sub.

(4)

Before the i-th bit of the minuend (0 ≤ i ≤ k − 1) reaches the subtraction neuron Sub, 3 spikes represent the number 1, and 0 spikes represent the number 0.

Therefore, the SNPS Π_BSSNP for binary subtraction designed in this paper includes input neuron, subtraction neuron, auxiliary neuron group, subtrahend input auxiliary neuron group, subtrahend input auxiliary neuron group, and minuend cache group of neurons. The structure of Π_BSSNP is shown in Figure 4, and its formal definition is shown in Formula (4).

Π_BSSNP = (O, σ_aux1, σ_aux2, …, σ_aux9, σ_num1, σ_num2, …, σ_numk−1, σ_numk,1, σ_numk,2, σ_numk,3, syn, in, out)

(4)

where

(1)

O = {a};

(2)

σ_Input = (0,R_Input), R_Input = {a→a};

(3)

σ_aux1 = (1,R_aux1), R_aux1 = {a→a};

(4)

σ_aux2 = (1,R_aux2), R_aux2 = {a→a};

(5)

σ_aux3 = (0,R_aux3), R_aux3 = {a^k→a²};

(6)

σ_aux4 = (0,R_aux4), R_aux4 = {a^k→a²};

(7)

σ_aux5 = (0,R_aux5), R_aux5 = {a→a; a³/a→λ};

(8)

σ_aux6 = (0,R_aux6), R_aux6 = {a→λ; a³/a→a};

(9)

σ_aux7 = (1,R_aux7), R_aux7 = {a→a};

(10)

σ_aux8 = (1,R_aux8), R_aux8 = {a→a};

(11)

σ_aux9 = (0,R_aux9), R_aux9 = {a^2k+1→a²};

(12)

σ_numi = (0,R_numi), R_numi = {a→a}, $i\in \left\{1,2,\cdots ,k-1\right\}$;

(13)

σ_numk,i = (0,R_numk,i), R_numk,i = {a→a}, $i\in \left\{1,2,3\right\}$;

(14)

σ_Sub = (0,R_Sub), R_Sub = {a→λ; a²/a→a; a³/a²→λ; a⁴→a; a⁵→λ; a⁶/a⁵→a};

(15)

syn = {(Input,aux_i)|$i\in \left\{5,6\right\}$}∪{(aux₁,aux₂)}∪{(aux₂,aux_i)|$i\in \left\{1,3,4\right\}$}∪{(aux₃,aux₆)}∪{(aux₄,aux_i)|$i\in \left\{2,5\right\}$}∪{(aux₆,Sub)}∪{(aux₇,aux₈)}∪{(aux₇,aux₉)}∪{(aux₇,Sub)}∪{(aux₈,aux₇)}∪{(aux₉,aux₇)}∪{(aux₅,num₁)}∪{(num_i,num_i+1)|$i\in \left\{1,2,\dots ,k-2\right\}$}}∪{(num_k−1,num_k,i)|$i\in \left\{1,2,3\right\}$}∪{(num_k,i,Sub)|$i\in \left\{1,2,3\right\}$};

(16)

in = input;

(17)

out = σ₀;

In Π_BSSNP, the functions of each neuron (neuron group) are as follows:

• Input neuron Input. Input receives binary strings from the environment and converts them to spikes in Π_BSSNP.
• Subtractive neuron Sub. The binary strings of the subtrahend and the minuend are subtracted bit by bit in the neuron Sub.
• Auxiliary neuron groups (aux₁, aux₂, aux₇, aux₈, aux₉). Continuously send a spike to neurons aux₃, aux₄, and Sub at each time slice.
• Minuend input auxiliary neuron group. The subtrahend is controlled to be accurately input into the minuend cache neuron, and the interference when the subtrahend is input is shielded.
• Minus input auxiliary neuron group. The subtrahend is controlled to be accurately input to the neuron Sub, and the interference when the subtrahend is input is shielded.
• Minuend cache neuron groups. The minuend is cached so that the corresponding binary bits of the minuend and the subtrahend are synchronously sent to the neuron Sub for operation.

It can be seen from the following theorem that Π_BSSNP can complete the subtraction of two k-bit binary strings as input.

Theorem 2. 

For the binary subtractor implemented by the SNPS shown in Figure 4, two natural numbers of length k (k ≥ 2) are input to its input neuron σ_Input in binary form from low to high, and this system can find the difference between two natural numbers.

Proof of Theorem 2. 

Let t represent the time slice length, t = 0 be the initial state of the system, X and Y be two arbitrary natural numbers, and $\mathrm{X}={\displaystyle \sum }_{\dot{i}=0}^{k-1}{x}_i{2}^i$, $\mathrm{Y}={\displaystyle \sum }_{\dot{i}=0}^{k-1}{y}_i{2}^i$. Readers can easily find that the input device composed of neurons σ_Input and neurons σ_aux1, σ_aux2, …, σ_aux6 is the same as in Section 3.1; will not be repeated here. Π_BSSNP implementation process is different from the adder in Section 3.1 as follows.

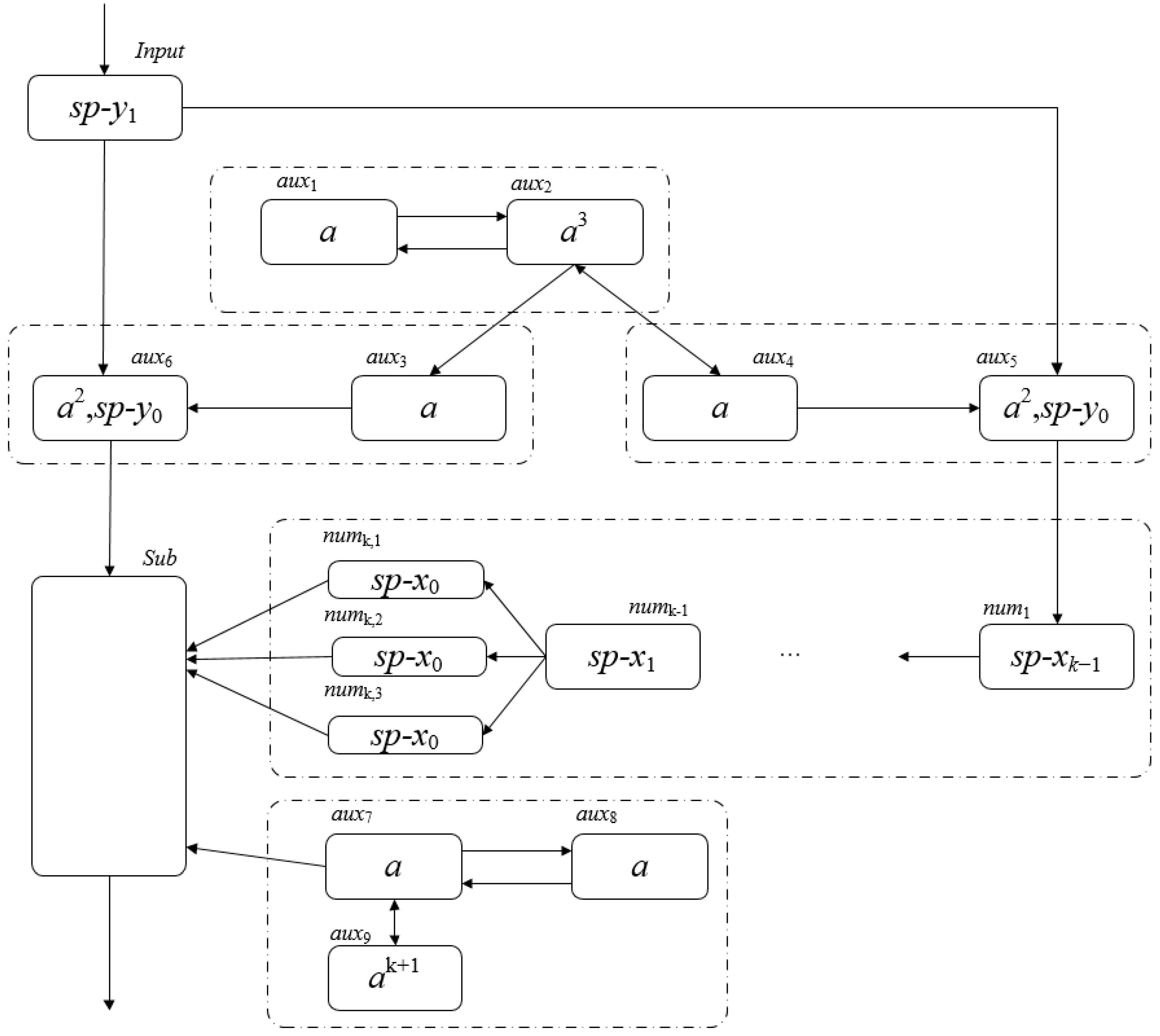
(1)

t = k + 1, the spike in σ_numj (1 ≤ j ≤ k − 1) is sp-x_k−j−1, and at the next time slice, σ_numk−1 will move to σ_numk,1, σ_numk,2, σ_numk,3 send spikes in σ_numk−1, respectively.

(2)

σ_aux7, σ_aux8 maintain a spike and σ_aux7 sends a spike to σ_Sub at each time slice. At t = k + 1, there are k spikes in σ_aux9. There are no spikes in σ_Sub.

(3)

When t = k + 2, the minuend is input into the minuend cache neuron group, and the pattern C_k+2 of Π_BSSNP is as shown in Figure 5.

(4)

From t = k + 3 to 2k + 2, σ_Sub simultaneously receives sp-x_i and sp-y_i (0 ≤ i ≤ k − 1) sequentially. Readers can refer to [13] for details of the subtraction operation in σ_Sub.

(5)

Starting from time t = k + 4, the environment starts to receive the calculation results in sequence.

(6)

t = 2k + 2, there are 2k + 1 spikes in σ_aux9, and the rule a^2k+1→a² is executed, which will consume 2k + 1 spikes and send two spikes to σ_aux7.

(7)

t = 2k + 3, there is 1 spike in σ_aux9, three spikes in σ_aux7, and one spike in σ_aux8, which will not change after that.

Because subtraction does not need to consider the carry operation of adding the highest digits of two natural numbers, there is no need to wait another time for the system to reach the termination pattern. It is not difficult for readers to verify that the system will reach the termination pattern at t = 2k + 3.

Based on the above description, readers can verify that for k ≥ 2, the SNPS Π_BSSNP for subtractor constructed above can correctly solve the difference between two natural numbers with a binary length of k, and the proof is complete. □

Figure 6 shows a Π_BSSNP structure for a three-bit binary subtraction. Based on this Π_BSSNP, the subtraction process of natural numbers 5 and 2 is listed in

Table 2. Π_BSSNP calculation process of the instance 101₂ − 010₂ = 011₂.

Step t	Input	aux1	aux2	aux3	aux4	aux5	aux6	aux7	aux8	aux9	num1	num2	num3, i (i = 1,2,3)	Sub	Output
0	-	1	1	0	0	0	0	1	1	0	0	0	0	0	-
1	1	1	1	0	0	0	0	1	1	0	0	0	0	0	-
2	0	1	1	1	1	1	1	1	1	1	0	0	0	1	-
3	1	1	1	2	2	0	1	1	1	2	1	0	0	1	-
4	0	1	1	3	3	1	1	1	1	3	0	1	0	1	-
5	1	1	3	1	1	2	2	1	1	4	1	0	1	1	-
6	0	0	4	1	1	3	3	1	1	5	0	1	0	4	-
7	-	0	4	1	1	2	2	1	1	6	0	0	1	2	1
8	-	0	4	1	1	2	2	1	1	7	0	0	0	5	1
9	-	0	4	1	1	2	2	3	1	1	0	0	0	1	0

, which shows the number of spikes contained in each neuron in Π_BSSNP (5,2). The two natural numbers expressed in binary form are: 101₂, 010₂, and 101₂ − 010₂ = 011₂. In Figure 6, the augend and the addend are input through the neuron Input, the auxiliary neuron group (aux₁, aux₂) continuously sends a spike to the neuron aux₃, aux₄, respectively, and the auxiliary neuron group (aux₁, aux₂) continuously sends a spike to the subtraction neuron Sub, the subtrahend input auxiliary neuron group (aux₄, aux₅) controls the subtrahend 5 (101) input to the subtrahend cache neuron group (num₁, num₂, num_3,1, num_3,2, num_3,3), the subtrahend input auxiliary neuron group (aux₃, aux₆) controls subtrahend 2 (010) input to neuron Sub, and finally subtraction operation is performed in neuron Sub.

In Table 2 column 1 likewise represents the system moment and columns 2–1 represent each neuron in the system. Each row of Table 2 represents the number of spikes in each neuron in the system at the corresponding moment. For example, the number in the first column of row 6 (step t = 5) is 1, indicating that the binary bit currently input to the neuron Input is 1. The numbers from the 11th column to the 13th column are 1, 0, 1, respectively, indicating that the binary bits of the minuend cache neuron group (num₁, num₂, num_3,1, num_3,2, num_3,3) are 1, 0, 1 respectively, and the input of minuend 5 (101) has been completed.

The Π_BSSNP designed in this section can complete the subtraction of two k-bit binary numbers within 2k + 3 time slices, and the number of neurons used is k + 13. The neurons in Π_BSSNP use a total of seven types of non-delay spiking rules and four types of forgetting rules.

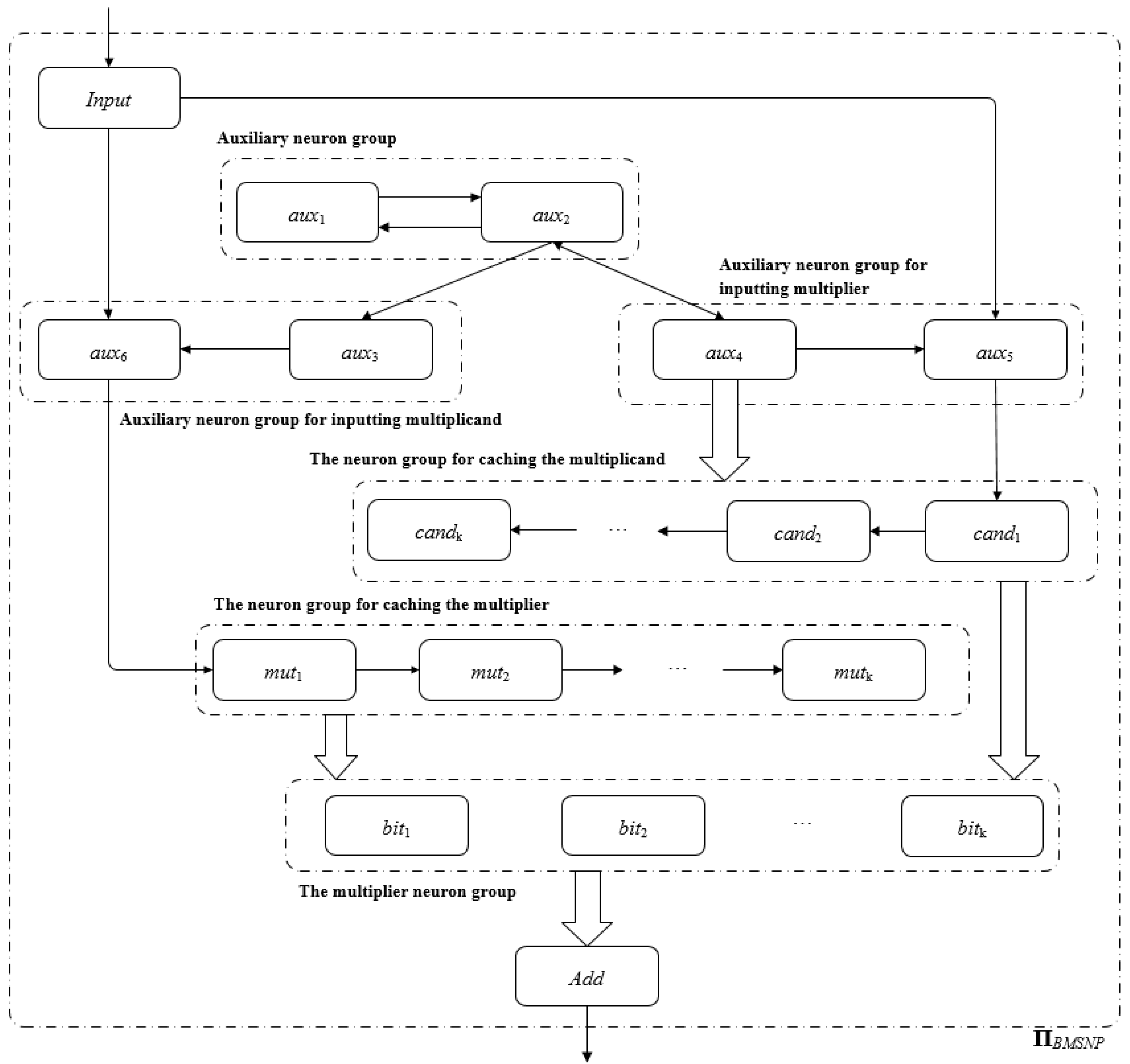
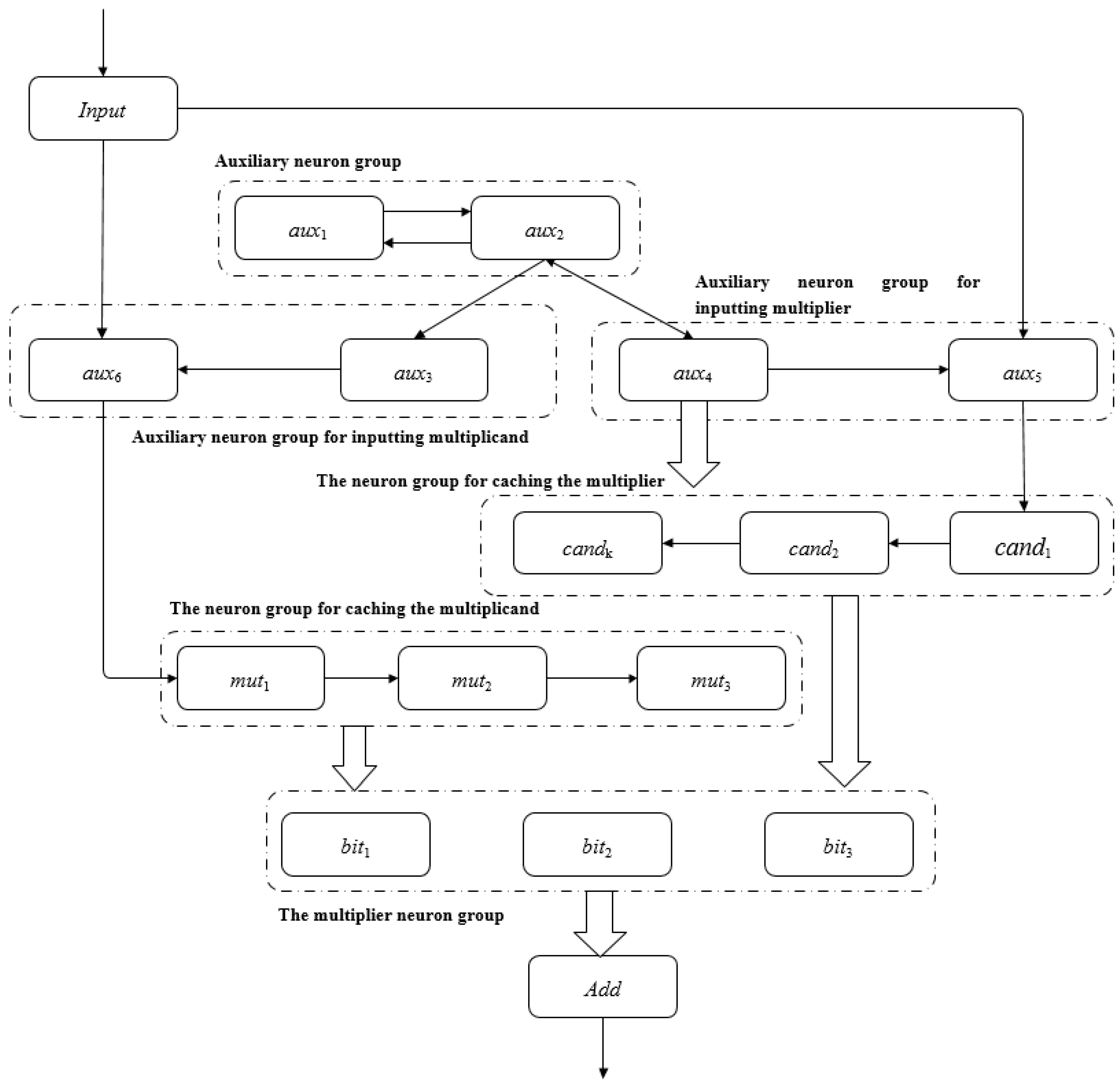
3.3. Binary Multiplication in SNP Systems

The basic idea of multiplication is to multiply each bit of two binary numbers, and the multiplied results will be added to be the final result according to the weight. In [30], the authors provide an SNPS for solving the product of any natural number within two k-bits. The SNPS for multiplication in their paper uses a large number of neurons, and the total time required for the calculation is not provided in detail. The basic idea of the binary multiplicative SNPS we designed is:

(1)

Through the input neuron Input, inputting the binary string of the multiplicand from the lowest bit to the highest bit. When the i-th bit (0 ≤ i ≤ k − 1) in the input string is 1, the neuron Input gets one spike; otherwise, it does not get a spike.

(2)

After each bit of the multiplicand is input, it is cached in the system. When all bits of the multiplicand are input, store the multiplicand in the multiplicand neuron group and wait for the input of the multiplier. After inputting the highest bit of the multiplicand, the multiplier is entered immediately.

(3)

After each bit of the multiplier is input, it is cached in the system and sent to the multiplicand neuron to perform multiplication with the corresponding binary bit of the multiplicand.

(4)

The stored multiplicand information in the multiplicand neuron group is not changed by the operation in (3).

(5)

Neuron Add calculates a binary bit of the multiplication result at every moment.

Therefore, the binary SNPS Π_BMSNP for multiplication designed in this paper includes input neurons, addition neurons, auxiliary neuron groups, multiplicand input auxiliary neuron groups, and multiplier input auxiliary neuron groups, along with a multiplicand cache neuron group, multiplicand neuron group, and multiplier cache neuron group. The structure of Π_BMSNP is shown in Figure 7, and its formal definition is shown in Formula (5).

Π_BMSNP =(O, σ_aux1, σ_aux2,…, σ_aux6, σ_cand1, σ_cand2, …, σ_candk, σ_mut1, σ_mut2, …, σ_mutk, σ_bit1, σ_bit2, …, σ_bitk, syn, in, out)

(5)

where

(1)

O = {a};

(2)

σ_Input = (0,R_Input), R_Input = {a→a};

(3)

σ_aux1 = (1,R_aux1), R_aux1 = {a→a};

(4)

σ_aux2 = (1,R_aux2), R_aux2 = {a→a};

(5)

σ_aux3 = (0,R_aux3), R_aux3 = {a^k→a²};

(6)

σ_aux4 = (0,R_aux4), R_aux4 = {a^k→a²};

(7)

σ_aux5 = (0,R_aux5), R_aux5 = {a→a; a³/a→λ};

(8)

σ_aux6 = (0,R_aux6), R_aux6 = {a→λ; a³/a→a};

(9)

σ_candi = (0,R_candi), R_candi = {a→a; a²→λ; a³→a²},$i\in \left\{1,2,\cdots ,k\right\}$;

(10)

σ_muti = (0,R_muti), R_muti = {a→a},$i\in \left\{1,2,\cdots ,k\right\}$;

(11)

σ_biti = (0,R_biti), R_biti = {a→λ; a³/a→a},$i\in \left\{1,2,\cdots ,k\right\}$;

(12)

σ_Add =(0,R_Add), R_Add = {a^2j/a^j→λ; a^2j+1/a^j+1→a},$j\in \left\{0,1,2,\cdots ,n\right\}$;

(13)

syn = {(Input,aux_i)|$i\in \left\{5,6\right\}$}∪{(aux₁,aux₂)}∪{(aux₂,aux_i)|$i\in \left\{1,3,4\right\}$}∪{(aux₃,aux₆)}∪{(aux₄,aux_i)|$i\in \left\{2,5\right\}$}∪{(aux₄,cand_i)|$i\in \left\{1,2,\cdots ,k\right\}$}∪{(aux₅,cand₁)}∪{(aux₆,mut₁)}∪{(cand_i,cand_i+1)|$i\in \left\{1,2,\dots ,k-1\right\}$}∪{(mut_i,mut_i+1) | $i\in \left\{1,2,\dots ,k-1\right\}$}∪{(bit_i,bit_i+1)|$i\in \left\{1,2,\dots ,k-1\right\}$}∪{(cand_i,bit_k-i+1) | $i\in \left\{1,2,\dots ,k\right\}$}∪{(mut_i,bit_i) | $i\in \left\{1,2,\dots ,k\right\}$}∪{(bit_i,Add) | $i\in \left\{1,2,\dots ,k\right\}$};

(14)

in = input;

(15)

out = Add;

In Π_BMSNP, the functions of each neuron (neuron group) are as follows:

• Input neuron Input. Input receives binary strings from the environment and converts them to spikes in Π_BMSNP.
• Addition neuron Add. The result of multiplying the multiplier by the multiplicand’s bits is summed in the Add neuron.
• Auxiliary neuron groups (aux₁, aux₂). Continuously send a spike to neurons aux₃ and aux₄ at each time slice.
• The multiplicand is input to the auxiliary neuron group. Control the multiplicand to be accurately input into the summand buffer neuron, shield the interference during multiplication input, and save the multiplicand in the multiplicand neuron group when the input of the highest bit of the multiplicand is completed.
• Multiply the input auxiliary neuron group. The control multiplier is accurately input into the multiplier cache neuron group, and the interference when the multiplier is input is shielded.
• Group of multiplicand cache neurons. Cache multiplicand.
• Group of multiplier cache neurons. The multiplier is buffered, and each binary bit of the control multiplier is multiplied by the multiplicand.
• Group of multiplicand neurons. The multiplicand is stored, and the multiplication operation of the multiplier and each binary bit of the multiplicand is performed.

It can be seen from the following theorem that Π_BMSNP can complete the multiplication of two k-bit binary strings as input.

Theorem 3. 

For the binary multiplier realized by the SNPS shown in Figure 7, two natural numbers of length k (k ≥ 2) are input to its input neuron σ_Input in binary form from low to high, and this system can correctly calculate the product of two natural numbers.

Proof of Theorem 3. 

Let t represent the time slice length, t = 0 the initial state of the system, X and Y two arbitrary natural numbers, and m and n two natural numbers less than or equal to k; then:

$$\mathrm{X}={{\displaystyle \sum }}_{\dot{i}=0}^{m-1}{x}_i{2}^i,\mathrm{Y}={{\displaystyle \sum }}_{j=0}^{n-1}{y}_j{2}^j,\mathrm{Z}=\mathrm{X}\times \mathrm{Y}$$

$$\begin{gathered} \mathrm{X}\times \mathrm{Y}=({{\displaystyle \sum }}_{\dot{i}=0}^{m-1}{x}_i{2}^i)\times ({{\displaystyle \sum }}_{\dot{i}=0}^{n-1}{y}_j{2}^j) \\ ={\displaystyle \sum }_{i=0}^{m-1}{\displaystyle \sum }_{j=0}^{n-1}{x}_i{y}_j{2}^{i+j}={\displaystyle \sum }_{\dot{i}=0}^{m-1}{y}_0{x}_i{2}^{i+0}+{\displaystyle \sum }_{\dot{i}=0}^{m-1}{y}_1{x}_i{2}^{i+1}+\dots +{\displaystyle \sum }_{\dot{i}=0}^{m-1}{y}_{n-1}{x}_i{2}^{i+n-1} \end{gathered}$$

From the above formula, it can be concluded that the operation of solving X × Y can be converted into solving n times the product of m digits and 1 digits, and the result of the product is shifted to the left by j bits according to the weight j of the multiplier y_j; then, the result of n times is shifted to the left summation. In fact, in the [30] the author did the same, using k² neurons to store the results of the n operations, and the storage process required k auxiliary neurons. The left shift of the product of the m-bit and 1-bit is achieved by adjusting the connections of neurons and finally adding the corresponding results n times.

In the SNPS for multiplication designed in this section, k² neurons are not used to store the results of these n operations. This paper uses a new control method to make full use of the parallelism of neuron calculations, and sequentially outputs the converted operation results Z from low to high. Finally, the correct operation result is obtained. The operation process of the SNPS multiplier shown in Figure 7 can be divided into the following three parts:

• Input the natural number X;
• Compute each bit of Z in parallel while inputting Y;
• Output each bit of Z from low to high in turn.

The execution process of Π_BMSNP is as follows:

(1)

From t = 0 to t = k + 1, the regular execution of Π_BMSNP and the change of spikes in each neuron include:

(i)

σ_Input accepts sp-x_i (0 ≤ i ≤ k − 1) and applies the corresponding rules to send sp-x_i to σ_aux5. During this period, σ_aux5 can only receive the spikes sent by σ_Input, and apply the rules to send the received spikes to σcand1 in turn. Similarly, σ_candj (1 ≤ j ≤ k − 2) sends the received spikes to σ_candj+1 and σ_bitj respectively.

(ii)

σ_aux6 accepts the spikes sent by σ_Input, if sp-x_i (0 ≤ i ≤ k − 1) = {a}, use the rule a→λ to forget this spike.

(iii)

σ_bitj (1 ≤ j ≤ k − 2) accepts spikes sent by σ_candj (1 ≤ j ≤ k − 2) and forgets them using the rule a→λ.

(iv)

σ_aux1 and σ_aux2 (starting to work at t = 1) each maintain one spike, and σ_aux3 and σ_aux4 each maintain k spikes at t = k + 1.

(v)

t = k + 1, σ_aux3 use the rule a^k→a² to send two spikes to σ_aux6, and σ_aux4 use the rule a^k→a² to send two spikes to σ_aux5 and σ_candj (1 ≤ j ≤ k) respectively. σ_Input accepts sp-y₀ and sends sp-y₀ to σ_aux6 according to the corresponding rules.

(vi)

There is no spike in σ_add, σ_muti (1 ≤ i ≤ k).

(2)

t = k + 2, the rule execution of Π_BMSNP and the change of spikes in each neuron include:

(i)

σ_Input accepts sp-y₁ and sends sp-y₀ to σ_aux5, σ_aux6 respectively. σ_aux5 sends sp-x_k−1 to σ_cand1 while receiving sp-y₀ and {a²} from σ_aux4. σ_candj (1 ≤ j ≤ k−1) accepts sp-x_k-j and sends sp-x_k-j−1, and σ_candk accepts sp-x₀. σ_candj (1 ≤ j ≤ k) receives the two spikes sent by σ_aux4, and σ_candj(1 ≤ j ≤ k) use the rule a³→a² or a→λ to send sp-x_j−1 to σ_bitj.

(ii)

σ_aux6 forgets sp-x_k−1 accepts both sp-y₀ (from σ_Input) and {a²} (from σ_aux3).

(iii)

σ_aux1 holds one spike, σ_aux2 gets three spikes (one spike from σ_aux1, two spikes from σ_aux4), σ_aux3 and σ_aux4 hold one spike.

(iv)

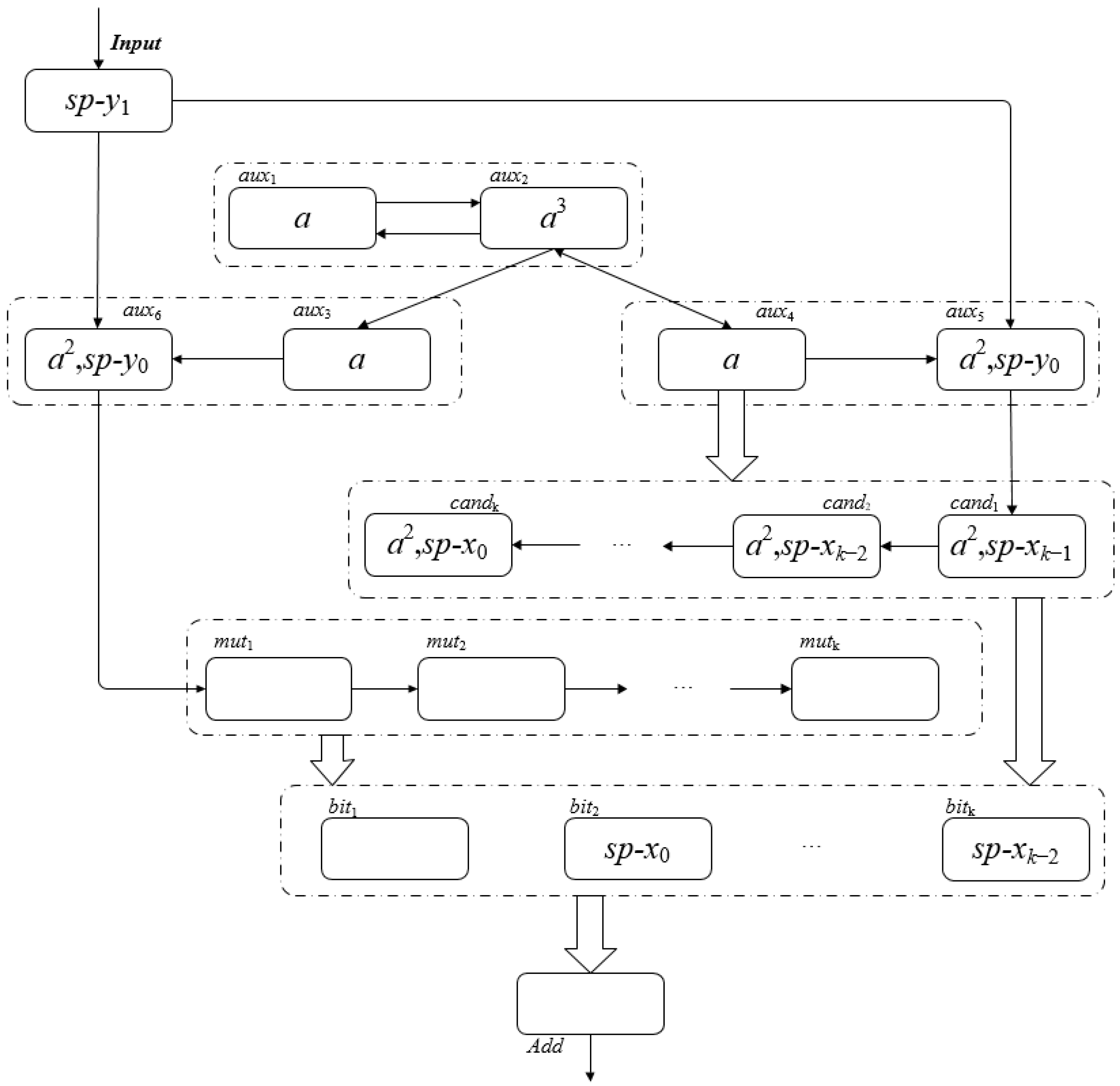
There is no spike in σ_add, σ_muti (1 ≤ i ≤ k).

At this point, the multiplicand has been input into the multiplicand cache neuron group, and we can get Figure 8, which shows the spikes contained in each neuron in the pattern C_k+2.

(3)

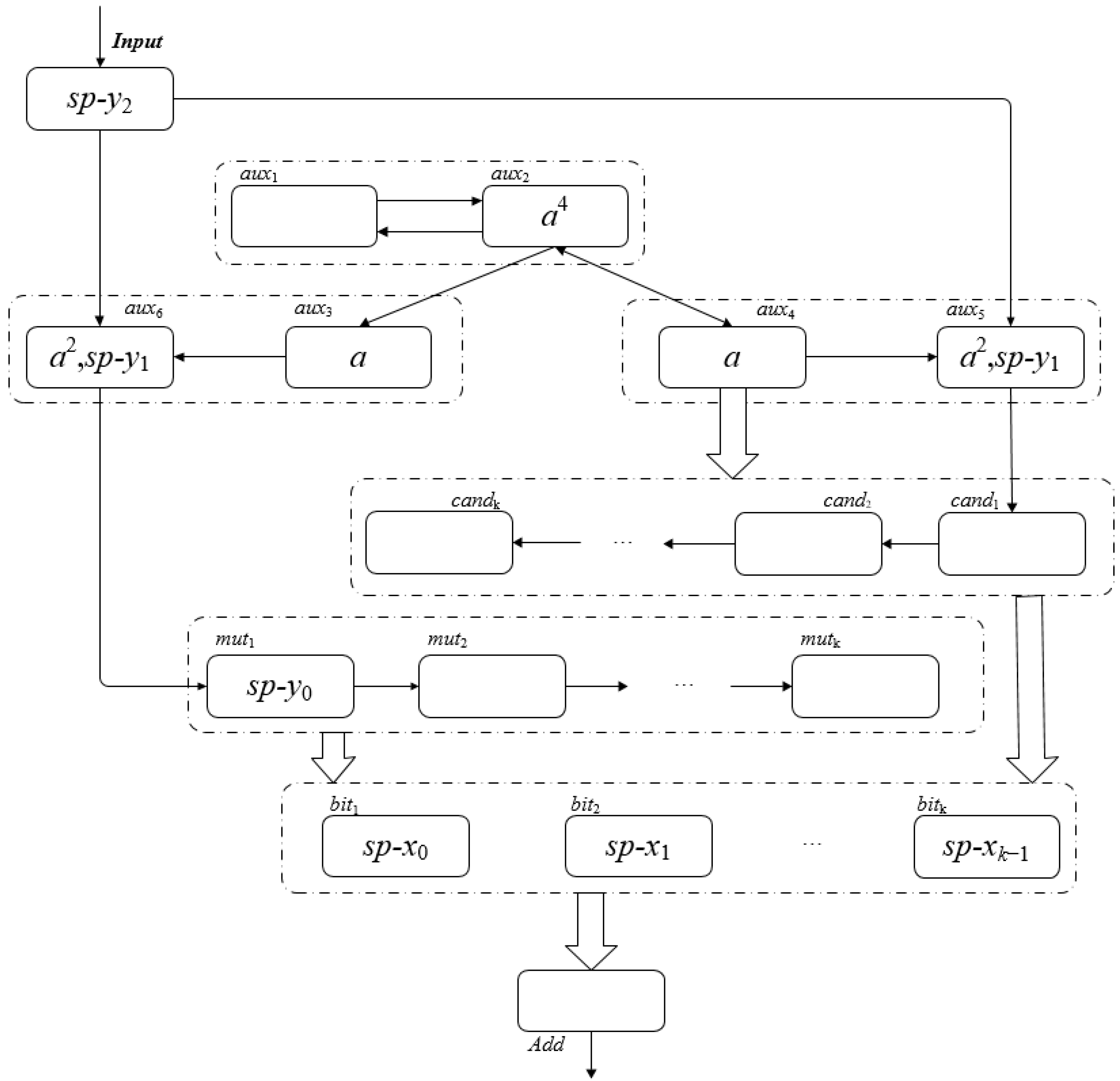
t = k + 3, the multiplicand has been input into the multiplicand neuron group, and the spike changes in each neuron of Π_BMSNP are shown in Figure 9:

(i)

σ_Input accepts sp-y₂ and sends sp-y₁ to σ_aux5 and σ_aux6, respectively.

(ii)

There are no spikes in σ_aux1 and four spikes in σ_aux4.

(iii)

σ_aux3 and σ_aux4 maintain one spike each.

(iv)

σ_aux5 receives the sp-y₁ sent by σ_Input, and use the corresponding rules in σ_aux5 to forget sp-y₀.

(v)

σ_aux6 receives the sp-y₁ sent by σ_Input and applies the corresponding rules in σ_aux6 to send sp-y₀ to σ_mut1.

(vi)

σ_mut1 receives sp-y₀ sent by σ_aux6.

(vii)

There is no spike in σ_candi (1 ≤ i ≤ k), σ_mutj (2 ≤ j ≤ k).

(viii)

sp-x_i−1 is received in σ_biti (1 ≤ i ≤ k).

(4)

From t = k + 4 to 3k + 5, the rule execution of Π_BMSNP and the change of spikes in each neuron include:

(i)

σ_Input sequentially accepts sp-y_j (3 ≤ j ≤ k − 1) and simultaneously use the rules to send sp-y_j−1 to σ_aux5 and σ_aux6.

(ii)

When the number of spikes in σ_aux5 is 3, the rule a³/a→λ is activated and consumes one spike, so there will always be two spikes in σ_aux5 and no spikes will be sent.

(iii)

There is no spike in σ_candi (1 ≤ i ≤ k).

(iv)

σ_aux6 sends sp-y_j (1 ≤ j ≤ k − 1) to σ_mut1 sequentially.

(v)

σ_muti (1 ≤ i ≤ k) sends sp-y_t+i-(k+5) to σ_muti+1 and σ_biti respectively. Where t is the current moment of Π_BMSNP. If t + i − (k + 5) < 0, it means that there is no spike in σ_muti, and no spike will be sent to σ_muti+1 and σ_biti.

(vi)

t = k + 4, σ_bit1 receives the sp-y₀ sent by σ_mut1, and performs the product operation of sp-y₀ and sp-x₀ in σ_bit1, and sends the operation result to σ_Add at the next time slice. Note that after the operation in σ_bit1, sp-x₀ is still stored in the neuron.

(vii)

t = k + 5, σ_bit1 receives the sp-y₁ sent by σ_mut1, performs the product operation of sp-y₁ and sp-x₀ in σ_bit1, and sends the operation result to σ_Add at the next time slice.

σ_Add receives the product operation result of sp-y₀ and sp-x₀, namely z₀, and sends z₀ to the environment at the next time slice.

(viii)

t = k + 6, z₀ is received in the environment.

σ_Add is summing the following operation results: sp-y₀ × sp-x₁, sp-y₁ × sp-x₀, the summation result is z₁, and the carry is kept in σ_Add.

The ongoing multiplication operation of Π_BMSNP: sp-y₀ × sp-x₂, sp-y₁ × sp-x₁, sp-y₂ × sp-x₀ they will be sent to σ_Add for summing operation at the next time, and the operation result is z₂.

(ix)

Similarly, t = k + 7, z₁ is received in the environment.

t = k + 8, z₂ is received in the environment.

t = k + i (9 ≤ i ≤ 2k + 3), z_i−6 is received in the environment.

t = 3k + 4, z_2k−2 is received in the environment.

Considering that a carry may occur when operating z_2k−2, the system reaches the termination configuration at t = 3k + 5.

Based on the above description, readers can verify that, for k ≥ 2, the SNPS multiplication constructed above can correctly solve the product of two natural numbers with a binary length of k, and the proof is complete. □

Figure 10 shows a Π_BMSNP structure for three-bit binary multiplication. Based on this Π_BMSNP, the multiplication process of the natural numbers 7 and 5 is listed in

Table 3. Π_BMSNP calculation process of the instance 111₂ × 101₂ = 100011₂.

Step t	Input	aux1	aux2	aux3	aux4	aux5	aux6	cand1	cand2	cand3	mut1	mut2	mut3	bit1	bit2	bit3	Add	Output
0	-	1	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	-
1	1	1	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	-
2	1	1	1	1	1	1	1	0	0	0	0	0	0	0	0	0	0	-
3	1	1	1	2	2	1	1	1	0	0	0	0	0	0	0	0	0	-
4	1	1	1	3	3	1	1	1	1	0	0	0	0	0	0	0	0	-
5	0	1	3	1	1	3	3	3	3	3	0	0	0	0	0	0	0	-
6	1	0	4	1	1	2	2	0	0	0	1	0	0	2	2	2	0	-
7	-	0	4	1	1	3	3	0	0	0	0	1	0	3	2	2	0	-
8	-	0	4	1	1	2	2	0	0	0	1	0	1	2	3	2	1	-
9	-	0	4	1	1	2	2	0	0	0	0	1	0	3	2	3	1	1
10	-	0	4	1	1	2	2	0	0	0	0	0	1	2	3	2	2	1
11	-	0	4	1	1	2	2	0	0	0	0	0	0	2	2	3	2	0
12	-	0	4	1	1	2	2	0	0	0	0	0	0	2	2	2	2	0
13	-	0	4	1	1	2	2	0	0	0	0	0	0	2	2	2	1	0
14	-	0	4	1	1	2	2	0	0	0	0	0	0	2	2	2	0	1

, which displays the spike counts in each neuron for each configuration in Π_BMSNP(7,5). These two natural numbers are expressed in binary form as: 111₂, 101₂, and 111₂ × 101₂ = 100011₂. In Figure 10, the multiplicand and the multiplier are input through the neuron Input, the auxiliary neuron group (aux₁, aux₂) continuously sends a spike to neurons aux₃ and aux₄ respectively, the multiplicand is input to the auxiliary neuron group (aux₄, aux₅) to control the multiplicand 7 (111) to be input to the multiplicand cache neuron group (cand₁, cand₂, cand₃), and after inputting the highest bit of the multiplier, it is stored in the multiplicand neuron group (bit₁, bit₂, bit₃) and the multiplier is input to the auxiliary neuron group (aux₃, aux₆) to control the multiplier 5 (101) input to the multiplier cache neuron group (mut₁, mut₂, mut₃. Multiplication is performed in the multiplier neuron, and the final neuron Add sums the results and outputs them to the environment.

In Table 3, column 1 likewise represents the system moment and columns 2 to last represent each neuron in the system. Each row of Table 3 represents the number of spikes in each neuron in the system at the corresponding moment. For example, the number in the first column of row 9 (step t = 8) is 0, indicating that the binary bit currently input to the neuron Input is 0. During the computation process of 111₂ × 101₂, from t = 1 to t = 3, each binary digit of the multiplicand 111 appears in the neuron input sequentially from low to high. At t = 6, the multiplicand is stored in the multiplier neuron group (bit₁, bit₂, bit₃). From t = 4 to t = 6, each binary digit of the multiplier 101 appears in the neuron input sequentially from low to high. At t = 8, the spike count from the 12th column to the 14th column (mut₁, mut₂, mut₃) is 1, 0, 1 respectively, representing the multiplier as 101. In the last column, from t = 9, the numbers 1, 1, 0, 0, 0, 1 are sequentially output to represent the final calculation result of 100011.

The Π_BMSNP designed in this section can complete the multiplication of two k-bit binary numbers within 3k + 5 time slices, and the number of neurons used is 3k + 8. The neurons in Π_BMSNP use a total of five types of non-delay spiking rules and four types of forgetting rules.

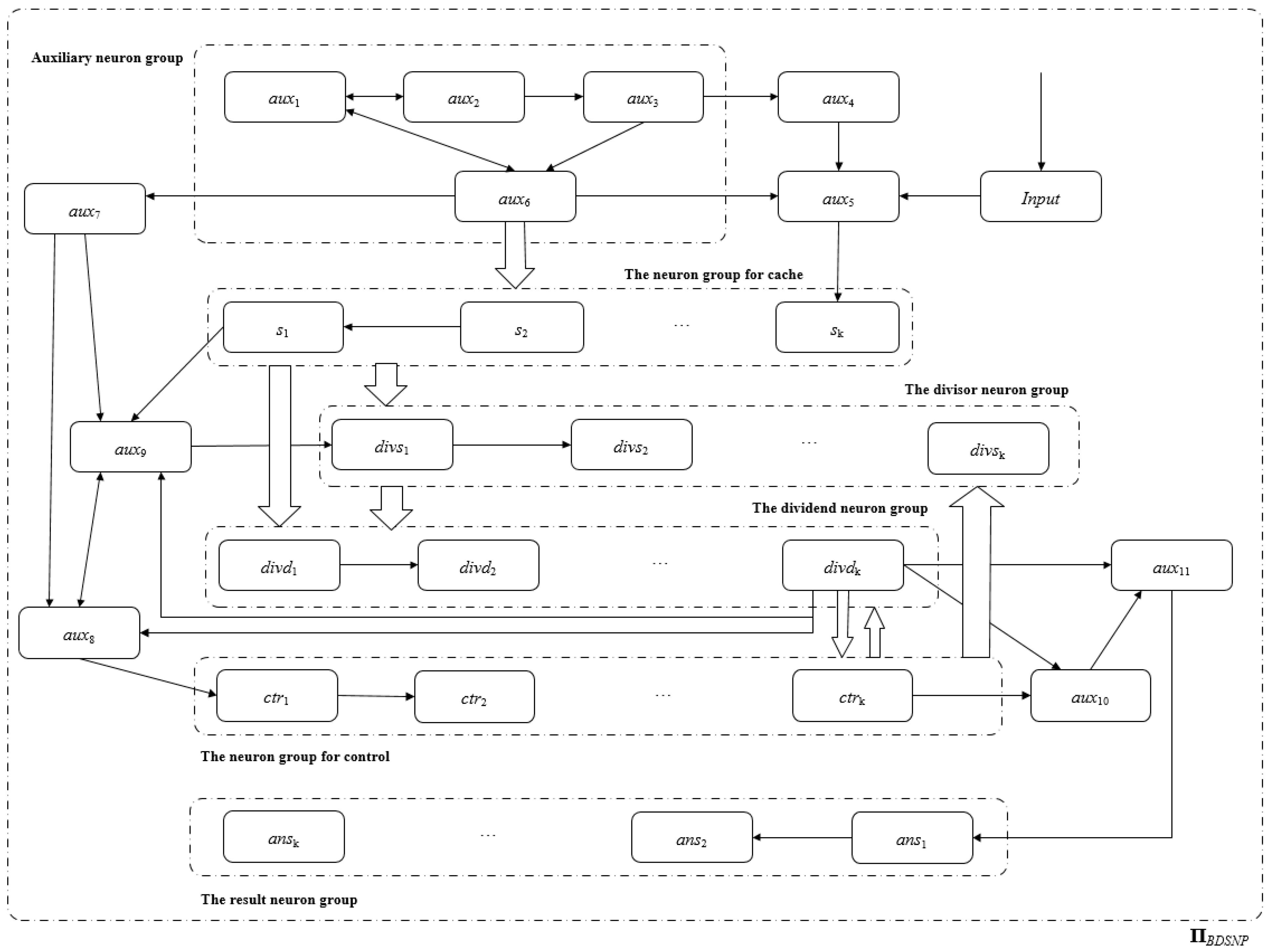
3.4. Binary Division in SNP Systems

Division is a basic method of arithmetic operation. The basic idea of division operations is to subtract the divisor from the dividend until the remainder is less than the divisor. At present, nobody has proposed an SNPS which encodes numbers as spike sequences for division. The basic idea of the binary division SPNS designed in this paper is as follows:

(1)

Through the input neuron, input the binary string of the dividend from the lowest bit to the highest bit. When the i-th bit (0 ≤ i ≤ k − 1) in the input string is 1, the neuron input gets one spike; otherwise, it does not get one spike.

(2)

After each digit of the dividend is input, it will be cached in the system. When all digits of the dividend are input, the dividend is stored in the dividend neuron group. Wait for the input of the divisor. Input the divisor immediately after the highest digit of the dividend is input.

(3)

After the divisor input is completed, save the divisor in the divisor neuron group. After the highest digit of the divisor is input, the control neuron group immediately sends the divisor to the dividend neuron group for subtraction. The stored dividend information in the dividend neuron group will be changed due to the subtraction operation.

(4)

For each subtraction operation, send a spike to the resulting neuron group.

(5)

Continue to carry out (4) in parallel until the highest bit of the dividend neuron group sends a borrow message to the control neuron group.

Therefore, the binary SNPS Π_BDSNP for division designed in this paper includes input neurons, result neuron groups, auxiliary neuron groups, dividend input auxiliary neuron groups, divisor input auxiliary neuron groups, and dividend cache neuron groups, along with a divisor neuron group, divisor cache neuron group, and divisor neuron group. The structure of Π_BDSNP is shown in Figure 11, and its formal definition is shown in Formula (6).

Π_BDSNP = (O, σ_aux1, σ_aux2,…, σ_aux11, σ_s1, σ_s2,…, σ_sk, σ_divs1, σ_divs2,…, σ_divsk, σ_ctr1, σ_ctr2, …, σ_ctrk, σ_divd1, σ_divd2, …, σ_divdk, σ_ans1, σ_ans2, …, σ_ansk,syn, in, out)

(6)

where

(1)

O = {a};

(2)

σ_Input = (0,R_Input), R_Input = {a→a; a³→a; a⁵→λ};

(3)

σ_aux1 = (1,R_aux1), R_aux1 = {a→a};

(4)

σ_aux2 = (1,R_aux2), R_aux2 = {a→a};

(5)

σ_aux3 = (0,R_aux3), R_aux3 = {a^2k−1→a};

(6)

σ_aux4 = (0,R_aux4), R_aux4 = {a→a};

(7)

σ_aux5 = (0,R_aux5), R_aux5 = {a→a; a²→λ; a³→a; a⁵→λ};

(8)

σ_aux6 = (0,R_aux6), R_aux6 = {a^k→a²; a^k+1→a³};

(9)

σ_aux7 = (0,R_aux7), R_aux7 = {a²→λ; a³→a³};

(10)

σ_aux8 = (2,R_aux8), R_aux8 = {a⁴→λ} ∪ {aⁱ→a⁵,$i\in \left\{5,6\right\}$} ∪ {a⁹→λ};

(11)

σ_aux9 = (0,R_aux9), R_aux9 = {aⁱ→λ | $i\in \left\{1,2,4\right\}$} ∪ {aⁱ→a⁵ | $i\in \left\{5,6,7,8\right\}$; a⁹→λ};

(12)

σ_aux10 = (0,R_aux10), R_aux10 = {a⁴→λ; a⁵→a; a⁹→λ};

(13)

σ_aux11 = (0,R_aux11), R_aux11 = {a→a; a⁴→λ; a⁵→λ};

(14)

σ_si = (0,R_si), R_si = {a→a; a²→λ; a³→a²; a⁴→a³} ∪ {a^j→λ | $j\in \left\{5,7,8\right\}$} |$i\in \left\{1,2,\cdots ,k\right\}$;

(15)

σ_divs1 = (0,R_divs1), R_divs1 = {a^j→λ | $j\in \left\{1,2\right\}$} ∪ {a⁵→a⁴; a⁸/a⁵→a⁵}

(16)

σ_divsi = (0,R_divsi), R_divsi = {a^j→λ | $j\in \left\{1,2\right\}$} ∪ {a^j→a⁴ | $j\in \left\{5,6\right\}$} ∪ {a^j/a⁵→a⁵ | $j\in \left\{8,9\right\}$} | $i\in \left\{2,3,\cdots ,k\right\}$;

(17)

σ_ctri = (0,R_ctri), R_ctri = {a⁴→λ; a⁵→a; a⁹→λ} | $i\in \left\{1,2,\cdots ,k\right\}$;

(18)

σ_divd1 = (0,R_divd1), R_divd1 = {a→λ; a^j/a→λ | $j\in \left\{3,5\right\}$} ∪ {a^j/a⁵→λ | $j\in \left\{7,9\right\}$} ∪ {a⁸/a⁴→a⁴; a¹⁰/a⁸→λ};

(19)

σ_divdi = (0,R_divdi), R_divdi = {a→λ; a^j/a→λ | $j\in \left\{3,5\right\}$; a^j/a⁵→λ,$j\in \left\{7,9\right\}$; a⁸/a⁴→a⁴; a¹⁰/a⁸→λ; a¹¹/a⁷→a⁴; a^j/a¹⁰→a⁴ | $j\in \left\{12,14\right\}$; a¹³/a¹¹→λ}, $i\in \left\{2,3,\cdots ,k\right\}$;

(20)

σ_ansi = (0,R_ansi), R_ansi = {a²→a}, $i\in \left\{1,2,\cdots ,k\right\}$;

(21)

syn = {(Input,aux₅)}∪{(aux₁,aux_i)|$i\in \left\{2,6\right\}$}∪{(aux₂,aux_i)|$i\in \left\{1,3\right\}$}∪{(aux₃,aux_i)|$i\in \left\{4,6\right\}$}∪{(aux₄,aux₅)}∪{(aux₅,s_k)}∪{(aux₆,aux_i)|$i\in \left\{1,5,7\right\}$}∪{(aux₆,s_i)|$i\in \left\{1,2,\dots ,k\right\}$}∪{(aux₇,aux_i)|$i\in \left\{9,10\right\}$}∪{(aux₈,aux₉)}∪{(aux₈,ctr₁)}∪{(aux₉,aux₈)}∪{(aux₉,divs₁)}∪{(aux₁₀,aux₁₁)}∪{(aux₁₁,ans₁)}∪{(s₁,aux₉)}∪{(s_i+1,s_i)|$i\in \left\{1,2,\dots ,k-1\right\}$}∪{(s_i,divd_i)|$i\in \left\{1,2,\dots ,k\right\}$}∪{(s_i,divs_i)|$i\in \left\{1,2,\dots ,k\right\}$}∪{(divs_i,divs_i+1)|$i\in \left\{1,2,\dots ,k-1\right\}$}∪{(divs_i,divd_i)|$i\in \left\{1,2,\dots ,k\right\}$}∪{(ctr_i,divs_i+1)|$i\in \left\{1,2,\dots ,k-1\right\}$}∪{(ctr_i,ctr_i+1)|$i\in \left\{1,2,\dots ,k-1\right\}$}∪{(ctr_i,divd_i)|$i\in \left\{1,2,\dots ,k\right\}$}∪{(ctr_k,aux₁₁)}∪{(divd_i,divd_i+1)|$i\in \left\{1,2,\dots ,k-1\right\}$}∪{(divd_k,ctr_i)|$i\in \left\{1,2,\dots ,k\right\}$}∪{(divd_k,aux_i)|$i\in \left\{9,10,12\right\}$}∪{(ans_i,ans_i+1)|$i\in \left\{1,2,\dots ,k-1\right\}$};

(22)

in = input;

(23)

out = ans_i|$i\in \left\{1,2,\cdots ,k\right\}$;

In Π_BDSNP, the functions of each neuron (neuron group) are as follows:

• Input neuron Input. Input receives binary strings from the environment and converts them to spikes in Π_BDSNP.
• Cache groups of neurons. Temporarily cache the dividend and the divisor. After the highest digit of the dividend is input into the system, the auxiliary neuron will save the dividend in the dividend neuron group. After the highest digit of the divisor is input into the system, the auxiliary neuron will save the divisor in the divisor neuron group.
• Auxiliary neuron group. The control dividend and divisor are stored in the dividend neuron group and the divisor neuron group, respectively.
• Dividend neuron group. Save the dividend, perform the operation of subtracting the divisor, and send a signal to the control neuron group if the subtraction is not enough.
• Divisor group of neurons. Save the divisor, and send the divisor to the dividend neuron group for subtraction.
• Groups of control neurons. Control the process of subtracting the dividend and the divisor, and stop when the result of the subtraction operation is less than the divisor.
• Resulting neuron groups. Counts the number of subtraction operations performed.

It can be seen from the following theorem that Π_BDSNP can complete the division of two k-bit binary strings as input.

Theorem 4. 

For the binary divider realized by the SNPS shown in Figure 11, two natural numbers of length k (k ≥ 2) are input to its input neuron σ_Input in binary form from low to high, and this system can correctly calculate the quotient of two natural numbers.

Proof of Theorem 4. 

Let t represent the time slice length, t = 0 the initial state of the system, X and Y any two natural numbers, X the dividend, and Y the divisor. Because division can be regarded as subtraction of the same number continuously, as shown in Figure 11, the binary divider is designed based on the idea of multiple subtraction; its operation process can be divided into the following three parts:

• Input dividend X and divisor Y;
• Loop controls the dividend to subtract the divisor until the dividend is smaller than the divisor;
• Count the number of subtractions, and convert the result into a binary form.

The execution process of Π_BDSNP is as follows:

(1)

t = 0, start sending the corresponding spike sp-x₀ of the lowest bit x₀ of X to σ_Input.

(2)

From t = 1 to t = k, the regular execution of Π_BDSNP and the change of spikes in each neuron include:

(i)

σ_Input accepts sp-x_i (0 ≤ i ≤ k −1 ) and use the corresponding rules to send sp-x_i to σ_aux5. During this period, σ_aux5 will only receive the spikes sent by σ_Input, and use the rules to send the received spikes to σ_sk in turn. Similarly, σ_sj (3 ≤ j ≤ k) sends the received spikes to σ_sj−1 in sequence.

(ii)

σ_aux1 and σ_aux2 maintain one spike each.

(iii)

t = k, σ_aux3 and σ_aux6 each contain k − 1 spikes.

(iv)

There are no spikes in σ_s1, σ_s2, σ_auxi |$i\in \left\{4,5,7,8,9,10,11\right\}$, σ_divsi, σ_ctri, σ_divdi, σ_ansi |$i\in \left\{1,2,\dots ,k\right\}$.

(3)

t = k + 1, the rule execution of Π_BDSNP and the change of spikes in each neuron include:

(i)

σ_Input accepts sp-y₀ and sends sp-y₀ to σ_aux5 according to the corresponding rules. σ_aux5 accepts sp-x_k−1 and sends sp-x_k−2, σ_sj (3 ≤ j ≤ k) accepts sp-x_k−j and sends sp-x_k−j−1, and σ_s2 accepts sp-x₀.

(ii)

There are k spikes in σ_aux3

(iii)

There are k spikes in σ_aux6, and the rule a^k→a² will be used to send two spikes each to σ_auxi|$i\in \left\{1,5,7\right\}$ and σ_sj (1 ≤ j ≤ k).

(4)

t = k + 2, the rule execution of Π_BDSNP and the change of spikes in each neuron include:

(i)

σ_Input accepts sp-y₁ and sends sp-y₀ to σ_aux5. σ_aux5 sends sp-x_k−1 to σ_sk while receiving sp-y₀ and {a²} from σ_aux6. σ_sj (1 ≤ j ≤ k) receives sp-x_j−1 and {a²} from σ_aux6.

(ii)

There are three spikes in σ_aux1 and k + 1 spikes in σ_aux3.

(iii)

There is one spike in σ_aux6. There are two spikes in σ_aux7, and we use the rule a²→λ to forget these two spikes.

At this time, the dividend has been input into the cache neuron group, and they will be sent to the dividend neuron group for storage at the next moment.

(5)

t = k + 3, σ_divdj (1 ≤ j ≤ k) receives sp-x_j−1, at this time sp-x_j−1 = {a²} means x_j−1 is 1, sp-x_j−1 = {λ} means that x_j−1 is 0.

(6)

From t = k + 4 to t = 2k + 3, the regular execution of Π_BDSNP and the change of spikes in each neuron include:

(i)

σ_sj (1 ≤ j ≤ k) sends the received spikes to σ_sj−1 in sequence.

(ii)

t = 2k, there are 2k−1 spikes in σ_aux3, the rule a^2k−1→a executes, sending one spike to σ_aux4.

(iii)

t = 2k + 1, there are k + 1 spikes in σ_aux6, the rule a^k+1→a³ is executed, and they are sent to σ_auxi|$i\in \left\{1,5,7\right\}$ and σ_sj (1 ≤ j ≤ k) respectively two spikes.

(iv)

When t = 2k + 2, σ_aux5 receives three spikes from σ_aux6 and one spike from σ_aux4.

There are four spikes in σ_aux1.

There are three spikes in σ_aux7.

σ_sj (1 ≤j ≤ k) will receive three spikes from sp-y_j−1 and σ_aux6. σ_sj (1 ≤ j ≤k) will send two spikes to σ_divdj and σ_aux9.

At this point, the divisors have been entered into the cache neuron group, and they will be sent to the divisor neuron group for storage at the next moment. sp-y_j−1 (1 ≤ j ≤ k) = {a³} means that x_j−1 is 1, and sp-x_j−1 = {λ} means that x_j−1 is 0.

(v)

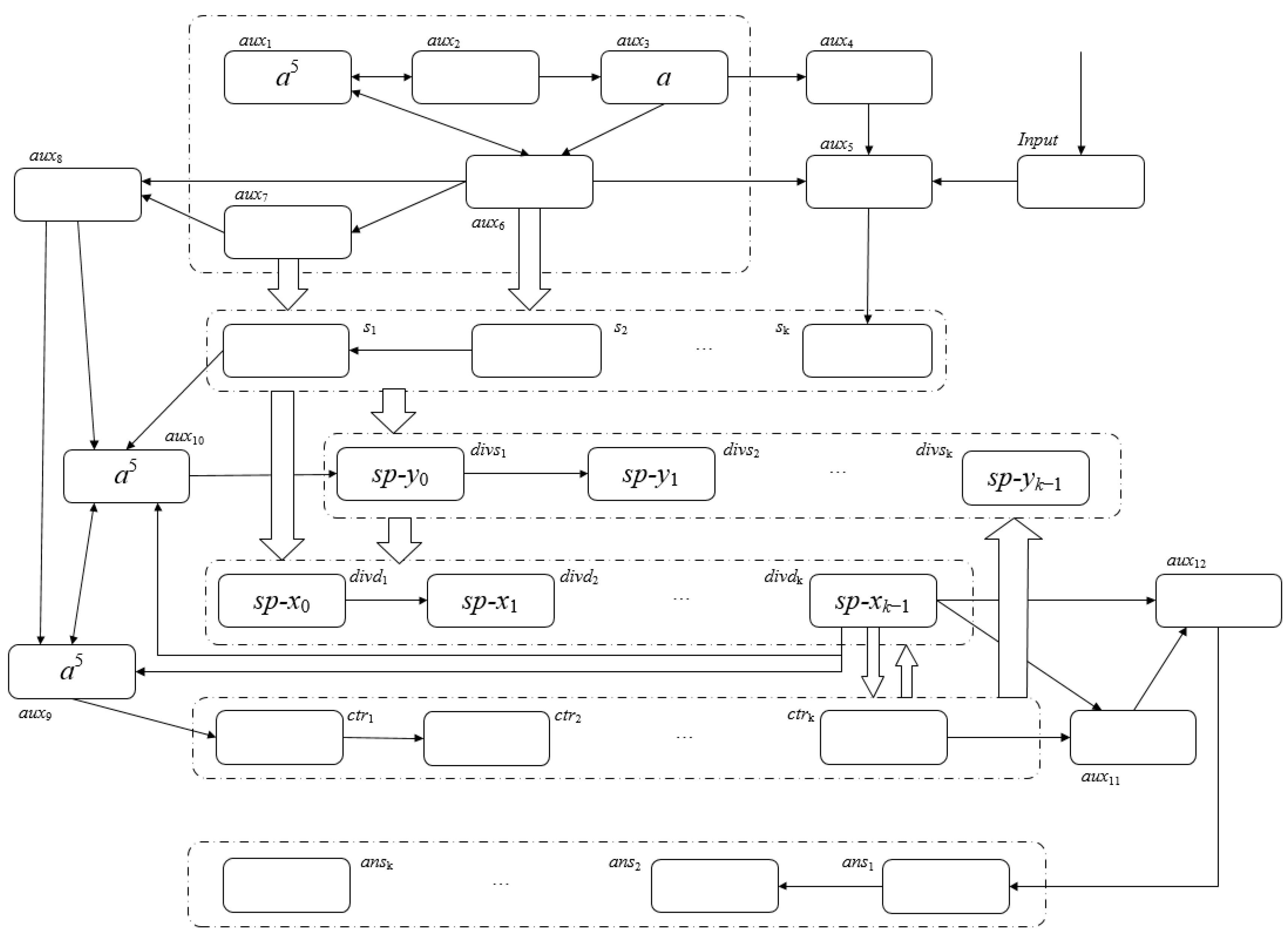
t = 2k + 3, σ_divsj (1 ≤ j ≤ k) receives the sp-y_j−1 sent by s_j, and the divisor is stored in the divisor neuron group.

There are five spikes in σ_aux9 (three from σ_aux7 and two from itself).

There are five spikes in σ_aux10 (three from σ_aux7 and two from σ_s1).

There are no spikes in σ_ctrj (1 ≤ j ≤ k).

σ_divdj (1 ≤ j ≤ k), receiving two spikes sent by s_j, after executing the corresponding rules in σ_divdj, sp-x_j−1 = {a⁴} it means that x_j−1 is 1, and sp-x_j−1 = {a²} means that x_j−1 is 0.

We can obtain Figure 12 now that both the dividend and the divisor have been entered into the system, which shows the spikes contained within the individual neurons in the pattern C_2k+3.

(7)

After t = 2k + 4, the regular execution of Π_BDSNP and the change of spikes in each neuron include:

(i)

t = 2k + 4, σ_divs1 receives five spikes from σ_aux10, σ_divs1 receives five spikes from σ_aux9, and prepares to send sp-y₀ to σ_divs1. σ_ctr1 sends one spike to σ_divs2 and σ_divd1 and σ_ctr2, respectively.

(ii)

t = 2k + 5, the difference operation between sp-x₀ and sp-y₀ is being performed in σ_divd1, and the operation result is kept in σ_divd1. If a borrow occurs, four spikes will be sent to σ_divd2 to participate in the calculation of sp-x₁ and sp-y₁ at the next time slice.σ_divs2 receives four spikes from σ_divs1 and one spike from σ_ctr1, and prepares to send sp-y₁ to σ_divs2. σ_ctr2 sends one spike to σ_divs3 and σ_divd2 and σ_ctr3, respectively.

(iii)

t = 2k + 6, the difference operation between sp-x₁ and sp-y₁ is being performed in σ_divd2, and the operation result is kept in σ_divd2. If a borrow occurs, four spikes will be sent to σ_divd3 to participate in the calculation of sp-x₂ and sp-y₂ at the next time slice.

(iv)

Similarly, it is not difficult to verify that t = 3k + 4, the difference operation of sp-x_k−1 and sp-y_k−1 is going on in σ_divdk. So far, the first subtraction operation is completed. If σ_divdk does not send 4 spikes to σ_aux12 (X ≥ Y), σ_aux11 will send one spike to σ_aux12, and σ_aux12 will send this spike to σ_ans1 at the next time slice.

(v)

Because the neurons of σ_divdi(1 ≤ i ≤ k) work in parallel, when t = 3k + 5, the second subtraction operation is completed. If σ_divdk does not send four spikes to σ_aux12 (X ≥ Y), σ_aux11 will send one spike to σ_aux12, and σ_aux12 will send this spike to σ_ans1 at the next time slice.

(vi)

The system will keep running until σ_divdk sends four spikes to σ_aux12, indicating that the current dividend is smaller than the divisor.

Through the above description, it is not difficult to see that the number of subtractions performed by this system will be sent to the neuron σ_ans1 successively over time, and the rule in the neuron σ_ansi (1 ≤ i ≤ k) is a²→a, which means every 2 enters 1; then, when the system reaches the termination pattern, the result of X quotient Y is stored in the neurons σ_ans1, σ_ans2, …, σ_ansk in binary form from low to high.

Based on the above description, readers can verify that for k ≥ 2 the SNP divider constructed above can correctly solve the quotient of two natural numbers with binary length k, and the proof is completed. □

Figure 13 shows the structure of a Π_BDSNP for three-digit binary division. Based on this Π_BDSNP, the division process of natural numbers 6 and 2 is listed in

Table 4. Π_BDSNP calculation process of the instance 110₂÷010₂ = 011₂.

Step t	Input	aux5	aux6	aux7	aux8	aux9	s3	s2	s1	divs1	divs2	divs3	divd1	divd2	divd3	aux10	aux11	ans3	ans2	ans1
0	-	0	0	0	2	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
1	0	0	0	0	2	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
2	1	0	1	0	2	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
3	1	1	2	0	2	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
4	0	1	3	0	2	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0
5	1	0	1	2	2	0	3	3	2	0	0	1	0	0	0	0	0	0	0	0
6	0	1	2	0	2	0	0	0	0	2	2	2	0	2	2	0	0	0	0	0
7	-	0	4	0	2	0	1	0	0	0	0	0	0	2	2	0	0	0	0	0
8	-	4	1	3	2	0	3	4	3	0	0	0	0	2	2	0	0	0	0	0
9	-	0	1	0	5	5	0	0	0	2	3	2	2	5	4	0	0	0	0	0
10	-	0	1	0	5	5	0	0	0	5	3	0	2	4	4	0	0	0	0	0
11	-	0	1	0	5	5	0	0	0	5	8	0	7	4	4	0	0	0	0	0
12	-	0	1	0	5	5	0	0	0	5	8	6	7	10	4	0	0	0	0	0
13	-	0	1	0	5	5	0	0	0	5	8	6	7	8	9	1	0	0	0	0
14	-	0	1	0	5	5	0	0	0	5	8	6	7	10	13	1	1	0	0	0
15	-	0	1	0	5	5	0	0	0	5	8	6	7	8	7	1	1	0	0	1
16	-	0	1	0	5	5	0	0	0	5	8	6	7	10	11	1	1	0	0	2
17	-	0	1	0	9	9	0	0	0	5	8	6	7	8	9	5	5	0	1	1
18	-	0	1	0	0	0	0	0	0	0	3	5	8	10	12	0	0	0	1	1

which shows the number of spikes contained in each neuron in Π_BDSNP(6,2). These two natural numbers are expressed in binary form: 110₂, 010₂, 110₂ ÷ 010₂ = 011₂. In Figure 13, the dividend and the divisor are input through the neuron Input, and both the dividend and the divisor are input to the cache neuron through the input auxiliary neuron group Tuple (s₁, s₂, s₃). The dividend is stored in the dividend neuron group (div₁, div₂, div₃), while the divisor is stored in the divisor neuron group (divs₁, divs₂, divs₃), and the control neuron after the input is completed The group immediately sends the divisor to the dividend neuron group for continuous subtraction operations and sends one spike to the result neuron group each time until the highest bit of the dividend neuron group sends a borrow message to the control neuron group, and the final result is stored in the result group of neurons.

In Table 4, likewise, column 1 represents the system moment and columns 2 to 1 represent each neuron in the system. Each row of Table 4 represents the number of spikes in each neuron in the system at the corresponding moment. It is not difficult to see that when t = 18 the resulting neuron group (the last three columns) in Table 4 has calculated the result (011) of dividing the last column of natural numbers 6 and 2.

The Π_BDSNP designed in this section can complete the division of two k-bit binary numbers within 2k + 4 time slices, and the number of neurons used is 5k + 12. The neurons in Π_BDSNP use a total of sixteen types of non-delay spiking rules and thirteen types of forgetting rules.

4. Comparison of Arithmetic Operations Realized by Various SNP Systems

In this section, we analyze and compare the excellent SNPS proposed in recent years for basic arithmetic operations; the results are shown in

Table 5. The number of neurons, time slices required, and number of rule types used for four arithmetic approaches.

Article	Input Type	Encoding	Add	Sub	Mut	Div	Rule Types
[28]	multiple inputs	time interval	10/-	12/-	21/-	25/-	4/4/12/15
[35]	multiple inputs	time-free	2/-	2/-	11/-	10/-	2/6/15/16
[29]	multiple inputs	spike train	3/(k + 1)	10/(k + 2)	13/(k + 7)	-/-	3/6/3/-
[31]	multiple inputs	spike train	7/(k + 2)	7/(k + 2)	(k2/2 + 15k/2 + 4)/ (2k + 5)	-/-	6/6/6/-
[30]	single input	spike train	(3k + 5)/(3k + 4)	-/-	(k2 + 5k + 3)/(4k + 2)	-/-	9/-/10/-
[36]	single input	spike train	(2k + 4)/(3k + 1)	-/-	5k/(3k + 5)	-/-	(5k − 1)/-/(9/2k + 7)/-
This work	single input	spike train	(k + 8)/(2k + 4)	(k + 13)/(2k + 3)	(3k + 8)/(3k + 5)	(5k + 12)/ (4k + quotient + 4)	6/11/9/29

Note: A/B, A represents the number of neurons used, B represents the number of time slices required for the operation. C/D/E/F, C represents the number of rules used for addition. Similarly, D, E, and F denote the number of rules used for subtraction, multiplication, and division, respectively.

. The statistical dimensions include the number of input neurons (NIN), the encoding method of operands (Encoding), the number of neurons used by the four basic operations (addition, subtraction, multiplication, and division), the number of time slices required to complete the operation, and the number of rule types (NRT). In operand input, when one input neuron is used it takes a long time to input two operands sequentially, but fewer neurons are used. When two input neurons are used, the input time consumed by parallel input of two operands is short, while the number of neurons is increased. There are two commonly used operand encodings: spike time interval-based encoding and spike sequence-based encoding. Spike time interval-based encoding is the conversion of a numerical value into time slices in the interval between two spikes, while spike sequence-based encoding is the conversion of numeric values into a specific sequence of characters, such as a binary sequence. When the system is input, the operand (value) is encoded into a corresponding spike sequence or spike interval. The calculation process is to process the spike. When the system outputs, the spike sequences or spike interval is decoded into a value. The number of rule types used refers to the number of rules using different representations, e.g., the rule a→a is only considered as 1 rule type even if it occurs in multiple neurons. The statistical results in bold in Table 5 are taken from the literature, while the rest are taken from the present study.

In Table 5, for example, the SNPS designed in [29] has multiple input neurons and the digital encoding method is spike sequences. The additive SNP system uses three neurons, the time required for the addition of two natural numbers with a length of k bits is k + 1, and the number of rules is three. Note that while the number of neurons required for multiplication in [29] is thirteen and the time required is k + 7, this multiplication SNPS can only fix one of the multipliers, which is fixed at 26. Due to the lack of an SNPS for implementing division operations in [29], the number of neurons, computation time, and number of rule types required for the division operation are marked with ‘-’.

In [28], the authors used the time interval encoding method, and the input number was represented by the time interval between two spike signals received by the input neuron. This is because the required time is related to the value of the input number, not its binary length, meaning that it cannot obtain the number of time slices required for the calculation. Similarly, [35] used the time-free encoding method to remove the precise execution time of the rules, making the solution of the problem independent of the execution time of the rules; thus, the time required for calculation cannot be obtained.

Refs. [17,31] used spike sequence encoding and two input neurons, meaning that the two operands do not need to be stored in the provided system, ensuring that the number of neurons used by addition and subtraction operations is constant and the calculation consumes a number of time slices k + 1 (or k + 2). The difference between the multiplication of [29] and [15] is that in [29] a multiplier is fixed to 26, while in [31] both multipliers can be input by input neurons, meaning that there is a significant number difference between the neurons and the time slices of consumption. Neither [29] nor [31] provide an SNPS for the division operation.

The work in [30,36] and in this paper, all of which employ spike sequence encoding and one input neuron, are comparable. Because the SNPS in this paper only saves the first operand, the calculation starts when the second operand arrives, which time improves the parallelism of the relevant neurons in the calculation process. Thus, for the number of neurons used in this paper both the time and computation time are less than the results in [30,36]. In addition, this paper presents SNPS for subtraction and division operations, which solves the open problem of how to design a divider based on the SNP system proposed in [30].

On the other hand, in the SNPS with one input neuron, the input of two k-bit operands requires 2k spikes; thus, considering the transmission of spikes and the output of calculation results, the basic arithmetic operation SNPS requires at least 2k + 2 time slices, meaning that the SNPS addition and multiplication designed in this paper have reached the optimum in terms of time consumption. Because the first operand of the input needs to be saved, and considering both the input neuron and the calculation neuron, the SNPS needs at least k + 2 neurons; thus, the SNPS addition and multiplication designed in this paper use a number of neurons that is close to optimum.

From the above analysis, we can see that, under the same encoding and input approach, the basic arithmetic operation SNPS designed in this paper has obvious advantages.

5. Conclusions and Future Work

Basic arithmetic operations are the basis of numerical calculations. In basic arithmetic operations, it is of great significance to study the simplification of computing components, reduce computing resources, and improve computing efficiency. Based on this, the present paper studies the problem of constructing a family of SNPS to realize the four basic arithmetic operations of addition, subtraction, multiplication, and division using only a single input neuron. Specifically: (1) by improving the parallelism of addition, this paper constructs a k-bit binary addition and multiplication with one input neuron. Among them, the number of neurons used by the adder is k + 8 and it takes 2k + 4 time slices, which is 50% and 33% less than similar systems, respectively; (2) the number of neurons used in the multiplication constructed in this paper is 3k + 8, and it takes 3k + 5 time slices, while the number of neurons used is 40% less than that of similar excellent systems; (3) a subtractive SNPS is designed, in which the number of neurons used and the time consumption are k + 13 and 2k + 3 time slices, respectively; (4) based on multiple subtraction, an SNPS for division for solving the quotient of two natural numbers of any binary length is constructed. The number of neurons required is 5k + 13 and the maximum time-consuming is 4k + quotient + 4 time slices, which solves the open problem proposed in [30] of how to design an SNPS to compute the division of two natural numbers. This paper designs a complete set of basic arithmetic operation SNPS, and has obvious advantages in the same type of system.

The system designed in this paper only considers the basic arithmetic operations of natural numbers, and further research can extend it to integers and even decimals. On the other hand, the SNPS for division that we have designed here is not optimal, and further work could optimize the system to reduce the time consumption and the number of neurons used. We are currently developing software for simulating the operation process of SNPS to accelerate the development of related SNPS systems and verify whether these systems are effective. In addition, an SNPS for expression evaluation, which requires the system to take different operations to complete compound operations, is being further developed.