Characteristic Analysis and Decision Model of Lane-Changing Game for Intelligent Connected Vehicles
Abstract
1. Introduction
2. Literature Review
2.1. Non-Cooperative Game Model
2.2. Cooperative Game Model
2.3. Extension of Game Lane-Change Model
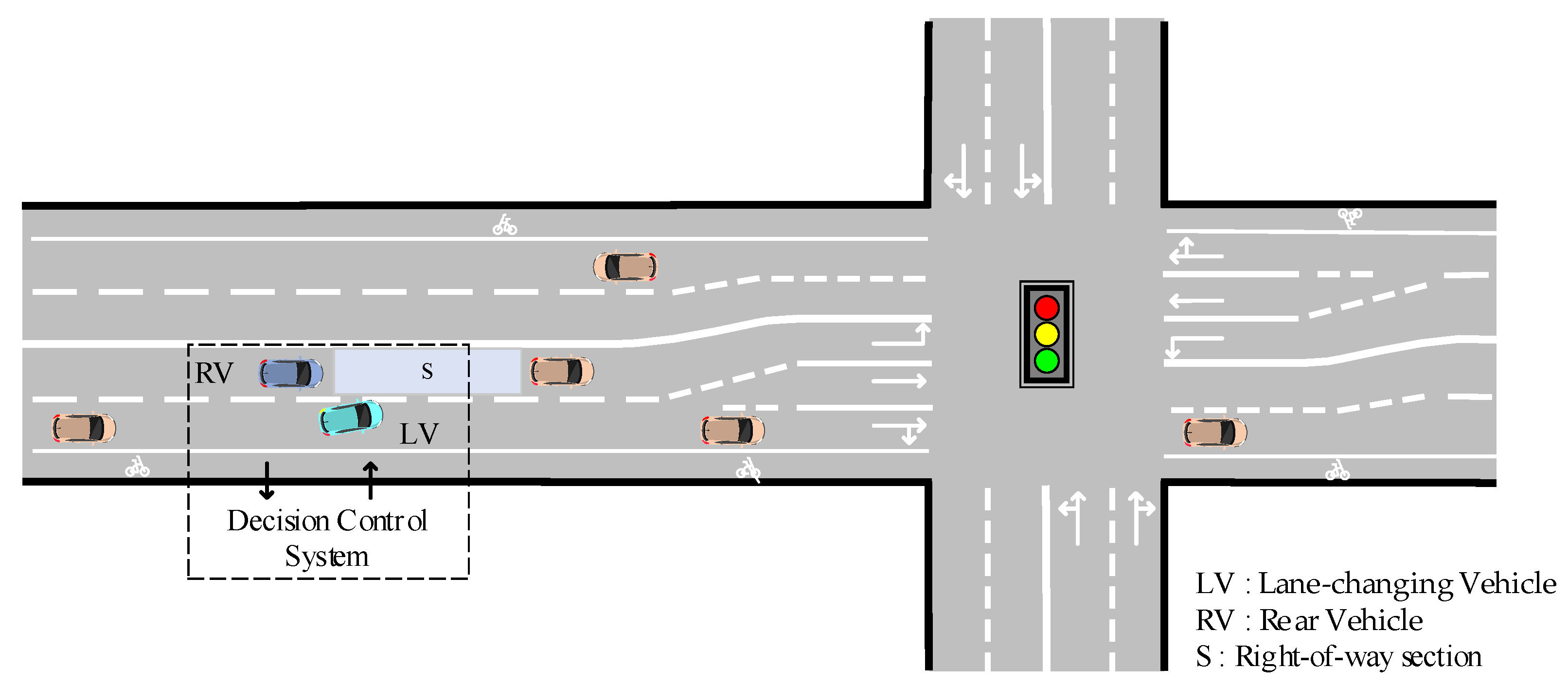
3. Characteristics of Vehicle Lane-Changing Game
4. Game Model
4.1. Definition of Right of Way
4.2. Game Components
4.2.1. Payoffs for Vehicle RV
4.2.2. Payoffs for Vehicle LV
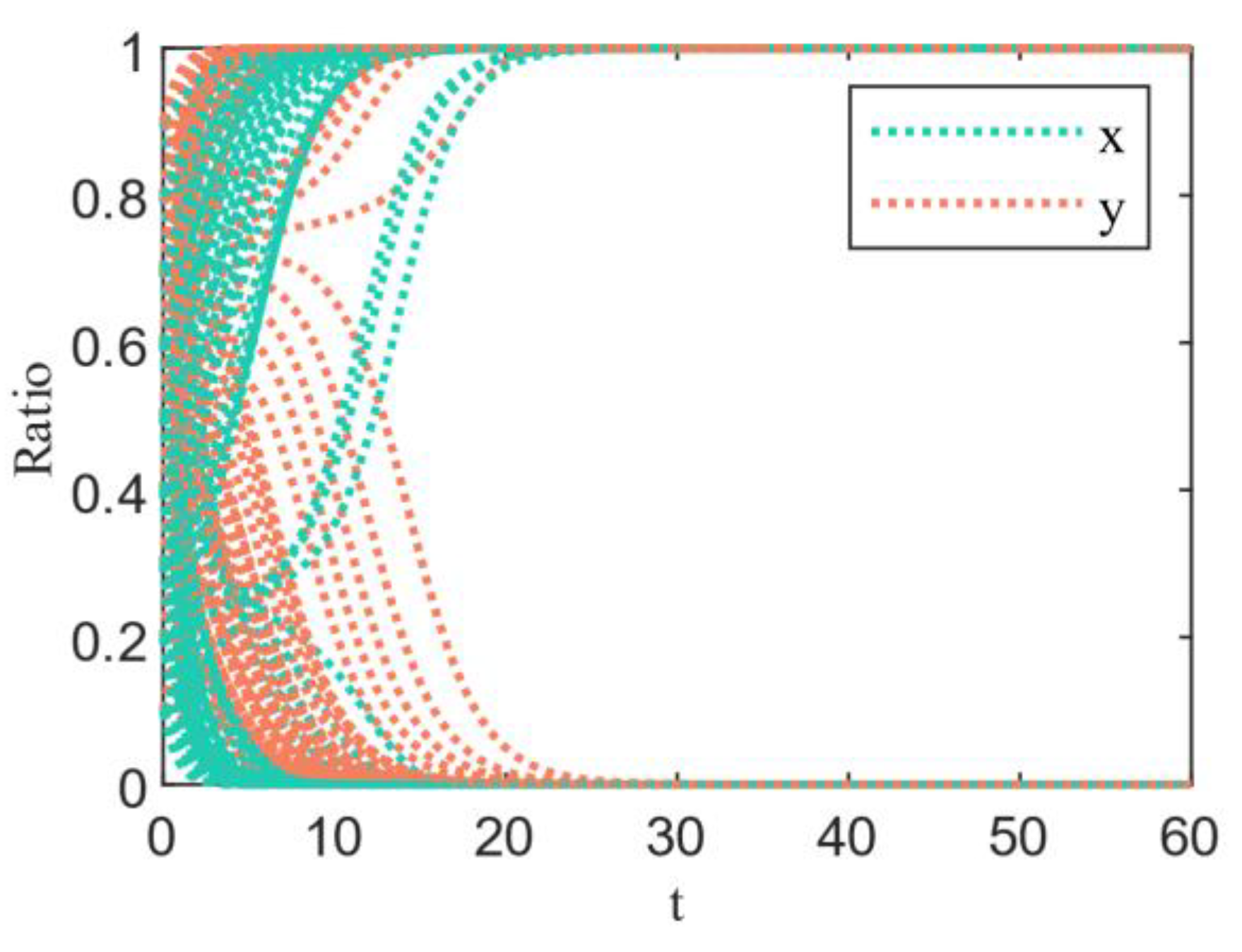
4.3. Game Equilibrium Analysis
5. Simulation Results and Analysis
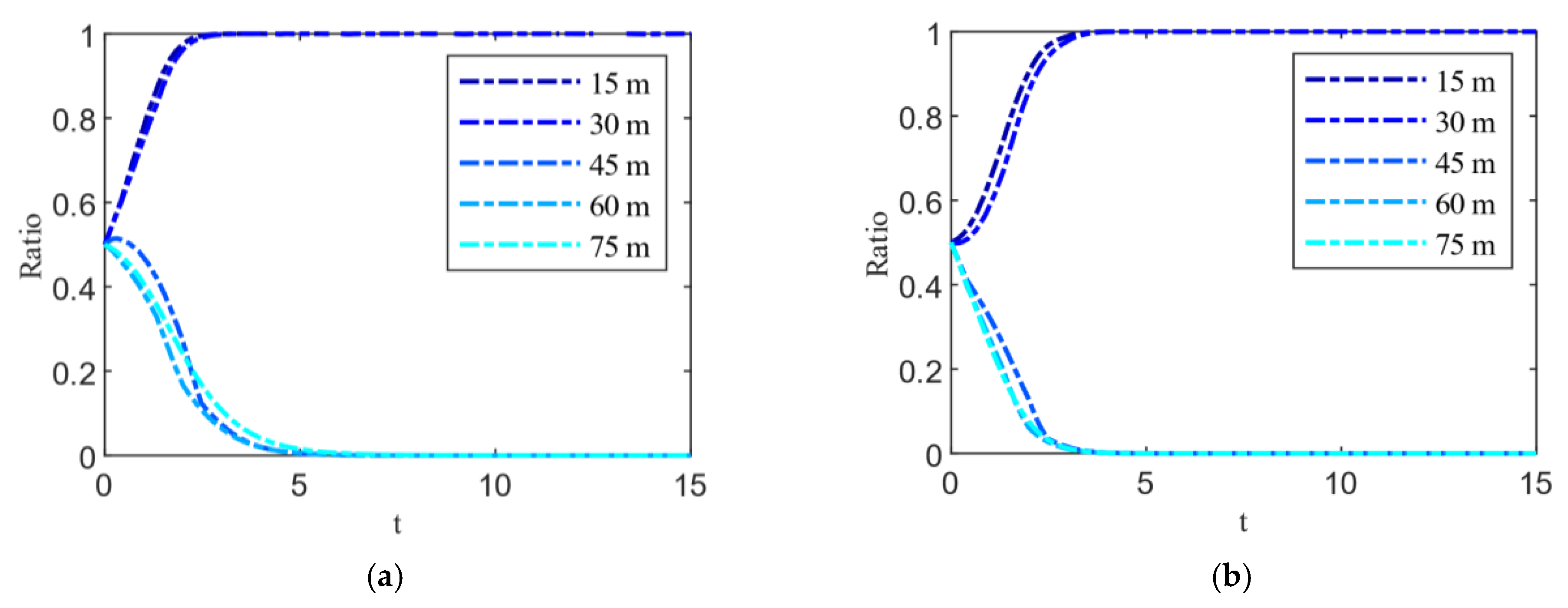
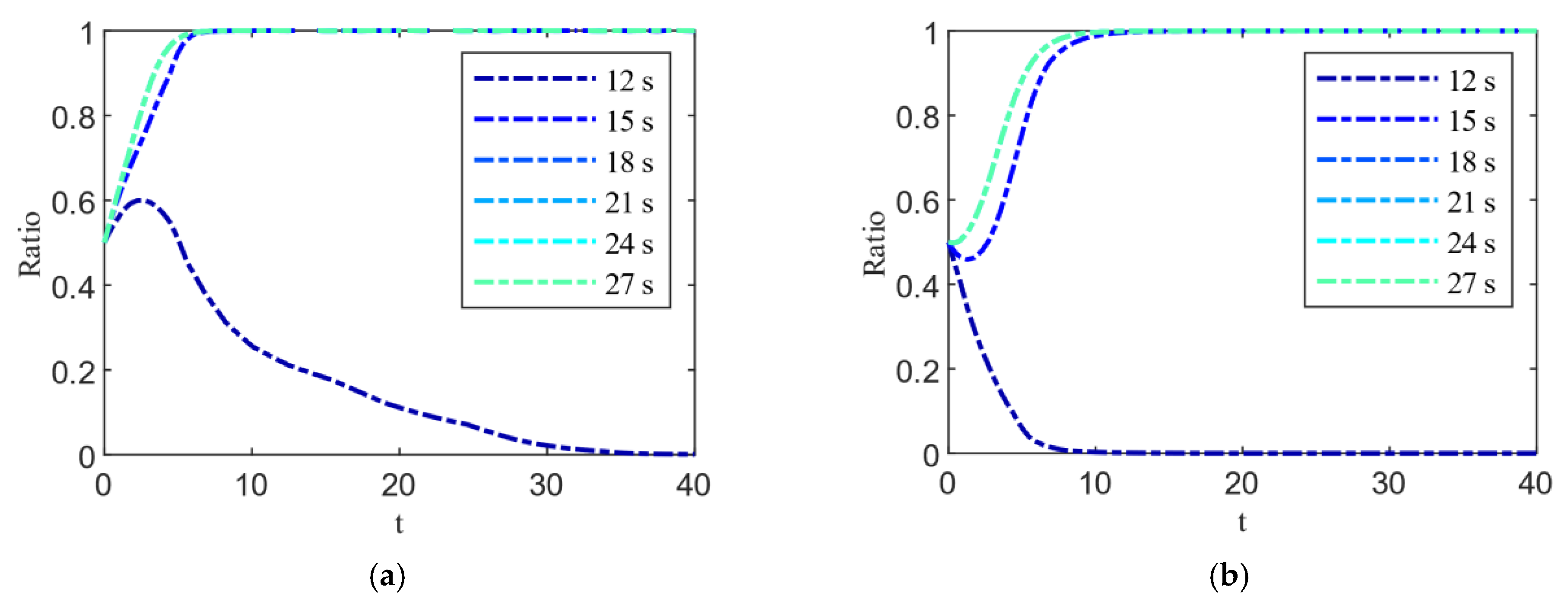
5.1. Sensitivity Analysis
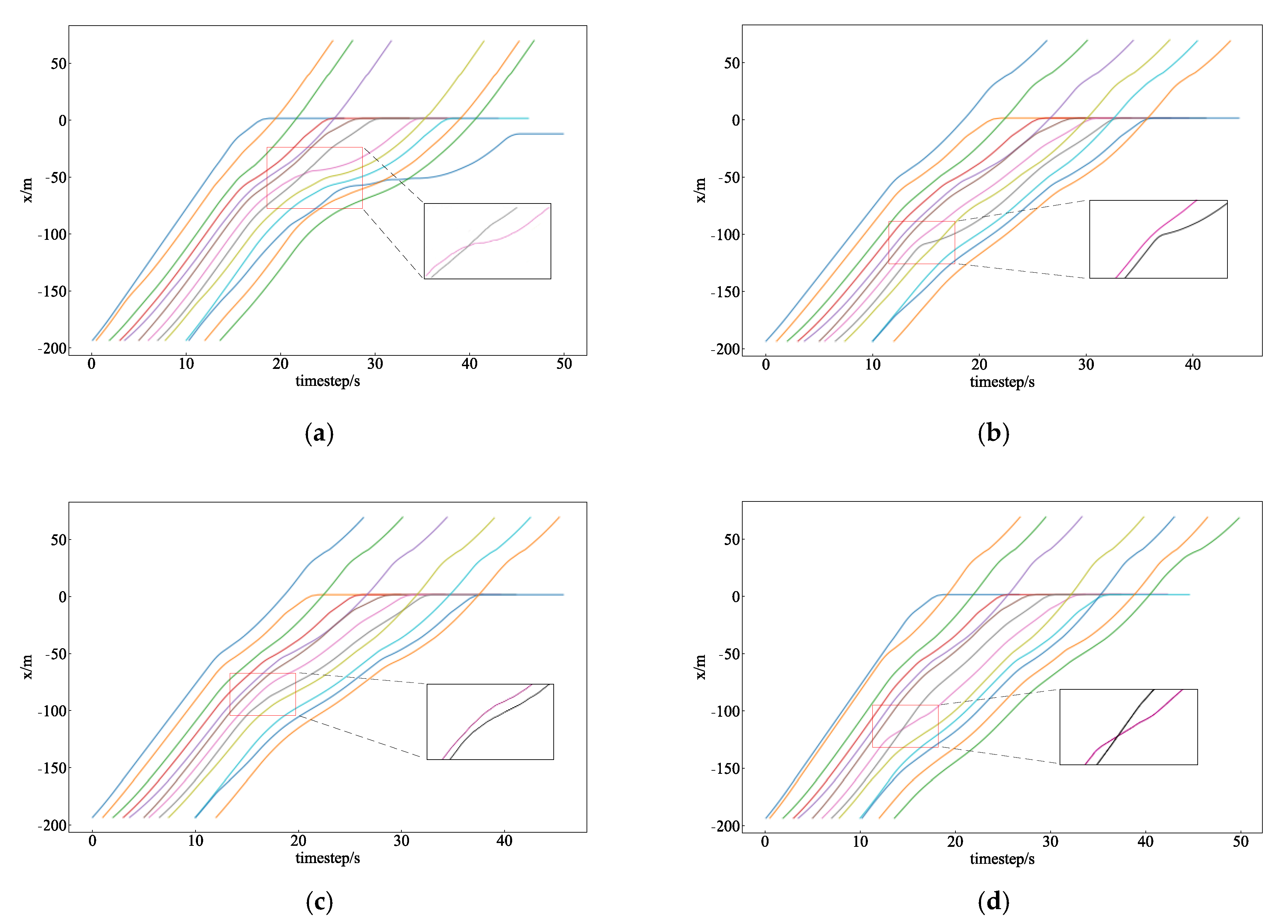
5.2. Analysis of Lane-Change Trajectory
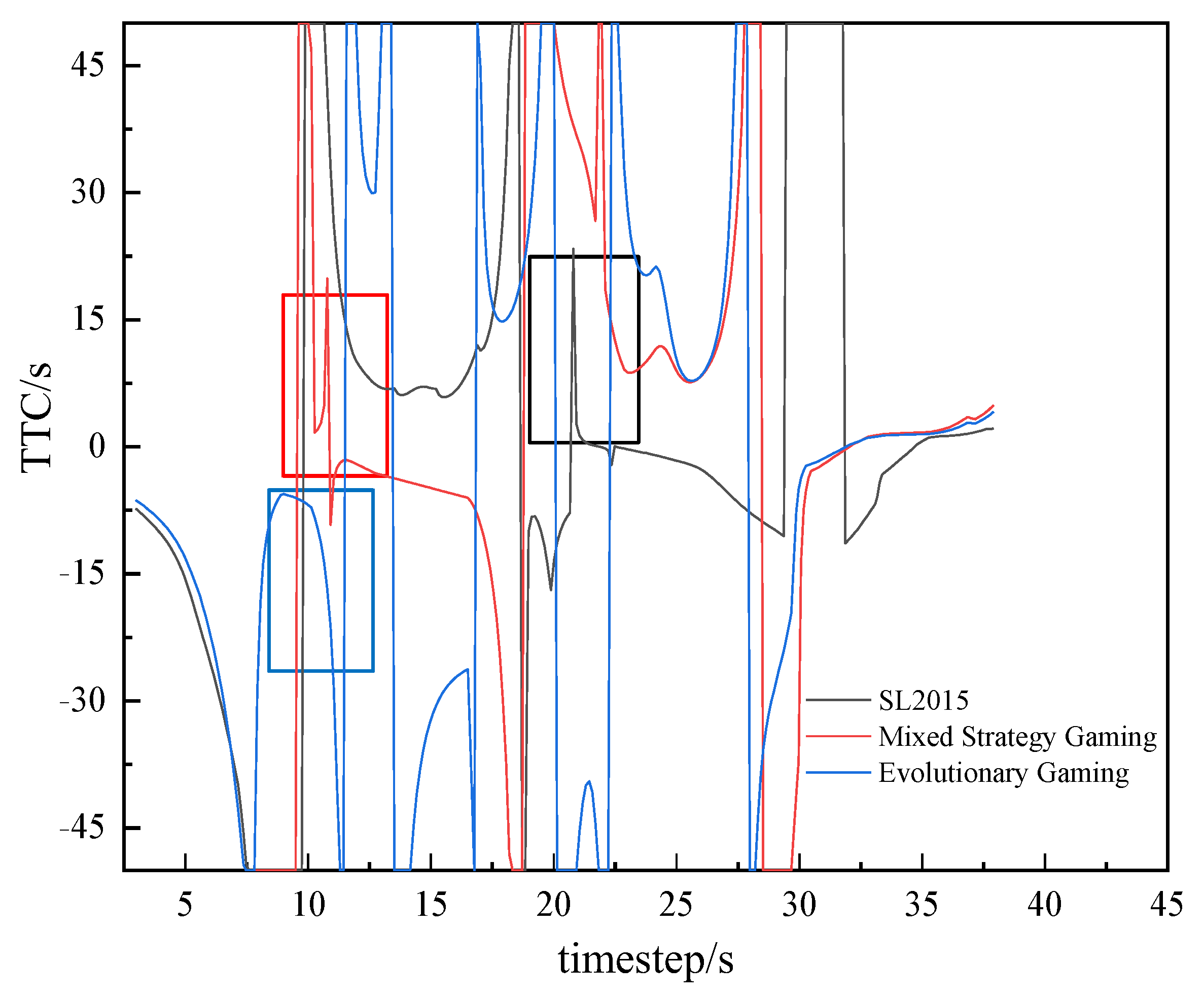
5.3. Analysis of Security
5.4. Threats to Validity
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, T.; Wang, C.; Fu, R.; Ma, Y.; Liu, Z.; Liu, T. Lane-Change Risk When the Subject Vehicle Is Faster Than the Following Vehicle: A Case Study on the Lane-Changing Warning Model Considering Different Driving Styles. Sustainability 2022, 14, 9938. [Google Scholar] [CrossRef]
- Mahmoud, R.; Yousuf, T.; Aloul, F.; Zualkernan, I. Internet of things (IoT) security: Current status, challenges, and prospective measures. In Proceedings of the 2015 10th International Conference for Internet Technology and Secured Transactions (ICITST), London, UK, 14–16 December 2015; pp. 336–341. [Google Scholar]
- Bures, M.; Klima, M.; Rechtberger, V.; Ahmed, B.S.; Hindy, H.; Bellekens, X. Review of Specific Features and Challenges in the Current Internet of Things Systems Impacting Their Security and Reliability. In Trends and Applications in Information Systems and Technologies; AISC: Chicago, IL, USA, 2021; Volume 1367, pp. 546–556. [Google Scholar]
- Sun, K.; Zhao, X.; Gong, S.; Wu, X. A Cooperative Lane Change Control Strategy for Connected and Automated Vehicles by Considering Preceding Vehicle Switching. Appl. Sci. 2023, 13, 2193. [Google Scholar] [CrossRef]
- Van den Beukel, A.P.; Van Driel, C.J.G.; Boelhouwer, A.; Veders, N.; Heffelaar, T. Assessment of Driving Proficiency When Drivers Utilize Assistance Systems—The Case of Adaptive Cruise Control. Safety 2021, 7, 33. [Google Scholar] [CrossRef]
- Ma, S.; Hu, J.; Wang, R.; Qu, S. Study on the Median Opening Length of a Freeway Work Zone Based on a Naturalistic Driving Experiment. Appl. Sci. 2023, 13, 851. [Google Scholar] [CrossRef]
- Kuang, Z.; Zhao, X.; Feng, L. Priority of Emergency Vehicle Dynamic Right-of-Way Control Method in Networked Environment. Appl. Sci. 2023, 13, 5883. [Google Scholar] [CrossRef]
- Wang, C.; Du, Y. Lane-Changing Strategy Based on a Novel Sliding Mode Control Approach for Connected Automated Vehicles. Appl. Sci. 2022, 12, 11000. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Y.; Zhu, H. Theory and Experiment of Cooperative Control at Multi-Intersections in Intelligent Connected Vehicle Environment: Review and Perspectives. Sustainability 2022, 14, 1542. [Google Scholar] [CrossRef]
- Chen, Q.J.; Xie, Y.X.; Ao, Y.; Li, T.G.; Chen, G.R.; Ren, S.F.; Wang, C. A deep neural network inverse solution to recover pre-crash impact data of car collisions. Transp. Res. Part C Emerg. Technol. 2021, 126, 103009. [Google Scholar] [CrossRef]
- Xie, Y.X.; Wu, C.T.; Li, B.Y.; Hu, X.; Li, S.F. A feed-forwarded neural network-based variational Bayesian learning approach for forensic analysis of traffic accident. Comput. Methods Appl. Mech. Eng. 2022, 397, 115148. [Google Scholar] [CrossRef]
- Qu, D.Y.; Zhang, K.K.; Song, H.; Dai, S.C. Analysis and Modeling of Lane-Changing Game Strategy for Autonomous Driving Vehicles. IEEE Access 2022, 10, 69531–69542. [Google Scholar] [CrossRef]
- Yao, R.H.; Du, X.J.; Zhang, W.S.; Zhang, H. Game Model of Lane Changing for Bus Exiting at Bus Bay Stops. J. Transp. Eng. 2022, 29, 319–329. [Google Scholar] [CrossRef]
- Arbis, D.; Dixit, V.V. Game theoretic model for lane changing: Incorporating conflict risks. Accid. Anal. Prev. 2019, 125, 158–164. [Google Scholar] [CrossRef] [PubMed]
- Dai, S.C.; Qu, D.Y.; Wang, Q.K.; Meng, Y.M.; Yang, Y.F. Characterization and model of Connected and Automated Vehicles lane-changing game on upstream sections of signalized intersections. Sci. Technol. Eng. 2023, 23, 4408–4416. [Google Scholar]
- Hang, P.; Lv, C.; Huang, C.; Xing, Y.; Hu, Z.X.; Cai, J.C. Human-like Lane-Change Decision Making for Automated Driving with a Game Theoretic Approach. In Proceedings of the 2020 4th CAA International Conference on Vehicular Control and Intelligence (CVCI), Hangzhou, China, 18–20 December 2020; pp. 708–713. [Google Scholar]
- Sun, K.; Zhao, X.M.; Wu, X. A cooperative lane change model for connected and autonomous vehicles on two lanes highway by considering the traffic efficiency on both lanes. Transp. Res. Int. Pers. 2021, 9, 100310. [Google Scholar] [CrossRef]
- Zheng, Y.; Ding, W.T.; Ran, B.; Qu, X. Coordinated decisions of discretionary lane change between connected and automated vehicles on freeways: A game theory-based lane change strategy. IET. Intell. Transp. Syst. 2020, 14, 1864–1870. [Google Scholar] [CrossRef]
- Liu, R.; Zhao, X.; Zhu, X.C.; Ma, J. A Human-like Shared Driving Strategy in Lane-Changing Scenario Using Cooperative LPV/MPC. IEEE Trans. Intell. Transp. Syst. 2023; in press. [Google Scholar] [CrossRef]
- Yu, Y.W.; Liu, S.K.; Wang, M.X. Multi-Player Dynamic Game-Based Automatic Lane-Changing Decision Model under Mixed Autonomous Vehicle and Human-Driven Vehicle Environment. Transp. Res. Rec. 2020, 2674, 165–183. [Google Scholar] [CrossRef]
- Pan, S.; Wang, Y.; Wang, K. A Game Theory-based Model Predictive Controller for Mandatory Lane Change of Multiple Vehicles. In Proceedings of the 2020 4th CAA International Conference on Vehicular Control and Intelligence (CVCI), Hangzhou, China, 18–20 December 2020; pp. 731–736. [Google Scholar]
- Hang, P.; Huang, C.; Hu, Z.X.; Lv, C. Decision Making for Connected Automated Vehicles at Urban Intersections Considering Social and Individual Benefits. Elec. Eng. Syst. Sci. 2022, 23, 22549–22562. [Google Scholar] [CrossRef]
- Smirnov, N.; Liu, Y.; Validi, A.; Morales-Alvarez, W.; Olaverri-Monreal, C. A Game Theory-Based Approach for Modeling Autonomous Vehicle Behavior in Congested, Urban Lane-Changing Scenarios. Sensors 2021, 21, 1523. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, J.; Liao, L.; Wu, G. Expressway Lane Change in Fog Environment by Dynamic Strategic Game. J. Adv. Transport. 2022, 22, 8612955. [Google Scholar] [CrossRef]
- Wang, G.; Hu, J.; Li, Z.; Li, L. Harmonious Lane Changing via Deep Reinforcement Learning. IEEE Trans. Intell. Transp. Syst. 2021, 23, 4642–4650. [Google Scholar] [CrossRef]
- Kang, K.; Rakha, H.A. A Repeated Game Freeway Lane Changing Model. Sensors 2020, 20, 1554. [Google Scholar] [CrossRef]
- Chen, W.; Ren, G.; Cao, Q.; Song, J.; Liu, Y.; Dong, C. A Game-Theory-Based Approach to Modeling Lane-Changing Interactions on Highway On-Ramps: Considering the Bounded Rationality of Drivers. Mathematics 2023, 11, 402. [Google Scholar] [CrossRef]
- Ye, M.; Li, P.; Yang, Z.; Liu, Y. Research on Lane Changing Game and Behavioral Decision Making Based on Driving Styles and Micro-Interaction Behaviors. Sensors 2022, 22, 6729. [Google Scholar] [CrossRef] [PubMed]
- Ji, K.; Orsag, M.; Han, K. Lane-Merging Strategy for a Self-Driving Car in Dense Traffic Using the Stackelberg Game Approach. Electronics 2021, 10, 894. [Google Scholar] [CrossRef]
- Milanés, V.; Shladover, S.E. Modeling cooperative and autonomous adaptive cruise control dynamic responses using experimental data. Transp. Res. Part C Emerg. Technol. 2014, 48, 285–300. [Google Scholar] [CrossRef]
- Sheikh, M.S.; Wang, J.; Regan, A. A game theory-based controller approach for identifying incidents caused by aberrant lane changing behavior. Phys. A Stat. Mech. Appl. 2021, 580, 126162. [Google Scholar] [CrossRef]
- Jiang, Y.S.; Hu, R.; Yao, Z.H.; Wu, P.C.; Luo, X.L. Stability and safety analysis for heterogeneous traffic flow composed of intelligent and connected vehicles. J. Beijing Jiaotong Univ. 2020, 44, 27–33. [Google Scholar]

| RV | ||
|---|---|---|
| LV | Give Way | Do Not Give Way |
| Change lanes | ||
| Do not change lanes | ||
| RV | ||
|---|---|---|
| LV | Give Way | Do Not Give Way |
| Change lanes | ||
| Do not change lanes | ||
| Equalization Point | Stability | ||
|---|---|---|---|
| (0, 0) | Stable point | ||
| (0, 1) | Instability point | ||
| (1, 0) | Instability point | ||
| (1, 1) | Stable point | ||
| 0 | Saddle point |
| Variable Name | Variable Meaning | Numerical Value |
|---|---|---|
| Simulation step/s | 0.1 | |
| Decision response time/s | 3.0 | |
| Vehicle length/m | 4.0 | |
| Maximum brake deceleration/(m·s−2) | 3.0 | |
| Maximum acceleration/(m·s−2) | 2.3 | |
| Road speed limit/(m·s−1) | 13.89 | |
| Minimum longitudinal distance/m | 2.5 | |
| Minimum lateral distance/m | 1.5 | |
| Signal cycle length/s | 132 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, D.; Dai, S.; Li, A.; Chen, Y.; Wei, C. Characteristic Analysis and Decision Model of Lane-Changing Game for Intelligent Connected Vehicles. Appl. Sci. 2023, 13, 8321. https://doi.org/10.3390/app13148321
Qu D, Dai S, Li A, Chen Y, Wei C. Characteristic Analysis and Decision Model of Lane-Changing Game for Intelligent Connected Vehicles. Applied Sciences. 2023; 13(14):8321. https://doi.org/10.3390/app13148321
Chicago/Turabian StyleQu, Dayi, Shouchen Dai, Aodi Li, Yicheng Chen, and Chuanbao Wei. 2023. "Characteristic Analysis and Decision Model of Lane-Changing Game for Intelligent Connected Vehicles" Applied Sciences 13, no. 14: 8321. https://doi.org/10.3390/app13148321
APA StyleQu, D., Dai, S., Li, A., Chen, Y., & Wei, C. (2023). Characteristic Analysis and Decision Model of Lane-Changing Game for Intelligent Connected Vehicles. Applied Sciences, 13(14), 8321. https://doi.org/10.3390/app13148321





