Abstract
Shear deformation plays an important role in certain structures, and neglecting shear deformation can affect the accuracy of structural response. This paper proposes a non-destructive damage evaluation method that considers shear deformation, based on static response, for identifying corrosion in beam-like structures. The influence of shear deformation on nodal displacement for simply supported beams with different cross-sections was analyzed. The results indicate that even small errors yield inaccurate identification results when neglecting shear deformation. To solve this problem, analytical displacements of the structure were determined based on the Timoshenko beam theory, and the objective function was established. Additionally, the damage identification results were obtained by minimizing the objective function using the interior point method. Several progressively complex examples were used to demonstrate the effectiveness of the proposed method in identifying damage in beam-like structures.
1. Introduction
Recent years have witnessed the rapid development of bridge construction, and bridges have become vital components involved in transporting infrastructure. Over time, in-service bridges will inevitably be damaged due to material aging, harsh natural environments, increasing traffic demands, as well as other extreme events, resulting in damage to the beam structure [1]. The American Society of Civil Engineers (ASCE) Infrastructure Report Card rates the bridge infrastructure in the United States as a C, with 7.5% of bridges being deemed structurally deficient [2]. Therefore, it is necessary to implement safety assessments effectively throughout the entire life cycle of bridges to ensure their integrity and reduce accident losses. Non-destructive damage evaluation (NDE) aims to identify damages in structures as early as possible to enable the taking on of appropriate measures to prevent further damage and avoid catastrophic failure. NDE provides a scientifically feasible solution for detecting the presence of damage in civil engineering structures [3,4,5].
Damage in the structure will lead to changes in some material parameters, such as cross-sectional area, moment of inertia, elastic modulus, and stiffness, thus affecting changes in structural static and dynamic properties, such as displacement, strain, mode shape, and natural frequency [6,7]. These damages can be identified by non-destructive testing of the structural response. According to different load cases, these tests can be divided into dynamic tests [8,9,10] and static tests [11,12,13,14].
The advantage of static-based NDE methods may include simplicity and effectiveness as they can provide high-precision results for structural damage identification. The NDE method based on the static response has attracted the attention of many scholars. Sanayei et al. [15,16] have been committed to structural parameter identification and damage assessment based on the static response, obtaining formulas for estimating structural parameters from static strain and conducting NDE on structures. Moreover, Xiao et al. [17,18] identified the damage for the truss structures using static response and proposed a stiffness separation method to simplify the damage identification of large-scale space truss structures. Deng et al. [19] proposed a damage identification method based on the correlation of the probability distribution of the quasi-static response data. This proposed method is validated by monitoring the strain and tension of bridge structures, and the results show that the method has good accuracy and robustness in identifying bridge structural damage. Zhu et al. [20] also proposed a method to identify structural damage based on the influence line of a sensor and an empirical Bayesian threshold estimator. This method utilizes the quasi-static displacement influence line to obtain displacement readings and infer load effects on the bridge. The accuracy of the method was verified through numerical simulation and field tests on bridges. Le et al. [21] investigated a new method for locating and quantifying damage in Euler–Bernoulli beams using the principle of static deflection changes. The effectiveness and reliability of this method have been verified through numerical simulations and experiments on multiple types of beams. Ma et al. [22] proposed a two-step non-model-based damage localization and quantification method to study the identification of beams. By using the static deflection changes caused by damage, the location of the damage is determined, and the crack depth is evaluated based on the characteristic expression of the rotational spring model. Numerical examples were used to verify that the proposed method can accurately locate and quantify the existing damage in the beam. Peng et al. [23] utilized static shear energy to detect damage in beam-like structures. They conducted simulated experiments using structural deflection data as measurement points on concrete beams with single and multiple damages, and the results showed that the algorithm provided a simple and effective method for locating defects in beam-like structures.
Beams are one of the most fundamental structural elements. The commonly employed theories for modeling the behavior of beams consist of the Euler–Bernoulli beam theory and the Timoshenko beam theory. The Euler–Bernoulli beam theory is often used in the analysis of long and slender beam structures, while the Timoshenko beam theory considers the effects of transverse rotatory inertia and shear deformation, so it is commonly used in the analysis of short and thick beam structures [24]. The classical Euler–Bernoulli beam theory is simplified in its analysis, while the Timoshenko beam theory provides a more accurate structural response [25,26,27]. In most cases, the impact of shear deformation on the structure is significantly smaller than that of the flexural one. Therefore, some studies tend to ignore the effect of shear deformation on the structure to simplify the calculation. However, in certain structures, such as deep beams, shear deformation may play a critical role [28,29]. In such structures, ignoring the impact of shear deformation on the structure may lead to some unreasonable rough results of measured data or model data in the structural analysis. Several studies revealed that even small variations in the model parameters or measurement data can lead to large errors in the identified damage locations and severities [30,31,32].
For this purpose, the NDE method based on the static response for beam-like structures was proposed in this paper, which considered the influence of shear deformation. Firstly, the NDE method and a principle based on static displacement response were introduced, and the influence of shear deformation during the process was also discussed. Then, an analysis was conducted on the effect of shear deformation on the nodal displacement response of a simply supported beam structure with different cross-sectional shapes and different damage scenarios. The proposed method was used for identifying corrosion in the beam elements of the structure, demonstrating its effectiveness and accuracy. Finally, the method was applied to the more complex beam-like structure for damage identification, and conclusions were drawn based on the results.
2. Formulation for Damage Identification
2.1. Element Stiffness Matrix Based on Timoshenko Beam Theory
Each node has three degrees of freedom (DoFs) in the 2D analysis, and the order of the stiffness matrix, , is 6 × 6 for a beam element with a uniform cross-section. In the element stiffness matrix of the Timoshenko beam theory, a dimensionless quantity dependent on the cross-sectional shape is provided as the shear coefficient, Ks. Based on published literature [33,34], the stiffness matrix of elements based on the Timoshenko beam theory can be expressed as follows:
In Equation (1), E, I, A, and L are the elastic modulus, the moment of inertia, the cross-sectional area, and the length of the member, respectively. The coefficient is known as the shear parameter, and can be expressed as
where G represents the shear modulus of the material, and As denotes the shear area, which is related to the shear coefficient, Ks. It should also be noted that different cross-sectional shapes have different values of As. For instance, for a rectangular cross-section, As equals 5/6 times the cross-sectional area A, while for a wide flange cross-section, As is calculated as the product of the thickness of the web and the width of the flange [35]. When the shear parameter () is equal to 0, Equation (1) reduces to the matrix that disregards shear deformation, i.e., the stiffness matrix of elements based on the Euler–Bernoulli beam theory.
2.2. Objective Function
The presented NDE method for identifying damages is founded on the stiffness method, which is an effective method for structural analysis. Since the physical parameters of the structure (such as the moment of inertia, cross-sectional area, and elastic modulus) are contained within the stiffness matrix, any damage to the structure may alter these parameters and can, consequently, affect the structural response. Therefore, any changes in the structural response can be utilized to identify these parameters. If the external force applied to the structure during non-destructive testing is known and some displacements have been accurately measured, then the stiffness method can be utilized to determine the values of unknown parameters. This process is also known as inverse analysis [36,37]. Assuming that some physical parameters in Equation (1) are unknown, the relationship between the structural stiffness matrix, displacements, and forces can be expressed as follows:
where represents the global forces; is the global stiffness matrix of the entire structure, which is obtained by assembling the stiffness matrices, , of all elements; and represents the global displacements.
The objective function for damage identification can be defined as the discrepancy between analytical displacement and measured displacement, and the objective function can be expressed as
In Equation (4), represents the ith measured displacement and represents the ith analytical displacement. The measured displacements and analytical displacements can be obtained by solving Equation (3). Furthermore, the unknown parameter can be obtained by minimizing the objective function. In this study, the interior point method was employed for optimizing the objective function, which is known for its superior computational speed, precision, and stability in tackling complex optimization problems [38].
2.3. Analysis Method for Damage Identification Results
The results of damage identification can be analyzed using mean relative error (MRE), which is a metric commonly used to evaluate the accuracy and precision of an estimation method [39]. The MRE measures the average percentage difference between the identified value and the actual value, which can be calculated using the following equation:
In Equation (5), N is the number of damaged elements, is the ith actual corrosion depth, and is the ith optimal value obtained by optimizing the objective function.
3. Effect of Shear Deformation on Nodal Displacement of a Simply Supported Beam
Figure 1 shows a three-element simply supported beam model, where the number of elements is denoted within the box, the number of nodes in the circle, and the DoFs of each node are represented by the number next to the arrow.
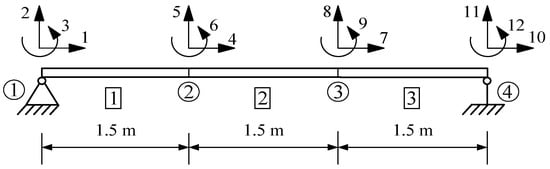
Figure 1.
Simply supported beam with three elements.
The beam under consideration has a length of 4.5 m and is modeled with three beam elements and four nodes, where each element length is set at 1.5 m. The modulus of elasticity (E) is 206 GPa and the shear modulus of the material (G) is 79.23077 GPa. According to the boundary conditions of the structure, node 1 restricts horizontal and vertical displacement, while node 4 only restricts vertical displacement. The external forces are applied as concentrated vertical forces of −50 kN at nodes 2 and 3. For analysis and comparison, two different cross-sectional shapes were considered, along with six varied damage scenarios. The dimension parameters of the cross-sectional shapes of the structure are given in Table 1.

Table 1.
The cross-sectional shapes and dimensions.
The data presented in Table 1 indicate that the wide flange cross-section and the rectangular cross-section have the same depth and width dimensions, resulting in the same depth-to-span ratio (h/L) of 0.033 for the structure.
Assuming that the beam elements are subjected to corrosion in the cross-sectional area, Table 2 presents the corresponding corrosion depths specified for each scenario from Scenario 1 to Scenario 6.

Table 2.
Damage scenarios.
Table 2 presents six distinct damage scenarios, with Scenarios 1, 2, and 3 involving damage to a single beam element, and Scenarios 4, 5, and 6 involving damage to two beam elements. The numbers in the table represent the corrosion depth of the beam elements.
The nodal displacements under six different damage scenarios were analyzed using the Euler–Bernoulli beam theory and the Timoshenko beam theory, respectively. Considering the large vertical displacement response of the simply supported beam structure, the relative errors in nodal displacements at DoFs 5 and 8 under different damage scenarios were analyzed. Figure 2 illustrates the relative error of vertical displacement based on two different beam theories. Specifically, Figure 2a displays the relative errors in nodal displacement at DoF 5 for simply supported beams with wide flange cross-section and rectangular cross-section, while Figure 2b displays the relative errors in nodal displacement at DoF 8 for the same structure.
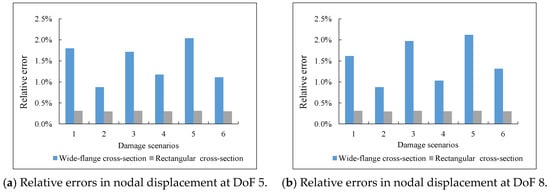
Figure 2.
Relative errors in nodal displacement under different damage scenarios.
From Figure 2a,b, it can be observed that shear deformation affects the nodal displacements of simply supported beams with wide flange cross-section and rectangular cross-section. For the simply supported beam with a wide flange cross-section, the relative errors in nodal displacements induced by shear deformation exhibit a variation under different damage scenarios. In particular, under Scenario 5, the maximum relative error is observed, with relative errors in DoFs 5 and 8 being 2.04% and 2.12%, respectively.
4. Damage Identification of Beam-like Structures Considering Shear Deformation
4.1. Example 1: Simply Supported Beam with Three Elements
Based on the discussion in the previous section, it is clear that shear deformation induces errors in the calculation of nodal displacements, and the impact of these errors on damage identification needs to be investigated further. This section focuses on investigating damage identification for the simply supported beam structure shown in Figure 1, which has the wide flange cross-section and the rectangular cross-section, as specified in Table 1. These structures are subjected to different damage scenarios, as listed in Table 2. Two different beam theories, the Euler–Bernoulli beam theory and the Timoshenko beam theory, are used for damage identification. In this study, the measured displacements for DoFs 5 and 8 were calculated based on the Timoshenko beam theory. Following the methodology presented in Section 2, the analytical displacements were obtained. Subsequently, the objective function shown in Equation (4) was established to identify the corrosion depth of beam elements. The interior point method was applied to optimize the objective function based on the current damage condition and cross-sectional dimensions of the beam elements, with boundary conditions set to zero and two with a starting point of one.
Table 3 presents the identification results for simply supported beams with wide flange cross-sections, including the iterations of objective functions based on both the Timoshenko beam theory and the Euler–Bernoulli beam theory, as well as the optimal value of the identified corrosion depth.

Table 3.
Identification results of the simply supported beam with a wide flange cross-section.
From the data in Table 3, it can be observed that the damage identification results obtained based on the Timoshenko beam theory are consistent with the corrosion depths given in Table 2. However, for Scenario 1 to Scenario 6, the damage identification results based on the Euler–Bernoulli beam theory show different degrees of deviation from the actual damage situation. The most significant errors in damage identification results occurred in Elements 1 and 3, with corrosion depths of 0.89 mm and 1.08 mm in Scenarios 1 and 3, respectively.
Table 4 presents the identification results for the simply supported beam with a rectangular cross-section.

Table 4.
Identification results of the simply supported beam with a rectangular cross-section.
Similar to previous findings, the data in Table 4 leads to the following conclusions: The damage identification results obtained based on the Timoshenko beam theory are consistent with the actual values of corrosion depth (Table 2). However, the damage identification results obtained based on the Euler–Bernoulli beam theory seem to have greater errors, especially for the identification of Element 2, where the corrosion depths in Scenarios 2, 4, and 6 are 1.28 mm.
To further analyze the obtained data, MRE analysis was conducted on the results obtained based on the Euler–Bernoulli beam theory. Table 5 shows the MRE of the damage identification results obtained based on the Euler–Bernoulli beam theory for two simply supported beams with different cross-sectional shapes.

Table 5.
The MRE of the results based on the Euler–Bernoulli beam theory.
From Table 5, it can be observed that for the simply supported beam with rectangular and wide flange cross-section, the largest MREs are 27.70% and 10.93%, respectively. In conclusion, it can be confirmed that the method based on the Timoshenko beam theory effectively improves the accuracy of damage identification results for simply supported beams with two different cross-sectional shapes.
4.2. Example 2: Simply Supported Beam with Five Elements
To further validate the proposed method, the simply supported beam depicted in Figure 3 was examined.
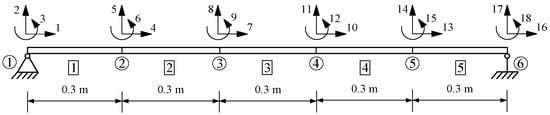
Figure 3.
Simply supported beam with five elements.
The beam has a length of 1.5 m and consists of five beam elements and six nodes, with each element being 0.3 m in length. According to the boundary conditions of the structure, node 1 restricts horizontal and vertical displacement, while node 6 restricts only vertical displacement. The material properties of this example correspond to that of the beam discussed in Section 4.1, with a rectangular cross-section shape (see Table 1). Moreover, two concentrated vertical forces of −100 kN were applied separately to nodes 2 and 5, and the damage scenarios of the structure are shown in Table 6.

Table 6.
Damage scenarios.
Table 6 provides three different scenarios of damage, where Scenario 1 involves damage to two beam elements, Scenario 2 involves damage to three beam elements, and Scenario 3 involves damage to four beam elements.
The proposed damage identification method, which takes into account shear deformation, is employed to identify damage in the structure. The objective function was formulated based on nodal displacements of DoFs 5, 8, 11, and 14. The boundary conditions of the interior point method range from 0 to 2, and the starting point is one. Figure 4a–c illustrate the identification results of corrosion depth for Scenario 1, Scenario 2, and Scenario 3, respectively.
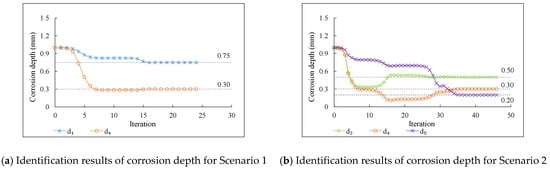
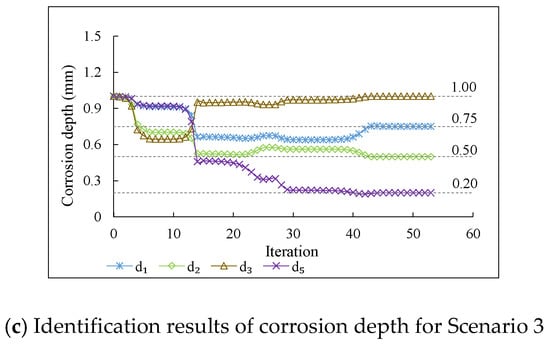
Figure 4.
Identification results of corrosion depth for different scenarios.
The horizontal axis of Figure 4 represents the number of iterations, and the vertical axis represents the corrosion depth of the beam elements. Additionally, the dashed lines indicate the actual corrosion depth of each element. As can be seen from Figure 4a, the objective function of Scenario 1 terminates after 24 iterations, and the final identification results of elements 1 and 4 match the actual corrosion depths perfectly. In Figure 4b, the objective function for Scenario 2 terminates after 46 iterations, and the damage of elements 2, 4, and 5 are successfully identified. Figure 4c shows the damage identification process for Scenario 3, where the objective function terminates after 53 iterations and the damage of all four beam elements is identified.
From the results presented in Figure 4, it can be concluded that the proposed method can effectively identify the damage of simply supported beams. Furthermore, Scenario 3 achieves the highest number of iterations among the three scenarios.
To provide a more intuitive display of the accuracy of damage identification, Figure 5 shows the trend of the MRE changes with iterations for Scenario 1, Scenario 2, and Scenario 3.
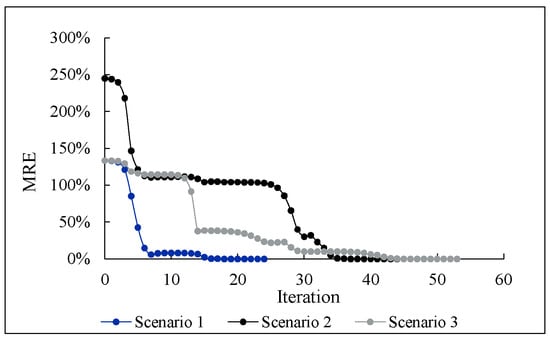
Figure 5.
The MRE during the identification for three different scenarios.
From Figure 5, it can be observed that the MRE decreases as iterations increase for all scenarios, indicating that the proposed damage identification method converges to a satisfactory solution.
4.3. Example 3: Simply Supported Overhanging Beam with Five Elements
To illustrate the effectiveness of the proposed method, a simply supported overhanging beam was studied. Figure 6 depicts the model used for identification, which is a simply supported overhanging beam with a length of 1.8 m, composed of six nodes and five beam elements.
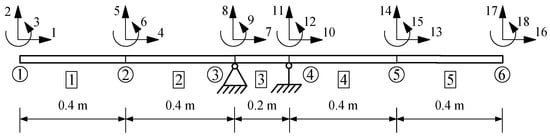
Figure 6.
Simply supported overhanging beam with five elements.
The material properties for this beam were the same as those used in previous examples, with a rectangular cross-sectional shape (see Table 1). The applied external forces consisted of concentrated vertical forces at nodes 1, 5, and 6, with magnitudes of −50 kN, −50 kN, and −100 kN, respectively. The damage scenarios of the structure are shown in Table 6.
The nodal displacements at DoFs 2, 5, 14, and 17 were selected as the necessary data for establishing the objective function. Figure 7a–c illustrate the identification process of three different damage scenarios using the objective function established based on the method that accounts for shear deformation.
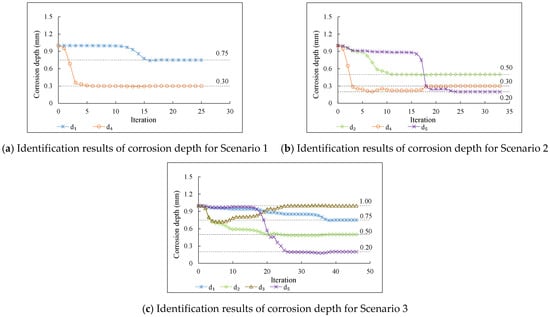
Figure 7.
Identification results of corrosion depth for different scenarios.
From Figure 7, it can be observed that the proposed damage detection method that accounts for shear deformation successfully identified the corrosion depths for all three damage scenarios. For damage Scenarios 1, 2, and 3, the objective function was iterated 25, 33, and 46 times, respectively, to complete the damage identification for two beam elements, three beam elements, and four beam elements.
The MRE of corrosion depth identification results for three different damage scenarios are given in Figure 8.
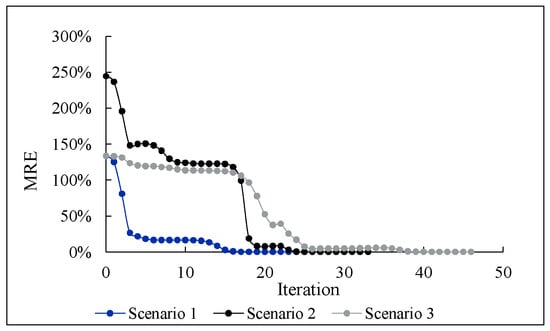
Figure 8.
The MRE during the identification for three different damage scenarios.
Figure 8 clearly shows the variation of MRE with iterations for all three damage scenarios, which eventually decrease to near-zero values. This indicates that the proposed method successfully identified structural damage in all scenarios, confirming its effectiveness and accuracy.
5. Conclusions
Overall, this paper proposed a non-destructive evaluation method based on the static response, which takes into account shear deformation to identify the corrosion in beam-like structures. Simply supported beams with a wide flange cross-section and a rectangular cross-section were used to demonstrate the influence of shear deformation on the nodal displacement response of structures. This example showed that the effect of shear deformation on the nodal displacements of simply supported beams is significant. Although the errors in nodal displacements caused by shear deformation in the simply supported beam with a rectangular cross-section may not be noticeable, it is enough to affect the accuracy of damage identification results. To investigate the influence of shear deformation on the accuracy of identification results, damage identification methods based on the Euler–Bernoulli beam theory and the Timoshenko beam theory were employed for this structure. The results showed that considering shear deformation effectively improved the accuracy of damage identification.
The proposed method was also applied to the complex beam-like structures to verify the accuracy, applicability, and effectiveness of damage identification. The results demonstrated that the method successfully identified the scenarios of damage for the beam-like structures.
Author Contributions
Conceptualization, X.M. and F.X.; Investigation, X.M., F.X., Y.Y. and G.S.C.; Writing—original draft, X.M.; Writing—review & editing, X.M., F.X., Y.Y., G.S.C. and Y.M.; Funding acquisition, F.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Jiangsu Province, China (Grant No. BK20200492).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ni, Y.Q.; Chen, R. Strain monitoring based bridge reliability assessment using parametric Bayesian mixture model. Eng. Struct. 2021, 226, 11406. [Google Scholar] [CrossRef]
- Dawood, T.; Zhu, Z.; Zayed, T. Computer vision–based model for moisture marks detection and recognition in subway networks. J. Comput. Civ. Eng. 2018, 32, 04017079. [Google Scholar] [CrossRef]
- Li, D.; Zhou, J.; Ou, J. Damage, nondestructive evaluation and rehabilitation of FRP composite-RC structure, A review. Constr. Build. Mater. 2020, 271, 121551. [Google Scholar] [CrossRef]
- Naito, H.; Sugiyama, R.; Bolander, J.E. Local Vibration Testing and Damage Evaluation for RC Bridge Decks. J. Struct. Eng. 2020, 146, 04020168. [Google Scholar] [CrossRef]
- Wang, J.; Xu, T.; Zhang, L.; Chang, T.; Zhang, J.; Yan, S.; Cui, H.L. Nondestructive damage evaluation of composites based on terahertz and X-ray image fusion. NDT E Int. Indep. Nondestruct. Test. Eval. 2022, 127, 102616. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, C.; Gu, X.; Li, J. A novel deep learning-based method for damage identification of smart building structures. Struct. Health Monit. 2019, 18, 143–163. [Google Scholar] [CrossRef]
- Hou, R.; Xia, Y. Review on the new development of vibration-based damage identification for civil engineering structures: 2010–2019. J. Sound Vib. 2021, 491, 115741. [Google Scholar] [CrossRef]
- Capponi, L.; Slavi, J.; Rossi, G.; Boltear, M. Thermoelasticity-based modal damage identification. Int. J. Fatigue 2020, 137, 105661. [Google Scholar] [CrossRef]
- Yang, X.; Ouyang, H.; Guo, X.; Cao, S. Modal Strain Energy-Based Model Updating Method for Damage Identification on Beam-Like Structures. J. Struct. Eng. 2020, 146, 04020246. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, J.; Lu, Z.R. A fast friction-model-inspired sparse regularization approach for damage identification with modal data. Comput. Struct. 2020, 227, 106142. [Google Scholar] [CrossRef]
- Lu, Z.R.; Zhou, J.; Wang, L.; Liu, J. Damage identification from static tests by eigenparameter decomposition and sparse regularization. Struct. Health Monit. 2019, 19, 147592171988098. [Google Scholar] [CrossRef]
- Xiao, F.; Fan, J.; Chen, G.S.; Hulsey, J.L. Bridge health monitoring and damage identification of truss bridge using strain measurements. Adv. Mech. Eng. 2019, 11, 1–7. [Google Scholar] [CrossRef]
- Xiao, F.; Zhu, W.; Meng, X.; Chen, G.S. Parameter identification of structures with different connections using static responses. Appl. Sci. 2022, 12, 5896. [Google Scholar] [CrossRef]
- Pathirage, C.S.N.; Li, J.; Li, L.; Hao, H.; Liu, W.; Wang, R. Development and application of a deep learning–based sparse autoencoder framework for structural damage identification. Struct. Health Monit. 2019, 18, 103–122. [Google Scholar] [CrossRef]
- Sanayei, M.; Saletnik, M.J. Parameter estimation of structures from static strain measurements I: Formulation. J. Struct. Eng. 1996, 122, 555–562. [Google Scholar] [CrossRef]
- Sanayei, M.; Phelps, J.E.; Sipple, J.D.; Bell, E.S.; Brenner, B.R. Instrumentation, nondestructive testing, and finite-element model updating for bridge evaluation using strain measurements. J. Bridge Eng. 2012, 17, 130–138. [Google Scholar] [CrossRef]
- Xiao, F.; Hulsey, J.L.; Chen, G.S.; Xiang, Y. Optimal static strain sensor placement for truss bridges. Int. J. Distrib. Sens. Netw. 2017, 13, 155014771770792. [Google Scholar] [CrossRef]
- Xiao, F.; Sun, H.; Mao, Y.; Chen, G.S. Damage identification of large-scale space truss structures based on stiffness separation method. Structures 2023, 53, 109–118. [Google Scholar] [CrossRef]
- Deng, F.; Wei, S.; Jin, X.; Chen, Z.; Li, H. Damage identification of long-span bridges based on the correlation of probability distribution of monitored quasi-static responses. Mech. Syst. Signal Process. 2023, 186, 109908. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, C.; Li, X. Structural damage detection of the bridge under moving loads with the quasi-static displacement influence line from one sensor. Measurement 2023, 211, 112599. [Google Scholar] [CrossRef]
- Le, N.T.; Thambiratnam, D.P.; Nguyen, A.; Chan, T.H.T. A new method for locating and quantifying damage in beams from static deflection changes. Eng. Struct. 2019, 180, 779–792. [Google Scholar] [CrossRef]
- Ma, Q.; Solís, M. Multiple damage identification in beams from full-field digital photogrammetry. J. Eng. Mech. 2019, 145, 04019054. [Google Scholar] [CrossRef]
- Peng, X.; Yang, Q. Damage detection in beam-like structures using static shear energy redistribution. Front. Struct. Civ. Eng. 2022, 16, 1552–1564. [Google Scholar] [CrossRef]
- Zhang, X.; Thompson, D.; Sheng, X. Differences between Euler-Bernoulli and Timoshenko beam formulations for calculating the effects of moving loads on a periodically supported beam. J. Sound Vib. 2020, 481, 115432. [Google Scholar] [CrossRef]
- Abbas, W.; Bakr, O.K.; Nassar, M.M.; Abdeen, M.; Shabrawy, M. Analysis of Tapered Timoshenko and Euler–BernoulliBeams on an Elastic Foundation with Moving Loads. J. Math. 2021, 2021, 6616707. [Google Scholar] [CrossRef]
- Larsen, M.L.; Adhikari, S.; Arora, V. Analysis of stochastically parameterized prestressed beams and frames. Eng. Struct. 2021, 249, 113312. [Google Scholar] [CrossRef]
- Luo, J.; Zhu, S.; Zhai, W. Exact closed-form solution for free vibration of Euler-Bernoulli and Timoshenko beams with intermediate elastic supports. Int. J. Mech. Sci. 2022, 213, 106842. [Google Scholar] [CrossRef]
- EN 1992-1-1; Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings. CEN: Brussels, Belgium, 2002.
- ACI Committee 318 Building Code Requirements for Structural Concrete and Commentary; American Concrete Institute: Detroit, MI, USA, 2000.
- Ding, Z.; Li, J.; Hao, H.; Lu, Z.R. Structural damage identification with uncertain modelling error and measurement noise by clustering based tree seeds algorithm. Eng. Struct. 2019, 185, 301–314. [Google Scholar] [CrossRef]
- Lu, Z.R.; Zhou, J.; Wang, L. On choice and effect of weight matrix for response sensitivity-based damage identification with measurement and model errors. Mech. Syst. Signal Process. 2019, 114, 1–24. [Google Scholar] [CrossRef]
- Seventekidis, P.; Giagopoulos, D. Model error effects in supervised damage identification of structures with numerically trained classifiers. Mech. Syst. Signal Process. 2023, 184, 109741. [Google Scholar] [CrossRef]
- Przemieniecki, J.S. Theory of Matrix Structural Analysis. Library of Congress Catalog Card Number 67; Courier Corporation: Gloucester, MA, USA, 1968. [Google Scholar]
- Logan, D.L. A First Course in the Finite Element Method, Enhanced Edition, SI Version; Cengage Learning: Boston, MA, USA, 2022. [Google Scholar]
- ANSI/AISC 360-10; Specification for Structural Steel Buildings. AISC: Chicago, IL, USA, 2010.
- Castillo, E.; Nogal, M.; Antonio Lozano-Galant, J.; Turmo, J. Solving some special cases of monomial ratio equations appearing frequently in physical and engineering problems. Math. Probl. Eng. 2016, 2016, 9764913. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks, a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2018, 378, 686–707. [Google Scholar] [CrossRef]
- Wambacq, J.; Maes, K.; Rezayat, A.; Guillaume, P.; Lombaert, G. Localization of dynamic forces on structures with an interior point method using group sparsity. Mech. Syst. Signal Process. 2018, 115, 593–606. [Google Scholar] [CrossRef]
- Tofallis, C. A better measure of relative prediction accuracy for model selection and model estimation. J. Oper. Res. Soc. 2015, 66, 1352–1362. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).