Earthquake Detection Using Stacked Normalized Recurrent Neural Network (SNRNN)

Featured Application

Earthquake Detection, Earthquake Early Warning System (EEWS), Processing of Seismic data.

Abstract

Earthquakes threaten people, homes, and infrastructure. Earthquake detection is a complex task because it does not show any specific pattern, unlike object detection from images. Convolutional neural networks have been widely used for earthquake detection but have problems like vanishing gradients, exploding, and parameter optimization. The ensemble learning approach combines multiple models, each of which attempts to compensate for the shortcomings of the others to enhance performance. This article proposes an ensemble learning model based on a stacked normalized recurrent neural network (SNRNN) for earthquake detection. The proposed model uses three recurrent neural network models (RNN, GRU, and LSTM) with batch normalization and layer normalization. After preprocessing the waveform data, the RNN, GRU, and LSTM extract the feature map sequentially. Batch normalization and layer normalization methods take place in mini-batches and input layers for stable and faster training of the model and improving its performance. We trained and tested the proposed model on 6574 events from 2000 to 2018 (18 years) in Turkey, a highly targeted region. The SNRNN achieves RMSE values of 3.16 and 3.24 for magnitude and depth detection. The SNRNN model outperforms the three baseline models, as seen by their low RMSE values.

1. Introduction

Natural disasters like earthquakes can be very damaging. They also trigger tsunamis, earthquakes, and fires, all of which can inflict significant damage and risk human and property safety. Earthquakes can have different effects on humans depending on the severity of the quake and the surrounding environment. Large earthquakes of six or above on the Richter scale are the scariest. Earthquakes have killed nearly 750,000 people worldwide since 1998. Many of these fatalities happened in nations hit hard by natural disasters, like Japan, China, and Indonesia. Automatic early earthquake detection using the data from seismic station sensors has emerged as an important area of research in recent years for emergency response [1]. The primary task in earthquake detection is to estimate an incoming event’s magnitude, depth, and location information. Emergency response and early earthquake warning systems (EEWSs) should be able to issue a warning or spread event information on the targeted area within seconds of the detection of seismic waves without the need for human intervention [2]. The number of seismic networks and monitoring sensors has steadily increased in recent years, and the continuous growth of seismic records calls for new processing algorithms that assist in solving problems in seismology. Several seismic networks with multiple stations, like the Southern California Seismic Network and the Turkey Network, have provided catalogs of earthquake events in the last decade. Seismology benefits significantly from a practical and comprehensive analysis of these catalogs. Using computational approaches like machine learning and deep learning is more promising for automatically predicting earthquakes [3].

Many different machine learning models, including decision trees (DTs), support vector machines (SVMs), and k-nearest neighbors (k-NNs), have been applied to the problem of earthquake detection. Ref. [4] used the SVM model for an on-site early warning system. Ref. [5] used k-means clustering techniques for earthquake magnitude detection from global earthquake catalogs. Ref. [6] used k-NN, SVM, DT, and random forest (RF) for earthquake detection and found that RF outperformed the other models. Several factors like feature selection method, dataset size, and class imbalance distribution affect the performance of machine learning models. To overcome the machine learning issues, deep learning has been introduced.

Deep learning is a subfield of machine learning. Like artificial neural networks, deep learning-based models use multiple layers to input and process data and output the results. Deep learning models are considered good when the dataset is complex and large because they employ several layers to deal with such data [6]. A convolutional neural network (CNN) was used to classify earthquake events into macro, micro, and artificial earthquakes. Ref. [1] presented a CNN and a graph convolutional network (GCN) based on deep learning models to detect earthquakes from multiple stations. Ref. [7] proposed a method that uses a CNN and graph partitioning algorithms to detect events with extremely low signal-to-noise ratios. Recurrent neural networks (RNNs) have a different architecture than CNNs. RNNs use various gates for different operations instead of convolutional and pooling operations. Ref. [8] used an RNN-based DeepShake model, and Ref. [9] used a CNN model to predict earthquake shaking intensity from ground motion observation. Ref. [10] used LSTM and BLSTM for magnitude detection. Ref. [2] proposed a transformer-based TEAM method that issues accurate and timely warnings. Model interpretation, hyperparameter tuning, and GPU-based special devices are significant issues with deep learning models. Past research studies propose three approaches to overcome the problems of deep learning and machine learning methods: layer or batch normalization, the attention mechanism in deep learning architectures, and ensemble learning.

Multiple or ensemble learning models have grown in computational intelligence in the last couple of decades. Different models (i.e., base classifiers) are organized sequentially or parallel to the design of a more powerful ensemble model. An ensemble model may consist of only machine learning models, deep learning models, or hybrid models. Ensemble-based studies report that ensemble models outperform the individual models of either machine learning or deep learning [9,11]. In machine learning-based ensemble studies, Ref. [11] proposed a machine learning-based ensemble method that combines SVM, k-NN, DT, and RF to design an ensemble model that can effectively detect earthquakes. Ref. [9] ensembled four machine learning models, AdaBoost, XGBoost, DT, and LightXGBoost, in a stack using multiple settings. Another stacked-based ensembled model was proposed in [10] to ensemble three models, bagging, AdaBoost, and stacking, for earthquake causality prediction. Ref. [12] ensembled a CNN and LSTM and proposed MagNet for earthquake magnitude estimation. Ref. [12] proposed an LSTM-GRU-based ensemble method that outperformed the LSTM and GRU on two datasets. Ref. [13] proposed a hybrid model and used SVM and three ANN models for earthquake prediction.

At different stations, the same earthquake event may be recorded differently. Applying normalization techniques like batch normalization and layer normalization can improve classification performance due to their normalization effects on raw seismic data. Within each layer, the feature maps are first standardized using the mean and standard deviation, and subsequently, these maps are transformed into standardized values using either a shift factor or a scale factor. Several recent studies showed that using layer normalization and batch normalization layers in deep learning models improves their computational and detection performance. Ref. [14] used batch normalization techniques in a GCNN model for earthquake source characterization. Ref. [15] showed that the training of a deep learning model can be enhanced using batch normalization. When a model uses layer normalization, all the cells receive the same feature distribution independently for each batch input. Ref. [16] used LSTM with an attention layer that effectively detected large-magnitude earthquake events and outperformed the LSTM and ANN models. Ref. [17] proposed an attention-based fully connected CNN model, and Ref. [16] used the attention layer in the LSTM model for earthquake detection. Ref. [15] applied batch normalization and attention layers in a GCNN model for magnitude detection.

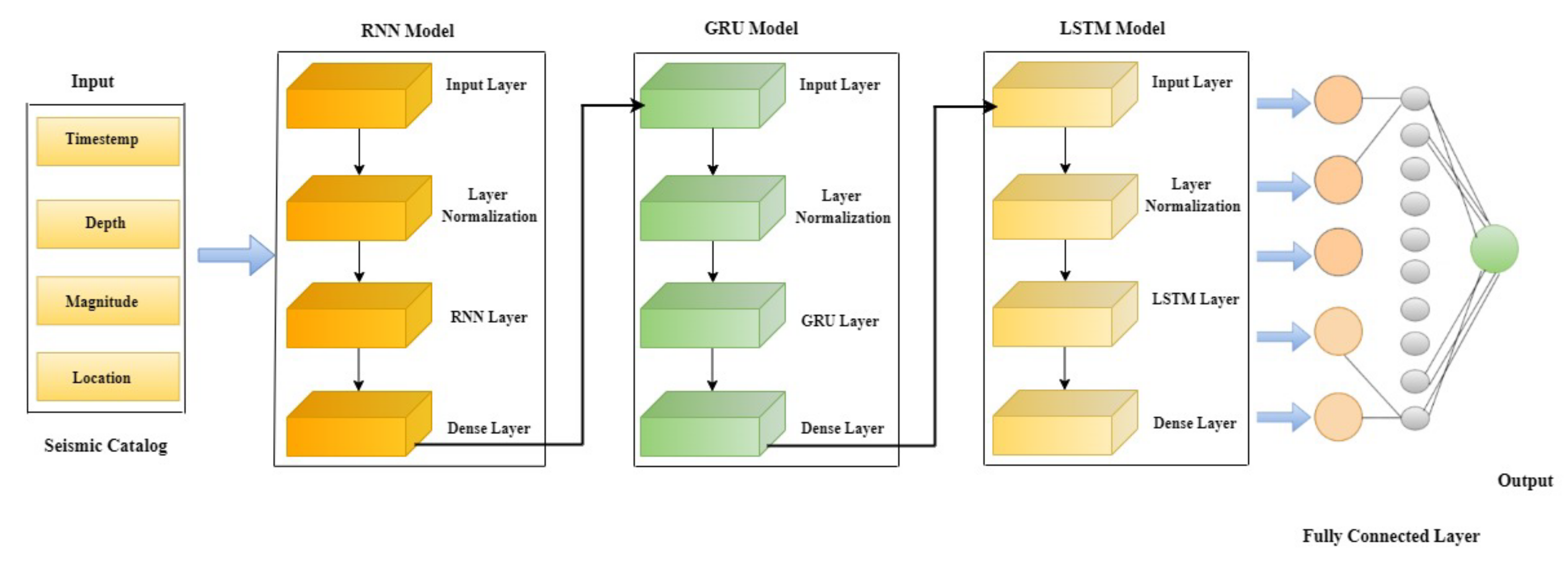
Taking advantage of both normalization and ensemble technique methods, in this study, we propose an RNN-based stacked normalized recurrent neural network (SNRNN) model that ensembles three recurrent neural network models in a stack: GRU, LSTM, and SimpleRNN. A GRU is an RNN model that uses less memory and is faster when the data have longer sequences. The LSTM and GRU used their gates to handle the gradient descent problem. The experimental results and their analysis show that the proposed model SNRNN is effective in earthquake detection tasks. The contribution of this study is as follows:

• We propose a deep learning model: a stacked normalized recurrent neural network (SNRNN), which is an ensemble model of three SimpleRNN, GRU, and LSTM models with normalization layers;
• We evaluate the performance of three individual RNN models and stacked RNN models using layer normalization and batch normalization methods;
• We compare the proposed SNRNN model to classic recurrent models and find that it outperformed all other models, achieving the lowest RMSE values.

2. Related Work

Earthquake detection using machine learning models such as SVM, DT, and k-NN has grown popular. Ref. [4] proposed an on-site EES for magnitude and ground velocity detection using multiple features and the SVM method. The early warning system issues alerts at different levels when the magnitude of an event exceeds a threshold value. Ref. [5] proposed an improved k-means clustering algorithm based on space-time-magnitude (STM) to cluster the earthquake events from global earthquake catalogs. The proposed model outperforms the modified k-means algorithm and the classic k-means method on various cluster sizes. Ref. [11] used k-NN, SVM, DT, and RF for earthquake detection, resulting in RF outperforming the other models. Several factors like feature selection method, dataset size, and class imbalance distribution affect the performance of machine learning models [17,18]. To overcome the machine learning issues, deep learning has been introduced.

Deep learning is a subfield of machine learning. Like artificial neural networks, deep learning-based models use multiple layers to input and process data and output the results. Deep learning models are considered good when the dataset is complex and significant because it employs several layers to deal with such data. Ref. [6] used a CNN for earthquake event classification into macro, micro, and artificial earthquakes. The proposed method outperformed the existing state-of-the-art methods on the Korean earthquake database. On the same database, the proposed CNN and GCN-based deep learning model of [1] outperformed the methods to detect earthquake events from multiple stations. Ref. [7] proposed a method that uses a CNN and graph partitioning algorithms to detect events with extremely low signal-to-noise ratios. Ref. [8] used an RNN-based DeepShake model, and Ref. [19] used a CNN model to predict the earthquake shaking intensity from ground motion observation. Ref. [20] used LSTM and BLSTM for magnitude prediction. Ref. [2] proposed a transformer-based TEAM method that issues accurate and timely warnings. Model interpretation, hyperparameter tuning, and GPU-based special devices are the major issues with deep learning models [14,15]. To overcome the issues of deep learning and machine learning methods, research studies propose three approaches: layer or batch normalization [3,15], the attention mechanism in deep learning architectures [6,21], and ensemble learning [9,11].

To efficiently train deep learning models, batch normalization is effective. It standardizes the layer outputs using data from each small training batch. It speeds up the training process by eliminating the necessity for the precise initialization of the parameters and enabling the use of high learning rates in a safe manner [15,22]. Several recent studies showed that using layer normalization and batch normalization in deep learning models improves their computational and detection performance. Ref. [14] used the batch normalization method in a GCNN model for earthquake source characterization. Ref. [15] showed that training of a deep learning model can be enhanced using batch normalization. Layer normalization is mainly used with RNN models to improve training and increase prediction [23]. When a model layer is normalized, all neurons receive the same distribution of features for the same input. Batching is no longer necessary when features and inputs to a particular layer are individually normalized [24,25]. This is why sequence models, such as RNNs, benefit significantly from layer normalization.

Earthquake detection is complex because it does not show any specific pattern, unlike object detection from images and text classification. The attention mechanism helps the deep learning model to give more attention to the most relevant and essential features from the input features for inference [6,26]. Ref. [16] used LSTM with an attention layer that effectively detects large-magnitude earthquake events and outperformed the LSTM and ANN models. Ref. [26] used a fully connected dense network with an attention layer to extract time–frequency features for earthquake detection from the Mediterranean dataset. Ref. [14] applied batch normalization and attention layers in a GCNN model for magnitude prediction. The results show that the proposed method outperformed the classical CNN and GCN models. Ref. [21] showed that the transformer model with an attention layer performs significantly better than the deep learning and traditional phase-picking and detection algorithms.

Instead of using a single model, we are interested in employing multiple models in a sequence to perform earthquake detection tasks, also known as ensemble learning or multiple classifier systems. Ensemble systems have gained popularity in computational intelligence and machine learning communities in recent decades. Ensemble systems have shown their efficacy and versatility in a wide range of problem areas and real-world applications like text classification [17], traffic accident detection [27], earthquake detection [28], and earthquake causality prediction [10]. In the last couple of decades, multiple classifier or ensemble learning systems have grown in computational intelligence. Ref. [11] proposed a machine learning-based ensemble method that combines SVM, k-NN, DT, and RF to design an ensemble model that can effectively detect earthquakes. Ref. [29] ensembled a CNN and LSTM and proposed MagNet for earthquake magnitude estimation. Ref. [12] proposed an LSTM-GRU-based ensemble method that outperformed the LSTM and GRU on two datasets. Ref. [9] ensembled four machine learning models, AdaBoost, XGBoost, DT, and LightXGBoost, in a stack using multiple settings. Ensemble-based studies report that ensemble models outperform individual models of either machine learning or deep learning.

There are two types of ensemble techniques: parallel and sequential. Base predictors are trained in parallel on the input, as shown in Figure 1a. The final result is determined by the majority voting method based on the results of the individual base models. The parallel ensemble utilizes many CPU cores, allowing for simultaneous predictions and model execution. As shown in Figure 1b, the base models used in the sequential ensemble technique are trained sequentially, with the output of one base model serving as the input to the next base model along with the input dataset. The next base model attempts to overcome the issues introduced by the preceding base model to enhance the accuracy of the overall detection system [18]. There are two possible types of base models: homogeneous and heterogeneous. In the homogenous learning environment, only one machine learning model (such as DT or NB) is trained in parallel or sequentially. However, many machine learning models are trained in parallel or sequentially in the heterogeneous learning environment. The ensemble learning strategy is advantageous when heterogeneous models are used as the base models [17]. The models under a heterogeneous approach can vary in terms of their feature sets, data for training, and evaluation criteria.

A summary of the related work is given in

Table 1. Related work with models using normalization, attention, or ensemble methods.

Papers	Models	Stations	Dataset	Normalization	Ensemble Type
[1]	CNN, GCN	Single	Korean	–	Convolutional
[2]	TEAM–Transformer	Multiple	Japan, Italy	–	–
[3]	GCN, BNGCNN	Multiple	Southern California	Batch	Convolutional
[5]	K-means clustering	Single	Global Seismic Data	–	–
[11]	EEPM	Single	India, Kenya, and Nepal	–	Machine learning
[6]	CNN	Multiple	South Korea	Batch, attention	–
[7]	Graph partitioning	Single	Waveform Data	–	No
[20]	Transformer	Multiple	Africa	Attention	–
[29]	MagNet (CRNN)	Multiple	STEAD	–	Convolutional, recurrent
[12]	LSTM, GRU	Single	Morocco, Japan, and Turkey	Layer	Recurrent
[9]	EEWPEnsembleStack	Multiple	Japan	–	Machine learning
[14]	BNGCNNAtt	Multiple	Alaska, Japan	Batch, attention	Convolutional
[16]	Attention-based LSTM	–	Japan	Attention	–
[26]	FCDNet	Multiple	STEAD	Batch, attention	Convolutional
[21]	Transformer, LSTM, CNN	Multiple	STEAD	–	Convolutional, recurrent
[19]	CNN	Multiple	Italy	–	–
[30]	LSTM	Multiple	Turkey	–	–

. Most of the studies used convolutional models rather than recurrent models. The attention mechanism is also used in most of the studies. Batch normalization is more popular than the layer normalization method. Batch normalization is effective with convolutional models, while layer normalization performs better with recurrent models. Most ensemble methods use convolutional models. Batch normalization is not an effective technique for a small batch size because it depends on batch size, while layer normalization is independent of batch size and can be applied to any batch size. Each feature in the mini-batch is normalized separately using batch normalization. When using layer normalization, all features are normalized independently for each input in the batch.

3. Stacked Normalized Recurrent Neural Network (SNRNN) Architecture

This section discusses, in detail, layer by layer, the proposed stacked normalized recurrent neural network model. The architecture of the SNRNN is shown in Figure 2. The first layer is the data layer, which receives the dataset and input to the proposed model. The second layer performs data preprocessing operations like removing irrelevant event information and splitting the dataset into training and testing subsets. The following three layers ensemble the SimpleRNN, GRU, and LSTM in a stack: The SimpleRNN model receives the preprocessed data and is trained on it to extract valuable features in the third layer. The fourth layer uses the GRU model to refine the features set output using the SimpleRNN. In the fifth layer, LSTM performs the final feature selection using its memory cells. The last layer is the output layer, which finally detects the earthquake event’s magnitude and depth.

3.1. Layer 1: Input Data

The dataset consists of fourteen attributes: event number, date and time, latitude, longitude, station number and name, magnitude, type, depth, source number, source description, reference, etc. We removed the irrelevant information and kept only the relevant information. As a result, we obtained five input attributes to feed into the proposed model: time, latitude, longitude, magnitude, magnitude type, and depth. To provide greater insight, the architecture of our model’s inputs and outputs is depicted in Figure 3. Following feature selection, the dataset was normalized using a min–max scaler. This scaler transforms the features by transforming their values to the interval [0, 1]. In this way, the original distribution shape was maintained. We split the dataset into training (75%) and testing (25%) subsets to train and test the model.

3.2. Layer 2: Recurrent Neural Network Model (RNN)

After preprocessing the dataset, it is given as input to the first SimpleRNN model. The normalization layer first normalizes feedback, and the normalized output is provided as input to the RNN layer. A dense layer is applied to the outcome of the RNN layer to produce the outcome. Layer normalization gives all neurons in a layer the same feature distribution for a given input. The need for batches is removed when normalization is performed across all features and for each piece of input to a given layer [25]. That is why layer normalization works so well with sequence models like RNNs. Finally, the dense layer works on the RNN layer to produce the output.

3.3. Layer 3: Gated Recurrent Unit Model (GRU)

The output of the RNN model is given to the next layer of the proposed architecture. At this layer, the GRU model is implemented. RNN faces exploding and vanishing gradient problems during backpropagation. GRU overcomes these problems using its gates. GRU is an RNN model with less memory and is faster than LSTM when the data have longer sequences. GRU is slower in training than ANN because GRU cell has more parameters than ANN cell. To address the gradient descent problem, GRUs employ the update gate and reset gate. Reset gates can recall previous knowledge learned and control what information is sent to the output. The model uses the update gate to determine how much information from the past should be transmitted to the future [31]. As the model can decide to replicate all the knowledge from the past, it eliminates the risk of the vanishing gradient problem, making this a very powerful model. As a first step, we used the following equation to get the updated gate state z_t for the time step t:

$$z_t=\sigma (W^{\left(z\right)}{x}_t+U^{\left(z\right)}{h}_{t-1})$$

(1)

The weight W_(z) of the network and the unit is applied to the input x_t when it is entered into the network. The same can be said for h_t−1, which, after being multiplied by its weight U_(z), stores information about the time before it (t − 1). The two sets of findings are combined and summed up, and then a sigmoid activation function is used to squeeze the total value into the range of 0 to 1. The purpose of the forget gate in the model is to determine how much of the information from the past should be ignored. The following equation was used to calculate the required information. This same formula describes the update gate, but the gate is used in a different way and with varying weights:

$$r_t=\sigma (W^{\left(r\right)}{x}_t+U^{\left(r\right)}{h}_{t-1})$$

(2)

3.4. Layer 4: Long Short-Term Memory Model (LSTM)

The long short-term memory (LSTM) model is the next layer of the proposed model. The LSTM is built up of many individual cells or units [16]. The hidden layer has many cells. The three gates of an LSTM cell are forgotten, input, and output. The forget gate keeps the cell state in memory, while the input and output gates handle incoming and outgoing data [30]. By utilizing these gates, LSTM can fix the issue of vanishing gradients. The following equations show the list of operations on the input sequence for the LSMT model:

$$i_t=\sigma (x_t{U}_i+h_{t-1 }{W}_i+b_{i })$$

(3)

$$f_t=\sigma (x_t{U}_f+h_{t-1}{W}_f+b_f)$$

(4)

$$o_t=\sigma (x_t{U}_o+h_{t-1}{W}_o+b_o)$$

(5)

$$q_t=tanh\left(x_t{U}_q+h_{t-1}{W}_q+b_{q }\right)$$

(6)

$$p_t=f_t\ast p_{t-1}+i_t\ast q_t$$

(7)

$$h_t=o_t\ast tanh\left(p_t\right)$$

(8)

$$r_t=\sigma \left(W^{\left(r\right)}{x}_t+U^{\left(r\right)}{h}_{t-1}\right)$$

(9)

$i_t$ is the output of the input gate, $o_t$ is the result of the output gate, and $f_t$ is the output of the forget gate. $i_t$, $o_t$, and $f_t$ are activated by the sigmoid function $\sigma$. These three results are the ensemble of input $x_t$and the preceding hidden state $h_{t-1}$ and the biased value $b$. A $tanh$ nonlinearity function is applied over the input $x_t$ and the previous hidden state $h_{t-1}$ to generate a temporary result $q_t$. The current step $t$ is then used to calculate the hidden step. Then, to obtain an updated version of the history $p_t$, $q_t$ is combined with history $p_{t-1}$ using the input gate $i_t$ and forgot gate $f_t$ in that order. In the end, the output gate $o_t$ will make use of the updated history $p_t$ to determine the final hidden state, which will serve as the output to the softmax layer, producing the outcome.

3.5. Layer 5: Output Layer

The last layer in the proposed architecture is the output layer which is a fully connected softmax layer. Here, the output of the LSTM model is the input of this layer. The outcome is the final detection made by the SNRNN model about the magnitude and depth of the earthquake event.

3.6. Layer Normalization

Layer normalization is a normalization technique that normalizes the inputs to a layer across the feature dimension, which can help improve the stability and performance of deep learning models. In our proposed model, we used layer normalization as a critical component to enhance the stacked normalized recurrent neural network (SNRNN) performance for earthquake detection. While batch normalization is another commonly used normalization technique, we chose layer normalization in our model due to its ability to normalize the inputs across different samples in a batch. This can be particularly useful when working with earthquake data.

4. Turkish Seismic Earthquake Dataset

In this study, we applied our methods to a seismic dataset gathered from Turkey. Turkey is well recognized for its active seismicity in a seismically active region. Regarding the number of people killed by earthquakes, Turkey is rated third in the globe, while in terms of the number of people affected, it is placed ninth. On average, it has at least one earthquake with a magnitude of 5 to 6 every year. Therefore, it is vital to analyze the earthquake data in this region and design an EEWS to detect an incoming earthquake accurately. The dataset was collected from the Disaster and Emergency Management Authority (AFAD) (https://deprem.afad.gov.tr/depremkatalogu?lang=en, accessed on 10 August 2022) catalog with the geographic parameters of latitude [35.67° to 42.38°] and longitude [25.85° to 45.14°]. The dataset consists of 6574 seismic events from 2000 to 2018 (18 years). The events were collected from different locations and stations in Turkey.

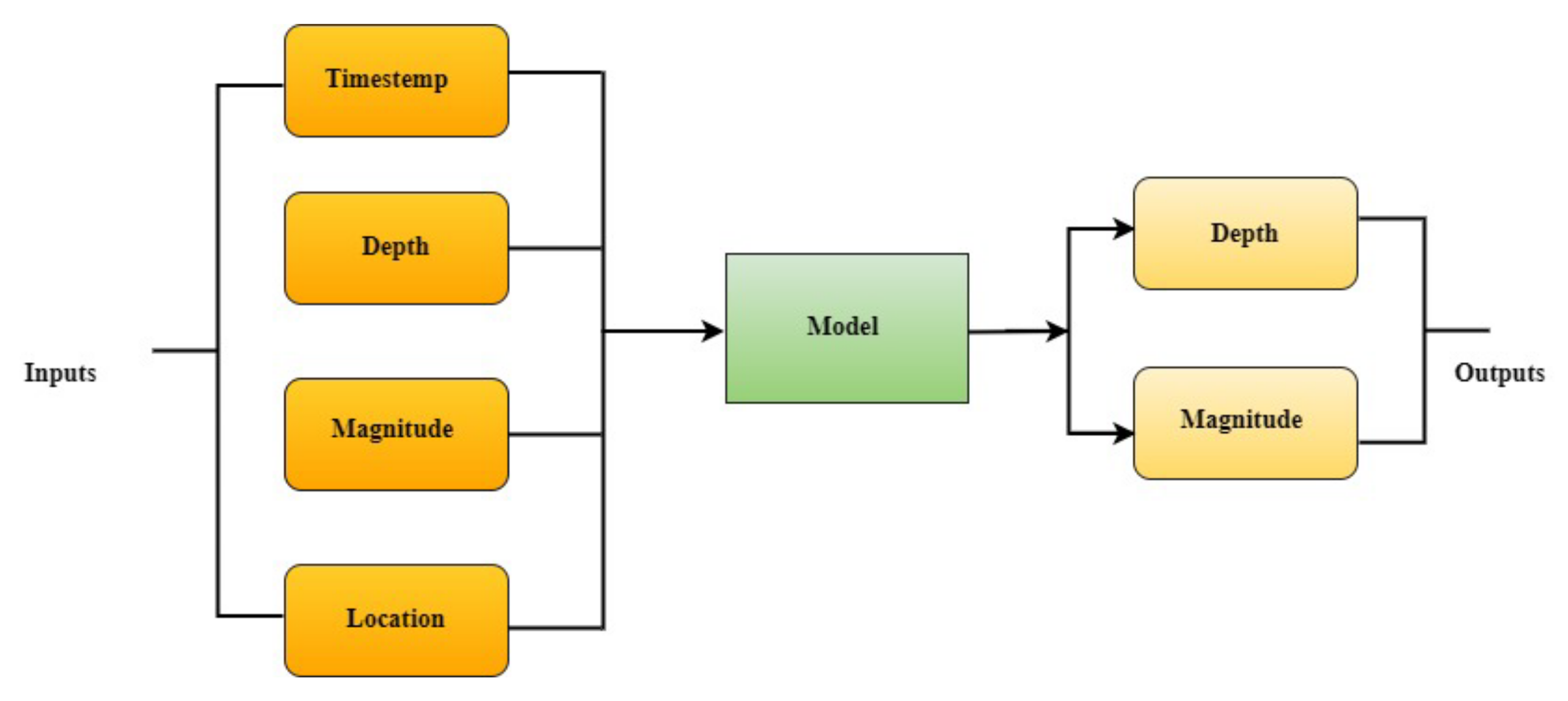
There are several features in the USGS dataset. We selected some of the most important and connected features and removed the others. The location information of all the events in the dataset is given in Figure 4. The locations of the high-magnitude (i.e., >7) seismic events are indicated on the map by red dots. The locations of the low-magnitude (i.e., <3) events are represented by white spots on the map. Green- and aqua-colored dots dominate the data, with a magnitude range of 4 to 6. Turkey’s border regions are the most likely to experience earthquakes due to their proximity to the fault lines. 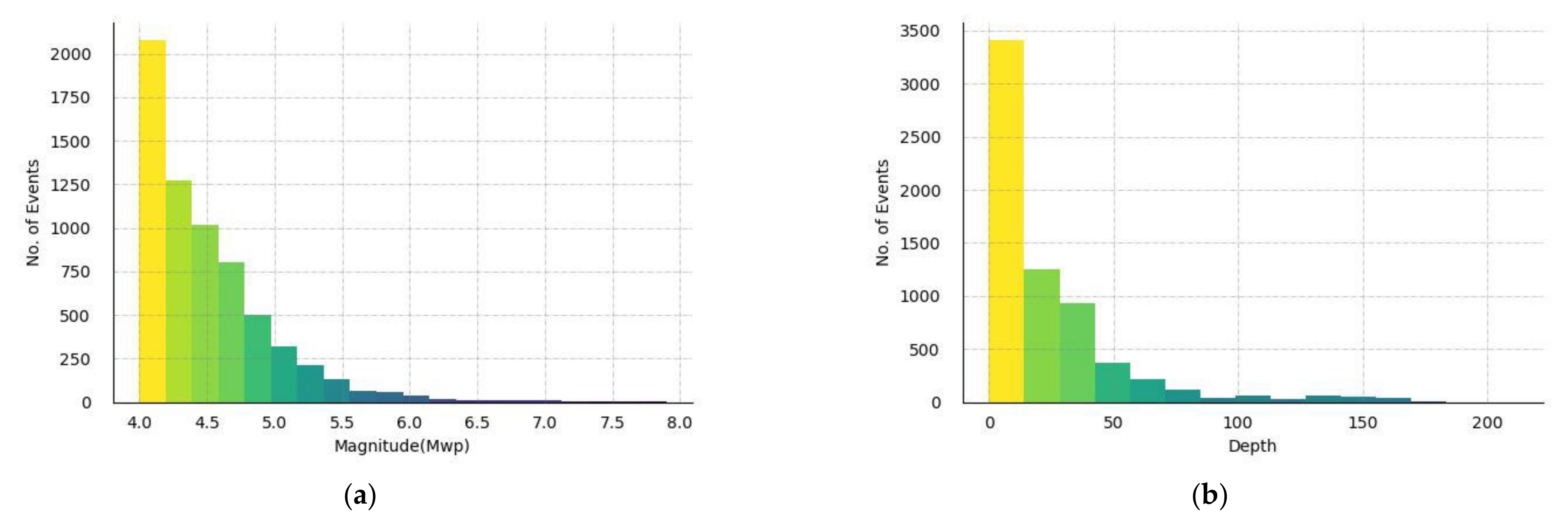Figure 5a shows a histogram showing the magnitude distribution in the dataset. The magnitude value ranges from 4.0 to 7.9, and the mean magnitude is 4.46. The dataset is dominated by events of magnitudes between 4.0 and 5.0. Figure 5b shows a histogram of the depth distribution of earthquake events. The depth ranges from 0.0 to 212 km, and the mean depth is 25 km. The majority of the events have a depth of less than 15 km.

In summary,

Table 2. Summary of the Turkey dataset.

Properties	Values	Properties	Values
Period	2000–2018	Min. and max. latitude	[35° to 43°]
No. of events	6575	Min. and max. longitude	[25° to 46°]
Maximum magnitude	7.9	Minimum magnitude	4.0
Mean magnitude	4.46	Dominate magnitude	4.0–5.0
Data split	75–25	Scaled min. and max. source depth	0 to 212 km
Dominate depth	<15 km	Mean depth	25 km

provides important statistical information on the seismic dataset related to earthquake events in Turkey. This information can improve our understanding of the region’s seismic activity and help us to develop more effective earthquake awareness and response strategies.

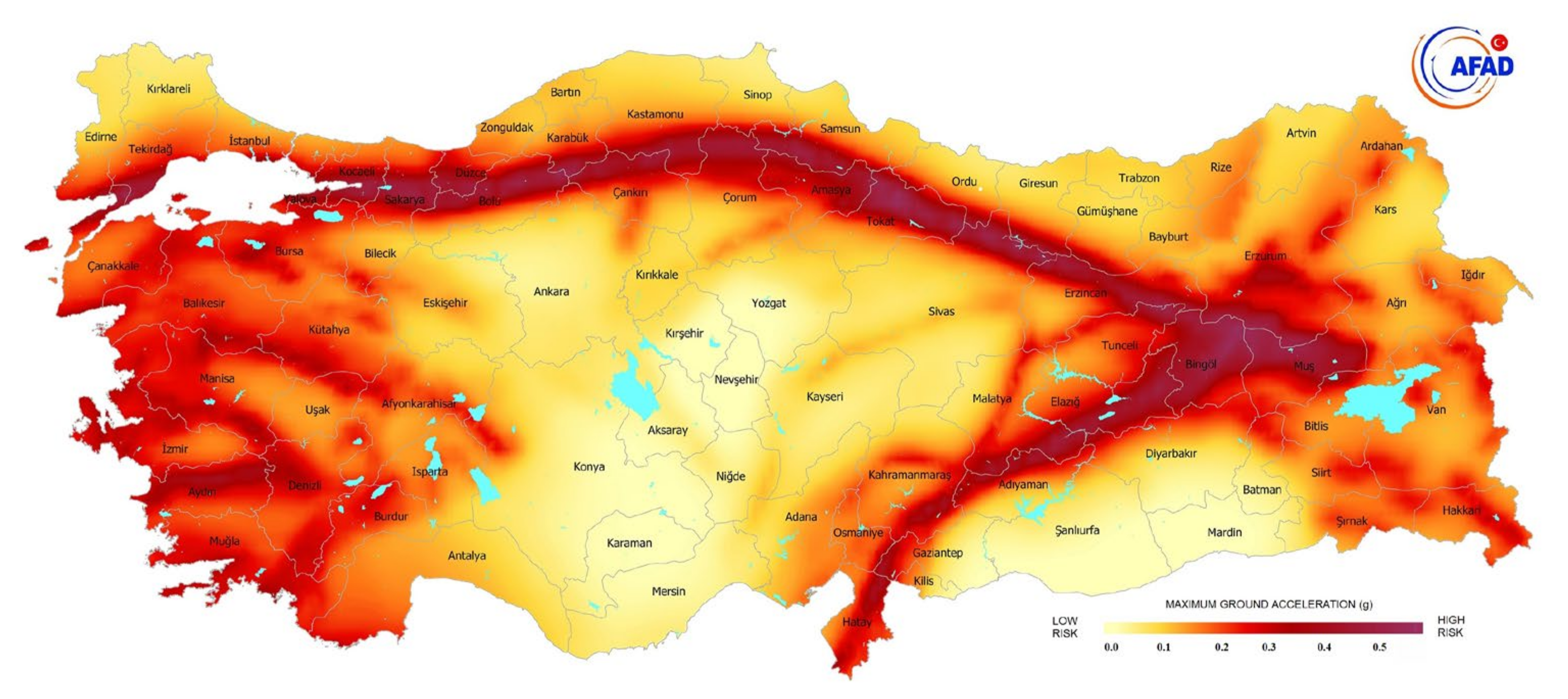
Figure 6 presents a risk map of the earthquake catalog of the Turkey region used in this study. A risk map is essential for predicting and mitigating the impacts of seismic events in the region. The map is constructed of peak accelerations, which are measures of the maximum shaking expected at a given location during an earthquake. The peak accelerations were calculated based on the characteristics of the earthquake catalog data, such as the magnitude, location, and depth of each earthquake event. By analyzing the earthquake catalog data and constructing the risk map, we can better understand the potential impact of future earthquakes in the region and help inform earthquake mitigation strategies. The risk map visually represents the distribution of seismic events in different regions of Turkey, with areas of higher hazard indicated in red and orange colors and areas of lower hazard in green and yellow.

5. Experiments and Discussion

In this section about the experiment and discussion, we first discuss the experimental settings and optimized parameters of the SimpleRNN, GRU, and LSTM. We discuss and analyze the individual models’ results with and without layer normalization and batch normalization methods. In the end, we discuss the results of our proposed SNRNN model.

All of the experiments were carried out, as a rule, on an Intel Core i7-7700 central processing unit operating at 3.60 gigahertz with 16 gigabytes of memory, an NVIDIA GeForce GTX 1080 graphics card, Windows 10, and Keras using the CUDA toolkit. The experiments were designed to compare the performance of three RNN models (SimpleRNN, GRU, and LSTM) with the proposed SNRNN model. The hyperparameters of these models, like batch size, dropout, and epochs, were tuned before the final experiments. These last parameters are shown in

Table 3. The hyperparameters of RNN, GRU, and LSTM models.

Parameters	RNN	GRU	LSTM
Batch size	64	32	64
Dropout	0.5	0.4	0.4
No. of epochs	20	16	15
Hidden units	32	64	32

. For all the models, we used the RMSE performance measure for network parameter optimization. RMSE is the improved form of mean square error (MSE) and can be calculated using the following equation:

$$\mathrm{RMSE}=\sqrt{\frac{{{\displaystyle \sum }}_{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2}{n}}$$

(10)

It is important to note that the unit scale of the observed data is preserved by the square root mistake. The ${\widehat{y}}_i$ in the equation represents the predicted values based on the model fit, and $y_i$ is the expected value. $n$ is the size of the values in the dataset. In addition to RMSE’s use in assessing quality, a random 75/25 split created a training and testing set from the whole dataset. From the training set, 25% of the data was used for validation during the training.

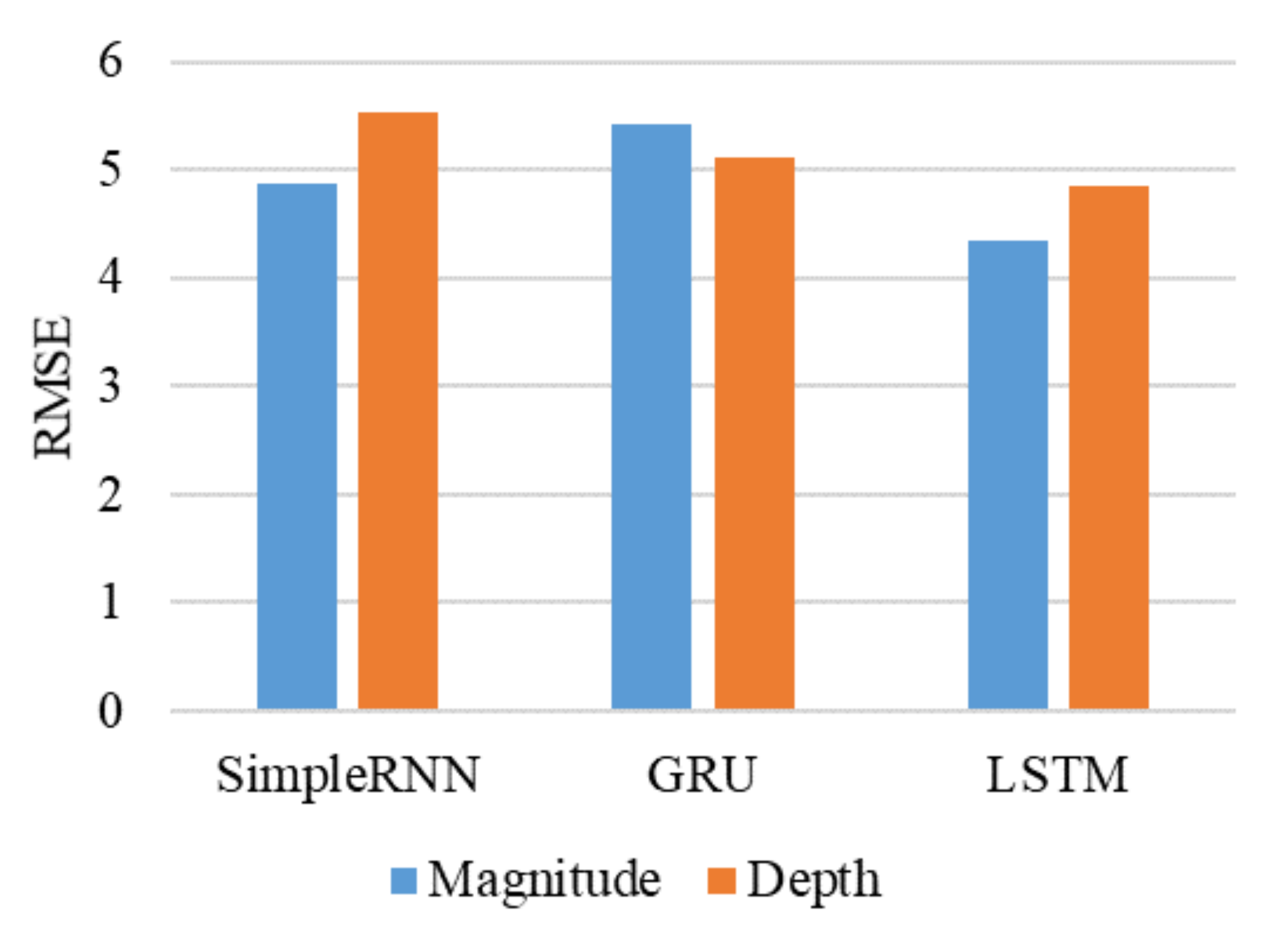
The first type of experiment compared the performance of the three RNN models: SimpleRNN, GRU, and LSTM. The RMSE values obtained by these models are shown in Figure 7. LSTM is usually considered suitable for time-series data. LSTM outperforms the GRU and SimpleRNN models in predicting magnitude and depth. LSTM achieves 4.35 and 4.84 RMSE values for magnitude and depth. The SimpleRNN does not perform well because of its vanishing gradient problems. The GRU and LSTM have gates to deal with vanishing gradient problems. Therefore, the GRU performed better than the SimpleRNN.

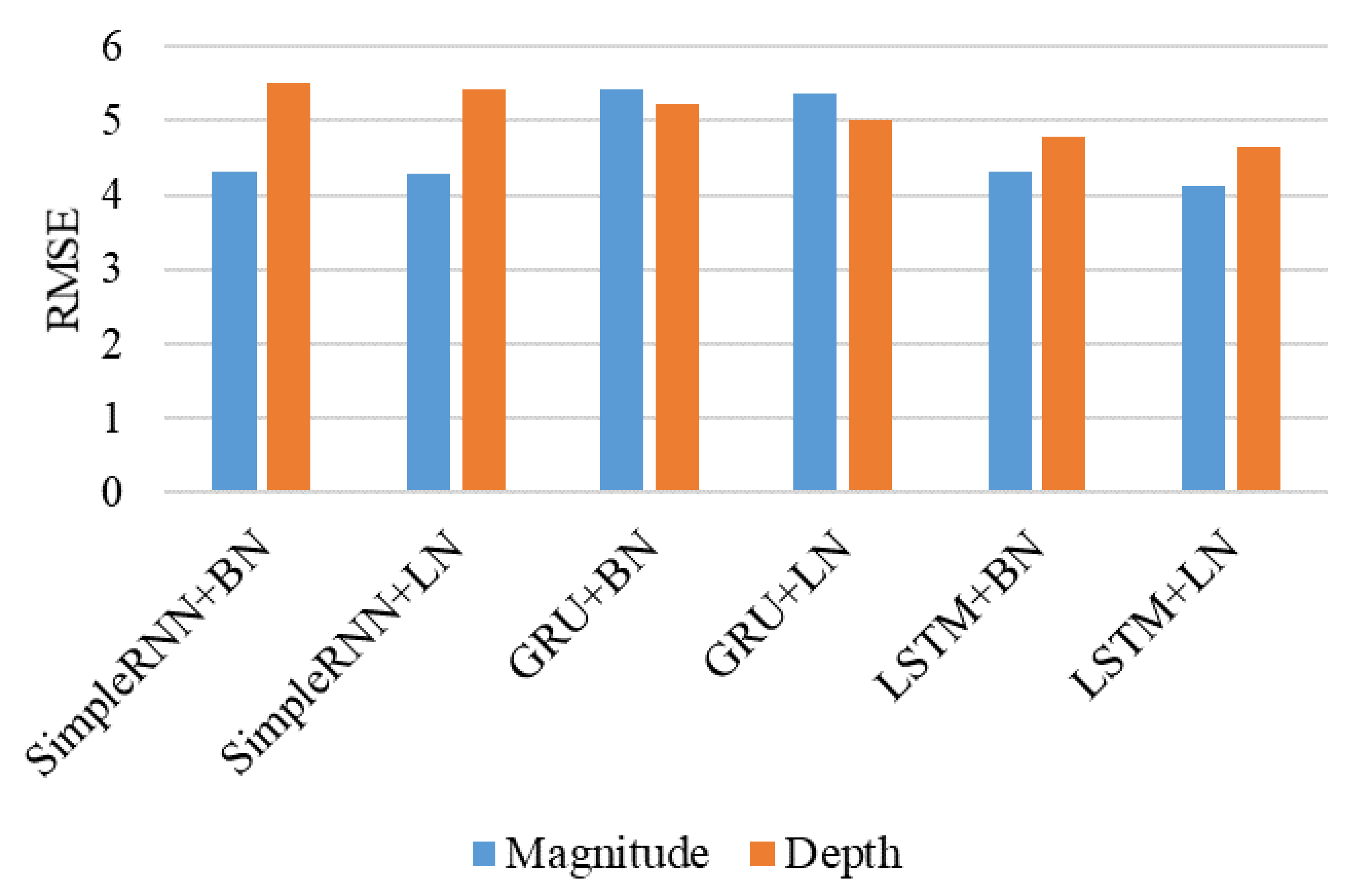
For the second type of experiment, we used the normalized models of the SimpleRNN, GRU, and LSTM to compare their performance. We added a batch normalization layer or the normalization layer to normalize the input and the mini-batches to train the model faster and increase performance. Again, LSTM+LN and LSTM+BN outperform the others in predicting magnitude and depth. LSTM+LN performs the best among all the models. It achieves 4.14 and 4.65 RMSE values for magnitude and depth, as shown in Figure 8. The models with batch normalization perform a little better than the standard models. When adding layer normalization to these models, all the models perform significantly better. Normalized GRU decreases its performance more than simple GRU. For the third type of experiment, we used the normalized models of the SimpleRNN, GRU, and LSTM to compare their performance. After analyzing the effects of the normalization techniques on the RNN models, we ensembled the SimpleRNN, GRU, and LSTM models in different settings to make a powerful and efficient stacked model.

The output of the first model was given as input to the second model, and so on. The results of the stacked models and individual models are shown in Figure 9. We conclude a significant decrease in the RMSE values of the stacked models compared to the individual models. Although the performance of stacking two models is better, stacking three models obtains the lowest RMSE values. From the results, we can easily conclude that ensemble methods are suitable for the task of magnitude and depth detection by overcoming the weaknesses of the base models.

The stacked RNN achieves the lowest RMSE values, 3.27 and 3.65, for magnitude and depth detection. Again, the GRU with either LSTM or the SimpleRNN does not show a high performance. In Figure 8 and Figure 9, we see that the stacked-based ensemble model significantly outperforms the individual models, and the models with the RNN models with normalization layers outperform the models with batch normalization layers. Finally, our proposed model, the stacked normalized RNN (SNRNN), is an ensemble model of the SimpleRNN, GRU, and LSTM models where each model has a normalization layer. Normalization is applied to the model input in the stack. The normalization layer normalizes each input in the batch independently across all the features. Batch normalization depends on the batch size, while normalization is independent of the batch size. The RMSE values show that the proposed model SNRNN (on top) outperforms all the models, where normalization helps to achieve 3.16 and 3.24 RMSE values for magnitude and depth detection. Our proposed SNRNN model takes advantage of both the ensemble learning and normalization techniques. All the results are summarized in

Table 4. Results of the baseline models and the proposed SNRNN model.

Model	Magnitude	Depth
SimpleRNN	4.87	5.52
GRU	5.41	5.12
LSTM	4.35	4.84
SimpleRNN+BN	4.32	5.5
SimpleRNN+LN	4.28	5.44
GRU+BN	5.42	5.24
GRU+LN	5.38	5.02
LSTM+BN	4.31	4.79
LSTM+LN	4.14	4.65
SimpleRNN+GRU	4.31	4.43
SimpleRNN+LSTM	3.78	4.32
GRU+LSTM	3.89	4.19
SimpleRNN+GRU+LSTM	3.27	3.65
SimpleRNN+GRU+NL	4.28	4.13
SimpleRNN+LSTM+NL	3.57	4.1
GRU+LSTM+NL	3.45	3.38
SimpleRNN+GRU+LSTM+NL	3.16	3.24

.

6. Conclusions and Future Work

Natural disasters like earthquakes can be very damaging. Automatic early earthquake detection using the data from seismic station sensors has emerged as an important area of research in recent years for emergency response. This article proposes a stacked-base ensemble method SNRNN for earthquake detection. This model, an ensemble of RNN, GRU, and LSTM base models, incorporating layer normalization techniques, can successfully detect the depth and magnitude of an earthquake event. After the data were preprocessed, the RNN, GRU, and LSTM sequentially extracted the feature map to make the final detection. Batch and layer normalization were utilized to achieve more consistent and faster training. Layer normalization was used to normalize features independently of the batch size. Therefore, layer normalization is more effective than batch normalization when using RNN-based models. We applied RNN, GRU, and LSTM models independently with both normalization methods. But the performance was lower than the proposed SNRNN model. After that, these models were ensembled to design a powerful model. We tested the proposed model on 6574 earthquake events from 2000 to 2018 in Turkey. The proposed model achieves 3.16 and 3.24 RMSE values for magnitude and depth detection. The RNN models outperform layer normalization over batch normalization. We also conclude that the ensemble model outperforms the individual model.

Researchers, seismologists, and the metrological department will all benefit from this innovative SNRNN by learning more about the potential of the ensemble method and how to apply many data mining techniques at once. In the future, we plan to apply similar ensemble techniques for earthquake detection with homogenous deep learning models. Further, the proposed model can be used for ground motion intensity detection.