A CP-ABE Scheme Based on Lattice LWE and Its Security Analysis

Abstract

In recent years, the research on ciphertext-policy attribute-based encryption (CP-ABE) scheme design based on learning with errors (LWE) has been a challenging problem, and many researchers have made a lot of attempts at it. At EUROCRYPT 2021, Datta, Komargodski, and Waters proposed the first provably secure direct CP-ABE construction that supports NC${}^1$ circuit access structures. Improving on their work, we propose a CP-ABE scheme. Technically, we use the new lattice two-stage sampling technique of Lai, Liu, and Wang (EUROCRYPT 2021) in the key generation phase instead of the extended trapdoor sampling technique. In this way, we obtain a CP-ABE scheme, which is at least as secure as the original scheme under the same conditions, and has a shorter ciphertext; we provide an innovative design idea for designing CP-ABE schemes only based on LWE, although this is only a partial theoretical work.

1. Introduction

In order to better realize the fine-grained access control of encrypted data, attribute-based encryption comes into being as a generalization of traditional public key encryption [1]. Attribute encryption has two variants, including ciphertext strategy and key strategy. In the ciphertext policy ABE, that is, the ciphertext is associated with the access policy, and the key is correlated to the attribute. While in the key policy ABE, the position of the access policy and the attribute is exactly opposite. However, there is one consistent point: decryption will be successful only if the attribute meets the access policy.

Since the concept of ABE was founded by Sahai et al. [2,3], it has been widely studied in cryptography and has many potential applications. Therefore, cryptographic researchers all over the world have been widely concerned by the design of the ABE scheme, which has given birth to a series of achievements that, on the whole, pursue various tradeoffs between expression, efficiency, security, and potential assumptions [4,5,6,7,8,9,10,11,12,13,14,15].

Most of the work mentioned above has been based on assumptions associated with bilinear mapping. It is necessary and normal to find structures based on other assumptions. On the one hand, they can not only make us more sure about the existence of the corresponding encryption scheme but also stimulate our enthusiasm for studying and developing new technologies, so as to further deepen our understanding of cryptographic primitives. On the other hand, in view of the known attacks of quantum computing on group-based cryptographic schemes [16], it is important to construct lattice-based attribute encryption to realize the security of quantum computing attacks. To this end, there are indeed several ABE schemes [4,5,8,10,11,14,17,18,19], which rely on other cryptographic assumptions rather than bilinear mappings as their underlying building blocks.

However, it is an indisputable fact that most of the existing ABE schemes based on LWE are ABE with a key strategy. Until the advent of reference [20], only a few LWE-based CP-ABE schemes had been constructed, and all of them were obtained through a special transformation with the help of the KP-ABE. However, this transformation will inevitably lead to some unsatisfactory results. For more details, please refer to [20].

Under the assumption that there is only LWE, improving the CP-ABE structure based on the general-purpose circuits described above has always been a challenging problem. In order to solve this question, several eye-catching jobs have been completed recently. For example, the work of [6,21,22] depends on LWE and bilinear groups. Work [9] lacks a safety certificate. Recently, a CP-ABE project on the basis of LWE was constructed in [22], although an indispensable part of the scheme remained the general circuit size limit. Reference [20] makes a conceptual contribution to this open and challenging issue. Their excellent work also draws on some innovative ideas from the work of [17,23]. In TCC 2013, Boyen et al. [17] proposed the first lattice-based attribute-based encryption construction (ABE) for NC${}^1$ circuits. Unfortunately, soon after, a loophole was discovered in the security; however, because of its technical novelty, it continues to be widely studied by many scholars. In particular, this is the first lattice-based ABE that uses the linear secret sharing scheme (LSSS) as a key tool to implement access control. In the scheme [23], Agrawal et al. proved that the scheme [17] is actually unsafe, and they gave an idea for repairing the security of the scheme by taking the notion of an admissible LSSS and instantiating it as the class of DNFs. After the work of [23], Datta et al. proposed the first CP-ABE scheme constructed in a direct manner and provided the complete security proof. It is a very innovative and creative work; it not only introduces new methods and techniques in concept but also popularizes and constructs new MA-ABE schemes.

The purpose of this paper is to propose an improved attribute-based encryption scheme based on the ciphertext policy (CP-ABE), which is modified on the basis of [20]. Technically, we use the two-stage sampling technique on the lattice in [24] instead of the extended trapdoor sampling technique in [20]. In this way, we obtain a CP-ABE scheme, which is at least as secure as the original scheme and has a shorter ciphertext.

The organization of the work of this article is listed below. In the second part, the relevant preliminary knowledge is given. In the third part, we give our CP-ABE scheme and the related proof of correctness and security.

2. Relevant Basic Knowledge

Here, we present several related concepts to facilitate readers to understand the full text. Consider a mapping $\mathrm{negl}:\mathbb{N}\to \mathbb{R}$. If there is a $N_c>0$ such that the formula of $\mathrm{negl}\left(x\right)<1/f\left(x\right)$ is always valid for all $f\left(x\right)>0$ and $x>N_c$, then $negl\left(x\right)$ is called a negligible function. In addition, for convenience, we use $\left[n\right]$ to represent the collection $\{1,\dots ,n\}$.

Let PPT denote the abbreviation of probabilistic polynomial time. Assuming that $\psi$ is a distribution, we will use the symbol $x\leftarrow \psi$ to indicate that x is randomly sampled on the basis of the distribution $\psi$. Assuming that Y is a set, we use the symbol $y\leftarrow Y$ to indicate that y is sampled on the elements of the set Y based on uniform distribution. Without losing generality, we use uppercase bold letters to represent matrices and lowercase bold letters to represent column vectors, such as $\mathbf{G}$ and $\mathbf{d}$. For convenience, we use ${\mathbf{G}}_l$ to represent the $l_{th}$ row of matrix $\mathbf{G}$, and, further, ${\mathbf{G}}_L$ represents a matrix that includes the set of ${\mathbf{G}}_l$ for all $l\in L$. Suppose $\mathbf{b}$ is a vector, we use the symbols $\parallel \mathbf{b}\parallel$ and ${\parallel \mathbf{z}\parallel }_{\infty }$ to represent its $l_2$ norm and $l_{\infty }$ norm, respectively.

2.1. Linear Secret Sharing Schemes with Linear Independence

This section is divided into two parts. In the first part, several essential definitions and characteristics of LSSSs are listed. In the second part, a new LSSS is presented, proposed in reference [25], and its definition will be listed later for the integrity of the article. This new LSSS has some interesting features, which can help us to design a CP-ABE scheme on the basis of the LWE hypothesis for all NC${}^1$ circuits.

2.1.1. Related Contents of LSSS

A secret sharing scheme means that the secret distributor divides the secret d into n parts using a specific algorithm and then distributes n shares to n participants. Authorized subsets of n participants can jointly reconstruct secrets, while other unauthorized subsets cannot.

Definition 1 

($\mathbf{Access}\mathbf{Structures}$, [25]). A collection $\mathbb{A}\subseteq 2^{\left[n\right]}\setminus \varphi$ of non-empty subsets of n participants labeled from one to n is called an access structure. The collections that belong to $\mathbb{A}$ are named the authorized collections, and the collections that do not belong to $\mathbb{A}$ are named the unauthorized collections. An access structure is deemed monotone in the case that the latter condition is satisfied. That is, for any two $C,E\in 2^{\left[n\right]}$, there is $E\in \mathbb{A}$ if there are $C\in \mathbb{A}$ and $C\subseteq E$.

A secret sharing scheme corresponding to a monotone access structure $\mathbb{A}$ can be regarded as a randomized algorithm whose input is a secret d and its output is n parts ${\mathrm{pa}}_1,\dots ,{\mathrm{pa}}_n$. These parts satisfy certain restrictions: that is, d can be determined by ${\left\{{\mathrm{pa}}_i\right\}}_{i\in A}$ for arbitrary $A\in \mathbb{A}$, while other sets are independent of d.

A secret sharing scheme corresponding to a non-monotone access structure $\mathbb{A}$ can be regarded as a randomized algorithm whose input is a secret d, and its output is $2n$ shares viewed as n pairs $({\mathrm{pa}}_{1,0},{\mathrm{pa}}_{1,1}),\dots ,({\mathrm{pa}}_{n,0},{\mathrm{pa}}_{n,1})$, these shares satisfy certain restrictions: that is, d can be determined by ${\left\{{\mathrm{pa}}_{i,1}\right\}}_{i\in A}\cup {\left\{{\mathrm{pa}}_{i,0}\right\}}_{i\notin A}$ for arbitrary $A\in \mathbb{A}$, while other sets are independent of d, which can be regarded as a transformation of the above concepts and algorithms.

Definition 2 

($\mathbf{Non}$-$\mathbf{monotone}\mathbf{LSSS}$, [25]). Let $\left[n\right]$ be a group of participants. Additionally, suppose $q\in \mathbb{N}$ is a prime power. The scheme described above is called non-monotone LSSS II over ${\mathbb{Z}}_q$ if the following conditions are true:

1. 

For $\rho \in \{0,1\}$ as well as $i\in \{1,\dots ,n\}$, each share ${\mathrm{pa}}_{i,\rho }$ of a secret $d\in {\mathbb{Z}}_q$ makes up a vector whose input is over ${\mathbb{Z}}_q$.

2. 

There must be a share-generating matrix, recorded as $\mathbf{G}\in {\mathbb{Z}}_q^{y\times t}$, and there is also a mapping η from $\left[y\right]$ to [2n]; η establishes an one-to-one mapping from the rows of $\mathbf{G}$ to the participants derived from $\left[n\right]$ and their corresponding negation (represented by $\{n+1,\dots ,2n\}$, respectively). This meets the conditions mentioned later, that is: Given a vector $\mathbf{v}={(d,{\alpha }_2,\dots ,{\alpha }_t)}^{\top }\in {\mathbb{Z}}_q^t$, then according to II , for the matrix $\mathbf{G}$ described above, there must be a vector representation of y shares of secret d that is equal to $\mathbf{pa}=\mathbf{G}·\mathbf{v}\in {\mathbb{Z}}_q^{y\times 1}$. For $\rho \in \{0,1\}$ as well as $i\in \{1,\dots ,n\}$, the part ${\mathrm{pa}}_{i,\rho }$ includes all of the ${\mathrm{pa}}_l$ values for which $\eta \left(l\right)=n(1-\rho )+i$ (in this way, all “1 shares" fall in the first n, and all “0 shares" fall in the last n). Then, $(\mathbf{G},\eta )$ will be named the LSSS policy about the access structure $\mathbb{A}$.

Based on the analysis of correctness and security in [25], we list the following conclusions. Correctness is achieved through the following condition: if $R\in \left[n\right]$ is authorized, the vector $(1,\underset{t-1}{\underbrace{0,\dots ,0}})\in {\mathbb{Z}}_q^t$ is in the span of the rows of ${\mathbf{G}}_{\widehat{R}}$ (where $\widehat{R}$$=R\cup \{i\in \{n+1,\dots ,2n\}\mid i-n\notin R\}$$\subset \left[2n\right]$). Security is achieved through the condition that if $R\in \left[n\right]$ is not authorized, then $(1,0,\dots ,0)$ cannot be expressed linearly by the rows of ${\mathbf{G}}_{\widehat{R}}$. In addition, in a case without authorization, there is a vector $\mathbf{t}\in {\mathbb{Z}}_q^t$, with the condition that its first components are ${\mathbf{t}}_1=1$ and ${\mathbf{G}}_{\widehat{R}}\mathbf{t}=\mathbf{0}$, of which $\mathbf{0}$ is the all 0 vector.

2.1.2. The Non-Monotone LSSS for NC${}^1$

We present a new non-monotone linear secret sharing scheme proposed in [25], which is suitable for all access structures that can be represented through NC${}^1$ circuits. This scheme possesses some very attractive and practical properties, as shown below:

-

Each element of the corresponding policy matrix is very small, and they all come from $\{-1,0,1\}$.

-

The secret can be rebuilt through a series of small coefficients are belong to $\{0,1\}$.

-

The rows corresponding to the access policy matrix that matches a collection that is not authorized are linearly independent.

$\mathbf{The}\mathbf{construction}$: We present the access structure $\mathbb{A}$ described by the NC${}^1$ circuit, which is adapted from [25]. The circuit can be represented through a Boolean formula with logarithmic depth, which is represented by AND, OR, and NOT gates. Then, we use De Morgan’s law to simplify the Boolean formula to a form with only OR and AND gates, marked by variables or their negation. The next step is to transform each gate node from top to bottom and from left to right, which can be seen as recursive. First, we initialize a global counter variable $c=2$ and increase the value of c by one after each door is marked. Next, we consider the specific operation flow of one of the doors. The outputs of wire x are marked as ${\mathbf{x}}_1=(1,0,\dots ,0)$ and ${\mathbf{x}}_2=(0,1,\dots ,0)$, and its sub-inputs are y (marked as ${\mathbf{y}}_1$ and ${\mathbf{y}}_2$) and z (marked as ${\mathbf{z}}_1$ and ${\mathbf{z}}_2$). The marker vectors of y and z are calculated from the marker vector of x according to the type of gate (as listed below). We calculate in turn until all the gate nodes are converted and put each vector of the lowest layer into a matrix $\mathbf{G}$ from top to down:

$\mathbf{AND}\mathbf{gate}$: ${\mathbf{y}}_1=0^c\parallel 1\parallel 0^{\tilde{k}-c-1}$, ${\mathbf{y}}_0={\mathbf{x}}_0$, ${\mathbf{z}}_1={\mathbf{x}}_1-{\mathbf{y}}_1$, ${\mathbf{z}}_0={\mathbf{x}}_0-{\mathbf{y}}_1$.

$\mathbf{OR}\mathbf{gate}$: ${\mathbf{y}}_1={\mathbf{x}}_1$, ${\mathbf{y}}_0=0^c\parallel 1\parallel 0^{\tilde{k}-c-1}$, ${\mathbf{z}}_1={\mathbf{x}}_1-{\mathbf{y}}_0$, ${\mathbf{z}}_0={\mathbf{x}}_0-{\mathbf{y}}_0$.

2.2. The Concept of CP-ABE

A CP-ABE scheme is defined by four PPT algorithms shown below, which have been adapted from the literature [9]:

• $\mathbf{Setup}(1^{\lambda },1^l)$: The setup algorithm is an algorithm whose input is the the security parameter $\lambda$, which is the input length l of the function f. Moreover its outputs are a master secret key MSK and a collection of exposed parameters PK.
• $\mathbf{Encrypt}$ (PK, $\mu$, f): The encryption program is an algorithm whose inputs are a public key PK, a message $\mu$, and a function f, and the output is a ciphertext CT.
• $\mathbf{Keygen}$ (MSK, x): The keygen algorithm is an algorithm that outputs the private key ${\mathrm{SK}}_x$ corresponding to the attribute x with the input of the MSK and the attribute x.
• $\mathbf{Decrypt}$ (PK, ${\mathrm{SK}}_x$, CT): The decryption program is an algorithm whose input is the public key PK, a secret key ${\mathrm{SK}}_x$, and a ciphertext CT. If and only if the attribute x satisfies $f\left(x\right)=1$, it will output the message $\mu$; otherwise, decryption fails.

Definition 3 

([9]). A CP-ABE scheme is correct if the equation shown below holds. Namely,

$$P_r\left[{\mu }^{\prime }=\mu \mathrm{bigg}|\begin{array}{c}\hfill (\mathrm{PK},\mathrm{MSK})\leftarrow Setup(1^{\lambda },1^l)\\ \hfill {\mathrm{SK}}_x\leftarrow Keygen(\mathrm{MSK},x)\\ \hfill CT\leftarrow Encryption(PK,\mu ,f)\\ \hfill {\mu }^{\prime }=\mathbf{Decrypt}(\mathrm{PK},\mathrm{CT},\mathrm{SK})\end{array}\right]=1-neg\left(1^{\lambda }\right).$$

In fact, CP-ABE schemes that implement the access structure $\mathbb{A}$ using an LSSS can be seen as an extension of the above definition. Namely, f is transformed into an access structure over the attribute collection. At the same time, the single attribute x in the definition above becomes a set S. By the same token, decryption can be successful only when certain conditions are met, that is, the attribute set S satisfies the access policy $\mathbb{A}$; otherwise, decryption fails.

$\mathbf{Security}$: Next, we present the security model of CP-ABE through the game between the challenger and the attacker shown below.

$\mathbf{Setup}$. After receiving the security parameters, the adversary submits an access structure $\mathbb{A}$, and then the challenger runs the setup algorithm and provides the resulting common parameters to the adversary.

$\mathbf{Phase}\mathbf{1}$. The adversary initiates a polynomial number of private key queries to the challenger, but a limitation of the attribute set is that the access structure $\mathbb{A}$ must not be met, and the challenger responds and gives the matching private key SK ←$\mathbf{Keygen}$(MSK, R).

$\mathbf{Challenge}$. The adversary provides two messages of equal lengths to the challenger, and then the challenger chooses a bit $b\in \{0,1\}$ with the probability of throwing coins at random and returns the ciphertext CT ←$\mathbf{Encrypt}$(PK, ${\mu }_b$, $\mathbb{A}$) to the adversary.

$\mathbf{Phase}\mathbf{2}$. This step is equivalent to the repetition of Phase 1.

$\mathbf{Guess}$. At the end of the game the adversary outputs a guess $b^{\prime }$ about b.

The probability advantage of an adversary $\mathcal{A}$ in the above game is defined as:

$${\mathrm{Adv}}_{\mathcal{A}}^{\mathrm{Sel}}\left(\lambda \right)=\mid \mathrm{Pr}[b=b^{\prime }]-1/2\mid .$$

(1)

Definition 4 

([20]). If for an arbitrary PPT adversary $\mathcal{A}$ and all $\lambda \in \mathbb{N}$, there exists a negligible function $\mathrm{negl}(·)$ such that ${\mathrm{Adv}}_{\mathcal{A}}^{\mathrm{Sel}}\le \mathrm{negl}(·)$ holds, then we call the CP-ABE scheme for LSSS-realizable access structures selectively secure.

Definition 5 

([20]). If a relaxed setting is made for the key query phase of the above scheme, that is, the rows in the generating matrix $\mathbf{G}$ corresponding to the attribute set sent by the adversary each key query must be linearly independent, namely, those attribute sets that do not meet the access policy are queried. Then it is said that the relaxed scheme is selectively secure under linear independence.

2.3. The Relevant Knowledge of Lattice

Here, we will give some lattice-related knowledge used in our CP-ABE construction. All of the relevant contents are adapted from the corresponding references. In order to save space, only an overview of lattice and Gaussian distributions is given here. For more details, please refer to [24]. A lattice whose dimension is m is a discrete additive subgroup of ${\mathbb{R}}^m$. For a matrix $\mathbf{A}\in {\mathbb{Z}}_q^{n\times m}$, where $n,m$, and q are integers greater than 0, ${\mathsf{\Lambda }}_q^{\perp }\left(\mathbf{A}\right)=\{\mathbf{y}\in {\mathbb{Z}}^m\mid \mathbf{Ay}=\mathbf{0}\left(modq\right)\}$ and ${\mathsf{\Lambda }}_q^{\mathbf{u}}\left(\mathbf{A}\right)=\{\mathbf{y}\in {\mathbb{Z}}^m\mid \mathbf{Ay}=\mathbf{u}\left(modq\right)\}$ are defined. Assume that $\sigma$ is an arbitrary real number greater than 0. The Gaussian distribution is a distribution interpreted by a probability distribution function $\rho \left(\mathbf{y}\right)=exp(-\pi \parallel \mathbf{y}-\mathbf{c}\parallel /{\sigma }^2)$ (where $\mathbf{c}\in {\mathbb{Z}}^n$), if a discrete set $V\subseteq {\mathbb{R}}^m$ is involved, then ${\rho }_{\sigma ,\mathbf{c}}\left(V\right)={\sum }_{\mathbf{y}\in V}{\rho }_{\sigma ,\mathbf{c}}\left(\mathbf{y}\right)$, and then ${\rho }_{V,\sigma ,\mathbf{c}}\left(\mathbf{y}\right)={\rho }_{\sigma ,\mathbf{c}}\left(\mathbf{y}\right)/{\rho }_{\sigma ,\mathbf{c}}\left(V\right)$ is defined as a Gaussian distribution whose parameter is $\sigma$ on the set V, represented by the symbol ${\mathcal{D}}_{V,\sigma }$. We use ${\tilde{\mathcal{D}}}_{V,\sigma }$ to represent the truncated Gaussian distribution, which is statistically indistinguishable from the Gaussian distribution ${\mathcal{D}}_{V,\sigma }$. The ${\tilde{\mathcal{D}}}_{V,\sigma }$ is the same as the ${\mathcal{D}}_{V,\sigma }$ except that when the $l_{\infty }$ norm exceeds $\sqrt{m}\sigma$, it will output 0.

Definition 6 

($\mathbf{Decisional}\mathbf{LWE}$ [10]). Select a λ as the security parameter, then let n, m, and q be functions of λ and positive integers at the same time. Therefore, suppose there is a probability distribution $\psi =\psi \left(\lambda \right)$ (in general, ψ is a distribution ${\mathcal{D}}_{\mathbb{Z},\alpha q}$ with the condition that $\alpha <1$) over $\mathbb{Z}$. The DLWE${}_{n,m,q,\psi }$ problem declares that for any $m=poly\left(n\right)$, in the case of $\mathbf{A}\leftarrow {\mathbb{Z}}_q^{n\times m},\mathbf{s}\leftarrow {\mathbb{Z}}_q^n$, $\mathbf{u}\leftarrow {\mathbb{Z}}_q^m$, and $\mathbf{e}\leftarrow {\psi }^m$, there will be a pair of distributions that are computationally indistinguishable as shown below:

$$(\mathbf{A},{\mathbf{s}}^{\top }\mathbf{A}+{\mathbf{e}}^{\top })\stackrel{\mathrm{c}}{\approx }(\mathbf{A},{\mathbf{u}}^{\top }).$$

Lemma 1 

($\mathbf{Leftover}\mathbf{Hash}\mathbf{Lemma}$ [25]). Let n and q be two functions from $\mathbb{N}$ to $\mathbb{N}$. Therefore, let $m>(n+1)logq+w(logn)$ and $l=l\left(n\right)$ be a function of n. Then, there are the two distributions shown below are statistically indistinguishable:

$$\begin{array}{cc}\hfill & {\mathcal{D}}_1\equiv \{(\mathbf{B},\mathbf{BS})\mid \mathbf{B}\leftarrow {\mathbb{Z}}_q^{n\times m},\mathbf{S}\leftarrow {\{-1,1\}}^{m\times l}\}\hfill \\ \hfill & {\mathcal{D}}_2\equiv \{(\mathbf{B},\mathbf{R})\mid \mathbf{B}\leftarrow {\mathbb{Z}}_q^{n\times m},\mathbf{R}\leftarrow {\mathbb{Z}}_q^{n\times l}\}\hfill \end{array}$$

Lemma 2 

($\mathbf{Smudging}$ [24]). Suppose n belongs to $\mathbb{N}$. For arbitrary $\mathbf{c}\in {\mathbb{Z}}^n$ and arbitrary real $\delta \ge \omega \left(\sqrt{logn}\right)$, there is always $SD({\mathcal{D}}_{{\mathbb{Z}}_n,\delta },{\mathcal{D}}_{{\mathbb{Z}}_n,\delta ,\mathbf{c}})\le \parallel \mathbf{c}\parallel /\delta$.

Lemma 3 

($\mathbf{Lattice}\mathbf{Trapdoor}$ [25]). A lattice trapdoor sampler is made up of a pair of algorithms, and the specific meaning and features are shown below:

1.

$\mathbf{TrapGen}(1^n,1^m,q)\mapsto (\mathbf{B},T_{\mathbf{B}})$: The purpose of the algorithm is to output a matrix $\mathbf{B}$ and its corresponding trapdoor $T_{\mathbf{B}}$, when the input is the dimension $n,m$ of the matrix and q. The output matrix $\mathbf{B}$ of this algorithm is indistinguishable from the matrix $\mathbf{C}$ of the same dimension which is randomly selected evenly in the same number field.

2.

$\mathbf{SamplePre}(\mathbf{B},T_{\mathbf{B}},\delta ,\mathbf{u})$: The goal of the algorithm is that when the input is matrix $\mathbf{B}$ and its corresponding trapdoor $T_{\mathbf{B}}$, a parameter $\delta \in \mathbb{R}$, $\mathbf{u}$, the algorithm can output a vector $\mathbf{t}\in {\mathbb{Z}}_q^m$, and the vector $\mathbf{t}$ must satisfy two conditions of $\mathbf{B}·\mathbf{t}=\mathbf{u}$ and $\parallel \mathbf{t}\parallel \le \sqrt{m}·\delta$. The pre-image $\mathbf{t}$ output by the algorithm is indistinguishable from the vector $\mathbf{d}$ selected according to the Gaussian distribution with parameter δ.

Lemma 4 

($\mathbf{SampleLeft}$ [24]). Let $m>n$, $q>2$ and suppose $\mathbf{C},\mathbf{D}\in {\mathbb{Z}}_q^{n\times m}$ are two full rank matrices; ${\mathbf{T}}_{\mathbf{C}}$ is a trapdoor matrix corresponding to $\mathbf{C}$. For a matrix $\mathbf{P}\in {\mathbb{Z}}_q^{n\times y}$ and $\theta \ge \parallel {\tilde{\mathbf{T}}}_{\mathbf{C}}\parallel ·\omega \left(\sqrt{logm}\right)$ (where ${\tilde{\mathbf{T}}}_{\mathbf{C}}$ is the Gram–Schmidt orthogonalization ${\mathbf{T}}_{\mathbf{C}}$ ), there must be a PPT algorithm SampleLeft $(\mathbf{C},{\mathbf{T}}_{\mathbf{C}},\mathbf{D},\mathbf{P},\theta )$ whose output is a matrix $\mathbf{Y}\in {\mathbb{Z}}_q^{2m\times y}$, and the matrix $\mathbf{Y}$ is statistically indistinguishable from the distribution of $D_{{\mathsf{\Lambda }}_q^{\mathbf{P}}(\mathbf{C}\mid \mathbf{D}),\theta }$.

Definition 7 

($\mathbf{New}\mathbf{Two}$-$\mathbf{Stage}\mathbf{Sampling}\mathbf{Method}$ [24]). Let $m>n\ge 1$, $q\ge 2$, and all are integers. Consider using $\delta ,\sigma \in \mathbb{R}$ and an arbitrary small norm matrix $\mathbf{S}\in {\mathbb{Z}}^{m\times m}$ as inputs, and the sampler operates sequentially according to the following two stages:

1. 

The first stage: (this stage has nothing to do with $\mathbf{S}$).

-

Select a matrix at a random $\mathbf{A}\leftarrow {\mathbb{Z}}_q^{n\times m}$;

-

Select a vector at a random $\mathbf{z}\leftarrow {\mathbb{Z}}_q^n$;

1. 

The second stage:

-

Select a vector $\mathbf{j}\leftarrow {\mathcal{D}}_{z^{n\times n},\delta }$;

-

Calculate $\mathbf{k}=\mathbf{z}-\mathbf{Aj}\left(modq\right)$;

-

Sample a random vector ${\mathbf{k}}^{\prime }=\left[\begin{array}{c}{\mathbf{k}}_1\\ {\mathbf{k}}_2\end{array}\right]\leftarrow {\mathcal{D}}_{{\mathsf{\Lambda }}_q^{\mathbf{k}}(\mathbf{A}\mid \mathbf{AS}),\sigma }$, to make the equation $(\mathbf{A},\mathbf{AS})$$·\left[\begin{array}{c}{\mathbf{k}}_1\\ {\mathbf{k}}_2\end{array}\right]=\mathbf{k}\left(modq\right)$ hold;

-

Let $\mathbf{h}=\left[\begin{array}{c}\mathbf{j}+{\mathbf{k}}_1\\ {\mathbf{k}}_2\end{array}\right]\in {\mathbb{Z}}^{2m}$, make the equation $[\mathbf{A},\mathbf{AS}]\mathbf{h}=\mathbf{z}\left(modq\right)$ hold;

-

Output the tuple $(\mathbf{A},\mathbf{AS},\mathbf{h},\mathbf{z})$.

This is an example of a quote.

3. Our Ciphertext-Policy ABE Scheme for NC${}^1$ Circuits Based on LWE

Here, we are going to show our CP-ABE scheme, which supports the access structure described through the NC${}^1$ circuit. The specific features and construction have been shown in Section 2.1.2.

First of all, we give the specific restrictions of each parameter in the scheme according to the proof of correctness and security. The $\mathbf{Setup}$ algorithm should select the appropriate parameters and noise distributions $n,m,\sigma ,q$ and ${\psi }_{lwe},{\psi }_1,{\psi }_2,{\psi }_{big}$, which meet the following conditions (fix any $0<ϵ<1/2$):

-

$\sigma <q,n=f\left(\lambda \right),{\psi }_{lwe}={\tilde{\mathcal{D}}}_{\mathbb{Z},\sigma },n·q/\sigma <2^{n^{ϵ}}$ (due to the LWE security)

-

$m>t_{max}nlogq+\omega (logn)+\lambda$  (due to the leftover hash lemma)

-

$\sigma \ge O\left(\sqrt{t_{max}nlogq}\right)·\omega \left(\sqrt{logm}\right)+\lambda$ (due to the trapdoor sampling)

-

${\psi }_1={\tilde{\mathcal{D}}}_{{\mathbb{Z}}_{\sigma }^{m-1}},{\psi }_2={\tilde{\mathcal{D}}}_{{\mathbb{Z}}_{\sigma }^m}$         (due to the trapdoor sampling)

-

${\psi }_{big}={\tilde{\mathcal{D}}}_{{\mathbb{Z}}^m,\delta }$, where $\delta \ge \sigma \sqrt{m}\parallel R\parallel ·{\lambda }^{w\left(1\right)}$  (due to the smudging/security)

-

$\mid \mathbb{U}\mid [\sqrt{2}{m}^{3/2}\sigma \left(\sqrt{2{\sigma }^2+2\sigma \delta +{\delta }^2}\right)+m^{3/2}\sigma \delta ]<q/4$ (due to the correctness)

Setup ($1^{\lambda }$): Take the security parameter $\lambda$, the maximum width $t_{max}=t_{max}\left(\lambda \right)$ of a linear secret sharing matrix corresponding to the scheme, and the attribute set $\mathbb{U}$ as inputs and perform the following steps in order:

• Select an LWE instance with the appropriate parameters $n,m,q$, as well as the distribution described above.
• Select a vector $\mathbf{x}\leftarrow {\mathbb{Z}}_q^n$ and select a series of random matrices ${\left\{{\mathbf{P}}_u\right\}}_{u\in \mathbb{U}}$ at the same time.
• Run algorithm $\mathbf{TrapGen}(1^n,1^m,q)$ to generate ${({\mathbf{A}}_u,{\mathbf{T}}_{{\mathbf{A}}_u})}_{u\in \mathbb{U}}$.
• Output the public parameters and master secret keys:

  $$\mathbf{PK}=(n,m,q,{\psi }_{lwe},{\psi }_2,{\psi }_{big},\mathbf{x},{\left\{{\mathbf{A}}_u\right\}}_{u\in \mathbb{U}},{\left\{{\mathbf{P}}_u\right\}}_{u\in \mathbb{U}}),\mathbf{MSK}=\left({\left\{{\mathbf{T}}_{{\mathbf{A}}_u}\right\}}_{u\in \mathbb{U}}\right).$$

$\mathbf{KeyGen}(\mathbf{MSK},$$U)$: With the master secret key and the collection of attributes $U\in \mathbb{U}$ as inputs, perform the following steps:

• Sample a $\widehat{\mathbf{w}}\leftarrow {\psi }_1$ and set the vector $\mathbf{w}=(1,\widehat{\mathbf{w}})\in {\mathbb{Z}}^m$.
• For each $u\in U$, sample matrix ${\mathbf{j}}_u\leftarrow {\tilde{\mathcal{D}}}_{{\mathbb{Z}}^m,\delta }$, at the same time, and, finally, let ${\mathbf{z}}_u={\mathbf{P}}_u\mathbf{w}-{\mathbf{A}}_u{\mathbf{j}}_u\left(modq\right)$.
• Sample ${\mathbf{S}}_u\leftarrow {\{-1,1\}}^{m\times m}$.
• Sample $\left[\begin{array}{c}{\mathbf{k}}_u\\ {\mathbf{g}}_u\end{array}\right]\leftarrow \mathbf{SampleLeft}({\mathbf{A}}_u,{\mathbf{A}}_u{\mathbf{S}}_u,{\mathbf{T}}_{{\mathbf{A}}_u},{\mathbf{z}}_u)$ for some parameter $\sigma$. In other words, choose $\left[\begin{array}{c}{\mathbf{k}}_u\\ {\mathbf{g}}_u\end{array}\right]$ to make the equation $[{\mathbf{A}}_u,{\mathbf{A}}_u{\mathbf{S}}_u]·\left[\begin{array}{c}{\mathbf{k}}_u\\ {\mathbf{g}}_u\end{array}\right]={\mathbf{z}}_u$ holds.
• Let ${\mathbf{h}}_u=\left[\begin{array}{c}{\mathbf{k}}_u+{\mathbf{j}}_u\\ {\mathbf{g}}_u\end{array}\right]$ and output $S{K}_f=(\mathbf{w},{\left\{{\mathbf{h}}_u\right\}}_{u\in U})$.

$\mathbf{Enc}(\mathbf{PK},\mu ,(\mathbf{G},\eta \left)\right)$: With the public parameters PK, a message $\mu \in \{0,1\}$ needs to be encrypted, and an LSSS access policy $(\mathbf{G},\eta$), generated from the previous transformation, are the inputs (that is to say, where $\mathbf{G}={\left({\mathbf{G}}_{i,l}\right)}_{y\times t_{max}}\in {\{-1,0,1\}}^{y\times t_{max}}\subset {\mathbb{Z}}_q^{y\times t_{max}}$). Perform the following steps in order:

• Sample vector $\mathbf{s}\leftarrow {\mathbb{Z}}_q^n$ and error vector ${\left\{{\mathbf{v}}_l\right\}}_{l\in \{2,\dots ,t_{max}\}}\leftarrow {\mathbb{Z}}_q^m$.
• In addition, continue to sample ${\left\{{\mathbf{e}}_i\right\}}_{i\in \left[y\right]}\leftarrow {\psi }_{lwe}^{2m}$ and ${\left\{{\widehat{\mathbf{e}}}_i\right\}}_{i\in \left[y\right]}\leftarrow {\psi }_{big}^m$, for every $i\in \left[y\right]$. Calculate ${\mathbf{c}}_i\in {\mathbb{Z}}_q^{2m},{\widehat{\mathbf{c}}}_i\in {\mathbb{Z}}_q^m$ as described below.

  $$\begin{array}{cc}\hfill & {\mathbf{c}}_i^{\top }={\mathbf{s}}^{\top }({\mathbf{A}}_{\eta \left(i\right)}\parallel {\mathbf{A}}_{\eta \left(i\right)}{\mathbf{S}}_{\eta \left(i\right)})+{\mathbf{e}}_i^{\top }\hfill \\ \hfill & {\widehat{\mathbf{c}}}_i^{\top }={\mathbf{G}}_{i,1}({\mathbf{s}}^{\top }\mathbf{x},\underset{m-1}{\underbrace{0,\dots ,0}})+\left[\sum _{l\in \{2,\dots ,t_{max}\}}{\mathbf{G}}_{i,l}{\mathbf{v}}_l^{\top }\right]-{\mathbf{s}}^{\top }{\mathbf{P}}_{\eta \left(i\right)}+{\widehat{\mathbf{e}}}_i^{\top }\hfill \end{array}$$
• Output the ciphertext $\mathbf{ct}=((\mathbf{G},\eta ),{\left\{{\mathbf{c}}_i\right\}}_{i\in \left[y\right]},{\left\{{\widehat{\mathbf{c}}}_i\right\}}_{i\in \left[y\right]},C=MSB\left({\mathbf{s}}^{\top }\mathbf{x}\right)\oplus \mu$).

$\mathbf{Dec}(\mathbf{SK},\mathbf{ct})$: With the private key and a ciphertext as inputs, perform the following algorithm steps in order:

• In the case that the vector (1, 0, …, 0) cannot be represented by the rows of $\mathbf{G}$ correlated to the attribute set U, the decryption will fail.
• Conversely, let $\Delta$ be a collection of the row labels of $\mathbf{G}$ with the condition that for any $i\in \Delta :\eta \left(i\right)\in U$. Hence, let ${\left\{{\xi }_i\right\}}_{i\in \Delta }\in \{0,1\}\in {\mathbb{Z}}_q$ be scalars with the condition that ${\sum }_{i\in \Delta }{\xi }_i{\mathbf{G}}_i=(1,0,\dots ,0)$, of which ${\mathbf{G}}_i$ is the $i^{th}$ row of $\mathbf{G}$.
• Calculate $Y^{{}^{\prime }}={\sum }_{i\in \Delta }{\xi }_i({\mathbf{c}}_i^{\top }{\mathbf{h}}_u+{\widehat{\mathbf{c}}}_i^{\top }\mathbf{w})$.
• ${\mu }^{\prime }=C\oplus MSB\left(Y^{{}^{\prime }}\right)$.

3.1. Correctness

Next, we will prove the correctness of the scheme. Given an attribute collection $U\subset \mathbb{U}$ and an arbitrary access policy $(\mathbf{G},\eta )$, where U forms an authorized set, calculate the following equation

$$Y^{\prime }=\sum _{i\in \Delta }{\xi }_i({\mathbf{c}}_i^{\top }{\mathbf{h}}_u+{\widehat{\mathbf{c}}}_i^{\top }\mathbf{w}).$$

By substituting the specific values of ${\left\{{\mathbf{c}}_i\right\}}_{i\in \left[y\right]}$ and ${\left\{{\widehat{\mathbf{c}}}_i\right\}}_{i\in \left[y\right]}$ into the above formula, we can obtain

$$\begin{array}{cc}\hfill & Y^{\prime }=\sum _{i\in \Delta }{\xi }_i{\mathbf{s}}^{\top }[{\mathbf{A}}_{\eta \left(i\right)}\parallel {\mathbf{A}}_{\eta \left(i\right)}{\mathbf{S}}_{\eta \left(i\right)}]{\mathbf{h}}_{\eta \left(i\right)}+\sum _{i\in \Delta }{\xi }_i({\mathbf{s}}^{\top }\mathbf{x},0,\dots ,0)\mathbf{w}+\hfill \\ \hfill & \sum _{i\in \Delta ,l\in \{2,\dots ,t_{max}\}}{\xi }_i{G}_{i,l}{\mathbf{v}}_l^{\top }\mathbf{w}-\sum _{i\in \Delta }{\xi }_i{\mathbf{s}}^{\top }{\mathbf{P}}_{\eta \left(i\right)}\mathbf{w}+\sum _{i\in \Delta }{\xi }_i{\mathbf{e}}_i{\mathbf{h}}_{\eta \left(i\right)}+\sum _{i\in \Delta }{\xi }_i{\widehat{\mathbf{e}}}_i\mathbf{w}.\hfill \end{array}$$

Here, let us review the previous key generation process. For each $u\in U$, ${\mathbf{h}}_u=\left[\begin{array}{c}{\mathbf{k}}_u+{\mathbf{j}}_u\\ {\mathbf{g}}_u\end{array}\right]$, and $[{\mathbf{A}}_u\parallel {\mathbf{A}}_u{\mathbf{S}}_u]·\left[\begin{array}{c}{\mathbf{k}}_u\\ {\mathbf{g}}_u\end{array}\right]={\mathbf{P}}_u\mathbf{w}-{\mathbf{A}}_u{\mathbf{j}}_u$ is established. That is to say, it holds that

$$[{\mathbf{A}}_{\eta \left(i\right)}\parallel {\mathbf{A}}_{\eta \left(i\right)}{\mathbf{S}}_{\eta \left(i\right)}]{\mathbf{h}}_{\eta \left(i\right)}={\mathbf{P}}_{{}_{\eta \left(i\right)}}\mathbf{w}.$$

Further, there will be

$$\begin{array}{cc}\hfill & Y^{\prime }=\sum _{i\in \Delta }{\xi }_i{\mathbf{s}}^{\top }{\mathbf{P}}_{\eta \left(i\right)}\mathbf{w}+\sum _{i\in \Delta }{\xi }_i{\mathbf{G}}_{i,1}({\mathbf{s}}^{\top }\mathbf{x},0,\dots ,0)\mathbf{w}\hfill \\ \hfill & +\sum _{i\in \Delta ,l\in \{2,\dots ,t_{max}\}}{\xi }_i{\mathbf{G}}_{i,j}{\mathbf{v}}_l^{\top }\mathbf{w}-\sum _{i\in \Delta }{\xi }_i{\mathbf{s}}^{\top }{\mathbf{P}}_{\eta \left(i\right)}\mathbf{w}+\sum _{i\in \Delta }{\xi }_i{\mathbf{e}}_i^{\top }{\mathbf{h}}_{\eta \left(i\right)}+\sum _{i\in \Delta }{\xi }_i{\widehat{\mathbf{e}}}_i^{\top }\mathbf{w}\hfill \\ \hfill & =\sum _{i\in \Delta }{\xi }_i{\mathbf{G}}_{i,1}({\mathbf{s}}^{\top }\mathbf{x},0,\dots ,0)\mathbf{w}+\sum _{i\in \Delta ,l\in \{2,\dots ,t_{max}\}}{\xi }_i{\mathbf{G}}_{i,l}{\mathbf{v}}_l^{\top }\mathbf{w}+\sum _{i\in \Delta }{\xi }_i{\mathbf{e}}_i^{\top }{\mathbf{h}}_{\eta \left(i\right)}+\sum _{i\in \Delta }{\xi }_i{\widehat{\mathbf{e}}}_i^{\top }\mathbf{w}\hfill \\ \hfill & =\left(\sum _{i\in \Delta }{\xi }_i{\mathbf{G}}_{i,1}\right)({\mathbf{s}}^{\top }\mathbf{x},0,\dots ,0)\mathbf{w}+\sum _{l\in \{2,\dots ,t_{max}\}}\left(\sum _{i\in \Delta }{\xi }_i{\mathbf{G}}_{i,l}\right){\mathbf{v}}_l^{\top }\mathbf{w}+\sum _{i\in \Delta }{\xi }_i{\mathbf{e}}_i^{\top }{\mathbf{h}}_{\eta \left(i\right)}+\hfill \\ & \sum _{i\in \Delta }{\xi }_i{\widehat{\mathbf{e}}}_i^{\top }\mathbf{w}.\hfill \end{array}$$

According to the above description, the formula ${\sum }_{i\in \Delta }{\xi }_i{\mathbf{G}}_{i,1}=1$ holds. Moreover, for $1<l\le t_{max}$, ${\sum }_{i\in \Delta }{\xi }_i{\mathbf{G}}_{i,l}=0$. Additionally, because of $\mathbf{w}=(1,\widehat{\mathbf{w}})$, then calculate $({\mathbf{s}}^{\top }\mathbf{x},0,\dots ,0)\mathbf{w}={\mathbf{s}}^{\top }\mathbf{x}$. Thus,

$$Y^{\prime }={\mathbf{s}}^{\top }\mathbf{x}+\sum _{i\in \Delta }{\xi }_i{\mathbf{e}}_i^{\top }{\mathbf{h}}_{\eta \left(i\right)}+\sum _{i\in \Delta }{\xi }_i{\widehat{\mathbf{e}}}_i^{\top }\mathbf{w}.$$

The correctness is based on the fact that the last two terms of the above two equations are very small and will not affect the MSB of ${\mathbf{s}}^{\top }\mathbf{x}$. In order to achieve this, we must make the following inequalities hold with extremely overwhelming probabilities:

-

$\Vert {\mathbf{e}}_i\Vert \le \sqrt{2m}\sigma :$ This is because the $2m$ coordinates of ${\mathbf{e}}_i$ are selected according ${\tilde{\mathcal{D}}}_{\mathbb{Z},\sigma }$.

-

$\Vert {\widehat{\mathbf{e}}}_i\Vert \le \sqrt{m}\delta :$ The reason for this is precisely because all the coordinates of ${\widehat{\mathbf{e}}}_i$ are selected according to ${\tilde{\mathcal{D}}}_{{\mathbb{Z}}^m,\delta }$, where $\delta \ge \sigma \sqrt{m}\parallel R\parallel ·{\lambda }^{w\left(1\right)}$.

-

$\Vert {\mathbf{h}}_{\eta \left(i\right)}\Vert \le m\sqrt{(2{\sigma }^2+2\sigma \delta +{\delta }^2)}:$ This is because the equation ${\mathbf{h}}_{\eta \left(i\right)}=\left[\begin{array}{c}{\mathbf{k}}_{\eta \left(i\right)}+{\mathbf{j}}_{\eta \left(i\right)}\\ {\mathbf{g}}_{\eta \left(i\right)}\end{array}\right]$ holds where (1) the selection of $\left[\begin{array}{c}{\mathbf{k}}_u\\ {\mathbf{g}}_u\end{array}\right]$ is based on a distribution that is statistically indistinguishable from ${\tilde{\mathcal{D}}}_{{\mathbb{Z}}^{2m},\sigma }$. Additionally, (2) ${\mathbf{j}}_u\leftarrow {\tilde{\mathcal{D}}}_{{\mathbb{Z}}^m,\delta }$.

-

$\parallel \mathbf{w}\parallel <m\sigma$: The reason is that $\mathbf{w}=(1,\widehat{\mathbf{w}})$, and $\widehat{\mathbf{w}}$ is selected by a distribution ${\tilde{\mathcal{D}}}_{{\mathbb{Z}}^{m-1},\sigma }$.

-

Based on the fact that ${\xi }_i\in \{0,1\}$, we can obtain:

$$\begin{array}{c}\hfill \sum _{i\in \Delta }{\xi }_i{\mathbf{e}}_i^{\top }{\mathbf{h}}_{\eta \left(i\right)}+\sum _{i\in \Delta }{\xi }_i{\widehat{\mathbf{e}}}_i^{\top }\mathbf{w}<\mid \mathbb{U}\mid [\sqrt{2}{m}^{3/2}\sigma \left(\sqrt{2{\sigma }^2+2\sigma \delta +{\delta }^2}\right)+m^{3/2}\sigma \delta ]<q/4.\end{array}$$

3.2. Security Analysisr

In this part, we will give the security analysis of the scheme in detail. The security proof of our scheme is carried out strictly according to the idea of the security proof in [20].

Theorem 1 

([20]). Under the condition that the LWE hypothesis is true, the CP-ABE scheme we present for all access structures described through NC${}^1$ circuits is selectively secure.

Theorem 2. 

Under the condition that the LWE assumption is true, the CP-ABE scheme we present is selectively secure under linear independence restriction.

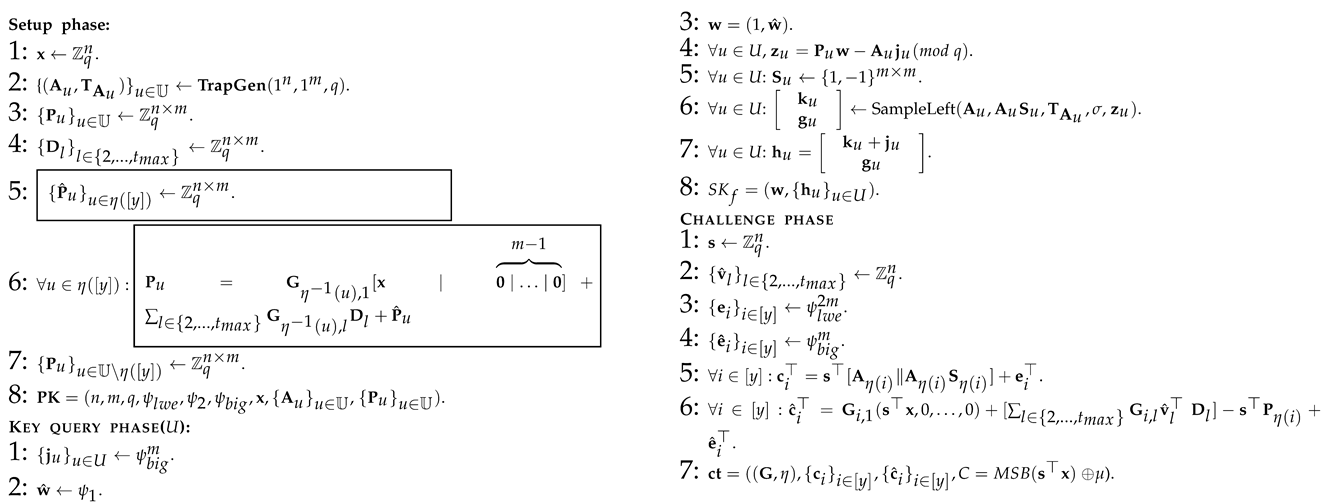
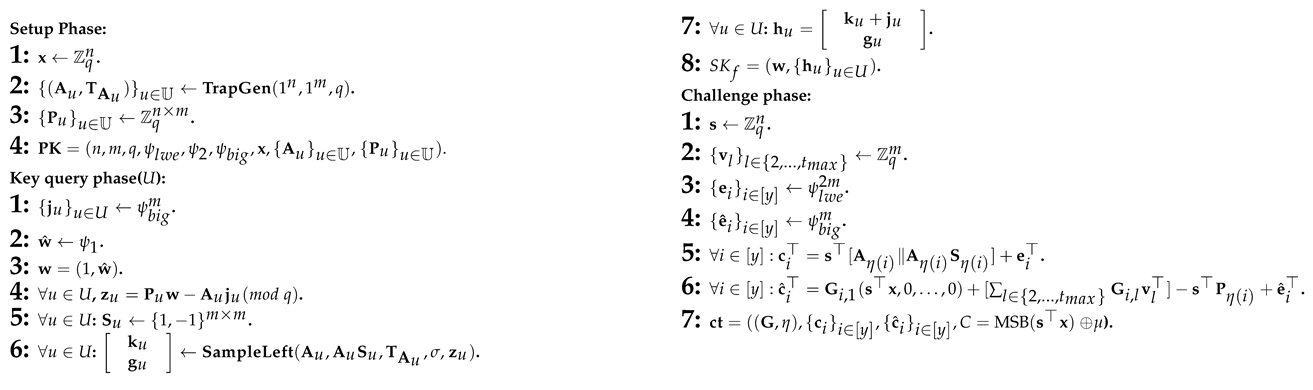Proof. 

To prove the correctness of Theorem 2, we considered a series of hybrid games, which are slightly different from each other. The first hybrid game matches the real choice security game under the linear independent restriction, and the final hybrid scheme is the one in which the advantage of the opponent is zero. By demonstrating that the advantages of the adversaries have only a completely negligible change between different consecutive hybrid games, we have finally proved the correctness of Theorem 2. Next, we will talk about the specific hybridization and analysis process. In order to facilitate the explanation, we first use 12 algorithm graphs to show, in detail, the process of 12 hybridizations in which all the symbols used are as defined above.

Secondly, we analyze the indistinguishability of any two adjacent hybridization processes in detail. For convenience, we introduce a probability function ${\beta }_{\mathcal{A},x}\left(\lambda \right):\mathbb{N}\to [0,1]$ for all adversaries $\mathcal{A}$, and any $x\in \{0,1,\dots ,11\}$ whose input is $1^{\lambda }$ and output is the probability of the opponent $\mathcal{A}$ correctly guesses the challenge bit $b\in \{0,1\}$ in each hybrid program. According to the definition of Algorithm 1, it is known that $\mid {\beta }_{\mathcal{A},0}\left(\lambda \right)-1/2\mid =Ad{v}_{\mathcal{A}}^{\mathrm{Sel}}\left(\lambda \right)$ for all $\lambda \in \mathbb{N}$. Furthermore, since the generated challenge ciphertext in Algorithm 12 does not disclose any information about the selection of challenge bits, it is known that ${\beta }_{\mathcal{A},11}=1/2$ for all $\lambda \in \mathbb{N}$.

Therefore, through the following series of analysis, we can conclude that for all $\lambda \in \mathbb{N}$, there is obviously

$$\begin{array}{c}\hfill Ad{v}_{\mathcal{A}}^{\mathrm{Sel}}\left(\lambda \right)\le \sum _{x\in \left[11\right]}\mid {\beta }_{\mathcal{A},x-1}\left(\lambda \right)-{\beta }_{\mathcal{A},x}\left(\lambda \right)\mid \le negl\left(\lambda \right)\end{array}$$

(2)

$\mathbf{Hybrid}\mathbf{0}$: This is the original selective weak security model of the CP-ABE scheme we constructed.

$\mathbf{Hybrid}\mathbf{1}$: This is similar to Algorithm 1, except for the three parts marked with a wireframe in Algorithm 2, and these changes are only semantic (As in Algorithm 1, ${\left\{{\mathbf{v}}_l\right\}}_{l\in \{2,\dots ,t_{max}\}}\leftarrow {\mathbb{Z}}_q^m$, Algorithm 2 replaces the original vector ${\left\{{\mathbf{v}}_l\right\}}_{l\in \{2,\dots ,t_{max}\}}$ with ${\widehat{\mathbf{v}}}_l^{\top }$${\mathbf{D}}_l$, where ${\left\{{\widehat{\mathbf{v}}}_l\right\}}_{l\in \{2,\dots ,t_{max}\}}\leftarrow {\mathbb{Z}}_q^n$ and ${\left\{{\mathbf{D}}_l\right\}}_{{}_{l\in \{2,\dots ,t_{max}\}}}\leftarrow {\mathbb{Z}}_q^{n\times m}$. The semantic changes involved later are also similar to the methods here), so there is obviously ${\beta }_{\mathcal{A},0}\left(\lambda \right)={\beta }_{\mathcal{A},1}\left(\lambda \right)$ for all adversaries $\mathcal{A}$.

$\mathbf{Hybrid}\mathbf{2}$: This is similar to Algorithm 2, except for the two parts marked with a wireframe in Algorithm 3, and these changes are only semantic, so there is obviously ${\beta }_{\mathcal{A},1}\left(\lambda \right)={\beta }_{\mathcal{A},2}\left(\lambda \right)$ for all adversary $\mathcal{A}$.

$\mathbf{Hybrid}\mathbf{3}$: This is similar to Algorithm 3, except for those parts marked with a wireframe in Algorithm 4. The indistinguishability of Algorithm 3 and Algorithm 4 stems from the leftover hash lemma (as shown in Lemma 1) and the basic fact that the sum of two random matrices is still a random matrix. So, there is obviously $\parallel {\beta }_{\mathcal{A},2}\left(\lambda \right)-{\beta }_{\mathcal{A},3}\left(\lambda \right)\parallel \le neg{l}_3\left(\lambda \right)$ for all adversaries $\mathcal{A}$.

$\mathbf{Hybrid}\mathbf{4}$: This is similar to Algorithm 4, except for those parts marked with a wireframe in Algorithm 5. It chooses another indistinguishable way to generate ${\left\{{\mathbf{D}}_j\right\}}_{{}_{j\in \{2,\dots ,t_{max}\}}}$, which stems from the trapdoor lattice sampler. So, there is obviously $\parallel {\beta }_{\mathcal{A},3}\left(\lambda \right)-{\beta }_{\mathcal{A},4}\left(\lambda \right)\parallel \le neg{l}_4\left(\lambda \right)$ for all adversaries $\mathcal{A}$.

$\mathbf{Hybrid}\mathbf{5}$: This is similar to Algorithm 5, except for several parts marked with wireframes in Algorithm 6, which can be summarized as the way in which $\left[\begin{array}{c}{\mathbf{k}}_u\\ {\mathbf{g}}_u\end{array}\right]$ is generated when answering the private key query of the adversary $\mathcal{A}$ for all $u\in U\cap \eta \left(y\right)$. This indistinguishably stems from the smudging lemma (Lemma 2), so we can deduce that $\parallel {\beta }_{\mathcal{A},4}\left(\lambda \right)-{\beta }_{\mathcal{A},5}\left(\lambda \right)\mid \le Q_{key}\left(\lambda \right)·\mid U\cap \eta \left(y\right)\mid ·2m·neg{l}_{smu}\left(\lambda \right)\le neg{l}_5\left(\lambda \right)$ for all adversaries $\mathcal{A}$ where $neg{l}_{smu}$ is a negligible function to measure the indistinguishability of two distributions under smudging and $Q_{key}$ represents the number of private key queries made. For example, for all of the $m\in \mathbb{N}$ and $\lambda \in \mathbb{N}$, when ${\mathcal{F}}_1\equiv \{{\mathbf{k}}_1\mid {\mathbf{k}}_1\leftarrow {\mathcal{D}}_{{\mathbb{Z}}^m,\delta }\}$, ${\mathcal{F}}_2\equiv \{{\mathbf{k}}_1+{\mathbf{k}}_2\mid {\mathbf{k}}_1\leftarrow {\mathcal{D}}_{{\mathbb{Z}}^m,\delta },{\mathbf{k}}_2\leftarrow {\mathcal{D}}_{{\mathbb{Z}}^m,\sigma }\},$ there is SD$({\mathcal{F}}_1,{\mathcal{F}}_2)\le m·neg{l}_{smu}\left(\lambda \right)$ (where $\delta \ge \sigma \sqrt{m}\parallel R\parallel ·{\lambda }^{w\left(1\right)}$).

$\mathbf{Hybrid}\mathbf{6}$: It is basically similar to Algorithm 6, just except the generation method of the vector $\mathbf{t}$ is different when answering the adversary $\mathcal{A}$. Here, in order to achieve the same purpose, we use the idea of Hybrid 6 in [20]. Namely, let $\mathbf{b}=(b_1,\dots ,b_{t_{max}})$ be a vector such that $b_1=1$ and ${\sum }_{l\in \{2,\dots ,t_{max}\}}{\mathbf{G}}_{{\eta }^{-1}\left(u\right),l}{b}_l=0$ for all $u\in U$. Note that by the game restriction, the set of rows of G with indices in ${\eta }^{-1}\left(U\right)$ must be unauthorized with respect to the access policy $(G,\eta )$, and, hence, the existence of such a vector $\mathbf{b}$ is guaranteed. We can find that the indistinguishability of Algorithm 6 and Algorithm 7 comes from the excellent characteristics of the trapdoor sampling of lattice. So, there is obviously $\parallel {\beta }_{\mathcal{A},5}\left(\lambda \right)-{\beta }_{\mathcal{A},6}\left(\lambda \right)\parallel \le neg{l}_6\left(\lambda \right)$ for all adversaries $\mathcal{A}$.

$\mathbf{Hybrid}\mathbf{7}$: This is similar to Algorithm 7, except for several parts marked with wireframes in Algorithm 8. Similar to the methods and goals of Hybrid 7 in [24], here, due to the restrictions of the game, for each secret key query of $\mathcal{A}$ corresponding to some attribute set $U\subset \mathbb{U}$, the rows of $\mathbf{G}$ with indices in $\eta U$ are linearly independent. These changes can also be seen as a simple semantic, so they are indistinguishable; therefore, there is obviously $\parallel p_{\mathcal{A},6}\left(\lambda \right)-p_{\mathcal{A},7}\left(\lambda \right)\parallel \le neg{l}_7\left(\lambda \right)$ for all adversaries $\mathcal{A}$.

$\mathbf{Hybrid}\mathbf{8}$: This is similar to Algorithm 8, except for several parts marked with wireframes in Algorithm 9, which can be summarized as the way in which ${\left[\begin{array}{c}{\mathbf{k}}_u\\ {\mathbf{g}}_u\end{array}\right]}_{u\in U\cap \rho \left(\right[y\left]\right)}$ is generated when answering the private key query of the adversary $\mathcal{A}$. The indistinguishability of Algorithm 8 and Algorithm 9 is derived from the excellent characteristics of the trapdoor sampling of lattice. So, there is obviously $\parallel p_{\mathcal{A},7}\left(\lambda \right)-p_{\mathcal{A},8}\left(\lambda \right)\parallel \le neg{l}_8\left(\lambda \right)$ for all adversaries $\mathcal{A}$.

$\mathbf{Hybrid}\mathbf{9}$: This is similar to Algorithm 9, except for the part marked with wireframes in Algorithm 10. Namely, the way to generate the matrices ${\left\{A_u\right\}}_{u\in \rho \left(\right[y\left]\right)}$ has been replaced. The indistinguishability of Algorithm 1 and Algorithm 2 is derived from the excellent characteristics of the trapdoor sampling of lattice as described earlier. So, there is obviously $\parallel {\beta }_{\mathcal{A},8}\left(\lambda \right)-{\beta }_{\mathcal{A},9}\left(\lambda \right)\parallel \le neg{l}_9\left(\lambda \right)$ for all adversaries $\mathcal{A}$.

$\mathbf{Hybrid}\mathbf{10}$: This is similar to Algorithm 10, except for the two parts marked with wireframes in Algorithm 11. Namely, the way to generate the vectors ${\widehat{\mathbf{e}}}_i$ in the ${\left\{{\widehat{\mathbf{c}}}_i\right\}}_{i\in \left[y\right]}$ has been replaced. The indistinguishability of Algorithm 10 and Algorithm 11 is derived from the smudging lemma (Lemma 2). So, there is obviously $\parallel {\beta }_{\mathcal{A},9}\left(\lambda \right)-{\beta }_{\mathcal{A},10}\left(\lambda \right)\parallel \le y·m·neg{l}_{smu}\le neg{l}_{10}\left(\lambda \right)$ for all adversaries $\mathcal{A}$.

$\mathbf{Hybrid}\mathbf{11}$: This is basically the same as Algorithm 11, except for a few framed parts, which are summarized as different ways of generating ciphertext in the challenge phase. In Algorithm 11, ${\left\{{\mathbf{c}}_i\right\}}_{i\in \left[y\right]}$ resembles a set of LWE${}_{n,q,\sigma }$ samples, and, here, we really want to use LWE to hide s. Assume that for any $i\in \left[y\right]$, $[{\mathbf{A}}_u,{\mathbf{A}}_u{\mathbf{S}}_u]=[{\mathbf{a}}_1,\dots ,{\mathbf{a}}_m,{\mathbf{a}}_{m+1},\dots ,{\mathbf{a}}_{2m}]$, then ${\mathbf{c}}_i=\mathbf{s}[{\mathbf{A}}_u,{\mathbf{A}}_u{\mathbf{S}}_u]+{\mathbf{e}}_i^{\top }=\mathbf{s}[{\mathbf{a}}_1,\dots ,{\mathbf{a}}_m,{\mathbf{a}}_{m+1},\dots ,{\mathbf{a}}_{2m}]+{\mathbf{e}}_i^{\top }=[\mathbf{s}{\mathbf{a}}_1+{\mathbf{e}}_{i,1},\dots ,\mathbf{s}{\mathbf{a}}_m+{\mathbf{e}}_{i,m},\mathbf{s}{\mathbf{a}}_{m+1}+{\mathbf{e}}_{i,m+1},\dots ,\mathbf{s}{\mathbf{a}}_{2m}+{\mathbf{e}}_{i,2m}]$. Because of the decisional LWE, we have that the selection of ${\left\{{\mathbf{c}}_i\right\}}_{i\in \left[y\right]}$ in Algorithm 11 and Algorithm 12 is indistinguishable. In addition, Algorithm 12 makes a semantic transformation with ${\widehat{\mathbf{v}}}_l=\mathbf{s}+{\mathbf{v}}_l^{\prime }$ so that ${\left\{{\widehat{\mathbf{c}}}_i\right\}}_{i\in \left[y\right]}$ gets rid of s and has the same distribution as the selection in Algorithm 11. In turn, if we look at $\mathbf{s}{\mathbf{x}}^{\top }$, because of $\mathbf{x}\leftarrow {\mathbb{Z}}_q^n$, we can make ${\mathbf{a}}_{2m+1}=\mathbf{x}$ and randomly select ${\mathbf{e}}_{2m+1}\leftarrow {\mathcal{D}}_{\mathbb{Z},\sigma }$. Then, there must be MSB$\left(\mathbf{s}{\mathbf{x}}^{\top }\right)$ = MSB$(\mathbf{s}{\mathbf{x}}^{\top }+{\mathbf{e}}_{2m+1})$. Then, according to the decisional LWE${}_{n,q,\sigma }$, we have that the distribution of MSB$\left(\mathbf{s}{\mathbf{x}}^{\top }\right)$ is indistinguishable from that of MSB$\left(\tau \right)$ (where $\tau \leftarrow {\mathbb{Z}}_q$). To sum up, the indistinguishability of Algorithm 11 and Algorithm 12 is derived from the LWE assumption. So, there is obviously $\parallel {\beta }_{\mathcal{A},10}\left(\lambda \right)-{\beta }_{\mathcal{A},11}\left(\lambda \right)\parallel \le neg{l}_{11}\left(\lambda \right)$ for all adversaries $\mathcal{A}$.    □

Algorithm 1 (Hybrid 0)

Algorithm 2 (Hybrid 1)

Algorithm 3  (Hybrid 2)

Algorithm 4  (Hybrid 3)

Algorithm 5  (Hybrid 4)

Algorithm 6  (Hybrid 5)

Algorithm 7  (Hybrid 6)

Algorithm 8  (Hybrid 7)

Algorithm 9  (Hybrid 8)

Algorithm 10  (Hybrid 9)

Algorithm 11  (Hybrid 10)

Algorithm 12  (Hybrid 11)

3.3. Comparison

For a long time before, the only known way to implement an LWE-based CP-ABE scheme was to convert a circuit-based KP-ABE scheme into a CP-ABE scheme, in which the access policies and sets of attributes were represented as circuits by using general circuits. However, this transformation essentially results in a CP-ABE with restricted access policy classes, whose parameters are far from ideal.

In recent years, people have tried to make some improvements to the CP-ABE based on the general-purpose circuits described above, while trying to get rid of other assumptions, and have wanted to design solutions only based on LWE. This is a step-by-step process, and, recently, there have been only a few exciting attempts, but these schemes themselves are not very efficient, and they are only attempts at the design level. There has not been too much consideration for specific contents, such as the key size or ciphertext size; therefore, here, we also make a comparison mainly from these levels, as shown below.

The reason why we say that our scheme is at least the same as the scheme [20] under the same parameters is that we can prove that the scheme can indeed achieve selective security. However, also because the use of two-stage sampling technology has been proven able to achieve a strong security, simple function encryption. The so-called strong security means that attackers can decrypt key queries before and after arbitrary challenges are issued in simulated security experiments. Here, we only give proof that the scheme is selectively secure. At the same time, in order to better illustrate the contribution of this scheme, we compare our scheme with some previous CP-ABE schemes, as shown in

Table 1. Comparison with the construction of some previous LWE-based CP-ABE schemes.

Scheme	Circuits	Access Structure	Assumption	Direct Design or Indirect	Only Based on LWE or Not	Security
[9]	UC *	Circuit encoding of BGG+	LWE	Indirect	Yes	Lack security proof
[6]	NC${}^1$	Circuit encoding of BGG+	Bilinear maps and LWE	Indirect	No	Ada-INDr
[21]	NC${}^1$	A nearly LSSS	LWE and KOALA *	Indirect	No	Very sel-security
[22]	UC *	Circuit encoding of BGG+	LWE	Indirect	Yes	Sel-secure
[20]	NC${}^1$	LSSS (non-monotone)	LWE	Direct	Yes	Sel-secure
Ours	NC${}^1$	LSSS (non-monotone)	LWE	Direct	Yes	(at least) Sel-secure

Note *: The UC in the figure above represents the general-purpose circuit, and the KOALA represents knowledge of orthogonality assumption. Direct means that a scheme is constructed directly, while indirect indicates that a scheme needs to be transformed by borrowing other KP-ABE schemes or functional encryption schemes (FE).

below.

Here, under the same parameters, we make a simple comparison between our scheme and the one in [20] in terms of the public key, private key, and ciphertext storage overhead. The results show that the ciphertext can be shortened to a certain extent by two-stage sampling technology. The specific comparison idea is as follows. Since the lengths of parts $(\mathbf{G},\eta )$ and $C=MSB\left({\mathbf{s}}^{\top }\mathbf{x}\right)\oplus \mu$ in the ciphertext of the two schemes are equal, we only compare parts ${\left\{{\mathbf{c}}_i\right\}}_{i\in \left[y\right]}$ and ${\left\{{\widehat{\mathbf{c}}}_i\right\}}_{i\in \left[y\right]}$, as shown in

Table 2. Comparison between our scheme and the scheme in [20] in terms of storage overhead under the same parameters.

Scheme	Public Key	Private Key	Ciphertext	Plaintex
[20]	$4\left|\mathbb{U}\right|mn\lceil {log}_{2}q\rceil$	$2m\left|U\right|\lceil {log}_2\left(\right|\sigma |+|\widehat{B}\left|\right)\rceil$	$y{t}_{\max }\lceil {log}_{2}3\rceil +4my\lceil {log}_{2}q\rceil$	1
Ours	$2\left|\mathbb{U}\right|mn\lceil logq\rceil$	$m\left|U\right|(\lceil {log}_2\left(\right|\sigma \left|\right)\rceil +\lceil {log}_2\left(\right|\sigma |+\left|\delta \right|)\rceil$)	$y{t}_{\max }\lceil {log}_{2}3\rceil +3my\lceil {log}_{2}q\rceil$	1

(since the value of the parameter “m” in our scheme is half that of the parameter “m” in their scheme, in order to make a unified comparison, we take the parameters in our scheme as the benchmark). In addition, we also find that the sizes of the public key and private key of our scheme are superior to those of the original scheme. However, because the efficiencies of all LWE-based CP-ABEs are relatively low, we mainly pay attention to the innovation of the scheme design itself. However, some other contents, such as key size, encryption cost, decryption cost, and so on, will not be considered for the time being. The performance optimization, computational complexity, and implementation of the scheme will be considered at a later time.

3.4. Example of Parameters Selection

In this section, we refer to the six constraints of the scheme parameters in the Section 3 of this paper, and, after a series of strict calculations, we give several groups of reasonable parameter choices, which are not necessarily optimal, for detail, please refer to

Table 3. Recommended parameters in our CP-ABE scheme.

${\mathit{t}}_{\mathit{max}}$	$\left|\mathbb{U}\right|$	$\mathit{\lambda }$	n	m	q	$\mathit{ϵ}$	$\mathit{\sigma }$	$\mathit{\delta }$
1 *	1	103	512	35,032	$2^{68}$	$1/7$	828	2.988 $\times {10}^9$
1 *	1	128	512	35,082	$2^{68}$	$1/7$	854	3.835 $\times {10}^9$
8	10	103	512	327,896	$2^{80}$	1/6	2580	1.1 $\times {10}^{10}$
8	20	103	512	327,896	$2^{80}$	1/6	2580	1.1 $\times {10}^{10}$
10	15	192	1024	435,595	2${}^{85}$	1/4	3048	2.55 $\times {10}^{11}$
8	20	256	1024	737,803	2${}^{90}$	1/10	4048	7.646 $\times {10}^{11}$

* Note: The data in rows 1 and 2 are for reference only.

as shown below.

3.5. A Simple Example of CP-ABE

Here, we consider a non-monotone Boolean formula $(A\bigwedge B)\bigvee (C\bigwedge D)$, whose root has a 1-label (1, 0, 0, 0, 0) and a 0-label (0, 1, 0, 0, 0). According to the construction principle of generating matrix G, we can determine that the policy is

$$G=\left(\begin{array}{ccccc}0& 0& 0& 1& 0\\ 0& 0& 1& 0& 0\\ 1& 0& 0& -1& 0\\ 0& 0& 1& -1& 0\\ 0& 0& 0& 0& 1\\ 0& 1& -1& 0& 0\\ 1& 0& -1& 0& -1\\ 0& 1& -1& 0& -1\end{array}\right)\begin{array}{c}{A}_1\\ A_0\\ B_1\\ B_0\\ C_1\\ C_0\\ D_1\\ D_0\end{array}$$

When the parameters $t_{max}=5,\left|U\right|=8,\lambda =103,n=512,m=327,896,ϵ=1/6,\sigma =$ 2580, and $\delta =1.1\times {10}^{10}$ are selected, respectively, a series of operations are carried out according to the requirements of the four steps of the scheme design in Section 3.1 above because we can easily find a set of ${\left\{w_i\right\}}_{i\in \left[8\right]}=(1,0,1,0,0,0,0,0)$ to make $G_i{w}_i=(1,0,0,0,0)$. Because the ciphertext generated by encryption is ${\left\{c_i\right\}}_{i\in \left[8\right]}$ and ${\left\{{\widehat{c}}_i\right\}}_{i\in \left[8\right]}$, therefore, according to the decryption algorithm, it can be calculated $Y^{{}^{\prime }}={\sum }_{i\in \Delta }{\xi }_i({\mathbf{c}}_i^{\top }{\mathbf{h}}_u+{\widehat{\mathbf{c}}}_i^{\top }\mathbf{w})$. After a series of simplification, we can obtain $Y^{{}^{\prime }}={\mathbf{sx}}^{\top }+{\mathbf{e}}_1^{\top }{\mathbf{h}}_{\eta \left(1\right)}+{\widehat{\mathbf{e}}}_1^{\top }\mathbf{t}+{\mathbf{e}}_3^{\top }{\mathbf{h}}_{\eta \left(3\right)}+{\widehat{\mathbf{e}}}_3^{{}^{\top }}\mathbf{h}$. Through the calculation, it is found that ${\mathbf{e}}_1^{\top }{\mathbf{h}}_{\eta \left(1\right)}+{\widehat{\mathbf{e}}}_1^{\top }\mathbf{t}+{\mathbf{e}}_3^{\top }{\mathbf{h}}_{\eta \left(3\right)}+{\widehat{\mathbf{e}}}_3^{{}^{\top }}\mathbf{h}<2.65\times {10}^{19}<q/4$; therefore, $MSB\left(Y^{{}^{\prime }}\right)=MSB\left({\mathbf{sx}}^{\top }\right)$, so it can be decrypted successfully.

4. Conclusions

In this paper, the CP-ABE scheme of [20] is improved by using a two-stage sampling algorithm, and a selectively secure CP-ABE scheme with shorter ciphertext is obtained. We prove the correctness of the scheme and give strict proof of security. At the same time, we also give a comparison of the computational cost between this scheme and the one in [20], and, in order to better understand the scheme, we recommend several groups of parameters through a series of strict calculations. Finally, we give a simple example to demonstrate the overall operation process of the algorithm. This scheme may provide some ideas for constructing other CP-ABE and multi-authority attribute encryption schemes, and the two-stage sampling algorithm involved in this scheme may be used in other cryptographic schemes to optimize the existing performance.