A Gaussian Process Decoder with Spectral Mixtures and a Locally Estimated Manifold for Data Visualization
Abstract
1. Introduction
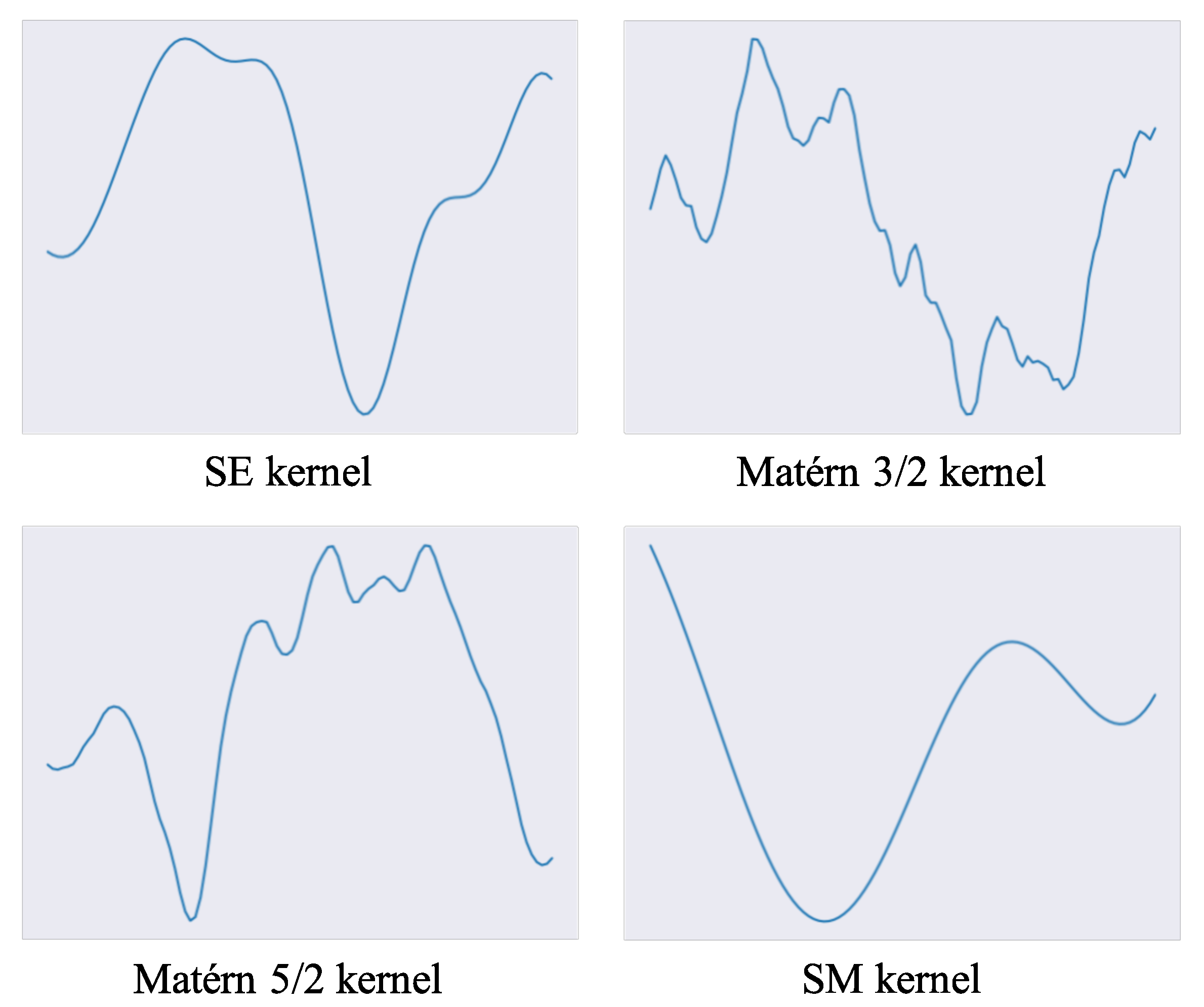
- Kernel function. We focus on the spectral mixture (SM) kernel [30] and introduce it into a GP-LVM. Generally, the SE kernel and Matérn kernel are applied to GP-LVMs, which are homogeneous kernels that only depend on the distance between latent features. In contrast, the SM kernel is a broader class kernel that depends on not only the distance but the periodicity of input features. Although the SM kernel has strong expressiveness compared to the SE and Matérn kernels, it has been applied to regression models and not to GP-LVMs. In this study, we develop the SM kernel for GP-LVMs and reveal its high ability for pattern discovery and visualization.
- Prior distribution. We focus on the use of a locally estimated manifold in the prior distribution. Local structures, such as the cluster structure, are crucial to improving the visibility of a low-dimensional representation. Therefore, we regularize low-dimensional embedding with the local estimation of the data manifold. Specifically, we locally approximate it with a neighborhood graph and regularize the low-dimensional representation with it. Through this strategy, we consider local structures and improve the visibility of low-dimensional representation. The regularization based on the graph Laplacian in supervised cases has been previously studied as the Gaussian process latent random field (GPLRF) [33], and we apply the GPLRF scheme in an unsupervised manner.
2. Related Works
2.1. Graph-Based Approaches
2.2. PCA-Based Approaches
3. Preliminary
3.1. Gaussian Process Latent Variable Model
3.2. Kernel Function
3.3. Uniform Manifold Approximation and Projection
4. Proposed Method
4.1. Model Formulation
4.2. Lower Bound of Log-Posterior Distribution
4.3. Optimization
5. Experiment
5.1. Experimental Setup
5.1.1. Dataset
- MNIST (http://yann.lecun.com/exdb/mnist/ (accessed on 25 July 2022)) contains 70K images of hand-written digits and labels corresponding to each digit. We randomly selected 20K images and colored embeddings along the corresponding labels. MNIST contains a cluster structure of each digit, and the embedding should preserve the cluster structure.
- COIL-20 [54] contains 1440 grayscale images of rotated objects. We used the first ten objects and colored embeddings along each object. Images of COIL-20 have a rotating structure, and the embedding should preserve it.
- DBPedia (https://wiki.dbpedia.org/ (accessed on 29 July 2022)) contains 530K Wikipedia articles classified into 14 categories. We used 20K random articles and extracted feature vectors by FastText following [37]. We colored the embedding following the category information, and the low-dimensional representation should preserve the cluster structure.
- Fashion MNIST (FMNIST) [55] contains 70K images of 10 kinds of fashion items and labels corresponding to each item. We randomly selected 20K images and colored embeddings to match the corresponding labels. Although FMNIST has a cluster structure similar to MNIST, the categories of FMNIST are more correlated than those of MNIST, and separating clusters in a low-dimensional representation is more difficult.
5.1.2. Comparative Methods
- PCA [3] is a classical method for dimensionality reduction and linearly derives its embedding. We compared our method with PCA as a benchmark method. Note that GP-LVM-based methods typically use PCA as the initial values of their latent variables.
- LE [34] is a classical graph-based approach and derives its low-dimensional embedding as the eigenvectors of the graph Laplacian. We used LE as the benchmark in the graph-based approaches.
- Bayesian GP-LVM (BGP-LVM) [16,25] is a GP-LVM that introduces the Bayesian inference into the latent variables. We used BGP-LVM as the baseline method and visualized the mean vectors as a low-dimensional representation. We used the RBF kernel in Equation (6) and standard normal density as the prior distribution following the original work [16].
- Potential of heat diffusion of affinity-based transition embedding (PHATE) [41] is a recently proposed graph-based approach and derives the neighborhood graph on the basis of the diffusion operation [56], enabling the global preservation of data. We used PHATE as a state-of-the-art method among the methods aimed at preserving global structures.
5.1.3. Evaluation
5.1.4. Training Procedure
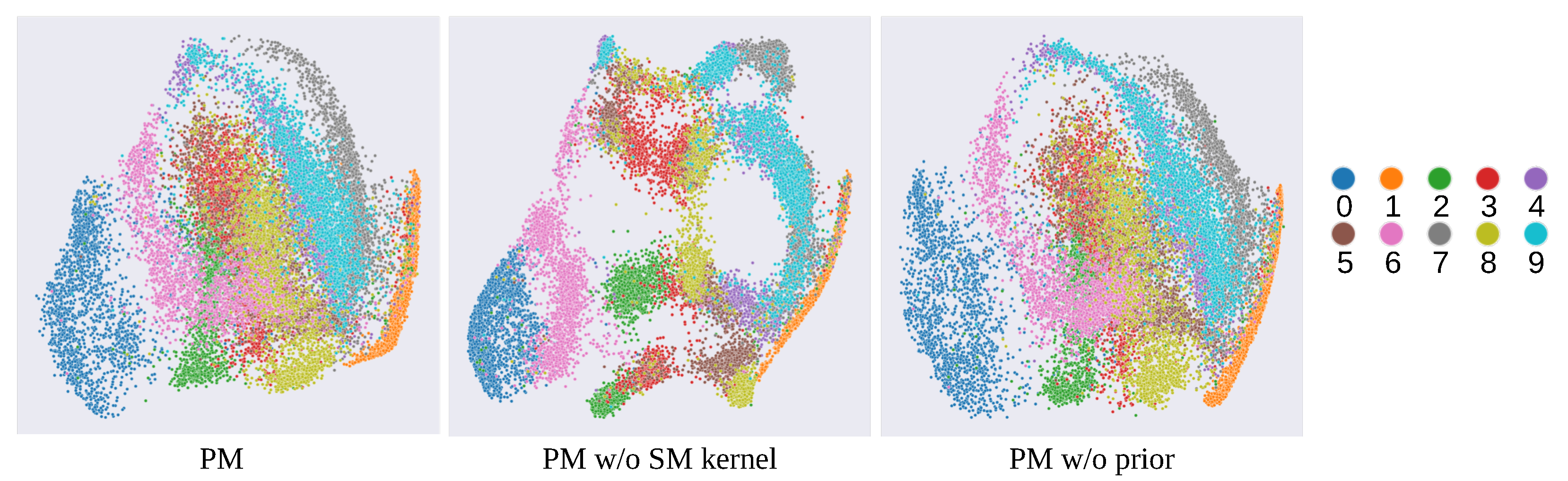
5.2. Ablation Study
5.3. Qualitative Results
5.4. Quantitative Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Van der Maaten, L.; Postma, E.; Van den Herik, J. Dimensionality reduction: A comparative. J. Mach. Learn Res. 2009, 10, 66–71. [Google Scholar]
- Hotelling, H. Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 1933, 24, 417–441. [Google Scholar] [CrossRef]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef] [PubMed]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Higgins, I.; Matthey, L.; Pal, A.; Burgess, C.; Glorot, X.; Botvinick, M.; Mohamed, S.; Lerchner, A. β-vae: Learning basic visual concepts with a constrained variational framework. In Proceedings of the International Conference on Learning Representations (ICLR), San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Sohl-Dickstein, J.; Weiss, E.; Maheswaranathan, N.; Ganguli, S. Deep unsupervised learning using nonequilibrium thermodynamics. In Proceedings of the International Conference on Machine Learning (ICML), Lille, France, 6–11 July 2015; pp. 2256–2265. [Google Scholar]
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. Adv. Neural Inf. Process. Syst. NeurIPS 2020, 33, 6840–6851. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Van der Maaten, L. Accelerating t-SNE using tree-based algorithms. J. Mach. Learn. Res. 2014, 15, 3221–3245. [Google Scholar]
- McInnes, L.; Healy, J.; Melville, J. UMAP: Uniform manifold approximation and projection for dimension reduction. arXiv 2018, arXiv:1802.03426. [Google Scholar]
- Kobak, D.; Berens, P. The art of using t-SNE for single-cell transcriptomics. Nat. Commun. 2019, 10, 5416. [Google Scholar] [CrossRef] [PubMed]
- Becht, E.; McInnes, L.; Healy, J.; Dutertre, C.A.; Kwok, I.W.; Ng, L.G.; Ginhoux, F.; Newell, E.W. Dimensionality reduction for visualizing single-cell data using UMAP. Nat. Biotechnol. 2019, 37, 38–44. [Google Scholar] [CrossRef]
- Lawrence, N.D. Probabilistic non-linear principal component analysis with Gaussian process latent variable models. J. Mach. Learn. Res. 2005, 6, 1783–1816. [Google Scholar]
- Titsias, M.; Lawrence, N.D. Bayesian Gaussian process latent variable model. In Proceedings of the International Conference on Artificial Intelligence and Statistics (AISTATS), Sardinia, Italy, 13–15 May 2010; pp. 844–851. [Google Scholar]
- Neal, R.M. Bayesian Learning for Neural Networks; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 118. [Google Scholar]
- Lee, J.; Bahri, Y.; Novak, R.; Schoenholz, S.S.; Pennington, J.; Sohl-Dickstein, J. Deep neural networks as Gaussian processes. arXiv 2017, arXiv:1711.00165. [Google Scholar]
- Märtens, K.; Campbell, K.; Yau, C. Decomposing feature-level variation with covariate Gaussian process latent variable models. In Proceedings of the International Conference on Machine Learning (ICML), Long Beach, CA, USA, 9–15 June 2019; pp. 4372–4381. [Google Scholar]
- Jensen, K.; Kao, T.C.; Tripodi, M.; Hennequin, G. Manifold GPLVMs for discovering non-Euclidean latent structure in neural data. Adv. Neural Inf. Process. Syst. 2020, 33, 22580–22592. [Google Scholar]
- Liu, Z. Visualizing single-cell RNA-seq data with semisupervised principal component analysis. Int. J. Mol. Sci. 2020, 21, 5797. [Google Scholar] [CrossRef]
- Jørgensen, M.; Hauberg, S. Isometric Gaussian process latent variable model for dissimilarity data. In Proceedings of the International Conference on Machine Learning (ICML), Sydney, Australia, 18–24 July 2021; pp. 5127–5136. [Google Scholar]
- Lalchand, V.; Ravuri, A.; Lawrence, N.D. Generalised GPLVM with stochastic variational inference. In Proceedings of the International Conference on Artificial Intelligence and Statistics (AISTATS), Virtual Event, 28–30 March 2022; pp. 7841–7864. [Google Scholar]
- Wang, J.M.; Fleet, D.J.; Hertzmann, A. Gaussian process dynamical models for human motion. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 30, 283–298. [Google Scholar] [CrossRef]
- Damianou, A.C.; Titsias, M.K.; Lawrence, N.D. Variational Inference for Latent Variables and Uncertain Inputs in Gaussian Processes. J. Mach. Learn. Res. 2016, 17, 1–62. [Google Scholar]
- Ferris, B.; Fox, D.; Lawrence, N. WiFi-SLAM using Gaussian process latent variable models. In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI), Hyderabad, India, 6–12 January 2007; pp. 2480–2485. [Google Scholar]
- Zhang, G.; Wang, P.; Chen, H.; Zhang, L. Wireless indoor localization using convolutional neural network and Gaussian process regression. Sensors 2019, 19, 2508. [Google Scholar] [CrossRef]
- Lu, C.; Tang, X. Surpassing human-level face verification performance on LFW with GaussianFace. In Proceedings of the AAAI conference on Artificial Intelligence (AAAI), Austin, TX, USA, 25–30 January 2015. [Google Scholar]
- Cho, Y.; Saul, L. Kernel methods for deep learning. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 7–10 December 2009. [Google Scholar]
- Wilson, A.; Adams, R. Gaussian process kernels for pattern discovery and extrapolation. In Proceedings of the International Conference on Machine Learning (ICML), Atlanta, GA, USA, 16–21 June 2013; pp. 1067–1075. [Google Scholar]
- Lloyd, J.; Duvenaud, D.; Grosse, R.; Tenenbaum, J.; Ghahramani, Z. Automatic construction and natural-language description of nonparametric regression models. In Proceedings of the AAAI Conference on Artificial Intelligence (AAAI), Quebec City, QC, Canada, 27–31 July 2014. [Google Scholar]
- Urtasun, R.; Darrell, T. Discriminative Gaussian process latent variable model for classification. In Proceedings of the International Conference on Machine Learning (ICML), Hong Kong, China, 19–22 August 2007; pp. 927–934. [Google Scholar]
- Zhong, G.; Li, W.J.; Yeung, D.Y.; Hou, X.; Liu, C.L. Gaussian process latent random field. In Proceedings of the AAAI Conference on Artificial Intelligence (AAAI), Atlanta, GA, USA, 11–15 July 2010; pp. 679–684. [Google Scholar]
- Belkin, M.; Niyogi, P. Laplacian eigenmaps for dimensionality reduction and data representation. Neural Comput. 2003, 15, 1373–1396. [Google Scholar] [CrossRef]
- Belkin, M.; Niyogi, P. Convergence of Laplacian eigenmaps. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 4–7 December 2006. [Google Scholar]
- Carreira-Perpinán, M.A. The Elastic Embedding Algorithm for Dimensionality Reduction. In Proceedings of the International Conference on Machine Learning (ICML), Haifa, Israel, 21–24 June 2010; pp. 167–174. [Google Scholar]
- Fu, C.; Zhang, Y.; Cai, D.; Ren, X. AtSNE: Efficient and robust visualization on gpu through hierarchical optimization. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AL, USA, 4–8 August 2019; pp. 176–186. [Google Scholar]
- Böhm, J.N.; Berens, P.; Kobak, D. Attraction-repulsion spectrum in neighbor embeddings. J. Mach. Learn. Res. 2022, 23, 1–32. [Google Scholar]
- Amid, E.; Warmuth, M.K. TriMap: Large-scale dimensionality reduction using triplets. arXiv 2019, arXiv:1910.00204. [Google Scholar]
- Wang, Y.; Huang, H.; Rudin, C.; Shaposhnik, Y. Understanding how dimension reduction tools work: An empirical approach to deciphering t-SNE, UMAP, TriMAP, and PaCMAP for data visualization. J. Mach. Learn. Res. 2021, 22, 9129–9201. [Google Scholar]
- Moon, K.R.; van Dijk, D.; Wang, Z.; Gigante, S.; Burkhardt, D.B.; Chen, W.S.; Yim, K.; Elzen, A.v.d.; Hirn, M.J.; Coifman, R.R.; et al. Visualizing structure and transitions in high-dimensional biological data. Nat. Biotechnol. 2019, 37, 1482–1492. [Google Scholar] [CrossRef] [PubMed]
- Tipping, M.E.; Bishop, C.M. Probabilistic principal component analysis. J. R. Stat. Soc. Ser. B Stat. Methodol. 1999, 61, 611–622. [Google Scholar] [CrossRef]
- Hofmann, T.; Schölkopf, B.; Smola, A.J. Kernel methods in machine learning. Ann. Stat. 2008, 36, 1171–1220. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Lawrence, N.D.; Moore, A.J. Hierarchical Gaussian process latent variable models. In Proceedings of the International Conference on Machine Learning (ICML), Corvallis, OR, USA, 20–24 June 2007; pp. 481–488. [Google Scholar]
- Quinonero-Candela, J.; Rasmussen, C.E. A unifying view of sparse approximate Gaussian process regression. J. Mach. Learn. Res. 2005, 6, 1939–1959. [Google Scholar]
- Titsias, M. Variational learning of inducing variables in sparse Gaussian processes. In Proceedings of the International Conference on Artificial intelligence and statistics (AISTATS), Clearwater Beach, FL, USA, 16–18 April 2009; pp. 567–574. [Google Scholar]
- Lawrence, N.D. Learning for larger datasets with the Gaussian process latent variable model. In Proceedings of the International Conference on Artificial Intelligence and Statistics (AISTATS), San Juan, Puerto Rico, 21–24 March 2007; pp. 243–250. [Google Scholar]
- Damianou, A.; Lawrence, N.D. Deep Gaussian processes. In Proceedings of the International Conference on Artificial Intelligence and Statistics (AISTATS), PMLR, Scottsdale, AZ, USA, 29 April–1 May 2013; pp. 207–215. [Google Scholar]
- Dai, Z.; Damianou, A.; González, J.; Lawrence, N. Variational auto-encoded deep Gaussian processes. In Proceedings of the International Conference on Learning Representation (ICLR), San Juan, Puerto Rico, 2–4 May 2016; pp. 1–11. [Google Scholar]
- Shewchuk, J.R. An Introduction to the Conjugate Gradient Method without the Agonizing Pain; Carnegie Mellon University: Pittsburgh, PA, USA, 1994. [Google Scholar]
- Zhu, C.; Byrd, R.H.; Lu, P.; Nocedal, J. Algorithm 778: L-BFGS-B: Fortran subroutines for large-scale bound-constrained optimization. ACM Trans. Math. Softw. 1997, 23, 550–560. [Google Scholar] [CrossRef]
- GPy. GPy: A Gaussian Process Framework in Python. 2012. Available online: http://github.com/SheffieldML/GPy (accessed on 26 June 2020).
- Nene, S.A.; Nayar, S.K.; Murase, H. Columbia Object Image Library (COIL-20); Technical Report CUCS-006-96; Columbia University: New York, NY, USA, 1996. [Google Scholar]
- Xiao, H.; Rasul, K.; Vollgraf, R. Fashion-MNIST: A novel image dataset for benchmarking machine learning algorithms. arXiv 2017, arXiv:1708.07747. [Google Scholar]
- Coifman, R.R.; Lafon, S. Diffusion maps. Appl. Comput. Harmon. Anal. 2006, 21, 5–30. [Google Scholar] [CrossRef]
- Venna, J.; Kaski, S. Neighborhood preservation in nonlinear projection methods: An experimental study. In Proceedings of the International Conference on Artificial Neural Networks (ICANN), Vienna, Austria, 21–25 August 2001; pp. 485–491. [Google Scholar]
- Espadoto, M.; Martins, R.M.; Kerren, A.; Hirata, N.S.; Telea, A.C. Toward a quantitative survey of dimension reduction techniques. IEEE Trans. Vis. Comput. Graph. 2019, 27, 2153–2173. [Google Scholar] [CrossRef] [PubMed]
- Zu, X.; Tao, Q. SpaceMAP: Visualizing High-dimensional Data by Space Expansion. In Proceedings of the International Conference on Machine Learning (ICML), Baltimore, MD, USA, 17–23 July 2022; pp. 27707–27723. [Google Scholar]
- Joia, P.; Coimbra, D.; Cuminato, J.A.; Paulovich, F.V.; Nonato, L.G. Local affine multidimensional projection. IEEE Trans. Vis. Comput. Graph. 2011, 17, 2563–2571. [Google Scholar] [CrossRef] [PubMed]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]

| Dataset | Samples | Dimensions | Categories | Type | Features |
|---|---|---|---|---|---|
| MNIST | 20,000 | 784 | 10 | Image | Pixels |
| COIL-20 | 720 | 16,384 | 10 | Image | Pixels |
| DBPedia | 20,000 | 100 | 14 | Text | FastText |
| FMNIST | 20,000 | 784 | 10 | Image | Pixels |
| Dataset | PCA | LE | t-SNE | BGP-LVM | PHATE | PM |
|---|---|---|---|---|---|---|
| MNIST | 0.738 | 0.756 | 0.994 | 0.823 | 0.871 | 0.881 |
| COIL-20 | 0.898 | 0.882 | 0.997 | 0.984 | 0.931 | 0.974 |
| DBPedia | 0.883 | 0.956 | 0.998 | 0.989 | 0.986 | 0.990 |
| FMNIST | 0.912 | 0.927 | 0.994 | 0.909 | 0.958 | 0.953 |
| Dataset | PCA | LE | t-SNE | BGP-LVM | PHATE | PM |
|---|---|---|---|---|---|---|
| MNIST | 0.503 | 0.431 | 0.349 | 0.464 | 0.368 | 0.512 |
| COIL-20 | 0.818 | 0.633 | 0.611 | 0.525 | 0.355 | 0.687 |
| DBPedia | 0.778 | 0.490 | 0.339 | 0.594 | 0.361 | 0.694 |
| FMNIST | 0.876 | 0.692 | 0.579 | 0.883 | 0.615 | 0.862 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Watanabe, K.; Maeda, K.; Ogawa, T.; Haseyama, M. A Gaussian Process Decoder with Spectral Mixtures and a Locally Estimated Manifold for Data Visualization. Appl. Sci. 2023, 13, 8018. https://doi.org/10.3390/app13148018
Watanabe K, Maeda K, Ogawa T, Haseyama M. A Gaussian Process Decoder with Spectral Mixtures and a Locally Estimated Manifold for Data Visualization. Applied Sciences. 2023; 13(14):8018. https://doi.org/10.3390/app13148018
Chicago/Turabian StyleWatanabe, Koshi, Keisuke Maeda, Takahiro Ogawa, and Miki Haseyama. 2023. "A Gaussian Process Decoder with Spectral Mixtures and a Locally Estimated Manifold for Data Visualization" Applied Sciences 13, no. 14: 8018. https://doi.org/10.3390/app13148018
APA StyleWatanabe, K., Maeda, K., Ogawa, T., & Haseyama, M. (2023). A Gaussian Process Decoder with Spectral Mixtures and a Locally Estimated Manifold for Data Visualization. Applied Sciences, 13(14), 8018. https://doi.org/10.3390/app13148018






