Dealing with Unreliable Annotations: A Noise-Robust Network for Semantic Segmentation through A Transformer-Improved Encoder and Convolution Decoder

Abstract

Conventional deep learning methods have shown promising results in the medical domain when trained on accurate ground truth data. Pragmatically, due to constraints like lack of time or annotator inexperience, the ground truth data obtained from clinical environments may not always be impeccably accurate. In this paper, we investigate whether the presence of noise in ground truth data can be mitigated. We propose an innovative and efficient approach that addresses the challenge posed by noise in segmentation labels. Our method consists of four key components within a deep learning framework. First, we introduce a Vision Transformer-based modified encoder combined with a convolution-based decoder for the segmentation network, capitalizing on the recent success of self-attention mechanisms. Second, we consider a public CT spine segmentation dataset and devise a preprocessing step to generate (and even exaggerate) noisy labels, simulating real-world clinical situations. Third, to counteract the influence of noisy labels, we incorporate an adaptive denoising learning strategy (ADL) into the network training. Finally, we demonstrate through experimental results that the proposed method achieves noise-robust performance, outperforming existing baseline segmentation methods across multiple evaluation metrics.

1. Introduction

Encoder–decoder network architecture has emerged as a dominant design in medical image segmentation, starting with U-Net, a fully symmetric variant [1]. The encoder in this architecture primarily focuses on extracting pixel location features via convolutional operations and downsampling. The decoder, conversely, reinstates spatial dimensions and pixel location information using deconvolutional operations. The copy-and-crop connection that exists between encoder and decoder layers facilitates the seamless transfer of multiscale semantic information. With this advanced framework, U-Net has been successfully deployed for segmenting a variety of regions within the human body, proving its efficacy across CT [2,3,4], ultrasound [5,6,7,8], and MRI modalities [9,10,11].

The segmentation capabilities of U-Net were later expanded upon by Çiçek, who introduced a 3D version capable of achieving volumetric segmentation through the extraction of sparsely annotated volumetric images [12]. Another significant advancement was made by Oktay, who introduced an attention gate model. This model enabled CNNs to automatically learn the structures of targets with diverse shapes and sizes [11]. The resultant attention U-Net-based model demonstrated superior sensitivity and accuracy while minimizing computational overhead. Kolarik also contributed to the development of the model by proposing a high-resolution Dense-UNet by comparing the performance of 2D and 3D convolutional operations within residual networks and densely connected networks, respectively [13].

Ongoing research related to various U-Net architectures such as residual networks, inception networks, densely connected networks, and feature normalization continues to advance the field [2,14,15,16]. The CNN-based U-Net has been ubiquitous in its application, which has led to the creation of a family of CNN-based U-Nets [2,3,13,14,15,17,18,19].

Vision Transformers (ViT) have garnered considerable attention as an influential architecture for diverse computer vision tasks, surpassing traditional CNNs in many instances [20]. Distinct from CNNs, which employ local convolutions to capture spatial information, ViTs utilize self-attention mechanisms [21] to simultaneously process both local and global contextual information. This attribute enables ViT networks to effectively capture intricate patterns and details, rendering them particularly suitable for medical image segmentation tasks that require a sufficient accurate delineation of complex structures [9,22,23,24,25]. Current ViT-improved segmentation networks in the literature are largely designed around a U-Net style architecture with self-attention layers. TransUNet [9] was introduced to address the bottleneck of UNet with ViT layers when processing high-level feature information. SwinUNet [22] was designed to utilize a promising shift-window-modified ViT [26] to construct a pure ViT-based UNet-style segmentation network. UNETR [23] introduced explored the ViT-based layer to tackle 3D medical semantic segmentation tasks.

The remarkable performance of both ViT- and CNN-based networks is possible mainly due to the availability of large volumes of high-quality data annotations. This need also constitutes a barrier to deploying advanced machine learning networks to clinical contexts.

Semisupervised learning (SSL) [6,24,27,28], and weakly supervised learning (WSL) [29,30,31], which aim to tackle the expensive cost of labeling data, have been explored to ViT and CNN, but their application in medical image segmentation still remains relatively underexplored, particularly in the context of noisy labels. The term noisy labels refers to inaccuracies and inconsistencies in the annotated ground truth data, and can significantly challenge network training and generalization [17,32,33]. In medical image segmentation, noisy labels are often inevitable due to factors such as interobserver variability, lack of experience of junior clinicians, and the sheer intricate nature of anatomical structures.

Figure 1 illustrates example CT spine images, corresponding ground truth segmentation masks, and simulated noisy labels. The annotation process may not output masks at a gold-standard level, but may rather generate labeled features that exhibit erosion or dilation of ideal contours, along with various elastic transformations. We refer to these alterations as noisy labels and conjecture their potential detrimental influence on the model’s performance. In actual clinical settings, these deviations from the gold standard are likely to be less dramatic.

By incorporating denoising techniques into the segmentation network, it becomes possible to develop noise-robust networks capable of effectively segmenting medical images in the presence of unreliable annotations. Consequently, this could lead to improved segmentation accuracy and enhanced clinical applicability, contributing to advancements in medical image analysis and diagnosis. Further investigation of ViT-based architectures, combined with sophisticated denoising techniques, may yield transformative outcomes in medical image segmentation, overcoming the limitations posed by noisy labels and facilitating more accurate and reliable diagnostic tools. The detailed noise-robust ViT-modified encoder–CNN decoder network proposed in this paper, named NR-UNet, is introduced in Section 2. The demonstration code is accessible at https://github.com/ziyangwang007/VIT4UNet.

There are four categories of contributions to this work:

1.

Inspired by the previous success of CNN and ViT, a ViT-based modified encoder and CNN-based decoder UNet-style segmentation network is proposed.

2.

To simulate real clinical scenarios, noise is manually added to the ground truth to create noisy labels, constructing a CT spine segmentation dataset with noisy labels for evaluation purposes.

3.

A simple and efficient adaptive denoising learning (ADL) is proposed for segmentation network to achieve a noise-robust segmentation framework.

4.

The proposed segmentation network with ADL attains competitive performance against other baseline methods across various evaluation metrics under the same data conditions with both accurate and noisy label sets.

2. Methods

The architecture of NR-UNet is depicted in Figure 2. This symmetrical architecture comprises encoders and decoders, denoted as ${\mathit{En}}_i$ and ${\mathit{De}}_i$, respectively, where $i\in [1,2,3,4]$ indicates the level of encoders and decoders. The transfer of feature maps is conducted between each level of $\mathit{En}$ and $\mathit{De}$, following the approach proposed by [1]. The CNN-based en/decoders consist of two-layer CNNs and batch normalization (BN) with up- or downsampling. The ViT-based encoders are designed to extract hidden high-level feature information in ${\mathit{En}}_4$ and use a bottleneck structure to further enhance feature learning, and 2-layer ViT is designed in each block. The ViT layer includes layer normalization (LN) [34], multihead self-attention (MSA), and multilayer perceptron (MLP), as described in [21]. The proposed ADL is briefly sketched in Figure 3, where a certain number of noisy labels are able to be detected and removed. We provide details on the segmentation network and adaptive denoising learning strategy in the sections below.

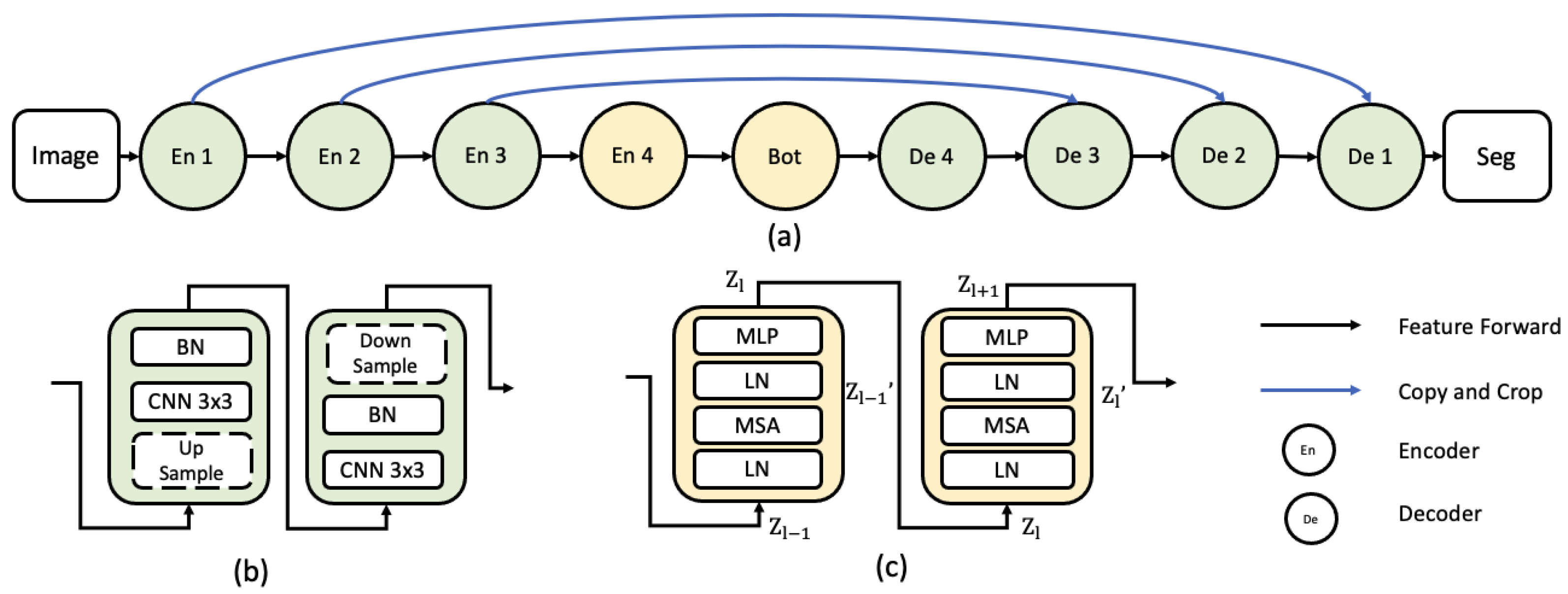
2.1. Vision Transformer Layer

In a ViT layer, an input feature map is first partitioned into a fixed number of non-overlapping patches. These patches are subsequently linearly embedded into a flattened vector, which serves as the input token for the transformer. A learnable positional encoding is added to the input token to incorporate spatial information. The encoded input tokens are then fed through a series of ViT layers, each comprising a MSA and a MLP. The MSA enables the model to capture long-range dependencies among input tokens, while the MLP refines the features extracted by the MSA. LN is applied within the ViT layers to stabilize the training process and promote model convergence. The basic ViT-based layer pipeline is shown in Figure 2c, and is described by the following six steps:

(i)

The process of tokenization converts the input image x of dimensions $H\times W$ into a sequence of flattened 2D patches denoted ${\{x_i^p\in {\mathbb{R}}^{P^2·C}\}}_{i=1,\cdots ,N}$. Each patch measures $P\times P$, and $N=\frac{H\times W}{P^2}$ accounts for the total number of image patches, thereby defining the input sequence length.

(ii)

These patches are subsequently mapped onto vectors $x^p$ in a latent D-dimensional embedding space using a trainable linear projection. To capture the spatial information inherent in the patches, learnable position embeddings are added to the patch embeddings, as follows:

$$z^0=[x_1^{p}E;x_2^{p}E;\cdots ;x_N^{p}E]+E_{\mathrm{pos}}$$

(1)

In this expression, $E\in {\mathbb{R}}^{(P^2·C)\times D}$ represents the patch embedding projection, $E_{\mathrm{pos}}\in {\mathbb{R}}^{N\times D}$ is the position embedding, and $z^0$ provides the feature map input to the first ViT layer.

(iii)

Comprising L layers, each incorporating an MSA and a MLP, the transformer encoder’s output from the $l^{th}$ layer is illustrated as

$$z_l^{{}^{\prime }}=\mathrm{MSA}\left(\mathrm{LN}\left(z_{l-1}\right)\right)+z_{l-1}$$

(2)

$$z_l=\mathrm{MLP}\left(\mathrm{LN}\left(z_l^{{}^{\prime }}\right)\right)+z_l^{{}^{\prime }}$$

(3)

where $\mathrm{LN}(·)$ stands for the layer normalization operator, and $z_l$ stands for the encoded image.

(iv)

The MLP is a fully connected feedforward neural network that consists of multiple layers of nodes. In the proposed NR-UNet, the MLP refines the features extracted by the MSA mechanism. The MLP involves two linear layers interspersed with a GELU activation function [35], defined as

$$\mathrm{MLP}\left(z_l^{{}^{\prime }}\right)={\mathrm{Linear}}_2\left(\mathrm{GELU}\left({\mathrm{Linear}}_1\left(z_l^{{}^{\prime }}\right)\right)\right)$$

(4)

In this equation, ${\mathrm{Linear}}_1$ and ${\mathrm{Linear}}_2$ denote the first and second linear layers. The subsequent MSA is composed of multiple self-attention heads that operate in parallel to capture different aspects of the input tokens. Each self-attention head calculates attention scores employing Query (Q), Key (K), and Value (V) matrices, which are derived from the input tokens via linear transformations:

The matrices Query (Q), Key (K), and Value (V) are derived from the input tokens $z_l^{{}^{\prime }}$ through linear transformations:

$$Q=z_l^{{}^{\prime }}{W}_Q, K=z_l^{{}^{\prime }}{W}_K, V=z_l^{{}^{\prime }}{W}_V$$

(5)

where $W_Q$, $W_K$, and $W_V$ are learnable weight matrices [21].

(v)

The attention scores are computed by taking the dot product of the Q and K matrices, subsequently scaling and normalizing through softmax:

$$\mathrm{Attention}(Q,K,V)=\mathrm{softmax}\left(\frac{Q{K}^{\top }}{\sqrt{d_k}}\right)V$$

(6)

where $d_k$ denotes the dimensionality of the Key vectors.

(vi)

The individual outputs of the self-attention heads are concatenated and linearly transformed to generate the final output of the MSA:

$$\mathrm{MSA}\left(z_l^{{}^{\prime }}\right)=\mathrm{Concat}({\mathrm{Head}}_1,\cdots ,{\mathrm{Head}}_H)W_O$$

(7)

where ${\mathrm{Head}}_i$ is the output of the i-th self-attention head, H is the total number of heads, and $W_O$ is another learnable weight matrix.

2.2. ViT Encoder to CNN Decoder

Drawing inspiration from [1,9,22], our proposed NR-UNet architecture combines a ViT-improved encoder with a CNN-based decoder into a hybrid segmentation network. The model initially employs a CNN for feature extraction, thereby creating an insightful feature map from the input image. However, instead of using raw images directly, it performs patch embedding on $1\times 1$ patches extracted from the CNN feature map. This methodological variation amplifies the importance of intermediate high-resolution CNN feature maps within the decoder pathway.

As outlined in [9], our model utilizes a cascaded upsampling path (CUP), which involves a series of upsampling actions to decode the concealed features, ultimately generating the final segmentation mask. The hidden feature sequence $z_L\in {\mathbb{R}}^{HW/P^2\times D}$ is first reshaped to $\frac{H}{P}\times \frac{W}{P}\times D$ dimensions, after which we construct the CUP by progressively stringing together several upsampling blocks. The purpose of these blocks is to methodically achieve full resolution, moving from $\frac{H}{P}\times \frac{W}{P}$ to $H\times W$. Each upsampling block consists of a $2\times$ upsampling operator, a 3 × 3 convolution layer, and a ReLU layer, executed in that order.

2.3. Noisy Labels

In order to evaluate the effectiveness of our proposed ADL in handling noisy labels, we simulate a scenario with imprecise annotations by introducing artificial noise into a dataset whose initial annotations are considered correct. The process of simulating noisy labels in our dataset is as follows:

a

Starting with a dataset containing perfect annotations, we randomly select a subset of annotations to be altered, and the ratio of noisy labels to the whole dataset is denoted as $\beta \in [0,1]$.

b

For the selected annotations, we apply image-processing operations such as erosion, dilation, and elastic transformation to generate noisy labels. These operations mimic the types of noise that could be present in real-world clinical scenarios, where annotations might be imperfect due to various factors. Erosion and dilation are fundamental morphological operations. Let A be the binary annotation mask and B be a structuring element. The erosion (⊖) and dilation (⊕) operations can be defined as

$$(A\ominus B)(x,y)=\underset{(i,j)\in B}{min}A(x-i,y-j)$$

(8)

$$(A\oplus B)(x,y)=\underset{(i,j)\in B}{max}A(x+i,y+j)$$

(9)

where $(x,y)$ represents the pixel coordinates in the image.

Elastic transformation is a nonlinear deformation technique that can simulate the local warping of shapes. Given an image $I(x,y)$ and two displacement fields $\mathsf{\Delta }x(x,y)$ and $\mathsf{\Delta }y(x,y)$, which are generated by Gaussian smoothing of random fields, an elastic transformation can be defined as

$$I_{\mathrm{transformed}}(x,y)=I(x+\alpha \mathsf{\Delta }x(x,y),y+\alpha \mathsf{\Delta }y(x,y))$$

(10)

where $\alpha$ is the deformation scale factor.

c

The altered annotations are then used to replace their corresponding original annotations in the dataset, creating a new dataset with a mix of perfect and noisy labels. By simulating noisy labels in this manner, we create a dataset that can challenge experiments, enabling us to assess the noise-robustness of our proposed method and compare its performance against existing high-performing techniques.

2.4. Adaptive Denoising Learning Strategy

In real-world applications, labels are inherently noisy, in the sense that they do not represent a precise ground truth. Our adaptive denoising learning (ADL) strategy is fairly straightforward, and yet efficient. To simulate different scenarios involving noise labels, a proportion $\beta$ of the provided ground truth masks in the training data (which are accurate) are replaced with noisy labels generated synthetically, as described in Section 2.3. These labels exhibit erosions, dilations, or elastic transformations, which are illustrated in Figure 1.

Drawing inspiration from O2U-Net [36], in every training epoch, we log the discrepancy between each prediction and its corresponding ground truth label. Labels accruing higher losses are more likely to be considered noisy, and are subsequently discarded at the epoch’s conclusion.

During the training process, our ADL strategy identifies and discards a specific quantity of labels with high loss values. As illustrated in Figure 3, a considerable quantity of noisy labels are detected and eliminated at the beginning of the training iteration; this quantity decreases gradually, as the training progresses. This reflects the transition of the training process from a state of underfitting to overfitting [17]. The number $N\left(t\right)$ of labels identified and removed at each epoch is calculated as

$$N\left(t\right)=\frac{\beta y}{k^2}(k-t)$$

(11)

In this equation, t corresponds to the current training epoch, $\beta$ represents the proportion of items in the training dataset subjected to noise, k stands for the total count of training epochs, and y indicates the total count of masks. By integrating ADL into the training process, we amplify the network’s robustness to noisy labels. This strategy, in turn, improves the model’s performance and clinical applicability.

3. Experiments and Results

3.1. Dataset

Our research makes use of a publicly available spine dataset, courtesy of the University of California Irvine Medical Centre’s School of Medicine and the National Institutes of Health [37]. This dataset includes CT scans from 10 individuals aged from 16 to 35 years. Each scan incorporates up to 600 slices of resolution 512 × 512 and interslice spacing of 1 mm. All images are normalized and resized to 256 × 256 pixels for uniformity. The dataset provides ground truth masks for each image, and a portion of these masks is subjected to noise (Section 2.3). Out of the 10 scans, 9 were used for training, which produced a total of 5043 images. The last scan, consisting of 552 images, was set aside for testing. Validation was conducted on 10% of the training data, ensuring no overlap occurred between the training and testing datasets.

3.2. Experimental Setup

The proposed NR-UNet was implemented using Python and Tensorflow, with experiments carried out on a system equipped with an Nvidia GeForce RTX 3090 GPU, with 24 GB memory, and an Intel CPU i9-10900K. In this experimental configuration, we utilized an input feature map of size $(256,256,1)$, with the number of CNNs on each layer of decoders set to 64, 128, 256, 512 for all U-shape encoder–decoder networks, incorporating two successive CNN layers within each encoder/decoder. With regards to the ViT-related design elements, we assigned an image patch-embedding dimension of 768, an MLP count of 1024, and 12 heads for the MSA. The bottleneck of the NR-UNet contained six ViT layers. Given that the downstream task was 2D image semantic segmentation (i.e., a per-pixel binary classification), the final layer was a 1 × 1 CNN layer. Runtimes for 50 epochs, including data transfer, ranged between 500 and 800 min. We opted for a training batch size of 4, and utilized the Adam optimizer, with a learning rate of ${10}^{-5}$. The chosen loss function relied on the Dice coefficient (Equation (12)), a frequently used metric for assessing overlap in semantic segmentation, particularly suited to managing the imbalance between a region of interest (ROI) and the background.

$${\mathcal{L}}_{\mathrm{Dice}}=1-\frac{2·{\sum }_{i=1}^N{y}_i\widehat{y}i}{{\sum }_{i=1}^N{y}_i+{\sum }_{i=1}^N{\widehat{y}}_i+\epsilon }$$

(12)

where $\epsilon$ is a small positive constant (e.g., ${10}^{-8}$) added to the denominator to prevent division by zero, $y_i$ denotes the ground truth mask, ${\widehat{y}}_i$ represents the predicted segmentation mask, and N is the total number of pixels in the image. This experimental setup allowed us to thoroughly investigate the contribution of the proposed adaptive denoising learning strategy to the overall performance of the NR-UNet in the context of medical image segmentation.

3.3. Metrics

Beyond the Dice coefficient, we evaluated the performance of NR-UNet using an assortment of standard overlap metrics: intersection over union (IoU), accuracy (Acc), precision (Pre), recall (Rec), and specificity (Spe). These evaluation measures are detailed in Equation (13), where TP, TN, FP, and FN represent the number of pixels classified as true positive, true negative, false positive, or false negative. The IoU measures the extent of the overlap between the predictions of our model and the ground truth; accuracy evaluates the overall correctness of the model’s predictions, with high accuracy in a medical context potentially signifying a model’s efficacy in distinguishing between different classes—a crucial factor for disease detection and treatment planning; precision and recall are crucial performance indicators that reflect a model’s proficiency in accurately identifying positive cases and evading false negatives, respectively. In the realm of medical image analysis, high precision ensures that positive detections are indeed relevant, thereby mitigating risks associated with false positives. Simultaneously, high recall improves the model’s capability to spot all areas of concern, minimizing overlooked detections. Specificity, on the other hand, quantifies the model’s capacity to correctly identify negative cases. Clinically, high specificity can curtail false-positive rates, thus preventing patients from undergoing unwarranted further examinations or treatments. Through the implementation of these diverse metrics, our intention is to offer an exhaustive evaluation of the proposed model’s performance, substantiating its potential value in clinical scenarios.

$$\begin{array}{cc}\hfill Dice& \hfill =\frac{2TP}{2TP+FP+FN}\hfill \\ \hfill IoU& \hfill =\frac{TP}{TP+FP+FN}\hfill \\ \hfill Accuracy& \hfill =\frac{TP+TN}{TP+TN+FP+FN}\hfill \\ \hfill Precision& \hfill =\frac{TP}{TP+FP}\hfill \\ \hfill Recall& \hfill =\frac{TP}{TP+FN}\hfill \\ \hfill Specificity& \hfill =\frac{TN}{TN+FP}\hfill \end{array}$$

(13)

3.4. Experiments in a Noise-Free Setup

Figure 4 illustrates eight examples of raw images, and the predicted result of a number of different networks, all training on accurate labels: UNet [1], residual UNet [13], dense UNet [13], MultiResUnet [19], LinkNet [38], FPN [39], UNet++ [2], UNet3+ [18], VNet [10], RARUNet [17], and QAPNet [3]. Our NR-UNet was compared with these for a setting of $\beta$ = 0 (hence, also training on accurate labels).

Batch normalization [40] and Dropout [41] were deployed after CNN layers for all UNet-based baseline methods for a fair comparison. A quantitative comparison of NR-UNet against the other ten baseline methods is given in

Table 1. Direct comparison against existing algorithms.

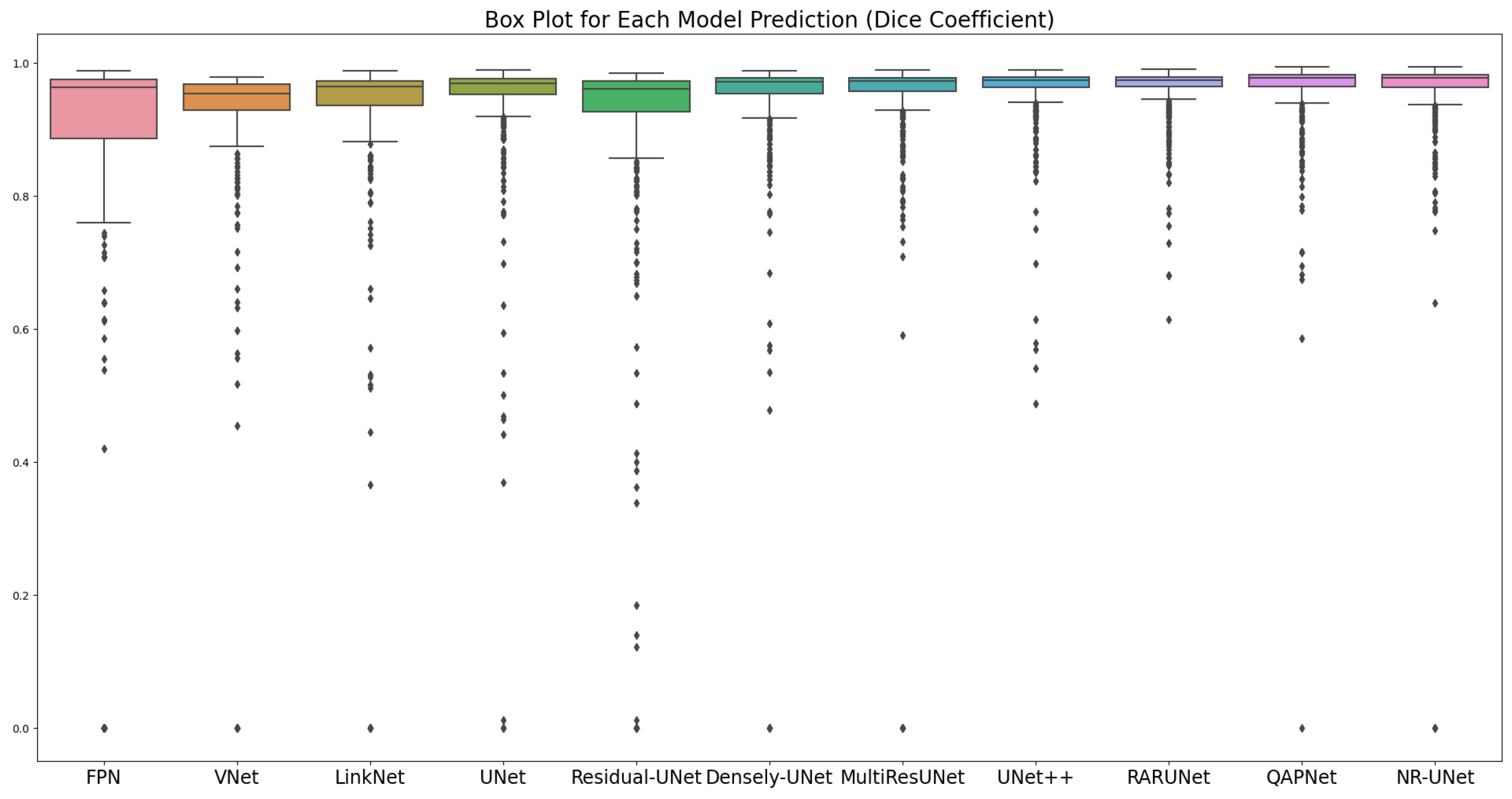
Network $\left(\mathit{\beta }=0\right)$	Dice	IoU	Acc	Pre	Rec	Spe	Par${10}^6$
FPN [39]	0.9373	0.8821	0.9944	0.9191	0.9563	0.9961	17.59
Residual UNet [13]	0.9416	0.8897	0.9949	0.9481	0.9353	0.9976	9.90
VNet [10]	0.9446	0.8950	0.9950	0.9202	0.9703	0.9961	14.74
LinkNet [38]	0.9524	0.9091	0.9959	0.9662	0.9390	0.9985	20.32
UNet [1]	0.9580	0.9193	0.9963	0.9619	0.9541	0.9983	8.64
Dense UNet [13]	0.9612	0.9252	0.9966	0.9600	0.9624	0.9982	15.47
MultiRes UNet [19]	0.9644	0.9312	0.9969	0.9633	0.9655	0.9983	7.76
UNet++ [2]	0.9659	0.9340	0.9970	0.9676	0.9642	0.9985	8.86
RARUNet [17]	0.9674	0.9369	0.9972	0.9721	0.9629	0.9987	11.79
QAPNet [3]	0.9690	0.9399	0.9973	0.9715	0.9666	0.9987	15.14
NR-UNet	0.9703	0.9424	0.9974	0.9740	0.9667	0.9988	182.90

. The best results are highlighted in bold.

In Figure 5, we present the box plot of the Dice coefficient for each model prediction. The Dice coefficient quantifies the performance of each model by assessing the overlap between the model prediction and the ground truth. The coefficients range between 0 and 1, where 1 signifies a perfect overlap between the prediction and the ground truth, and 0 signifies no overlap. The variation in box heights and positions provides an overview of the performance differences across the models. A higher median and a narrower box suggest that a model has a high overall performance and a consistent prediction quality across different slices. Additionally, pairwise t-tests were conducted to determine the statistical significance of the differences in Dice coefficients between NR-UNet and UNet, where the t-statistic is $2.64$ and the p-value is $0.0085$. A low p-value (typically < 0.05) indicates a statistically significant difference in performance between two models. A comparison of the training progress of NR-UNet against UNet is depicted in Figure 6. The line charts illustrate the evolution of loss on the training set (in blue) and the validation set (in red). On the y-axis, each type of loss is plotted against the number of training epochs on the x-axis.

3.5. Experiments in a Noisy Setup

To evaluate the impact of the proposed ADL contribution, our core experiments assessed the algorithms’ robustness to noise in the annotations.

Table 2. Ablation studies of adaptive denoising learning via various segmentation networks under different proportions of noisy labels.

Proportion ($\mathit{\beta }$)	Network	ADL	Dice	IoU
75%	Residual UNet	✗	0.7962	0.6614
		✓	0.8210	0.6964
75%	UNet	✗	0.8004	0.6672
		✓	0.8337	0.7148
75%	NR-UNet	✗	0.8196	0.6943
		✓	0.8466	0.7340
50%	Residual UNet	✗	0.8179	0.6919
		✓	0.8453	0.7321
50%	UNet	✗	0.8188	0.6932
		✓	0.8564	0.7489
50%	NR-UNet	✗	0.8362	0.7185
		✓	0.8832	0.7908
25%	Residual UNet	✗	0.9002	0.8185
		✓	0.9213	0.8541
25%	UNet	✗	0.9084	0.8322
		✓	0.9303	0.8697
25%	Dense UNet	✗	0.9096	0.8342
		✓	0.9284	0.8664
25%	NR-UNet	✗	0.9101	0.8350
		✓	0.9532	0.9106

specifically examines the effect of the ADL strategy. `Proportion’ represents the percentage $\beta$ of noisy labels introduced into the training dataset, with various other proportions also tested beyond those shown in the table (but omitted here to avoid clutter). The ‘Network’ column demonstrates that different networks were employed for training separately, and the presence of a module implementing the ADL strategy (annotated with check marks) improves performance across the board. Whilst in Table 1, the various networks performed similarly, it is evident from Table 2 that our proposed ADL strategy mitigates the impact of noisy labels, bringing the segmentation performance to levels that can be considered acceptable in many practical applications. Eight example predictions by NR-UNet under different data situations (i.e., different ratio $\beta$ of noisy labels) are sketched in Figure 7. In this setup, NR-UNet is noticeably more effective than its counterparts. By comparing the outcomes of different algorithms and varying the proportion of noisy labels introduced into the training dataset, we gain valuable insights into the robustness and adaptability of our method in addressing the challenges posed to medical image segmentation tasks by noisy annotations.

4. Conclusions

Our research into the impact of noise in annotation labels suggests that for certain semantic segmentation tasks, near-perfect hand-drawn contours are not a strict necessity. Through our experiments, we show that the proposed NR-UNet, coupled with the ADL strategy, performs competitively under varying levels of label noise.

While the results from the proposed NR-UNet and ADL strategy are promising, there is room for further improvement. As part of our future work, we plan to broaden the applicability of the NR-UNet and ADL strategy to other medical imaging modalities, such as MRI and ultrasound. We will also assess how generalizable they are across a wider range of clinical applications. These methods can also be used in conjunction with weakly supervised learning tasks, improving the reliability of safety-critical scenarios like medical screening or diagnosis on the strength of minimal hand-annotation requirements.