Decreasing the Rail Potential of High-Speed Railways Using Ground Wires
Abstract
:Featured Application
Abstract
1. Introduction
2. Theoretical Review
3. Rail Potential Problem in High-Speed Railways
3.1. Characteristics
- Large train current. In a 350 km/h EMU with 16 cars, the peak current of the train can exceed 800 A, which is about twice the current of the most powerful electric locomotive.
- Large short-circuit current in traction networks. In China, most substations of high-speed railways obtain electric power from 220 kV grids, which normally have a high short-circuit level. When a fault takes place near the substation, the short-circuit current will be limited only by the impedance of the traction transformer. For a 63 MVA single-phase transformer with a 10.5% impedance, this current will reach up to 20 kA.
- High rail–ground leakage resistance. High-speed railways mainly adopt a ballastless track, which normally has high rail–ground leakage resistance. As an example, in terms of the Japanese material, a value of 100~500 Ω·km has been reported for the Shinkansen, compared to 2~5 Ω·km for normal lines [19].
3.2. Possible Solutions
- Bonding the rails of different tracks sufficiently.
- Increasing the connections between the rail and PW (called CPW in some studies).
- Grounding the PW using OCS post foundations.
- Laying one or two directly buried bare wires, which are adequately connected to the rail and PW.
- Utilizing the foundation grounding resistance of various structures along the railway.
- Constructing a special grounding pole along the railway.
4. Electric Parameter Calculation
4.1. Calculation of Conductor Internal Impedance
4.2. Calculation of Impedance of Overhead Conductor–Earth Circuit
4.3. Electric Parameters of Directly Buried Ground Wires
4.4. Theory of Multiconductor Transmission Lines
5. Results
5.1. Network Conditions
- Two equal AT sections with a 15 km interval;
- A 55 kV source with a 10,000 MVA short-circuit level;
- A 90 MVA single-phase transformer with a 10.5 percent impedance;
- AT leakage impedance of 0.1 + j0.45 Ω;
- Substation and section post grounding resistance of 0.5 Ω;
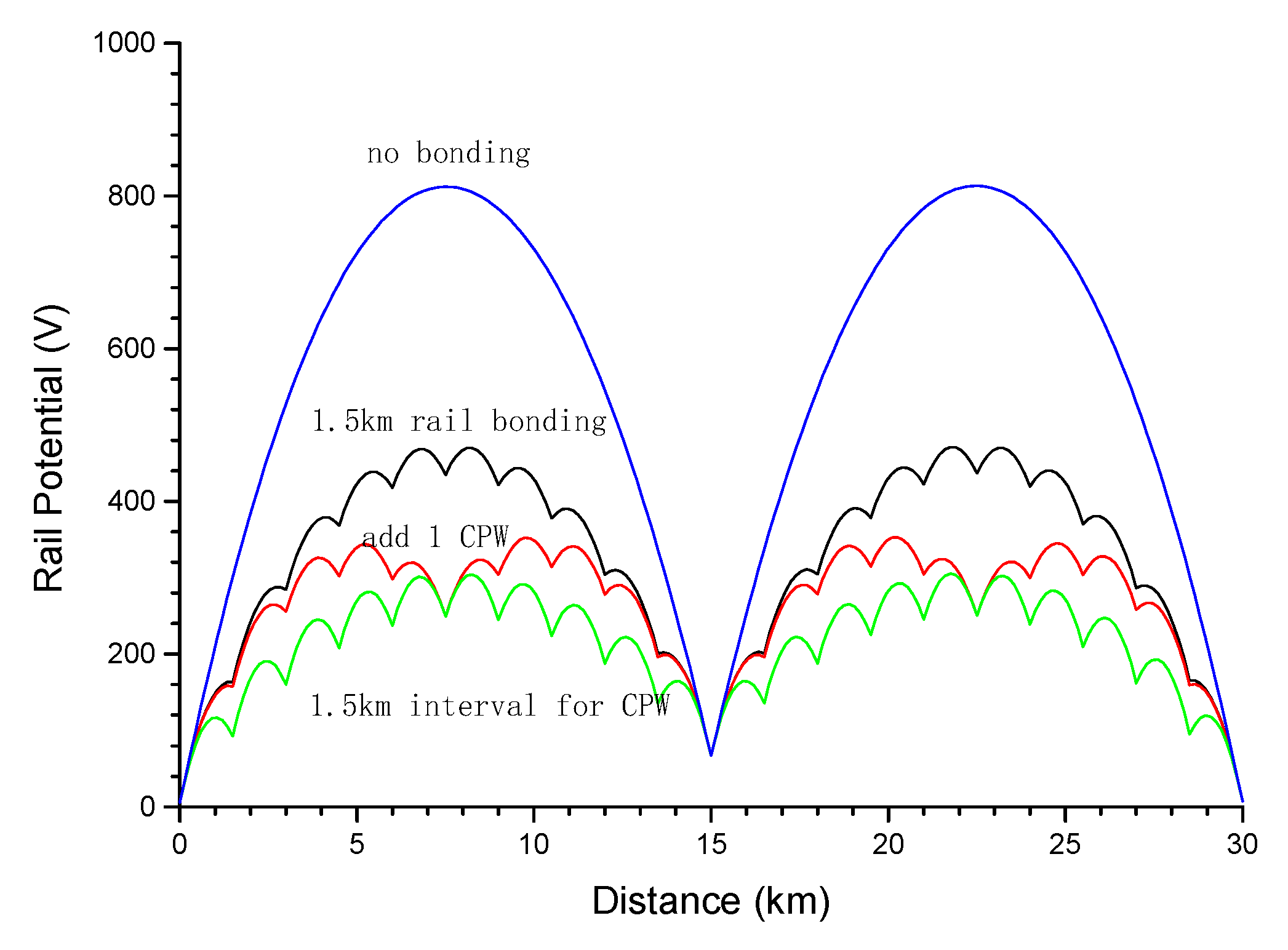
- Interval of 1.5 km for the cross-bonding of two track rails;
- Rail–ground leakage resistance of 100 Ω·km;
- Earth resistivity of 100 Ω·m;
- A PW insulated with an OCS post (see Figure 5 for OCS conductors);
- Train current of 1000 A with a power factor of 0.97.


5.2. Effect of Bonding
5.3. Rail–Ground Leakage Resistance
5.4. OCS Post Resistance
5.5. Effect of Directly Buried Ground Wire
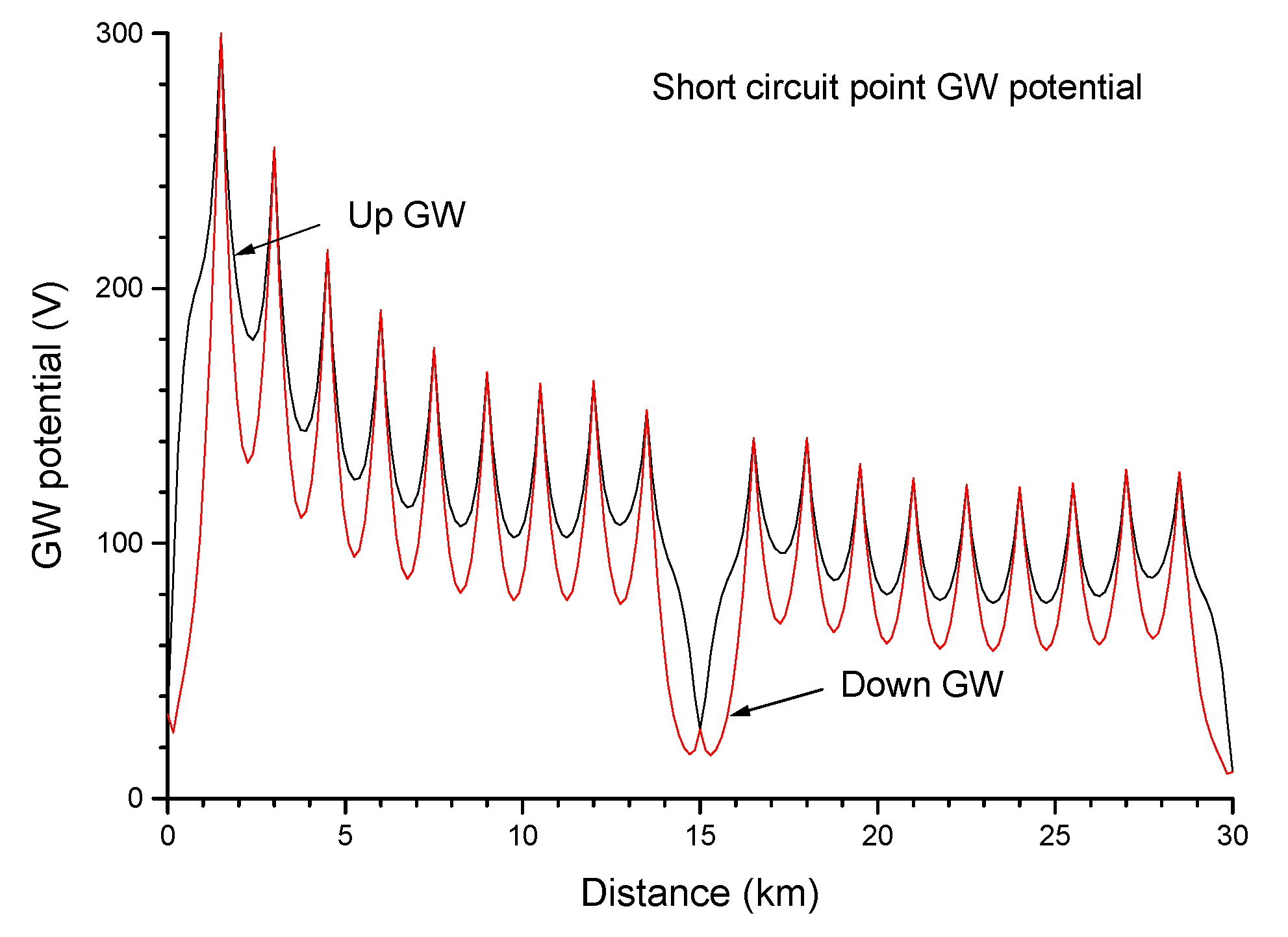
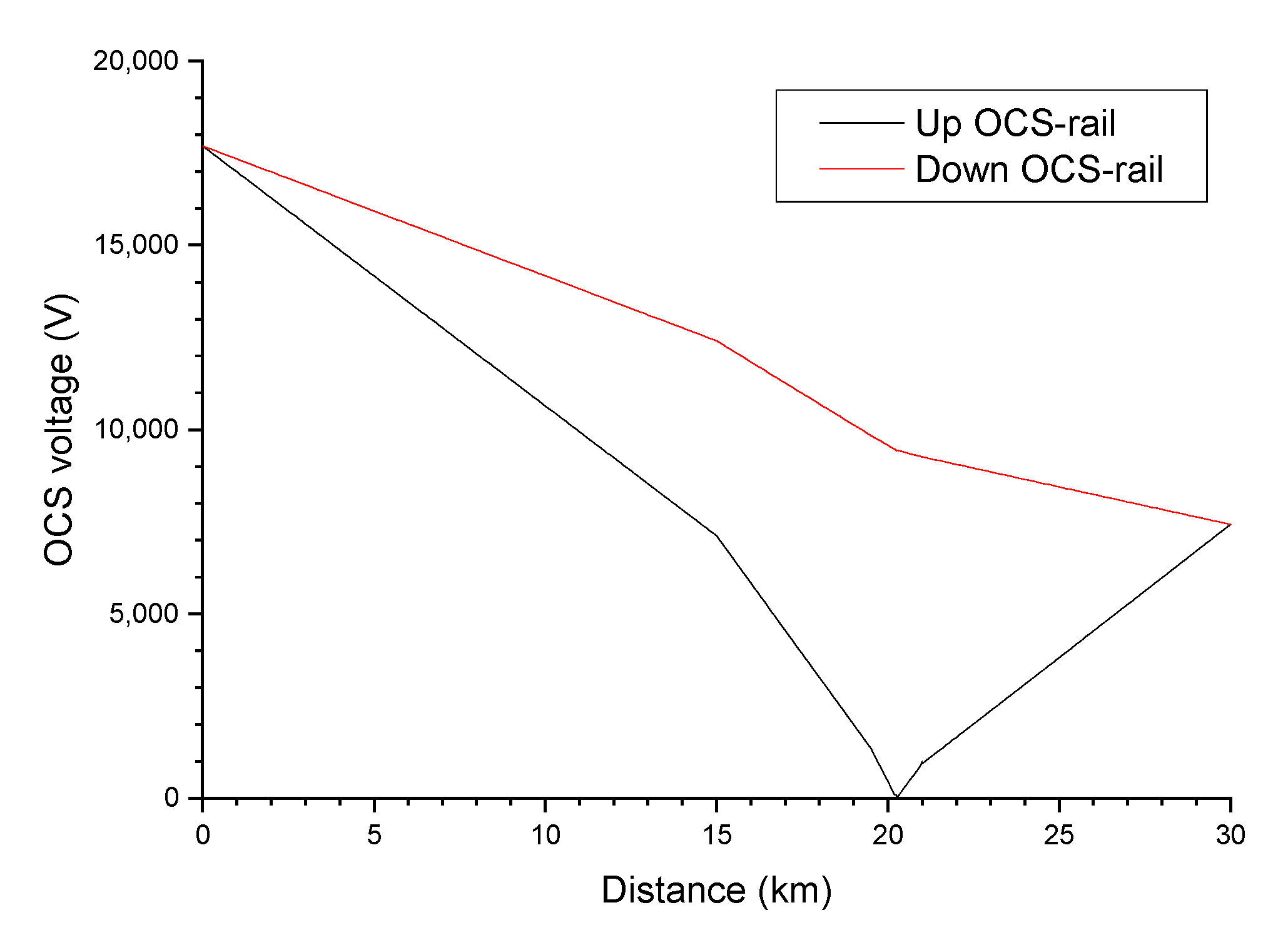
5.6. T–R Short Circuit
5.7. T–PW Short Circuit
6. Field Test
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| AT | auto-transformer |
| BT | booster transformer |
| CC | coaxial cable |
| CPW | connector of protective wire |
| CW | contact wire |
| EMI | electromagnetic interference |
| EMU | electric multiple unit |
| GW | ground wire |
| Iθ | current and phase angle |
| OCS | overhead catenary system |
| MW | messenger wire |
| NF | negative feeder |
| PDL | passenger dedicated line |
| PF | positive feeder |
| PQ | active power and reactive power |
| PW | protection wire |
| T–PW | trolley (contact wire)–protection wire |
| T–R | trolley (contact wire)–rail |
| T–R+NF | trolley (contact wire)–rail + negative feedback |
References
- Gu, J.; Yang, X.; Zheng, T.Q.; Shang, Z.; Zhao, Z.; Guo, W. Negative Resistance Converter Traction Power System for Reducing Rail Potential and Stray Current in the Urban Rail Transit. IEEE Trans. Transp. Electrif. 2021, 7, 225–239. [Google Scholar] [CrossRef]
- Huang, K.; Liu, Z.; Zhu, F.; Deng, Y. Grounding Behavior and Optimization Analysis of Electric Multiple Units in High-Speed Railways. IEEE Trans. Transp. Electrif. 2021, 7, 240–255. [Google Scholar] [CrossRef]
- Natarajan, R.; Imece, A.; Popoff, J.; Agarwal, K.; Meliopoulos, P.S. Analysis of grounding systems for electric traction. IEEE Trans. Power Deliv. 2001, 16, 389–393. [Google Scholar] [CrossRef]
- Kiesling, F.; Puschman, R.; Schmieder, A. Contact Lines for Electric Railways, Planning Design Implementation; Siemens: Munich, Germany, 2001. [Google Scholar]
- Biesenack, H.; George, G.; Hofmann, G.; Schmidder, A. Electric Railway Traction Power Supply Systems (Translated by Guangfeng Qi); China Railway Press: Beijing, China, 2019. [Google Scholar]
- Gu, J.; Yang, X.; Zheng, T.Q.; Xia, X.; Zhao, Z.; Chen, M. Rail Potential and Stray Current Mitigation for Urban Rail Transit With Multiple Trains Under Multiple Conditions. IEEE Trans. Transp. Electrif. 2022, 8, 1684–1694. [Google Scholar] [CrossRef]
- Wang, M.; Yang, X.; Zheng, T.Q.; Ni, M. DC Autotransformer-Based Traction Power Supply for Urban Transit Rail Potential and Stray Current Mitigation. IEEE Trans. Transp. Electrif. 2020, 6, 762–773. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, G.; Qiu, R.; Liu, Z.; Yao, N. Distribution Correction Model of Urban Rail Return System Considering Rail Skin Effect. IEEE Trans. Transp. Electrif. 2021, 7, 883–891. [Google Scholar] [CrossRef]
- Chen, M.; Fu, H.; Xie, C.; Liu, W.; Xu, W. Analysis of Rail Potential Characteristics of AC/DC Dual-system Traction Power Supply System. Xinan Jiaotong Daxue Xuebao J. Southwest Jiaotong Univ. 2022, 57, 729–736. [Google Scholar] [CrossRef]
- Kaleybar, H.J.; Brenna, M.; Foiadelli, F.; Fazel, S.S.; Zaninelli, D. Power Quality Phenomena in Electric Railway Power Supply Systems: An Exhaustive Framework and Classification. Energies 2020, 13, 6662. [Google Scholar] [CrossRef]
- Song, S. Study on the Feature of Running-through Earth Wire and Impact on Traction Currents Distribution in High-speed Railway; Beijing Jiaotong University: Beijing, China, 2017. (In Chinese) [Google Scholar]
- Yang, B. Comprehensive Simulation of AT Traction Power Supply and Integrated Grounding System; Beijing Jiaotong University: Beijing, China, 2014. (In Chinese) [Google Scholar]
- Wu, G.; Gao, G.; Dong, A.; Zhou, L.; Cao, X.; Wang, W.; Wang, B.; Tang, Y.; Chen, J. Study on the Performance of Integrated Grounding Line in High-Speed Railway. IEEE Trans. Power Deliv. 2011, 26, 1803–1810. [Google Scholar] [CrossRef]
- Ning, B.; Tang, T.; Dong, H.; Wen, D.; Liu, D.; Gao, S.; Wang, J. An Introduction to Parallel Control and Management for High-Speed Railway Systems. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1473–1483. [Google Scholar] [CrossRef]
- Guemes, J.A.; Hernando, F.E. Method for calculating the ground resistance of grounding grids using FEM. IEEE Trans. Power Deliv. 2004, 19, 595–600. [Google Scholar] [CrossRef]
- Guemes-Alonso, J.A.; Hernando-Fernandez, F.E.; Rodriguez-Bona, F.; Ruiz-Moll, J.M. A practical approach for determining the ground resistance of grounding grids. IEEE Trans. Power Deliv. 2006, 21, 1261–1266. [Google Scholar] [CrossRef]
- Huang, W.; He, Z.; Hu, H.; Wang, Q. Study on Distribution Coefficient of Traction Return Current in High-Speed Railway. Energy Power Eng. 2013, 5, 1253–1258. [Google Scholar] [CrossRef]
- Riordan, J. Current propagation in electric railway propulsion systems. AIEE Trans. 1932, 51, 1011–1019. [Google Scholar] [CrossRef]
- Watanabe, H.; Mochinaga, Y. Rail potential and countermeasures for rail potential suppression of electric railways. Railw. Tech. Res. Rep. 1978. [Google Scholar]
- Qi, G.; Xin, C. Voltage and Current Distribution of Rail Circuit and the Integrated Grounding System for High Speed Railway Traction Network; Southwest Jiaotong University Press: Chengdu, China, 2012. [Google Scholar]
- Zhao, T.; Wu, M. Electric power characteristics of all-parallel AT traction power supply system. In Proceedings of the 2011 International Conference on Transportation, Mechanical, and Electrical Engineering (TMEE), Changchun, China, 16–18 December 2011. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, M.; Liu, Q. A Novel Power Flow Algorithm for Traction Power Supply Systems Based on the Thévenin Equivalent. Energies 2018, 11, 126. [Google Scholar] [CrossRef] [Green Version]
- Mingli, W.; Yu, F. Numerical calculations of internal impedance of solid and tubular cylindrical conductors under large parameters. IEEE Proc. Gener. Transm. Distrib. 2004, 151, 67–72. [Google Scholar] [CrossRef]
- Carson, J.R. Wave propagation in overhead wires with ground return. Bell Syst. Tech. J. 1926, 5, 539–554. [Google Scholar] [CrossRef]
- PoIlaczek, F. Uber das Feld einer unendlich langen wechselstrom-durchflossenen Einfachleitung. Elekt. Nachr. Tech. 1926, 3, 339–359. (In German) [Google Scholar]
- Dommel, H.W. EMTP Theory Book, 2nd ed.; Microtran Power System Analysis Corporation: Vancouver, BC, Canada, 1992. [Google Scholar]
- CCITT. Directives Concerning the Protection of Telecommunication Lines against Harmful Effects from Electric Power and Electrified Railway Lines; International Telecommunication Union: Geneva, Switzerland, 1989; Volumes I and IV. [Google Scholar]
- Sunde, E.D. Earth Conduction Effects in Transmission Systems; D. Van Nostrand Company, Inc.: New York, NY, USA, 1949. [Google Scholar]

















| Wire Type | Maximal Rail Potential | Maximal GW Current |
|---|---|---|
| TJ25 | 89.7 V | 74.8 A |
| TJ35 | 88.5 V | 94.2 A |
| TJ50 | 87.3 V | 118 A |
| TJ70 | 86.4 V | 142 A |
| TJ95 | 85.9 V | 162 A |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, G.; Song, K. Decreasing the Rail Potential of High-Speed Railways Using Ground Wires. Appl. Sci. 2023, 13, 7944. https://doi.org/10.3390/app13137944
Wu G, Song K. Decreasing the Rail Potential of High-Speed Railways Using Ground Wires. Applied Sciences. 2023; 13(13):7944. https://doi.org/10.3390/app13137944
Chicago/Turabian StyleWu, Guanting, and Kejian Song. 2023. "Decreasing the Rail Potential of High-Speed Railways Using Ground Wires" Applied Sciences 13, no. 13: 7944. https://doi.org/10.3390/app13137944
APA StyleWu, G., & Song, K. (2023). Decreasing the Rail Potential of High-Speed Railways Using Ground Wires. Applied Sciences, 13(13), 7944. https://doi.org/10.3390/app13137944






