Obtaining the Effective Dielectric Permittivity of a Conducting Surface in the Terahertz Range via the Characteristics of Surface Plasmon Polaritons

Featured Application

Surface plasmon refractometry of conducting surfaces applied in terahertz plasmonic integrated circuits and communication lines.

Abstract

With the intensive development of data transmitting and processing devices in the terahertz (THz) frequency range, an important part of which are integrated plasmonic components and communication lines, it becomes necessary to measure correctly the optical constants of their conductive surfaces. In this paper, we describe a reliable method for determining the effective permittivity ε_m of a metal surface from the measured characteristics (refractive and absorption indices) of THz surface plasmon polaritons (SPPs). The novelty of the method is the conduction of measurements on a metal surface with a dielectric layer of subwavelength thickness, suppressing the radiative losses of SPPs, which are not taken into account by the SPP dispersion equation. The method is tested on a number of flat “gold sputtering–zinc sulfide layer–air” structures with the use of the THz radiation (λ₀ = 141 μm) from the Novosibirsk free electron laser (NovoFEL). The SPP characteristics are determined from interferograms measured with a plasmon Michelson interferometer. It is found that the method allows a significant increase in the accuracy of the ε_m in comparison with measurements on the same metal surface without a dielectric layer.

1. Introduction

The value of the dielectric permittivity of the surface of metal and the metallized elements of optical circuits may differ significantly from that calculated by the Drude model, especially in the infrared (IR) and terahertz (THz) ranges, where the reflectivity of noble metals tends to 100% and the anomalous skin effect manifests itself in a weak form [1,2]. In addition, in the THz range, the reflectivity of a metal surface (directly related to its dielectric constant) strongly depends on the quality and preparation of the mirror surface [3,4,5]. Therefore, in order to model correctly the operation of optical systems, it is necessary to use a measured value of the dielectric constant of the given reflective surface of metal (metallized) elements, not reference data.

For frequencies in the visible and near-IR ranges, a number of methods are known (reflectometry, polarimetry, conductometry, ellipsometry, Fourier spectroscopy, and calorimetry) for the determination of the dielectric permittivity of thin-layer and bulk conducting samples [6,7]. However, since a weakly pronounced anomalous skin effect occurs in metals at THz frequencies [8], their dielectric permittivity is no longer adequately described by the Drude model, and the results of its calculation via the above methods and Kramers–Kronig relations are of low reliability and in poor agreement [2,9]. For example, the results of measurements of reflectivity coincide with calculations based on conductometric measurements and Kramers–Kronig transformations only for very pure metals with minimal roughness and without oxide layers [3].

The waveguide method, in which a thin layer of the metal under study is deposited onto a plate dielectric waveguide, has proved to be more reliable in the far IR range [10]. However, with this method, the radiation interacts with the metal surface (within the skin layer, whose depth at THz frequencies does not exceed 100 nm [4]) adjacent to the plate, not bordering with the environment.

New possibilities for the refractometry of metals have opened up with the proposal to use surface plasmon polaritons (SPPs) for this purpose. SPPs are a kind of surface electromagnetic waves, which exist at the interface between media, one of which (metal) contains conduction electrons and has a negative dielectric permittivity [11]. The SPP characteristics (field distribution, attenuation coefficient, and phase velocity) are determined mainly by the optical constants of the metal and the ratio of the SPP frequency ω to the plasma frequency ω_p of the metal: the greater their difference (in the THz range, the ω_p is about three orders of magnitude greater than the ω), the lower the SPP decay and the closer the SPP phase velocity to the velocity of the corresponding plane wave in the medium adjoining the metal. This makes THz SPPs promising for use in high-speed lines for data transmission and processing [12,13,14]. With the discovery of the ability of a structured (by holes, relief, or other ordered inhomogeneities) metal surface to direct THz SPPs with high attenuation and high field concentration in the near-surface region, it became possible to create both active and passive microdevices in which information is carried by SPPs [15,16,17].

First, due to the attenuated total reflection (ATR) phenomenon, SPPs were applied to the determination of the optical constants of metals with high conductivity in the visible range, both transparent metal layers [18,19,20] and bulk samples [21]. Later on, a similar technique was tested in the mid-IR range for a transparent layer of palladium (a transition metal with a reflectivity of about 90%) [22]. However, for noble metals, because of their high conductivity, this technique is not applicable, since the propagation length L_s (the distance at which the wave intensity decreases by a factor of e ≈ 2.718) of infrared SPPs reaches several centimeters, which leads to the distortion of the reflected beam due to the re-emission of SPPs into the ATR prism.

A fundamentally new method for the SPP refractometry of metal surfaces in the IR range was proposed in [23]. The method includes the measurement of the propagation length of monochromatic SPPs over a bare metal surface (L₀) and the same surface containing a thin non-absorbing film (L) of known thickness d and refractive index n_layer and then the calculation of the optical constants of the metal using the L₀, L, d, and n_layer values and the radiation wavelength λ₀ via simultaneous solution of the SPP dispersion equations for two- and three-layer structures [11]. However, the reliability of the results obtained via such a technique is low, since it implicitly assumes (in the derivation of the dispersion equations) that the observed attenuation of the SPPs is due solely to the Joule losses in the metal, while in reality it also involves other significant mechanisms of dissipation of the SPP energy: scattering on the inhomogeneities and surface roughness, scattering on the granules of the near-surface layer of the metal, and heat losses due to the skin effect.

In the THz range, it was proposed to determine the dielectric permittivity of the surface of non-transparent metal objects from measured SPP characteristics such as the propagation length and depth of the field penetration into the environment adjacent to the metal [24]. However, this technique also does not take into account the influence of the SPP energy dissipation on the inhomogeneities of a real surface on both measured quantities, which reduces the reliability of the results.

New prospects for the refractometry of metals seemed to appear in connection with the development in the early 1990s of the THz time-domain spectroscopy (THz TDS) [25,26]. A significant advantage of the TDS method in comparison with those mentioned above lies in the measurement of not the power but rather the amplitude and phase of the probing THz radiation in the form of a picosecond pulse. After interaction with the sample, the broadband THz radiation is strobed by femtosecond light pulses (for the triggering of the THz radiation photodetector), which yields the time dependence of the photocurrent. The full inverse Fourier transform of this dependence makes it possible to obtain both the amplitude and phase spectrum of the reflected (transmitted) radiation in the entire THz range. The method has been tested for the THz refractometry in a transmission/reflection geometry of transparent metal layers (up to 120 nm thick) on terahertz spectrometers with a wide dynamic range and with the use of reference dielectric plates [27,28]. Along with the advantages, which are impressive at first glance, the TDS method has a number of disadvantages: (1) the impossibility of studying metal samples with roughness, at which the reflected radiation is scattered; (2) the strict requirements for the parallelism of the faces of the substrates; and (3) the long measurement time because of the need to average the measurement results over a large number of pulses because of the stringent requirements for the synchronism and identity of THz and light pulses [29].

There were attempts to combine the possibilities of the SPP refractometry and TDS spectroscopy for studying the surfaces of metals and semiconductors in the THz range [30,31,32]. A THz radiation pulse was converted into a pulse of broadband SPPs, and after they traveled a macroscopic distance over the sample, the SPPs were inversely converted into bulk radiation, which was detected, and the resulting photocurrent dependence on time was processed by the standard TDS method. However, test measurements have demonstrated the fundamental impossibility of integrating the capabilities of the SPP and TDS methods in real conditions. The main reason is parasitic radiation, both from the conversion (coupling) elements and from the SPP track (because of inhomogeneities on the real surface). As a result, the photodetector receives a “mixture” of bulk waves (BWs) from the conversion output element and the BWs generated at the coupling input element and on surface inhomogeneities on the SPP track. As a result, the signal-to-noise ratio and measurement accuracy become very low [32].

It is important to note that in all the works we know on the refractometry of metal surfaces, the metal dielectric permittivity value ε_m in the THz range, as determined from an analysis of the spectrum of radiation reflected from or transmitted through the studied metal layer, is two to three orders of magnitude greater than the εm values found from the characteristics of the SPPs for the same surface [2]. The main reason for this difference is apparently the different length of interaction of the radiation with the sample under study. Indeed, in the transmission/reflection geometry, the interaction length is equal to the sample thickness (in the case of transmission, the thickness of metal films is up to 120 nm), which is several times greater than the skin layer thickness δ_skin of metal (for gold, δ_skin ≈ 40 nm). The grainy surface structure, inherent in an evaporated metal [33,34], as well as the roughness and small defects on optically polished substrates, form an optically-inhomogeneous surface layer of the metal with a thickness comparable to δ_s [35]. The optical constants of such a layer can differ significantly from the constants of the metal below it, composing the majority (in thickness) of the metal layer. Therefore, it is the metal under the transition layer that makes the main contribution to the transmission/reflection coefficient, and consequently, the optical constants obtained from the analysis of the transmission/reflection spectra are closer to the bulk metal constants, which are well described by the Drude model [27,28].

As for the THz SPP refractometry method, the field of the surface wave generated by the probing radiation penetrates into the metal only to the depth δ_m ≈ δ_s [36]. Therefore, the SPP characteristics are determined mainly by the optical properties of the transition layer of the metal. As a result, the effect of inhomogeneities and surface defects on the SPP characteristics exceeds that on the characteristics of the reflected probing radiation. In addition, taking into account the resonant enhancement of the field in the near-surface region during SPP-enhanced photon generation and the difference in the distribution of the fields of the SPPs and the reflected plane wave (the δ_m value is slightly less than δ_s) [11], we can assume that the collisional frequency ω_τ of the conduction electrons for the SPPs exceeds this value for a plane wave of probing radiation incident on the metal.

Therefore, in our opinion, it can be stated that the value of the effective permittivity ε_m of the metal surface depends not only on the manufacturing and processing of the metal surface but also on the method of its determination. More precisely, it depends on the nature of the interaction of the probing radiation with the object of study. Due to the intensive mastering of the THz range and the creation of THz plasmonic devices in recent years, the development of the THz SPP refractometry method is of particular relevance. In this paper, we consider the possibility of determining the effective (averaged over the surface layer) dielectric permittivity of metals and highly doped semiconductors (which provide a macroscopic SPP propagation length) at THz frequencies from the refractive index n_s and absorption index κ_s for the SPPs directed by this surface, as measured with a plasmon Michelson interferometer (where ${\tilde{n}}_{\mathrm{s}}=n_{\mathrm{s}}+i·{\kappa }_{\mathrm{s}}$ is the SPP complex refractive index).

2. Materials and Methods

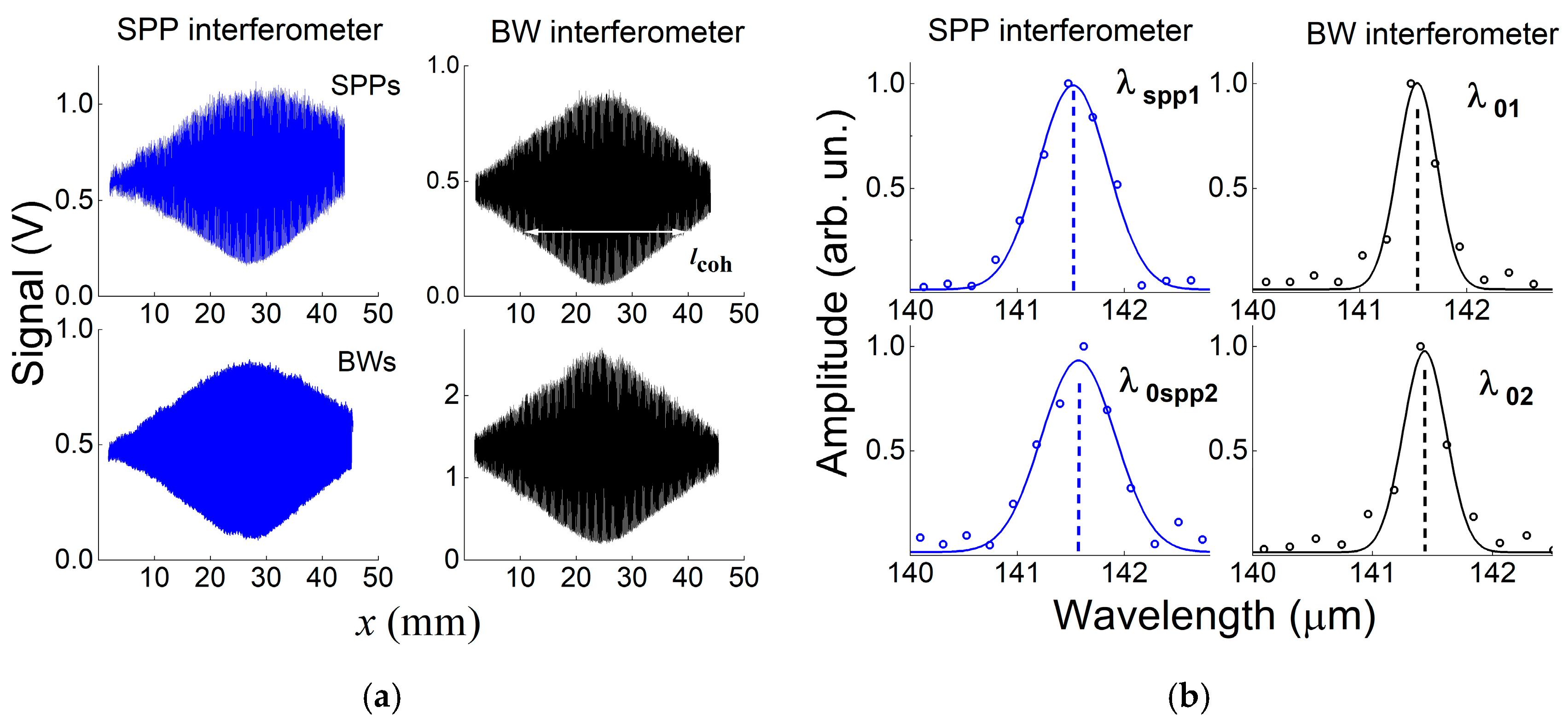
2.1. Experimental Setup

To measure the characteristics of THz surface plasmon polaritons (SPPs), we developed and created a plasmon Michelson interferometer, the schematic diagram of which is shown in [37,38], the results of the first testing are presented in [39], and a detailed description of the SPP interferometer, its technical characteristics and measurement technique are presented in the paper [40]. The source of radiation was a unique installation of the Budker Institute of Nuclear Physics SB RAS, the Novosibirsk free electron laser (NovoFEL) [41], which generates a periodic sequence of 100-ps pulses with a frequency of 5.6 MHz. The NovoFEL radiation was linearly polarized and fully coherent in the beam cross-section; the temporal coherence was 30 ÷ 100 ps (depending on the operating mode of the laser). The radiation wavelength was λ₀ = 141 µm, with a line width of less than 1%. The average radiation power at the input to the interferometer was 30 ÷ 40 W, and the diameter of the Gaussian beam was 12 mm.

The use of the interferometer, similarly to the classical Michelson interferometer, relies on an analysis of the interferogram formed not by bulk waves but by collinear SPP beams directed by the surface under study. The real part of the SPP refractive index n_s was determined from a comparison of the NovoFEL emission spectrum with the SPP spectrum resulting from the Fourier analysis of the interferogram.

In the normal mode of NovoFEL operation, the emission spectrum is not stable enough: the wavelength shift can be of up to 0.2 μm during measurements. For the variations in the laser radiation spectrum to be taken into account, the interferogram formed by the NovoFEL radiation beams was recorded simultaneously with the plasmon interferogram. For this purpose, a Michelson interferometer for bulk waves (BWs) [39] was added to the scheme of the plasmon interferometer (Figure 1).

The p-component corresponding to the SPP polarization was extracted from the NovoFEL radiation beam entering the input of the installation (the lithographic polarizer P₁ was used). The polypropylene film beam splitter BS₁ split the linearly polarized radiation into two beams. The cylindrical mirror CL focused the transmitted beam on the edge of the flat substrate of the plasmon interferometer, where, due to diffraction, the radiation was converted into SPPs. The mirror M₅ directed the reflected beam, the intensity of which was controlled by the polarizer P₂, to the BW interferometer.

In the plasmon interferometer, fixed (M₁) and movable (M₂) mirrors were used (40 × 20 × 5 mm³ glass plates with gold coating on the reflecting faces), and a 40 × 25 × 1 mm³ plane-parallel plate BS₂ of Zeonex polyimide, at an angle of 45° to the incident SPP beam, served as an SPP beam splitter [42]. The lower faces of the mirrors and the beam splitter were optically polished and closely adhered to the substrate, providing optical contact with its surface.

At the exit from the plasmon interferometer, the combined collinear SPP beams from both arms passed onto the convex surface of the cylindrical out-coupling element adjacent to the end of the substrate for the conversion of the SPPs into BWs. The element was a 1/8 of a cylinder with a curvature radius of 60 mm; its convex polished surface contained a 300 nm layer of gold coated with a ZnS layer 1 μm thick. Having reached the opposite edge of the convex face of the element, the resulting SPP beam diffracted on it and was converted into BWs, which were registered by the radiation detector. The choice of such a specific coupling element was made due to the need for the spatial separation of the BWs generated by the SPPs at the out-coupling edge of this element from the parasitic BWs arising at (1) the conversion of the NovoFEL radiation into SPPs (accompanied by the formation of high-intensity diffracted BWs) [43], (2) the diffraction of the SPPs on the splitter and mirrors of the interferometer [44], and (3) the transition of the SPPs from the substrate to the out-coupling element. Moreover, an additional source of parasitic BWs was the scattering [45] of the SPPs on the roughness and optical inhomogeneities of the substrate surface, leading to the appearance of the radiative losses of the SPPs [35]. An additional and effective screen from the parasitic BWs was a foam “gate” (35 mm long and 1 mm high) placed on the substrate at the point of its contact with the conversion out-coupling element.

The detection of the interfering BWs generated by the SPP beams on the free edge of the out-coupling element was done using an optoacoustic detector (Golay Cell, TYDEX, St. Petersburg, Russia) of high sensitivity (NEP ≈ 1.4 × 10⁻¹⁰ W/Hz^1/2 [46]). The need to use a highly sensitive receiver was due to the low signal intensity, large energy losses of the SPPs during their diffraction on the circuit elements, and the SPP attenuation during propagation along the sample surface.

In the BW interferometer, the beams lost energy insignificantly (only in the reflection from the splitter BS₃). Thus, a less sensitive single-pixel pyroelectric receiver MG-33 (Novosibirsk Plant of Semiconductor Devices Vostok, Novosibirsk, Russia) was used to record the BW interferograms [47,48]. The radiation directed onto its 1 × 1 mm² sensitive element was collected by a TPX lens with a focal length of 50 mm.

Since the receivers applied can register only a time-varying radiation flux, a mechanical obturator was placed at the input of the setup, which modulated the radiation intensity with a frequency of 100 Hz. The signals from each receiver were recorded by two synchronous detectors (SR-830, Stanford Research Systems, Sunnyvale, CA, USA), from the outputs of which the signals were sent to the two-channel digital oscilloscope (Handyscope 3, TiePie, Sneek, The Netherlands), which operated in the recorder mode. The measured time dependences were digitized and written to a file.

The movable mirrors M₂ and M₄ were attached to the platforms of the motorized stages (Standa, Vilnius, Lithuania), which shifted the mirrors along the x axis during scanning with a step of 2.5 μm. The scanning speed chosen was the highest possible (100 steps per second), at which the detectors had time to correctly register the recorded signals. The recording time for one pair of interferograms corresponding to a displacement of the movable mirrors by 30 mm was about 2 min.

2.2. Sample Fabrication and Testing

The samples were 100 × 150 × 11 mm³ flat glass plates, whose upper faces (100 × 150 mm²) were optically polished. By means of magnetron sputtering in an argon atmosphere at a pressure of 3 × 10⁻³ mbar with the use of a BOC Edwards Auto 500 device (Bolton, UK), an adhesive chromium sublayer (10 nm thick) was first deposited onto the polished face (heated to a temperature of 120 °C), and then a layer of gold (grade 99.999%) 300 nm thick was applied. The layers were sputtered sequentially from two different magnetrons without time delays. A layer of zinc sulfide (ZnS) that was uniform in thickness (up to 3 µm) was deposited onto the top of the gold via electron-beam evaporation (from a molybdenum crucible). The sequential deposition of the layers was done in one technological cycle, without the removal of the substrate from the vacuum chamber. The thickness of the samples was measured with a “Spektr” ellipsometer developed by the Institute of Semiconductor Physics SB RAS [49].

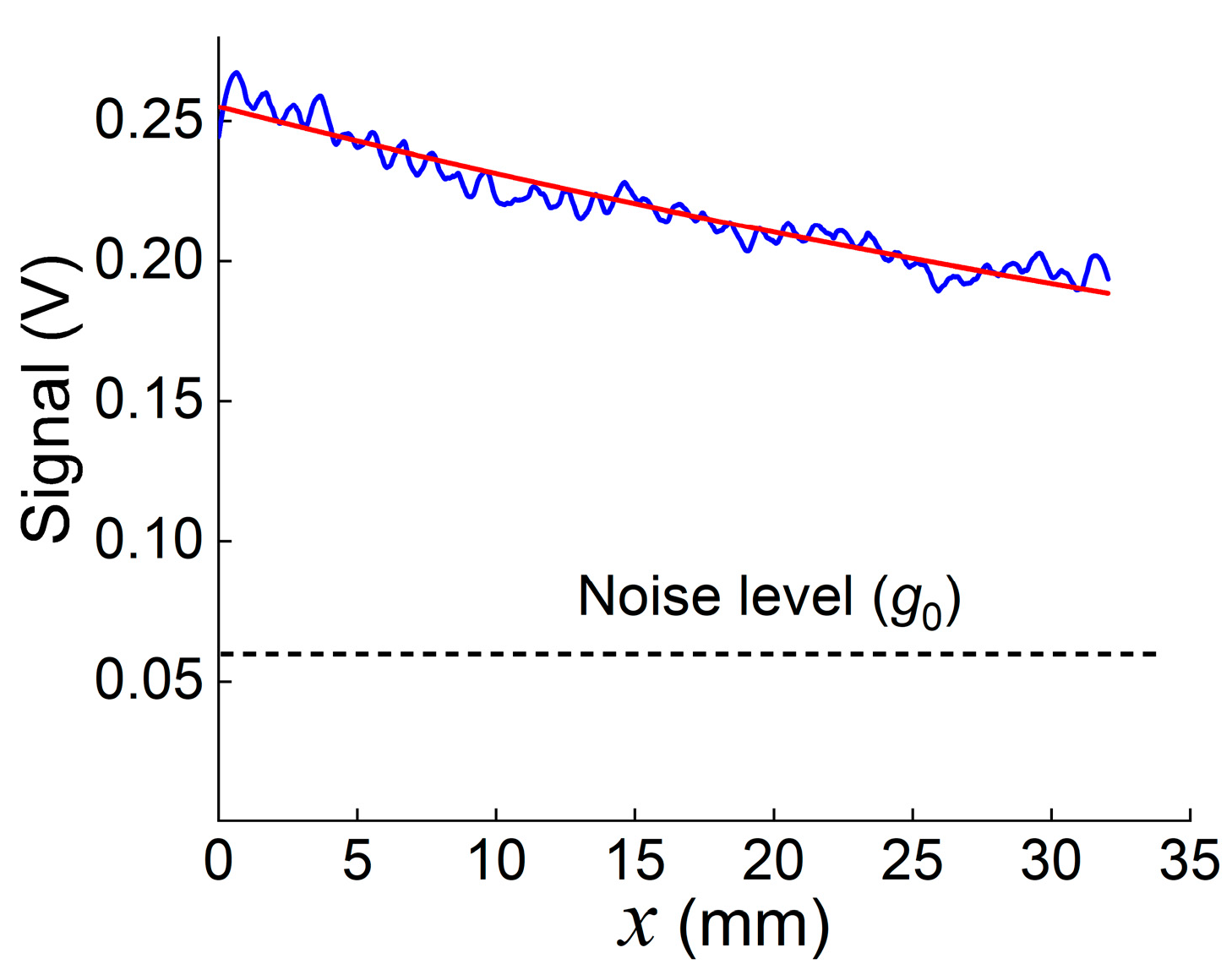
2.3. Experimental Data Processing

Before the terahertz measurements, the optical circuits of both interferometers were adjusted with respect to the collimated beam of a diode laser (λ₀ = 635 nm). The adjustment was done with high accuracy, since the difference in the refractive indices of the SPPs on the samples, whose ZnS coatings differed in the thickness by 100 nm, was about 10⁻⁴. In addition, after the placement of another sample (with a ZnS layer of a different thickness), it was necessary to re-adjust the SPP interferometer circuit, which took a lot of time because of the high accuracy maintained. To reduce the adjustment time and take into account the slight misalignment between the interferometers, we carried out the measurements in two stages. First, two interferograms were measured simultaneously (on the plasmon and BW interferometers), in accordance with the scheme described in Section 2.1, when the SPPs propagated along the sample surface. During the second stage of the measurements, the NovoFEL radiation in the plasmon interferometer was not converted into SPPs; rather, it was directed straight to the beam splitter BS₂ to result in an interferogram formed by the source radiation in the environment (air). Simultaneously with that, an interferogram was recorded on the BW interferometer. Thus, with the two stages of the measurements, for each sample (differing in terms of the thickness of the ZnS layer), two pairs of interferograms were obtained. Moreover, for the collection of statistics, the measurements were repeated four times with each of the samples.

Figure 2a shows an example of the SPP and BW interferograms. As the movable mirrors of the interferometers move along the x axis, the amplitudes of the sinusoids first increase, then reach the maximum, and then decrease in the final section of the scanning. This is a typical symmetric form of the autocorrelation function for a coherent radiation source [50]. The amplitude envelope has a Gaussian profile, the width of which determines the length (duration) of coherence, which was 27 mm (90 ps) in this experiment. This is close to the maximum duration of the NovoFEL radiation pulse at operation in a stable mode (100 ps).

By means of the Fourier transform, the SPP and NovoFEL radiation spectra were calculated from the interferograms (Figure 2b). The circles indicate the results of the calculations of the components of the Fourier spectrum. The number of calculation points was determined by the length of the measured interferograms, which depends on the coherence length of the NovoFEL radiation (l_coh ≈ 27 mm). Next, the spectra were approximated with a Gaussian function of the form $f(x)=A·\exp \left[-\frac{1}{2}{\left(\frac{x - x_{\mathrm{c}}}{w}\right)}^2\right]+f_0$ and normalized to the value (A + f₀). The w value defined the width of the spectrum. The value of the parameter x_c, which describes the position of the central line of the spectrum, corresponded to the desired wavelength. The plots in Figure 3 show the following wavelengths (central lines of the spectra): λ_spp1 and λ_0spp2, found from the interferograms obtained on the plasmon interferometer with and without SPP excitation, respectively; and λ₀₁ and λ₀₂, the corresponding wavelengths of the NovoFEL radiation in air, as determined with the BW interferometer.

Since the complex refractive index of the SPPs is defined as the ratio of the SPP wave number k_s to the wave number of the radiation from the source in vacuum k₀ = 2π/λ₀,

$${\tilde{n}}_{\mathrm{s}}=\frac{k_{\mathrm{s}}}{k_0}=n_{\mathrm{s}}+i·{\kappa }_{\mathrm{s}}$$

(1)

the real part n_s was found from the spectra shown in Figure 3 using the following formula:

$$n_{\mathrm{s}}=\left(\frac{{\mathsf{\lambda }}_{\mathrm{spp}1}/{\mathsf{\lambda }}_{0\mathrm{spp}2}}{{\mathsf{\lambda }}_{01}/{\mathsf{\lambda }}_{02}}\right)·\mathrm{Re}\left({\tilde{n}}_{\mathrm{a}}\right)$$

(2)

where the normalization to λ₀₁/λ₀₂ takes into account the shift in the NovoFEL generation spectrum that could occur during the time between recordings of the interferograms with and without SPP excitation (see Section 2.1). The factor $\mathrm{Re}\left({\tilde{n}}_{\mathrm{a}}\right)$ in Expression (2) makes it possible to take into account the fact that the laser radiation propagates not in vacuum but in air with the complex refractive index ${\tilde{n}}_{\mathrm{a}}=1.0002726+i·0.0000039$ [51,52]. For each sample, the average value of n_s was found from four sets of interferograms.

To find the κ_s value, we measured the attenuation of the SPP intensity at the displacement of the movable mirror M₂ (see Figure 1) in the plasmon interferometer. In this case, the fixed mirror M₁ was covered by an absorbing plate. A typical dependence, as measured on a sample with a ZnS layer 470 nm thick, is shown in Figure 3. The figure also shows the result of the approximation of the measurement results with a function of the form $g(x)=B·\exp \left(2x/L_{\mathrm{s}}\right)+g_0$, where L_s is the SPP propagation length. The exponent takes into account the 2x increase in the SPP path at the displacement of the mirror by x. The noise level g₀ was measured in the experiment and was set as an approximation parameter. For each sample, the average SPP propagation length L_av over four measurements was found and the κ_s value was calculated using the formula [11]

$${\mathsf{\kappa }}_{\mathrm{s}}=\frac{{\mathsf{\lambda }}_0}{4\mathsf{\pi }·L_{\mathrm{av}}}$$

(3)

3. Results

The experiments were carried out with a set of samples with flat substrates containing non-transparent layers of sputtered gold coated with a ZnS layer of thickness d = 0–3000 nm. Figure 4a,b show the real part without unity n_s − 1 and the imaginary part κ_s of the SPP refractive index, respectively, which were found via the above methods, versus the d value. In these figures, the black lines show the calculated dependences obtained via the numerical solution of the dispersion equation for the “gold–ZnS layer–air” structure at λ₀ = 141 μm. In these calculations, the refractive index of ZnS was taken as $n_{\mathrm{d}}=2.943+i·0.01$ [7], and the gold permittivity ε_m was calculated by the Drude model with the use of the reference values of the plasma frequency ω_p = 1.37 × 10¹⁶ s⁻¹ and frequency of the collisions of the conduction electrons ω_τ = 4.05 × 10¹³ s⁻¹ [1]:

$${\epsilon }_{\mathrm{m}}(\omega )=1-\frac{{\omega }_p{}^2}{{\omega }^2+{\omega }_{\mathsf{\tau }}{}^2}+i·\frac{{\omega }_{\tau }·{\omega }_p{}^2}{\omega ·({\omega }^2+{\omega }_{\mathsf{\tau }}{}^2)}$$

(4)

where ω = 2πc/λ₀ = 1.34 × 10¹³ s⁻¹ (c is the speed of light in a vacuum).

From Figure 4a, one can see that the value of n_s − 1 monotonically increases with d, with all its experimental values lying above the calculated curve, which indicates that the real part Re(ε_m) of the dielectric constant of the deposited gold is less than the value predicted by the Drude model—according to the SPP theory, a decrease in the Re(ε_m) must be accompanied by an increase in the n_s.

Note that the determination errors for n_s − 1 for small thicknesses of ZnS (d ≤ 300 nm) and d = 3000 nm are noticeably larger than those for 300 nm < d < 3000 nm. The reason for this is the low intensity of the useful signal from the SPPs due to the low efficiency of the SPP generation in the plasmon interferometer at such thicknesses of the dielectric layer.

The value of the SPP refractive index on uncoated gold was n_s ≈ 1.0005, which corresponds to the SPP phase velocity ϑ_ph = c/n_s ≈ 0.9995 c. Similar values of SPP phase velocities were also obtained for thick aluminum wire in experiments performed on a TDS spectrometer [53], where ϑ_ph was determined from the time delay of a THz SPP pulse relative to a light pulse propagating in air.

As for the imaginary part κ_s of the SPP refractive index, which characterizes the SPP decay, at an increase in the thickness d of the cover layer, the measured values (blue circles in Figure 4b) first decrease, reach the minimum at d ≈ 300 nm, and then grow monotonically. This behavior of κ_s was explained in [35] and is associated with the decrease in the radiative losses of the SPPs at the deposition of a dielectric layer onto the metal surface. At some d = d₀ (300 nm in our case), the integral losses of the SPPs reach the minimum, and at d > d₀, their growth is due to the predominance of the Joule losses over the radiative losses because of the monotonic increase in the fraction of the SPP field energy transferred into the metal with d growth.

A small discrepancy between the experimental values of κ_s and the numerical solution at d > d₀ can be caused by the thickness inhomogeneity of the ZnS coating, which can lead to the inaccuracy of the measurements of the absorption part of the refractive index of the SPPs. Due to peculiarities of the ZnS deposition technique, at large thicknesses of ZnS, the inhomogeneity is higher, so the discrepancy with the theory can be more noticeable.

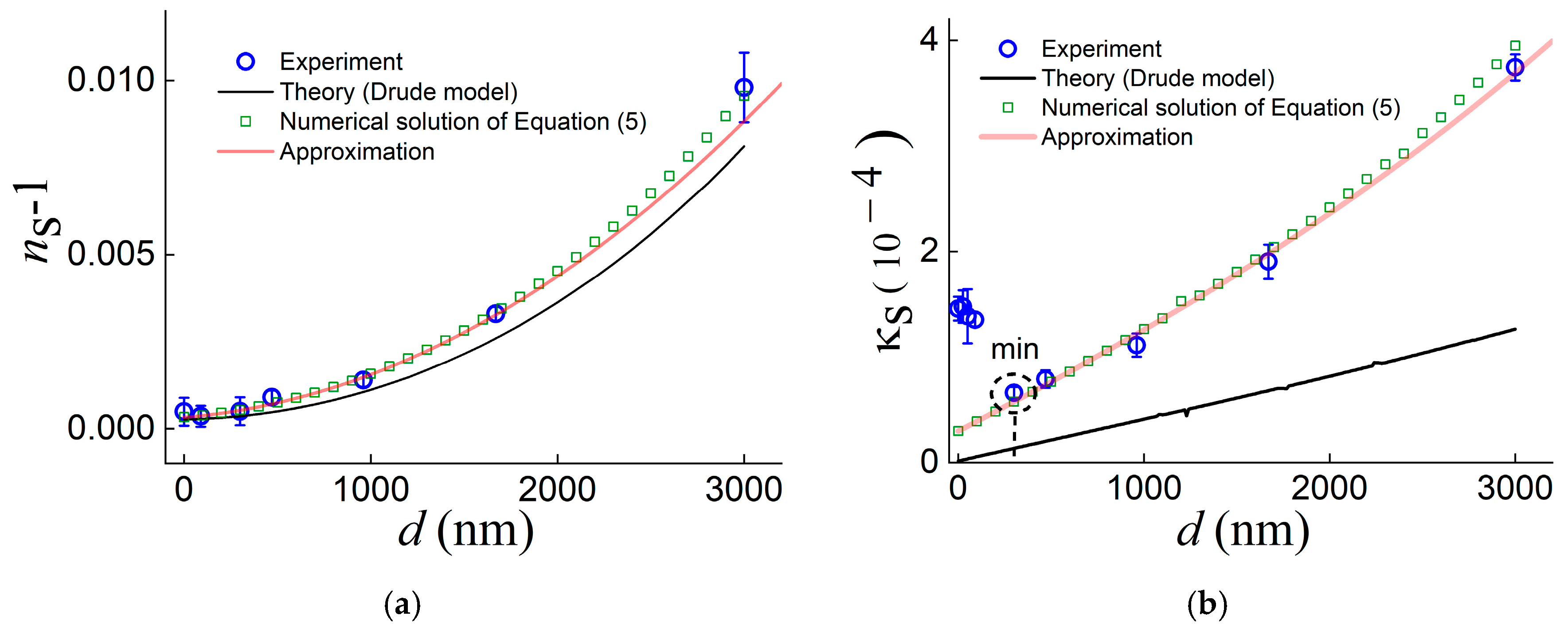
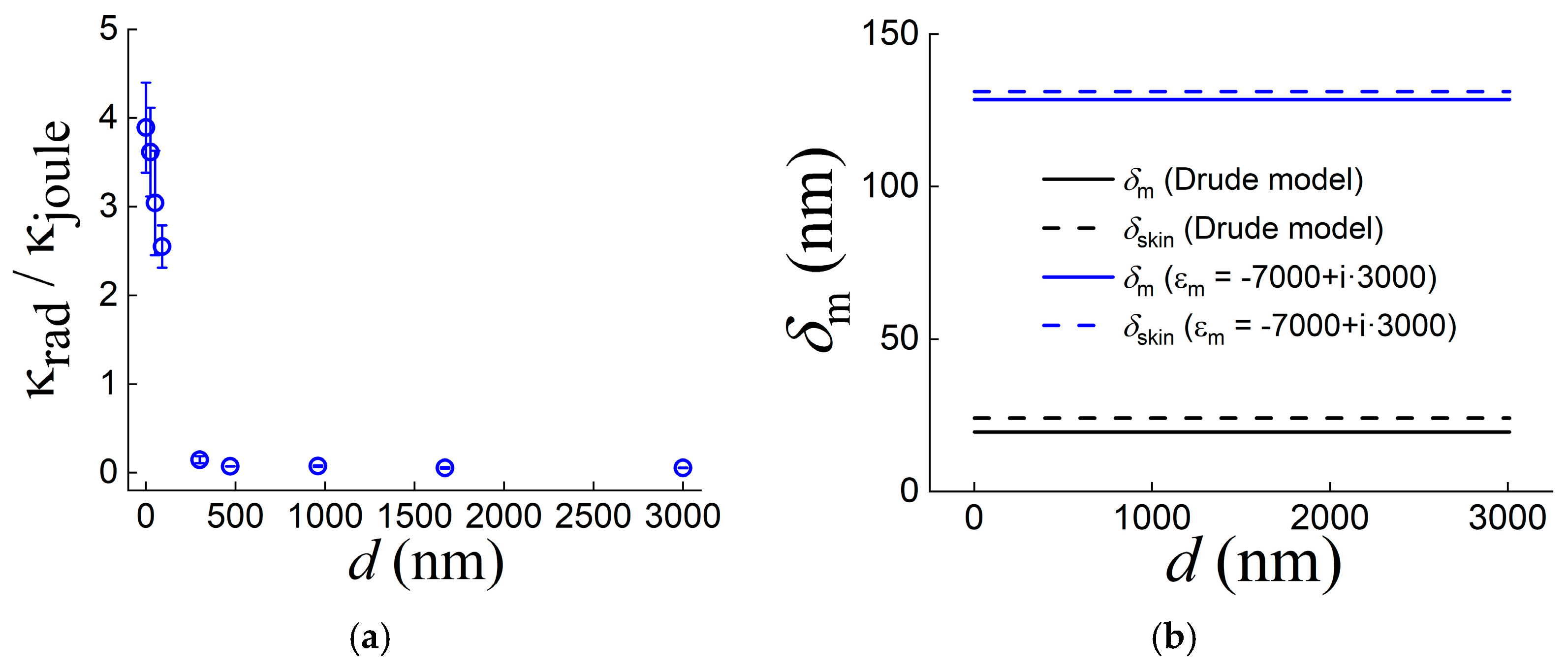
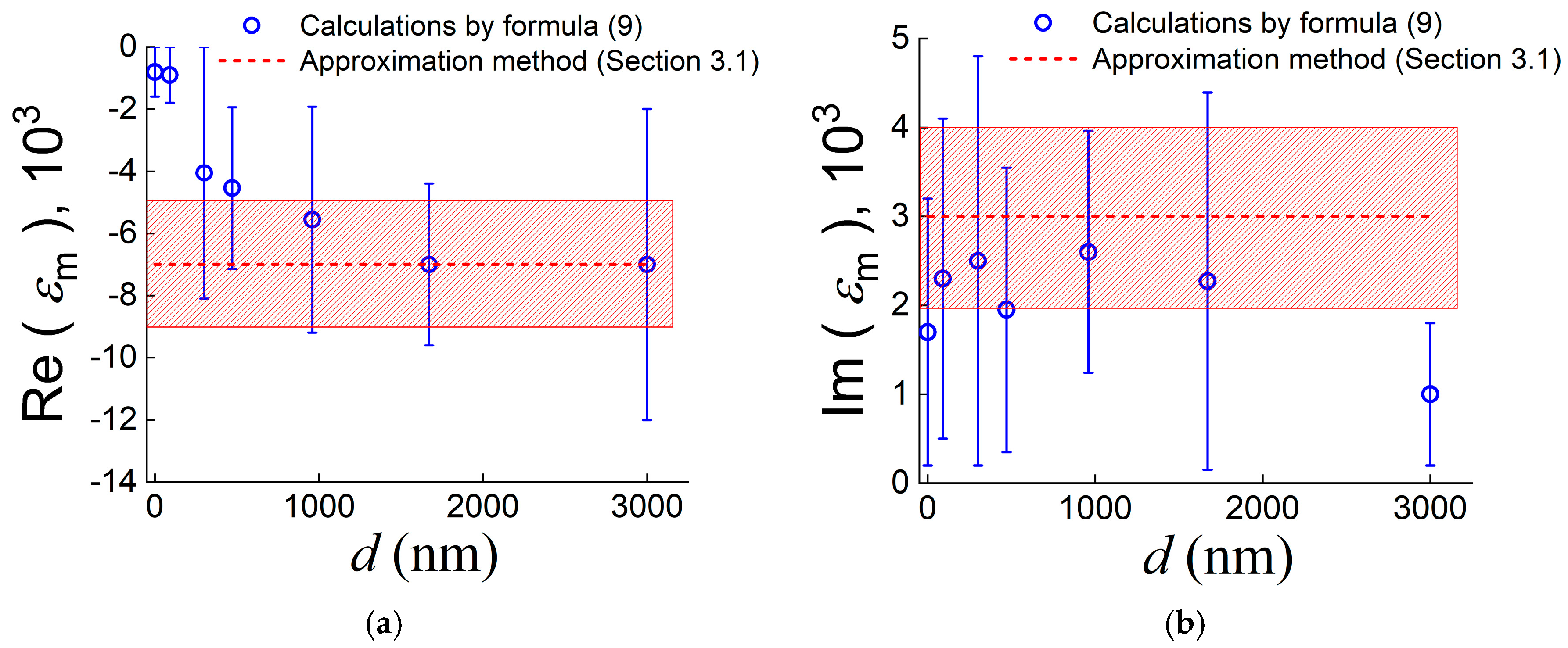
3.1. Determination of the Permittivity of the Metal Surface from the SPP Characteristics on a Set of Samples with a Dielectric Layer of Various Thicknesses

In this section, we consider an approximation method for finding the metal permittivity, which uses the ${\tilde{n}}_{\mathrm{s}}$ values found for a set of samples with ZnS coatings of various thicknesses.

To determine the effective permittivity ε_m of a metal surface guiding the SPPs and containing a thin-layer coating of thickness d with permittivity ε_d from the found complex refractive index ${\tilde{n}}_{\mathrm{s}}$ of the SPPs, it is necessary to solve (with respect to ε_m) the SPP dispersion equation for the three-layer structure “metal–dielectric layer–environment” [54]:

$$\tanh \left(k_0·d·\sqrt{{\tilde{n}}_{\mathrm{s}}{}^2-{\epsilon }_{\mathrm{d}}}\right)=-\frac{\sqrt{{\tilde{n}}_{\mathrm{s}}{}^2-{\epsilon }_{\mathrm{d}}}\times \left(\frac{\sqrt{{\tilde{n}}_{\mathrm{s}}{}^2 - {\epsilon }_{\mathrm{a}}}}{{\epsilon }_{\mathrm{a}}}+\frac{\sqrt{{\tilde{n}}_{\mathrm{s}}{}^2 - {\epsilon }_{\mathrm{m}}}}{{\epsilon }_{\mathrm{m}}}\right)}{{\epsilon }_{\mathrm{d}}·\left(\frac{\sqrt{{\tilde{n}}_{\mathrm{s}}{}^2 - {\epsilon }_{\mathrm{a}}}·\sqrt{{\tilde{n}}_{\mathrm{s}}{}^2 - {\epsilon }_{\mathrm{m}}}}{{\epsilon }_{\mathrm{a}}·{\epsilon }_{\mathrm{m}}}+\frac{{\tilde{n}}_{\mathrm{s}}{}^2 - {\epsilon }_{\mathrm{d}}}{{\epsilon }_{\mathrm{d}}{}^2}\right)}$$

(5)

where ε_a is the permittivity of the environment.

Transcendental Equation (5) can be solved numerically, although the solution is very sensitive to small variations in the ${\tilde{n}}_{\mathrm{s}}$ within the measurement error, which can result in a large error in the determination of the metal permittivity ε_m. Therefore, we have developed an ε_m determination method based on the approximation of the (n_s − 1)(d) and κ_s(d) dependences measured for a series of samples with different ZnS coating thicknesses.

In the THz range ε_m >> ε_d, ε_a, the $k_{0}d<<1/\sqrt{{\epsilon }_{\mathrm{m}}}$ condition is met at d << λ. Expanding both parts of Equation (5) into a Taylor series with respect to a small correction to the refractive index ${\tilde{n}}_{\mathrm{s}}$ because of the dielectric coating on the metal, we obtain an approximate formula for calculating the surface impedance of the three-layer structure (see Appendix A):

$$\xi \approx \frac{i\times \left({\epsilon }_{\mathrm{d}}·\sqrt{-\frac{{\epsilon }_{\mathrm{m}}{}^2}{{\epsilon }_{\mathrm{a}}{ + \mathsf{\epsilon }}_{\mathrm{m}}}}\times \left({\epsilon }_{\mathrm{a}}+{\epsilon }_{\mathrm{m}}\right)+k_{0}d·{\epsilon }_{\mathrm{m}}\times \left[{\epsilon }_{\mathrm{a}}\left({\epsilon }_{\mathrm{m}}-{\epsilon }_{\mathrm{d}}\right)-{\epsilon }_{\mathrm{m}}{\epsilon }_{\mathrm{d}}\right]\right)}{{\epsilon }_{\mathrm{d}}·\left({\epsilon }_{\mathrm{a}}+{\epsilon }_{\mathrm{m}}\right)\times \left(k_{0}d·{\epsilon }_{\mathrm{d}}\sqrt{-\frac{{\epsilon }_{\mathrm{m}}{}^2}{{\epsilon }_{\mathrm{a}} + {\epsilon }_{\mathrm{m}}}}+{\epsilon }_{\mathrm{m}}\right)}$$

(6)

where

$${\tilde{n}}_{\mathrm{s}}=\sqrt{{\epsilon }_{\mathrm{a}}-{\left({\epsilon }_{\mathrm{a}}\xi \right)}^2}$$

(7)

The dependences of n_s − 1 and κ_s on the ZnS layer thickness d were found using Formulas (6) and (7) for the gold permittivity ε_m calculated according to the Drude model (blue lines in Figure 5). In the figure, the red lines show the results of the numerical solution of Equation (5). It can be seen that at d ≤ 1500 nm, the approximate and exact solutions practically coincide, while at 1500 nm < d ≤ 3000 nm, they differ by no more than 8%.

Then, the experimental dependences (n_s − 1)(d) and κ_s(d) were approximated by means of a MATLAB program, using the least squares method to find the minimum deviations of the experimental values from the corresponding functions $\mathrm{Re}\left({\tilde{n}}_{\mathrm{s}}-1\right)$ and $\mathrm{Im}\left({\tilde{n}}_{\mathrm{s}}\right)$ (${\tilde{n}}_{\mathrm{s}}$ was found by Formula (7)). The real and imaginary parts of the gold permittivity ε_m were varied as parameters. The search for the solution for both functions was performed in the range of ZnS layer thicknesses 300 nm ≤ d ≤ 1670 nm. The domain of the functions did not include small thicknesses (d < 300 nm) when the SPP decay is governed by the radiative losses, which are not taken into account by Equation (5). At d = 3000 nm, the approximate formula gives noticeable deviations from the exact solution.

As a result of the approximation, the permeability of the deposited gold was found: the real part was Re(ε_m) ≈ −7000 ± 3000, while the imaginary was Im(ε_m) ≈ 3000 ± 1300. The approximation dependences (n_s − 1)(d) and κ_s(d) are shown by the gray lines in Figure 4. The large errors (of up to 40%) in the determination of the ε_m by this method are due to the closeness of the refractive index n_s of the THz SPPs to the refractive index of air, which necessitates a higher accuracy in finding the n_s value.

In Figure 4, the green squares show the results for the numerical solution of the dispersion Equation (5) via the downhill method [55] at ε_m = −7000 + i·3000. It can be seen that the results of the calculation at d ≤ 1700 nm almost coincide with the curves obtained by the approximate Formula (7), which indicates the possibility of its effective application for evaluation calculations of the complex refractive index of THz SPPs in a three-layer structure in the presence of a dielectric coating layer of subwavelength thickness on the metal.

It was already noted above that the presence of a dielectric layer on the metal surface leads to an increase in the fraction of the SPP field energy transferred into the metal. In this case, the depth δ_m of the penetration of the SPP field into the metal is practically independent of the coating thickness, as evidenced by the graphs in Figure 6b, as obtained from the solution of Equation (5) for the “gold–ZnS layer of thickness d–air” structure. It can be seen that with the gold permeability found via the approximation method from the experimental results, the δ_m value is approximately six times greater than that for the permeability calculated by the Drude model. Therefore, for the deposited gold layer to be non-transparent for the THz SPP field (which excludes the effect of the substrate on the SPP characteristics), its thickness must be 200–300 nm at least.

From the plot of κ_s(d) in Figure 6a, it can be seen that at small thicknesses d < 300 nm, the loss of the SPPs in the experiment is much greater than the calculations predict. This is explained by the presence of the radiative losses of the SPPs, which are not taken into account either by the approximate formulas or by the dispersion equation. Starting from d ≈ 300 nm (where the minimum of the integral losses of the SPPs is reached and their radiative losses become relatively small compared with the Joule losses), the measured values of the absorption coefficient of the SPPs approach the calculated dependence.

Based on this interpretation of the existence of the minimum of the losses κ_s(d) and the assumption that other mechanisms of losses contribute negligibly to the total SPP decay, the SPP radiative losses can be estimated by the following formula:

$${\kappa }_{\mathrm{rad}}={\kappa }_{\mathrm{s}}-{\kappa }_{\mathrm{Joule}}$$

(8)

where κ_s is the total SPP losses measured in the experiment; and κ_Joule is the Joule SPP losses determined from the solution of Equation (5).

Figure 6a shows the ratio of the radiative losses estimated by Formula (8) to the Joule losses at different thicknesses d of the ZnS layer, as calculated from the solution of Equation (5) with the substitution of ε_m = −7000 + i·3000 (found via the approximation method) into it. In this case, in the absence of a dielectric layer on the metal surface, the radiative losses exceed the Joule losses by about four-fold. However, as the d grows, this ratio decreases monotonically to zero at d ≥ 960 nm, when the SPP decay is determined mainly by the losses in the metal.

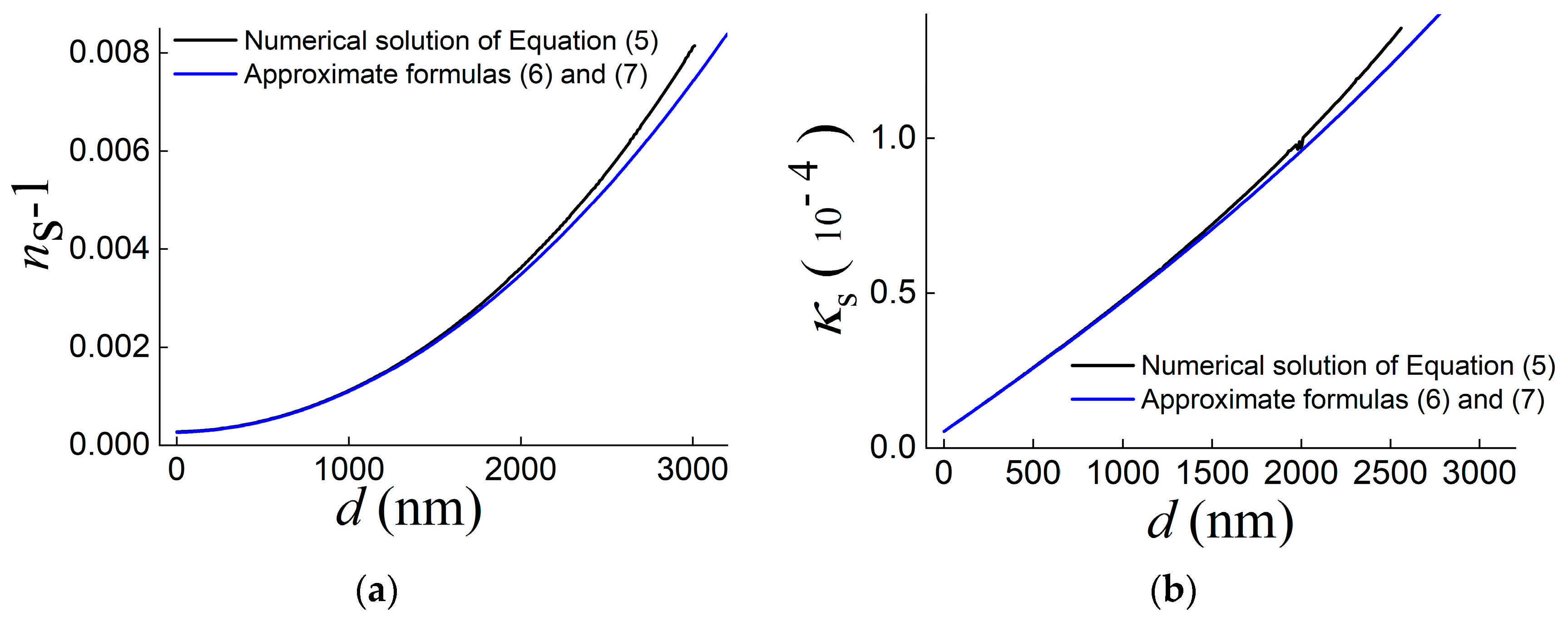
3.2. Determination of the Effective Dielectric Constant of the Metal Surface from SPP Characteristics on One Sample

In Section 3.1, we described an estimation of the dielectric permittivity of metal ε_m via the application of the approximation method to the measurements of the characteristics of the THz SPPs on a set of samples with different thicknesses of dielectric layers on the metal surface. Despite its rather high reliability, this method is very laborious for the rapid assessment of the dielectric constant of metal (metallized) optical surfaces. Therefore, it is desirable (in view of practical applications) to have a method for the determination of ε_m from the complex refractive index ${\tilde{n}}_{\mathrm{s}}=n_{\mathrm{s}}+i{\kappa }_{\mathrm{s}}$ of the THz SPPs, as found from the measurements of its real and imaginary parts on only one sample.

From Equation (5), we obtained an approximate formula for calculating the ε_m from the measured characteristics of the SPPs (see Appendix A):

$${\epsilon }_{\mathrm{m}}\approx -\frac{{\epsilon }_{\mathrm{d}}{}^2}{{\left[k_0·d·\left({\epsilon }_{\mathrm{a}}-{\epsilon }_{\mathrm{d}}\right)+i·{\epsilon }_{\mathrm{d}}·\xi \right]}^2}$$

(9)

where the surface impedance ξ is found from Formula (6).

As was established above, the radiative losses make a predominant contribution to the SPP decay on a metal without a dielectric coating layer, which leads to large errors in the determination of the ε_m. Therefore, it is necessary to find a layer thickness d range in which the error in the determination of the ε_m is not so large. For this purpose, the permittivity ε_m of the deposited gold was calculated using Formula (9) with the substitution of the experimentally determined values of ${\tilde{n}}_{\mathrm{s}}$ for samples with different thicknesses d of the ZnS layer.

The found values of the real Re(ε_m) and imaginary Im(ε_m) parts of the gold permittivity are shown by the blue circles in Figure 7. The errors on the graphs correspond to the maximum permittivity deviations calculated in the ranges of the experimental values n_s ± Δn_s and κ_s ± Δκ_s, where Δn_s and Δκ_s are the corresponding measurement errors. It can be seen that the values of the Re(ε_m) and Im(ε_m) at small thicknesses of the ZnS layer (d < 300 nm) differ greatly from the approximation values, while at d ≥ 300 nm, they approach the approximation values asymptotically (except for the Im(ε_m) at d = 3000 nm, where already Formula (9) gives insufficiently reliable results compared with the exact solution of the dispersion Equation (5) and the increased inaccuracy of the measurements of the imaginary part of the refractive index of the SPPs due to the inhomogeneity of the ZnS film over the thickness). This character of the dependence ε_m(d) can be explained by the fact that Formula (9) does not take into account the radiative losses of the SPPs. At larger thicknesses of the dielectric layer, when the radiative losses become much less than the thermal losses, Formula (9) describes the experiment much better.

Note that according to the performed calculations, the real part Re(ε_m) of the permittivity of gold without a ZnS coating layer (d = 0) turned out to be equal to −800 (see Figure 7). This value of Re(ε_m) is in agreement with the estimates given in earlier publications on the THz SPP refractometry of deposited gold without a dielectric coating layer, as implemented on a TDS spectrometer [31] and with FEL radiation [24]. However, as follows from the above, this value of the Re(ε_m) differs from its real value of −7000 almost 10 times. In our opinion, the erroneous estimation of the Re(ε_m) in previous works on the THz SPP refractometry was because of the unaccounted for significant radiative losses of the SPPs on a metal surface free without a coating layer.

It is important to note that the obtained errors for the metal effective permittivity (see Figure 7) are very large (reach 50%). It is clear that its more reliable determination via the proposed method of the SPP refractometry requires higher accuracy in terms of finding the real part of the SPP refractive index from the recorded interferograms. For the accuracy of the determination of the metal permittivity to be 20% (for thicknesses d ≥ 500 nm), it is necessary to determine the n_s with an error not worse than 10⁻⁴ (with an actual error of 10% for the κ_s, which depends on the signal-to-noise ratio, adjustment, and stability of the intensity of NovoFEL radiation). For such accuracy for the n_s, the stability of the radiation source in terms of the wavelength during the recording of the interferogram must not be worse than 0.01 µm (for λ₀ = 141 µm), while the width of the generation line must be an order of magnitude smaller than 1.0 ÷ 1.5 µm in the normal operation mode. This can be achieved via the reduction of the measurement time with faster and more sensitive detectors, as well as with sources of coherent THz radiation that are more stable than FELs, such as gas lasers [56], backward wave oscillators [57], gyrotrons [58], and quantum-cascade lasers [59].

Note that it is possible to increase the stability of the NovoFEL radiation to temporal variations in the radiation wavelength at an operation in the mode of negative detuning of the electron bunch repetition rate from the repetition rate of light pulses inside the FEL optical resonator, accompanied by a decrease in the average radiation power [60]. In operation in this mode, a stable single-mode generation regime was established, the linewidth of which reached the maximum possible narrow value (0.25%) [50], while the wavelength shift in 15 min was not more than 0.1 of the width of the generated radiation spectrum (0.04 μm at λ₀ = 141 µm), which is close to the desired accuracy. However, to achieve such a generation mode, a long and laborious adjustment of the NovoFEL parameters is necessary.

In addition, the precision of the translation stages, which shift the movable mirrors M₂ and M₅ (Figure 1), has a significant effect on the accuracy of the interferometric measurements. The positioners from Standa, which we used in this work, with a displacement of 30 mm (the characteristic scan length of the interferograms in our experiments) can give an error of 10 µm [61], at which the measurement error of the refractive index of the SPPs reaches up to 0.0003, which does not satisfy the required accuracy. Applying translation stages with encoders or more precise positioners can significantly increase the accuracy of the measurements.

4. Conclusions

The studies performed have shown that for the correct determination of the effective permittivity ε_m of a metal surface via the proposed method of terahertz (THz) plasmon interferometric refractometry or by other methods based on an analysis of the characteristics of surface plasmon polaritons (SPPs), the measurements must be performed in the presence of a dielectric layer with a uniform thickness on the metal. The thickness of the dielectric coating should be large enough for the radiative losses because of the SPP scattering on the surface roughness and inhomogeneities to be significantly less than the Joule losses of the SPPs in the metal, although not large enough to make it impossible to measure the SPP decay with an acceptable accuracy. The choice of the optimal thickness of the dielectric layer depends on many factors [62]: the type of the metal, its state (surface of bulk or deposited metal), substrate roughness, optical homogeneity of the metal film, and the optical density of the dielectric. The proposed method of the plasmon refractometry of a conducting surface can be applied not only to metals but also to other materials used in THz plasmonics (doped semiconductors [31], graphene [63], dielectrics on absorption lines, etc.), which provide the macroscopic propagation length of the surface wave. Using the ε_m value found via the method proposed will enable more adequate modeling of the operation of the elements and devices of THz plasmonics, plasmonic sensors, and communication lines.