Research on Dynamic Process and Droplet Splash of Laser-Induced Cavitation Bubble Collapse within a Droplet
Abstract
:1. Introduction
2. Experimental System and Definition
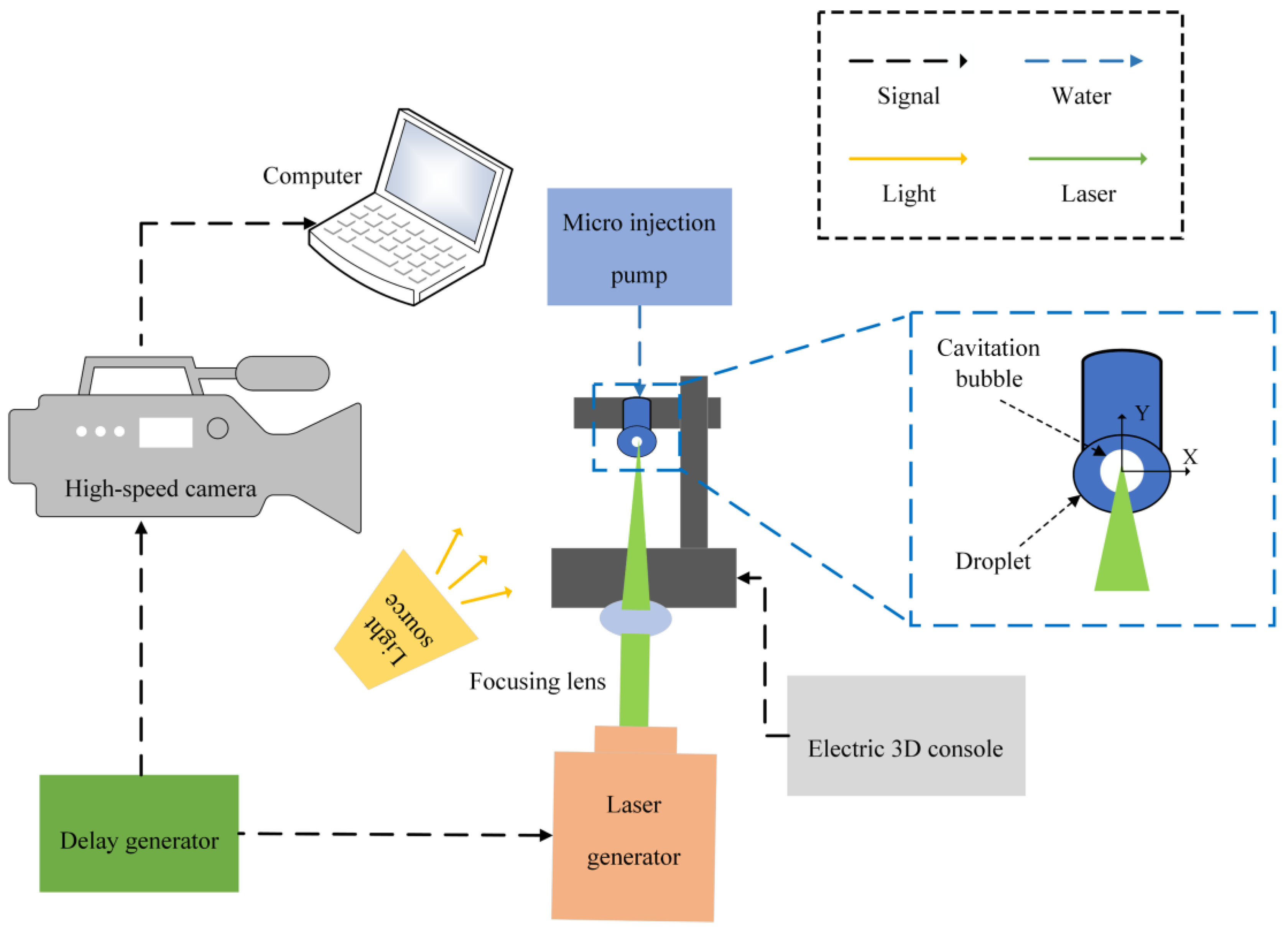
2.1. Experimental System
2.2. Definition of Feature Points and Radius Ratio
2.3. Three Typical Splash Cases
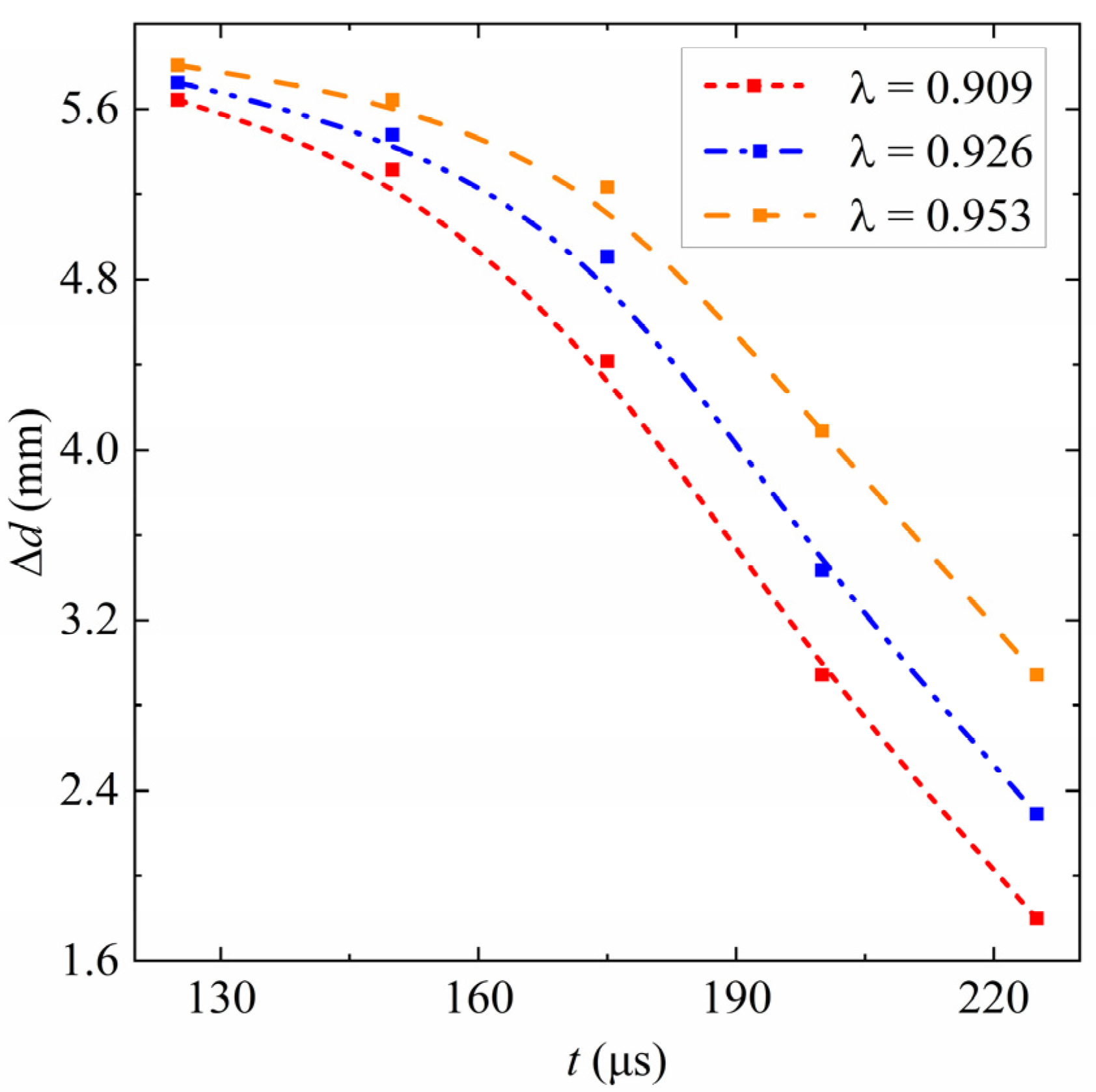
3. Quantitative Analysis of No Splash
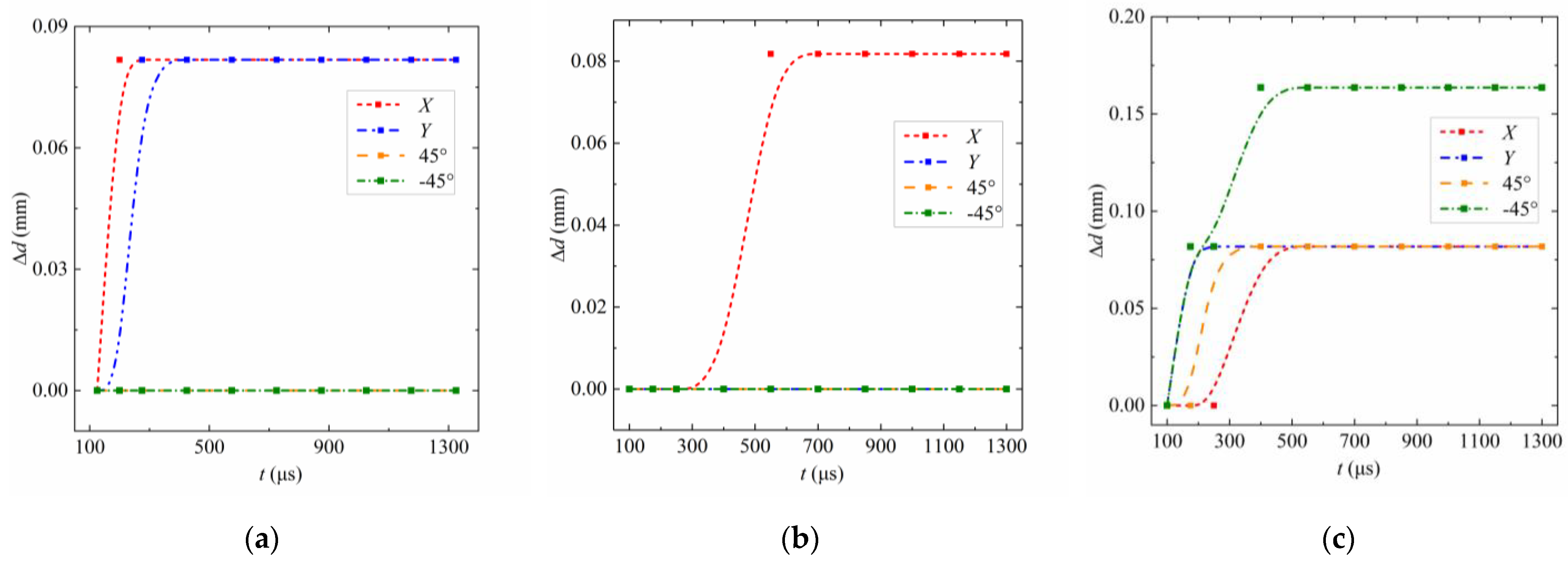
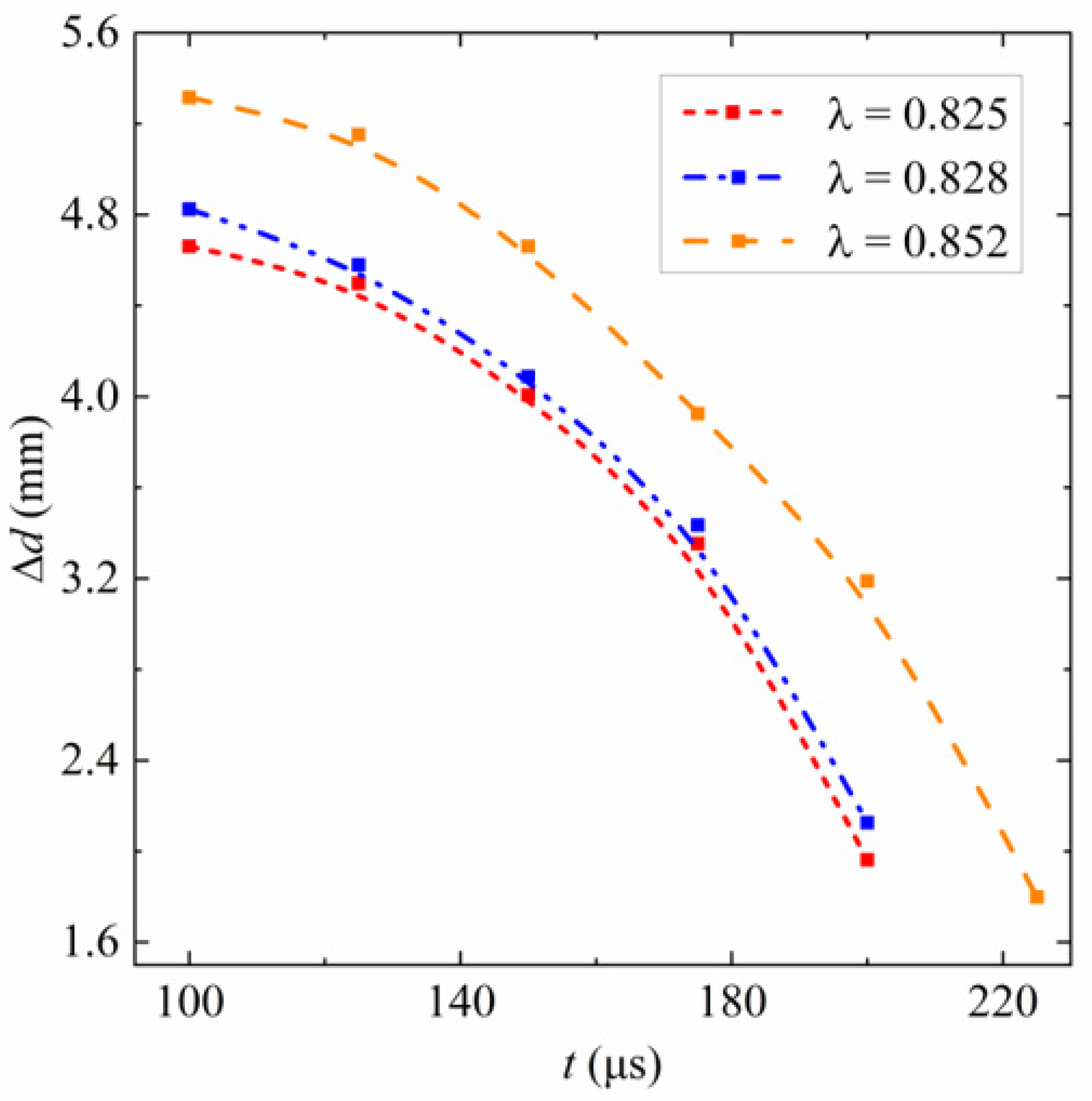
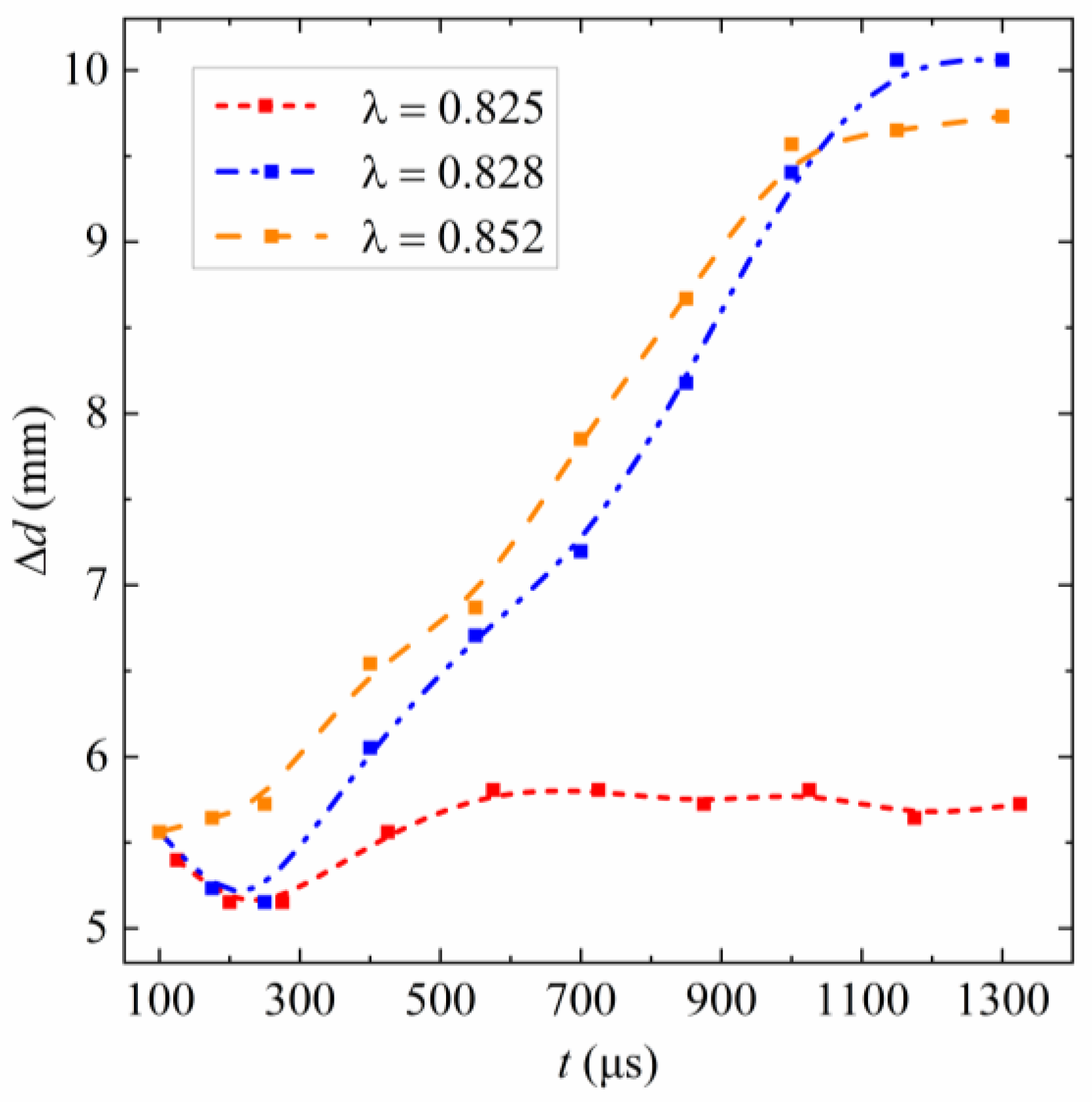
3.1. Bubble Feature Points
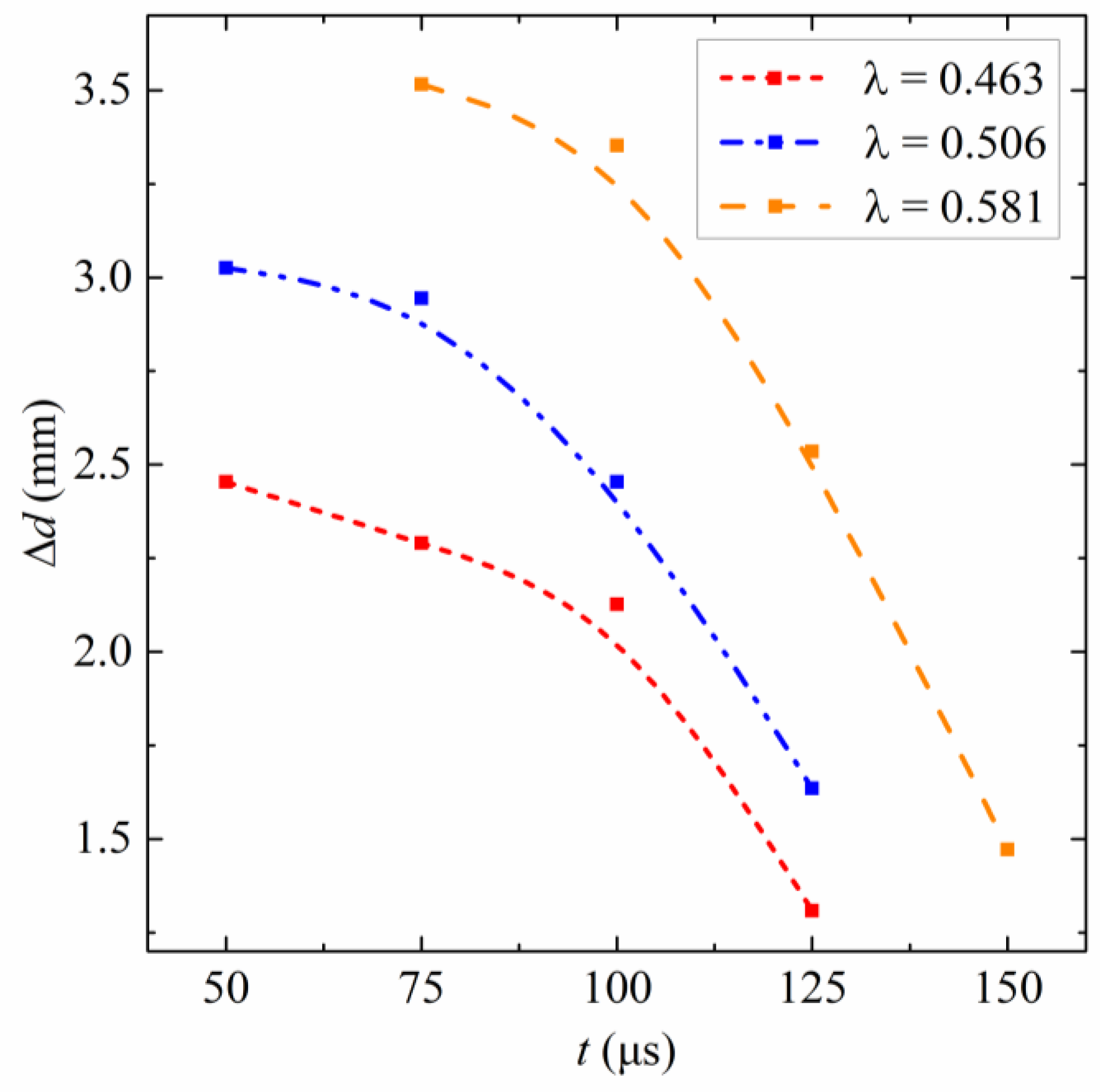
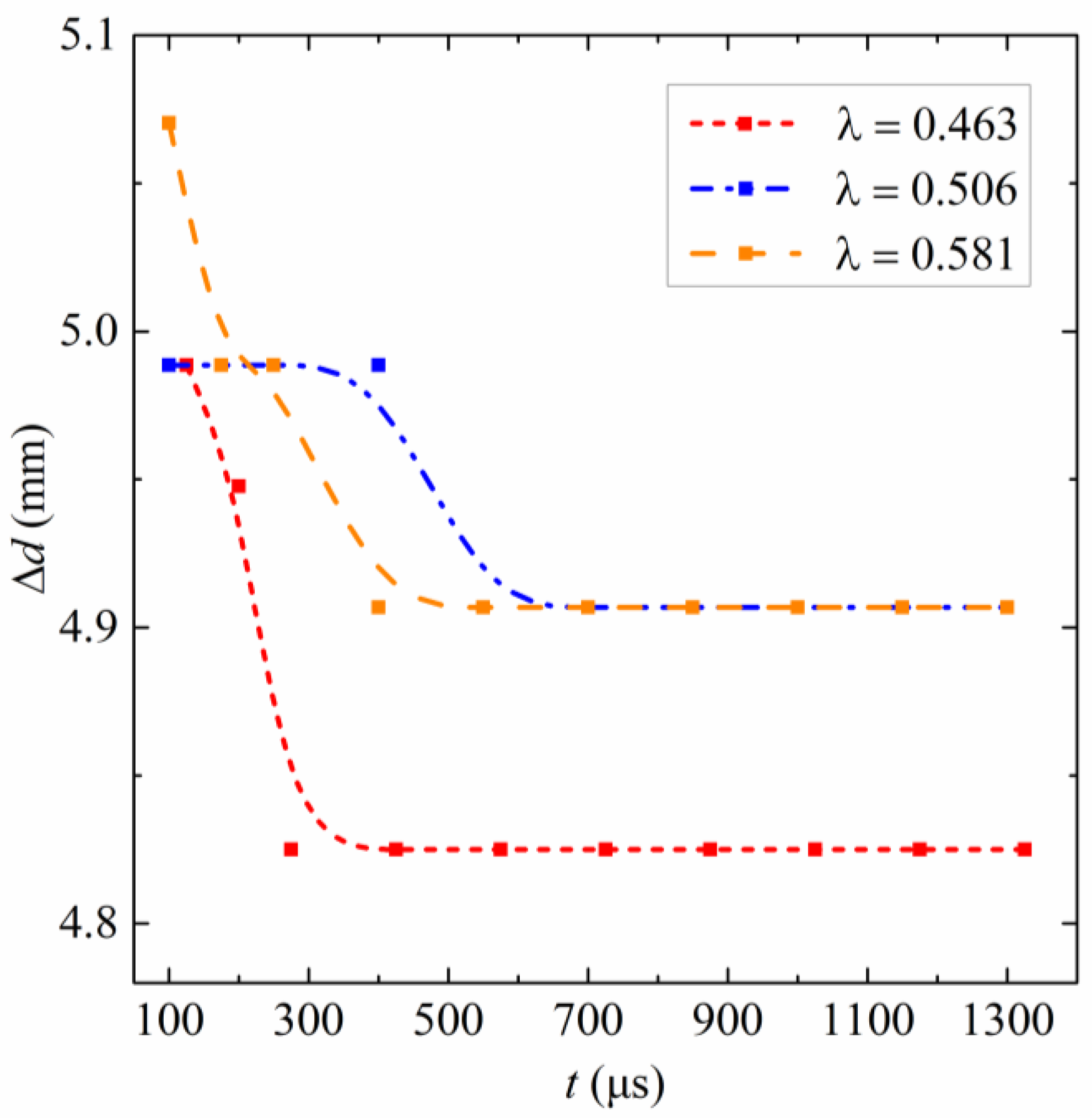
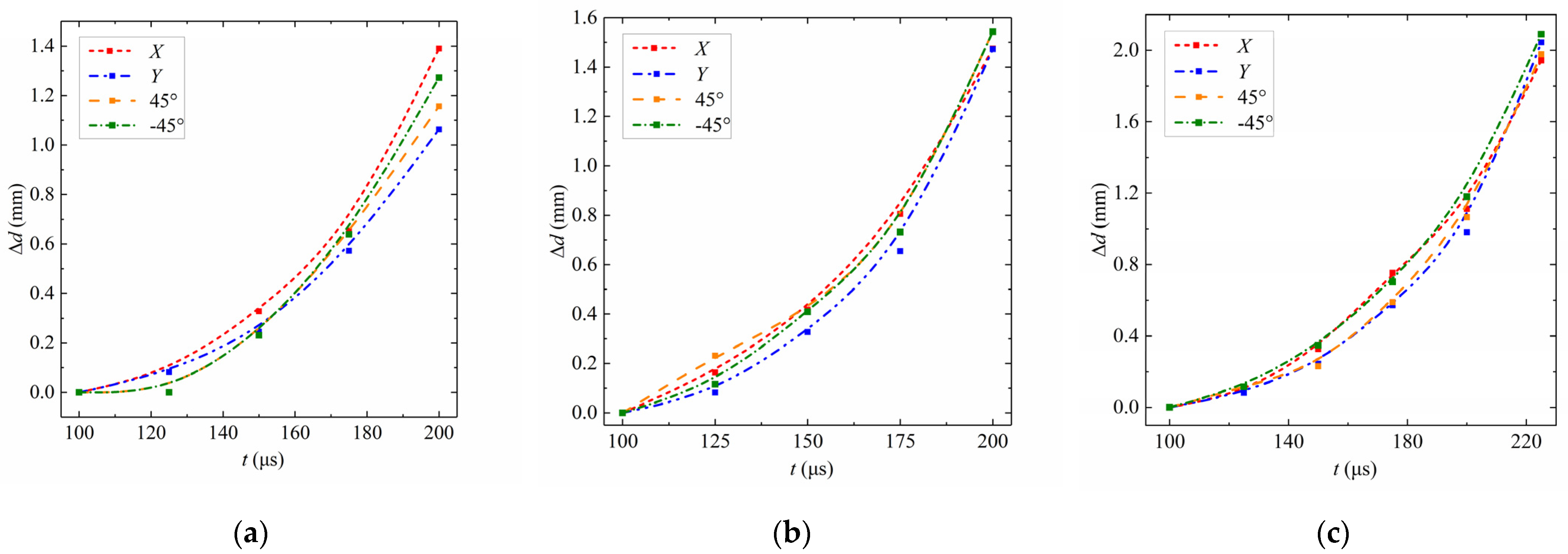
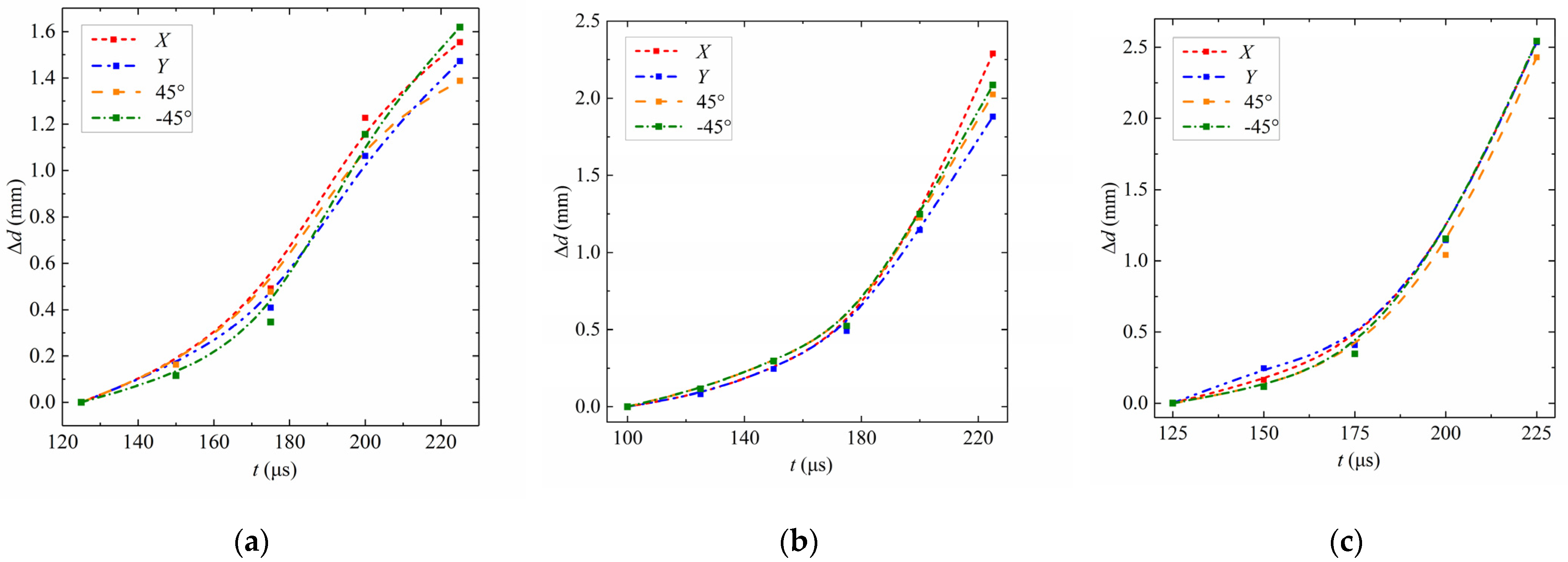
3.2. Droplet Feature Points
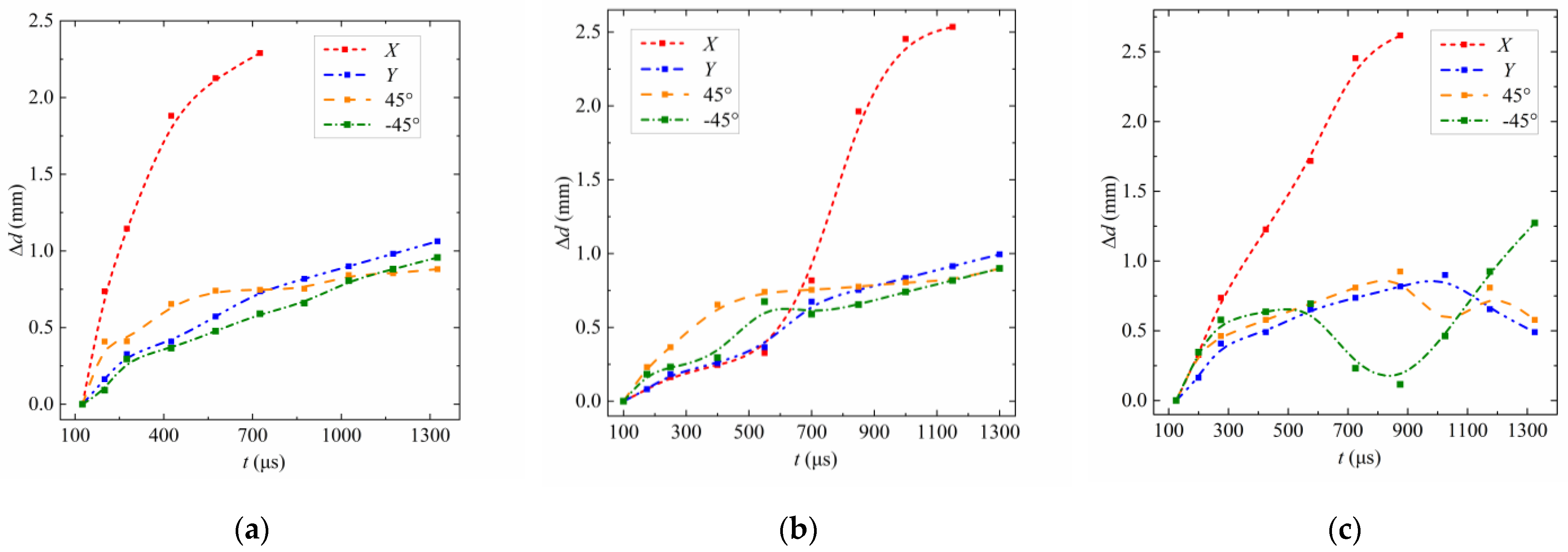
4. Quantitative Analysis of Scattering Splash
4.1. Bubble Feature Points
4.2. Droplet Feature Points
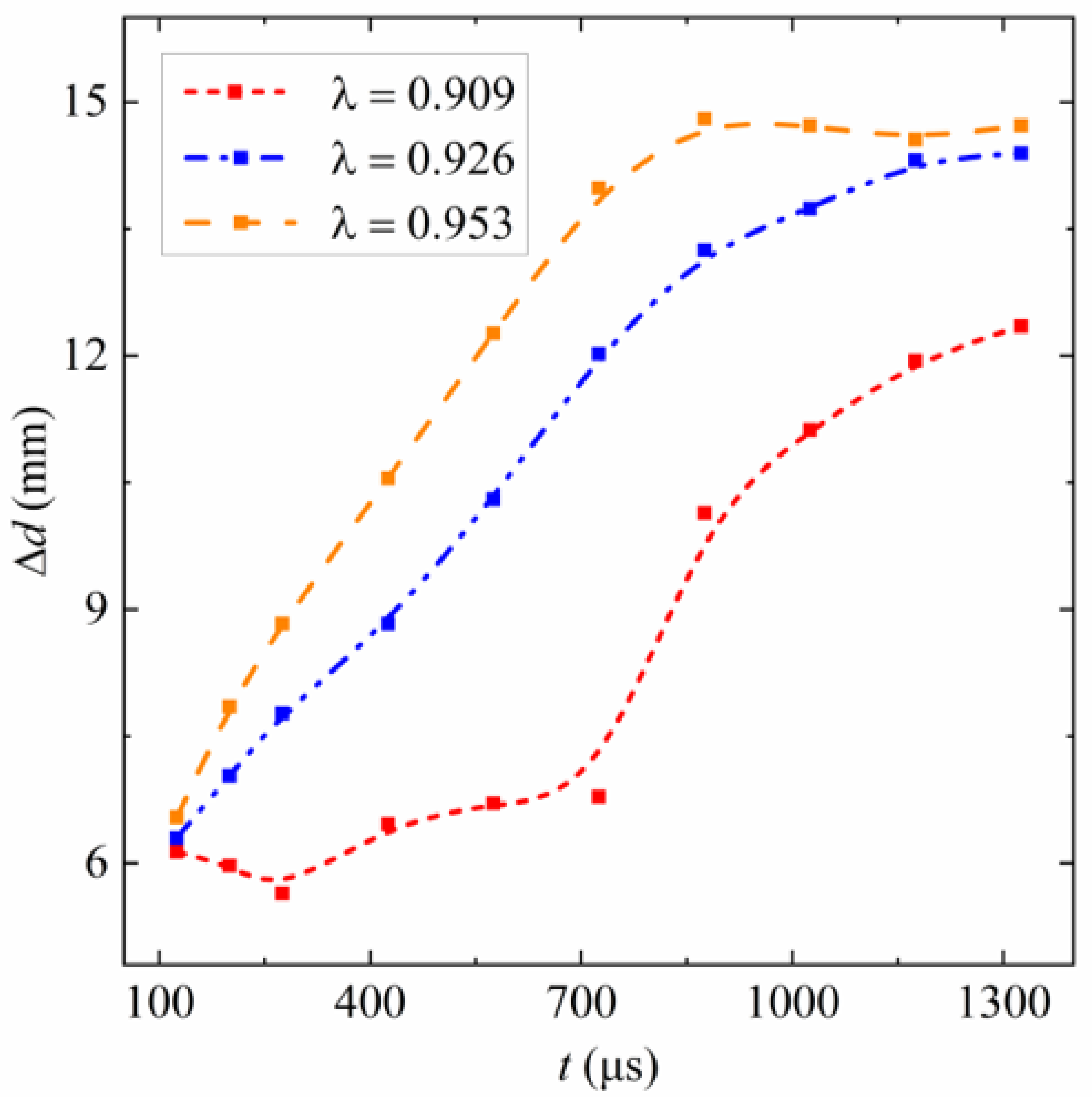
5. Quantitative Analysis of Composite Splash
5.1. Bubble Feature Points
5.2. Droplet Feature Points
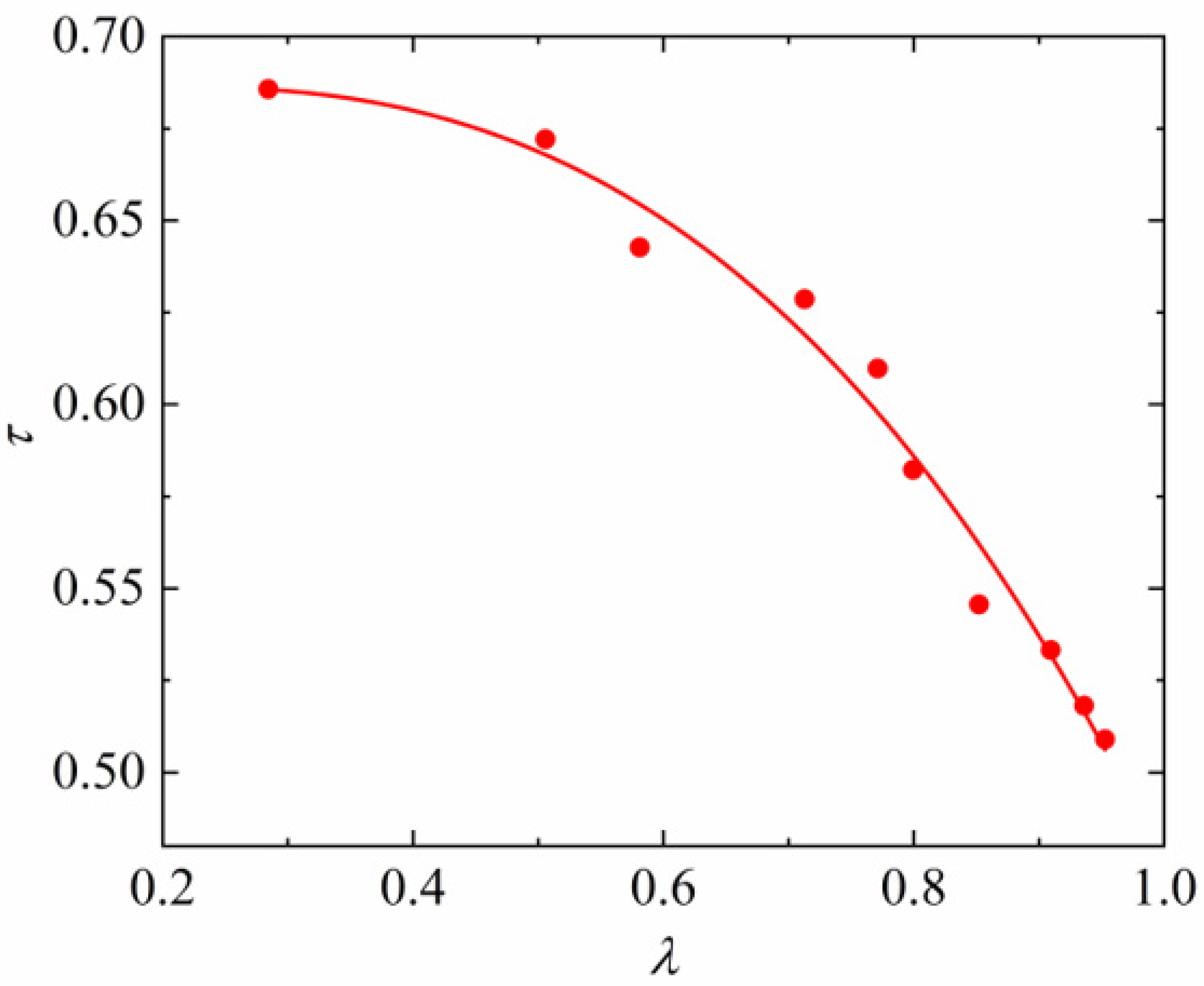
6. Discussion of Collapse Time
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Salvador, F.J.; Martínez-López, J.; Caballer, M.; De Alfonso, C. Study of the influence of the needle lift on the internal flow and cavitation phenomenon in diesel injector nozzles by CFD using RANS methods. Energy Conv. Manag. 2013, 66, 246–256. [Google Scholar] [CrossRef] [Green Version]
- Som, S.; Ramirez, A.I.; Longman, D.E.; Aggarwal, S.K. Effect of nozzle orifice geometry on spray, combustion, and emission characteristics under diesel engine conditions. Fuel 2011, 90, 1267–1276. [Google Scholar] [CrossRef]
- Blessing, M.; König, G.; Krüger, C.; Michels, U.; Schwarz, V. Analysis of Flow and Cavitation Phenomena in Diesel Injection Nozzles and Its Effects on Spray and Mixture Formation. SAE Trans. 2003, 112, 1694–1706. [Google Scholar]
- Wang, X.; Su, W. A numerical study of cavitating flows in high-pressure diesel injection nozzle holes using a two-fluid model. Sci. Bull. 2009, 54, 1655–1662. [Google Scholar] [CrossRef]
- He, Z.; Zhong, W.; Wang, Q.; Jiang, Z.; Fu, Y. An investigation of transient nature of the cavitating flow in injector nozzles. Appl. Therm. Eng. 2013, 54, 56–64. [Google Scholar] [CrossRef]
- Ghiji, M.; Goldsworthy, L.; Brandner, P.A.; Garaniya, V.; Hield, P. Analysis of diesel spray dynamics using a compressible Eulerian/VOF/LES model and microscopic shadowgraphy. Fuel 2017, 188, 352–366. [Google Scholar] [CrossRef] [Green Version]
- Suh, H.K.; Lee, C.S. Effect of cavitation in nozzle orifice on the diesel fuel atomization characteristics. Int. J. Heat Fluid Flow 2008, 29, 1001–1009. [Google Scholar] [CrossRef]
- Yan, W. Experimental Study on Atomization Characteristics of Diesel Engine under Different Environmental Pressure and Temperature. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2018. [Google Scholar]
- Payri, R.; Garcia, J.; Salvador, F.; Gimeno, J. Using spray momentum flux measurements to understand the influence of diesel nozzle geometry on spray characteristics. Fuel 2005, 84, 551–561. [Google Scholar] [CrossRef]
- Lv, M.; Ning, Z.; Yan, K. The Instability of Vapor Bubble Growth within the Diesel Droplet under the Condition of Supercavitation. Adv. Mater. Res. 2012, 512–515, 477–480. [Google Scholar] [CrossRef]
- Kodama, T.; Tomita, Y. Cavitation bubble behavior and bubble–shock wave interaction near a gelatin surface as a study of in vivo bubble dynamics. Appl. Phys. B 2000, 70, 139–149. [Google Scholar] [CrossRef]
- Sankin, G.N.; Zhong, P. Interaction between shock wave and single inertial bubbles near an elastic boundary. Phys. Rev. E Cover. Stat. Nonlinear Biol. Soft Matter Phys. 2006, 74, 46304. [Google Scholar] [CrossRef] [Green Version]
- Arora, A.; Hakim, I.; Baxter, J.; Rathnasingham, R.; Srinivasan, R.; Fletcher, D.A.; Mitragotri, S. Needle-free delivery of macromolecules across the skin by nanoliter-volume pulsed microjets. Proc. Natl. Acad. Sci. USA 2007, 104, 4255–4260. [Google Scholar] [CrossRef] [PubMed]
- Baxter, J.; Mitragotri, S. Needle-free liquid jet injections: Mechanisms and applications. Expert Rev. Med. Devices 2014, 3, 565–574. [Google Scholar] [CrossRef] [PubMed]
- Fletcher, D.A.; Palanker, D.V.; Huie, P.; Miller, J.; Marmor, M.F.; Blumenkranz, M.S. Intravascular drug delivery with a pulsed liquid microjet. Arch. Ophthalmol. 2002, 120, 1206–1208. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Zhu, B.; Huang, J.; Xiang, X.; Tang, Y.; Ma, L.; Yan, F.; Cheng, C.; Qiu, L. Ultrasound-targeted microbubble destruction augmented synergistic therapy of rheumatoid arthritisvia targeted liposomes. J. Mat. Chem. B 2020, 8, 5245–5256. [Google Scholar] [CrossRef]
- Martin, G.D.; Hoath, S.D.; Hutchings, I.M. Inkjet printing-the physics of manipulating liquid jets and drops. J. Phys. Conf. Ser. 2008, 105, 12001. [Google Scholar] [CrossRef]
- de Gans, B.J.; Duineveld, P.C.; Schubert, U.S. Inkjet Printing of Polymers: State of the Art and Future Developments. Adv. Mater. 2004, 16, 203–213. [Google Scholar] [CrossRef]
- Patrascioiu, A.; Fernández-Pradas, J.M.; Palla-Papavlu, A.; Morenza, J.L.; Serra, P. Laser-generated liquid microjets: Correlation between bubble dynamics and liquid ejection. Microfluid. Nanofluid. 2014, 16, 55–63. [Google Scholar] [CrossRef]
- Brown, M.S.; Kattamis, N.T.; Arnold, C.B. Time-resolved dynamics of laser-induced micro-jets from thin liquid films. Microfluid. Nanofluid. 2011, 11, 199–207. [Google Scholar] [CrossRef]
- Obreschkow, D.; Kobel, P.; Dorsaz, N.; de Bosset, A.; Nicollier, C.; Farhat, M. Cavitation bubble dynamics inside liquid drops in microgravity. Phys. Rev. Lett. 2006, 97, 94502. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Wang, S.P.; Zhang, A.M. Experimental study on the interaction between bubble and free surface using a high-voltage spark generator. Phys. Fluids 2016, 28, 32109. [Google Scholar] [CrossRef]
- Gonzalez Avila, S.R.; Ohl, C. Fragmentation of acoustically levitating droplets by laser-induced cavitation bubbles. J. Fluid Mech. 2016, 805, 551–576. [Google Scholar] [CrossRef]
- Lindau, O.; Lauterborn, W. Cinematographic observation of the collapse and rebound of a laser-produced cavitation bubble near a wall. J. Fluid Mech. 2003, 479, 327–348. [Google Scholar] [CrossRef]
- Liu, X.M.; He, J.; Lu, J.; Ni, X.W. Effect of surface tension on a liquid-jet produced by the collapse of a laser-induced bubble against a rigid boundary. Opt. Laser Technol. 2009, 41, 21–24. [Google Scholar] [CrossRef]
- Lü, M.; Ning, Z.; Yan, K.; Fu, J.; Song, Y.; Sun, C. Breakup of cavitation bubbles within the diesel droplet. Chin. J. Mech. Eng. 2014, 27, 198–204. [Google Scholar] [CrossRef]
- Kobel, P.; Obreschkow, D.; de Bosset, A.; Dorsaz, N.; Farhat, M. Techniques for generating centimetric drops in microgravity and application to cavitation studies. Exp. Fluids 2009, 47, 39–48. [Google Scholar] [CrossRef] [Green Version]
- Luo, X.; Gong, H.; Cao, J.; Yin, H.; Yan, Y.; He, L. Enhanced separation of water-in-oil emulsions using ultrasonic standing waves. Chem. Eng. Sci. 2019, 203, 285–292. [Google Scholar] [CrossRef]
- Kang, Y.J.; Cho, Y. Gravity-capillary jet-like surface waves generated by an underwater bubble. J. Fluid Mech. 2019, 866, 841–864. [Google Scholar] [CrossRef]
- Liang, Y.; Jiang, Y.; Wen, C.; Liu, Y. Interaction of a planar shock wave and a water droplet embedded with a vapour cavity. J. Fluid Mech. 2020, 885, R6. [Google Scholar] [CrossRef]
- Zeng, Q.; Gonzalez-Avila, S.R.; Voorde, S.T.; Ohl, C. Jetting of viscous droplets from cavitation-induced Rayleigh-Taylor instability. J. Fluid Mech. 2018, 846, 916–943. [Google Scholar] [CrossRef]
- Wang, J.; Li, H.; Guo, W.; Wang, Z.; Du, T.; Wang, Y.; Abe, A.; Huang, C. Rayleigh-Taylor instability of cylindrical water droplet induced by laser-produced cavitation bubble. J. Fluid Mech. 2021, 919, A42. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Zhang, X.; Zhang, S.; Wang, H.; Zha, K.; Li, Z.; Zhang, Y. Research on Dynamic Process and Droplet Splash of Laser-Induced Cavitation Bubble Collapse within a Droplet. Appl. Sci. 2023, 13, 7862. https://doi.org/10.3390/app13137862
Zhang Y, Zhang X, Zhang S, Wang H, Zha K, Li Z, Zhang Y. Research on Dynamic Process and Droplet Splash of Laser-Induced Cavitation Bubble Collapse within a Droplet. Applied Sciences. 2023; 13(13):7862. https://doi.org/10.3390/app13137862
Chicago/Turabian StyleZhang, Yuning, Xiaofei Zhang, Shurui Zhang, Hongbo Wang, Kehui Zha, Zhaohao Li, and Yuning Zhang. 2023. "Research on Dynamic Process and Droplet Splash of Laser-Induced Cavitation Bubble Collapse within a Droplet" Applied Sciences 13, no. 13: 7862. https://doi.org/10.3390/app13137862
APA StyleZhang, Y., Zhang, X., Zhang, S., Wang, H., Zha, K., Li, Z., & Zhang, Y. (2023). Research on Dynamic Process and Droplet Splash of Laser-Induced Cavitation Bubble Collapse within a Droplet. Applied Sciences, 13(13), 7862. https://doi.org/10.3390/app13137862




