Cooperative Jamming-Assisted Untrusted Relaying Based on Game Theory for Next-Generation Communication Systems
Abstract
:1. Introduction
Literature Review Comparison
- We investigate the secrecy rate of the PU and the utility rate of the CJs/SUs, based on the locations of the CJs for the AF-based untrusted relaying case.
- The model of the Stackelberg game between PU and CJs, as well as that of the power control game among CJs, are derived and investigated when an untrusted relaying terminal is employed.
- We extend the CJST scheme in [48] to the case where the eavesdropper is considered to be an untrusted relay. We further extend the single CJ-assisted UR-CJST scheme [51] to multiple CJs, which we refer to as Untrusted Relaying-aided Multiple Cooperative Jammers-based Simultaneous Transmission (UR-MCJST).
- Finally, an Untrusted Relaying-aided Multiple Cooperative Jammers-based Time-Division Transmission (UR-MCJTDT) scheme is proposed, where time division is considered in the utility phase. The performances of both UR-MCJST and UR-MCJTDT schemes are investigated.
2. System Model
2.1. Cooperative Jamming Model
2.2. Stackelberg Game Model
3. Transmission Scenarios
3.1. UR-MCJST Scenario
3.2. UR-MCJTDT Scenario
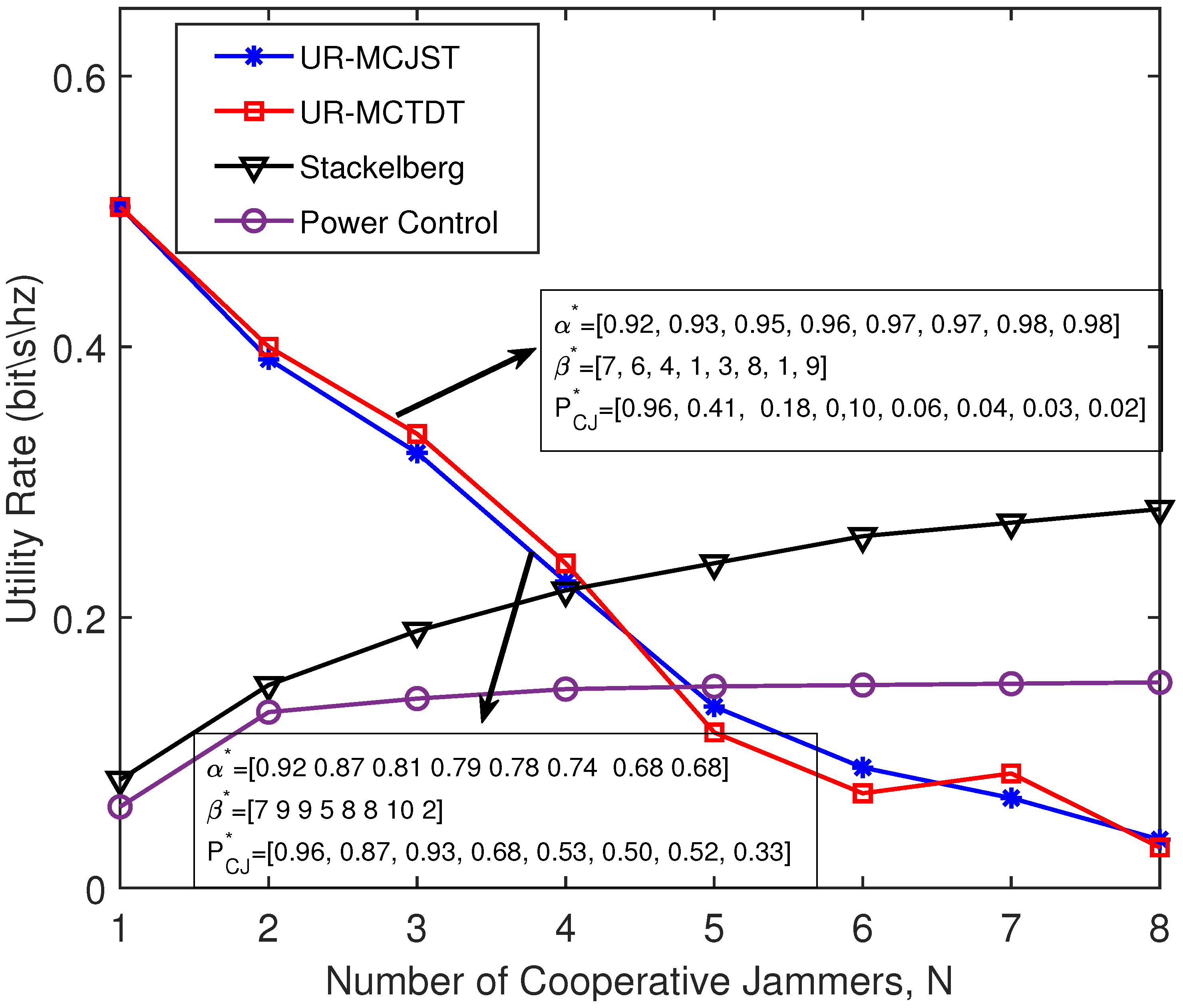
4. Results and Discussions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zou, Y.; Zhu, J.; Wang, X.; Hanzo, L. A Survey on Wireless Security: Technical Challenges, Recent Advances, and Future Trends. Proc. IEEE 2016, 104, 1727–1765. [Google Scholar] [CrossRef]
- Shannon, C.E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Wyner, A.D. The wiretap channel. Bell Syst. Tech. J. 1975, 54, 1355–1387. [Google Scholar] [CrossRef]
- Csiszar, J.; Korner, J. Broadcast channels with confidential messages. IEEE Trans. Inf. Theory 1978, 24, 339–348. [Google Scholar] [CrossRef] [Green Version]
- Mucchi, L.; Jayousi, S.; Caputo, S.; Panayirci, E.; Shahabuddin, S.; Bechtold, J.; Morales, I.; Stoica, R.A.; Abreu, G.; Haas, H. Physical-Layer Security in 6G Networks. IEEE Open J. Commun. Soc. 2021, 2, 1901–1914. [Google Scholar] [CrossRef]
- Yang, N.; Wang, L.; Geraci, G.; Elkashlan, M.; Yuan, J.; Renzo, M.D. Safeguarding 5G wireless communication networks using physical layer security. IEEE Commun. Mag. 2015, 53, 20–27. [Google Scholar] [CrossRef]
- Kong, Z.; Yang, S.; Wang, D.; Hanzo, L. Robust Beamforming and Jamming for Enhancing the Physical Layer Security of Full Duplex Radios. IEEE Trans. Inf. Forensics Secur. 2019, 14, 3151–3159. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Rajendran, S.; Sun, Z.; Woods, R.; Hanzo, L. Physical Layer Security for the Internet of Things: Authentication and Key Generation. IEEE Wirel. Commun. 2019, 26, 92–98. [Google Scholar] [CrossRef] [Green Version]
- Tekin, E.; Yener, A. The general Gaussian multiple-access and two-way wiretap channels: Achievable rates and Cooperative Jamming. IEEE Trans. Inf. Theory 2008, 54, 2735–2751. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.; Tao, M.; Kennedy, R. Cooperative jamming for secrecy in decentralized wireless networks. In Proceedings of the IEEE International Conference on Communications (ICC), Ottawa, ON, Canada, 10–15 June 2012; pp. 2339–2344. [Google Scholar] [CrossRef]
- Zhou, Y.; Yeoh, P.L.; Chen, H.; Li, Y.; Schober, R.; Zhuo, L.; Vucetic, B. Improving Physical Layer Security via a UAV Friendly Jammer for Unknown Eavesdropper Location. IEEE Trans. Veh. Technol. 2018, 67, 11280–11284. [Google Scholar] [CrossRef]
- Li, A.; Wu, Q.; Zhang, R. UAV-enabled cooperative jamming for improving secrecy of ground wiretap channel. IEEE Wirel. Commun. Lett. 2018, 8, 181–184. [Google Scholar] [CrossRef] [Green Version]
- Sun, X.; Ng, D.W.K.; Ding, Z.; Xu, Y.; Zhong, Z. Physical layer security in UAV systems: Challenges and opportunities. arXiv 2019, arXiv:1909.06785. [Google Scholar] [CrossRef] [Green Version]
- Sendonaris, A.; Erkip, E.; Aazhang, B. User Cooperation Diversity Part I: System Description. IEEE Trans. Commun. 2003, 51, 1927–1938. [Google Scholar] [CrossRef] [Green Version]
- Laneman, N.; Tse, D.N.C.; Wornell, G.W. Cooperative diversity in wireless networks: Efficient protocols and outage behavior. IEEE Trans. Inf. Theory 2004, 50, 3062–3080. [Google Scholar] [CrossRef]
- Dohler, M.; Li, Y. Cooperative Communications: Hardware, Channel and PHY; John Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Ng, S.X.; Li, Y.; Vucetic, B.; Hanzo, L. Distributed Irregular Codes Relying on Decode-and-Forward Relays as Code Components. IEEE Trans. Veh. Technol. 2015, 64, 4579–4588. [Google Scholar] [CrossRef] [Green Version]
- Khan, A.U.; Abbas, G.; Abbas, Z.H.; Bilal, M.; Shah, S.C.; Song, H. Reliability Analysis of Cognitive Radio Networks With Reserved Spectrum for 6G-IoT. IEEE Trans. Netw. Serv. Manag. 2022, 19, 2726–2737. [Google Scholar] [CrossRef]
- Khan, A.U.; Abbas, G.; Abbas, Z.H.; Khan, W.U.; Waqas, M. Spectrum utilization efficiency in CRNs with hybrid spectrum access and channel reservation: A comprehensive analysis under prioritized traffic. Future Gener. Comput. Syst. 2021, 125, 726–742. [Google Scholar] [CrossRef]
- Haykin, S. Cognitive radio: Brain-empowered wireless communications. IEEE J. Sel. Areas Commun. 2005, 23, 201–220. [Google Scholar] [CrossRef]
- Chen, Y.; Yu, G.; Zhang, Z.; Chen, H.; Qiu, P. On cognitive radio networks with opportunistic power control strategies in fading channels. IEEE Trans. Wirel. Commun. 2008, 7, 2752–2761. [Google Scholar] [CrossRef]
- Letaief, K.B.; Zhang, W. Cooperative Communications for Cognitive Radio Networks. Proc. IEEE 2009, 97, 878–893. [Google Scholar] [CrossRef] [Green Version]
- Goldsmith, A.; Jafar, S.A.; Maric, I.; Srinivasa, S. Breaking Spectrum Gridlock With Cognitive Radios: An Information Theoretic Perspective. Proc. IEEE 2009, 97, 894–914. [Google Scholar] [CrossRef]
- Zaidi, S.A.R.; McLernon, D.C.; Ghogho, M. Breaking the Area Spectral Efficiency Wall in Cognitive Underlay Networks. IEEE J. Sel. Areas Commun. 2014, 32, 2205–2221. [Google Scholar] [CrossRef]
- Nie, J.; Luo, J.; Xiong, Z.; Niyato, D.; Wang, P. A Stackelberg Game Approach Toward Socially-Aware Incentive Mechanisms for Mobile Crowdsensing. IEEE Trans. Wirel. Commun. 2019, 18, 724–738. [Google Scholar] [CrossRef]
- Li, F.; Yao, H.; Du, J.; Jiang, C.; Qian, Y. Stackelberg Game-Based Computation Offloading in Social and Cognitive Industrial Internet of Things. IEEE Trans. Ind. Inform. 2020, 16, 5444–5455. [Google Scholar] [CrossRef]
- Tang, L.; Chen, H.; Li, Q. Social Tie Based Cooperative Jamming for Physical Layer Security. IEEE Commun. Lett. 2015, 19, 1790–1793. [Google Scholar] [CrossRef]
- Krikidis, I.; Thompson, J.S.; McLaughlin, S. Relay selection for secure cooperative networks with jamming. IEEE Trans. Wirel. Commun. 2009, 8, 5003–5011. [Google Scholar] [CrossRef]
- Bao, V.N.Q.; Linh-Trung, N.; Debbah, M. Relay selection schemes for dual-hop networks under security constraints with multiple eavesdroppers. IEEE Trans. Wirel. Commun. 2013, 12, 6076–6085. [Google Scholar] [CrossRef] [Green Version]
- Dong, L.; Han, Z.; Petropulu, A.P.; Poor, H.V. Improving wireless physical layer security via cooperating relays. IEEE Trans. Signal Process. 2010, 58, 1875–1888. [Google Scholar] [CrossRef]
- Liang, W.; Ng, S.X.; Hanzo, L. Cooperative Overlay Spectrum Access in Cognitive Radio Networks. IEEE Commun. Surv. Tutor. 2017, 19, 1924–1944. [Google Scholar] [CrossRef] [Green Version]
- Ali, B.; Zamir, N.; Butt, M.F.U.; Ng, S.X. Physical layer security: Friendly jamming in an untrusted relay scenario. In Proceedings of the 2016 24th European Signal Processing Conference (EUSIPCO), Budapest, Hungary, 28 August–2 September 2016; pp. 958–962. [Google Scholar] [CrossRef] [Green Version]
- Ali, B.; Zamir, N.; Ng, S.X.; Butt, M.F.U. Distributed Matching Algorithms: Maximizing Secrecy in the Presence of Untrusted Relay. Radioengineering 2017, 26, 601–610. [Google Scholar] [CrossRef]
- Saad, W.; Zhou, X.; Maham, B.; Basar, T.; Poor, H.V. Tree Formation with Physical Layer Security Considerations in Wireless Multi-Hop Networks. IEEE Trans. Wirel. Commun. 2012, 11, 3980–3991. [Google Scholar] [CrossRef] [Green Version]
- He, X.; Yener, A. Cooperation with an untrusted relay: A secrecy perspective. IEEE Trans. Inf. Theory 2010, 56, 3807–3827. [Google Scholar] [CrossRef] [Green Version]
- Moya Osorio, D.P.; Alves, H.; Benitez Olivo, E.E. On the Secrecy Performance and Power Allocation in Relaying Networks With Untrusted Relay in the Partial Secrecy Regime. IEEE Trans. Inf. Forensics Secur. 2020, 15, 2268–2281. [Google Scholar] [CrossRef] [Green Version]
- Kuhestani, A.; Mohammadi, A.; Yeoh, P.L. Optimal Power Allocation and Secrecy Sum Rate in Two-Way Untrusted Relaying Networks With an External Jammer. IEEE Trans. Commun. 2018, 66, 2671–2684. [Google Scholar] [CrossRef]
- Zhao, R.; Tan, X.; Chen, D.H.; He, Y.C.; Ding, Z. Secrecy Performance of Untrusted Relay Systems With a Full-Duplex Jamming Destination. IEEE Trans. Veh. Technol. 2018, 67, 11511–11524. [Google Scholar] [CrossRef]
- Jiang, W.; Gong, Y.; Xiao, Q.; Liao, Y. Secrecy Rate Maximization for Untrusted Relay Networks With Nonorthogonal Cooperative Transmission Protocols. IEEE Trans. Veh. Technol. 2018, 67, 6325–6339. [Google Scholar] [CrossRef]
- Sun, L.; Zhang, T.; Li, Y.; Niu, H. Performance study of two-hop amplify-and-forward systems with untrustworthy relay nodes. IEEE Trans. Veh. Technol. 2012, 61, 3801–3807. [Google Scholar] [CrossRef]
- Yan, S.; Yang, N.; Land, I.; Malaney, R.; Yuan, J. Three Artificial-Noise-Aided Secure Transmission Schemes in Wiretap Channels. IEEE Trans. Veh. Technol. 2018, 67, 3669–3673. [Google Scholar] [CrossRef] [Green Version]
- Lai, L.; Gamal, H.L. The relay–eavesdropper channel: Cooperation for secrecy. IEEE Trans. Inf. Theory 2008, 54, 4005–4019. [Google Scholar] [CrossRef]
- Ekrem, E.; Ulukus, S. Secrecy in cooperative relay broadcast channels. IEEE Trans. Inf. Theory 2011, 57, 137–155. [Google Scholar] [CrossRef] [Green Version]
- Khodakarami, H.; Lahouti, F. Link Adaptation with Untrusted Relay Assignment: Design and Performance Analysis. IEEE Trans. Commun. 2013, 61, 4874–4883. [Google Scholar] [CrossRef]
- Sun, L.; Ren, P.; Du, Q.; Wang, Y.; Gao, Z. Security-Aware Relaying Scheme for Cooperative Networks With Untrusted Relay Nodes. IEEE Commun. Lett. 2015, 19, 463–466. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, K.J.R. An Information Secrecy Game in Cognitive Radio Networks. IEEE Trans. Inf. Forensics Secur. 2011, 6, 831–842. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R.; Song, L.; Han, Z.; Jiao, B. Physical Layer Security for Two-Way Untrusted Relaying With Friendly Jammers. IEEE Trans. Veh. Technol. 2012, 61, 3693–3704. [Google Scholar] [CrossRef]
- Stanojev, I.; Yener, A. Improving Secrecy Rate via Spectrum Leasing for Friendly Jamming. IEEE Trans. Wirel. Commun. 2013, 12, 134–145. [Google Scholar] [CrossRef] [Green Version]
- Al-Talabani, A.; Deng, Y.; Nallanathan, A.; Nguyen, H.X. Enhancing Secrecy Rate in Cognitive Radio Networks via Multilevel Stackelberg Game. IEEE Commun. Lett. 2016, 20, 1112–1115. [Google Scholar] [CrossRef] [Green Version]
- Jeon, H.; McLaughlin, S.W.; Kim, I.M.; Ha, J. Secure Communications with Untrusted Secondary Nodes in Cognitive Radio Networks. IEEE Trans. Wirel. Commun. 2014, 13, 1790–1805. [Google Scholar] [CrossRef]
- Zamir, N.; Ali, B.; Butt, M.F.U.; Ng, S.X. Improving secrecy rate via cooperative jamming based on Nash Equilibrium. In Proceedings of the 24th European Signal Processing Conference (EUSIPCO), Budapest, Hungary, 28 August–2 September 2016; pp. 235–239. [Google Scholar] [CrossRef] [Green Version]
- Moradikia, M.; Bastami, H.; Kuhestani, A.; Behroozi, H.; Hanzo, L. Cooperative Secure Transmission Relying on Optimal Power Allocation in the Presence of Untrusted Relays, A Passive Eavesdropper and Hardware Impairments. IEEE Access 2019, 7, 116942–116964. [Google Scholar] [CrossRef]
- Izanlou, M.; Mohammadi, A.; Dosaranian-Moghadam, M. Impact of imperfect channel state information on the physical layer security in D2D wireless networks using untrusted relays. Wirel. Pers. Commun. 2021, 116, 341–368. [Google Scholar] [CrossRef]
- Hayajneh, M.; Gulliver, T.A. Physical Layer Security in Two-Way SWIPT Relay Networks with Imperfect CSI and a Friendly Jammer. Entropy 2023, 25, 122. [Google Scholar] [CrossRef]
- Ali, B. Rate Optimization and Resource Allocation in Cooperative Cognitive Radio Networks. Ph.D. Thesis, COMSATS Institute of Information Technology Islamabad, Islamabad, Pakistan, 2017. [Google Scholar]
- Ochiai, P.M.H.; Tarokh, V. Design and analysis of collaborative diversity protocols for wireless sensor networks. In Proceedings of the IEEE Vehicular Technology Conference, (VTC-04 Fall), Los Angeles, CA, USA, 26–29 September 2004; pp. 4645–4649. [Google Scholar] [CrossRef]
- Osborne, M.J.; Rubenstein, A. A Course in Game Theory; MIT Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Simeone, O.; Stanojev, I.; Savazzi, S.; Bar-Ness, Y.; Spagnolini, U.; Pickholtz, R. Spectrum Leasing to Cooperating Secondary Ad Hoc Networks. IEEE J. Sel. Areas Commun. 2008, 26, 203–213. [Google Scholar] [CrossRef]






| S/No. | Related Works | Relaying | Untrusted Relay / Eve | No. of Relays () | Cognitive Radio | Simultaneous Transmission | Time-Division Transmission | Is Known to the D | Jamming Node |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Krikidis et al. 2009 [28] | ✓ | E | S | ✗ | ✗ | ✗ | ✗ | R |
| 2 | Dong et al. 2010 [30] | ✓ | E | M | ✗ | ✗ | ✗ | ✓ | R |
| 3 | He et al. 2010 [35] | ✓ | S | ✗ | ✗ | ✗ | ✗ | ||
| 4 | Ekrem et al. 2011 [43] | ✓ | E | S | ✗ | ✗ | ✗ | ✗ | |
| 5 | Wu et al. 2011 [46] | ✗ | E | ✗ | ✓ | ✓ | ✗ | ✓ | |
| 6 | Sun et al. 2012 [40] | ✓ | S | ✗ | ✗ | ✗ | ✓ | D | |
| 7 | Zhang et al. 2012 [47] | ✓ | S | ✗ | ✗ | ✗ | ✓ | ||
| 8 | Saad et al. 2012 [34] | ✗ | E | ✗ | ✗ | ✗ | ✗ | ✗ | |
| 9 | Khodakarami et al. 2013 [44] | ✓ | M | ✗ | ✗ | ✗ | ✗ | ||
| 10 | Bao et al. 2013 [29] | ✓ | E | S | ✗ | ✗ | ✗ | ✗ | |
| 11 | Stanojev et al. 2013 [48] | ✓ | E | S | ✓ | ✓ | ✗ | ✓ | |
| 12 | Jeon et al. 2014 [50] | ✓ | act as a | S | ✓ | ✗ | ✗ | ✗ | |
| 13 | Sun et al. 2015 [45] | ✓ | S | ✗ | ✗ | ✗ | ✓ | D | |
| 14 | Al-Talabani et al. 2016 [49] | ✓ | E | S | ✓ | ✓ | ✗ | ✓ | |
| 15 | Zamir et al. 2016 [51] | ✓ | S | ✓ | ✓ | ✗ | ✓ | ||
| 16 | Ali et al. 2017 [33] | ✓ | S | ✗ | ✗ | ✗ | ✓ | ||
| 17 | Zhou et al. 2018 [11] | ✗ | E | ✗ | ✗ | ✗ | ✗ | ✗ | |
| 18 | Li et al. 2018 [12] | ✗ | E | ✗ | ✗ | ✗ | ✗ | ✗ | |
| 19 | Kuhestani et al. 2018 [37] | ✓ | M | ✗ | ✗ | ✗ | ✓ | ||
| 20 | Zhao et al. 2018 [38] | ✓ | S | ✗ | ✗ | ✗ | ✓ | ||
| 21 | Jiang et al. 2018 [39] | ✓ | S | ✗ | ✗ | ✗ | ✓ | D | |
| 22 | Yan et al. 2018 [41] | ✗ | E | ✗ | ✗ | ✗ | ✗ | S | |
| 23 | Osorio et al. 2020 [36] | ✓ | S | ✗ | ✗ | ✗ | ✓ | D | |
| 24 | Izanlou et al. 2021 [53] | ✓ | S | ✗ | ✗ | ✗ | ✓ | ||
| 25 | Hayajneh et al. 2023 [54] | ✓ | E | S | ✗ | ✗ | ✗ | ✓ | |
| 26 | Our proposed scheme | ✓ | S | ✓ | ✓ | ✓ | ✓ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zamir, N.; Ali, B.; Butt, M.F.U.; Javed, M.A.; Lee, B.M.; Ng, S.X. Cooperative Jamming-Assisted Untrusted Relaying Based on Game Theory for Next-Generation Communication Systems. Appl. Sci. 2023, 13, 7863. https://doi.org/10.3390/app13137863
Zamir N, Ali B, Butt MFU, Javed MA, Lee BM, Ng SX. Cooperative Jamming-Assisted Untrusted Relaying Based on Game Theory for Next-Generation Communication Systems. Applied Sciences. 2023; 13(13):7863. https://doi.org/10.3390/app13137863
Chicago/Turabian StyleZamir, Nida, Bakhtiar Ali, Muhammad Fasih Uddin Butt, Muhammad Awais Javed, Byung Moo Lee, and Soon Xin Ng. 2023. "Cooperative Jamming-Assisted Untrusted Relaying Based on Game Theory for Next-Generation Communication Systems" Applied Sciences 13, no. 13: 7863. https://doi.org/10.3390/app13137863
APA StyleZamir, N., Ali, B., Butt, M. F. U., Javed, M. A., Lee, B. M., & Ng, S. X. (2023). Cooperative Jamming-Assisted Untrusted Relaying Based on Game Theory for Next-Generation Communication Systems. Applied Sciences, 13(13), 7863. https://doi.org/10.3390/app13137863






