An Optimized Hybrid Transformer for Enhanced Ultra-Fine-Grained Thin Sections Categorization via Integrated Region-to-Region and Token-to-Token Approaches
Abstract
1. Introduction
2. Materials and Methods
2.1. Dataset Source
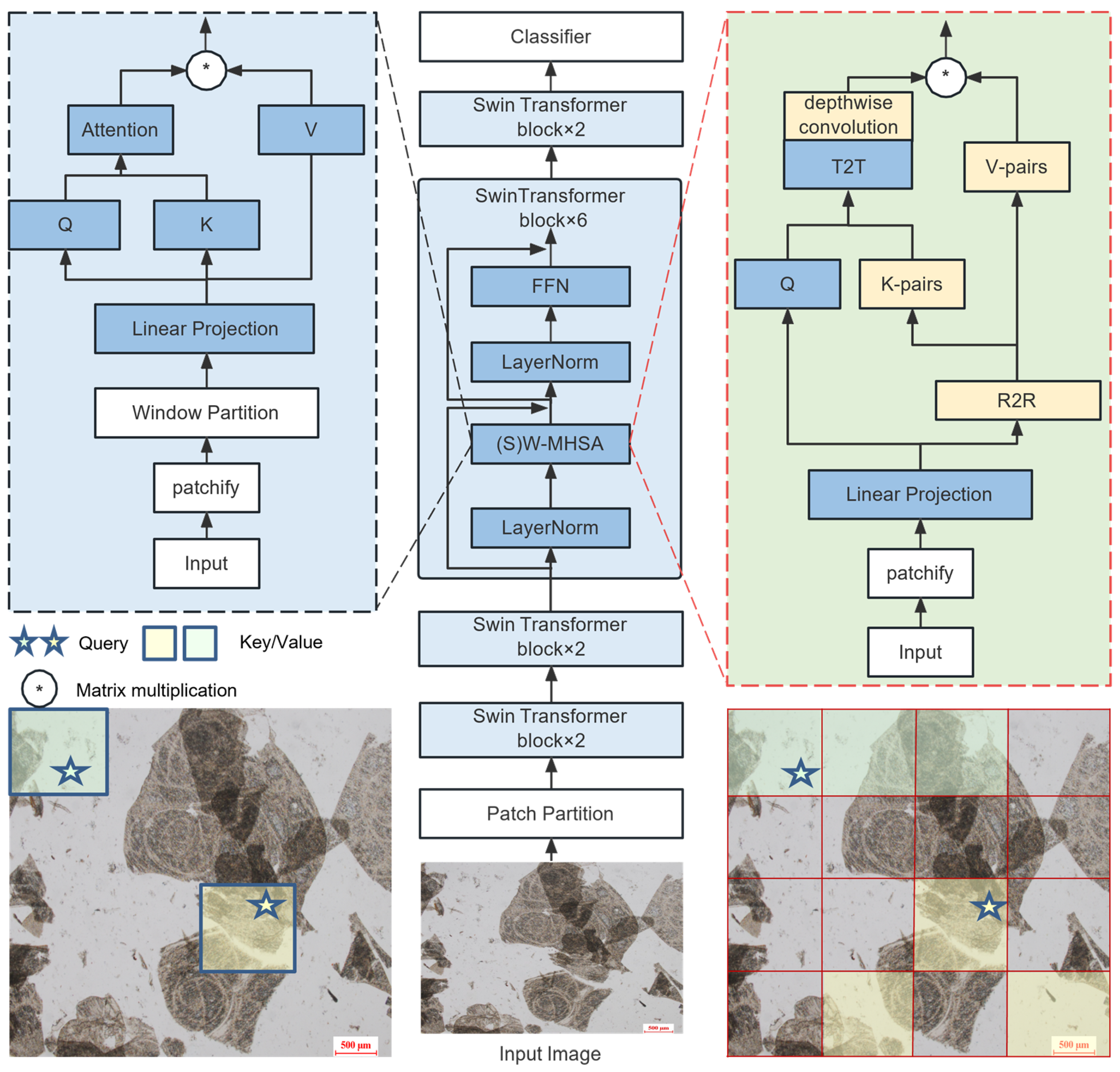
2.2. Methods
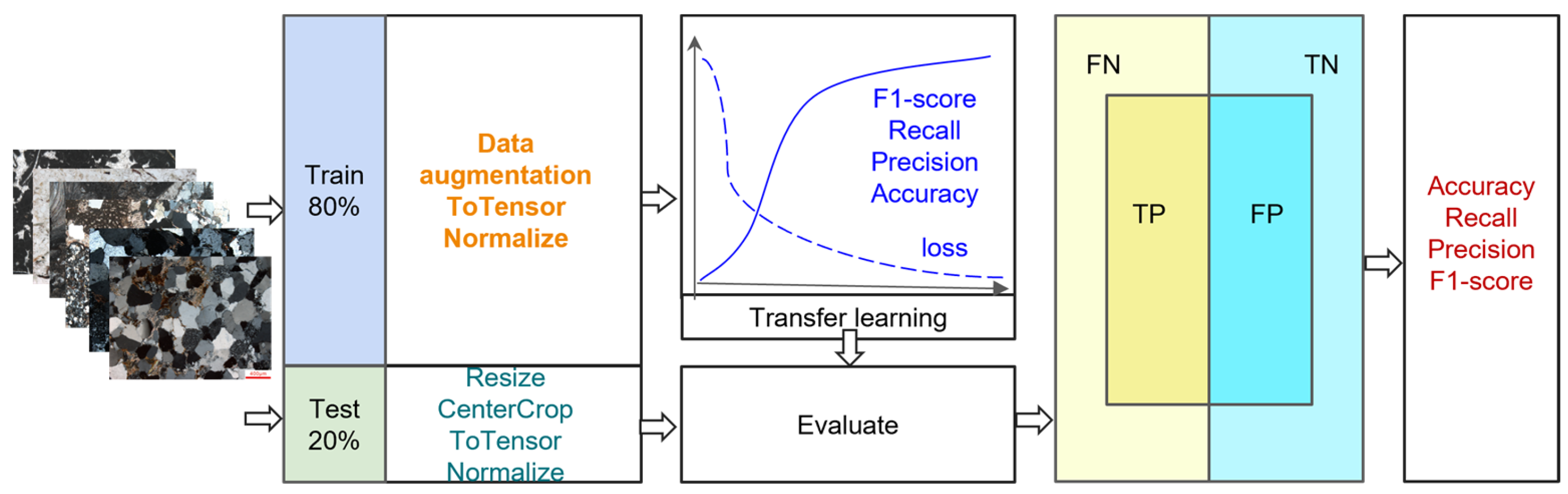
2.3. Experimental Setup and Evaluation Criteria
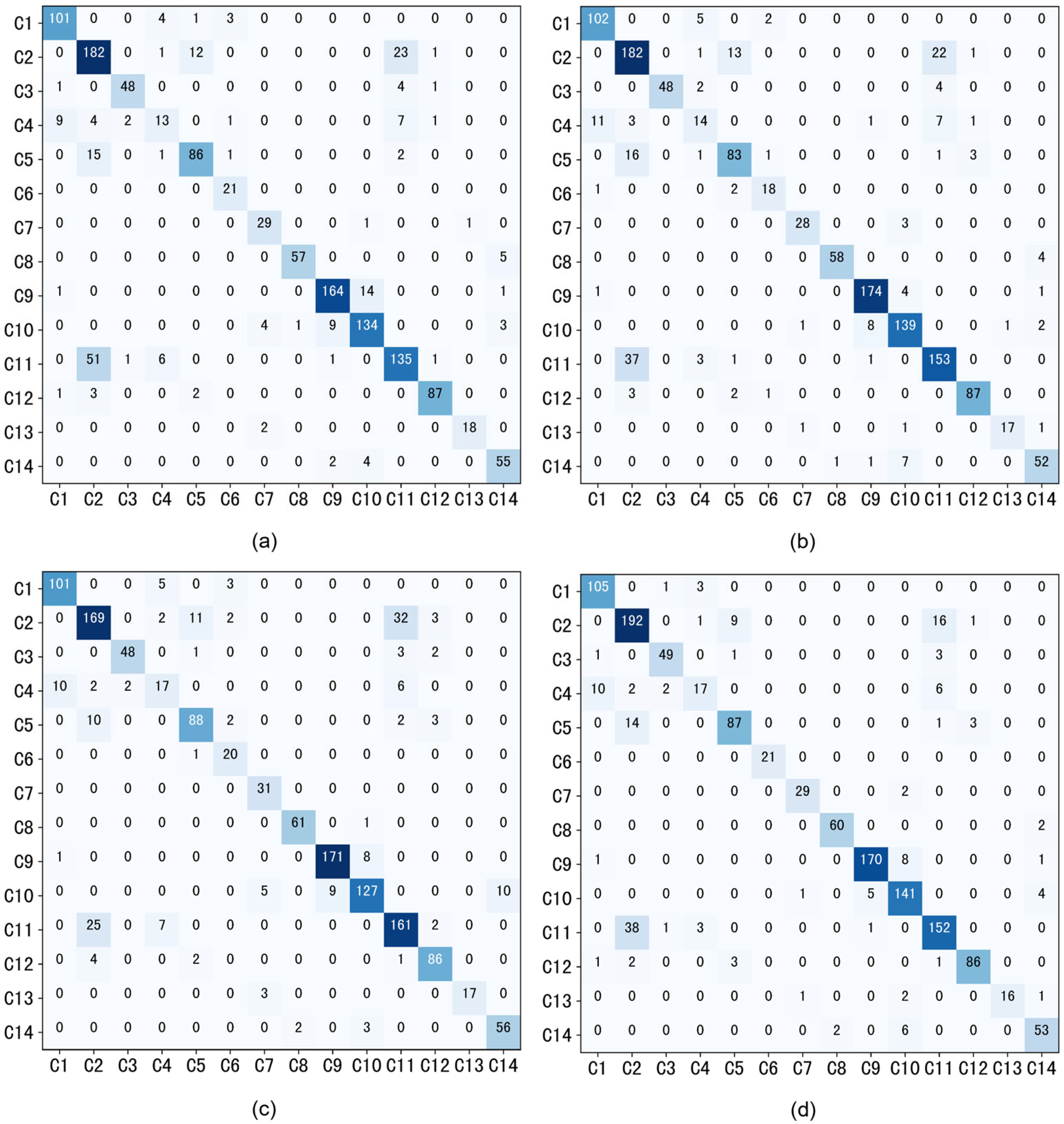
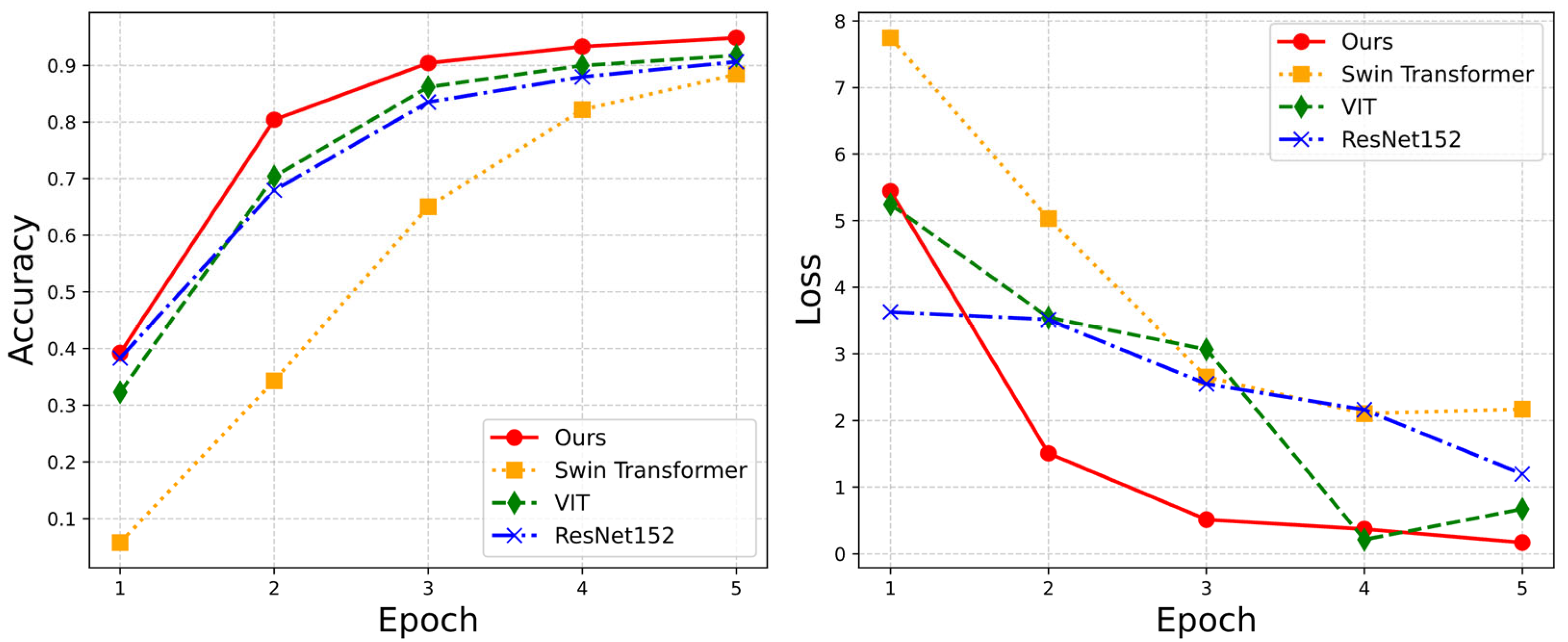
3. Results
4. Discussion
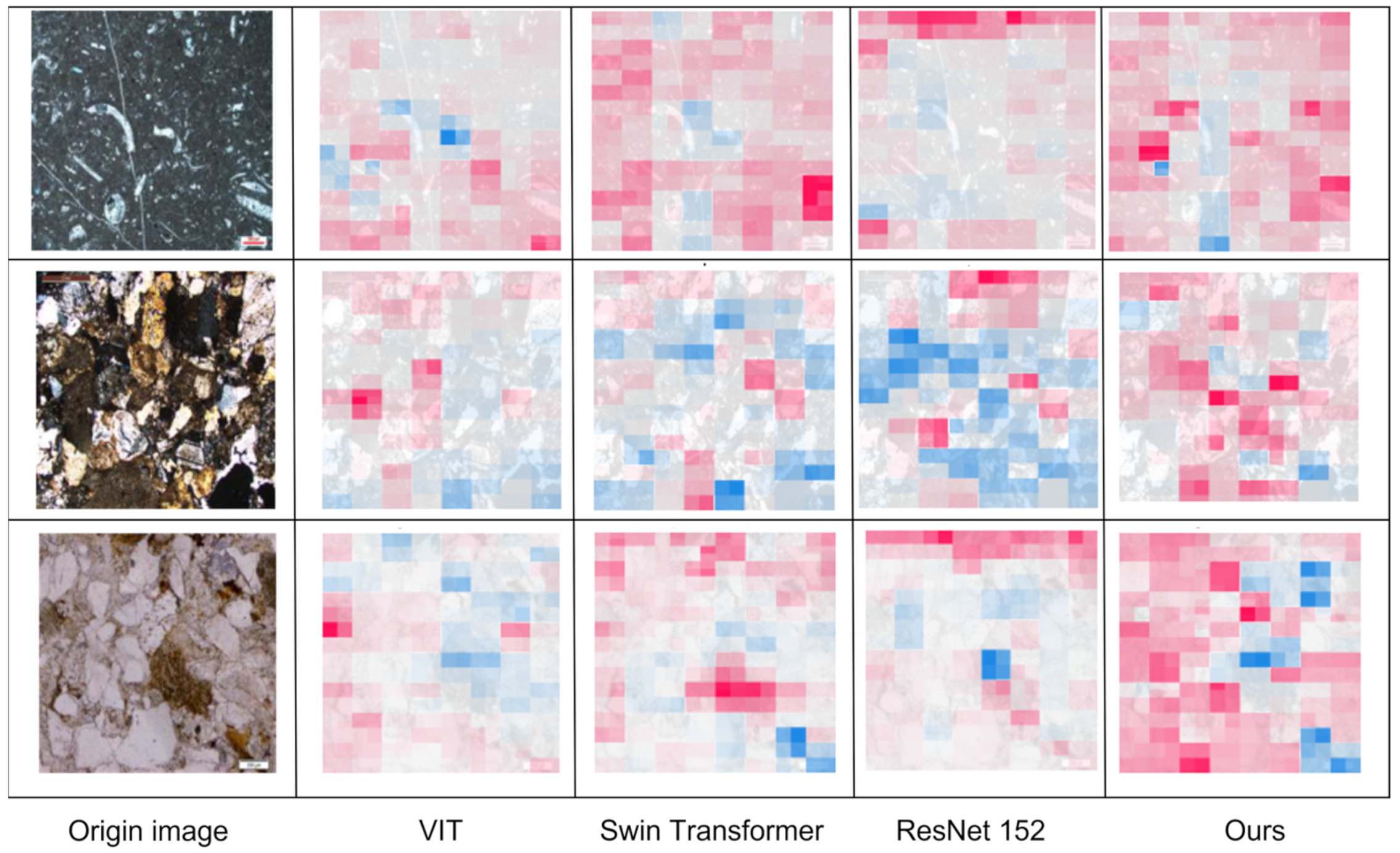
4.1. Explainable Analysis with SHAP
4.2. Model Complexity Analysis
4.3. Generalization Analysis
4.4. Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xu, Z.; Ma, W.; Lin, P.; Hua, Y. Deep Learning of Rock Microscopic Images for Intelligent Lithology Identification: Neural Network Comparison and Selection. J. Rock Mech. Geotech. Eng. 2022, 14, 1140–1152. [Google Scholar] [CrossRef]
- Liu, N.; Huang, T.; Gao, J.; Xu, Z.; Wang, D.; Li, F. Quantum-Enhanced Deep Learning-Based Lithology Interpretation from Well Logs. IEEE Trans. Geosci. Remote Sens. 2021, 60, 4503213. [Google Scholar] [CrossRef]
- Pi, Z.; Zhou, Z.; Li, X.; Wang, S. Digital Image Processing Method for Characterization of Fractures, Fragments, and Particles of Soil/Rock-like Materials. Mathematics 2021, 9, 815. [Google Scholar] [CrossRef]
- Martínez-Martínez, J.; Corbí, H.; Martin-Rojas, I.; Baeza-Carratalá, J.F.; Giannetti, A. Stratigraphy, Petrophysical Characterization and 3D Geological Modelling of the Historical Quarry of Nueva Tabarca Island (Western Mediterranean): Implications on Heritage Conservation. Eng. Geol. 2017, 231, 88–99. [Google Scholar] [CrossRef]
- Izadi, H.; Sadri, J.; Bayati, M. An Intelligent System for Mineral Identification in Thin Sections Based on a Cascade Approach. Comput. Geosci. 2017, 99, 37–49. [Google Scholar] [CrossRef]
- Vaneghi, R.G.; Saberhosseini, S.E.; Dyskin, A.V.; Thoeni, K.; Sharifzadeh, M.; Sarmadivaleh, M. Sources of Variability in Laboratory Rock Test Results. J. Rock Mech. Geotech. Eng. 2021, 13, 985–1001. [Google Scholar] [CrossRef]
- Thompson, S.; Fueten, F.; Bockus, D. Mineral Identification Using Artificial Neural Networks and the Rotating Polarizer Stage. Comput. Geosci. 2001, 27, 1081–1089. [Google Scholar] [CrossRef]
- Singh, N.; Singh, T.; Tiwary, A.; Sarkar, K.M. Textural Identification of Basaltic Rock Mass Using Image Processing and Neural Network. Comput. Geosci. 2010, 14, 301–310. [Google Scholar] [CrossRef]
- Chatterjee, S. Vision-Based Rock-Type Classification of Limestone Using Multi-Class Support Vector Machine. Appl. Intell. 2013, 39, 14–27. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, M.; Han, S.; Ren, Q.; Shi, J. Intelligent Identification for Rock-Mineral Microscopic Images Using Ensemble Machine Learning Algorithms. Sensors 2019, 19, 3914. [Google Scholar] [CrossRef]
- Polat, Ö.; Polat, A.; Ekici, T. Automatic Classification of Volcanic Rocks from Thin Section Images Using Transfer Learning Networks. Neural Comput. Appl. 2021, 33, 11531–11540. [Google Scholar] [CrossRef]
- Alzubaidi, F.; Mostaghimi, P.; Swietojanski, P.; Clark, S.R.; Armstrong, R.T. Automated Lithology Classification from Drill Core Images Using Convolutional Neural Networks. J. Pet. Sci. Eng. 2021, 197, 107933. [Google Scholar] [CrossRef]
- Ma, H.; Han, G.; Peng, L.; Zhu, L.; Shu, J. Rock Thin Sections Identification Based on Improved Squeeze-and-Excitation Networks Model. Comput. Geosci. 2021, 152, 104780. [Google Scholar] [CrossRef]
- Li, D.; Zhao, J.; Ma, J. Experimental Studies on Rock Thin-Section Image Classification by Deep Learning-Based Approaches. Mathematics 2022, 10, 2317. [Google Scholar] [CrossRef]
- De Lima, R.P.; Duarte, D.; Nicholson, C.; Slatt, R.; Marfurt, K.J. Petrographic Microfacies Classification with Deep Convolutional Neural Networks. Comput. Geosci. 2020, 142, 104481. [Google Scholar] [CrossRef]
- YU, X. Ultra-Fine-Grained Visual Categorization. PhD Thesis, Griffith University, Australia, 2021. [Google Scholar]
- Liang, Y.; Cui, Q.; Luo, X.; Xie, Z. Research on Classification of Fine-Grained Rock Images Based on Deep Learning. Comput. Intell. Neurosci. 2021, 2021, 5779740. [Google Scholar] [CrossRef]
- Yu, X.; Wang, J.; Zhao, Y.; Gao, Y. Mix-ViT: Mixing Attentive Vision Transformer for Ultra-Fine-Grained Visual Categorization. Pattern Recognition 2023, 135, 109131. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. arXiv 2017, arXiv:1706.03762. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image Is Worth 16 × 16 Words: Transformers for Image Recognition at Scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer Using Shifted Windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 10012–10022. [Google Scholar]
- Zheng, Y.; Jiao, L.; Wu, W.; Zhang, C. Petrographic Recognition and Classification of Bioclastic Carbonate Thin Sections Based on Attention Mechanism. Geoenergy Sci. Eng. 2023, 225, 211712. [Google Scholar] [CrossRef]
- Huang, Z.; Su, L.; Wu, J.; Chen, Y. Rock Image Classification Based on EfficientNet and Triplet Attention Mechanism. Appl. Sci. 2023, 13, 3180. [Google Scholar] [CrossRef]
- Xu, Y.; Hu, X.; Sun, G.; A Photomicrograph Dataset of Mid-Cretaceous Langshan Formation from the Northern Lhasa Terrane, Tibet. Science Data Bank. Available online: https://www.scidb.cn/en/detail?dataSetId=724638692169220096 (accessed on 10 May 2022).
- Han, Z.; Hu, X.; A Photomicrograph Dataset of the Early-Middle Jurassic Rocks under Thin Section in the Tibetan Tethys Himalaya. Science Data Bank. Available online: https://www.scidb.cn/en/detail?dataSetId=722014393801375744 (accessed on 10 May 2022).
- Hu, X.; Data Set of Polarizing Micrographs of Late Cretaceous-Eocene Rock Slices in the Western Tarim Basin, Xinjiang. Science Data Bank. Available online: https://www.scidb.cn/en/detail?dataSetId=683352400798416896 (accessed on 10 May 2022).
- Zhang, Y.; An, W.; Hu, X.; A Photomicrograph Dataset of Cretaceous Siliciclastic Rocks from Xigaze Forearc Basin, Southern Tibet. Science Data Bank. Available online: https://www.scidb.cn/en/detail?dataSetId=731595076429414400 (accessed on 10 May 2022).
- Lai, W.; Zhang, Y.; Hu, X.; Sun, G.; Photomicrograph Dataset of Cretaceous Siliciclastic Rocks from the Central-Northern Lhasa Terrane. Tibet Science Data Bank. Available online: https://www.scidb.cn/en/detail?dataSetId=684034823831945216 (accessed on 10 May 2022).
- Liu, Y.; Hou, M.; Liu, X.; Qi, Z.; A Micrograph Dataset of Buried Hills and Overlying Glutenite in Bozhong Sag, Bohai Bay Basin. Science Data Bank. Available online: https://www.scidb.cn/en/detail?dataSetId=752623639467130880 (accessed on 10 May 2022).
- Du, X.; Microscopic Image Data Set of Xujiahe Gas Reservoir in Northeast Sichuan. Science Data Bank. Available online: https://www.scidb.cn/en/detail?dataSetId=b068f97abd9b4b6da1558bcc20337632 (accessed on 10 May 2022).
- Shi, G.; Hu, Z.; Li, Y.; Liu, C.; Guan, J.; Chen, H.; Hou, M.; Wang, F.; A Sandstone Microscopical Images Dataset of He-8 Member of Upper Paleozoic in Northeast Ordos Basin. Science Data Bank. Available online: https://www.scidb.cn/en/detail?dataSetId=727528044247384064 (accessed on 10 May 2022).
- Li, P.; Li, Y.; Cheng, X.; Wang, Y.; Li, C.; Liu, Z.; A Photomicrograph Dataset of Upper Paleozoic Tight Sandstone from Linxing Block, Eastern Margin of Ordos Basin. Science Data Bank. Available online: https://www.scidb.cn/en/detail?dataSetId=727601552654598144 (accessed on 10 May 2022).
- Cai, W.; Hou, M.; Chen, H.; Liu, Y.; A Micrograph Dataset of Terrigenous Clastic Rocks of Upper Devonian Lower Carboniferous Wutong Group in Southern Lower Yangtze. Science Data Bank. Available online: https://www.scidb.cn/en/detail?dataSetId=732987889075355648 (accessed on 10 May 2022).
- Feng, W.; He, F.; Zhou, Y.; Yang, J.; A Microscopic Image Dataset of Permian Volcanolithic Fragment Bearing Sandstones from SouthWest China. Science Data Bank. Available online: https://www.scidb.cn/en/detail?dataSetId=703351065692602368 (accessed on 10 May 2022).
- Ma, Q.; Chai, R.; Yang, J.; Du, Y.; Dai, X.; A Microscopic Image Dataset of Mesozoic Metamorphic Grains Bearing Sandstones from Mid-Yangtze, China. Science Data Bank. Available online: https://www.scidb.cn/en/detail?dataSetId=727525043063488512 (accessed on 10 May 2022).
- Dunham, R.J. Classification of sedimentary rocks according to depositional texture. In Classification of Carbonate Rocks, Memoir 1, American; Ham, W.E., Ed.; Association of Petroleum Geologists: Tulsa, OK, USA, 1962; pp. 108–121. [Google Scholar]
- Embry, A.F.; Klovan, J.E. A Late Devonian Reef Tract on Northeastern Banks Island, NWT. Bull. Can. Pet. Geol. 1971, 19, 730–781. [Google Scholar]
- Garzanti, E. From Static to Dynamic Provenance Analysis—Sedimentary Petrology Upgraded. Sediment. Geol. 2016, 336, 3–13. [Google Scholar] [CrossRef]
- Lai, W.; Jiang, J.; Qiu, J.; Yu, J.; Hu, X.; A Photomicrograph Dataset of Rocks for Petrology Teaching at Nanjing University. Science Data Bank. Available online: https://www.scidb.cn/en/detail?dataSetId=732953783604084736 (accessed on 10 May 2022).
- Zhu, L.; Wang, X.; Ke, Z.; Zhang, W.; Lau, R.W. BiFormer: Vision Transformer with Bi-Level Routing Attention. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 10323–10333. [Google Scholar]
- Yuan, L.; Chen, Y.; Wang, T.; Yu, W.; Shi, Y.; Jiang, Z.-H.; Tay, F.E.; Feng, J.; Yan, S. Tokens-to-Token Vit: Training Vision Transformers from Scratch on Imagenet. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 558–567. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the Inception Architecture for Computer Vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar]
- Loshchilov, I.; Hutter, F. Decoupled Weight Decay Regularization. arXiv 2017, arXiv:1711.05101. [Google Scholar]
- Nohara, Y.; Matsumoto, K.; Soejima, H.; Nakashima, N. Explanation of Machine Learning Models Using Shapley Additive Explanation and Application for Real Data in Hospital. Comput. Methods Programs Biomed. 2022, 214, 106584. [Google Scholar] [CrossRef]
- Rodríguez-Pérez, R.; Bajorath, J. Interpretation of Compound Activity Predictions from Complex Machine Learning Models Using Local Approximations and Shapley Values. J. Med. Chem. 2019, 63, 8761–8777. [Google Scholar] [CrossRef]
- Steiner, A.; Kolesnikov, A.; Zhai, X.; Wightman, R.; Uszkoreit, J.; Beyer, L. How to Train Your Vit? Data, Augmentation, and Regularization in Vision Transformers. arXiv 2021, arXiv:2106.10270. [Google Scholar]
- Xu, Z.; Liu, R.; Yang, S.; Chai, Z.; Yuan, C. Learning Imbalanced Data with Vision Transformers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 15793–15803. [Google Scholar]

| Dataset | ID | Class | Numbers | ||
|---|---|---|---|---|---|
| Subclass Number | Train | Test | |||
| Dataset1 | C1 | Debris Feldspar Sandstone | 1 | 11,353 | 1360 |
| C2 | Debris Quartz Sandstone | 1 | |||
| C3 | Debris Sandstone | 1 | |||
| C4 | Feldspar Debris Sandstone | 1 | |||
| C5 | Feldspar Quartz Sandstone | 1 | |||
| C6 | Feldspar Sandstone | 1 | |||
| C7 | Quartz Debris Sandstone | 1 | |||
| C8 | Quartz Sandstone | 1 | |||
| C9 | Floatstone limestone | 1 | |||
| C10 | Grain Limestone | 1 | |||
| C11 | Micritic Limestone | 1 | |||
| C12 | Packstone Limestone | 1 | |||
| C13 | Quartz Debris Sandstone | 1 | |||
| C14 | Quartz Sandstone | 1 | |||
| Dataset2 | Metamorphic Rock | 40 | 2185 | 449 | |
| Sedimentary Rock | 28 | ||||
| Volcanic Rock | 40 | ||||
| ResNet152 | ViT | Swin Transformer | Ours | |
|---|---|---|---|---|
| macro avg | 86.65% | 85.00% | 84.50% | 87.07% |
| weighted avg | 86.17% | 84.45% | 86.32% | 88.04% |
| Categories Metrics (%) | Models | ||||
|---|---|---|---|---|---|
| ResNet-152 | ViT | Swin Transformer | Ours | ||
| C1 | Precision | 0.9018 | 0.8938 | 0.8870 | 0.8898 |
| Recall | 0.9266 | 0.9266 | 0.9358 | 0.9633 | |
| F1-score | 0.9140 | 0.9099 | 0.9107 | 0.9251 | |
| C2 | Precision | 0.8048 | 0.7137 | 0.7552 | 0.7742 |
| Recall | 0.7717 | 0.8311 | 0.8311 | 0.8767 | |
| F1-score | 0.7879 | 0.7679 | 0.7913 | 0.8223 | |
| C3 | Precision | 0.9600 | 0.9412 | 1.0000 | 0.9245 |
| Recall | 0.8889 | 0.8889 | 0.8889 | 0.9074 | |
| F1-score | 0.9231 | 0.9143 | 0.9412 | 0.9159 | |
| C4 | Precision | 0.5484 | 0.5200 | 0.5385 | 0.7083 |
| Recall | 0.4595 | 0.3514 | 0.3784 | 0.4595 | |
| F1-score | 0.5000 | 0.4194 | 0.4444 | 0.5574 | |
| C5 | Precision | 0.8544 | 0.8515 | 0.8218 | 0.8700 |
| Recall | 0.8381 | 0.8190 | 0.7905 | 0.8286 | |
| F1-score | 0.8462 | 0.8350 | 0.8058 | 0.8488 | |
| C6 | Precision | 0.7407 | 0.8077 | 0.8182 | 1.0000 |
| Recall | 0.9524 | 1.0000 | 0.8571 | 1.0000 | |
| F1-score | 0.8333 | 0.8936 | 0.8372 | 1.0000 | |
| C7 | Precision | 0.7949 | 0.8286 | 0.9333 | 0.9355 |
| Recall | 1.0000 | 0.9355 | 0.9032 | 0.9355 | |
| F1-score | 0.8857 | 0.8788 | 0.9180 | 0.9355 | |
| C8 | Precision | 0.9683 | 0.9828 | 0.9831 | 0.9677 |
| Recall | 0.9839 | 0.9194 | 0.9355 | 0.9677 | |
| F1-score | 0.9760 | 0.9500 | 0.9587 | 0.9677 | |
| C9 | Precision | 0.9500 | 0.9318 | 0.9405 | 0.9659 |
| Recall | 0.9500 | 0.9111 | 0.9667 | 0.9444 | |
| F1-score | 0.9500 | 0.9213 | 0.9534 | 0.9551 | |
| C10 | Precision | 0.9137 | 0.8758 | 0.9026 | 0.8868 |
| Recall | 0.8411 | 0.8874 | 0.9205 | 0.9338 | |
| F1-score | 0.8759 | 0.8816 | 0.9115 | 0.9097 | |
| C11 | Precision | 0.7854 | 0.7895 | 0.8182 | 0.8492 |
| Recall | 0.8256 | 0.6923 | 0.7846 | 0.7795 | |
| F1-score | 0.8050 | 0.7377 | 0.8010 | 0.8128 | |
| C12 | Precision | 0.8958 | 0.9560 | 0.9457 | 0.9556 |
| Recall | 0.9247 | 0.9355 | 0.9355 | 0.9247 | |
| F1-score | 0.9101 | 0.9457 | 0.9405 | 0.9399 | |
| C13 | Precision | 1.0000 | 0.9474 | 0.9444 | 1.0000 |
| Recall | 0.8500 | 0.9000 | 0.8500 | 0.8000 | |
| F1-score | 0.9189 | 0.9231 | 0.8947 | 0.8889 | |
| C14 | Precision | 0.8485 | 0.8594 | 0.8667 | 0.8689 |
| Recall | 0.9180 | 0.9016 | 0.8525 | 0.8689 | |
| F1-score | 0.8819 | 0.8800 | 0.8595 | 0.8689 | |
| macro avg | Precision | 0.8548 | 0.8499 | 0.8682 | 0.8997 |
| Recall | 0.8665 | 0.8500 | 0.8450 | 0.8707 | |
| F1-score | 0.8577 | 0.8470 | 0.8549 | 0.8820 | |
| weighted avg | Precision | 0.8623 | 0.8453 | 0.8626 | 0.8813 |
| Recall | 0.8617 | 0.8445 | 0.8632 | 0.8804 | |
| F1-score | 0.8609 | 0.8428 | 0.8619 | 0.8790 | |
| Models | Average Runtime (MS) | Params(M) | GFLOPs | Input Size | Model Size |
|---|---|---|---|---|---|
| ResNet152 | 52.34 | 58.2 | 23.20 | 224 × 224 | 222.8 |
| ViT | 14.84 | 58.1 | 22.57 | 224 × 224 | 330.3 |
| Swin Transformer | 32.39 | 19.6 | 5.96 | 224 × 224 | 108.2 |
| Ours | 23.53 | 21.9 | 6.70 | 224 × 224 | 108.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Wang, S. An Optimized Hybrid Transformer for Enhanced Ultra-Fine-Grained Thin Sections Categorization via Integrated Region-to-Region and Token-to-Token Approaches. Appl. Sci. 2023, 13, 7853. https://doi.org/10.3390/app13137853
Zhang H, Wang S. An Optimized Hybrid Transformer for Enhanced Ultra-Fine-Grained Thin Sections Categorization via Integrated Region-to-Region and Token-to-Token Approaches. Applied Sciences. 2023; 13(13):7853. https://doi.org/10.3390/app13137853
Chicago/Turabian StyleZhang, Hongmei, and Shuiqing Wang. 2023. "An Optimized Hybrid Transformer for Enhanced Ultra-Fine-Grained Thin Sections Categorization via Integrated Region-to-Region and Token-to-Token Approaches" Applied Sciences 13, no. 13: 7853. https://doi.org/10.3390/app13137853
APA StyleZhang, H., & Wang, S. (2023). An Optimized Hybrid Transformer for Enhanced Ultra-Fine-Grained Thin Sections Categorization via Integrated Region-to-Region and Token-to-Token Approaches. Applied Sciences, 13(13), 7853. https://doi.org/10.3390/app13137853





