Influence of the Mechanism of Fluid-Structure Interaction on Stiffness of Static Pressure Spindles and Slides

Abstract

The stiffness of static pressure spindles and slides is affected by the phenomenon of fluid-structure interaction (FSI). Many methods have been proposed to calculate the stiffness with FSI considered. However, the influence of FSI on stiffness is still unknown. This paper studies the lateral stiffness of an aerostatic slide. The relationship between the lateral stiffness of the aerostatic slide, the lateral bearings, and the solid structure is deduced. According to the relationship, this paper proposes a theory that reveals the influence mechanism of FSI on the stiffness of static pressure spindles and slides. The proposed theory is also valid for the normal stiffness of the aerostatic slide and the thrust stiffness of an aerostatic spindle.

1. Introduction

Static pressure spindles and slides are key parts in ultra-precision machine tools [1,2,3,4]. Their stiffness is an important performance indicator for the machine tools. Static pressure spindles and slides are supported and lubricated by static pressure bearings that include aerostatic and hydrostatic bearings, which mainly use air and oil as lubricants [5,6,7,8]. The performance of static pressure bearings can be accurately calculated based on the computational fluid dynamics (CFD) method [9,10,11,12,13]. However, the stiffness of static pressure spindles and slides is not that of their supporting bearings due to the influence of FSI, which is a common phenomenon in many fields [14,15,16,17]. This is because the solid structures of static pressure spindles and slides are not rigid. They deform under the support forces from the supporting bearings, which will change the shapes and dimensions of the bearings and thus affect the stiffness.

For the static pressure spindles and slides with small dimensions and stiffness, their solid deformation under the supporting forces is generally small, and the effect of FSI can be ignored. However, for static pressure spindles and slides with large dimensions and high load-carrying capacity, their solid deformation is large, and thus the effect of FSI has to be considered, or the calculation results may have a significant error. Researchers have proposed some methods to consider the effect of FSI on the stiffness of static pressure spindles and slides. Some researchers use a transient FSI method to study the stiffness of static pressure spindles [18,19,20,21]. This method can well simulate structural deformation. However, many iterations are required to achieve convergence, which requires much computation time. Some researchers propose a steady FSI method to study the thrust stiffness of static pressure spindles, which can save lots of computation time compared with the transient method [22]. Because the structural stiffness of static pressure slides is relatively small, the influence of FSI is generally great. Some researchers adopt the transient FSI method to research the normal [23,24] and lateral stiffness [25] of static pressure slides.

These FSI methods can calculate the stiffness of static pressure spindles and slides accurately. However, the influence of FSI on stiffness is still unknown. When a static pressure spindle or slide is designed, designers have to calculate the stiffness under different design parameters to find the suitable parameters, which will prolong the design cycle. This paper aims to reveal the influence of FSI on the stiffness of static pressure spindles and slides. The lateral stiffness of an aerostatic slide is analyzed. Its relationship with the lateral stiffness of the solid structure and supporting bearings is deduced. A theory for the stiffness of static pressure spindles and slides with FSI considered is proposed. The theory is proven to be valid for the normal stiffness of the aerostatic slide and the thrust stiffness of an aerostatic spindle.

2. Lateral Stiffness of an Aerostatic Slide

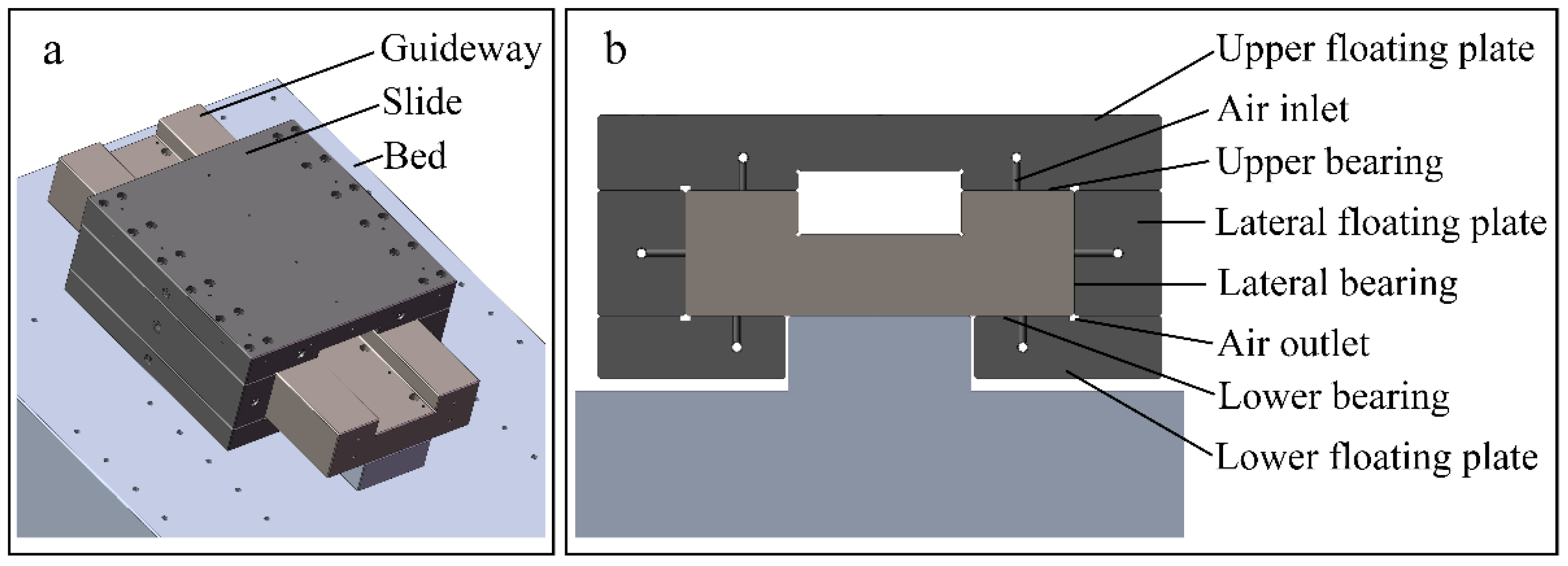
The studied aerostatic slide is from an ultra-precision machine tool, which is shown in Figure 1. Two lateral aerostatic bearings support the slide in the lateral direction and the other four aerostatic bearings in the normal direction. The lateral and normal directions are the horizontal and vertical directions in Figure 1b, respectively.

Under external and supporting forces, the displacement and deformation of the slide in the normal and lateral directions can change the shapes and dimensions of the six supporting bearings and thus affect the stiffness of the aerostatic slide. In the cutting process, the external lateral force on the slide is mainly from the cutting force, which is small. Its effect on the lateral stiffness of the aerostatic slide can be ignored. Besides, the linear motor counteracts the external force in the feed direction. Only the external force in the normal direction, F_n, and the supporting forces from the bearings should be considered. The external moment is small and can also be ignored. Therefore, for the upper or lower bearings, the supporting forces from the left and right bearings are equal. The upper and lower supporting forces, F₁ and F₂, are from the two upper and lower bearings, which are applied on the contact surfaces between the slide and supporting bearings in the normal direction. Hence, the supporting forces from the single upper and lower bearings are F₁/2 and F₂/2, respectively. If a very small external lateral force, F_s, is applied on the barycenter of the slide as shown in Figure 2, the slide will move a distance, d. Then the film thickness of the left lateral bearing, h_3L, decreases, and thus the left lateral supporting force, F_3L, increases. On the contrary, the film thickness of the right lateral bearing, h_3R, increases and the right lateral supporting force, F_3R, decreases. The resultant forces of F_3L and F_3R will change from 0 to a force that is equal in magnitude but opposite in direction to F_s, making the slide static again. The relationship between F_s and the two lateral supporting forces is shown as:

$$F_{3\mathrm{L}}=F_{3\mathrm{R}}+F_{\mathrm{s}}$$

(1)

The lateral stiffness of the aerostatic slide, k_s, is the derivative of F_s with respect to d, which can be written as:

$$k_{\mathrm{s}}=\underset{d\to 0}{\lim }\frac{F_{\mathrm{s}}}{d}$$

(2)

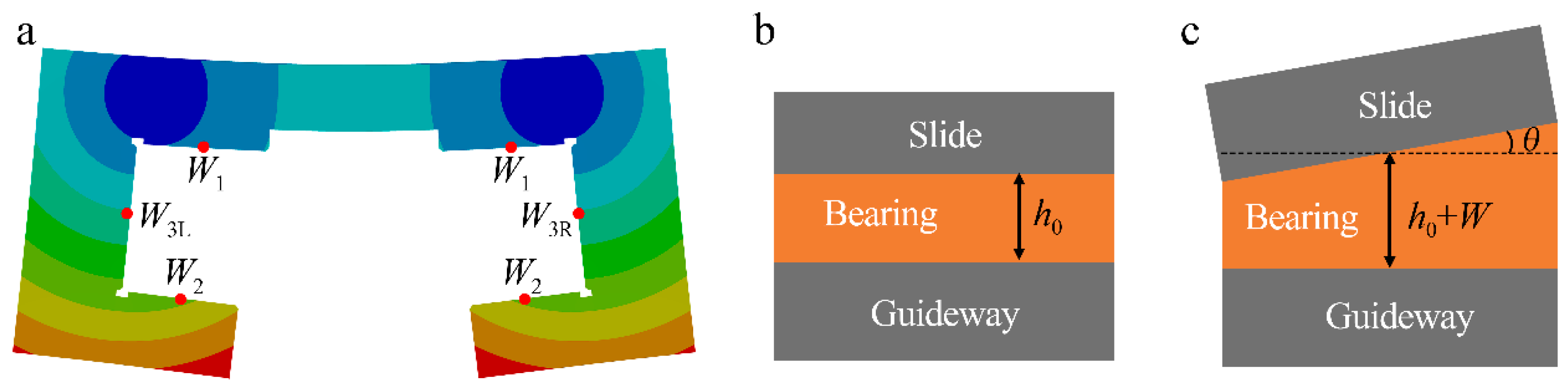
When high-pressure air is supplied to the bearings, the slide will deform under the six supporting forces, as shown in Figure 3a. W₁ and W₂ are the deformation values of the upper and lower supporting surfaces’ center lines parallel to the feed direction in the film thickness direction. W_3L and W_3R are the deformation values of the left and right lateral supporting surfaces’ center lines. The shapes of the six air films will change from cuboid to wedge, which can be defined by two parameters for every air film. One is the deformation value of the supporting surfaces’ center line parallel to the feed direction in the film thickness direction, W. The other one is the wedge angle, θ. The shapes of the supporting bearing before and after the slide deforms are shown in Figure 3b,c, where h₀ represents the designed film thickness. The solid deformation of the supporting surface can be seen as the superposition of the supporting surface moving along the film thickness direction by W and rotating around the center line by θ. W changes the film thickness of the aerostatic bearing and θ changes the shape. In fact, the wedge angles of the six supporting bearings are less than 200 μrad and hardly change the supporting forces. If the wedge angle of the lower supporting bearing increases from 0 to 200 μrad, its supporting force only increases by 1.16%, and thus the influence of wedge angle on the supporting forces can be ignored. The supporting force from the bearing can be obtained by calculating the CFD model of the bearing, whose film thickness is h₀ plus W.

The left and right lateral film thicknesses, h_3L and h_3R, can be expressed as:

$$\left\{\begin{array}{c}{h}_{3\mathrm{L}}=h_0+W_{3\mathrm{L}}-d\\ h_{3\mathrm{R}}=h_0+W_{3\mathrm{R}}+d\end{array}\right.$$

(3)

d can be obtained from Equation (3), as shown in:

$$d=\frac{h_{3\mathrm{R}}-h_{3\mathrm{L}}+W_{3\mathrm{L}}-W_{3\mathrm{R}}}{2}$$

(4)

When the external lateral force is 0, F_3L is equal to F_3R. In this case, W_3L is equal to W_3R. The relationship between W_3L or W_3R and the supporting forces can be obtained by the finite element method, which is shown as Equation (5). In this equation, W₃ represents W_3L or W_3R, and F₃ is equal to F_3L and F_3R.

$$W_3=-5.084\times {10}^{-4}{F}_1+6.866\times {10}^{-4}{F}_2+2.885\times {10}^{-3}{F}_3$$

(5)

The functional relationship in Equation (5) is linear because the solid deformation is small and the structural material is linear. The change in F_3L hardly changes W_3R, and the change in F_3R hardly changes W_3L. When the external lateral force is small, Equation (5) can be rewritten as:

$$\left\{\begin{array}{c}{W}_{3\mathrm{L}}=-5.084\times {10}^{-4}{F}_1+6.866\times {10}^{-4}{F}_2+2.885\times {10}^{-3}{F}_{3\mathrm{L}}\\ W_{3\mathrm{R}}=-5.084\times {10}^{-4}{F}_1+6.866\times {10}^{-4}{F}_2+2.885\times {10}^{-3}{F}_{3\mathrm{R}}\end{array}\right.$$

(6)

Subtracting W_3R from W_3L in Equation (6) gives Equation (7), where λ is 2.885 × 10⁻³.

$$W_{3\mathrm{L}}-W_{3\mathrm{R}}=\lambda (F_{3\mathrm{L}}-F_{3\mathrm{R}})$$

(7)

The supporting force from the bearing decreases with the increase in film thickness. The relationship between the supporting force and the film thickness can be obtained by the CFD method. The design parameters of the left and right lateral bearings are identical. The functional relationship between F_3L and h_3L, f, is equal to that between F_3R and h_3R, as shown in:

$$\left\{\begin{array}{c}{F}_{3\mathrm{L}}=f(h_{3\mathrm{L}})\\ F_{3\mathrm{R}}=f(h_{3\mathrm{R}})\end{array}\right.$$

(8)

Combining Equations (1), (2), (4), (7) and (8) yields:

$$k_{\mathrm{s}}=\underset{d\to 0}{\lim }2\frac{f(h_{3\mathrm{L}})-f(h_{3\mathrm{R}})}{h_{3\mathrm{R}}-h_{3\mathrm{L}}+\lambda \left[f(h_{3\mathrm{L}})-f(h_{3\mathrm{R}})\right]}$$

(9)

Equation (9) can be written as:

$$k_{\mathrm{s}}=\underset{d\to 0}{\lim }\frac{2}{\frac{h_{3\mathrm{R}}-h_{3\mathrm{L}}}{f(h_{3\mathrm{L}})-f(h_{3\mathrm{R}})}+\lambda }$$

(10)

For a lateral supporting bearing whose film thickness is h, its thrust stiffness, k_fs, is the derivative of the opposite number of its supporting force with respect to h, as shown in:

$$k_{\mathrm{fs}}=\underset{\Delta h\to 0}{\lim }-\frac{f(h+\Delta h)-f(h)}{\Delta h}$$

(11)

Substituting for h and ∆h in Equation (11) using h = h_3L and ∆h = h_3R − h_3L gives:

$$k_{\mathrm{fs}}=\underset{(h_{3\mathrm{R}}-h_{3\mathrm{L}})\to 0}{\lim }\frac{f(h_{3\mathrm{L}})-f(h_{3\mathrm{R}})}{h_{3\mathrm{R}}-h_{3\mathrm{L}}}$$

(12)

The lateral structural stiffness, k_ss, is defined as the derivative of F₃ with respect to W₃. The change in F₃ barely changes F₁ and F₂. k_ss can be deduced by Equation (5), as shown in:

$$k_{\mathrm{ss}}=\frac{\partial F_3}{\partial W_3}=\frac{1}{\lambda }$$

(13)

When h_3R − h_3L tends towards 0, d tends towards 0, and vice versa. The two tendencies are identical. Combining Equations (10), (12) and (13) gives:

$$k_{\mathrm{s}}=\frac{2k_{\mathrm{fs}}{k}_{\mathrm{ss}}}{k_{\mathrm{fs}}+k_{\mathrm{ss}}}$$

(14)

It can be seen that k_s can be directly induced if k_fs and k_ss are known. The lateral stiffness of the aerostatic slide has a functional relationship with that of the lateral bearings and solid structure. The lateral bearing can be regarded as a linearly elastic body in the film thickness direction when its film thickness changes a little, which is similar to a spring in the lateral direction. The lateral supporting surface deforms under the lateral supporting force, and the relationship between W₃ and F₃ is linear, which is similar to a spring deforming under an external force. In fact, Equation (14) can be obtained directly if the lateral bearings are seen as two springs and the slide is seen as an assembly consisting of a rigid body and two springs, as shown in Figure 4. One end of the spring representing the lateral bearing connects the guideway, and the other end connects the spring representing the slide. The stiffness constants of the springs representing the lateral bearing and slide are k_fs and k_ss, respectively.

The structure of the slide and the two lateral bearings is elastic in the lateral direction. When a lateral force is applied on the slide, the two lateral floating plates will deform to counteract a part of the force, and the film thicknesses of the two lateral bearings will change to counteract the rest of the force. Therefore, the lateral stiffness of the aerostatic slide derives from both the solid structure and the supporting bearings. Therefore, this paper proposes a theory for the stiffness of the aerostatic spindle and slide, which is that the stiffness derives from both the solid structure and the supporting bearings and can be obtained by seeing the supporting bearings and the solid structure as springs.

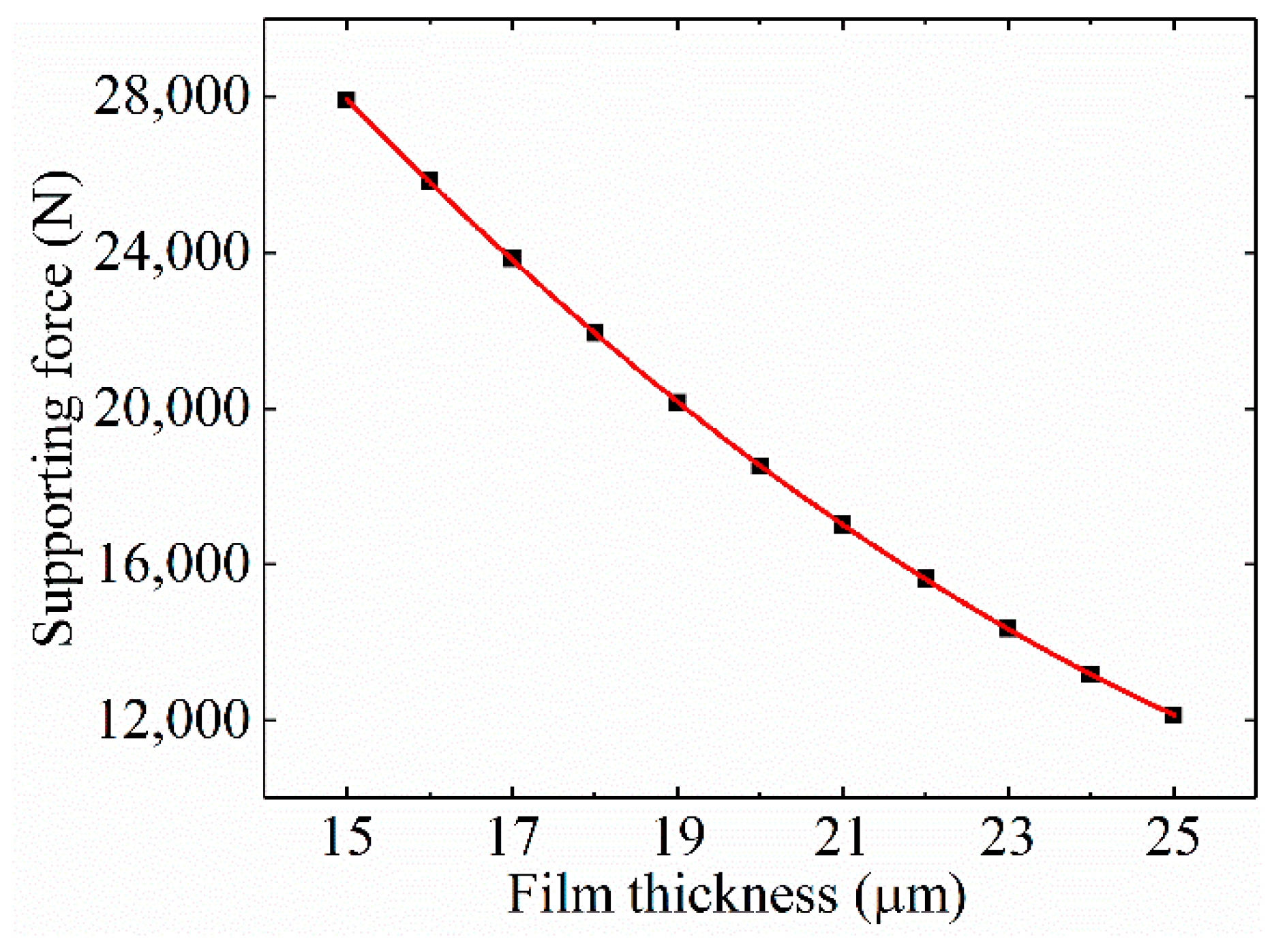
The lateral stiffness will be calculated based on Equation (14) to verify the proposed theory. The film thickness of the lateral bearing can be calculated by the transient FSI method, which is 20.61 μm when the slide bears no load; namely, F_n is the gravity of the slide. The lateral support forces with the lateral film thickness, h₃, in the range of 18 μm to 25 μm can be calculated by the CFD method, which are shown in Figure 5. The functional relationship between F₃ and h₃ can be obtained through 2-order polynomial fitting, as shown in Equation (15). The fitting curve is shown as the red curve in Figure 5.

$$F_3=15.273h_3{}^2-945.11h_3+16227.2$$

(15)

k_fs is the derivative of the opposite number of F₃ with respect to h₃, as shown in:

$$k_{\mathrm{fs}}=-30.546h_3+945.11$$

(16)

k_fs can be obtained by substituting h₃ = 20.61 into Equation (16), which is 315.56 N/μm. k_ss can be obtained based on Equation (13), which is 346.62 N/μm. Therefore, k_s is 330.4 N/μm according to Equation (14), which is significantly less than double k_fs.

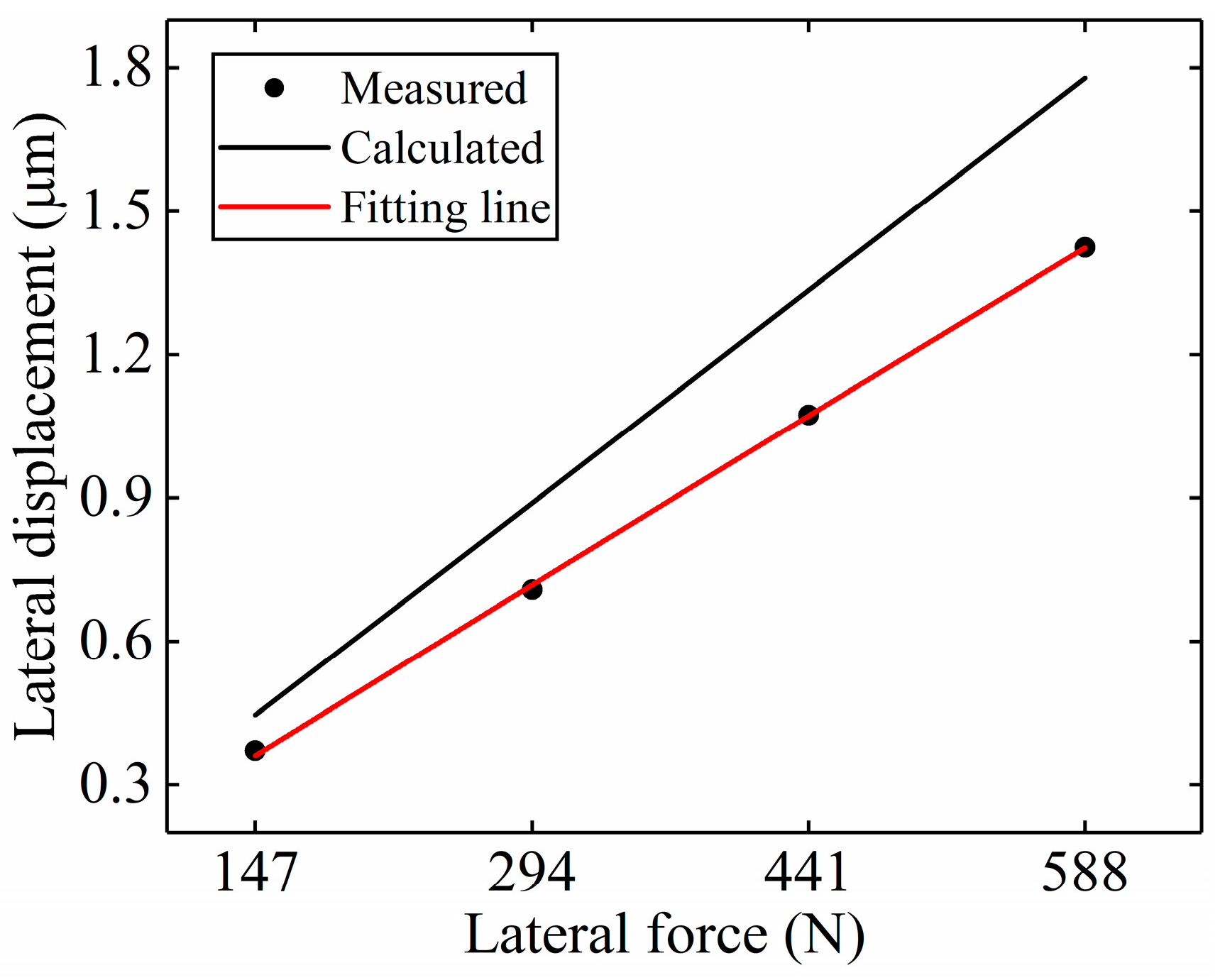
The tests for the lateral stiffness of the aerostatic slide are conducted to verify the calculation. The lateral displacements of the slide under four external lateral forces are measured to obtain the lateral stiffness. Eight steel blocks are used to apply the lateral forces, as shown in Figure 6. The gravity of the steel blocks is converted into lateral force by two pulleys. The mass of each steel block is 7.5 kg. Four lateral forces can be applied by using two, four, six, and eight steel blocks, which are 147 N, 294 N, 441 N, and 588 N, respectively. A capacitive displacement sensor is used to measure the lateral displacements. To decrease the influence of the solid deformation, the measuring position is in the middle of the upper surface of the slide.

For each external lateral force, the measurement is repeated five times. The lateral displacements under the four lateral forces are shown in

Table 1. Lateral displacements under different external lateral forces (μm).

Lateral Force	1	2	3	4	5	Average Value
147 N	0.373	0.366	0.375	0.374	0.368	0.3712
294 N	0.713	0.715	0.711	0.706	0.695	0.7080
441 N	1.079	1.066	1.067	1.069	1.091	1.0744
588 N	1.444	1.421	1.431	1.422	1.402	1.4240

.

Figure 7 shows the lateral displacements under the four lateral forces, which are measured and calculated based on the proposed theory. The measured lateral displacements are fitted by a proportional function. The fitting line is shown as the red line in Figure 7. The slope of the fitting line is 0.00246. Hence, the measured lateral stiffness is 406.5 N/μm, which approaches the calculation. The error between them is 18.7%.

3. Normal Stiffness of an Aerostatic Slide

The lateral stiffness of the aerostatic slide follows the proposed theory well. The proposed theory should be valid for the stiffness of the aerostatic slide in other directions. This section will prove the theory of normal stiffness. According to the proposed theory, the two upper supporting bearings are seen as two springs whose stiffness, k_fn1, is the thrust stiffness of the upper bearing. Similarly, the two lower supporting bearings are seen as two springs whose stiffness, k_fn2, is the thrust stiffness of the lower bearing. The slide is seen as an assembly consisting of a rigid body and four springs that connect to the four springs representing the upper and lower bearings, as shown in Figure 8. The stiffness of the springs connecting to the springs representing the upper bearings, k_sn1, is the derivative of the supporting force from the upper bearing with respect to W₁. The stiffness of the springs connecting to the springs representing the lower bearings, k_sn2, is the derivative of the supporting force from the lower bearing with respect to W₂. The normal stiffness of the aerostatic slide can be directly obtained from Figure 8, as shown in Equation (17), which will be verified to prove that the proposed theory is also valid for the normal stiffness of the aerostatic slide.

$$k_{\mathrm{n}}=\frac{2k_{\mathrm{fn}1}{k}_{\mathrm{sn}1}}{k_{\mathrm{fn}1}+k_{\mathrm{sn}1}}+\frac{2k_{\mathrm{fn}2}{k}_{\mathrm{sn}2}}{k_{\mathrm{fn}2}+k_{\mathrm{sn}2}}$$

(17)

When the external normal force, which is F_n in Figure 2, changes, the slide will displace in the normal direction to make the slide stable again. Supposing the change of F_n is ∆F_n and the corresponding displacement of the slide is d, the normal stiffness of the aerostatic slide, k_n, can be expressed as:

$$k_{\mathrm{n}}=\underset{d\to 0}{\lim }\frac{\Delta F_{\mathrm{n}}}{d}$$

(18)

If ∆F_n is positive, the slide will displace in the gravity direction. Then the upper supporting force F₁ will increase and F₂ will decrease to counteract ∆F_n. Let the changes in F₁ and F₂ be ∆F₁ and ∆F₂, respectively. ∆F_n is equal to ∆F₁ minus ∆F₂. Hence Equation (18) can be rewritten as:

$$k_{\mathrm{n}}=\underset{d\to 0}{\lim }\frac{\Delta F_1-\Delta F_2}{d}$$

(19)

The supporting forces from the single upper and lower bearings are F₁/2 and F₂/2, respectively. Because ∆F₁ and ∆F₂ are very small, k_sn1 and k_sn2 can be expressed as Equation (20), where ∆W₁ and ∆W₂ are the changes of W₁ and W₂ due to the changes of F₁ and F₂.

$$\left\{\begin{array}{c}{k}_{\mathrm{sn}1}=\frac{\Delta F_1}{2\Delta W_1}\\ k_{\mathrm{sn}2}=\frac{\Delta F_2}{2\Delta W_2}\end{array}\right.$$

(20)

The changes in the film thicknesses of the upper and lower supporting bearings, ∆h₁ and ∆h₂, can be obtained based on ∆W₁, ∆W₂, and d, as shown in:

$$\left\{\begin{array}{c}\Delta h_1=\Delta W_1-d\\ \Delta h_2=\Delta W_2+d\end{array}\right.$$

(21)

k_fn1 and k_fn2 are the opposite numbers of the derivatives of F₁/2 and F₂/2 with respect to h₁ and h₂, respectively, as shown in:

$$\left\{\begin{array}{c}{k}_{\mathrm{fn}1}=\underset{\Delta h_1\to 0}{\lim }-\frac{\Delta F_1}{2\Delta h_1}\\ k_{\mathrm{fn}2}=\underset{\Delta h_2\to 0}{\lim }-\frac{\Delta F_2}{2\Delta h_2}\end{array}\right.$$

(22)

Substituting for ∆h₁ and ∆h₂ in Equation (21) using Equation (22), and ∆W₁ and ∆W₂ using Equation (20), gives:

$$\left\{\begin{array}{c}d=\frac{\Delta F_1}{2k_{\mathrm{sn}1}}+\frac{\Delta F_1}{2k_{\mathrm{fn}1}}\\ d=-\frac{\Delta F_2}{2k_{\mathrm{sn}2}}-\frac{\Delta F_2}{2k_{\mathrm{fn}2}}\end{array}\right.$$

(23)

Substituting Equation (23) into Equation (19) can give Equation (17). Hence, the proposed theory is valid for the normal stiffness of the aerostatic slide.

4. Thrust Stiffness of the Aerostatic Spindle

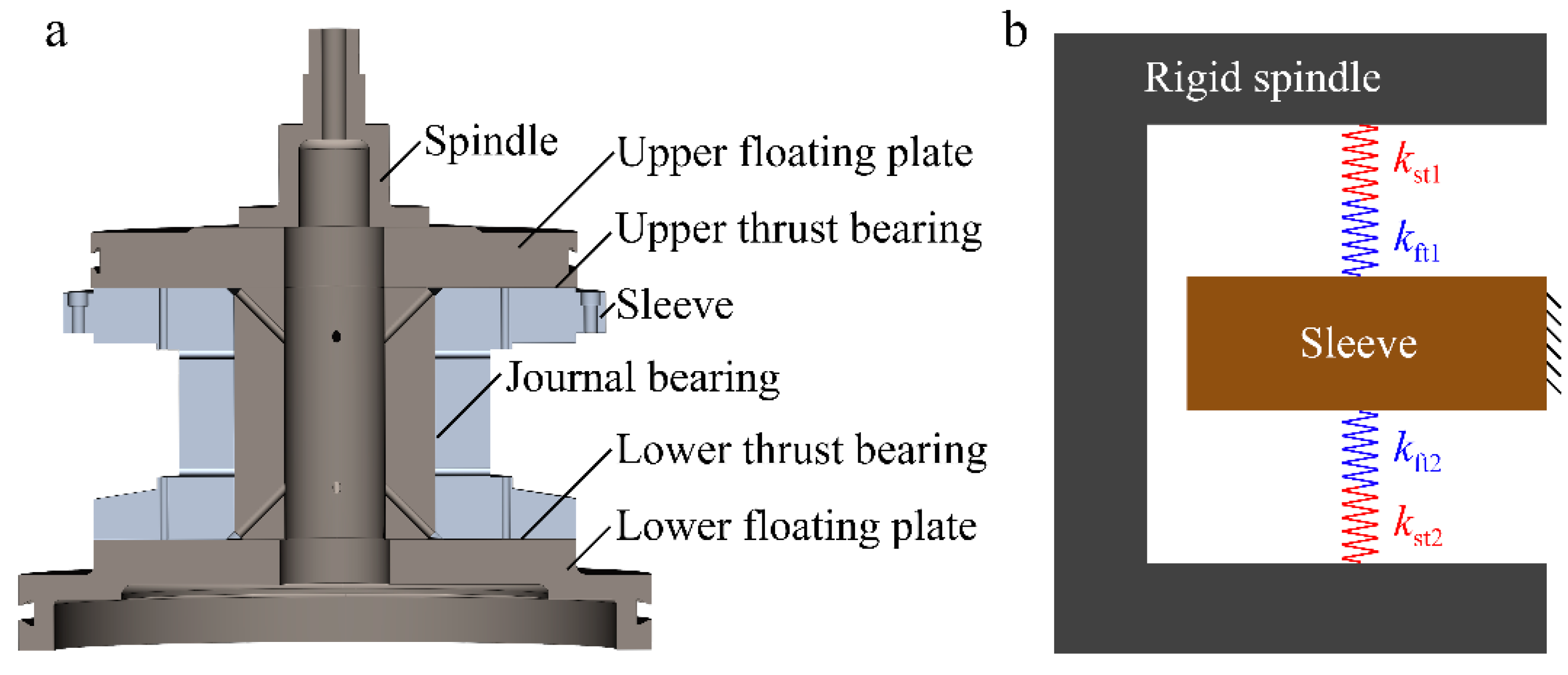
This section will analyze whether the proposed theory is valid for the thrust stiffness of the aerostatic spindle. The studied aerostatic spindle is from a fly-cutting machine tool. Its configuration is shown in Figure 9a. The aerostatic spindle is H-shaped. Two thrust bearings support the spindle in the axial direction. According to the proposed theory, the upper and lower supporting bearings are seen as two springs whose stiffness constants, k_ft1 and k_ft2, are the thrust stiffness values of the upper and lower bearings, respectively. The spindle is seen as an assembly consisting of a rigid body and two springs that connect to the two springs representing the upper and lower thrust bearings, as shown in Figure 9b. The spindle and sleeve will deform under the supporting forces from the upper and lower thrust bearings, F₁ and F₂. The deformation of the sleeve is small compared with the spindle, which will be ignored. The stiffness constants of the springs connecting to the springs representing the upper and lower bearings, k_st1 and k_st2, are the derivatives of F₁ and F₂ with respect to W₁ and W₂, respectively, which are the axial deformation values of the middle rings of the upper and lower supporting surfaces.

The thrust stiffness of the spindle, k_t, can be directly obtained from Figure 9b, as shown in:

$$k_{\mathrm{t}}=\frac{k_{\mathrm{ft}1}{k}_{\mathrm{st}1}}{k_{\mathrm{ft}1}+k_{\mathrm{st}1}}+\frac{k_{\mathrm{ft}2}{k}_{\mathrm{st}2}}{k_{\mathrm{ft}2}+k_{\mathrm{st}2}}$$

(24)

Similar to the normal stiffness of the aerostatic slide, Equation (24) can be verified in the same way. The thrust stiffness calculated by the steady FSI method is 2043.5 N/μm, which accords with the experimental result of 2224.9 N/μm [22]. The thrust stiffness will be calculated based on Equation (24), which will be contrasted with 2043.5 N/μm. The film thicknesses of the upper and lower thrust bearings can be obtained based on the transient FSI method, which are 18.76 μm and 20.43 μm, respectively. The design dimensions of the upper and lower bearings are identical. The supporting forces from the upper or lower thrust bearing under the film thicknesses from 10 μm to 25 μm can be obtained based on the CFD method, as shown in Figure 10.

The relationship between the supporting force and the film thickness can be obtained by 2-order polynomial fitting, as shown in Equation (25). The fitting curve is shown as the red curve in Figure 10.

$$F=59.974h^2-3978.54h+74121.0$$

(25)

k_ft1 and k_ft2 are the opposite numbers of the derivatives of F₁ and F₂ with respect to h₁ and h₂, respectively. The opposite number of the derivative of F with respect to h is shown as:

$$-\frac{dF}{dh}=-119.948h+3978.54$$

(26)

k_ft1 and k_ft2 can be obtained by substituting h = 18.76 μm and h = 20.43 μm into Equation (26), which are 1728.32 N/μm and 1528.00 N/μm, respectively. The changes in the lower and radial supporting forces barely deform the upper floating plate. Moroever, the changes in the upper and radial supporting forces barely deform the lower floating plate. Therefore, based on the finite element method, k_st1 and k_st2 can be obtained by calculating the solid deformation under the upper and lower supporting forces, which are 3866.31 N/μm and 2876.13 N/μm, respectively. Substituting the values of k_ft1, k_ft2, k_st1, and k_st2 into Equation (24) gives k_t = 2192.3 N/μm, which is nearly identical to the normal stiffness values obtained by the steady FSI method and experiment.

5. Discussion

The proposed theory is also valid for the stiffness of the static pressure spindle and slide in other directions, which can also be verified. However, the influence of FSI on the radial stiffness of static pressure spindles is generally small. This is because the small radial solid deformation hardly changes the shape and dimensions of the journal bearing, and the radial structural stiffness is large. Moreover, for the angular stiffness of static pressure spindles and slides, the supporting forces change the shapes and dimensions of the supporting bearings and thus change the angular stiffness of the bearings. However, the external moment is basically counteracted by the reaction moment due to the deformation of the supporting bearings. In other words, the angular structural stiffness is much greater than the angular stiffness of the supporting bearings. The angular stiffness of the static spindle or slide is nearly equal to that of their supporting bearings. For the above reasons, the proposed theory for the stiffness in these directions will not be introduced in this paper.

Based on the proposed theory, there are two ways to enhance the stiffness of the static pressure spindle and slide. One is to increase the stiffness of the supporting bearings, and the other is to increase the structural stiffness. For a system with only a supporting bearing, suppose the structural stiffness is λ times the stiffness of the bearing. According to the proposed theory, the system stiffness, k, is shown in Equation (27) where k_f is the stiffness of the bearing.

$$k=\frac{\lambda }{1+\lambda }{k}_{\mathrm{f}}$$

(27)

The ratio of k to k_f is λ/(1 + λ), which increases with the increase of λ, as shown in Figure 11. It can be seen that when λ is less than 2, the ratio grows fast with the increase of λ. But when λ is greater than 4, the growth of the ratio slows considerably. Increasing the structural stiffness will inevitably increase the dimensions and mass of the solid, which will decrease the natural frequencies and degrade the drive properties of the spindle and slide. Therefore, λ should be in a reasonable range. This paper suggests that λ should be around 3. When λ is 3, the system stiffness is 75% of the stiffness of the bearing. When λ is greater than 4, the increase of λ will not enhance the system stiffness effectively. In this case, increasing k_f will be a more proper way to enhance k.

When the structure of a static pressure spindle or slide is confirmed, the next step is to choose suitable structural dimensions s and a designed film thickness h₀, which are critical at the design stage. To make the stiffness value of the static pressure spindle or slide k_c reach the designed value k, lots of k_c under different structural dimensions and designed film thicknesses have been calculated to find the suitable parameters based on the conventional method, as shown in Figure 12a. It can be seen that the conventional method is a little bit blind and inefficient. For this problem, a method based on the proposed theory is proposed to choose suitable structural dimensions and designed film thickness, as shown in Figure 12b. First, the bearing and structural stiffness values, k_f and k_s, can be obtained on the basis of k and λ, and thus the actual film thickness after the solid deforms h and structural dimensions s can be determined, respectively. Then, based on the FSI method, the designed film thickness h₀ can also be obtained. Hence, s and h₀ can be determined on the basis of k and λ. It can be seen that the method based on the proposed theory is more efficient than the conventional method.

6. Conclusions

This paper studies the influence mechanism of FSI on the stiffness of static pressure spindles and slides. First, the lateral stiffness of an aerostatic slide with FSI considered is analyzed. Its relationship with the lateral stiffness of the supporting bearings and solid structure is deduced. According to the relationship, a theory revealing the influence mechanism of FSI on the stiffness of static pressure spindles and slides is proposed. The proposed theory discovers that stiffness derives from both the solid structure and the supporting bearings and can be obtained by seeing the supporting bearings and the structure as springs. Then the lateral stiffness is measured to verify the theory.

Second, based on the proposed theory, the relationship between the normal stiffness of the aerostatic slide, the normal supporting bearings, and the solid structure is obtained. Afterward, the relationship is verified. Besides, the thrust stiffness of an aerostatic spindle is calculated based on the proposed theory, which accords with that based on the steady FSI method. In the end, the influence of the ratio of the structural stiffness to the stiffness of the supporting bearing on the system stiffness is analyzed. This paper suggests the ratio should be around 3.