A Review of the Dynamics Progress of Bubble Collapse within Droplet and Droplet Splash
Abstract
:1. Introduction
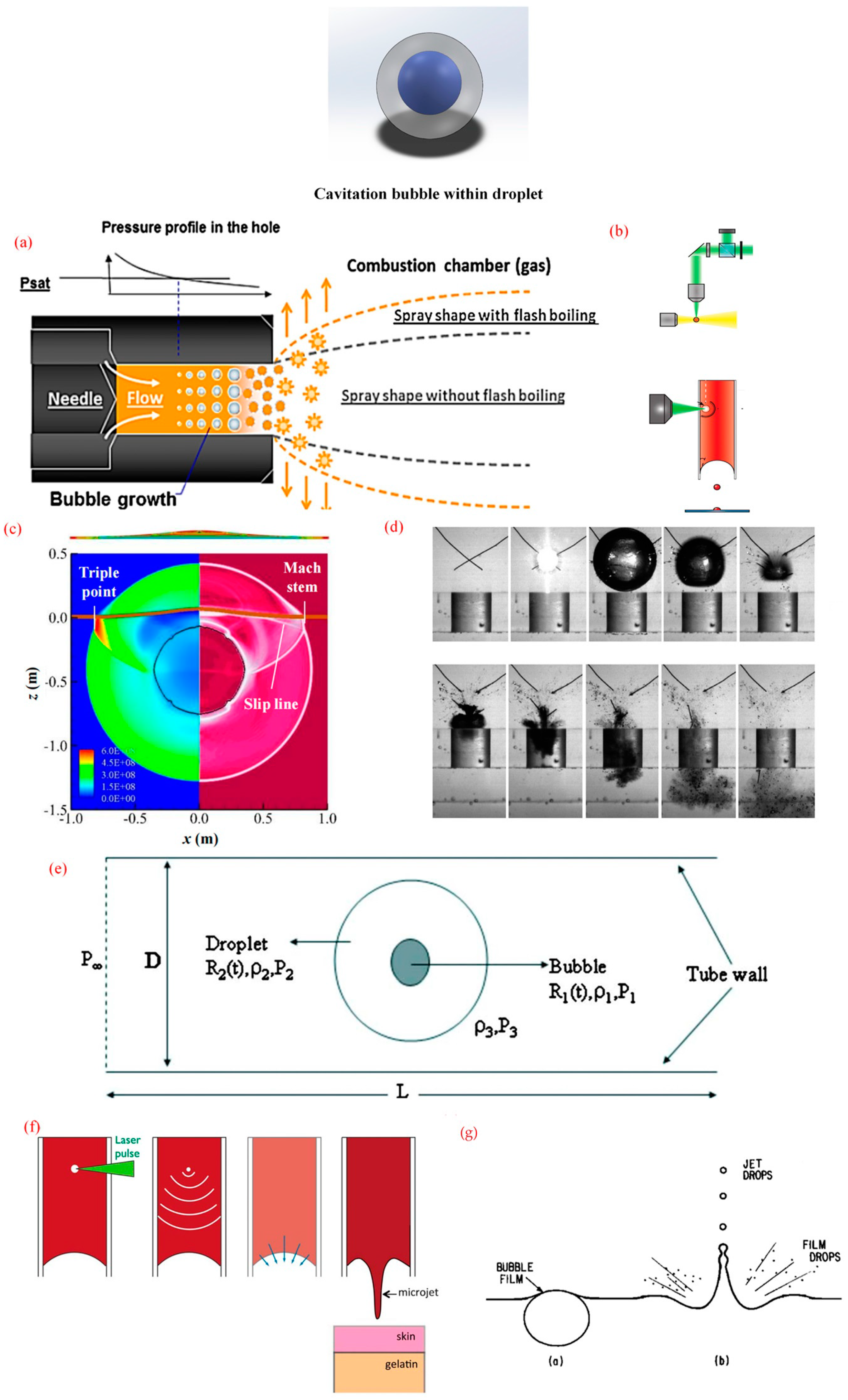
2. Typical Forms of Cavitation Bubble Collapse
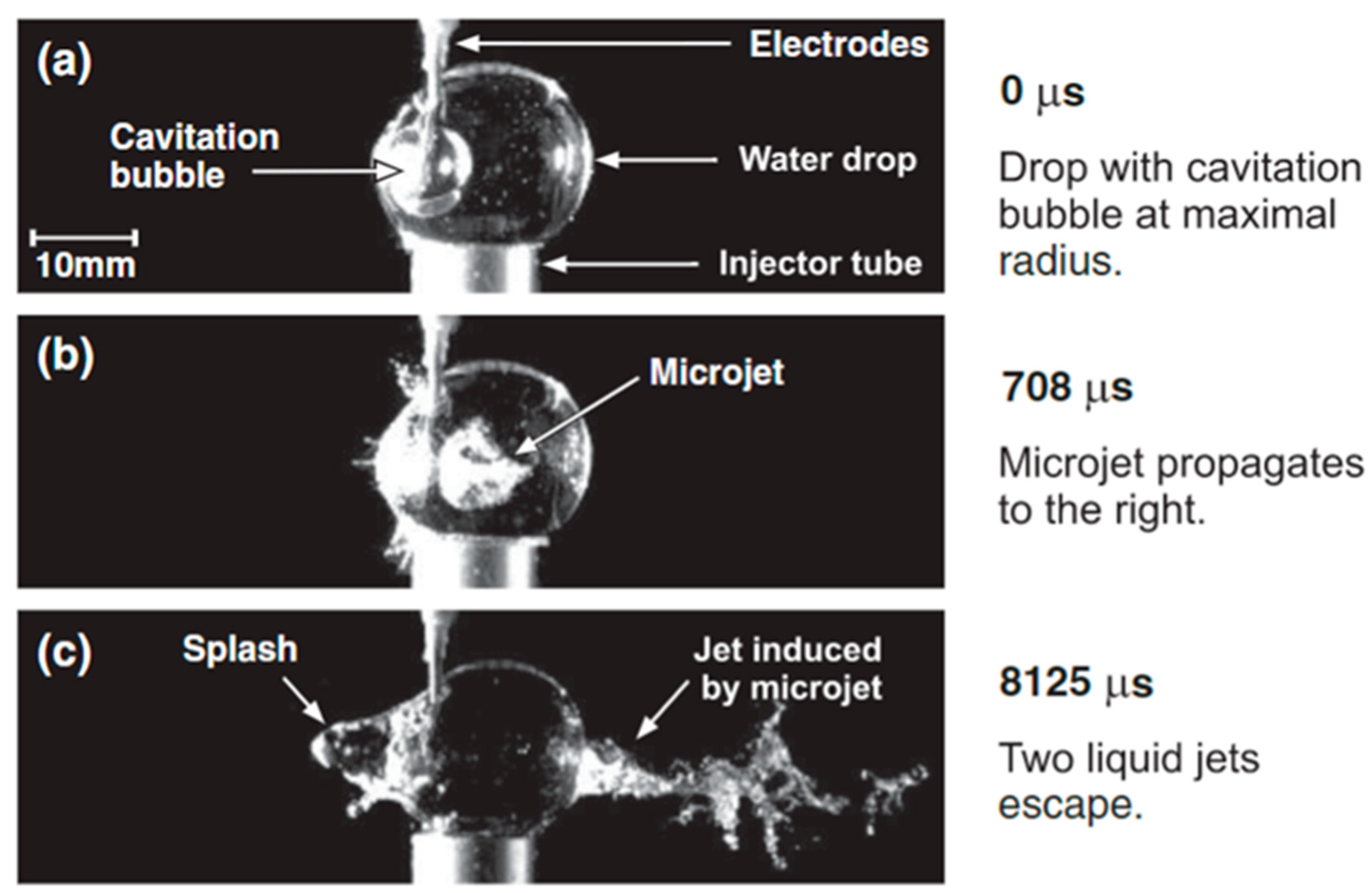
2.1. Microjets
2.2. Bubble Migration
2.3. Microbubble Cloud
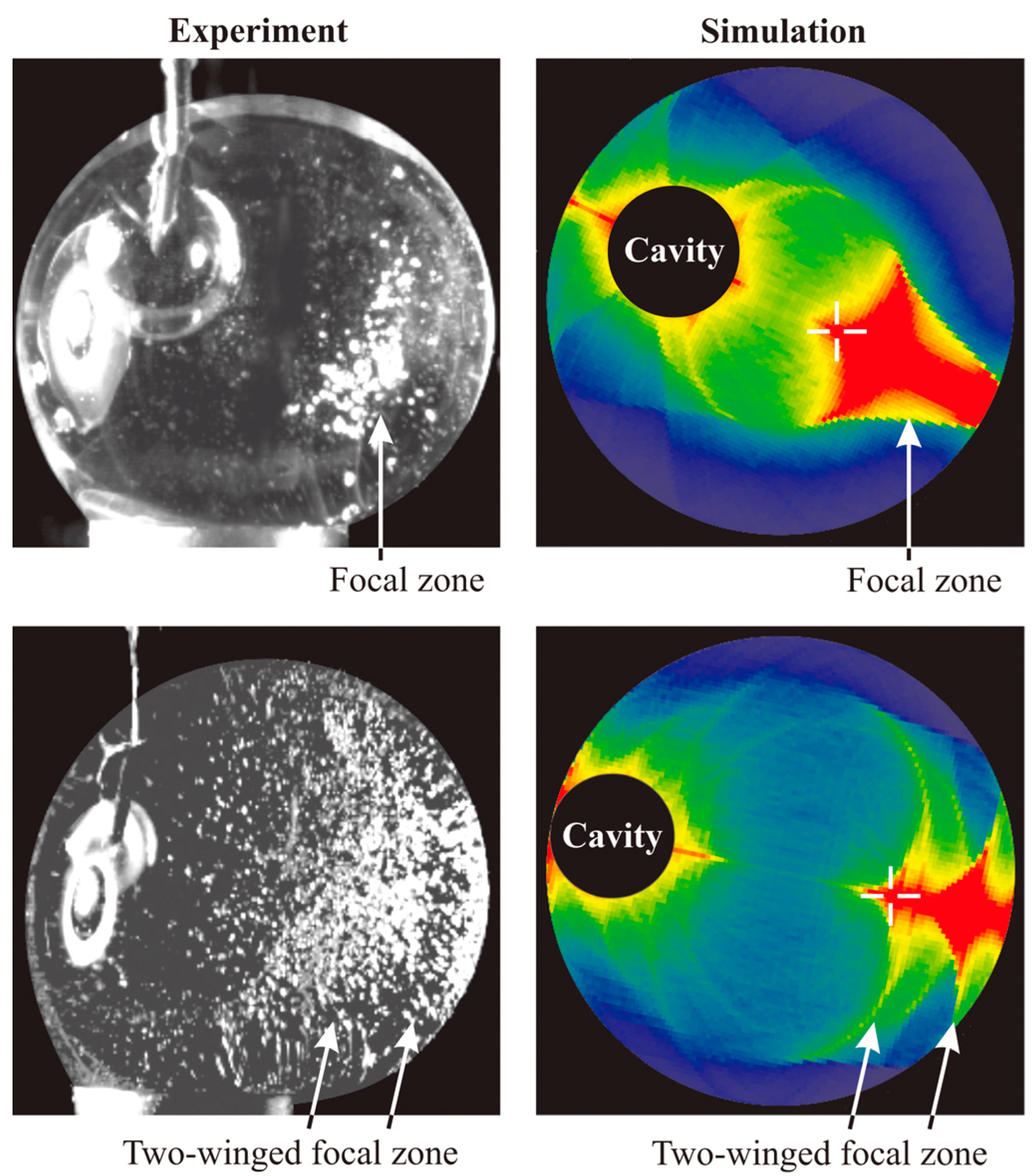
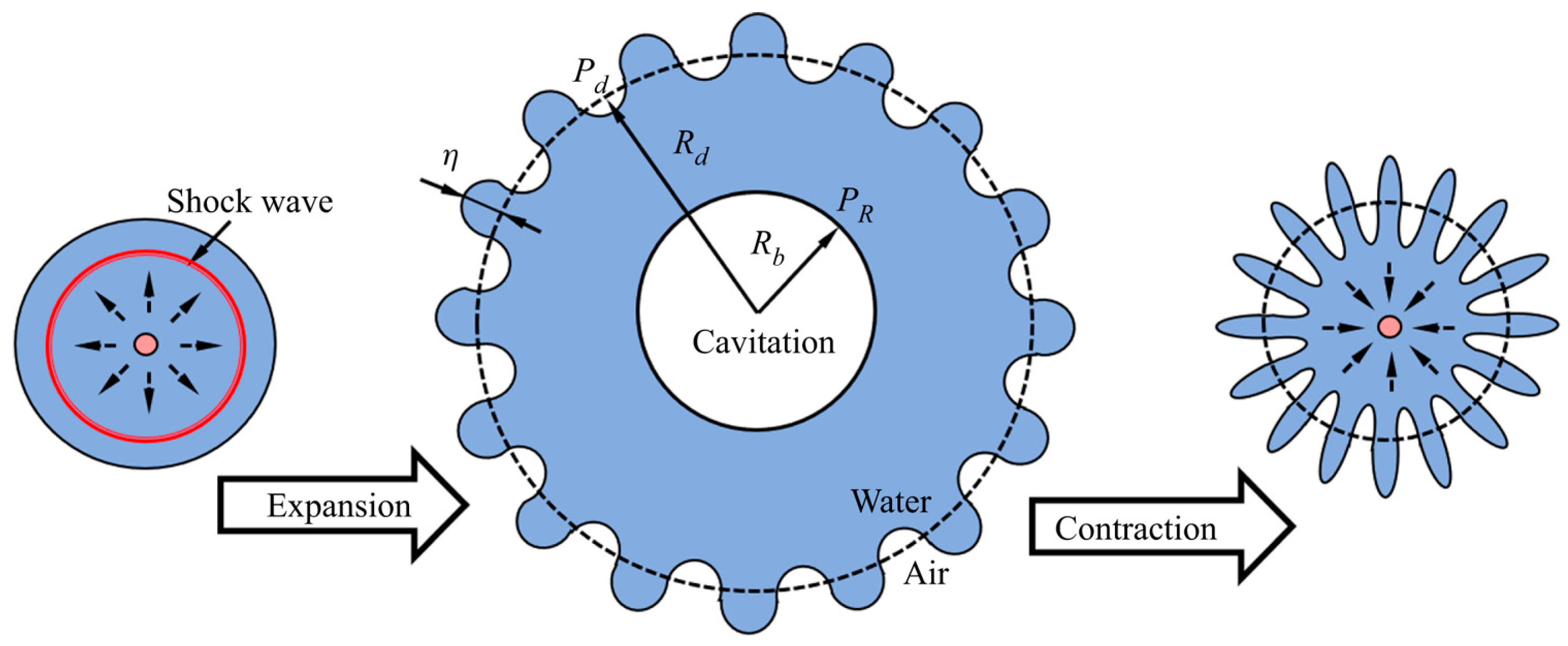
3. Shock Wave of Bubble Collapse
3.1. Form of Shock Wave
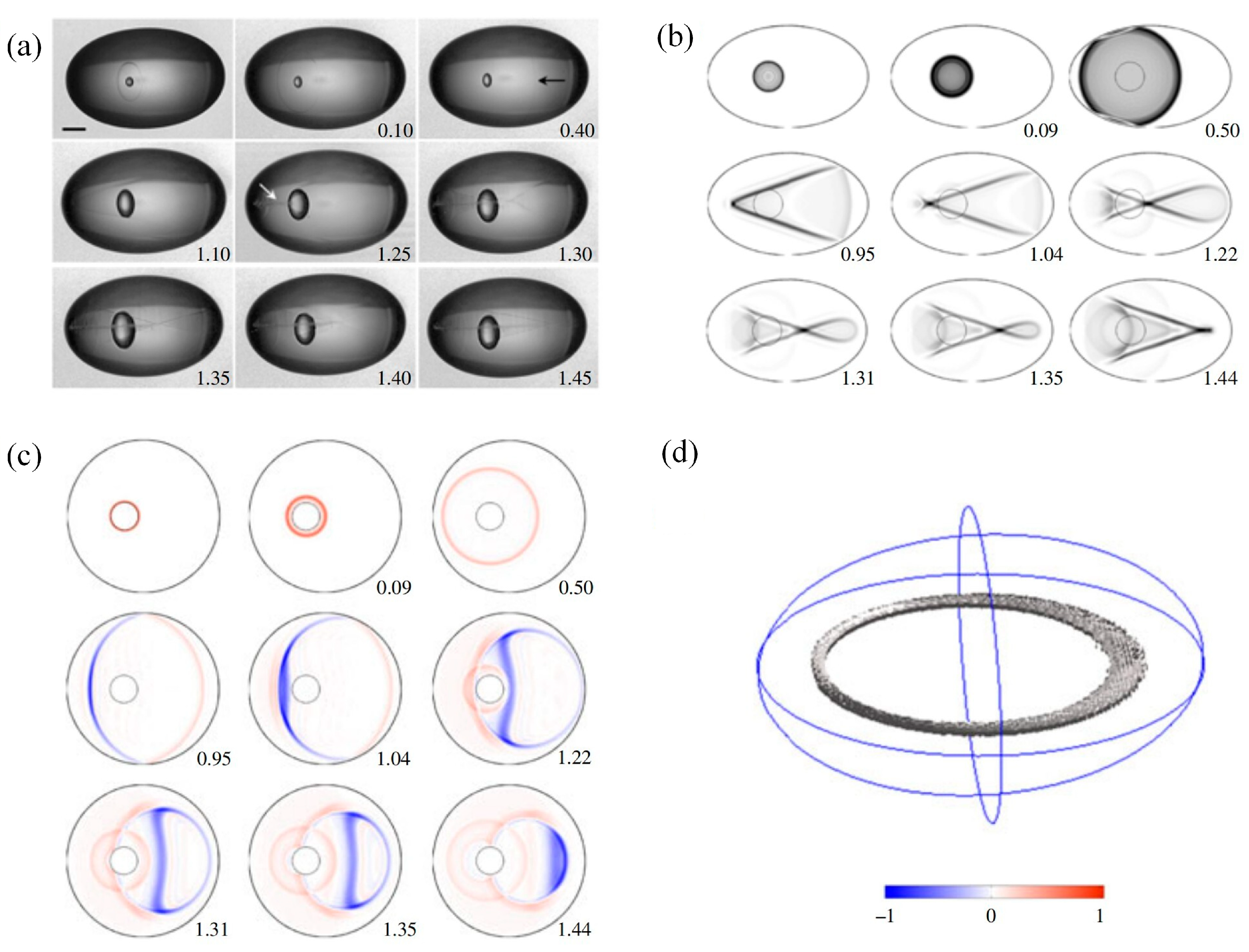
3.2. Evolution of Shock Wave
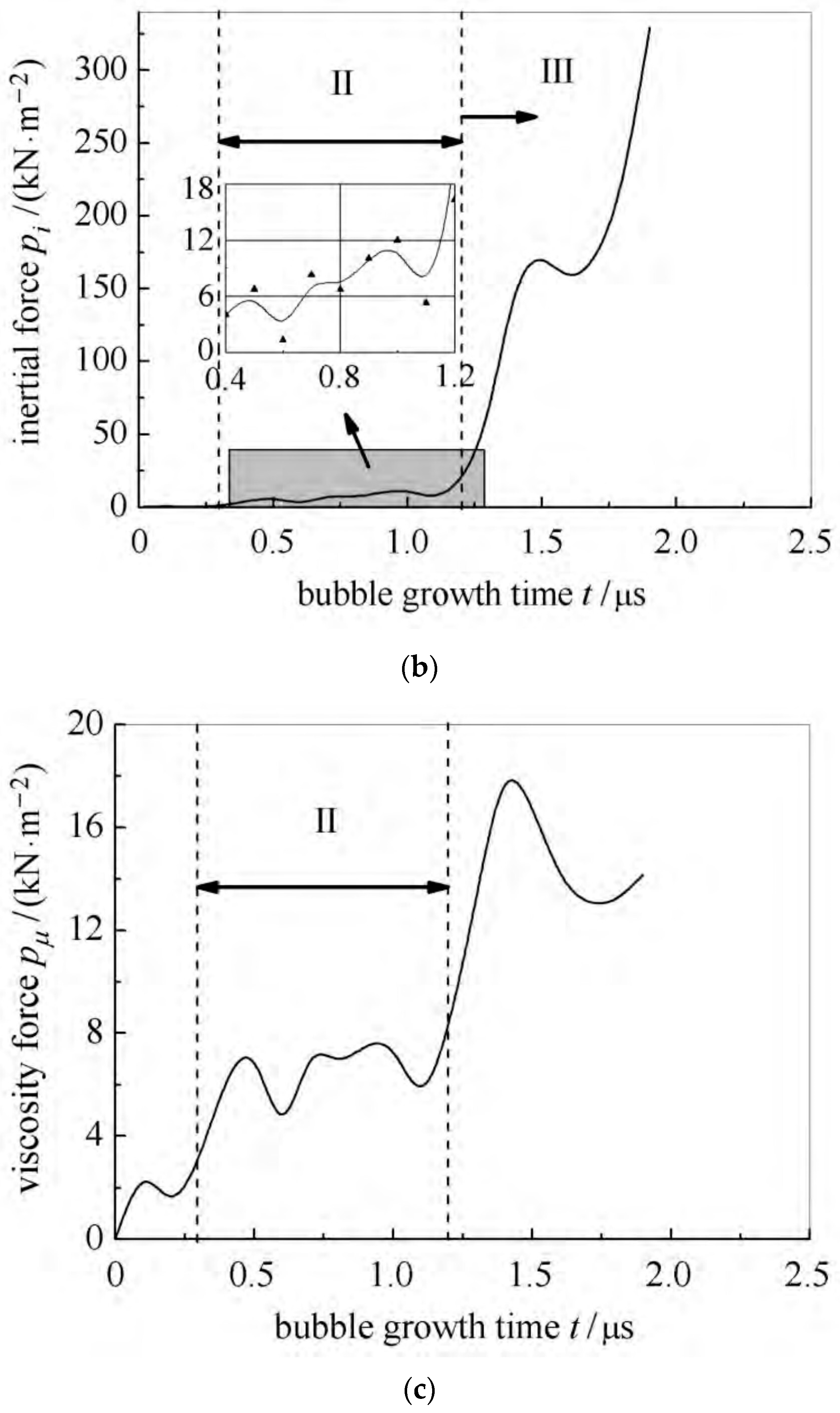
3.3. Force in The Early Stage of Collapse
3.3.1. Types of Force
3.3.2. Distribution of Force
4. Typical Forms of Droplet Splash
4.1. Experimental System
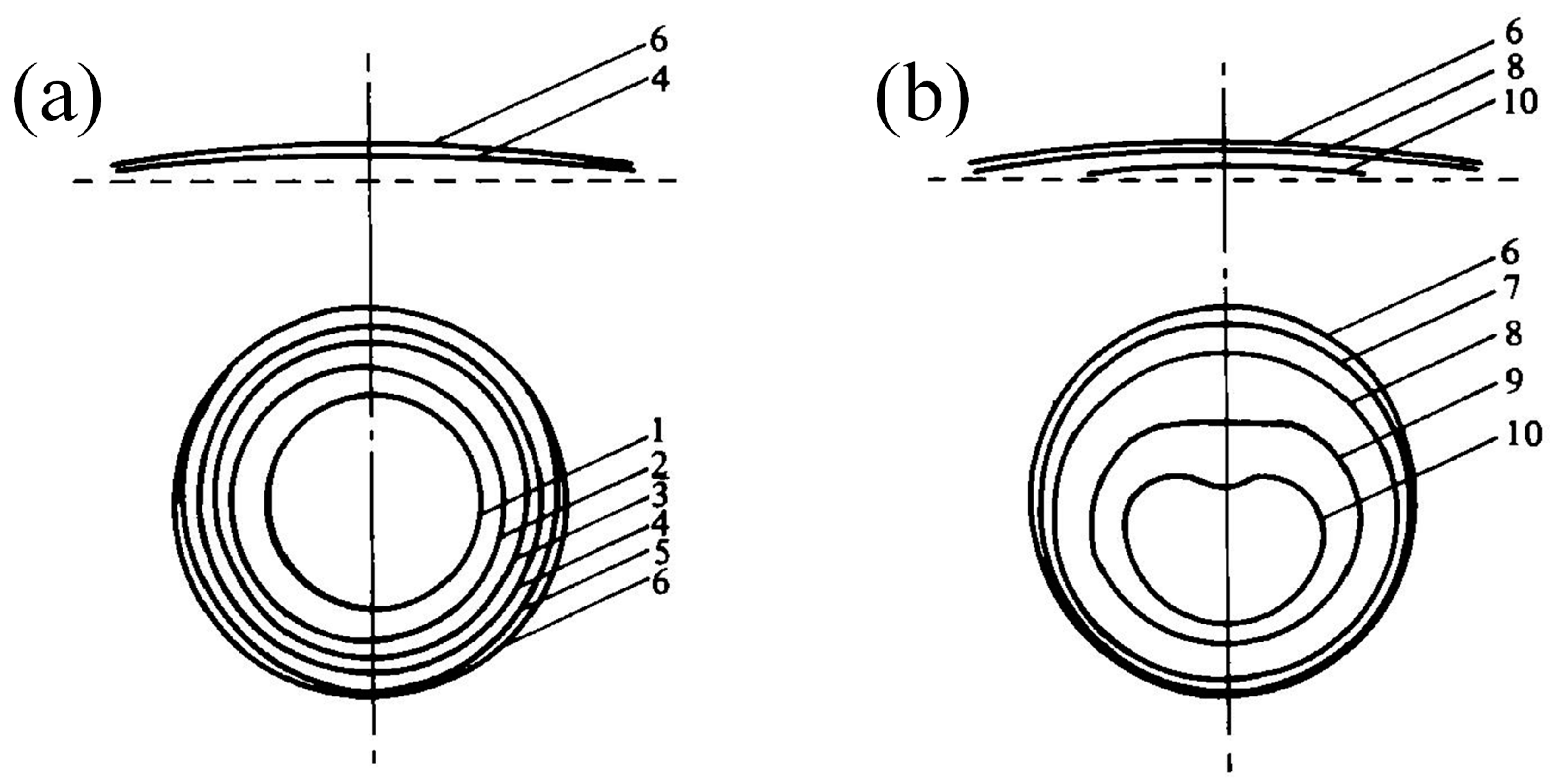
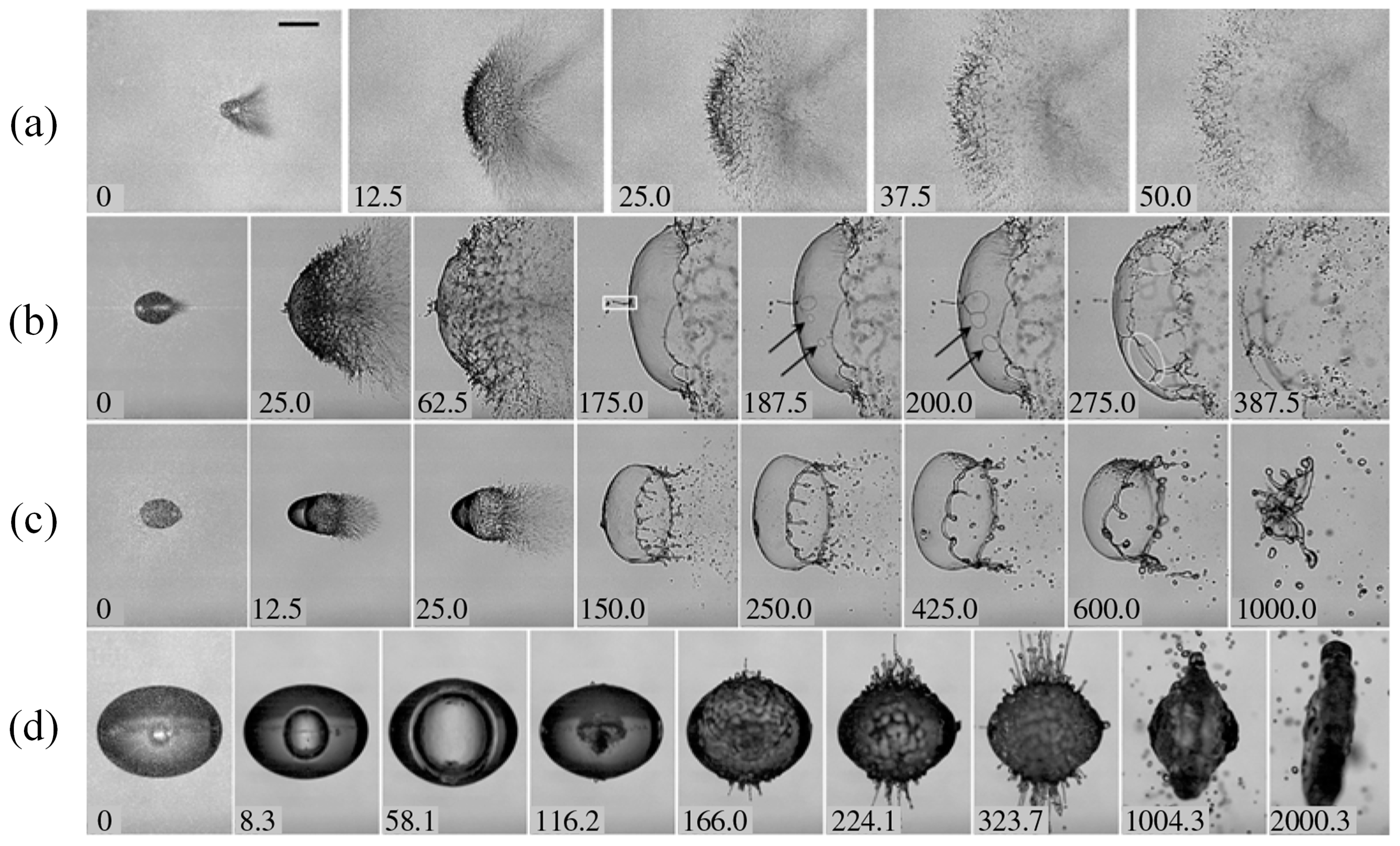
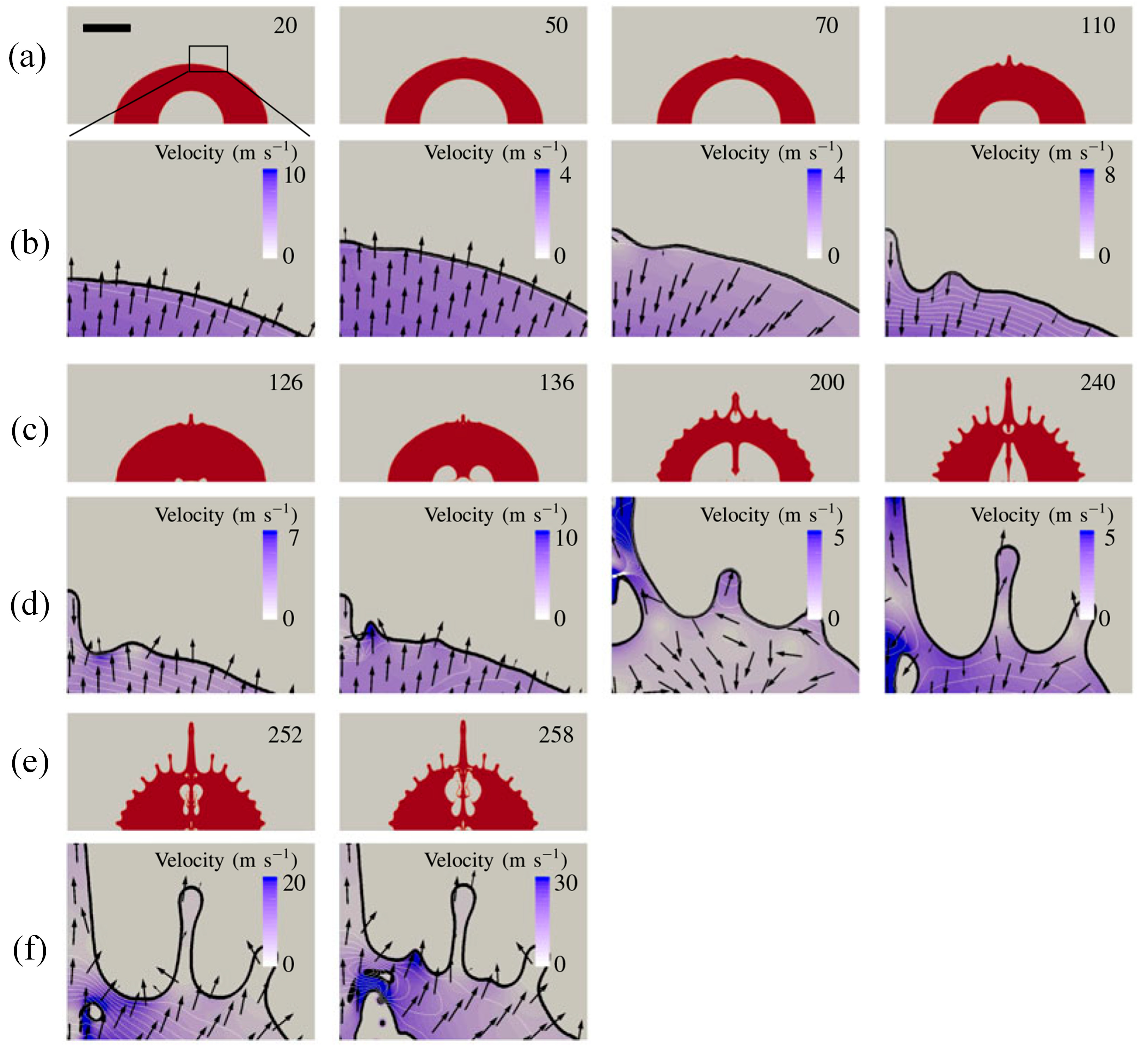
4.2. Typical Splash Forms
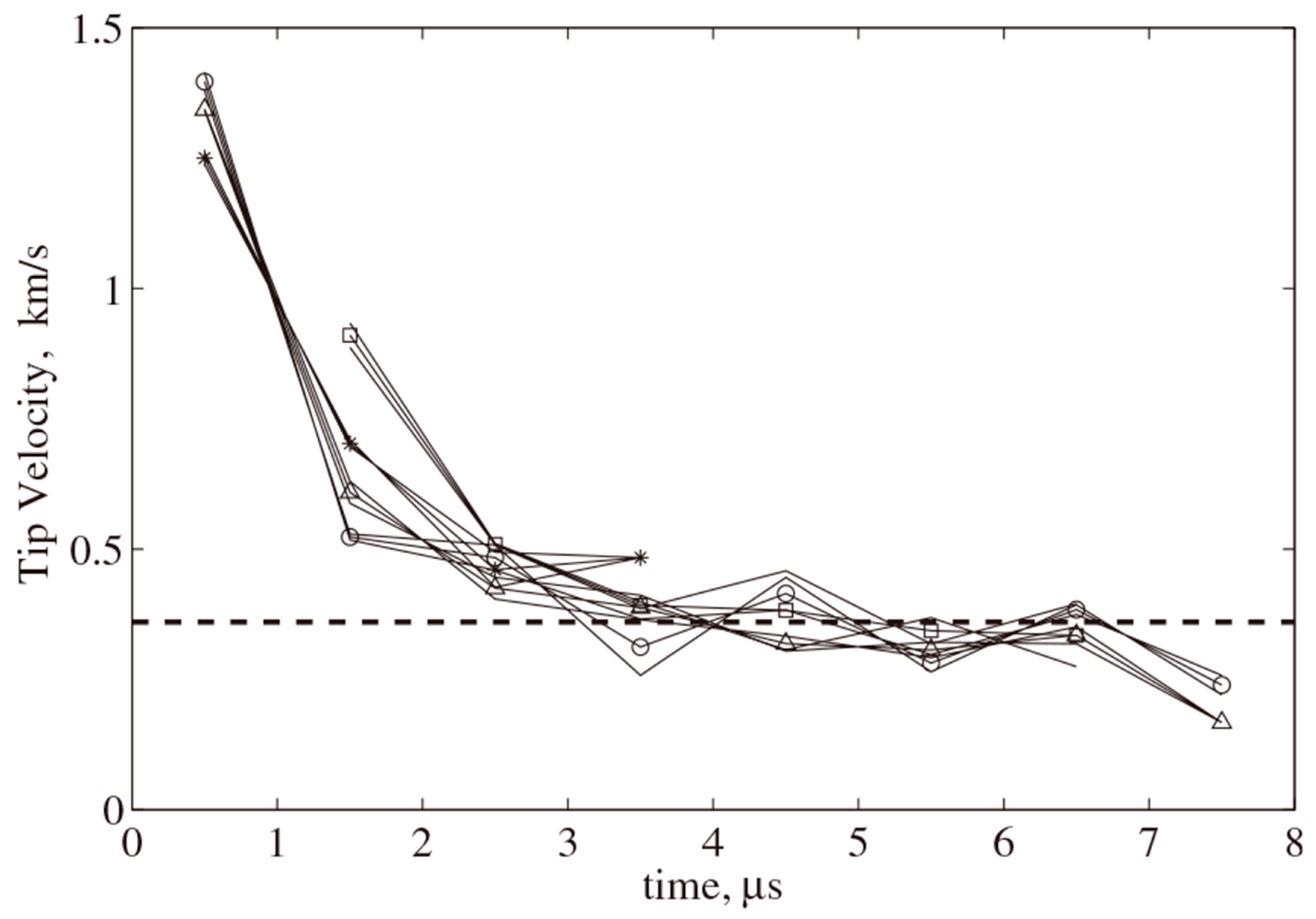
5. Splash Velocity
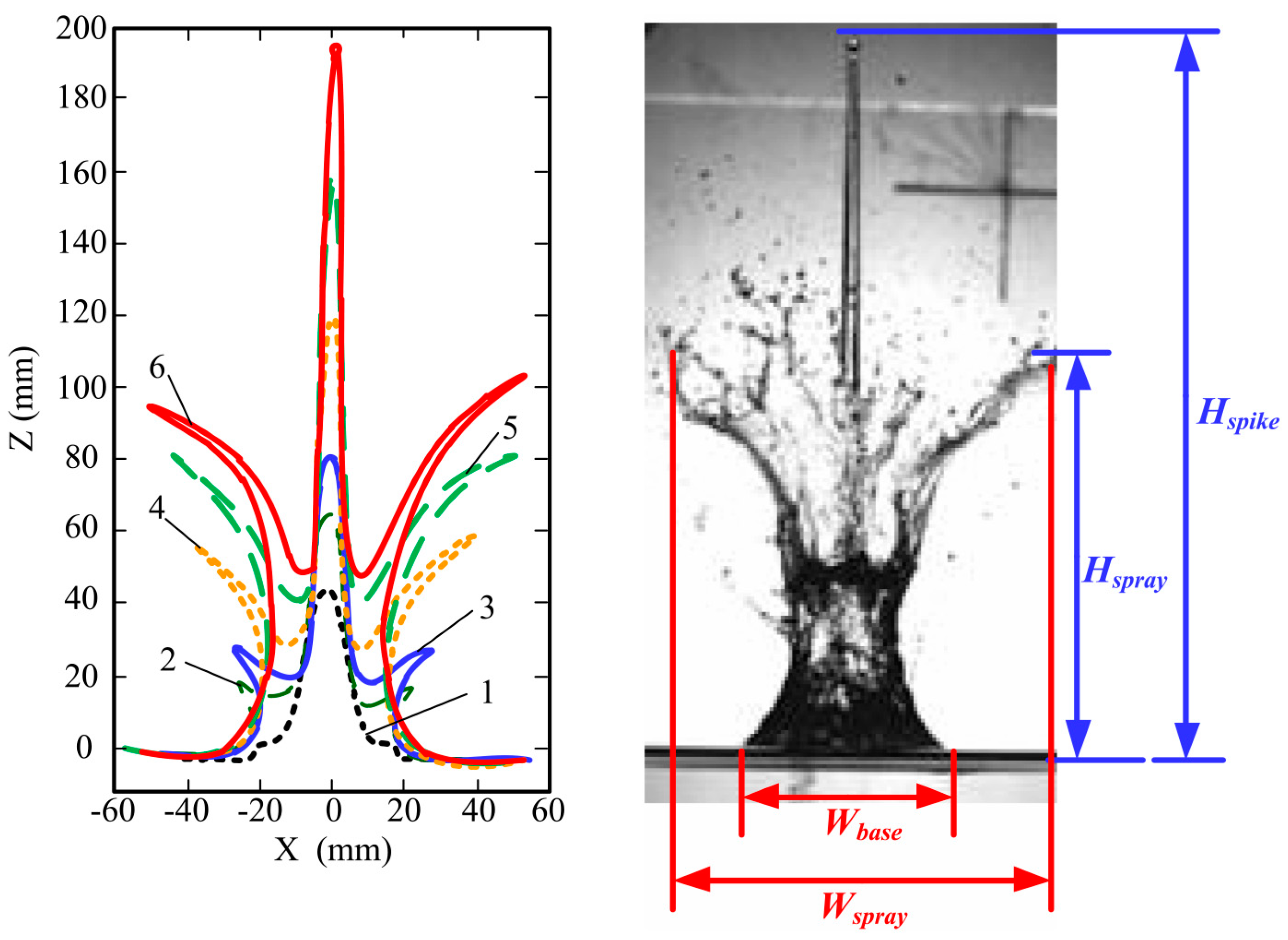
5.1. Definition of Splash Structure
5.2. Comparison of Splash Velocity
5.3. Splash Flow Field
5.4. Splash Mechanism
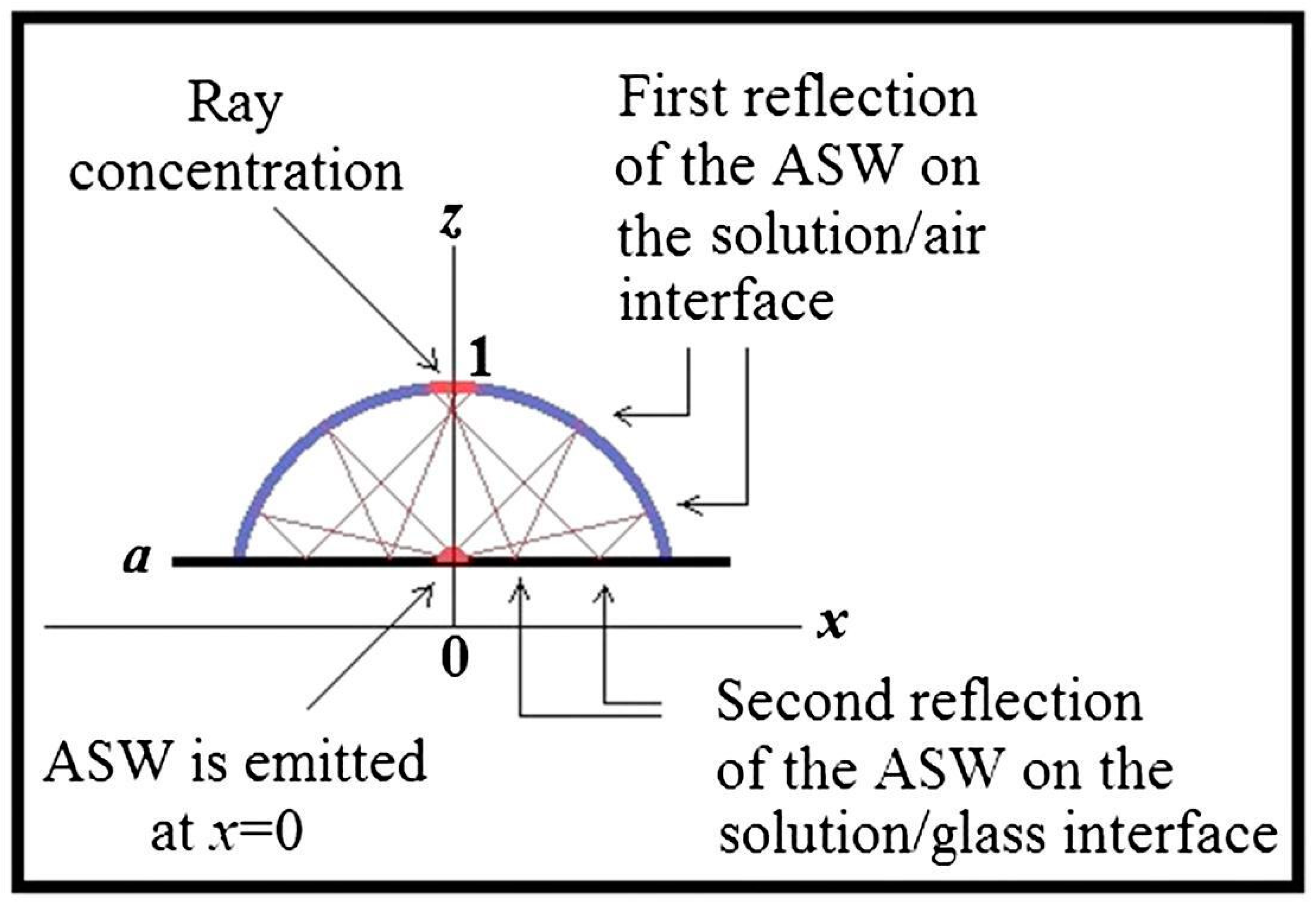
5.4.1. Singularity Theory of Interface Depression
5.4.2. Taylor Instability Mechanism
6. Splash Direction
6.1. Splash Direction Control
6.2. Splash Direction Mechanism
7. Conclusions and Perspecitves
7.1. Conclusions
7.2. Perspective
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guo, W.; Li, H.; Wang, J.; Wang, Y.; Huang, C. Reserch progress on interaction between a single cavitation and free surface. Chin. J. Theor. Appl. Mech. 2019, 51, 1682–1698. [Google Scholar]
- Wang, S.; Zhang, A.; Liu, Y.; Zhang, S.; Cui, P. Bubble dynamics and its applications. J. Hydrodyn. 2018, 30, 975–991. [Google Scholar] [CrossRef]
- Suh, H.K.; Lee, C.S. Effect of cavitation in nozzle orifice on the diesel fuel atomization characteristics. Int. J. Heat Fluid Flow 2008, 29, 1001–1009. [Google Scholar] [CrossRef]
- Payri, F.; Bermúdez, V.; Payri, R.; Salvador, F.J. The influence of cavitation on the internal flow and the spray characteristics in diesel injection nozzles. Fuel 2004, 83, 419–431. [Google Scholar] [CrossRef]
- Watanabe, H.; Nishikori, M.; Hayashi, T.; Suzuki, M.; Kakehashi, N.; Ikemoto, M. Visualization analysis of relationship between vortex flow and cavitation behavior in diesel nozzle. Int. J. Engine Res. 2015, 16, 5–12. [Google Scholar] [CrossRef]
- Wu, Z.; Shi, Z.; Zhao, H.; Yao, F.; Liu, H.; Li, W.; Xu, J. Effects of bubbles in the liquid jet on the air-blast atomization. Fuel 2020, 266, 117117. [Google Scholar] [CrossRef]
- Lü, M.; Ning, Z.; Yan, K.; Fu, J.; Song, Y.; Sun, C. Breakup of cavitation bubbles within the diesel droplet. Chin. J. Mech. Eng. 2014, 27, 198–204. [Google Scholar] [CrossRef]
- Yang, X.; Xue, R.; Wang, N.; Huang, Z.; Zhang, H.; Liu, X.; Chen, L.; Hou, Y. Review of internal cavitating flow in injection nozzles, external atomization and cooling in liquid nitrogen spray cooling systems. Cryogenics 2023, 131, 103661. [Google Scholar] [CrossRef]
- Delrot, P.; Modestino, M.A.; Gallaire, F.; Psaltis, D.; Moser, C. Inkjet Printing of Viscous Monodisperse Microdroplets by Laser-Induced Flow Focusing. Phys. Rev. Appl. 2016, 6, 024003. [Google Scholar] [CrossRef] [Green Version]
- Fraters, A.; van den Berg, M.; de Loore, Y.; Reinten, H.; Wijshoff, H.; Lohse, D.; Versluis, M.; Segers, T. Inkjet Nozzle Failure by Heterogeneous Nucleation: Bubble Entrainment, Cavitation, and Diffusive Growth. Phys. Rev. Appl. 2019, 12, 064019. [Google Scholar] [CrossRef] [Green Version]
- Delrot, P.; Modestino, M.A.; Psaltis, D.; Moser, C.; Gu, B.; Helvajian, H.; Piqué, A. Laser-assisted inkjet printing of highly viscous fluids with sub-nozzle resolution. In Proceedings of the Laser 3D Manufacturing III, San Francisco, CA, USA, 4 December 2016. [Google Scholar]
- Kondo, T.; Ando, K. One-way-coupling simulation of cavitation accompanied by high-speed droplet impact. Phys. Fluids 2016, 28, 33303. [Google Scholar] [CrossRef]
- Martin, G.D.; Hoath, S.D.; Hutchings, I.M. Inkjet printing—The physics of manipulating liquid jets and drops. J. Phys. Conf. Ser. 2008, 105, 12001. [Google Scholar] [CrossRef]
- Zhang, Z.F.; Wang, C.; Wang, L.K.; Zhang, A.M.; Silberschmidt, V.V. Underwater explosion of cylindrical charge near plates: Analysis of pressure characteristics and cavitation effects. Int. J. Impact Eng. 2018, 121, 91–105. [Google Scholar] [CrossRef] [Green Version]
- Ming, F.R.; Zhang, A.M.; Xue, Y.Z.; Wang, S.P. Damage characteristics of ship structures subjected to shockwaves of underwater contact explosions. Ocean Eng. 2016, 117, 359–382. [Google Scholar] [CrossRef]
- Liu, N.N.; Wu, W.B.; Zhang, A.M.; Liu, Y.L. Experimental and numerical investigation on bubble dynamics near a free surface and a circular opening of plate. Phys. Fluids 2017, 29, 107102. [Google Scholar] [CrossRef]
- Zhang, A.; Wang, S.; Peng, Y.; Ming, F.; Liu, Y. Research progress in underwater explosion and its damage to ship structures. Chin. J. Ship Res. 2019, 14, 1–13. [Google Scholar]
- Lew, K.S.F.; Klaseboer, E.; Khoo, B.C. A collapsing bubble-induced micropump: An experimental study. Sens. Actuators A Phys. 2007, 133, 161–172. [Google Scholar] [CrossRef]
- Khoo, B.C.; Klaseboer, E.; Hung, K.C. A collapsing bubble-induced micro-pump using the jetting effect. Sens. Actuators A Phys. 2005, 118, 152–161. [Google Scholar] [CrossRef]
- Dijkink, R.; Ohl, C. Laser-induced cavitation based micropump. Lab Chip 2008, 8, 1676. [Google Scholar] [CrossRef] [PubMed]
- Karri, B.; Pillai, K.S.; Klaseboer, E.; Ohl, S.; Khoo, B.C. Collapsing bubble induced pumping in a viscous fluid. Sens. Actuators A Phys. 2011, 169, 151–163. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Wu, Y. A review of rotating stall in reversible pump turbine. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 1181–1204. [Google Scholar] [CrossRef]
- Fabiilli, M.L.; Haworth, K.J.; Fakhri, N.H.; Kripfgans, O.D.; Carson, P.L.; Fowlkes, J.B. The role of inertial cavitation in acoustic droplet vaporization. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 1006–1017. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Yang, D.; Zhang, Q.; Guo, X.; Raymond, J.L.; Roy, R.A.; Zhang, D.; Tu, J. The influence of droplet concentration on phase change and inertial cavitation thresholds associated with acoustic droplet vaporization. J. Acoust. Soc. Am. 2020, 148, L375–L381. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.; Pitt, W.G. Acoustic Droplet Vaporization in Biology and Medicine. Biomed. Res. Int. 2013, 2013, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Qamar, A.; Wong, Z.Z.; Fowlkes, J.B.; Bull, J.L. Dynamics of acoustic droplet vaporization in gas embolotherapy. Appl. Phys. Lett. 2010, 96, 143702. [Google Scholar] [CrossRef] [Green Version]
- Lacour, T.; Valier-Brasier, T.; Coulouvrat, F. Ultimate fate of a dynamical bubble/droplet system following acoustic vaporization. Phys. Fluids 2020, 32, 51702. [Google Scholar] [CrossRef]
- Sivakumar, M.; Tang, S.Y.; Tan, K.W. Cavitation technology—A greener processing technique for the generation of pharmaceutical nanoemulsions. Ultrason. Sonochem. 2014, 21, 2069–2083. [Google Scholar] [CrossRef]
- Kang, S.; Huang, Y.; Yeh, C. Characterization of Acoustic Droplet Vaporization for Control of Bubble Generation Under Flow Conditions. Ultrasound Med. Biol. 2014, 40, 551–561. [Google Scholar] [CrossRef]
- Jean-Michel, E.; Ayache, B. Therapeutic Ultrasound, 1st ed.; Springer International Publishing: Cham, Switzerland, 2016; pp. 157–362. [Google Scholar]
- Wong, Z.Z.; Kripfgans, O.D.; Qamar, A.; Fowlkes, J.B.; Bull, J.L. Bubble evolution in acoustic droplet vaporization at physiological temperature via ultra-high speed imaging. Soft Matter 2011, 7, 4009. [Google Scholar] [CrossRef]
- Wang, L.Y.; Zheng, S.S. Advances in low-frequency ultrasound combined with microbubbles in targeted tumor therapy. J. Zhejiang Univ. Sci. B 2019, 20, 291–299. [Google Scholar] [CrossRef]
- Jagadeesh, G.; Prakash, G.D.; Rakesh, S.G.; Allam, U.S.; Krishna, M.G.; Eswarappa, S.M.; Chakravortty, D. Needleless Vaccine Delivery Using Micro-Shock Waves. Clin. Vaccine Immunol. 2011, 18, 539–545. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schramm-Baxter, J.; Mitragotri, S. Needle-free jet injections: Dependence of jet penetration and dispersion in the skin on jet power. J. Control. Release 2004, 97, 527–535. [Google Scholar] [CrossRef] [PubMed]
- Stachowiak, J.C.; Li, T.H.; Arora, A.; Mitragotri, S.; Fletcher, D.A. Dynamic control of needle-free jet injection. J. Control. Release 2009, 135, 104–112. [Google Scholar] [CrossRef] [PubMed]
- Tagawa, Y.; Oudalov, N.; El, G.A.; Sun, C.; Lohse, D. Needle-free injection into skin and soft matter with highly focused microjets. Lab Chip 2013, 13, 1357–1363. [Google Scholar] [CrossRef] [Green Version]
- Rosselló, J.M.; Ohl, C. Bullet jet as a tool for soft matter piercing and needle-free liquid injection. Biomed. Opt. Express 2022, 13, 5202. [Google Scholar] [CrossRef]
- Kudryavtsev, V.N.; Makin, V.K. Impact of Ocean Spray on the Dynamics of the Marine Atmospheric Boundary Layer. Bound.-Lay. Meteorol. 2011, 140, 383–410. [Google Scholar] [CrossRef] [Green Version]
- Fabrice, V. Ocean Spray. Annu. Rev. Fluid Mech. 2015, 47, 507–538. [Google Scholar]
- Ramon, J.C.; Duncan, C.B. Bubble and Aerosol Spectra Produced by a Laboratory ‘Breaking Wave’. J. Geophys. Res. 2015, 47, 507–538. [Google Scholar]
- François, R.; George, A. Film drop distributions from bubbles bursting in seawater. J. Geophys. Res. Ocean 1991, 96, 10681–10688. [Google Scholar]
- Blanchard, D.C.; Syzdek, L.D. Film drop production as a function of bubble size. J. Geophys. Res. 1988, 93, 3649–3654. [Google Scholar] [CrossRef]
- Resch, F.J.; Darrozes, J.S.; Afeti, G.M. Marine liquid aerosol production from bursting of air bubbles. J. Geophys. Res. 1986, 91, 1019–1029. [Google Scholar] [CrossRef]
- Khan, M.M.; Hélie, J.; Gorokhovski, M.; Sheikh, N.A. Experimental and numerical study of flash boiling in gasoline direct injection sprays. Appl. Therm. Eng. 2017, 123, 377–389. [Google Scholar] [CrossRef]
- Obreschkow, D.; Kobel, P.; Dorsaz, N.; de Bosset, A.; Nicollier, C.; Farhat, M. Cavitation bubble dynamics inside liquid drops in microgravity. Phys. Rev. Lett. 2006, 97, 94502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Robert, E.; Lettry, J.; Farhat, M.; Monkewitz, P.A.; Avellan, F. Cavitation bubble behavior inside a liquid jet. Phys. Fluids 2007, 19, 67106. [Google Scholar] [CrossRef]
- Kobel, P.; Obreschkow, D.; de Bosset, A.; Dorsaz, N.; Farhat, M. Techniques for generating centimetric drops in microgravity and application to cavitation studies. Exp. Fluids 2009, 47, 39–48. [Google Scholar] [CrossRef] [Green Version]
- Blake, J.R.; Taib, B.B.; Doherty, G. Transient cavities near boundaries Part 2. Free surface. J. Fluid Mech. 1987, 181, 197–212. [Google Scholar] [CrossRef]
- Liu, J.L.; Xiao, W.; Yao, X.L.; Huang, X.H. Dynamics of a bubble in a liquid fully confined by an elastic boundary. Phys. Fluids 2021, 33, 63303. [Google Scholar] [CrossRef]
- Obreschkow, D.; Dorsaz, N.; Kobel, P.; de Bosset, A.; Tinguely, M.; Field, J.; Farhat, M. Confined shocks inside isolated liquid volumes: A new path of erosion? Phys. Fluids 2011, 23, 101702. [Google Scholar] [CrossRef] [Green Version]
- Lindinger, A.; Hagen, J.; Socaciu, L.D.; Bernhardt, T.M.; Woste, L.; Duft, D.; Leisner, T. Time-resolved explosion dynamics of H2O droplets induced by femtosecond laser pulses. Appl. Opt. 2004, 43, 5263–5269. [Google Scholar] [CrossRef]
- Gonzalez Avila, S.R.; Ohl, C. Fragmentation of acoustically levitating droplets by laser-induced cavitation bubbles. J. Fluid Mech. 2016, 805, 551–576. [Google Scholar] [CrossRef]
- Heijnen, L.; Quinto-Su, P.A.; Zhao, X.; Ohl, C.D. Cavitation within a droplet. Phys. Fluids 2009, 21, 91102. [Google Scholar] [CrossRef] [Green Version]
- Rosselló, J.M.; Reese, H.; Ohl, C. Dynamics of pulsed laser-induced cavities on a liquid–gas interface: From a conical splash to a ‘bullet’ jet. J. Fluid Mech. 2022, 939, A35. [Google Scholar] [CrossRef]
- Padilla-Martinez, J.P.; Ramirez-San-Juan, J.C.; Berrospe-Rodriguez, C.; Korneev, N.; Aguilar, G.; Zaca-Moran, P.; Ramos-Garcia, R. Controllable direction of liquid jets generated by thermocavitation within a droplet. Appl. Opt. 2017, 56, 7167–7173. [Google Scholar] [CrossRef]
- Mohamed, F. What We Learned from Cavitation Bubbles in Microgravity, 1st ed.; IntechOpen: London, UK, 2020; pp. 12–17. [Google Scholar]
- Farhat, M.; Obreschkow, D.; Kobel, P.; Dorsaz, N.; De Bosset, A. Interaction of a cavitation bubble with a spherical free surface. In Proceedings of the Sixth International Symposium on Cavitation, Wageningen, The Netherlands, 11–15 September 2006. [Google Scholar]
- Zeng, Q.; Gonzalez-Avila, S.R.; Voorde, S.T.; Ohl, C. Jetting of viscous droplets from cavitation-induced Rayleigh–Taylor instability. J. Fluid Mech. 2018, 846, 916–943. [Google Scholar] [CrossRef]
- Thoroddsen, S.T.; Takehara, K.; Etoh, T.G.; Ohl, C.D. Spray and microjets produced by focusing a laser pulse into a hemispherical drop. Phys. Fluids 2009, 21, 112101. [Google Scholar] [CrossRef] [Green Version]
- Supponen, O.; Obreschkow, D.; Kobel, P.; Farhat, M. Detailed Jet Dynamics in a Collapsing Bubble. J. Phys. Conf. Ser. 2015, 656, 12038. [Google Scholar] [CrossRef]
- Patrascioiu, A.; Fernández-Pradas, J.M.; Palla-Papavlu, A.; Morenza, J.L.; Serra, P. Laser-generated liquid microjets: Correlation between bubble dynamics and liquid ejection. Microfluid. Nanofluid. 2014, 16, 55–63. [Google Scholar] [CrossRef]
- Lindau, O.; Lauterborn, W. Cinematographic observation of the collapse and rebound of a laser-produced cavitation bubble near a wall. J. Fluid Mech. 2003, 479, 327–348. [Google Scholar] [CrossRef]
- Li, S.; Han, R.; Zhang, A.M.; Wang, Q.X. Analysis of pressure field generated by a collapsing bubble. Ocean Eng. 2016, 117, 22–38. [Google Scholar] [CrossRef]
- Supponen, O.; Obreschkow, D.; Tinguely, M.; Kobel, P.; Dorsaz, N.; Farhat, M. Scaling laws for jets of single cavitation bubbles. J. Fluid Mech. 2016, 802, 263–293. [Google Scholar] [CrossRef] [Green Version]
- Robinson, P.B.; Blake, J.R.; Kodama, T.; Shima, A.; Tomita, Y. Interaction of cavitation bubbles with a free surface. J. Appl. Phys. 2001, 89, 8225–8237. [Google Scholar] [CrossRef]
- Blake, J.R.; Gibson, D.C. Growth and collapse of a vapour cavity near a free surface. J. Fluid Mech. 1981, 111, 123–140. [Google Scholar] [CrossRef]
- Lauterborn, W.; Vogel, A. Shock Wave Emission by Laser Generated Bubbles; Springer: Berlin/Heidelberg, Germany, 2013; pp. 67–103. [Google Scholar]
- Vogel, A.; Busch, S.; Parlitz, U. Shock wave emission and cavitation bubble generation by picosecond and nanosecond optical breakdown in water. J. Acoust. Soc. Am. 1996, 100, 148–165. [Google Scholar] [CrossRef]
- Sankin, G.N.; Simmons, W.N.; Zhu, S.L.; Zhong, P. Shock wave interaction with laser-generated single bubbles. Phys. Rev. Lett. 2005, 95, 34501. [Google Scholar] [CrossRef]
- Akhatov, I.; Lindau, O.; Topolnikov, A.; Mettin, R.; Vakhitova, N.; Lauterborn, W. Collapse and rebound of a laser-induced cavitation bubble. Phys. Fluids 2001, 13, 2805–2819. [Google Scholar] [CrossRef] [Green Version]
- Chahine, G.L.; Kapahi, A.; Choi, J.; Hsiao, C. Modeling of surface cleaning by cavitation bubble dynamics and collapse. Ultrason. Sonochem. 2016, 29, 528–549. [Google Scholar] [CrossRef] [PubMed]
- Philipp, A.; Lauterborn, W. Cavitation erosion by single laser-produced bubbles. J. Fluid Mech. 1998, 361, 75–116. [Google Scholar] [CrossRef]
- Supponen, O.; Obreschkow, D.; Kobel, P.; Tinguely, M.; Dorsaz, N.; Farhat, M. Shock waves from nonspherical cavitation bubbles. Phys. Rev. Fluids 2017, 2, 093601. [Google Scholar] [CrossRef] [Green Version]
- Brujan, E.A.; Keen, G.S.; Vogel, A.; Blake, J.R. The final stage of the collapse of a cavitation bubble close to a rigid boundary. Phys. Fluids 2002, 14, 85–92. [Google Scholar] [CrossRef] [Green Version]
- Krivokorytov, M.S.; Vinokhodov, A.Y.; Sidelnikov, Y.V.; Krivtsun, V.M.; Kompanets, V.O.; Lash, A.A.; Koshelev, K.N.; Medvedev, V.V. Cavitation and spallation in liquid metal droplets produced by subpicosecond pulsed laser radiation. Phys. Rev. E 2017, 95, 31101. [Google Scholar] [CrossRef]
- Ohl, S.; Klaseboer, E.; Khoo, B.C. Bubbles with shock waves and ultrasound: A review. Interface Focus 2015, 5, 20150019. [Google Scholar] [CrossRef]
- Lv, M.; Ning, Z.; Sun, C. Study on the growth and collapse of cavitation bubble within a droplet. Chin. J. Theor. Appl. Mech. 2016, 48, 857–866. [Google Scholar]
- Pain, A.; Hui Terence Goh, B.; Klaseboer, E.; Ohl, S.; Cheong Khoo, B. Jets in quiescent bubbles caused by a nearby oscillating bubble. J. Appl. Phys. 2012, 111, 54912. [Google Scholar] [CrossRef]
- Moghtadernejad, S.; Lee, C.; Jadidi, M. An Introduction of Droplet Impact Dynamics to Engineering Students. Fluids 2020, 5, 107. [Google Scholar] [CrossRef]
- Pearson, A.; Cox, E.; Blake, J.R.; Otto, S.R. Bubble interactions near a free surface. Eng. Anal. Bound. Elem. 2004, 28, 295–313. [Google Scholar] [CrossRef]
- Kiyama, A.; Tagawa, Y.; Ando, K.; Kameda, M. Effects of a water hammer and cavitation on jet formation in a test tube. J. Fluid Mech. 2016, 787, 224–236. [Google Scholar] [CrossRef] [Green Version]
- Longuet-Higgins, M.S. Bubbles, breaking waves and hyperbolic jets at a free surface. J. Fluid Mech. 1983, 127, 103–121. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, S.P.; Zhang, A.M. Experimental study on the interaction between bubble and free surface using a high-voltage spark generator. Phys. Fluids 2016, 28, 32109. [Google Scholar] [CrossRef]
- Dadvand, A.; Khoo, B.C.; Shervani-Tabar, M.T. A collapsing bubble-induced microinjector: An experimental study. Exp. Fluids 2009, 46, 419–434. [Google Scholar] [CrossRef]
- Robles, V.; Gutierrez-Herrera, E.; Devia-Cruz, L.F.; Banks, D.; Camacho-Lopez, S.; Aguilar, G. Soft material perforation via double-bubble laser-induced cavitation microjets. Phys. Fluids 2020, 32, 42005. [Google Scholar] [CrossRef] [Green Version]
- Kang, Y.J.; Cho, Y. Gravity–capillary jet-like surface waves generated by an underwater bubble. J. Fluid Mech. 2019, 866, 841–864. [Google Scholar] [CrossRef]
- Reuter, F.; Ohl, C. Supersonic needle-jet generation with single cavitation bubbles. Appl. Phys. Lett. 2021, 118, 134103. [Google Scholar] [CrossRef]
- Bempedelis, N.; Zhou, J.; Andersson, M.; Ventikos, Y. Numerical and experimental investigation into the dynamics of a bubble-free-surface system. Phys. Rev. Fluids 2021, 6, 013606. [Google Scholar] [CrossRef]
- Li, J.; Rong, J. Bubble and free surface dynamics in shallow underwater explosion. Ocean Eng. 2011, 38, 1861–1868. [Google Scholar] [CrossRef]
- Li, T.; Zhang, A.; Wang, S.; Li, S.; Liu, W. Bubble interactions and bursting behaviors near a free surface. Phys. Fluids 2019, 31, 42104. [Google Scholar]
- Han, B.; Köhler, K.; Jungnickel, K.; Mettin, R.; Lauterborn, W.; Vogel, A. Dynamics of laser-induced bubble pairs. J. Fluid Mech. 2015, 771, 706–742. [Google Scholar] [CrossRef] [Green Version]
- Chen, R.C.; Yu, Y.T.; Su, K.W.; Chen, J.F.; Chen, Y.F. Exploration of water jet generated by Q-switched laser induced water breakdown with different depths beneath a flat free surface. Opt. Express 2013, 21, 445–453. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Li, H.; Guo, W.; Wang, Z.; Du, T.; Wang, Y.; Abe, A.; Huang, C. Rayleigh–Taylor instability of cylindrical water droplet induced by laser-produced cavitation bubble. J. Fluid Mech. 2021, 919, A42. [Google Scholar] [CrossRef]
- Lauterborn, W.; Kurz, T.; Mettin, R.; Ohl, C. Advances in Chemical Physics, 1st ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1999; pp. 333–350. [Google Scholar]
- Padilla-Martinez, J.P.; Ramirez-San-Juan, J.C.; Korneev, N.; Banks, D.; Aguilar, G.; Ramos-Garcia, R. Breaking the Rayleigh-Plateau instability limit using thermocavitation within a droplet. At. Spray 2013, 23, 487–503. [Google Scholar] [CrossRef]
- Tan, M.K.; Friend, J.R.; Yeo, L.Y. Interfacial jetting phenomena induced by focused surface vibrations. Phys. Rev. Lett. 2009, 103, 24501. [Google Scholar] [CrossRef] [Green Version]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Zhang, X.; Zhang, S.; Ying, J.; Yang, Y.; Wang, H.; Li, Z.; Zhang, Y. A Review of the Dynamics Progress of Bubble Collapse within Droplet and Droplet Splash. Appl. Sci. 2023, 13, 7822. https://doi.org/10.3390/app13137822
Zhang Y, Zhang X, Zhang S, Ying J, Yang Y, Wang H, Li Z, Zhang Y. A Review of the Dynamics Progress of Bubble Collapse within Droplet and Droplet Splash. Applied Sciences. 2023; 13(13):7822. https://doi.org/10.3390/app13137822
Chicago/Turabian StyleZhang, Yuning, Xiaofei Zhang, Shurui Zhang, Jiaze Ying, Yihao Yang, Hongbo Wang, Zhaohao Li, and Yuning Zhang. 2023. "A Review of the Dynamics Progress of Bubble Collapse within Droplet and Droplet Splash" Applied Sciences 13, no. 13: 7822. https://doi.org/10.3390/app13137822
APA StyleZhang, Y., Zhang, X., Zhang, S., Ying, J., Yang, Y., Wang, H., Li, Z., & Zhang, Y. (2023). A Review of the Dynamics Progress of Bubble Collapse within Droplet and Droplet Splash. Applied Sciences, 13(13), 7822. https://doi.org/10.3390/app13137822




