The Use of Empirical Mode Decomposition on Heart Rate Variability Signals to Assess Autonomic Neuropathy Progression in Type 2 Diabetes
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
2.2. ECG and PPG Recording and Processing
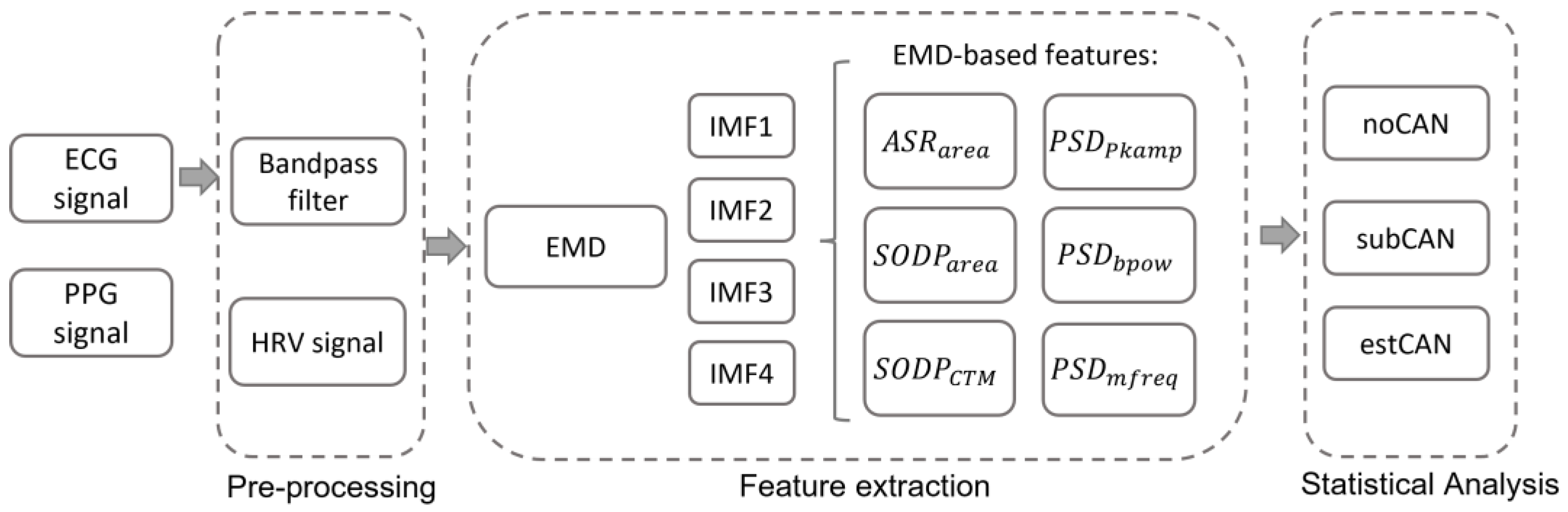
2.3. Feature Extraction
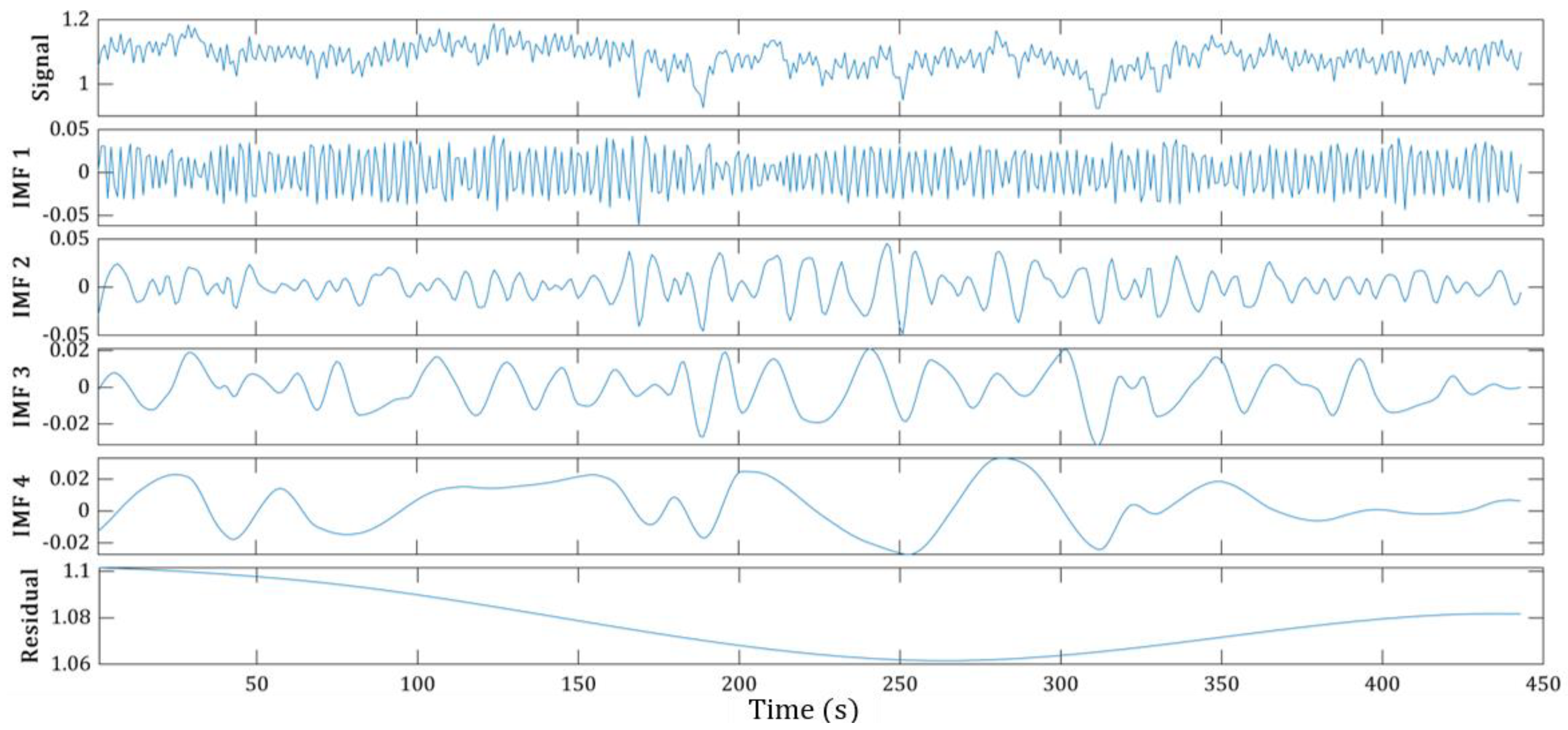
2.3.1. Empirical Mode Decomposition
- (i)
- Identify the signal maxima and minima;
- (ii)
- Compute the interpolated upper and lower envelopes and the instantaneous local mean of the envelopes;
- (iii)
- Subtract the obtained local mean from the original signal x(t) to obtain the first component ;
- (iv)
- Check whether the component satisfies the two basic conditions of the IMF:
- The number of extrema—maxima and minima—and the number of zero-crossings in a signal should be either equal or differ by a maximum of one;
- At any point, the mean value of two envelopes, one formed by connecting local maxima and the other by local minima, should be zero.
- (v)
- Repeat steps (i)–(iii) until it satisfies the conditions of the IMF (or by applying a stopping criterion such as the number of repetitions);
- (vi)
- Repeat steps (i)–(iii) again for the calculation of the next IMFs, until no more components can be extracted (or by removing criteria such as the number of required IMFs).
2.3.2. The Features of EMD-Derived IMFs
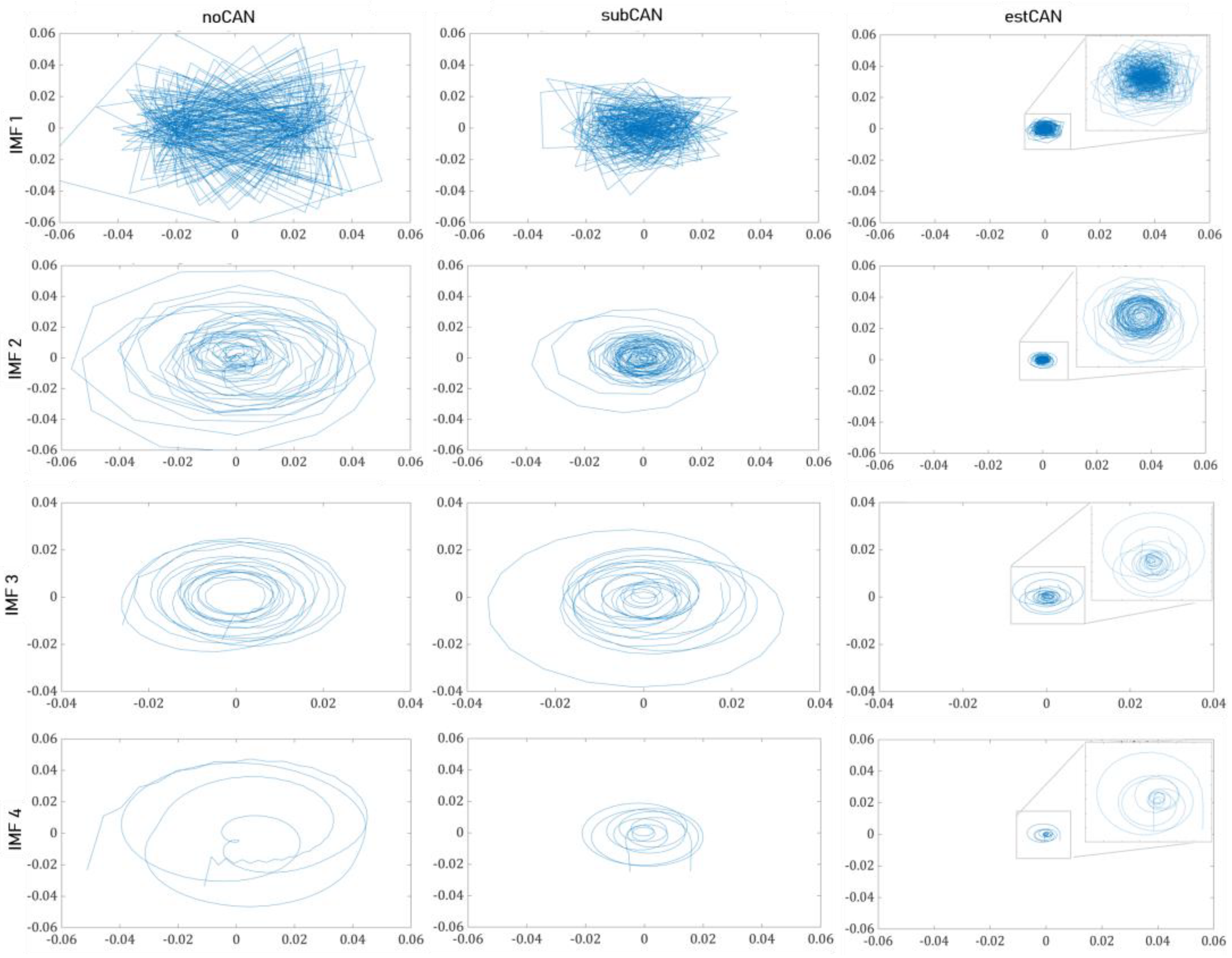
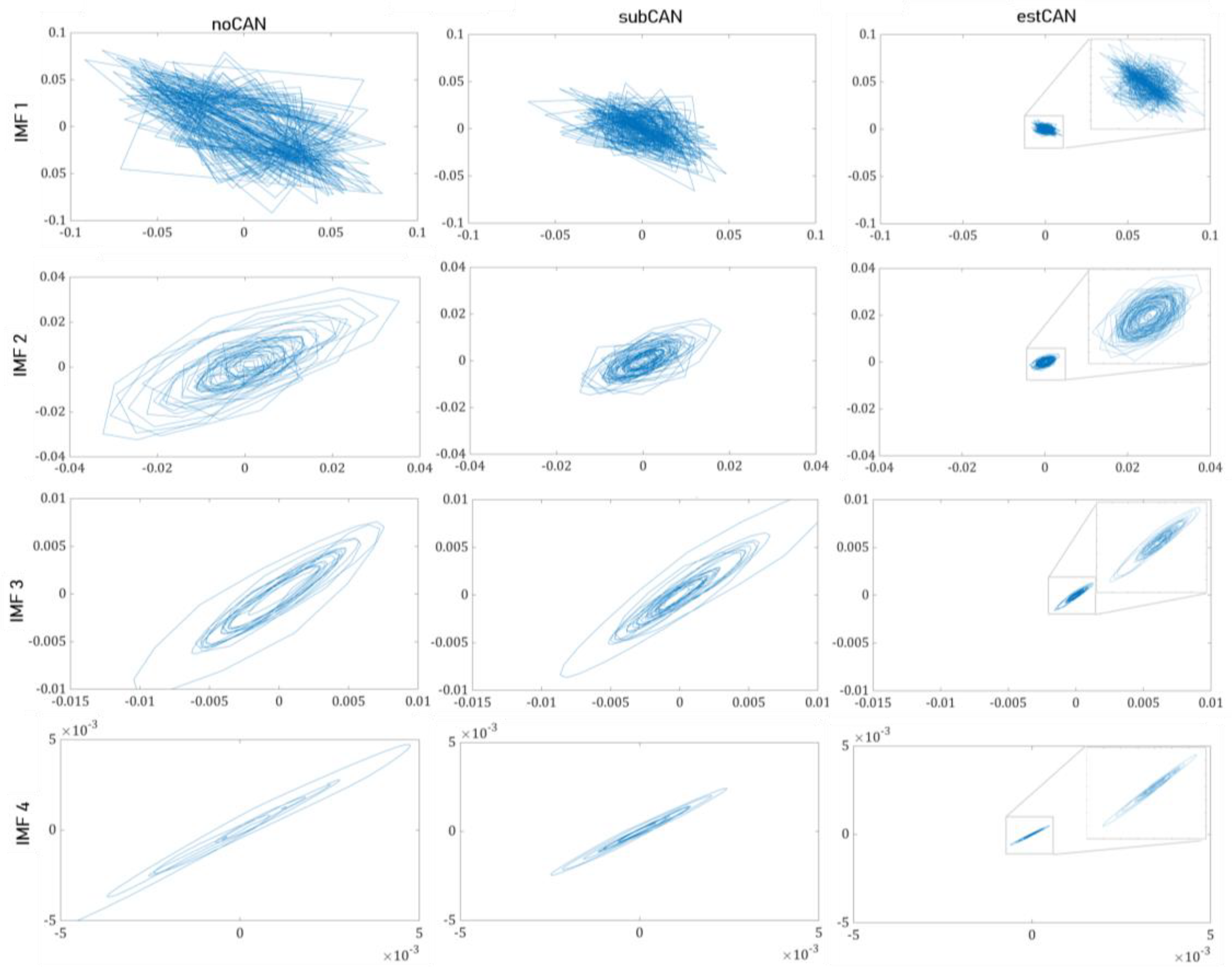
- The area of analytical signal representation ()
- The second-order difference plots ()
- Power spectral density estimation (, and )
2.4. Statistical Analysis
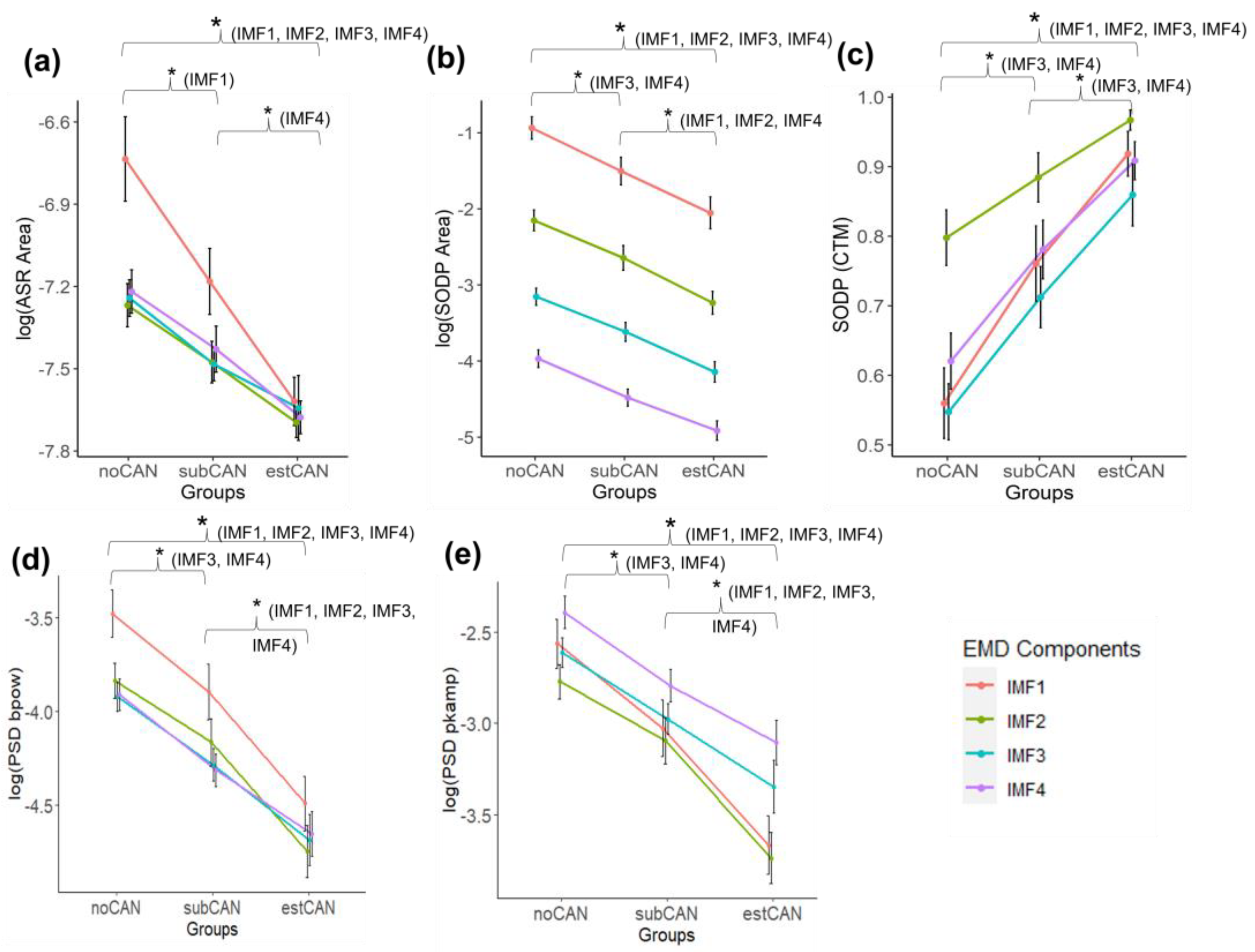
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- International Diabetes Federation. IDF Diabetes Atlas, 10th ed.; International Diabetes Federation: Brussels, Belgium, 2021. [Google Scholar]
- American Diabetes Association. 2. Classification and Diagnosis of Diabetes: Standards of Medical Care in Diabetes–2021. Diabetes Care 2021, 44 (Suppl. S1), S15–S33. [Google Scholar] [CrossRef]
- Vinik, A.I.; Erbas, T.; Casellini, C.M. Diabetic Cardiac Autonomic Neuropathy, Inflammation and Cardiovascular Disease. J. Diabetes Investig. 2013, 4, 4–18. [Google Scholar] [CrossRef] [PubMed]
- Fisher, V.L.; Tahrani, A.A. Cardiac Autonomic Neuropathy in Patients with Diabetes Mellitus: Current Perspectives. Diabetes Metab. Syndr. Obes. 2017, 10, 419–434. [Google Scholar] [CrossRef] [PubMed]
- Williams, S.; Raheim, S.A.; Khan, M.I.; Rubab, U.; Kanagala, P.; Zhao, S.S.; Marshall, A.; Brown, E.; Alam, U. Cardiac Autonomic Neuropathy in Type 1 and 2 Diabetes: Epidemiology, Pathophysiology, and Management. Clin. Ther. 2022, 44, 2022. [Google Scholar] [CrossRef]
- O’Brien, I.A.; O’Hare, P.; Corrall, R.J.M. Heart Rate Variability in Healthy Subjects: Effect of Age and the Derivation of Normal Ranges for Tests of Autonomic Function. Heart 1986, 55, 348–354. [Google Scholar] [CrossRef] [PubMed]
- Vinik, A.I.; Casellini, C.; Parson, H.K.; Colberg, S.R.; Nevoret, M.-L. Cardiac Autonomic Neuropathy in Diabetes: A Predictor of Cardiometabolic Events. Front. Neurosci. 2018, 12, 591. [Google Scholar] [CrossRef]
- Ang, L.; Dillon, B.; Mizokami-Stout, K.; Pop-Busui, R. Cardiovascular Autonomic Neuropathy: A Silent Killer with Long Reach. Auton. Neurosci. 2020, 225, 102646. [Google Scholar] [CrossRef]
- Spallone, V. Update on the Impact, Diagnosis and Management of Cardiovascular Autonomic Neuropathy in Diabetes: What Is Defined, What Is New, and What Is Unmet. Diabetes Metab. J. 2019, 43, 3. [Google Scholar] [CrossRef]
- Acharya, R.; Kannathal, N.; Krishnan, S.M. Comprehensive Analysis of Cardiac Health Using Heart Rate Signals. Physiol. Meas. 2004, 25, 1139–1151. [Google Scholar] [CrossRef]
- Rolim, L.C.; de Souza, J.S.T.; Dib, S.A. Tests for Early Diagnosis of Cardiovascular Autonomic Neuropathy: Critical Analysis and Relevance. Front. Endocrinol. 2013, 4, 2–5. [Google Scholar] [CrossRef]
- Pop-Busui, R.; Backlund, J.Y.C.; Bebu, I.; Braffett, B.H.; Lorenzi, G.; White, N.H.; Lachin, J.M.; Soliman, E.Z. Utility of Using Electrocardiogram Measures of Heart Rate Variability as a Measure of Cardiovascular Autonomic Neuropathy in Type 1 Diabetes Patients. J. Diabetes Investig. 2022, 13, 125–133. [Google Scholar] [CrossRef]
- Castiglioni, P.; Faini, A.; Nys, A.; De Busser, R.; Scherrenberg, M.; Baldussu, E.; Parati, G.; Dendale, P. Heart Rate Variability for the Early Detection of Cardiac Autonomic Dysfunction in Type 1 Diabetes. Front. Physiol. 2022, 13, 1319. [Google Scholar] [CrossRef]
- Cardoso, C.R.L.; de Oliveira, V.A.G.; Leite, N.C.; Salles, G.F. Prognostic Importance of Cardiovascular Autonomic Neuropathy on Cardiovascular and Mortality Outcomes in Individuals with Type 2 Diabetes: The Rio de Janeiro Type 2 Diabetes Cohort. Diabetes Res. Clin. Pract. 2023, 196, 110232. [Google Scholar] [CrossRef]
- Benichou, T.; Pereira, B.; Mermillod, M.; Tauveron, I.; Pfabigan, D.; Maqdasy, S.; Dutheil, F. Heart Rate Variability in Type 2 Diabetes Mellitus: A Systematic Review and Meta-Analysis. PLoS ONE 2018, 13, e0195166. [Google Scholar] [CrossRef] [PubMed]
- Sassi, R.; Cerutti, S.; Lombardi, F.; Malik, M.; Huikuri, H.V.; Peng, C.-K.; Schmidt, G.; Yamamoto, Y.; Gorenek, B.; Lip, G.Y.H.; et al. Advances in Heart Rate Variability Signal Analysis: Joint Position Statement by the e-Cardiology ESC Working Group and the European Heart Rhythm Association Co-Endorsed by the Asia Pacific Heart Rhythm Society. Europace 2015, 17, 1341–1353. [Google Scholar] [CrossRef]
- Bravi, A.; Longtin, A.; Seely, A.J. Review and Classification of Variability Analysis Techniques with Clinical Applications. Biomed. Eng. Online. 2011, 10, 90. [Google Scholar] [CrossRef]
- Faust, O.; Acharya, U.R.; Molinari, F.; Chattopadhyay, S.; Tamura, T. Linear and Nonlinear Analysis of Cardiac Health in Diabetic Subjects. Biomed. Signal. Process. Control. 2012, 7, 295–302. [Google Scholar] [CrossRef]
- Jelinek, H.F.; Md Imam, H.; Al-Aubaidy, H.; Khandoker, A.H. Association of Cardiovascular Risk Using Nonlinear Heart Rate Variability Measures with the Framingham Risk Score in a Rural Population. Front. Physiol. 2013, 4, 186. [Google Scholar] [CrossRef]
- Rajendra Acharya, U.; Faust, O.; Adib Kadri, N.; Suri, J.S.; Yu, W. Automated Identification of Normal and Diabetes Heart Rate Signals Using Nonlinear Measures. Comput. Biol. Med. 2013, 43, 1523–1529. [Google Scholar] [CrossRef] [PubMed]
- Khandoker, A.H.; Jelinek, H.F.; Palaniswami, M. Identifying Diabetic Patients with Cardiac Autonomic Neuropathy by Heart Rate Complexity Analysis. Biomed. Eng. Online 2009, 8, 3. [Google Scholar] [CrossRef] [PubMed]
- Roy, B.; Ghatak, S. Nonlinear Methods to Assess Changes in Heart Rate Variability in Type 2 Diabetic Patients—PubMed. Arq. Bras. Cardiol. 2013, 101, 317–327. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Maheshwari, S.; Kumar, A. Empirical Mode Decomposition: Theory & Applications. Int. J. Electron. Electr. Eng. 2014, 7, 873–878. [Google Scholar]
- Bajaj, V.; Pachori, R.B. Classification of Seizure and Nonseizure EEG Signals Using Empirical Mode Decomposition. IEEE Trans. Inf. Technol. Biomed. 2012, 16, 1135–1142. [Google Scholar] [CrossRef]
- Pachori, R.B.; Patidar, S. Epileptic Seizure Classification in EEG Signals Using Second-Order Difference Plot of Intrinsic Mode Functions. Comput. Methods Programs Biomed. 2014, 113, 494–502. [Google Scholar] [CrossRef]
- Salankar, N.; Mishra, P.; Garg, L. Emotion Recognition from EEG Signals Using Empirical Mode Decomposition and Second-Order Difference Plot. Biomed. Signal. Process. Control. 2021, 65, 102389. [Google Scholar] [CrossRef]
- Abdulrahman, A.; Baykara, M.; Alakus, T.B. A Novel Approach for Emotion Recognition Based on EEG Signal Using Deep Learning. Appl. Sci. 2022, 12, 10028. [Google Scholar] [CrossRef]
- Hadoush, H.; Alafeef, M.; Abdulhay, E. Automated Identification for Autism Severity Level: EEG Analysis Using Empirical Mode Decomposition and Second Order Difference Plot. Behav. Brain Res. 2019, 362, 240–248. [Google Scholar] [CrossRef] [PubMed]
- Mishra, V.K.; Bajaj, V.; Kumar, A.; Singh, G.K. Analysis of ALS and Normal EMG Signals Based on Empirical Mode Decomposition. IET Sci. Meas. Technol. 2016, 10, 963–971. [Google Scholar] [CrossRef]
- Mishra, V.K.; Bajaj, V.; Kumar, A.; Sharma, D.; Singh, G.K. An Efficient Method for Analysis of EMG Signals Using Improved Empirical Mode Decomposition. AEU—Int. J. Electron. Commun. 2017, 72, 200–209. [Google Scholar] [CrossRef]
- Naik, G.R.; Selvan, S.E.; Nguyen, H.T. Single-Channel EMG Classification with Ensemble-Empirical-Mode-Decomposition-Based ICA for Diagnosing Neuromuscular Disorders. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 24, 734–743. [Google Scholar] [CrossRef]
- Dubey, R.; Kumar, M.; Upadhyay, A.; Pachori, R.B. Automated Diagnosis of Muscle Diseases from EMG Signals Using Empirical Mode Decomposition Based Method. Biomed. Signal. Process. Control. 2022, 71, 103098. [Google Scholar] [CrossRef]
- Hasan, N.I.; Bhattacharjee, A. Deep Learning Approach to Cardiovascular Disease Classification Employing Modified ECG Signal from Empirical Mode Decomposition. Biomed. Signal. Process. Control. 2019, 52, 128–140. [Google Scholar] [CrossRef]
- Rakshit, M.; Das, S. An Efficient ECG Denoising Methodology Using Empirical Mode Decomposition and Adaptive Switching Mean Filter. Biomed. Signal. Process. Control. 2018, 40, 140–148. [Google Scholar] [CrossRef]
- Kumar, S.; Panigrahy, D.; Sahu, P.K. Denoising of Electrocardiogram (ECG) Signal by Using Empirical Mode Decomposition (EMD) with Non-Local Mean (NLM) Technique. Biocybern. Biomed. Eng. 2018, 38, 297–312. [Google Scholar] [CrossRef]
- Mohanty, M.; Dash, M.; Biswal, P.; Sabut, S. Classification of Ventricular Arrhythmias Using Empirical Mode Decomposition and Machine Learning Algorithms. Prog. Artif. Intell. 2021, 10, 489–504. [Google Scholar] [CrossRef]
- -Bautista, C.; Rangel-Rodriguez, M.A.; Perez-Sanchez, A.H.; Amezquita-Sanchez, A.V.; Granados-Lieberman, J.P.; Valtierra-Rodriguez, D.; Bak, E.; Centeno-Bautista, M.A.; Rangel-Rodriguez, A.H.; Perez-Sanchez, A.V.; et al. Electrocardiogram Analysis by Means of Empirical Mode Decomposition-Based Methods and Convolutional Neural Networks for Sudden Cardiac Death Detection. Appl. Sci. 2023, 13, 3569. [Google Scholar] [CrossRef]
- Soh, D.C.K.; Ng, E.Y.K.; Jahmunah, V.; Oh, S.L.; San, T.R.; Acharya, U.R. A Computational Intelligence Tool for the Detection of Hypertension Using Empirical Mode Decomposition. Comput. Biol. Med. 2020, 118, 103630. [Google Scholar] [CrossRef]
- Barnova, K.; Martinek, R.; Jaros, R.; Kahankova, R.; Matonia, A.; Jezewski, M.; Czabanski, R.; Horoba, K.; Jezewski, J. A Novel Algorithm Based on Ensemble Empirical Mode Decomposition for Non-Invasive Fetal ECG Extraction. PLoS ONE 2021, 16, e0256154. [Google Scholar] [CrossRef]
- Echeverria, J.C.; Crowe, J.A.; Woolfson, I.M.S.; Hayes-Gill, I.B.R. Application of Empirical Mode Decomposition to Heart Rate Variability Analysis. Med. Biol. Eng. Comput. 2001, 39, 471–479. [Google Scholar] [CrossRef]
- Souza Neto, E.P.; Custaud, M.A.; Cejka, J.C.; Abry, P.; Frutoso, J.; Gharib, C.; Flandrin, P. Assessment of Cardiovascular Autonomic Control by the Empirical Mode Decomposition. Methods Inf. Med. 2004, 43, 60–65. [Google Scholar] [CrossRef] [PubMed]
- Pachori, R.B.; Avinash, P.; Shashank, K.; Sharma, R.; Acharya, U.R. Application of Empirical Mode Decomposition for Analysis of Normal and Diabetic RR-Interval Signals. Expert. Syst. Appl. 2015, 42, 4567–4581. [Google Scholar] [CrossRef]
- Pachori, R.B.; Kumar, M.; Avinash, P.; Shashank, K.; Acharya, U.R. An Improved Online Paradigm for Screening of Diabetic Patients Using RR-Interval Signals. J. Mech. Med. Biol. 2016, 16, 1640003. [Google Scholar] [CrossRef]
- Acharya, U.R.; Fujita, H.; Sudarshan, V.K.; Lih Oh, S.; Muhammad, A.; Koh, J.E.W.; Hong Tan, J.; Chua, C.K.; Poo Chua, K.; San Tan, R. Application of Empirical Mode Decomposition (EMD) for Automated Identification of Congestive Heart Failure Using Heart Rate Signals. Neural Comput. Appl. 2017, 28, 3073–3094. [Google Scholar] [CrossRef]
- Sood, S.; Kumar, M.; Pachori, R.B.; Acharya, U.R. Application of Empirical Mode Decomposition-Based Features for Analysis of Normal and CAD Heart Rate Signals. J. Mech. Med. Biol. 2016, 16, 1640002. [Google Scholar] [CrossRef]
- Shi, M.; He, H.; Geng, W.; Wu, R.; Zhan, C.; Jin, Y.; Zhu, F.; Ren, S.; Shen, B. Early Detection of Sudden Cardiac Death by Using Ensemble Empirical Mode Decomposition-Based Entropy and Classical Linear Features from Heart Rate Variability Signals. Front. Physiol. 2020, 11, 118. [Google Scholar] [CrossRef]
- Erdfelder, E.; Faul, F.; Buchner, A.; Lang, A.G. Statistical Power Analyses Using G*Power 3.1: Tests for Correlation and Regression Analyses. Behav. Res. Methods 2009, 41, 1149–1160. [Google Scholar] [CrossRef]
- Borowik, E.; Grabowicz, W.; Grycewicz, T.; Lubiński, A. Clinical Usefulness of Baroreflex Sensitivity Test in the Detection of Cardiovascular Autonomic Neuropathy in Patients with Type 2 Diabetes Mellitus. Pol. Merkur. Lek. 2015, 39, 277–280. [Google Scholar]
- Kück, J.-L.; Bönhof, G.J.; Strom, A.; Zaharia, O.-P.; Müssig, K.; Szendroedi, J.; Roden, M.; Ziegler, D. Impairment in Baroreflex Sensitivity in Recent-Onset Type 2 Diabetes without Progression over 5 Years. Diabetes 2020, 69, 1011–1019. [Google Scholar] [CrossRef]
- Petry, D.; de Godoy Marques, C.M.; Marques, J.L.B. Baroreflex Sensitivity with Different Lags for the Evaluation of Cardiovascular Autonomic Neuropathy in Subjects with Diabetes. Comput. Biol. Med. 2020, 127, 104098. [Google Scholar] [CrossRef]
- Ewing, D.J.; Campbell, I.W.; Clarke, B.F. Assessment of Cardiovascular Effects in Diabetic Autonomic Neuropathy and Prognostic Implications. Ann. Intern. Med. 1980, 92, 308–311. [Google Scholar] [CrossRef] [PubMed]
- Rajala, S.; Lindholm, H.; Taipalus, T. Comparison of Photoplethysmogram Measured from Wrist and Finger and the Effect of Measurement Location on Pulse Arrival Time. Physiol. Meas. 2018, 39, 075010. [Google Scholar] [CrossRef] [PubMed]
- Kuusela, T. Methodological Aspects of Baroreflex Sensitivity Analysis. In Heart Rate Variability (HRV) Signal Analysis: Clinical Applications; Kamath, M.V., Watanabe, M.A., Upton, A.R.M., Eds.; CRC Press: Boca Raton, FL, USA, 2012; pp. 43–58. [Google Scholar] [CrossRef]
- Tank, J.; Baevski, R.M.; Fender, A.; Baevski, A.R.; Graves, K.F.; Ploewka, K.; Weck, M. Reference Values of Indices of Spontaneous Baroreceptor Reflex Sensitivity. Am. J. Hypertens. 2000, 13, 268–275. [Google Scholar] [CrossRef] [PubMed]
- Kardos, A.; Watterich, G.; de Menezes, R.; Csanády, M.; Casadei, B.; Rudas, L. Determinants of Spontaneous Baroreflex Sensitivity in a Healthy Working Population. Hypertension 2001, 37, 911–916. [Google Scholar] [CrossRef] [PubMed]
- Pan, J.; Tompkins, W.J. A Real-Time QRS Detection Algorithm. IEEE Trans. Biomed. Eng. 1985, 3, 230–236. [Google Scholar] [CrossRef]
- Vest, A.N.; Da Poian, G.; Li, Q.; Liu, C.; Nemati, S.; Shah, A.J.; Clifford, G.D. An Open-Source Benchmarked Toolbox for Cardiovascular Waveform and Interval Analysis. Physiol. Meas. 2018, 39, aae021. [Google Scholar] [CrossRef]
- Lai, Y.-C.; Ye, N. Recent Developments in Chaotic Time Series Analysis. Int. J. Bifurc. Chaos 2003, 13, 1383–1422. [Google Scholar] [CrossRef]
- Cohen, M.E.; Hudson, D.L.; Deedwania, P.C. Applying Continuous Chaotic Modeling to Cardiac Signal Analysis. IEEE Eng. Med. Biol. Mag. 1996, 15, 97–102. [Google Scholar] [CrossRef]
- Cavalheiro, G.L.; Almeida, M.F.S.; Pereira, A.A.; Andrade, A.O. Study of Age-Related Changes in Postural Control during Quiet Standing through Linear Discriminant Analysis. Biomed. Eng. Online 2009, 8, 35. [Google Scholar] [CrossRef]
- Subasi, A. Practical Guide for Biomedical Signals Analysis Using Machine Learning Techniques: A MATLAB Based Approach; Academic Press: Cambridge, MA, USA, 2019. [Google Scholar]
- Orini, M.; Barbieri, R.; Nardelli, M.; Scilingo, E.P.; Valenza, G. Introduction to Complex Cardiovascular Physiology. In Complexity and Nonlinearity in Cardiovascular Signals; Barbieri, R., Scilingo, E.P., Valenza, G., Eds.; Springer: Cham, Switzerland, 2017; pp. 3–44. ISBN 9783319587097. [Google Scholar]
- Coopmans, C.; Zhou, T.L.; Henry, R.M.A.; Heijman, J.; Schaper, N.C.; Koster, A.; Schram, M.T.; van der Kallen, C.J.H.; Wesselius, A.; den Engelsman, R.J.A. Both Prediabetes and Type 2 Diabetes Are Associated with Lower Heart Rate Variability: The Maastricht Study. Diabetes Care 2020, 43, 1126–1133. [Google Scholar] [CrossRef]
- Frattola, A.; Parati, G.; Gamba, P.; Paleari, F.; Mauri, G.; di Rienzo, M.; Castiglioni, P.; Mancia, G. Time and Frequency Domain Estimates of Spontaneous Baroreflex Sensitivity Provide Early Detection of Autonomic Dysfunction in Diabetes Mellitus. Diabetologia 1997, 40, 1470–1475. [Google Scholar] [CrossRef]
- Pan, W.; He, A.; Feng, K.; Li, Y.; Wu, D.; Liu, G. Multi-Frequency Components Entropy as Novel Heart Rate Variability Indices in Congestive Heart Failure Assessment. IEEE Access. 2019, 7, 37708–37717. [Google Scholar] [CrossRef]
- Chen, M.; He, A.; Feng, K.; Liu, G.; Wang, Q. Empirical Mode Decomposition as a Novel Approach to Study Heart Rate Variability in Congestive Heart Failure Assessment. Entropy 2019, 21, 1169. [Google Scholar] [CrossRef]
- Shaffer, F.; Ginsberg, J.P. An Overview of Heart Rate Variability Metrics and Norms. Front. Public Health 2017, 5, 258. [Google Scholar] [CrossRef]
- Balcıoğlu, A.S. Diabetes and Cardiac Autonomic Neuropathy: Clinical Manifestations, Cardiovascular Consequences, Diagnosis and Treatment. World J. Diabetes 2015, 6, 80. [Google Scholar] [CrossRef]
- Vinik, A.I.; Ziegler, D. Diabetic Cardiovascular Autonomic Neuropathy. Circulation 2007, 115, 387–397. [Google Scholar] [CrossRef]
- Pop-Busui, R. Cardiac Autonomic Neuropathy in Diabetes: A Clinical Perspective. Diabetes Care 2010, 33, 434. [Google Scholar] [CrossRef] [PubMed]
- Khandoker, A.H.; Jelinek, H.F.; Moritani, T.; Palaniswami, M. Association of Cardiac Autonomic Neuropathy with Alteration of Sympatho-Vagal Balance through Heart Rate Variability Analysis. Med. Eng. Phys. 2010, 32, 161–167. [Google Scholar] [CrossRef] [PubMed]
- Alkhodari, M.; Rashid, M.; Mukit, M.A.; Ahmed, K.I.; Mostafa, R.; Parveen, S.; Khandoker, A.H. Screening Cardiovascular Autonomic Neuropathy in Diabetic Patients with Microvascular Complications Using Machine Learning: A 24-Hour Heart Rate Variability Study. IEEE Access. 2021, 9, 119171–119187. [Google Scholar] [CrossRef]
- Carricarte Naranjo, C.; Sanchez-Rodriguez, L.M.; Brown Martínez, M.; Estévez Báez, M.; Machado García, A. Permutation Entropy Analysis of Heart Rate Variability for the Assessment of Cardiovascular Autonomic Neuropathy in Type 1 Diabetes Mellitus. Comput. Biol. Med. 2017, 86, 90–97. [Google Scholar] [CrossRef]
- Lin, K.; Wei, L.; Huang, Z.; Zeng, Q. Combination of Ewing Test, Heart Rate Variability, and Heart Rate Turbulence Analysis for Early Diagnosis of Diabetic Cardiac Autonomic Neuropathy. Medicine 2017, 96, e8296. [Google Scholar] [CrossRef] [PubMed]
- Selvan, S.S.; Arjunan, S.P.; Swaminathan, R.; Kumar, D.K. Complexity Analysis in the PR, QT, RR and ST Segments of ECG for Early Assessment of Severity in Cardiac Autonomic Neuropathy. Appl. Sci. 2022, 12, 5746. [Google Scholar] [CrossRef]
- Cornforth, D.; Jelinek, H.F.; Tarvainen, M. A Comparison of Nonlinear Measures for the Detection of Cardiac Autonomic Neuropathy from Heart Rate Variability. Entropy 2015, 17, 1425–1440. [Google Scholar] [CrossRef]
- Jelinek, H.F.; Cornforth, D.J.; Tarvainen, M.P.; Khalaf, K. Investigation of Linear and Nonlinear Properties of a Heartbeat Time Series Using Multiscale Rényi Entropy. Entropy 2019, 21, 727. [Google Scholar] [CrossRef]

| noCAN | subCAN | estCAN | |
|---|---|---|---|
| n | 20 | 20 | 20 |
| Age (yrs) | 60.1 ± 4.5 | 62.0 ± 7.0 | 57.0 ± 8.4 |
| Gender | 7F/13M | 12F/8M | 10F/10M |
| DM duration (yrs) | 13.2 ± 9.5 | 13.9 ± 9.8 | 17.6 ± 9.3 |
| HbA1c (mmol/mol) | 89 ± 22 | 71 ± 31 | 99 ± 19 |
| Feature | Group | ||||
|---|---|---|---|---|---|
| ) | noCAN | −6.777 ± 0.770 b | −7.399 ± 0.338 b | −7.424 ± 0.287 b | −7.300 ± 0.432 ab |
| subCAN | −7.199 ± 0.540 c | −7.580 ± 0.282 | −7.609 ± 0.204 | −7.616 ± 0.263 a | |
| estCAN | −7.655 ± 0.382 bc | −7.739 ± 0.268 b | −7.694 ± 0.450 b | −7.712 ± 0.224 b | |
| ) | noCAN | −0.654 ± 0.665 b | −1.878 ± 0.609 b | −2.810 ± 0.488 ab | −3.598 ± 0.527 ab |
| subCAN | −1.957 ± 0.802 c | −2.374 ± 0.740 c | −3.294 ± 0.584 a | −4.071 ± 0.557 ac | |
| estCAN | −1.086 ± 0.759 bc | −2.963 ± 0.703 bc | −3.733 ± 0.733 b | −4.551 ± 0.621 bc | |
| noCAN | 0.773 ± 0.268 b | 0.887 ± 0.173 b | 0.317 ± 0.180 ab | 0.694 ± 0.234 ab | |
| subCAN | 0.887 ± 0.209 | 0.941 ± 0.105 | 0.531 ± 0.276 ac | 0.868 ± 0.143 ac | |
| estCAN | 0.981 ± 0.037 b | 0.987 ± 0.029 b | 0.750 ± 0.253 bc | 0.947 ± 0.089 bc | |
| ) | noCAN | −3.480 ± 0.574 b | −3.839 ± 0.432 b | −3.921 ± 0.370 ab | −3.912 ± 0.390 ab |
| subCAN | −3.897 ± 0.668 c | −4.166 ± 0.564 c | −4.288 ± 0.388 ac | −4.314 ± 0.382 ac | |
| estCAN | −4.492 ± 0.654 bc | −4.749 ± 0.622 bc | −4.687 ± 0.612 bc | −4.655 ± 0.527 bc | |
| ) | noCAN | −2.562 ± 0.617 b | −2.771 ± 0.435 b | −2.613 ± 0.379 ab | −2.392 ± 0.403 ab |
| subCAN | −3.028 ± 0.692 c | −3.094 ± 0.570 c | −2.975 ± 0.368 ac | −2.793 ± 0.391 ac | |
| estCAN | −3.667 ± 0.724 bc | −3.741 ± 0.626 bc | −3.349 ± 0.644 bc | −3.106 ± 0.551 bc | |
| noCAN | 0.290 ± 0.051 | 0.097 ± 0.019 | 0.041 ± 0.010 | 0.018 ± 0.003 | |
| subCAN | 0.266 ± 0.054 | 0.090 ± 0.029 | 0.039 ± 0.121 | 0.019 ± 0.006 | |
| estCAN | 0.285 ± 0.0463 | 0.098 ± 0.031 | 0.039 ± 0.008 | 0.017 ± 0.004 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cossul, S.; Andreis, F.R.; Favretto, M.A.; Marques, J.L.B. The Use of Empirical Mode Decomposition on Heart Rate Variability Signals to Assess Autonomic Neuropathy Progression in Type 2 Diabetes. Appl. Sci. 2023, 13, 7824. https://doi.org/10.3390/app13137824
Cossul S, Andreis FR, Favretto MA, Marques JLB. The Use of Empirical Mode Decomposition on Heart Rate Variability Signals to Assess Autonomic Neuropathy Progression in Type 2 Diabetes. Applied Sciences. 2023; 13(13):7824. https://doi.org/10.3390/app13137824
Chicago/Turabian StyleCossul, Sandra, Felipe Rettore Andreis, Mateus Andre Favretto, and Jefferson Luiz Brum Marques. 2023. "The Use of Empirical Mode Decomposition on Heart Rate Variability Signals to Assess Autonomic Neuropathy Progression in Type 2 Diabetes" Applied Sciences 13, no. 13: 7824. https://doi.org/10.3390/app13137824
APA StyleCossul, S., Andreis, F. R., Favretto, M. A., & Marques, J. L. B. (2023). The Use of Empirical Mode Decomposition on Heart Rate Variability Signals to Assess Autonomic Neuropathy Progression in Type 2 Diabetes. Applied Sciences, 13(13), 7824. https://doi.org/10.3390/app13137824






