A Coordinate-Regression-Based Deep Learning Model for Catheter Detection during Structural Heart Interventions

Featured Application

Assisting surgeons by automatically detecting the position of the catheter tip based on fluoroscopic images during minimally invasive surgeries.

Abstract

With a growing geriatric population estimated to triple by 2050, minimally invasive procedures that are image-guided are becoming both more popular and necessary for treating a variety of diseases. To lower the learning curve for new procedures, it is necessary to develop better guidance systems and methods to analyze procedure performance. Since fluoroscopy remains the primary mode of visualizations, the ability to perform catheter tracking from fluoroscopic images is an important part of this endeavor. This paper explores the use of deep learning to perform the landmark detection of a catheter from fluoroscopic images in 3D-printed heart models. We show that a two-stage deep-convolutional-neural-network-based model architecture can provide improved performance by initially locating a region of interest before determining the coordinates of the catheter tip within the image. This model has an average error of less than 2% of the image resolution and can be performed within 4 milliseconds, allowing for its potential use for real-time intraprocedural tracking. Coordinate regression models have the advantage of directly outputting values that can be used for quantitative tracking in future applications and are easier to create ground truth values (~50× faster), as compared to semantic segmentation models that require entire masks to be made. Therefore, we believe this work has better long-term potential to be used for a broader class of cardiac devices, catheters, and guidewires.

1. Introduction

With a growing geriatric population estimated to triple by 2050, minimally invasive procedures that are image-guided are becoming both more popular and necessary for treating a variety of diseases [1,2,3]. Currently, over 400 million individuals worldwide are suffering from cardiovascular disease [4], and the number of annual deaths is estimated to be 23.3 million by 2030 [5]. Of these, well over a million patients will undergo a minimally invasive percutaneous procedure to address a structural heart defect, which is defined as an abnormality of the cardiac wall, valve, chamber, or one of the major arteries of the heart [6]. Despite being minimally invasive, these procedures can still result in death or life-threatening complications due to accidental punctures and device embolization, or can have limited efficacy due to the misalignment of an implanted device [7]. Percutaneous and minimally invasive procedures are used for a wide variety of cardiovascular ailments and are typically guided by imaging modalities, such as X-ray fluoroscopy and echocardiography [8], since they provide real-time imaging [9]. However, most organs are transparent to fluoroscopy, so contrast agents, which transiently opacify structures of interest, must be used to visualize the surrounding tissue. Furthermore, fluoroscopy only provides a two-dimensional (2D) projection of the catheter and device, and, therefore, no information on their depth [10]. Echocardiography can directly image anatomic structures and blood flow, so it is often used as a complementary imaging modality. Although this method can provide useful intraoperative 2D and 3D images, this technology requires skilled operators and general anesthesia is a prerequisite for transesophageal echocardiographic (TEE) guidance. The limitations of these techniques increase the complexity of procedures, which often require the interventionalist to determine the position of the catheter/device by analyzing multiple imaging angles and modalities [11,12]. The added coordination of different specialties also increases resource utilization and costs. Preoperative 3D imaging modalities provide detailed anatomic information and are often displayed on separate screens or overlaid on real-time imaging modalities to improve image-guided interventions [9,12,13]. However, this method of fusion imaging obstructs the view of the real-time image during the procedure [12]. Furthermore, all of these images are displayed on 2D screens, which fundamentally mitigate the ability to perceive depth and orientation [14].

Our group [15,16,17], among others [18,19,20,21], have shown the promise of augmented and mixed-reality visualization to address the limitations in depth perception for cardiac interventions by using 3D holographic headsets. In order to leverage mixed-reality technology as a navigation tool for fluoroscopy-guided percutaneous procedures, catheter tracking is a cornerstone of the image guidance system. In our earlier publications, we demonstrated a mixed-reality-based training simulator for structural heart disease interventions using a 3D-printed heart phantom [15]. In this work, the catheter was coupled, at three distinct locations along its distal end, with three electromagnetic (EM) sensors, each allowing the real-time simultaneous tracking of three spatial positions (X, Y, and Z) and three orientation angles (azimuth, elevation, and roll). Although utilizing EM sensors is advantageous for portability and to minimize radiation from fluoroscopy, affordable systems (<USD 10 k) have a low accuracy (up to ~5 mm) and require manual integration of sensors into a catheter, and thus are not a general solution to address the many types of cardiac interventional devices available on the market.

To address these limitations with EM sensor tracking, we previously presented a novel deep-learning-driven method for tracking a catheter in a 3D-printed heart phantom from biplane fluoroscopic images that were acquired during a mock procedure [17]. In this work, we trained a U-Net [22] model on the 3D-printed heart phantom to segment a radiopaque marker at the tip of the catheter. A postprocessing step was used to analytically calculate the Z-coordinate by leveraging the two simultaneous views of the catheter. Although this was an accurate method to perform the tip detection of a catheter, it is not scalable to many types of catheters and/or devices, since semantic segmentation models require the time-consuming manual annotation of ground truth images. Annotating masks (i.e., selecting all pixels in the catheter tip) takes ~50 times longer than defining the landmark as a single point on the image. We, therefore, explored the use of coordinate regression models that directly output the X- and Y-coordinate of the catheter tip, while utilizing the same analytical Z-coordinate calculation. This method has the benefits of simpler ground truth annotations and mitigating the need for the postprocessing of the output mask.

Deep convolutional neural networks (CNNs) have been applied to a multitude of computer vision problems. In medical imaging, CNNs have been effective in many tasks, such as classification [23], localization [24], tracking [25], and image segmentation [22,26]. Ronneberger et al. [22] proposed the U-Net [22], which replaced the pooling operators in fully convolutional networks (FCNs) [27] with up-sampling operators, allowing the input image resolution to be retained in the output. The performance of the U-Net [22] for segmenting medical images, notably with even small training datasets, demonstrated the potential of such an encoder–decoder architecture. The U-Net [22] was later applied to other medical settings, including the Xenopus kidney [28], MRI volume segmentation of the prostate [29], retinal vessels, liver and tumors in CT scans, ischemic stroke lesion, and intervertebral disc and pancreas [30,31,32,33,34,35,36,37,38,39,40,41].

Landmark localization plays a vital role in medical image analysis. Several deep learning methods have been proposed for landmark localization that employ regression or classification [42,43,44,45,46,47,48]. In regression-based localization, a hard threshold is utilized to detect the presence of a landmark in image slices, patches, or voxels. This threshold converts the model’s coordinate prediction (pixel-wise or mm-based) to the assigned annotated labels. Therefore, these methods usually rely on the careful consideration of a final threshold value, which may be data- or task-specific. Zheng et al. [49] localized a landmark by classifying image voxels with multilayer perceptrons, while Xu et al. [50] localized landmarks based on their relative position (up, down, left, or right) to the landmark of interest. In another work, Yang et al. [51] predicted the location of a landmark based on intersecting the classification outputs from all axial, coronal, and sagittal image slices. Another existing approach for coordinate regression is to generate a heatmap output from a CNN and apply a loss directly to the heatmap rather than the numerical coordinates [52]. Even though this approach offers good spatial generalization, it has the drawback that gradient flow begins at the heatmap rather than at the numerical coordinates. This creates a disconnect between the heatmap loss optimization and the true goal of reducing the coordinate error distances [52]. Another coordinate regression approach is to utilize fully connected (FC) layers that produce numerical coordinates [53]. Most notably, FC layers allow end-to-end backpropagation from the predicted numerical coordinates to the input image. However, the fully connected layer weights are highly dependent on the spatial distribution of the inputs during training. To address this issue, our group used another approach that leveraged a segmentation network followed by a postprocessing step [17]. Despite providing promising results, the time-consuming process of making masks for the ground truth labels prevented the long-term scalability of this work for other devices and expanding the dataset to allow for greater generalizability (multiple scanners, background images from patients, etc.). Thus, we propose pursuing a direct identification of the catheter tip without any masking annotation/analysis.

There has also been some work involving coordinate regression in medical imaging in recent years, including localizing in areas related to neurology [54] and arthrology [55] sciences. Dünnwald et al. conducted segmentation and localization on the locus coeruleus (LC), a small nucleus in the brain stem. They proposed CoRe-Unet, a type of 3D U-Net to predict coordinates of a voxel in the input volume. The network relies on correlating prominent structures to detect the actual position of the LC through a localization network trained to detect the center-of-mass (COM) coordinates [56]. Li et al. [55] also focused on landmark detection in the temporomandibular joints (TJ) through a two-stage end-to-end localization network based on an attention-guided mechanism. Their method includes global and local stages, based on learning both local features around landmarks and estimating landmark coordinates. The network consists of a differentiable spatial to numerical transform (DSNT) layer attached to a 3D U-Net, enabling the conversion of heatmaps to coordinate detection [55]. Despite some achievements in the mentioned line of work, models based on heatmap analysis have two main drawbacks: they are computationally expensive and are sensitive to outliers, whilst coordinate regression provides a faster estimation of the landmark [57].

There has been work involving guidewire tracking, usually used in combination with catheter tracking in related studies. Researchers indicate that many frameworks used for catheter tracking can also be applied to guidewire tracking [58]. Traditional methods in endovascular and neurosurgery fields have guided researchers to use either intensity- and learning-based models or the segmentation and movement of the guidewire [58,59,60,61,62]. However, with emergent segmentation and deep learning techniques, new approaches have taken a turn in this direction. These techniques range from supervised to unsupervised methods. Supervised methods can consist of instance segmentation, region of interest [63,64,65,66], two-stage region of interest, and target segmentation [67], whilst unsupervised methods have used optical flow and a U-Net trained in a Siamese network [68]. Although all these methods are relevant to the field, they include semantic segmentation, which falls out of the scope of this paper.

In another work, researchers utilized a CNN to explore the possibility to detect motion between two fluoroscopic frames in catheterization procedures [69]. They were able to compare their CNN-based catheter tip detection with normalized cross correlation (CC) and found a mean absolute error (MAE) of 8.7 ± 2.5 pixels or 3.0 ± 0.9 mm between methods, with the CNN outperforming CC. However, the researchers state that the correlation between the predictions and tracking results is not obvious. In another study, automated catheter localization for ultrasound-guided high-dose-rate prostate brachytherapy was pursued. They used a U-NET model to localize implanted catheters on transverse images on 3500 manually localized implanted catheters. They reported 80% reconstruction accuracy within 2 mm along 90% of the catheter length; however, they also mentioned that the catheter tip was often not detected and required extrapolation [70].

To overcome the issues in the previously pursued works, this paper presents the implementation of a landmark localization method using coordinate regression for catheter detection from fluoroscopic images acquired during a mock procedure in a 3D-printed heart phantom.

We can summarize the motivation of the paper as follows:

• Tracking the tip of a catheter for future use in a mixed-reality navigation system.
• Addressing the limited accuracy, low availability, and high cost of EM sensor tracking systems.
• Proposing a catheter tip coordinate regression detection methodology leveraging deep convolutional neural networks to reduce the time-consuming task of generating ground truth masks.

2. Materials and Methods

2.1. Dataset

We collected a fluoroscopic image dataset for our custom-made, 3D-printed heart model during a mock procedure in the catheterization lab at NewYork-Presbyterian Hospital. The custom model contained a heart that was transparent under X-ray and a metal spray-painted spine that was visible under X-ray, which is the same as in our previous publication [15]. In addition, some metal spheres were present as fiducial markers, but those were not used in this study. It should be noted that the 3D-printed heart model was within an acrylic box that produced additional artifacts seen in the image, but these artifacts will not be present in clinical images. Our dataset contained a total of 3408 JPEG images at 512 × 512 spatial resolution, where the catheter was moved along the entire range of the image. In all images, the entire catheter tip was visible. The dataset included 62 paired images which were taken from different views at the same time. These 124 images were used to test the model in 3D space. Image contrast, clarity, and brightness varied across sets taken on different days.

To prove that landmark detection can be achieved, we initially focused solely on the radiopaque marker band of the catheter tip. The marker band formed different shapes depending on the angle of the image, and, therefore, can be seen as a rectangle with varying width, a thin-walled circle, or an oval. The catheter can also take on different shapes in the image as it is curved, rotated, and translated by the user (Figure 1).

The dataset (containing 3408 images) was randomly divided into three sets: training (2182 images), validation (546 images), and test (680 images). In addition, we had an additional set, the “fixed-test” set, which was based on removing any incorrectly predicted regions from the first stage of the 2-stage network architecture (to determine the best base accuracy of the second stage of the network). For deep learning model evaluation, 20% of the samples were set aside at the beginning as the test set. The training and validation sets consisted of the remaining 80% of the samples, which were trained and evaluated based on a 5-fold cross-validation technique. Therefore, in each iteration, 80% of the training and validation samples were dedicated to training the model and 20% of them were set as the validation set. The best parameters for the training process were chosen based on best practices and the assessment of the validation outcomes. The training parameters included the number of layers, neurons in each layer, and epochs, and the learning rate. The best values for these parameters were achieved by varying them and checking for the best accuracy in the outcome. The detailed architecture is discussed in Section B.

2.2. Architectures

The CNN-based models developed for this problem are intended to locate the center of the marker band in less time than the frame rate of the acquisition system (generally 15 frames per second). Since it is understood that landmark detection will be more accurate on detailed images, we implemented two deep networks working in series. The first network, called the region selection network, predicts a subregion of the image that contains the marker band; a second network, called the localizer network, finds the exact position of the landmark (outputting its X- and Y-coordinates). Although the two networks were used sequentially during inference, training was performed separately. This way, the image was used in more detail without using the larger field of view of the entire image. The details of these networks are explained in the following two sections.

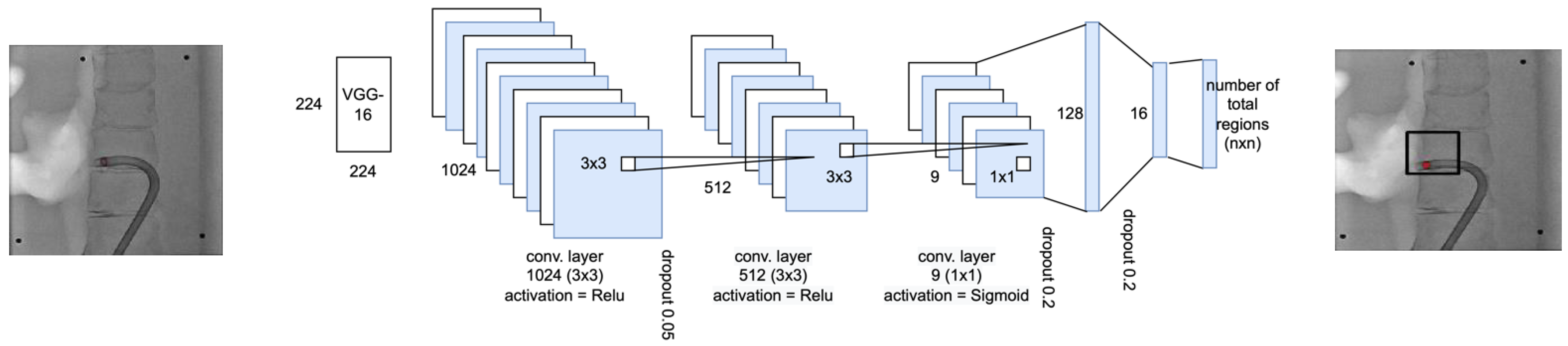
2.2.1. Region Selection Network

The region selection network seeks to detect the region of the image that contains the marker band of the catheter. To select the target region, the images are first divided into n columns and n rows. Since the model is supervised, it needs the ground truth positions of the targets in the new splitting system. Therefore, the target positions are converted to the region number in which it resides. Thus, the model output is an n × n vector with a softmax activation, with each element representing the probability of the target point being in that region.

The network consists of a VGG-16 [71] backbone followed by three convolution layers and three fully connected layers. The first convolution layer consists of a 3 × 3 kernel with 1024 channels, followed by a rectified linear unit (ReLU) activation function. The second layer includes a 3 × 3 kernel, 512 channels, and a ReLU activation function. The final layer consists of a 1 × 1 kernel, 9 channels, and a sigmoid activation function (Figure 2). Afterward, three fully connected (FC) layers are implemented. These layers have 128, 16, and n × n (representing the total region number) neurons. The FC layers have a dropout probability of 0.20 and 0.05 as shown in Figure 2.

The input images were originally 512 × 512 pixels. However, as the input to a VGG network [71] is an image with dimensions 224 × 224 × 3, we initially resized our images to be in accordance with the VGG dimensions. For transfer learning purposes, the weights of all layers were frozen with weights pretrained on ImageNet [72], whilst the remaining layers of the network were fine-tuned on our dataset. Training was performed with 80 epochs per 5-fold split (where the highest accuracy was achieved), with the longest training occurring with 400 epochs. The Adam optimizer was used with a 0.00001 constant learning rate, and we used a cross-entropy loss function.

2.2.2. Localizer Network

The localizer network finds the best point in the image for the center of the marker band in the selected region. In this network (Figure 3), the input is a region of the original image that was selected in the first network, albeit it is the ground truth region in the training procedure. These subimages are loaded with a higher resolution to match the needed size of 224 × 224 pixels. The network’s output is the X- and Y-coordinates of this subimage (i.e., between 0 and 223). Since the landmark location is in the local coordinate system of the subimage, it is then converted to the global coordinates of the original image. The architecture of this network is similar to the previous network apart from the last layer, which now has two FC layers with 9 and 2 neurons, respectively. Here, training is performed with 100 epochs per 5-fold split (with the lowest radial distance error as cost function), with the longest training occurring with 500 epochs. The network’s output provides a prediction based on the last two neurons, which represent the X- and Y-coordinates of the landmark in the local coordinate system of the subimage.

2.3. Dual Network Inference

During inference, the two networks work in series (Figure 4), where the first network receives the images sequentially with a size of 224 × 244 pixels and designates the region in which the landmark has the highest probability of existing. It should be noted that if this first network predicts incorrectly, the second network will not be able to select the correct catheter tip. The selected region’s resolution is updated to match the VGG-16 network architecture and entered as the 224 × 224 × 3 input to the network. This provides a connection between the localizer network and the predicted landmark’s coordinates of the region. A transformation occurs to convert the network output to the local landmark coordinates (marked as the center of the marker and indicated with a red arrow) and, consequently, the global coordinates of the original image.

Both networks’ designs were implemented in Google Colab utilizing the Python programming language. Google hosted Colab for the artificial intelligent applications with many inbuilt libraries and free GPU and TPU accelerators. Concerning hardware acceleration, we ran the model on Colab with a GPU which proved to have the highest efficiency. Colab also offers TPU computing; however, the TPU takes up a considerably more training time compared to the GPU mode typically in small batch sizes.

3. Results and Discussion

The overall contribution of this work is showing how a two-stage architecture can improve the accuracy of landmark detection for a coordinate regression network. Figure 5 shows the distribution of errors that occur for all input images (indicated by the number of samples in the vertical axis) for when only a single region (i.e., the entire image) is fed into the second stage versus nine regions. As can be seen, the results for nine regions had a distribution that was shifted towards the left, indicating a higher accuracy as compared to the distribution of one region, which was further shown by their average accuracy of 1.75 pixels and 7.36 pixels, respectively. Therefore, utilizing the two-stage architecture is necessary to optimize the accuracy of this landmark detection.

To further optimize the performance of this two-stage architecture, we varied the size of the square region array from n = 3 (9 regions) to n = 10 (100 regions). Figure 6 shows the accuracy of the region selection network for their training, validation, and test sets, for each of the characterized region sizes. Training and validation sets are the last sets provided by the 5-fold validation. As can be seen, with an increase in the number of regions, the accuracy of detection for the first stage decreased. The incorrect predictions were usually occurring when the marker band was located at the border of the region, such that it was overlapping with another region (Figure 7). In this example of the figure, the model was predicting from 25 possible regions, and predicted correctly in the figure on the left (Figure 7A) but incorrectly in the figure on the right (Figure 7B). To state a simple example, in the case of 100 regions, the model misclassified 11 (out of 680) images. In brief, almost all the predicted regions touched the catheter tip, even if they did not point to the correct region.

In the localizer network, the expectation is to predict the exact location of the center of the marker band within the target region. Figure 8 presents the outcomes obtained from the network. This chart indicates the averages of errors between the ground truth coordinate and the predicted landmark coordinate by the model. This error is reported separately for the training, validation, test, and fixed-test results. The “fixed-test” results remove all the incorrectly selected regions to demonstrate the highest accuracy the second model can achieve. The error is reported based on the 512 × 512 pixel size versions of the original images. The test dataset contained the average of the results of both the correctly and incorrectly selected regions.

Overall, the data convey two overall trends: (i) the larger the region number, the less accurately the region selection performs, and (ii) the larger the region number, the more accurately the localizer network performs. Given these two trends, it is seen that either n = 5 or n = 7 provides the optimal results, with n = 7 providing the highest accuracy for the fixed-test set. These conclusions are further supported by the plots in Figure A1, which show the distribution of error for all points; it can be seen that the majority of images were accurately predicted, with a minimal number of large outliers. As we plotted these errors with their ground truth coordinates of the image (Figure A2), we did not see any obvious trends due to spatial positioning within the image.

The inference time to predict landmark position in this model (both networks consecutively) is 4 milliseconds on average. The frame rate of the acquisition system is typically 15 frames per second (67 ms). Therefore, the inference time is significantly less than the system’s acquisition rate and this method can be used for real-time catheter tracking. Compared to other well-known networks, the results of average accuracy, average training time, and average inference time of some models are shown in

Table 1. Comparison of proposed method, in terms of accuracy, training time, and inference time, with other methods.

Model	Region Number	Mean Error	Standard Deviation of Error	Training Time	Inference Time	Output Type
		Pixels from 512 × 512 Image		Average for Each Image
Mobile Net [73]	5 × 5	19.29	9.77	3.8 s	3.6 ms	Landmark
ResNet [74]	5 × 5	3.35	6.23	4.9 s	4.4 ms	Landmark
Dense Net [75]	5 × 5	3.86	7.29	21.5 s	11.2 ms	Landmark
U-Net [17]	1	1.00	6.13	0.2 s	10 ms	Mask
VGG [71]	1	7.36	4.90	2.1 s	1.7 ms	Landmark

. Our method, which is the two-stage and VGG-based model, outperforms all the mentioned models.

4. Conclusions

We have shown that landmark detection using coordinate regression deep learning models can be used to perform catheter localizing on fluoroscopy images. Our results suggest that these models can provide ~1% positional accuracy at speeds much faster (>10×) than commercial acquisition systems used in cardiac interventions, and have the fastest training and inference times compared to other models. Furthermore, our method requires less time in preparing ground truth training datasets as compared to semantic segmentation methods (as typically used for U-Net). Although the results are promising, there are several limitations that need future improvement before these models can be used for clinical applications: (i) Nonclinical images: These models were trained on images acquired from 3D-printed models and, thus, do not have clinically relevant backgrounds; thus, clinical use should only be performed after the model has been optimized and validated on clinical images. (ii) Limited degrees of freedom: Currently, the model only predicts a single point on the catheter, giving a single 3D coordinate but no orientation; future models should predict two or more points to allow for the catheter’s 3D orientation to be calculated. (iii) Generalizability: This model was trained on a set of images acquired from a single type of catheter, imaging system, and phantom model; future work needs to train the model on an expanded set of data. (iv) Accelerating and parallel processing must be considered in future works.

Despite the limitations listed above, this work provides the primary advantage of developing deep learning models that can be optimized without the tedious task of developing image masks, as typically needed by U-Net models [22]. Furthermore, these models can be used to perform catheter tracking for training purposes for custom 3D-printed heart models [15] or on commercial training systems (Biomodex Inc., Paris, France).