An Extended Membrane System with Monodirectional Tissue-like P Systems and Enhanced Particle Swarm Optimization for Data Clustering
Abstract
:1. Introduction
2. Tissue-like P Systems
2.1. TPs with Evolutional Symport/Antiport and Promoters
- (1)
- is nonempty finite set of alphabets consisting of elements, and all elements in this alphabet are called objects;
- (2)
- is a finite alphabet set of , which represents objects initially placed in the environment, such that ;
- (3)
- is the structure of the P system, which consists of membranes;
- (4)
- are finite multisets of objects over , initially placed in membranes, where , for ;
- (5)
- is a finite set of communication rules for the system, which contains two kinds of rules with promoters of the following restrictions.
- ①
- Evolutional symport rules with promoters: , where , , ,, . It can only be applied to a configuration if both the multiset of objects and promoter objects appear in the same existing membrane . When such an evolutional symport rule with promoters associated with membrane and membrane is employed, the multiset of objects under the presence of promoter objects in membrane is simultaneously sent to membrane and evolved into new objects ;
- ②
- Evolutional antiport rules with promoters: , where , , ,, . It can only be applied to a configuration if both and appear in the same existing membrane , and another membrane in the same configuration contains . When such an evolutional antiport rule with promoters associated with and is employed, under the presence of in is simultaneously sent to and evolved into , at the same time, in is also simultaneously sent to and evolved into new objects ;
- (6)
- represents an input membrane or region, where ;
- (7)
- represents an output membrane or region, where .
2.2. MTPs with Evolutional Symport and Promoters
3. Improved Particle Swarm Optimization
3.1. Environmental Factors
3.2. Crossover Operator
4. The Proposed ECPSO-MTP
4.1. The Common Framework of ECPSO-MTP
- (1)
- is a non-empty, finite alphabet for objects;
- (2)
- is a finite alphabet set for objects that are initially placed in the input membrane;
- (3)
- is the structure of the ECPSO-MTP, which contains elementary membranes;
- (4)
- are finite multisets for objects that are initially placed in elementary membranes, where , for ;
- (5)
- is the finite set of evolution rules for objects in the proposed ECPSO-MTP, where . is a finite subset of associated with membrane , for or , and is of the form: , for . When such an evolution rule in is applied, objects in evolve into ;
- (6)
- is the finite set of communication rules for objects in the proposed ECPSO-MTP, where . is a finite subset of associated with using the evolutional symport with promoters of MTP. Specifically, and is of the form: , or , where , , , , ;
- (7)
- is the input membrane of the proposed ECPSO-MTP;
- (8)
- is the output membrane of the proposed ECPSO-MTP. When the computation of this extended P system is completed, objects in the output membrane will be sent to the environment , which is regarded as the final computational result of the system. The membrane structure of the proposed ECPSO-MTP is graphically depicted in Figure 1.
4.2. Evolution Rules
4.3. Communication Rules
4.3.1. Forward Communication Rules
4.3.2. Backward Communication Rules
4.4. Computation of Proposed ECPSO-MTP
- (1)
- Initialization
- (2)
- Evolution mechanism for to
- (3)
- Forward communication mechanism from to
- (4)
- Evolution mechanism for
- (5)
- Forward commutation mechanism from to
- (6)
- Backward communication mechanism from to
- (7)
- Termination and output
| Algorithm 1 ECPSO-MTP |
| Input: , ; |
| (1) Initialization <1> Velocity and position initialized |
| for to |
| Velocity of object : ; |
| Position of object : ; end |
| <2> Local and global best updated |
| for to |
| for to Update local best of objects according to Equation (10); Update global best of object according to Equation (11); |
| end end |
| (2) Evolution mechanism for to |
| <1> Velocity and position updated |
| for to |
| for to |
| Update velocity of object based on a randomly selection strategy according to Equations (6)–(8); |
| Update position of object according to Equation (9); end |
| end <2> Local and global best updated (3) Forward communication mechanism from to |
| if |
| for to |
| ; |
| end |
| end |
| (4) Evolution mechanism for |
| <1> Position updated |
| Update position of object in according to Equations (3)–(5); |
| <2> Local best updated |
| (5) Forward commutation mechanism from to |
| if |
| ; |
| end |
| (6) Backward communication mechanism from to if |
| for to |
| ; |
| end |
| end (7) Termination and output |
| if |
| Best position of P system: ; |
| Best Fitness of P system:; |
| end |
| Output: Best position of P system; best fitness of P system; |
4.5. Complexity Analysis
5. The Proposed ECPSO-MTP for Data Clustering
5.1. Test Datasets
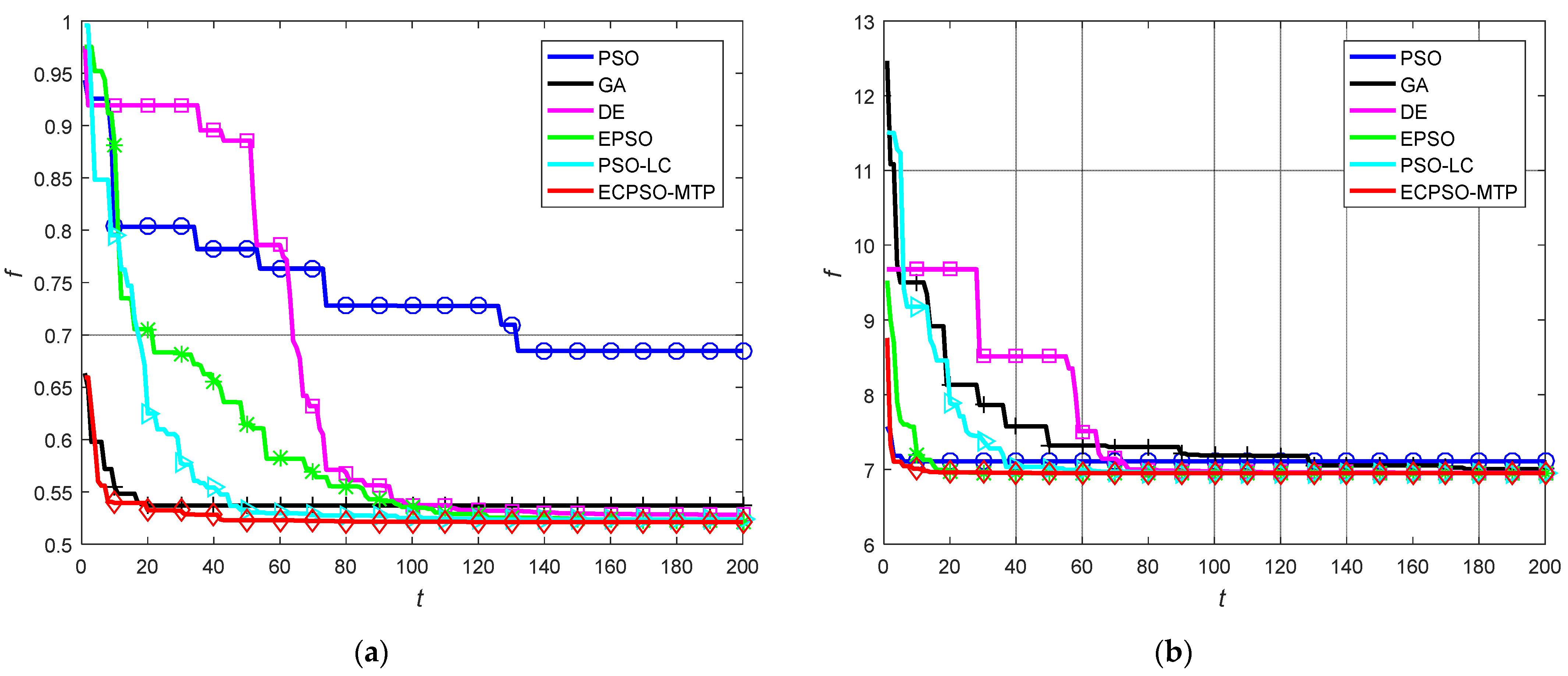
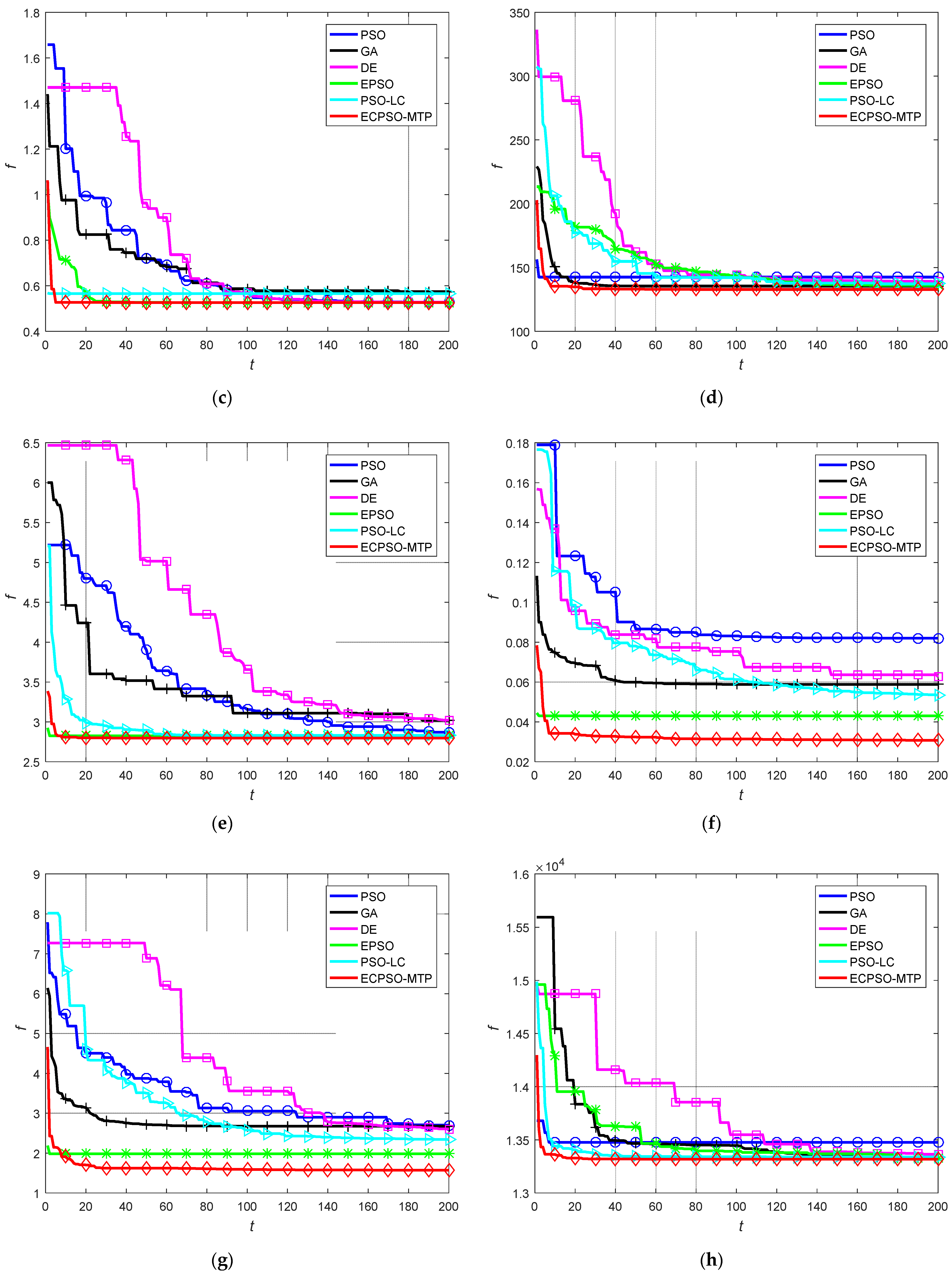
5.2. Comparison with Other Exisitng Approaches
5.3. Friedman Test Statistics
6. The Proposed ECPSO-MTP for Image Segmentation
6.1. Test Images
6.2. Comparison with Other Clustering Approaches
6.3. Friedman Test Statistics
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Păun, G. Membrane computing: An introduction. Theor. Comput. Sci. 2002, 287, 73–100. [Google Scholar] [CrossRef] [Green Version]
- Păun, G. Computing with membranes. J. Comput. Syst. Sci. 2000, 61, 108–143. [Google Scholar] [CrossRef] [Green Version]
- Pan, L.; Zeng, L.; Song, T. Membrane Computing an Introduction, 1st ed.; Huazhong University of Science and Technology Press: Wuhan, China, 2012; pp. 1–10. [Google Scholar]
- Păun, G. Membrane computing and economics: A General View. Int. J. Comput. Commun. Control. 2016, 11, 105–112. [Google Scholar] [CrossRef]
- Freund, R.; Păun, G.; Mario, J. Tissue P systems with channel states. Theor. Comput. Sci. 2005, 330, 101–116. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.Y.; Song, B.S.; Zeng, X.X. Rule synchronization for monodirectional tissue-like P systems with channel states. Inf. Comput. 2022, 285, 104895. [Google Scholar] [CrossRef]
- Păun, A.; Păun, G. The power of communication P systems with symport/antiport. New Gener. Comput. 2002, 20, 295–305. [Google Scholar] [CrossRef]
- Jiang, Z.N.; Liu, X.Y.; Zang, W.K. A kernel-based intuitionistic weight fuzzy k-modes algorithm using coupled chained P system combines DNA genetic rules for categorical data. Neurocomputing 2023, 528, 84–96. [Google Scholar] [CrossRef]
- Song, B.; Hu, Y.; Adorna, H.N.; Xu, F. A quick survey of tissue-like P systems. Rom. J. Inf. Sci. Technol. 2018, 21, 310–321. [Google Scholar]
- Kujur, S.S.; Sahana, S.K. Medical image registration utilizing tissue P systems. Front. Pharmacol. 2022, 13, 949872. [Google Scholar] [CrossRef]
- Martin, O.D.; Cabrera, V.L.; Mario, J.P. The environment as a frontier of efficiency in tissue P systems with communication rules. Theor. Comput. Sci. 2023, 956, 113812. [Google Scholar] [CrossRef]
- Pan, L.Q.; Song, B.S.; Zandron, C. On the computational efficiency of tissue P systems with evolutional symport/antiport rules. Knowl. Based Syst. 2023, 262, 110266. [Google Scholar] [CrossRef]
- Luo, Y.; Guo, P.; Jiang, Y.; Zhang, Y. Timed homeostasis tissue-Like P systems with evolutional symport/antiport rules. IEEE Access 2020, 8, 131414–131424. [Google Scholar] [CrossRef]
- Orellana-Martín, D.; Valencia-Cabrera, L.; Song, B.; Pan, L.; Pérez-Jiménez, M.J. Tissue P systems with evolutional communication rules with two objects in the left-hand side. Nat. Comput. 2023, 22, 119–132. [Google Scholar] [CrossRef]
- Song, B.S.; Pan, L.Q. The computational power of tissue-like P systems with promoters. Theor. Comput. Sci. 2016, 641, 43–52. [Google Scholar] [CrossRef]
- Song, B.; Zeng, X.; Jiang, M.; Pérez-Jiménez, M.J. Monodirectional tissue P systems with promoters. IEEE Trans. Cybern. 2021, 51, 438–450. [Google Scholar] [CrossRef]
- Song, B.S.; Zeng, X.X.; Paton, R.A. Monodirectional tissue P systems with channel states. Inf. Sci. 2021, 546, 206–219. [Google Scholar] [CrossRef]
- Song, B.S.; Li, K.L.; Zeng, X.X. Monodirectional evolutional symport tissue P systems with promoters and cell division. IEEE Trans. Parallel Distrib. Syst. 2022, 33, 332–342. [Google Scholar] [CrossRef]
- Song, B.S.; Li, K.L.; Zeng, X.X. Monodirectional evolutional symport tissue P systems with channel states and cell division. Sci. China-Inf. Sci. 2023, 66, 139104. [Google Scholar] [CrossRef]
- Zhang, G.; Jiménez, M.; Gheorghe, G. Real-Life Applications with Membrane Computing, 1st ed.; Springer Press: Berlin/Heidelberg, Germany, 2017; pp. 11–12. [Google Scholar]
- Tian, X.; Liu, X.Y. Improved hybrid heuristic algorithm inspired by tissue-like membrane system to solve job shop scheduling problem. Processes 2021, 20, 219. [Google Scholar] [CrossRef]
- Zhang, G.X.; Chen, J.X.; Gheorghe, M. QA hybrid approach based on differential evolution and tissue membrane systems for solving constrained manufacturing parameter optimization problems. Appl. Soft Comput. 2013, 13, 1528–1542. [Google Scholar] [CrossRef]
- Peng, H.; Shi, P.; Wang, J.; Riscos-Núñez, A.; Pérez-Jiménez, M.J. Multiobjective fuzzy clustering approach based on tissue-like membrane systems. Knowl. Based Syst. 2017, 125, 74–82. [Google Scholar] [CrossRef]
- Lagos-Eulogio, P.; Seck-Tuoh-Mora, J.C.; Hernandez-Romero, N.; Medina-Marin, J. A new design method for adaptive IIR system identification using hybrid CPSO and DE. Nonlinear Dyn. 2017, 88, 2371–2389. [Google Scholar] [CrossRef]
- Wang, L.; Liu, X.; Qu, J.; Zhao, Y.; Jiang, Z.; Wang, N. An extended tissue-like P System based on membrane systems and quantum-behaved particle swarm optimization for image segmentation. Processes 2022, 10, 287. [Google Scholar] [CrossRef]
- Luo, Y.G.; Guo, P.; Zhang, M.Z. A framework of ant colony P system. IEEE Access 2019, 7, 157655–157666. [Google Scholar] [CrossRef]
- Peng, H.; Wang, J. A hybrid approach based on tissue P systems and artificial bee colony for IIR system identification. Neural Comput. Appl. 2017, 28, 2675–2685. [Google Scholar] [CrossRef]
- Chen, H.J.; Liu, X.Y. An improved multi-view spectral clustering based on tissue-like P systems. Sci. Rep. 2022, 12, 18616. [Google Scholar] [CrossRef]
- Sharif, E.A.; Agoyi, M. Using tissue-like P system to solve the nurse rostering problem at the medical centre of the national university of malaysia. Appl. Nanosci. 2022, 2022, 3145. [Google Scholar] [CrossRef]
- Issac, T.; Silas, S.; Rajsingh, E.B. Investigative prototyping a tissue P system for solving distributed task assignment problem in heterogeneous wireless sensor network. J. King Saud Univ. -Comput. Inf. Sci. 2022, 34, 3685–3702. [Google Scholar] [CrossRef]
- Chen, H.J.; Liu, X.Y. Reweighted multi-view clustering with tissue-like P system. PLoS ONE 2023, 18, e269878. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Kassoul, K.; Zufferey, N.; Cheikhrouhou, N.; Belhaouari, S.B. Exponential particle swarm optimization for global optimization. IEEE Access 2022, 10, 78320–78344. [Google Scholar] [CrossRef]
- Wang, D.S.; Tan, D.P.; Liu, L. Particle swarm optimization algorithm: An overview. Soft Comput. 2017, 22, 387–408. [Google Scholar] [CrossRef]
- Bi, J.X.; Zhao, M.O.; Chai, D.S. PSOSVRPos: WiFi indoor positioning using SVR optimized by PSO. Expert Syst. Appl. 2023, 222, 119778. [Google Scholar] [CrossRef]
- Anbarasi, M.P.; Kanthalakshmi, S. Power maximization in standalone photovoltaic system: An adaptive PSO approach. Soft Comput. 2023, 27, 8223–8232. [Google Scholar] [CrossRef]
- Peng, J.; Li, Y.; Kang, H.; Shen, Y.; Sun, X.; Chen, Q. Impact of population topology on particle swarm optimization and its variants: An information propagation perspective. Swarm Evol. Comput. 2022, 69, 100990. [Google Scholar] [CrossRef]
- Harrison, K.; Engelbrecht, A.; Berman, B. Self-adaptive particle swarm optimization: A review and analysis of convergence. Swarm Intell. 2018, 12, 187–226. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.; Zhou, X.; Ran, X.; Liu, Y.; Deng, W.; Deng, W. Co-evolutionary competitive swarm optimizer with three-phase for large-scale complex optimization problem. Inf. Sci. 2023, 619, 2–18. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, Y.; Chan, T.H.; Li, X.; Zhao, S. A particle swarm optimization algorithm with sigmoid increasing inertia weight for structural damage identification. Appl. Sci. Basel 2022, 12, 3429. [Google Scholar] [CrossRef]
- Wang, J.; Wang, X.; Li, X.; Yi, J. A hybrid particle swarm optimization algorithm with dynamic adjustment of inertia weight based on a new feature selection method to optimize SVM parameters. Entropy 2023, 25, 531. [Google Scholar] [CrossRef] [PubMed]
- Duan, Y.; Chen, N.; Chang, L.; Ni, Y.; Kumar, S.V.N.S.; Zhang, P. CAPSO: Chaos adaptive particle swarm optimization algorithm. IEEE Access 2022, 10, 29393–29405. [Google Scholar] [CrossRef]
- Molaei, S.; Moazen, H.; Najjar-Ghabel, S.; Farzinvash, L. Particle swarm optimization with an enhanced learning strategy and crossover operator. Knowl. Based Syst. 2021, 215, 106768. [Google Scholar] [CrossRef]
- Pan, L.Q.; Zhao, Y.; Li, L.H. Neighborhood-based particle swarm optimization with discrete crossover for nonlinear equation systems. Swarm Evol. Comput. 2022, 69, 101019. [Google Scholar] [CrossRef]
- Das, P.K.; Jena, P.K. Multi-robot path planning using improved particle swarm optimization algorithm through novel evolutionary operators. Appl. Soft Comput. 2020, 92, 106312. [Google Scholar] [CrossRef]
- Pu, H.; Song, T.; Schonfeld, P.; Li, W.; Zhang, H.; Hu, J.; Peng, X.; Wang, J. Mountain railway alignment optimization using stepwise & hybrid particle swarm optimization incorporating genetic operators. Appl. Soft Comput. 2019, 78, 41–57. [Google Scholar]
- Gu, Q.; Wang, Q.; Chen, L.; Li, X.; Li, X. A dynamic neighborhood balancing-based multi-objective particle swarm optimization for multi-modal problems. Expert Syst. Appl. 2022, 205, 117313. [Google Scholar] [CrossRef]
- Moazen, H.; Molaei, S.; Farzinvash, L.; Sabaei, M. PSO-ELPM: PSO with elite learning, enhanced parameter updating, and exponential mutation operator. Inf. Sci. 2023, 628, 70–91. [Google Scholar] [CrossRef]
- Lynn, N.; Suganthan, P.N. Heterogeneous comprehensive learning particle swarm optimization with enhanced exploration and exploitation. Swarm Evol. Comput. 2015, 24, 11–24. [Google Scholar] [CrossRef]
- Cao, Y.L.; Zhang, H. Comprehensive learning particle swarm optimization algorithm with local search for multimodal functions. IEEE Trans. Evol. Comput. 2019, 23, 718–731. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, H.; Li, K.; Lin, Z.; Yang, J.; Shen, X.-L. A hybrid particle swarm optimization algorithm using adaptive learning strategy. Inf. Sci. 2018, 436, 162–177. [Google Scholar] [CrossRef]
- Zhou, X.; Zhou, S.; Han, Y.; Zhu, S. Levy flight-based inverse adaptive comprehensive learning particle swarm optimization. Math. Biosci. Eng. 2022, 19, 5241–5268. [Google Scholar] [CrossRef]
- Ge, Q.; Guo, C.; Jiang, H.; Lu, Z.; Yao, G.; Zhang, J.; Hua, Q. Industrial power load forecasting method based on reinforcement learning and PSO-LSSVM. IEEE Trans. Cybern. 2022, 52, 1112–1124. [Google Scholar] [CrossRef]
- Li, W.; Liang, P.; Sun, B.; Sun, Y.; Huang, Y. Reinforcement learning-based particle swarm optimization with neighborhood differential mutation strategy. Swarm Evol. Comput. 2023, 78, 101274. [Google Scholar] [CrossRef]
- Lu, L.W.; Zhang, J.; Sheng, J.A. Enhanced multi-swarm cooperative particle swarm optimizer. Swarm Evol. Comput. 2022, 69, 100989. [Google Scholar] [CrossRef]
- Li, D.; Wang, L.; Guo, W.; Zhang, M.; Hu, B.; Wu, Q. A particle swarm optimizer with dynamic balance of convergence and diversity for large-scale optimization. Appl. Soft Comput. 2023, 32, 109852. [Google Scholar] [CrossRef]
- Zhang, Y.; Gong, D.W.; Ding, Z.H. Handling multi-objective optimization problems with a multi-swarm cooperative particle swarm optimizer. Expert Syst. Appl. 2011, 38, 13933–13941. [Google Scholar] [CrossRef]
- Li, T.; Shi, J.; Deng, W.; Hu, Z. Pyramid particle swarm optimization with novel strategies of competition and cooperation. Appl. Soft Comput. 2022, 121, 108731. [Google Scholar] [CrossRef]
- Song, W.; Ma, W.; Qiao, G. Particle swarm optimization algorithm with environmental factors for clustering analysis. Soft Comput. 2017, 21, 283–293. [Google Scholar] [CrossRef]
- Nenavath, H.; Jatoth, E.K. Hybridizing sine cosine algorithm with differential evolution for global optimization and object tracking. Appl. Soft Comput. 2018, 62, 1019–1043. [Google Scholar] [CrossRef]
- Pozna, C.; Precup, R.-E.; Horvath, E.; Petriu, E.M. Hybrid particle filter-particle swarm optimization algorithm and application to fuzzy controlled servo systems. IEEE Trans. Fuzzy Syst. 2022, 30, 4286–4297. [Google Scholar] [CrossRef]
- Song, B.S.; Zhang, C.; Pan, L.Q. Tissue-like P systems with evolutional symport/antiport rules. Inf. Sci. 2017, 378, 177–193. [Google Scholar] [CrossRef]
- Pan, T.; Xu, J.; Jiang, S.; Xu, F. Cell-like spiking neural P systems with evolution rules. Soft Comput. 2019, 23, 5401–5409. [Google Scholar] [CrossRef]
- Artificial Datasets. Available online: https://www.isical.ac.in/content/research-data (accessed on 16 June 2020).
- UCI Repository of Machine Learning Databases. Available online: http://archive.ics.uci.edu/ml/datasets.php (accessed on 20 July 2022).
- Peng, H.; Wang, J.; Shi, P.; Pérez-Jiménez, M.J.; Riscos-Núñez, A. An extended membrane system with active membranes to solve automatic fuzzy clustering problems. Int. J. Neural Syst. 2016, 26, 1650004. [Google Scholar] [CrossRef]
- Malinen, M.I.; Franti, P. Clustering by analytic functions. Inf. Sci. 2012, 217, 31–38. [Google Scholar] [CrossRef]
- Tang, Y.; Huang, J.; Pedrycz, W.; Li, B.; Ren, F. A fuzzy cluster validity index induced by triple center relation. IEEE Trans. Cybern. 2023, 99, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Ge, F.H.; Liu, X.Y. Density peaks clustering algorithm based on a divergence distance and tissue-Like P System. Appl. Sci. Basel 2023, 13, 2293. [Google Scholar] [CrossRef]
- Kumari, B.; Kumar, S. Chaotic gradient artificial bee colony for text clustering. Soft Comput. 2016, 20, 1113–1126. [Google Scholar]
- Friedman, M. The use of Ranks to avoid the assumption of normality implicit in the analysis of variance. Publ. Am. Stat. Assoc. 1937, 32, 675–701. [Google Scholar] [CrossRef]
- The Berkeley Segmentation Dataset and Benchmark. Available online: https://www2.eecs.berkeley.edu/Research/Projects/CS/vision/grouping/segbench/ (accessed on 13 October 2021).
- Achanta, R.; Shaji, A.; Smith, K.; Lucchi, A.; Fua, P.; Süsstrunk, S. SLIC superpixels compared to state-of-the-art superipixel methods. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2274–2282. [Google Scholar] [CrossRef] [Green Version]















| Datasets | Data Instances | Features | Clusters |
|---|---|---|---|
| Data_9_2 | 900 | 2 | 9 |
| Square4 | 1000 | 2 | 4 |
| Iris | 150 | 4 | 3 |
| Newthyroid | 215 | 5 | 3 |
| Seeds | 210 | 7 | 3 |
| Yeast | 1484 | 8 | 10 |
| Glass | 214 | 9 | 6 |
| Wine | 178 | 13 | 3 |
| Parameters | Comparative Approaches | |||||
|---|---|---|---|---|---|---|
| PSO | GA | DE | EPSO | PSO-LC | ECPSO-MTP | |
| 200 | 200 | 200 | 200 | 200 | 200 | |
| 200 | 200 | 200 | 200 | 200 | 200 | |
| 2,2 | N | N | 0.6,3 | (0,1) | 2,2 | |
| N | N | N | (0,1) | N | N | |
| (0,1) | N | N | (0,1) | N | (0,1) | |
| N | N | N | (0,1) | N | N | |
| 0.4,1.2 | N | N | 0.4,0.6 | N | 0.4,1.2 | |
| N | N | N | N | 0.99 | N | |
| N | 0.6 | 0.6 | N | N | N | |
| N | 0.02 | N | N | N | N | |
| N | N | N | N | 0.994 | 0.994 | |
| N | N | N | N | 0.995 | 0.995 | |
| N | N | (0.5,1) | N | N | N | |
| N | N | N | N | N | 10 [66] | |
| Datasets | Statistics | Comparative Approaches | |||||
|---|---|---|---|---|---|---|---|
| PSO | GA | DE | EPSO | PSO-LC | ECPSO-MTP | ||
| Data_9_2 | Worst | 0.7260 | 0.5597 | 0.6505 | 0.5240 | 0.6223 | 0.5248 |
| Best | 0.6476 | 0.5240 | 0.5230 | 0.5215 | 0.5218 | 0.5212 | |
| Mean | 0.6854 | 0.5407 | 0.5361 | 0.5222 | 0.5343 | 0.5214 | |
| S.D. | 0.0184 | 0.0079 | 0.0275 | 0.0006 | 0.0252 | 0.0007 | |
| Square4 | Worst | 7.3164 | 7.0736 | 6.9807 | 6.9520 | 6.9525 | 6.9520 |
| Best | 6.9780 | 6.9733 | 6.9520 | 6.9519 | 6.9519 | 6.9519 | |
| Mean | 7.1100 | 7.0195 | 6.9569 | 6.9519 | 6.9520 | 6.9519 | |
| S.D. | 0.0862 | 0.0274 | 0.0051 | 6.81 × 10−6 | 8.59 × 10−5 | 5.49 × 10−6 | |
| Iris | Worst | 1.0158 | 0.5873 | 0.9578 | 0.6619 | 0.5729 | 0.5263 |
| Best | 0.5268 | 0.5450 | 0.5266 | 0.5263 | 0.5287 | 0.5263 | |
| Mean | 0.5663 | 0.5621 | 0.5433 | 0.5357 | 0.5418 | 0.5263 | |
| S.D. | 0.1178 | 0.0099 | 0.0614 | 0.0236 | 0.0103 | 1.09 × 10−5 | |
| Newthyroid | Worst | 152.0870 | 157.1877 | 175.1488 | 136.4225 | 138.1924 | 132.9317 |
| Best | 135.9901 | 133.9973 | 133.1129 | 132.8665 | 135.0995 | 132.8379 | |
| Mean | 143.5047 | 139.2553 | 137.6728 | 133.9052 | 136.5018 | 132.8426 | |
| S.D. | 4.3043 | 4.6420 | 7.2724 | 1.2267 | 0.7346 | 0.0187 | |
| Seeds | Worst | 4.8188 | 3.0923 | 3.0838 | 3.0387 | 3.2346 | 2.7968 |
| Best | 2.8261 | 2.9253 | 2.8306 | 2.8119 | 2.7975 | 2.7968 | |
| Mean | 3.2956 | 3.0059 | 2.9215 | 2.8862 | 2.9042 | 2.7968 | |
| S.D. | 0.7528 | 0.0382 | 0.0467 | 0.0530 | 0.1070 | 2.03 × 10−6 | |
| Yeast | Worst | 0.0822 | 0.0797 | 0.0661 | 0.0465 | 0.0668 | 0.0341 |
| Best | 0.0521 | 0.0578 | 0.0586 | 0.0388 | 0.0494 | 0.0306 | |
| Mean | 0.0721 | 0.0674 | 0.0623 | 0.0427 | 0.0585 | 0.0315 | |
| S.D. | 0.0082 | 0.0076 | 0.0016 | 0.0019 | 0.0043 | 0.0008 | |
| Glass | Worst | 5.0427 | 3.3902 | 2.7652 | 2.2345 | 3.8383 | 1.6684 |
| Best | 2.7025 | 2.1930 | 2.4661 | 1.7229 | 2.3312 | 1.5705 | |
| Mean | 3.5114 | 2.6536 | 2.6326 | 2.0258 | 2.6359 | 1.5795 | |
| S.D. | 0.5915 | 0.3020 | 0.0713 | 0.1198 | 0.2870 | 0.0241 | |
| Wine | Worst | 13,616.9408 | 13,415.0092 | 14,752.6728 | 13,362.1693 | 13,396.0147 | 13,318.5101 |
| Best | 13,318.6675 | 13,327.0278 | 13,320.7178 | 13,325.9217 | 13,327.5156 | 13,318.4817 | |
| Mean | 13,407.7736 | 13,361.6433 | 13,355.5274 | 13,340.4952 | 13,353.1583 | 13,318.4858 | |
| S.D. | 61.9835 | 18.9552 | 201.6508 | 8.3583 | 18.6450 | 0.0057 | |
| Datasets | Statistics | Comparative Approaches | |||||
|---|---|---|---|---|---|---|---|
| PSO | GA | DE | EPSO | PSO-LC | ECPSO-MTP | ||
| Data_9_2 | Mean | 0.8413 | 0.9128 | 0.9179 | 0.9212 | 0.9144 | 0.9214 |
| S.D. | 0.0382 | 0.0078 | 0.0304 | 0.0022 | 0.0201 | 0.0015 | |
| Square4 | Mean | 0.9313 | 0.9333 | 0.9346 | 0.9350 | 0.9350 | 0.9350 |
| S.D. | 0.0033 | 0.0027 | 0.0018 | 3.36 × 10−16 | 0.0001 | 3.36 × 10−16 | |
| Iris | Mean | 0.8771 | 0.8923 | 0.8857 | 0.8907 | 0.8932 | 0.8933 |
| S.D. | 0.0551 | 0.0106 | 0.0319 | 0.0056 | 0.0107 | 0.0026 | |
| Newthyroid | Mean | 0.8007 | 0.8361 | 0.8536 | 0.8541 | 0.8502 | 0.8605 |
| S.D. | 0.0448 | 0.0144 | 0.0273 | 0.0392 | 0.0298 | 7.85 × 10−16 | |
| Seeds | Mean | 0.8510 | 0.8879 | 0.8929 | 0.8952 | 0.8947 | 0.8976 |
| S.D. | 0.0906 | 0.0077 | 0.0065 | 0.0119 | 0.0084 | 7.85 × 10−16 | |
| Yeast | Mean | 0.3494 | 0.3559 | 0.3925 | 0.4385 | 0.3785 | 0.5044 |
| S.D. | 0.0260 | 0.0266 | 0.0287 | 0.0235 | 0.0179 | 0.0215 | |
| Glass | Mean | 0.4911 | 0.4967 | 0.5185 | 0.5355 | 0.4965 | 0.5877 |
| S.D. | 0.0450 | 0.0199 | 0.0154 | 0.0222 | 0.0152 | 0.0062 | |
| Wine | Mean | 0.7013 | 0.7016 | 0.7018 | 0.7022 | 0.7022 | 0.7022 |
| S.D. | 0.0058 | 0.0022 | 0.0041 | 2.24 × 10−16 | 2.24 × 10−16 | 2.24 × 10−16 | |
| Datasets | Comparative Approaches | |||||
|---|---|---|---|---|---|---|
| PSO | GA | DE | EPSO | PSO-LC | ECPSO-MTP | |
| Data_9_2 | 6 | 5 | 4 | 2 | 3 | 1 |
| Square4 | 6 | 5 | 4 | 1 | 3 | 1 |
| Iris | 6 | 5 | 4 | 2 | 3 | 1 |
| Newthyroid | 6 | 5 | 4 | 2 | 3 | 1 |
| Seeds | 6 | 5 | 4 | 2 | 3 | 1 |
| Yeast | 6 | 5 | 4 | 2 | 3 | 1 |
| Glass | 6 | 5 | 3 | 2 | 4 | 1 |
| Wine | 6 | 5 | 4 | 2 | 3 | 1 |
| Total Rank | 48 | 40 | 31 | 15 | 25 | 8 |
| Average Rank | 6 | 5 | 3.875 | 1.875 | 3.125 | 1 |
| Deviation | 2.5 | 1.5 | 0.375 | −1.625 | −0.375 | −2.5 |
| Image | Statistics | Comparative Approaches | |||
|---|---|---|---|---|---|
| K-Means | SC | PSO | ECPSO-MTP | ||
| Lawn | Worst | 0.9933 | 0.9937 | 0.9934 | 0.9943 |
| Best | 0.9933 | 0.9937 | 0.9934 | 0.9943 | |
| Mean | 0.9933 | 0.9937 | 0.9934 | 0.9943 | |
| S.D. | 2.28 × 10−16 | 2.34 × 10−16 | 5.61 × 10−16 | 3.42 × 10−16 | |
| Agaric | Worst | 0.9477 | 0.9517 | 0.9485 | 0.9567 |
| Best | 0.9477 | 0.9517 | 0.9485 | 0.9567 | |
| Mean | 0.9477 | 0.9517 | 0.9485 | 0.9567 | |
| S.D. | 1.24 × 10−16 | 2.65 × 10−16 | 4.49 × 10−16 | 3.16 × 10−16 | |
| Church | Worst | 0.7892 | 0.8902 | 0.7876 | 0.7967 |
| Best | 0.8646 | 0.8902 | 0.8903 | 0.8962 | |
| Mean | 0.8593 | 0.8902 | 0.8641 | 0.8903 | |
| S.D. | 0.0147 | 1.12 × 10−16 | 0.0445 | 0.0239 | |
| Castle | Worst | 0.9302 | 0.9411 | 0.9327 | 0.9413 |
| Best | 0.9377 | 0.9411 | 0.9377 | 0.9413 | |
| Mean | 0.9346 | 0.9411 | 0.9368 | 0.9413 | |
| S.D. | 0.0033 | 3.36 × 10−16 | 0.0019 | 4.49 × 10−16 | |
| Elephants | Worst | 0.6930 | 0.8881 | 0.7669 | 0.7624 |
| Best | 0.9248 | 0.8940 | 0.7820 | 0.9248 | |
| Mean | 0.7802 | 0.8882 | 0.7807 | 0.8978 | |
| S.D. | 0.0862 | 0.0008 | 0.0029 | 0.0558 | |
| Lane | Worst | 0.8205 | 0.9668 | 0.8318 | 0.8241 |
| Best | 0.9730 | 0.9730 | 0.9730 | 0.9795 | |
| Mean | 0.9124 | 0.9676 | 0.9537 | 0.9696 | |
| S.D. | 0.0668 | 0.0027 | 0.0482 | 0.0671 | |
| Starfish | Worst | 0.4805 | 0.5232 | 0.4910 | 0.5911 |
| Best | 0.5860 | 0.7259 | 0.6287 | 0.8435 | |
| Mean | 0.5597 | 0.6233 | 0.5829 | 0.6344 | |
| S.D. | 0.0406 | 0.0620 | 0.0183 | 0.0639 | |
| Pyramid | Worst | 0.7200 | 0.7366 | 0.7497 | 0.7914 |
| Best | 0.7661 | 0.8394 | 0.7594 | 0.8410 | |
| Mean | 0.7533 | 0.7648 | 0.7551 | 0.8354 | |
| S.D. | 0.0157 | 0.0421 | 0.0038 | 0.0073 | |
| Images | Comparative Approaches | |||
|---|---|---|---|---|
| K-Means | SC | PSO | ECPSO-MTP | |
| Lawn | 4 | 2 | 3 | 1 |
| Agaric | 4 | 2 | 3 | 1 |
| Church | 4 | 2 | 3 | 1 |
| Castle | 4 | 2 | 3 | 1 |
| Elephants | 4 | 2 | 3 | 1 |
| Lane | 4 | 2 | 3 | 1 |
| Starfish | 4 | 2 | 3 | 1 |
| Pyramid | 4 | 2 | 3 | 1 |
| Total Rank | 32 | 16 | 24 | 8 |
| Average Rank | 4 | 2 | 3 | 1 |
| Deviation | 1.5 | −0.5 | 0.5 | −1.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Liu, X.; Qu, J.; Zhao, Y.; Gao, L.; Ren, Q. An Extended Membrane System with Monodirectional Tissue-like P Systems and Enhanced Particle Swarm Optimization for Data Clustering. Appl. Sci. 2023, 13, 7755. https://doi.org/10.3390/app13137755
Wang L, Liu X, Qu J, Zhao Y, Gao L, Ren Q. An Extended Membrane System with Monodirectional Tissue-like P Systems and Enhanced Particle Swarm Optimization for Data Clustering. Applied Sciences. 2023; 13(13):7755. https://doi.org/10.3390/app13137755
Chicago/Turabian StyleWang, Lin, Xiyu Liu, Jianhua Qu, Yuzhen Zhao, Liang Gao, and Qianqian Ren. 2023. "An Extended Membrane System with Monodirectional Tissue-like P Systems and Enhanced Particle Swarm Optimization for Data Clustering" Applied Sciences 13, no. 13: 7755. https://doi.org/10.3390/app13137755
APA StyleWang, L., Liu, X., Qu, J., Zhao, Y., Gao, L., & Ren, Q. (2023). An Extended Membrane System with Monodirectional Tissue-like P Systems and Enhanced Particle Swarm Optimization for Data Clustering. Applied Sciences, 13(13), 7755. https://doi.org/10.3390/app13137755







