An Optical Implementation of Quantum Bit Commitment Using Infinite-Dimensional Systems
Abstract
1. Introduction
2. Results
2.1. The Theoretical Description of the Protocol
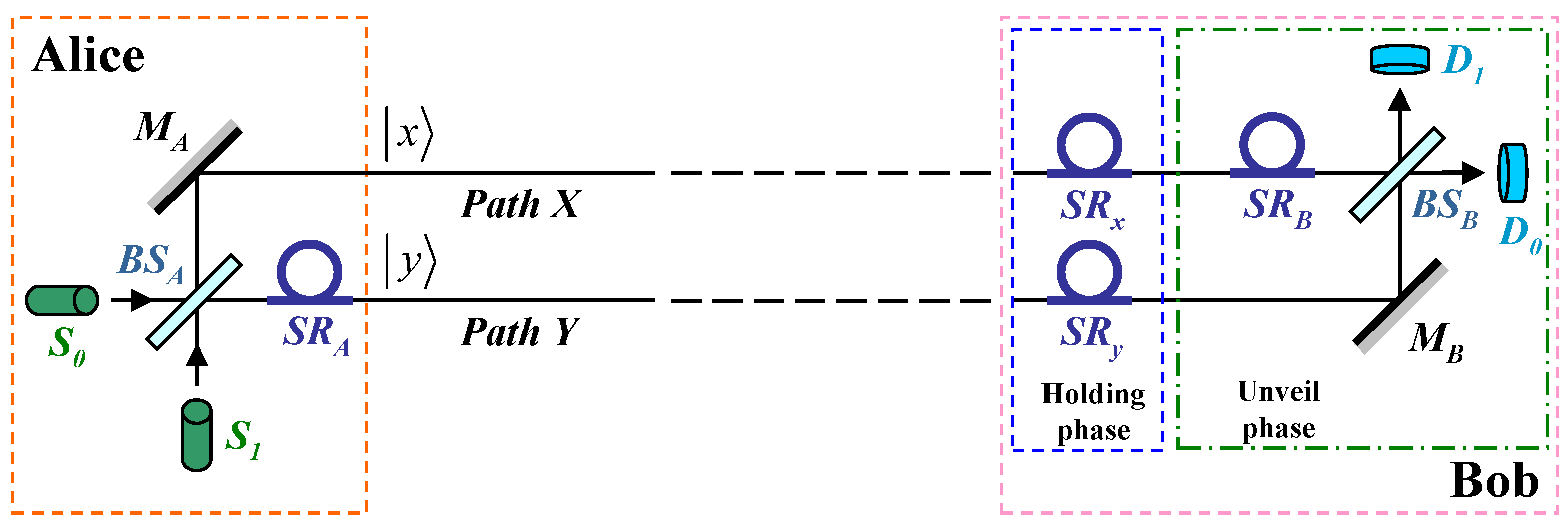
2.2. The Experimental Implementation
2.3. The Relationship between the Two Protocols
2.4. Feasibility
2.5. Practical Difficulties
3. Discussion
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BC | Bit Commitment |
| QBC | Quantum Bit Commitment |
| MLC | Mayers–Lo–Chau |
| HJW | Hughston–Jozsa–Wootters |
| MZ | Mach–Zehnder |
| QKD | Quantum Key Distribution |
| QCT | Quantum Coin Tossing |
Appendix A. Confidence Interval of the Error Rate
Appendix B. Quantum Coin Tossing as an Application
References
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. In Proceedings of the IEEE International Conference on Computers, Systems, and Signal Processing, Bangalore, India, 9–12 December 1984; IEEE: New York, NY, USA, 1984; p. 175. [Google Scholar]
- Brassard, G.; Crépeau, C.; Jozsa, R.; Langlois, D. A quantum bit commitment scheme provably unbreakable by both parties. In Proceedings of the 34th Annual IEEE Symposium on Foundations of Computer Science, Palo Alto, CA, USA, 3–5 November 1993; IEEE: Los Alamitos, CA, USA, 1993; p. 362. [Google Scholar]
- Rabin, M.O. How to Exchange Secrets by Oblivious Transfer; Technical Report TR-81; Aiken Computation Laboratory, Harvard University: Cambridge, MA, USA, 1981; Available online: http://eprint.iacr.org/2005/187.pdf (accessed on 18 March 2010).
- Even, S.; Goldreich, O.; Lempel, A. A randomized protocol for signing contracts (Extended abstract). In Advances in Cryptology, Proceedings of the Crypto ’82, Santa Barbara, CA, USA, 23–25 August 1982; Chaum, D., Rivest, R.L., Sherman, A.T., Eds.; Plenum: New York, NY, USA, 1982; p. 205. [Google Scholar]
- Kilian, J. Founding cryptography on oblivious transfer. In Proceedings of the 1988 ACM Annual Symposium on Theory of Computing, Chicago, IL, USA, 2–4 May 1988; ACM: New York, NY, USA, 1988; p. 20. [Google Scholar]
- Mayers, D. The trouble with quantum bit commitment. arXiv 1996, arXiv:quant-ph/9603015v3. [Google Scholar]
- Mayers, D. Unconditionally secure quantum bit commitment is impossible. Phys. Rev. Lett. 1997, 78, 3414. [Google Scholar] [CrossRef]
- Lo, H.-K.; Chau, H.F. Is quantum bit commitment really possible? Phys. Rev. Lett. 1997, 78, 3410. [Google Scholar] [CrossRef]
- Crépeau, C. What is going on with quantum bit commitment? In Proceedings of the Pragocrypt ’96: 1st International Conference on the Theory and Applications of Cryptology, Prague, Czech Republic, 3–7 November 1996. [Google Scholar]
- Chau, H.F.; Lo, H.-K. Making an empty promise with a quantum computer. Fortsch. Phys. 1998, 46, 507. [Google Scholar] [CrossRef]
- Lo, H.-K.; Chau, H.F. Why quantum bit commitment and ideal quantum coin tossing are impossible. Physica D 1998, 120, 177. [Google Scholar] [CrossRef]
- Brassard, G.; Crépeau, C.; Mayers, D.; Salvail, L. The security of quantum bit commitment schemes. In Proceedings of the Randomized Algorithms, Satellite Workshop of 23rd International Symposium on Mathematical Foundations of Computer Science, Brno, Czech Republic, 24–28 August 1998. [Google Scholar]
- Bub, J. The quantum bit commitment theorem. Found. Phys. 2001, 31, 735. [Google Scholar] [CrossRef]
- Broadbent, A.; Schaffner, C. Quantum cryptography beyond quantum key distribution. Designs Codes Cryptogr. 2016, 78, 351. [Google Scholar] [CrossRef]
- Brassard, G.; Crépeau, C.; Mayers, D.; Salvail, L. A brief review on the impossibility of quantum bit commitment. arXiv 1997, arXiv:quant-ph/9712023v1. [Google Scholar]
- Brassard, G.; Crépeau, C.; Mayers, D.; Salvail, L. Defeating classical bit commitments with a quantum computer. arXiv 1998, arXiv:quant-ph/9806031v1. [Google Scholar]
- Damgård, I.; Kilian, J.; Salvail, L. On the (im)possibility of basing oblivious transfer and bit commitment on weakened security assumptions. In Advances in Cryptology, Proceedings of the EUROCRYPT ’99, Prague, Czech Republic, 2–6 May 1999; LNCS; Springer: Berlin/Heidelberg, Germany, 1999; Volume 1592, pp. 56–73. [Google Scholar]
- Kent, A. Impossibility of unconditionally secure commitment of a certified classical bit. Phys. Rev. A 2000, 61, 042301. [Google Scholar] [CrossRef]
- Canetti, R.; Fischlin, M. Universally composable commitments. Lect. Notes Comput. Sci. 2001, 2139, 19. [Google Scholar]
- Kent, A. Why classical certification is impossible in a quantum world. Quantum Inf. Process. 2012, 11, 493. [Google Scholar] [CrossRef]
- Spekkens, R.W.; Rudolph, T. Degrees of concealment and bindingness in quantum bit commitment protocols. Phys. Rev. A 2001, 65, 012310. [Google Scholar] [CrossRef]
- Spekkens, R.W.; Rudolph, T. Optimization of coherent attacks in generalizations of the BB84 quantum bit commitment protocol. Quant. Inf. Comput. 2002, 2, 66. [Google Scholar] [CrossRef]
- D’Ariano, G.M. The quantum bit commitment: A finite open system approach for a complete classification of protocols. arXiv 2002, arXiv:quant-ph/0209149v1. [Google Scholar]
- D’Ariano, G.M. The quantum bit commitment: A complete classification of protocols. arXiv 2002, arXiv:quant-ph/0209150v1. [Google Scholar]
- Chailloux, A.; Kerenidis, I. Optimal bounds for quantum bit commitment. In Proceedings of the 52nd IEEE Symposium on Foundations of Computer Science, Palm Springs, CA, USA, 22–25 October 2011; p. 354. [Google Scholar]
- D’Ariano, G.M.; Kretschmann, D.; Schlingemann, D.; Werner, R.F. Reexamination of quantum bit commitment: The possible and the impossible. Phys. Rev. A 2007, 76, 032328. [Google Scholar] [CrossRef]
- Chiribella, G.; D’Ariano, G.M.; Perinotti, P.; Schlingemann, D.M.; Werner, R.F. A short impossibility proof of quantum bit commitment. Phys. Lett. A 2013, 377, 1076. [Google Scholar] [CrossRef]
- Mayers, D. Superselection rules in quantum cryptography. arXiv 2002, arXiv:quant-ph/0212159v2. [Google Scholar]
- Kitaev, A.; Mayers, D.; Preskill, J. Superselection rules and quantum protocols. Phys. Rev. A 2004, 69, 052326. [Google Scholar] [CrossRef]
- Halvorson, H. Remote preparation of arbitrary ensembles and quantum bit commitment. J. Math. Phys. 2004, 45, 4920. [Google Scholar] [CrossRef]
- Disilvestro, L.; Markham, D. Quantum protocols within Spekkens’ toy model. Phys. Rev. A 2017, 95, 052324. [Google Scholar] [CrossRef]
- Cheung, C.-Y. Secret parameters in quantum bit commitment. arXiv 2005, arXiv:quant-ph/0508180v2. [Google Scholar] [CrossRef]
- Cheung, C.-Y. Insecurity of quantum bit commitment with secret parameters. Int. J. Mod. Phys. B 2007, 21, 4271. [Google Scholar] [CrossRef]
- Cheung, C.-Y. On the question of secret probability distributions in quantum bit commitment. Chin. J. Phys. 2019, 58, 320. [Google Scholar] [CrossRef]
- Magnin, L.; Magniez, F.; Leverrier, A.; Cerf, N.J. Strong no-go theorem for Gaussian quantum bit commitment. Phys. Rev. A 2010, 81, 010302. [Google Scholar] [CrossRef]
- Modi, K.; Pati, A.K.; De, A.S.; Sen, U. Masking quantum information is impossible. Phys. Rev. Lett. 2018, 120, 230501. [Google Scholar] [CrossRef]
- Bhowmick, S.; Srivastav, A.; Pati, A.K. No-masking theorem for observables and no-bit commitment. arXiv 2022, arXiv:2209.12261v1. [Google Scholar]
- Vilasini, V.; Portmann, C.; del Rio, L. Composable security in relativistic quantum cryptography. New J. Phys. 2019, 21, 043057. [Google Scholar] [CrossRef]
- Chiribella, G.; D’Ariano, G.M.; Perinotti, P. Probabilistic theories with purification. Phys. Rev. A 2010, 81, 062348. [Google Scholar] [CrossRef]
- Li, Q.; Li, C.-Q.; Long, D.-Y.; Chan, W.H.; Wu, C.-H. On the impossibility of non-static quantum bit commitment between two parties. Quantum Inf. Process. 2012, 11, 519. [Google Scholar] [CrossRef]
- Gutoski, G.; Rosmanis, A.; Sikora, J. Fidelity of quantum strategies with applications to cryptography. Quantum 2018, 2, 89. [Google Scholar] [CrossRef]
- Sikora, J.; Selby, J. A simple proof of the impossibility of bit-commitment in generalised probabilistic theories using cone programming. Phys. Rev. A 2018, 97, 042302. [Google Scholar] [CrossRef]
- Nagy, M.; Nagy, N. An information-theoretic perspective on the quantum bit commitment impossibility theorem. Entropy 2018, 20, 193. [Google Scholar] [CrossRef]
- Sun, X.; He, F.; Wang, Q. Impossibility of quantum bit commitment, a categorical perspective. Axioms 2020, 9, 28. [Google Scholar] [CrossRef]
- He, G.P. Secure quantum bit commitment against empty promises. Phys. Rev. A 2006, 74, 022332. [Google Scholar] [CrossRef]
- He, G.P. Quantum key distribution based on orthogonal states allows secure quantum bit commitment. J. Phys. A Math. Theor. 2011, 44, 445305. [Google Scholar] [CrossRef]
- He, G.P. Simplified quantum bit commitment using single photon nonlocality. Quantum Inf. Process. 2014, 13, 2195. [Google Scholar] [CrossRef]
- He, G.P. Chapter 4: Density matrices in quantum bit commitment. In Understanding Density Matrices; Danielsen, N.V., Ed.; Nova Science Publishers: New York, NY, USA, 2019; pp. 139–164. [Google Scholar]
- Yuen, H.P. An unconditionally secure quantum bit commitment protocol. arXiv 2012, arXiv:1212.0938v1. [Google Scholar]
- Srikanth, R. Quantum bit commitment and the reality of the quantum state. Found. Phys. 2018, 48, 92. [Google Scholar] [CrossRef]
- Cheung, C.-Y. Unconditionally secure quantum bit commitment using modified double-slit and unstable particles. arXiv 2023, arXiv:2305.12902v1. [Google Scholar]
- Hughston, L.P.; Jozsa, R.; Wootters, W.K. A complete classification of quantum ensembles having a given density matrix. Phys. Lett. A 1993, 183, 14. [Google Scholar] [CrossRef]
- Uhlmann, A. The “transition probability” in the state space of a *-algebra. Rep. Math. Phys. 1976, 9, 273. [Google Scholar] [CrossRef]
- Kirkpatrick, K.A. The Schrödinger-HJW Theorem. Found. Phys. Lett. 2006, 19, 95. [Google Scholar] [CrossRef]
- He, G.P. Chaos in quantum steering in high-dimensional systems. Phys. Rev. A 2018, 97, 042340. [Google Scholar] [CrossRef]
- He, G.P. Unconditionally secure quantum bit commitment based on the uncertainty principle. Proc. R. Soc. A 2019, 475, 20180543. [Google Scholar]
- Goldenberg, L.; Vaidman, L. Quantum cryptography based on orthogonal states. Phys. Rev. Lett. 1995, 75, 1239. [Google Scholar] [CrossRef]
- Koashi, M.; Imoto, N. Quantum cryptography based on split transmission of one-bit information in two steps. Phys. Rev. Lett. 1997, 79, 2383. [Google Scholar] [CrossRef]
- Xu, S.-W.; Sun, Y.; Lin, S. Quantum private query based on single-photon interference. Quantum Inf. Process. 2016, 15, 3301. [Google Scholar] [CrossRef]
- Avella, A.; Brida, G.; Degiovanni, I.P.; Genovese, M.; Gramegna, M.; Traina, P. Experimental quantum-cryptography scheme based on orthogonal states. Phys. Rev. A 2010, 82, 062309. [Google Scholar] [CrossRef]
- Danan, A.; Vaidman, L. Practical quantum bit commitment protocol. Quantum Inf. Process. 2012, 11, 769. [Google Scholar] [CrossRef]
- Ng, N.H.Y.; Joshi, S.K.; Chia, C.M.; Kurtsiefer, C.; Wehner, S. Experimental implementation of bit commitment in the noisy-storage model. Nat. Commun. 2012, 3, 1326. [Google Scholar] [CrossRef]
- Nikolopoulos, G.M. Optical scheme for cryptographic commitments with physical unclonable keys. Opt. Express. 2019, 27, 29367. [Google Scholar] [CrossRef]
- Shakhovoy, R.; Puplauskis, M.; Sharoglazova, V.; Duplinskiy, A.; Sych, D.; Maksimova, E.; Hydyrova, S.; Tumachek, A.; Mironov, Y.; Kovalyuk, V.; et al. Phase randomness in a semiconductor laser: Issue of quantum random-number generation. Phys. Rev. A 2023, 107, 012616. [Google Scholar] [CrossRef]
- Clifton, R.; Bub, J.; Halvorson, H. Characterizing quantum theory in terms of information-theoretic constraints. Found. Phys. 2003, 33, 1561. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, G.P. An Optical Implementation of Quantum Bit Commitment Using Infinite-Dimensional Systems. Appl. Sci. 2023, 13, 7692. https://doi.org/10.3390/app13137692
He GP. An Optical Implementation of Quantum Bit Commitment Using Infinite-Dimensional Systems. Applied Sciences. 2023; 13(13):7692. https://doi.org/10.3390/app13137692
Chicago/Turabian StyleHe, Guang Ping. 2023. "An Optical Implementation of Quantum Bit Commitment Using Infinite-Dimensional Systems" Applied Sciences 13, no. 13: 7692. https://doi.org/10.3390/app13137692
APA StyleHe, G. P. (2023). An Optical Implementation of Quantum Bit Commitment Using Infinite-Dimensional Systems. Applied Sciences, 13(13), 7692. https://doi.org/10.3390/app13137692




