Experimental Study on Remaining Useful Life Prediction of Lithium-Ion Batteries Based on Three Regression Models for Electric Vehicle Application

Abstract

This paper presents three regression models that predict the lithium-ion battery life for electric cars based on a supervised machine learning regression algorithm. The linear regression, bagging regressor, and random forest regressor models will be compared for the capacity prediction of lithium-ion batteries based on voltage-dependent per-cell modeling. When sufficient test data are available, three linear regression learning algorithms will train this model to give a promising battery capacity prediction result. The effectiveness of the three linear regression models will be demonstrated experimentally. The experiment table system is built with an NVIDIA Jetson Nano 4 GB Developer Kit B01, a battery, an Arduino, and a voltage sensor. The random forest regressor model has evaluated the model’s accuracy based on the average of the square of the difference between the initial value and the predicted value in the data set (MSE (mean square error)) and RMSE (root mean squared error), which is smaller than the linear regression model and bagging regressor model (MSE is 516.332762; RMSE is 22.722957). The linear regression model with MSE and RMSE is the biggest (MSE is 22060.500669; RMSE is 148.527777). This result allows the random forest regressor model to remain helpful in predicting the life of lithium-ion batteries. Moreover, this result allows rapid identification of battery manufacturing processes and will enable users to decide to replace defective batteries when deterioration in battery performance and lifespan is identified.

1. Introduction

Due to the benefits of high energy density, low self-discharge characteristics, fast charging, high-capacity, low-pollution, and long-life lithium-ion batteries (LIB) have recently received much attention in research and application. As a result, their market share is steadily growing [1,2,3]. These exceptional characteristics have drawn several scientists to research battery power management in recent years [4,5]. In particular, the battery’s state of health (SOH) is utilized to gauge its aging and anticipate how long it will last during the storm’s charge and discharge cycles. Through the design of materials and the evaluation of battery life, this approach may speed up the development of novel electrode materials with increased capacity and energy [6]. Physical modeling and data collection are used to forecast universal batteries’ capacity and capacity loss [7]. Math is used in model-based approaches. To accurately represent the battery’s decay law, the model is chosen by the battery’s physical or experimental deterioration process [8]. The data generated by impedance were analyzed using fuzzy logic in reference [9]. The integral of the discharge or charge current is used to determine the battery’s remaining power using the Coulomb (CC) technique of calculating capacity over time, which is frequently used for straightforward computations [10]. Based on a modified Randle circuit model, the authors of [11] created a non-linear model of the battery by employing circuit characteristics such as resistors, capacitors, and inductors to forecast the depletion of battery capacity. However, interference from other integrated system components impacts measurement accuracy [12]. Additionally, according to reference [13], for analogous circuit models with several complicated characteristics, the lifespan prediction model, in conjunction with innovative filtering technology, will forecast the reduction in battery capacity. The battery cell is complex, varied, and mysterious.

An empirical exponential and polynomial regression model were also suggested in reference [14,15,16] to track the trend of battery cell degradation throughout the battery cell’s life based on the analysis of experimental data and utilize a filtering approach to tweak the model parameters live. According to [17], a novel model using a Kalman filter and regression vector was created to forecast the battery’s short-term capacity and cycle life. Additionally, the literature has established a novel prediction technique based on multiple filtering interaction models [18] to estimate battery cycle life. Many battery capacity models employ the multi-model interaction modeling technique for various state equations. Here, it is discovered that these model-based techniques have made significant strides toward high performance. Experimental evidence supports this finding. The battery-degrading accuracy of the physical model, however, limits the accuracy and robustness of these models [19,20].

Artificial intelligence (AI) techniques are now often used in state prediction, voice recognition, natural language processing, and picture and image processing. Machine learning (ML) uses a traditional neural network, but algorithms follow the system. To predict the SOH of Li-ion battery packs, scientists also coupled the effectiveness of ML with training schemes and clever tweaks. As a result, the suggested technique is paired with the Gaussian network process (NGP) model [21,22,23,24,25] in this study, which considers the battery’s degradation under various operating situations. The regression model is used to predict the target values as continuous values. This model also has far-reaching applications, from house price prediction, e-commerce valuation systems, weather forecasts, and stock market predictions to image resolution conversion, super-high automatic encoder learning features, and image compression [26,27,28,29,30]. In this paper, we used linear regression, bagging regressor, and random forest regressor models. Three models will be compared to predict the capacity of lithium-ion batteries based on voltage-dependent per-cell modeling. When sufficient test data are available, three linear regression learning algorithms will train this model to give a promising battery capacity prediction result. The effectiveness of the three linear regression models will be demonstrated experimentally. First, the study predicts, based on the correlation analysis, that the average power loss in the battery’s early cycles is connected to the lifespan of the charge and discharge cycles. The developed model (ML) is then used to forecast the cycle life of the Li-ion battery. The results of our study are based on the characteristics of the first 100 charging and discharging cycles to determine the battery’s capacity. Consequently, battery production methods may be quickly detected, and consumers can choose to replace bad batteries when performance and longevity start to decline.

The article is divided into the following six parts: first, Section 2 illustrates the extraction of the battery’s physical components. Battery psychological characteristics are discussed in Section 3. Section 4 explores the three ML regression approaches that are presented. The results of the experiment and assessment are shown in Section 5. Lastly, Section 6 is the conclusion and includes a discussion of the possible future developments of our research results.

2. Electric Vehicles Battery Key Parameters

2.1. Variance of Temperature

The surface temperature increases during heat generation, remains constant, and varies during the discharge phase. This temperature is created by I_2R and the chemical reaction. As the battery capacity declines, the temperature increases, leading to a large thermal variance. The temperature variance in each cycle is calculated by the Formula (1).

$$T=E{\left(T_t-\mu \right)}^2$$

(1)

where E is the electromotive force, and T_i is the ith temperature sample in n cycles.

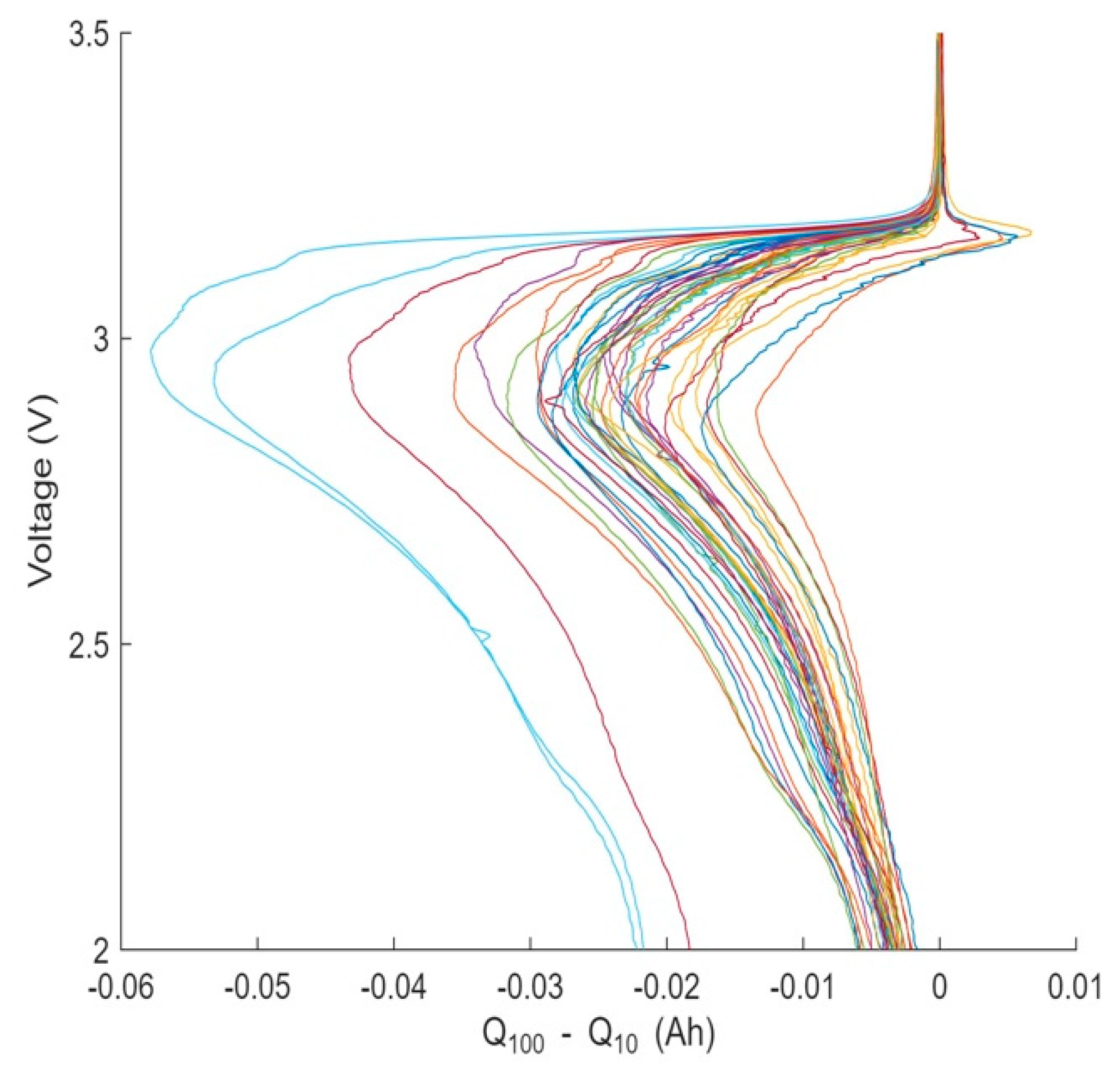
2.2. Discharge Voltage Variance

As the voltage discharges faster, the battery capacity declines. The discharge voltage variance in each cycle is written as Formula (3).

$$V=E{\left(V_t-\mu \right)}^2$$

(2)

where E is the electromotive force, and V_i is the ith voltage sample in n cycles.

3. Physical Characteristics of Battery Lithium-Ion

The hue of the angles and the measured discharge capacity curves vary over the spectrum across the battery life cycle shown in Figure 1.

The connection between the predicted discharge capacity and the total number of cycles throughout the battery life is shown in Figure 1. Early processes in the battery’s life cause its ability to decline gradually, while later cycles cause it to drain quickly. The power characteristics were also discovered to be alternating, indicating that the capacity and battery life models are not linear. Therefore, the research suggests a model based on fundamental physical characteristics and the premature discharge of the storm to calculate the battery’s life precisely. We predict the battery life using the battery capacity formula at each cycle (3) based on the beginning values in Part 2 (voltage, current, temperature, etc.). The recipe demonstrates the link between first-cycle discharge and battery life.

$$P_{jk}={\displaystyle \sum _{i=2}^{n}U(t_i)(Q(t_i)-Q(t_{i-1}))/(t_n-t_1)}$$

(3)

where $P_{jk}$ is the battery capacity at each cycle; U(t) is the discharge voltage; Q(t) is the discharged power; t is the discharge time at each cycle to determine the average power; j is the jth battery; and k is the number of discharge cycles.

Based on Figure 1, it can be seen that the capacity curves of the battery cells decline in the early cycles because of the slight increase in capacity during the early discharge phase. Therefore, to study the relationship between the characteristics and the subsequent period related to the battery cycle life, this paper uses data from 10 to 100 cycles. Figure 1 shows the curve. Power P indicates that the attenuation of the battery is minimal during the whole cycle. This paper uses variance statistics to convert the attenuation fluctuation of the average power P_j of each battery from 10 to 110 cycles into energy P_Dj to establish the relationship corresponding to the period L_j. The relationship between P_Dj and L_j is determined through Equation (4).

$${\rho }_{p_D,L}=\frac{E(P_{D}L)-E(P_D)E(L)}{\sqrt{E(P^2{}_D)-{(E(P_D))}^2}\sqrt{E(L^2)-{(E(L))}^2}}$$

(4)

Each voltage–discharge power relationship is different from the 100th and 10th cycles $\Delta Q_{100-10}(V)$, as shown in Figure 2.

4. Regression Models Life Prediction of Lithium-Ion Batteries

4.1. Linear Regression

Linear regression is a method to predict the dependent variable (y) based on the value of the independent variable (x). This means that linear regression should have a linear relationship between the independent variable and the non-independent variable, and the effect of a change in the values of the independent variables should further affect the dependent variables. Some properties of linear regression are that the regression line always passes through the mean of the independent variable (x) and the standard of the dependent variable (y). The regression line minimizes the sum of the “area of errors”. The sum of areas measures the response/dependent variable (y) ratio variation. The amount of variation inherent in the reaction can be considered before regression is performed [19,20,21].

The linear regression model is shown in Figure 3, and the steps are as follows:

Step 1: Define input data characteristics;

Step 2: Analyze the correlation of the data;

Step 3: Estimate the model;

Step 4: Determine the fitting line;

Step 5: Analyze the model;

Step 6: Test the model with tested data;

Step 7: Calculate with metric types of sampled data.

The paper uses a simple linear regression model to predict the remaining life of the battery cell. This model provides accurate results. The linear model has the form of Formula (5).

$${\widehat{y}}_i={\widehat{w}}^T{x}_i+\beta$$

(5)

where ${\widehat{y}}_i$ is the period forecast of the ith battery cell, the feedback variable; x_i is the feature vector p for the ith battery cell, the predictor variable; ŵ is a vector of p-dimensional model coefficients; and $\beta$ is the regression coefficient.

When applying regression techniques, a penalty function is added to the least squares optimization formula to avoid overfitting. linear regression uses an elastic network to fit and select the model by finding the sparse coefficient vectors. The linear regression formula using an elastic network has the following form as Equation (6):

$$\widehat{w}={\min }_w{\parallel y-Xw-\beta \parallel }_2^2+\lambda P(w)$$

(6)

where the min function represents finding the value of w that minimizes the argument, y is the n-dimensional vector of the observed battery life, X is the n × p matrix of objects, and λ is a non-negative directional quantity. Inside ${\parallel y-Xw\parallel }_2^2$ are the smallest regular squares. P(w) depends on the elastic network regression technique.

$$P(w)=\frac{1-\alpha }{2}{\parallel w\parallel }_2^2+\alpha {\parallel w\parallel }_1$$

(7)

where $\alpha$ is the scalar coefficient between 0 and 1.

One way to gauge how “good” a model fits a given data set is to calculate the square root mean square error (RMSE). RMSE is a known metric that averages predicted values that are far from observed values. RMSE and mean percent error were chosen to evaluate the performance of the model. RMSE is calculated as Formula (8) as follows:

$$RMSE=\sqrt{\frac{1}{n}}{\displaystyle \sum _{i=1}^n{(y_i-{\widehat{y}}_i)}^2}$$

(8)

where y is the observed lifetime, $\widehat{y}$ is the predicted period, and n is the total number of samples. The average percentage error is determined by Formula (9):

$$\%erro=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\frac{(y_i-{\widehat{y}}_i)}{y_i}}^{}}\times 100$$

(9)

The linear regression model is written using Python code, as shown below:

• def regression_matrics(y_test, y_pred):
•  # calculate errors
•  mse = mean_squared_error(y_test, y_pred)
• rmse = mean_squared_error(y_test, y_pred, squared=False)
• mae = mean_absolute_error(y_test, y_pred)
•  # report error
• print(f’Mean Squared Error: {mse}’)
• print(f’Root Mean Square Error: {rmse}’)
• print(f’Mean Absolute Error: {mae}’)

4.2. Random Forest Regressor

Random forest is an algorithm that belongs to the group of supervised learning algorithms used in two problems: classification and regression. The general idea of the algorithm is it is a combination of many decision trees; however, for each decision tree, there is randomness, so the prediction result is a combination of many decision trees. In building an algorithm for the regression problem, the implementation steps are still the same, only the output of the problem is a constant value, and it will be averaged from the output points. The structure of the random forest regressor algorithm is shown in Figure 4.

Build a Random Forest Regression Algorithm

It prepares the data: It will randomly take n data points from the data set. This technique is called bootstrapping. It takes a sample from the data set without throwing it away but still leaves it in the original data until we divide enough n data sets; these n data sets may overlap. After enough n data, we randomly pick k attributes (k < n), new data, enough n data, and enough k attributes. For each data set with k attributes, it will build each decision tree submodel.

The decision tree construction process is based on randomness, so the results of the trees in the random forest algorithm are different.

RMSE is calculated using Formula (8), and the average percentage error is determined by Formula (9).

The result is the union of all the previously trained decision trees.

The random forest regressor model is written using Python code, as shown below:

• rfr = RandomForestRegressor(random_state=2301, n_estimators=100)
• rfr.fit(X_train, y_train)
• print(rfr.score(X_train, y_train))
• print(rfr.score(X_test, y_test))
• rfr_pred = rfr.predict(X_test)
• rfr_rmse = np.sqrt(mean_squared_error(y_test, rfr_pred))
• print(rfr_rmse)

4.3. Decision Tree Regressor

A decision tree regressor is a supervised learning algorithm, and it can be used in two problems: classification and regression. Building an algorithm based on a given training data set is about determining the questions and their order. A unique feature is that the algorithm can work with unordered discrete categorical variables. Decision trees also work with data with feature vectors that include absolute and numeric attributes. The data also do not need to be normalized regarding training.

In the decision tree regression problem, this algorithm can perform two regression or classification tasks.

The decision tree algorithm works like this:

−

Step 1: Create an empty binary tree;

−

Step 2: Select features to split;

−

Step 3: If there are no more questions, make a prediction;

−

Step 4: Recursion from Step 2.

There are two problems to solve in this algorithm: (1) feature selection and (2) when to stop recursion.

(1)

Feature selection: To solve this problem, we calculate the MSE cost (mixedness). We will rely on this MSE cost to choose the feature accordingly. It will calculate from the root node and then calculate the intermediate nodes; if the error cost of that split feature is the smallest, then choose that feature.

(2)

Stop the recursion: The max depth parameter is in this task tree when the request limit is reached, or divide the tree so it cannot be divided anymore.

RMSE is calculated as Formula (8), and the average percentage error is determined by Formula (9).

The decision tree regressor model is written using Python code, as shown below:

• dtr = DecisionTreeRegressor(random_state=2301)
• dtr.fit(X_train, y_train)
• dtr.fit(X_train, y_train)
• print(dtr.score(X_train, y_train))
• print(dtr.score(X_test, y_test))
• dtr_pred = dtr.predict(X_test)
• dtr_rmse = np.sqrt(mean_squared_error(y_test, dtr_pred))
• print(dtr_rmse)

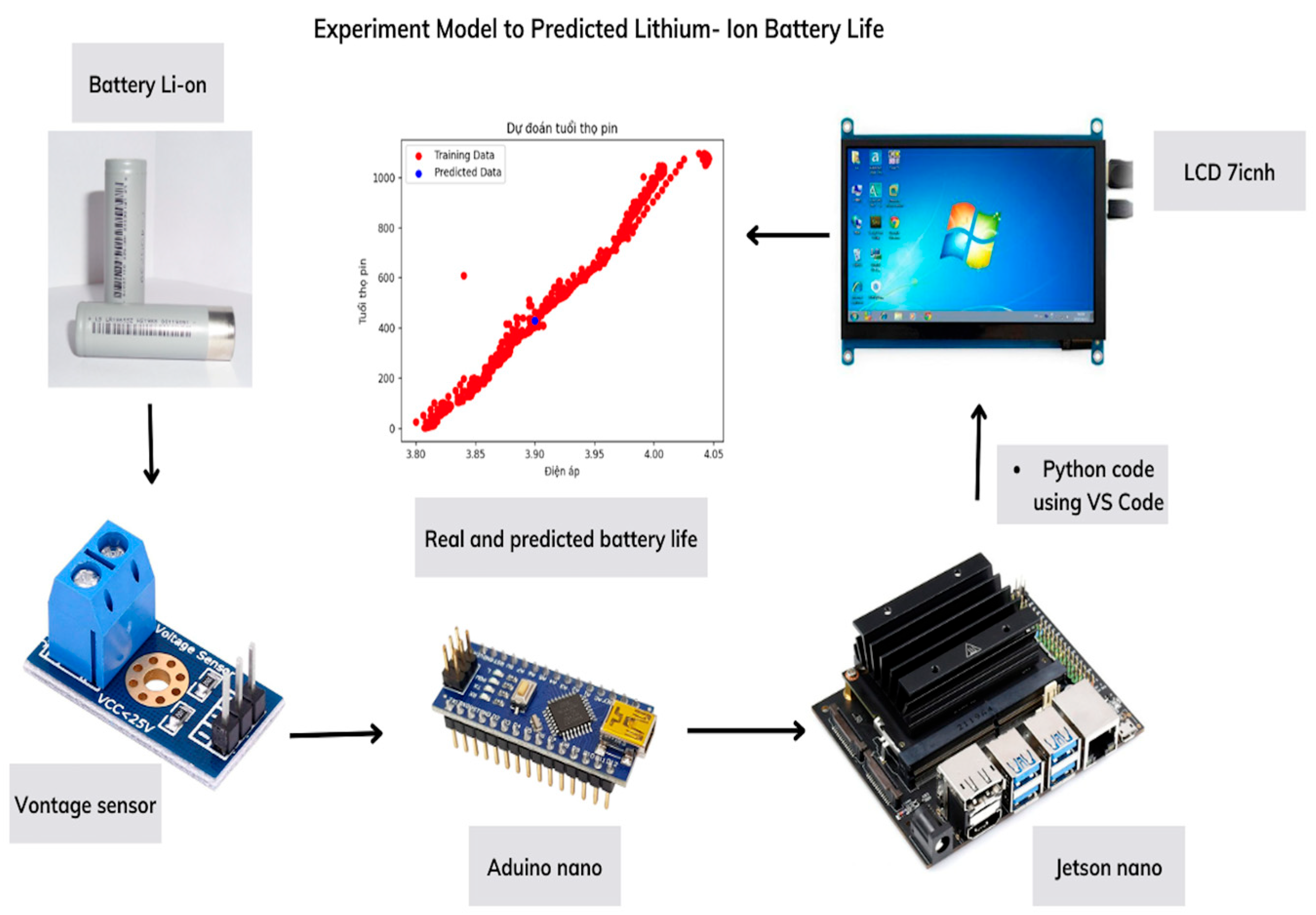
5. Experiment Results and Discussion

We built an experimental table as shown in Figure 5 and Figure 6. The parameters of the battery to estimate its life are as follows:

−

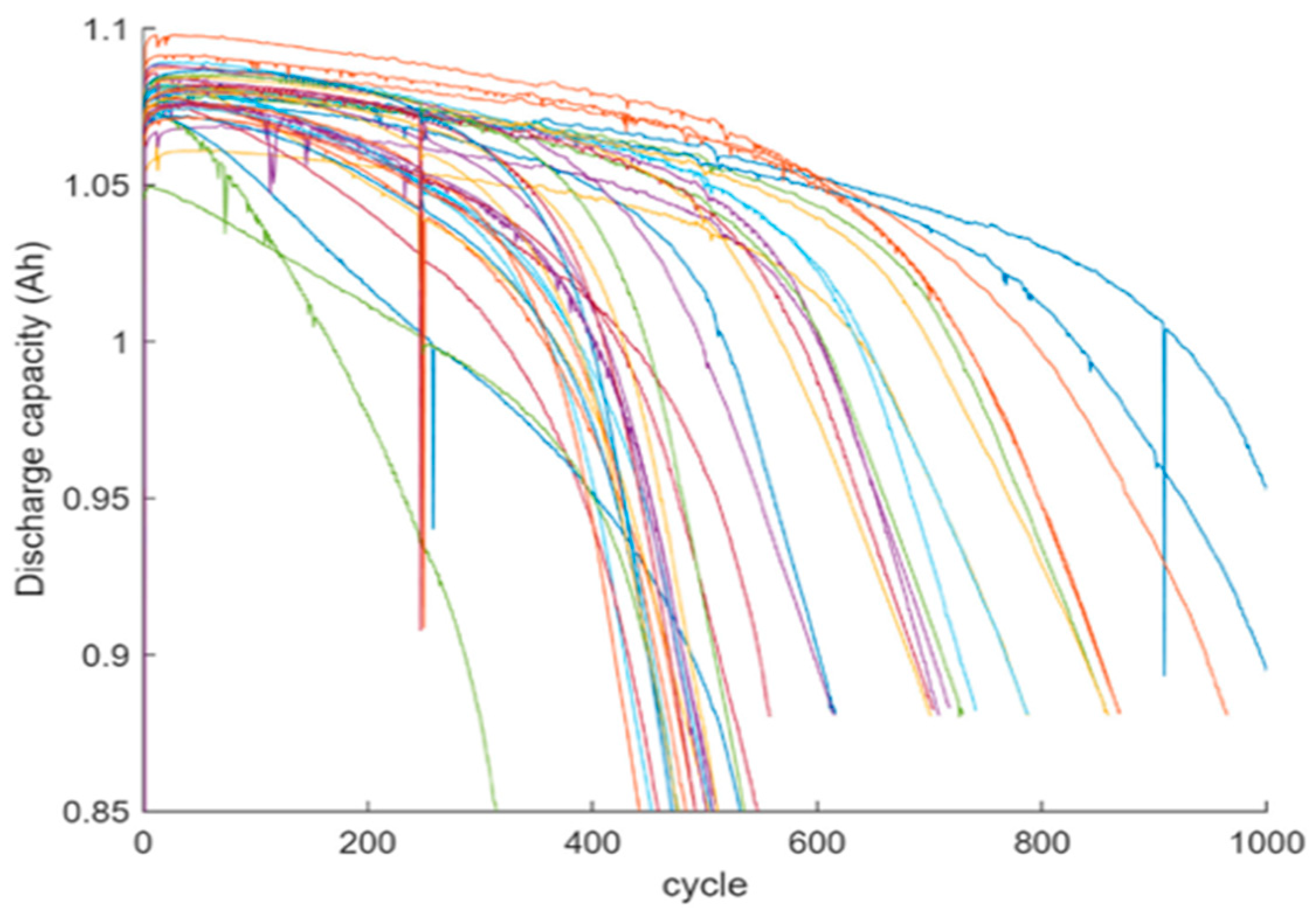
Cycle Index: number of cycles.

−

Decrement 3.8–4.05 V(s).

−

Max. Voltage Discharge (V): 4.05 V.

−

Min. Voltage Charge (V): 3.8 V.

−

Combo NVIDIA Jetson Nano Developer Kit B01: GPU: 128-core Maxwell, CPU: Quad-core ARM A57 @ 1.43 GHz, Memory 4 GB 64 bits LPDDR4 25,6 GB/s.

Time constant current (s): After being tested, the model could accurately calculate the battery’s voltage in one hour. This data could be further extrapolated to estimate the entire life cycle. Power management can become more approachable and effective by adding machine learning to clever battery technology.

The parameters of the battery are: Maximum discharge voltage (V) of 4.05 V and minimum charging voltage (V) of 3.8 V. The experimental scenario was conducted in three cases below, comparing two predictive models: linear regression and bagging regression.

−

Case 1: Predict lithium-ion battery capacity when the maximum voltage is equal to 4 V (when the battery is working without load).

−

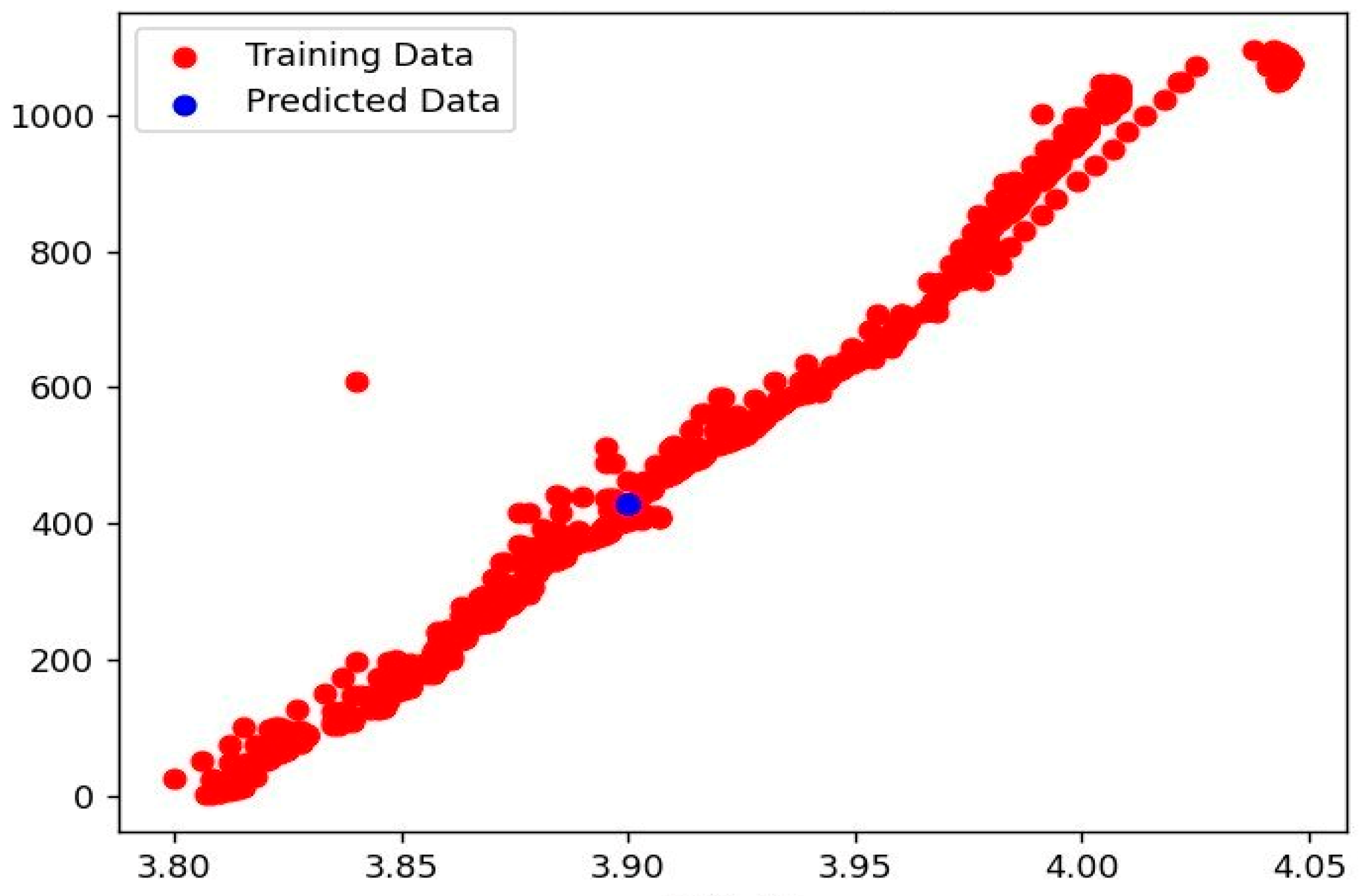
Case 2: Predict lithium-ion battery capacity at the time of maximum voltage equal to 3.9 V (batteries power a DC motor with parameters: No-load current at 12 V and 0.92 A, no-load speed at 1200 rpm, no-load current at 24 V and 1.46 A, and no-load speed at 2000 rpm. It is recommended to use a 12 V, 10 A source for a stable motor).

−

Case 3: Forecast of Li-ion battery capacity at the time of maximum voltage equal to 3.8 V (No-load current at 12 V and 0.92 A, no-load speed at 1200 rpm, no-load current at 24 V and 1.46 A, and no-load speed at 2000 rpm. It is recommended to use a 12 V, 10 A source for a stable motor).

The experimental results for the linear regression model, random forest regressor model, and decision tree regressor model are shown in Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15.

(a)

The experimental results of linear regression model.

Figure 7. Prediction of lithium-ion battery capacity at the maximum voltage equal to 4 V.

Figure 7. Prediction of lithium-ion battery capacity at the maximum voltage equal to 4 V.

Figure 8. Prediction of lithium-ion battery capacity at the maximum voltage equal to 3.9 V.

Figure 8. Prediction of lithium-ion battery capacity at the maximum voltage equal to 3.9 V.

Figure 9. Prediction of lithium-ion battery capacity at the maximum voltage equal to 3.8 V.

Figure 9. Prediction of lithium-ion battery capacity at the maximum voltage equal to 3.8 V.

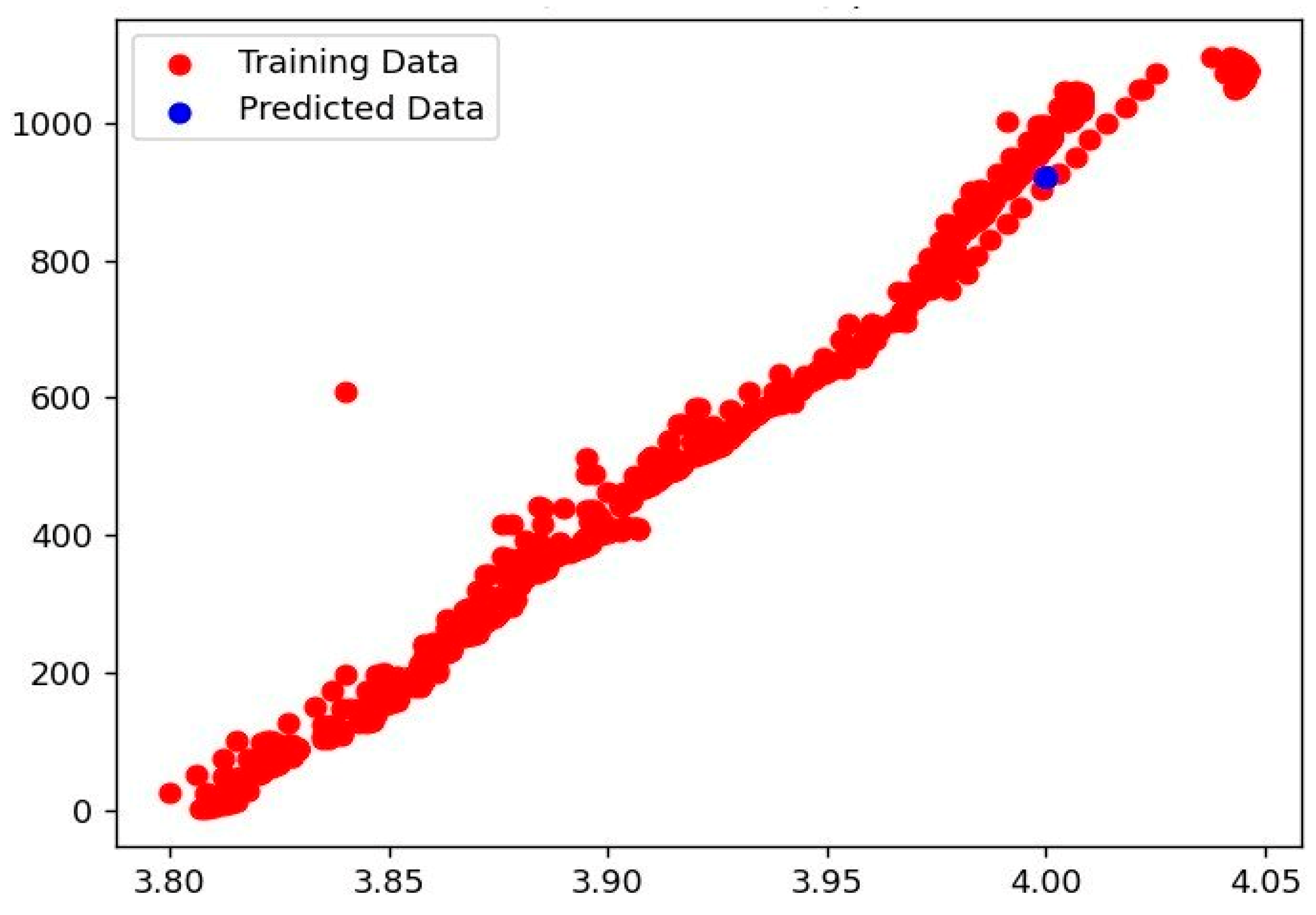
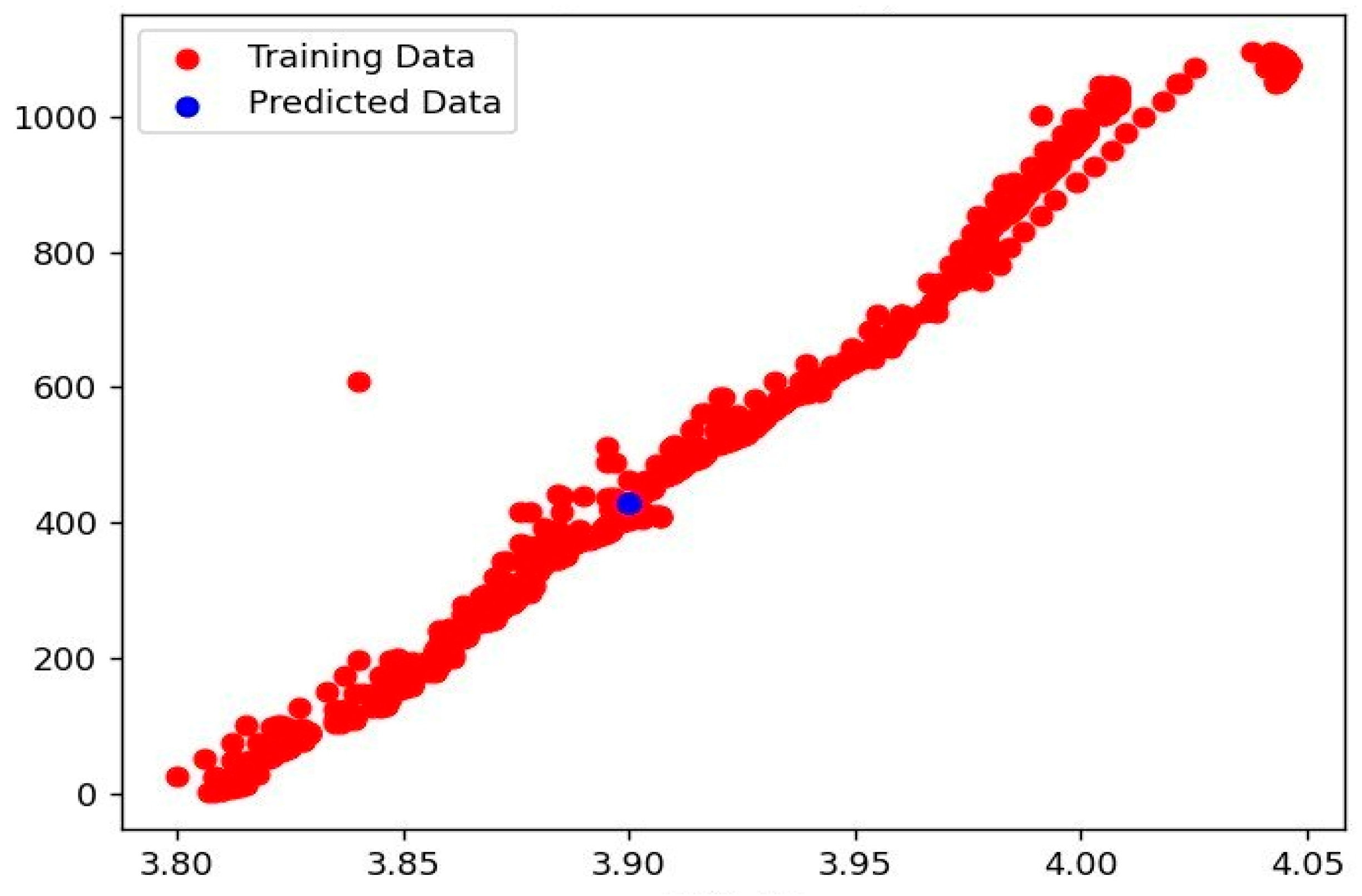
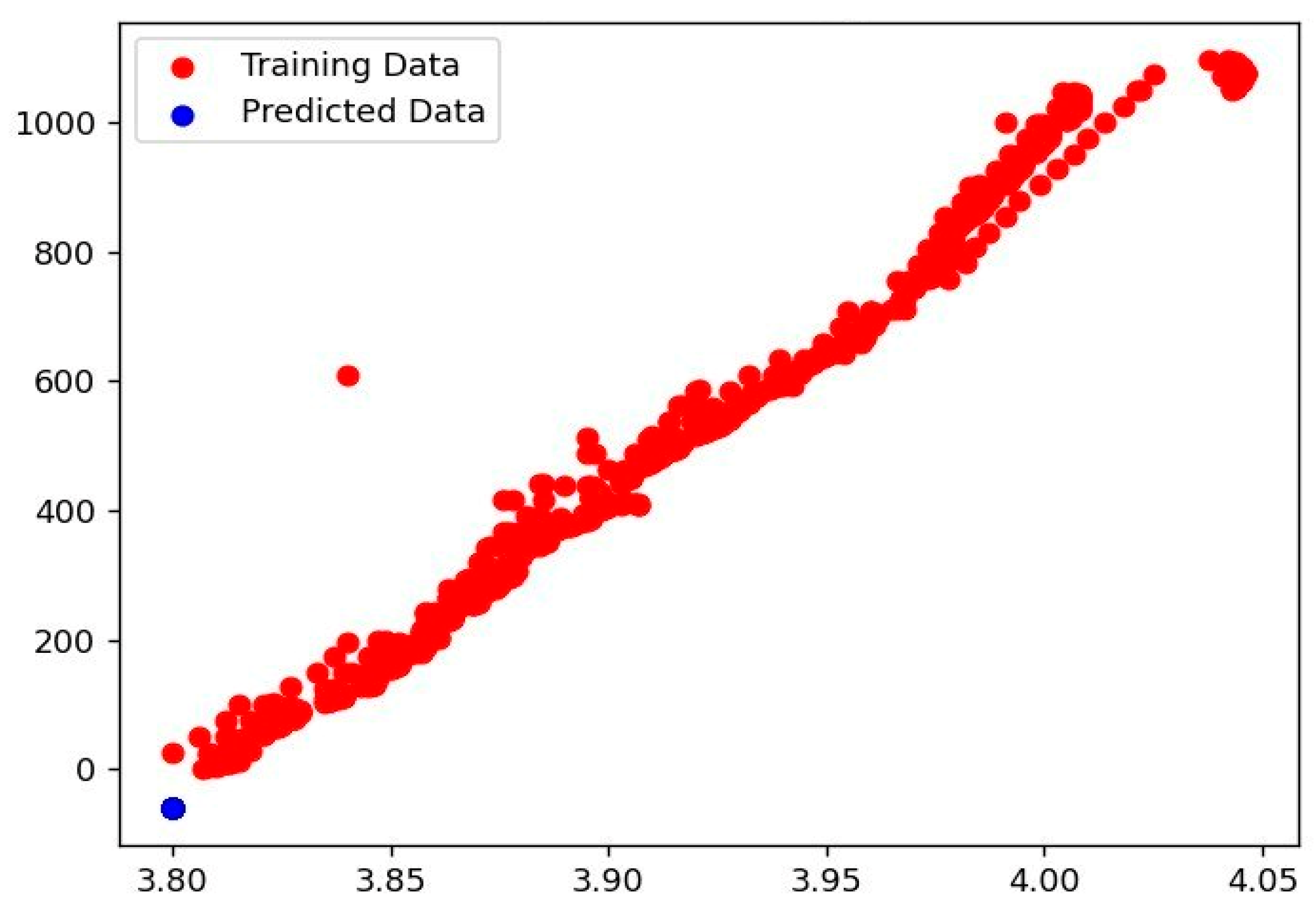
(b)

The experimental results of random forest regressor

Figure 10. Prediction of lithium-ion battery capacity at the maximum voltage equal to 4 V.

Figure 10. Prediction of lithium-ion battery capacity at the maximum voltage equal to 4 V.

Figure 11. Prediction of lithium-ion battery capacity at the maximum voltage equal to 3.8 V.

Figure 11. Prediction of lithium-ion battery capacity at the maximum voltage equal to 3.8 V.

Figure 12. Prediction of lithium-ion battery capacity at the maximum voltage equal to 3.8 V.

Figure 12. Prediction of lithium-ion battery capacity at the maximum voltage equal to 3.8 V.

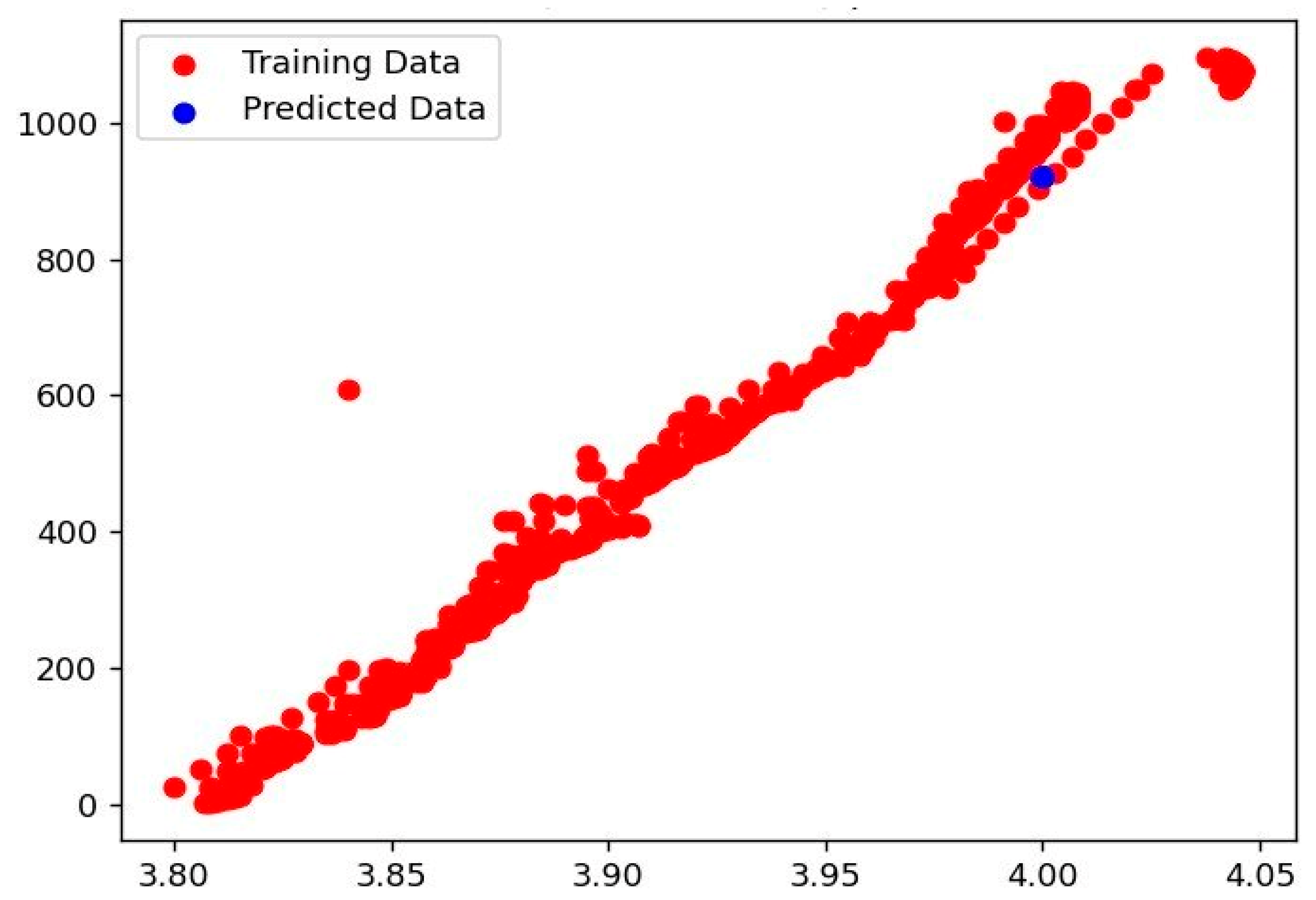
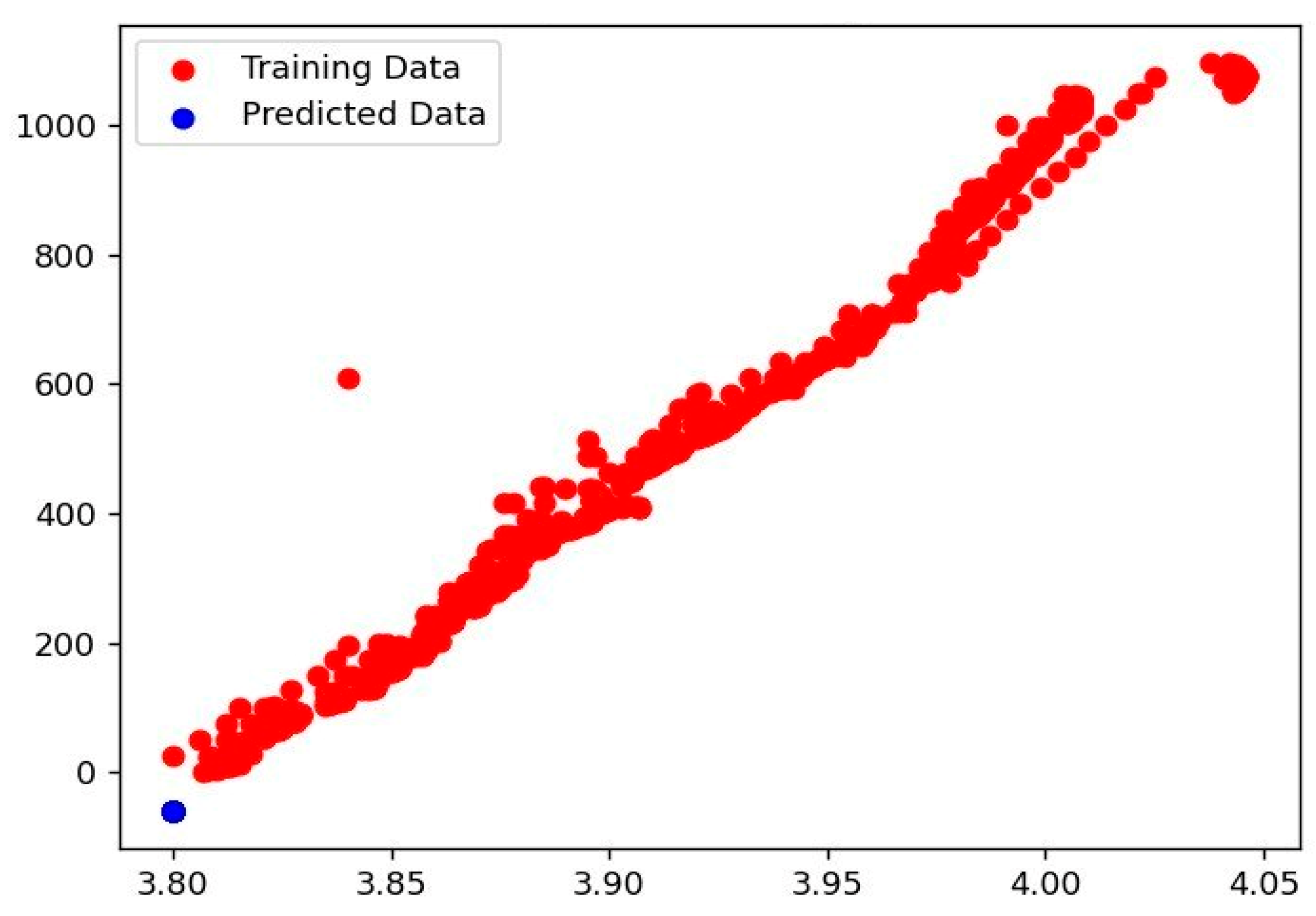
(c)

The experimental results for decision tree regressor model.

Figure 13. Prediction of lithium-ion battery capacity at the maximum voltage equal to 4 V.

Figure 13. Prediction of lithium-ion battery capacity at the maximum voltage equal to 4 V.

Figure 14. Prediction of lithium-ion battery capacity at the maximum voltage equal to 3.8 V.

Figure 14. Prediction of lithium-ion battery capacity at the maximum voltage equal to 3.8 V.

Figure 15. Prediction of lithium-ion battery capacity at the maximum voltage equal to 3.8 V.

Figure 15. Prediction of lithium-ion battery capacity at the maximum voltage equal to 3.8 V.

The MSE and RMSE results of three regression models are shown in

Table 1. The MSE and RMSE results of three regression models.

Regression Model	MSE	RMSE
Linear Regression	22,060.500669	148.527777
Random Forest Regressor	516.332762	22.722957
Decision Tree Regressor	1337.112429	36.566548

.

Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15 show that the experimental results in the two empirical cases for the three regressor models have similar results. This means every training point in the above graph is close to the diagonal. Therefore, the trained model resembles linear regression theory. According to the training model, the higher the rated voltage, the better the battery life. For example, the life of a battery is 1000 discharge cycles at 4 V. Meanwhile, the battery life is 500 discharge cycles at 3.9 V. However, considering the accuracy of the model, it was found that the random forest regressor model has evaluated the model’s accuracy based on the average of the square of the difference between the initial value and the predicted value in the data set (MSE—mean square error), which is smaller than the linear regression and decision tree regressor models (516.332762). The linear regression model with MSE is the biggest (22060.500669). This result allows the random forest regressor model to remain helpful for the life prediction of lithium-ion batteries.

6. Conclusions

This paper proposes a battery life prediction using a linear regression model, a random forest regressor model, and a decision tree regressor model with features designed based on a lithium-ion battery’s voltage. The prediction results show high accuracy for lithium-ion batteries under different battery capacity conditions. All parts can be achieved in one discharge cycle. This advantage allows for an accurate lifecycle prediction model without historical data, making it more practical in real-world applications. The computation time is reasonable to achieve real-time prediction results. This approach is well suited when lithium-ion batteries serve as energy storage or backup devices, such as in data centers and grid-level energy storage. For the proposed solution to improve predictive performance more accurately and reliably in the future, the research team will compare many machine learning or deep learning models to predict the battery’s remaining capacity. At the same time, the lithium-ion battery life prediction model combines more designed features based on the lithium-ion battery’s voltage, current, temperature, and discharge time.