Machine Learning-Based Shoveling Trajectory Optimization of Wheel Loader for Fuel Consumption Reduction
Abstract
1. Introduction
2. Shoveling Experiments and Analysis
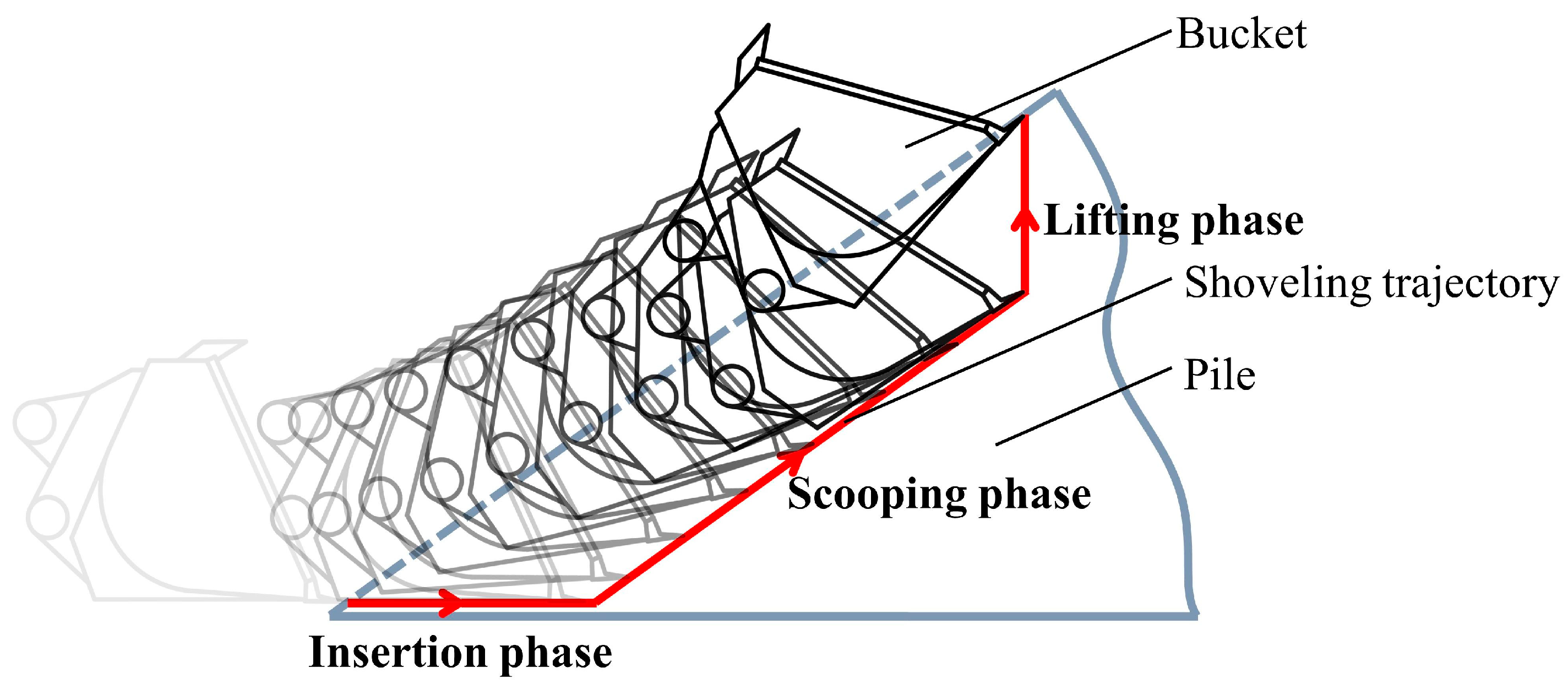
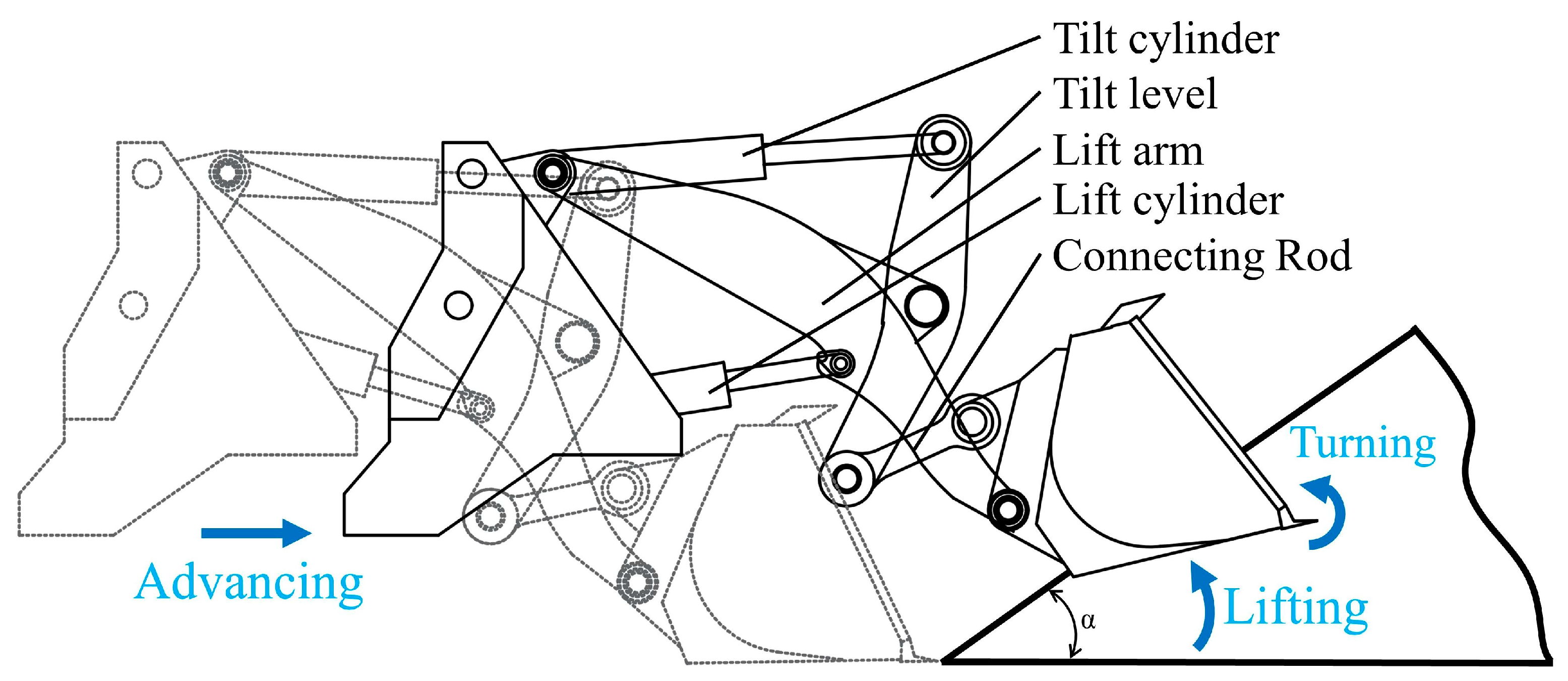
2.1. Shoveling Principle and Experiment Design
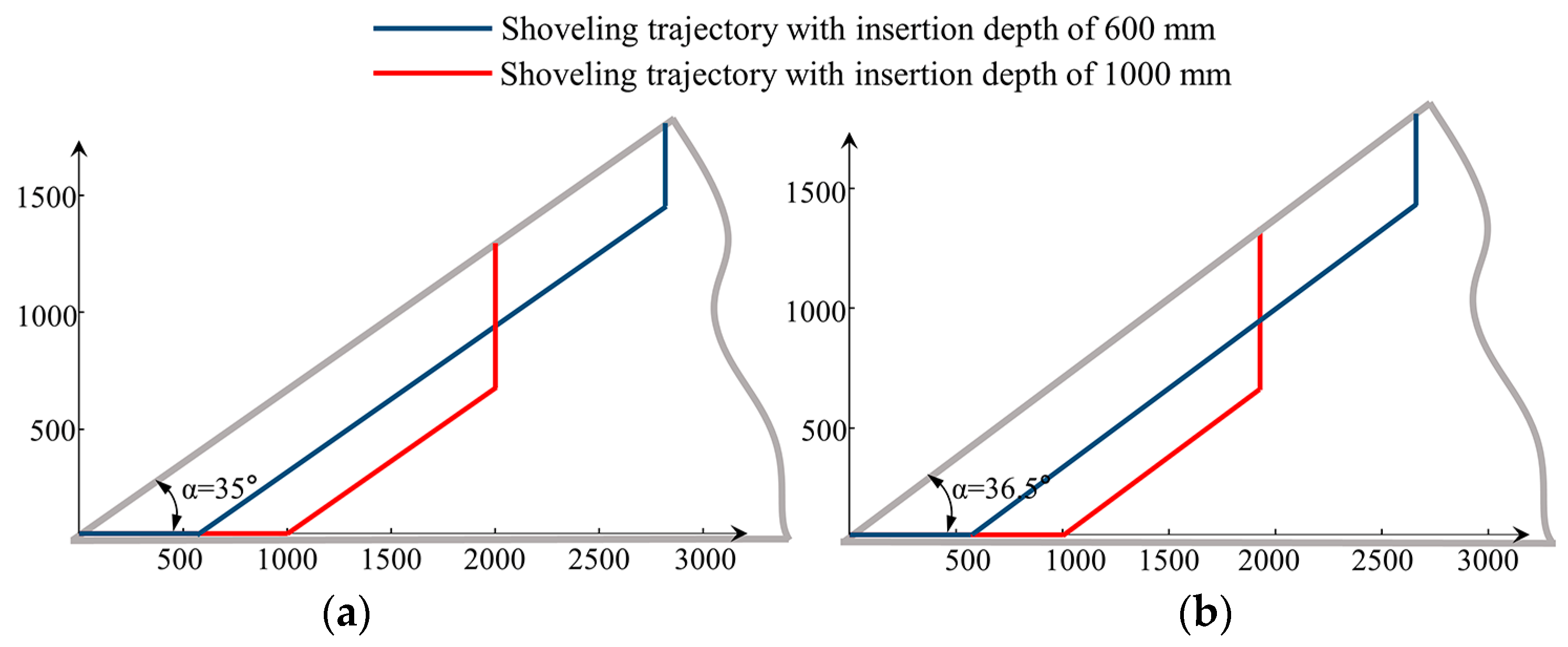
2.2. Trajectory Planning
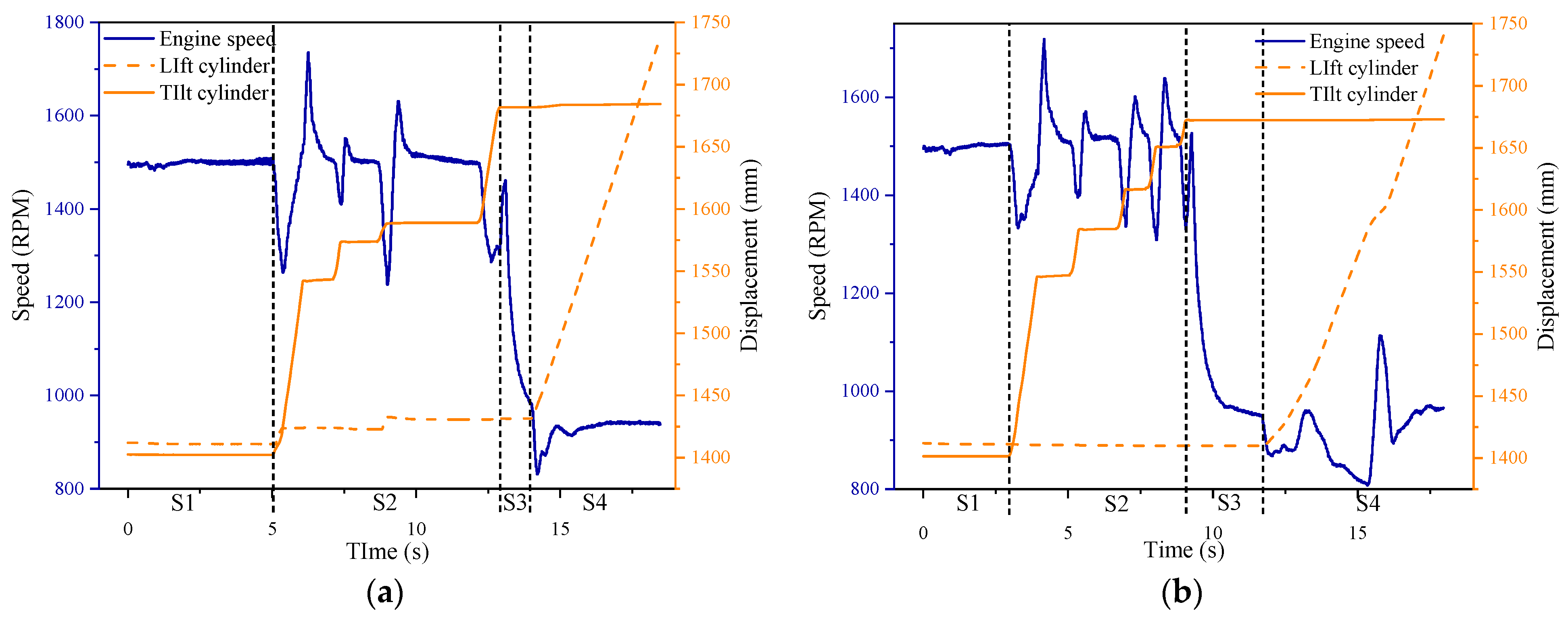
2.3. Engine Speed Analysis
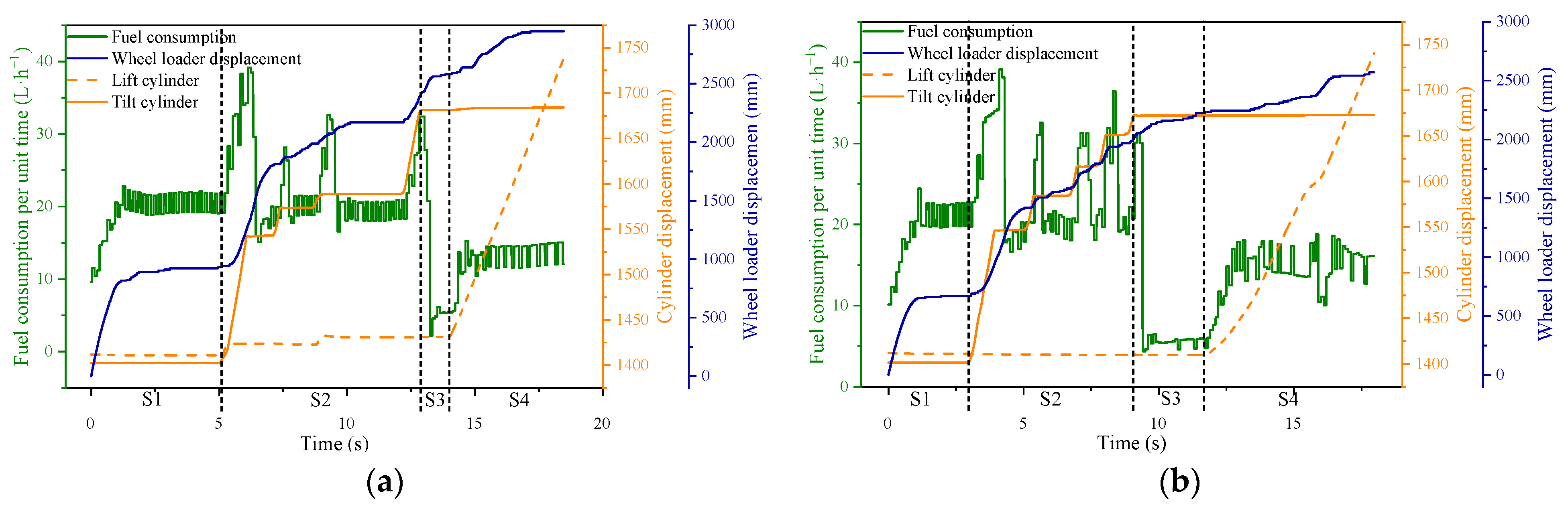
- Insertion phase: There is no change in the displacement of the lift cylinder and the displacement of the tilt cylinder. The engine speed is maintained at 1500 RPM, but a smaller oscillation will occur. This oscillation is more violent at the beginning of the insertion phase. However, as the insertion depth increases, it gradually calms down and stays at 1500 RPM.
- Scooping phase: The displacement of the tilt cylinder increases rapidly, and the displacement of the lift cylinder steps up. With the increasing displacement of the cylinder, there is a large change in engine speed. When the displacement of the cylinder starts to increase, the engine speed decreases at first, then increases rapidly and is higher than 1500 RPM. When the displacement of the cylinder is stable, the engine speed also falls back to 1500 RPM rapidly.
- Stopping phase: The displacement of the tilt cylinder and lift cylinder has no change, and the engine speed decreases to a lower state in a short time.
- Lifting phase: The displacement of the lift cylinder increases rapidly, and the displacement of the tilt cylinder is almost unchanged. The engine speed decreases to the lowest point in the whole shoveling process in a short period and then increases.
2.4. Fuel Consumption Analysis
- Insertion phase: The wheel loader is inserted into the pile at a certain distance with traction. In the early insertion phase, the insertion speed of the wheel loader is fast. However, as the insertion depth increases, the resistance to the bucket also increases rapidly, and the wheel loader insertion speed gradually decreases. Meanwhile, the fuel consumption per unit of time rises rapidly after the insertion of the pile and then remains in a relatively stable state.
- Scooping phase: The wheel loader continues to keep moving forward. In the early scooping phase, the wheel loader can move forward rapidly because the material is scooped up by the bucket to provide space for the wheel loader to move forward. In the later scooping phase, the wheel loader advances at a slower speed due to resistance. It is obvious that when the lift cylinder and tilt cylinder remain unchanged, the fuel consumption per unit time remains at a relatively stable level. The fuel consumption per unit time increases rapidly when the displacement of the lift cylinder and tilt cylinder increases and then is in a stable state.
- Stopping phase: The resistance of the wheel loader increases sharply, and the wheel loader is forced to stop moving forward. However, to prevent the wheel loader from moving backward, the wheel loader will continue to keep moving ahead and move forward for a short distance. The fuel consumption per unit time is then reduced to the lowest state during the entire shoveling operation.
- Lifting phase: The wheel loader is subjected to inertia in the process of lifting the bucket and continues to keep moving forward. And the fuel consumption per unit time increases with the displacement of the lift cylinder and then remains stable.
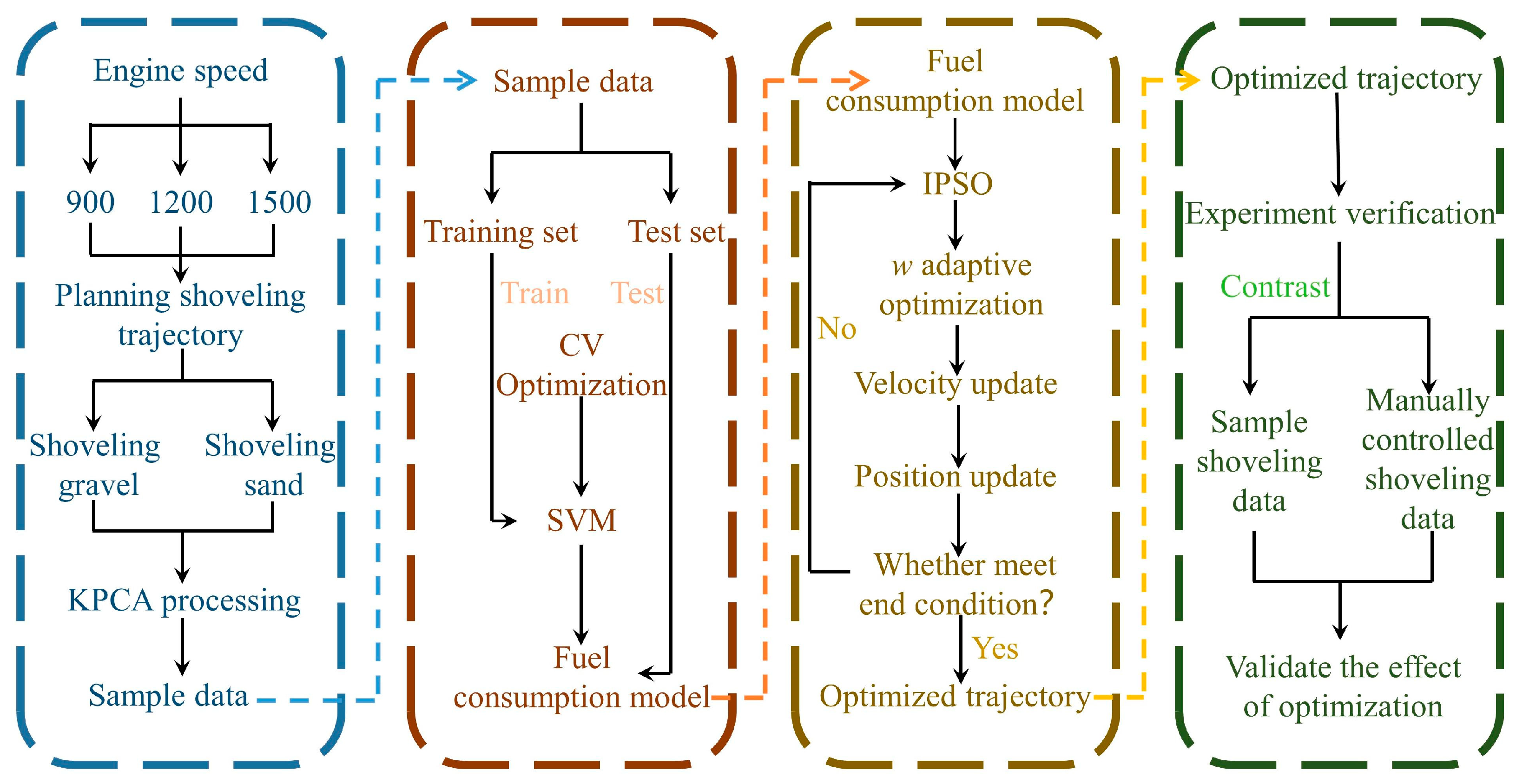
3. Research Methodology
3.1. KPCA and GRA
- Select the parent sequence Y and the subsequence X.
- To eliminate the influence of the magnitude, the parent sequence and the subsequence are normalized, and the normalized parent sequence is recorded as Y′ and the subsequence is recorded as X′.
- The formula is shown in Equation (9) to calculate the grey relation coefficient.where ρ is the discriminant coefficient, which takes values from 0 to 1 and is taken as 0.5 in this paper.
3.2. SVM
| Algorithm 1 K-fold Cross Validation |
| 1: begin |
| 2: bestaccuracy; cbest; gbest; |
| 3: for c = cmin2:cmax2 |
| 4: for g = gmin2:gmax2 |
| 5: divide the dataset equally into K groups; |
| 6: for = 1:K |
| 7: divide the dataset equally into K groups; |
| 8: train(K) as the test set, the rest as the training set; |
| 9: record the accuracy of the test set ace(K); |
| 10: end; |
| 11: cv = (ace(1) + ace(2) + ⋯ + ace(K))/K; |
| 12: if cv > bestaccuracy |
| 13: bestaccuracy = cv; cbest = c; gbest = g; |
| 14: end; |
| 15: end; |
| 16: end; |
| 17: end. |
3.3. IPSO
4. SVM Fuel Consumption Model and IPSO Optimization
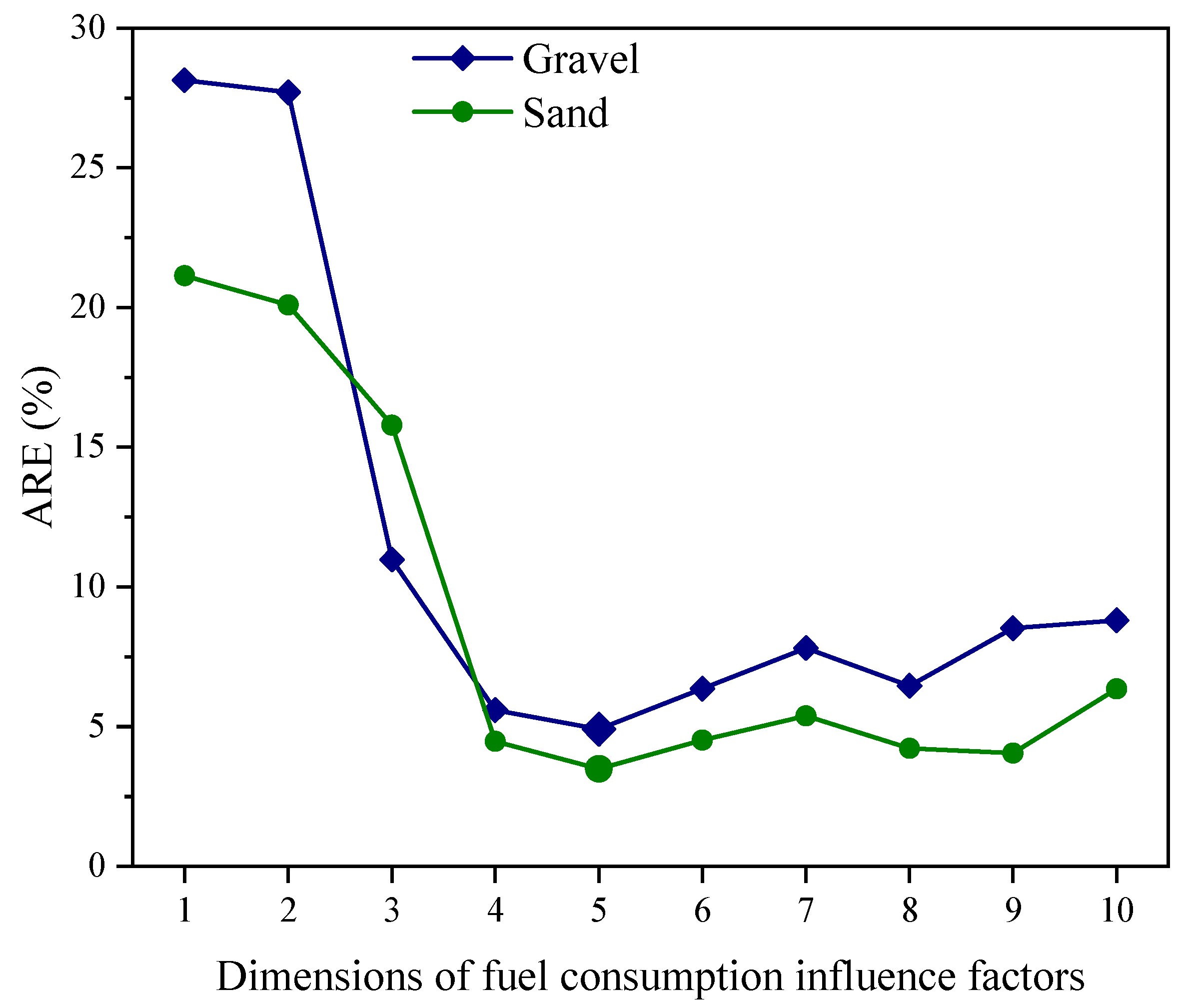
4.1. KPCA Processing and GRA Verification
4.2. SVM Model
4.3. IPSO Optimization Process
5. Validation Experiment and Discussion
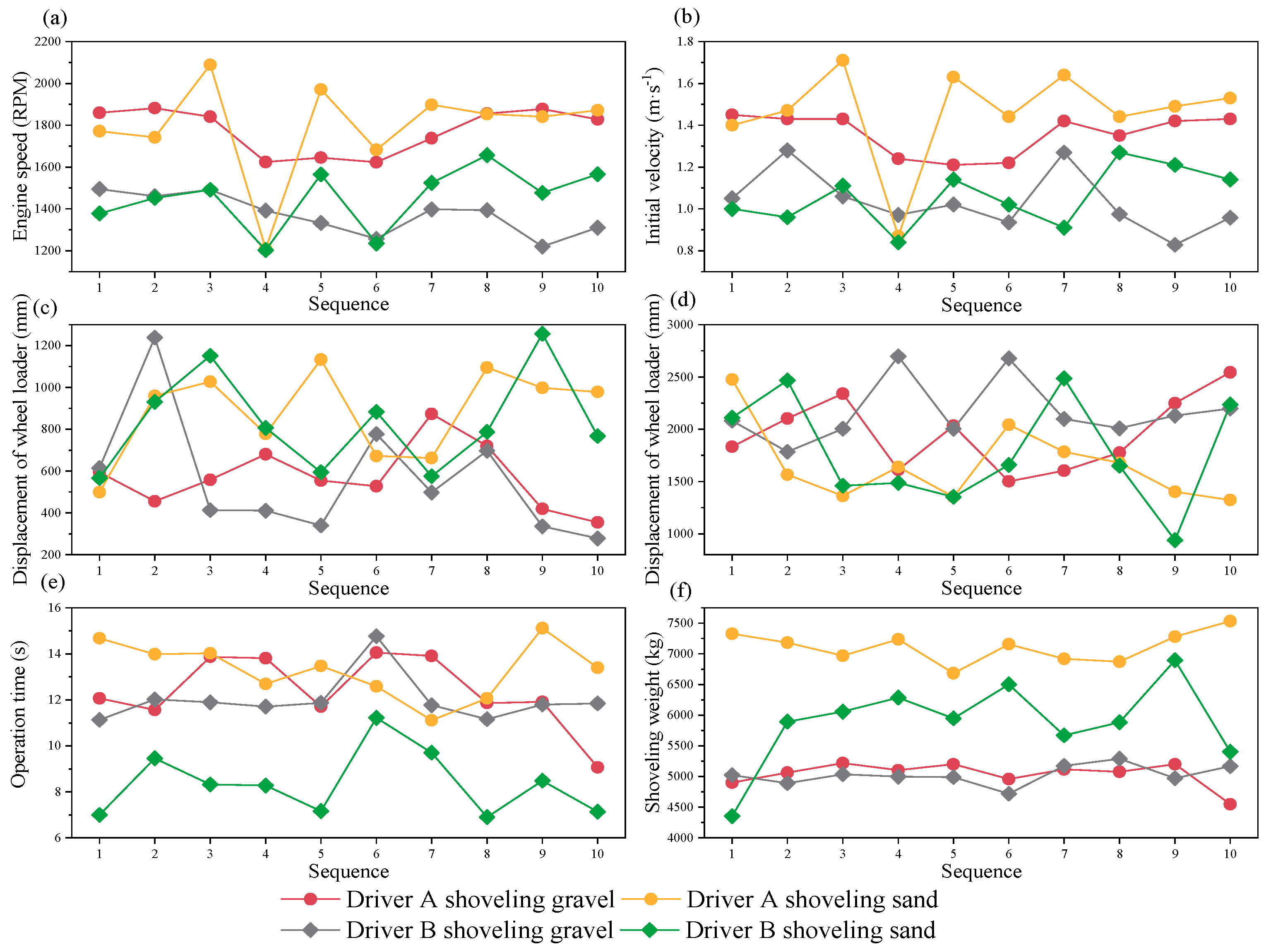
5.1. Validation Experiment
5.2. Discussion
6. Conclusions
- In this study, the factors with a strong influence on the fuel consumption of shoveling operations are screened by experimental analysis and KPCA. The factors with a strong influence are initial velocity, the wheel loader displacement in the insertion phase, the shoveling weight, the operation time, and the wheel loader displacement in the scooping phase. KPCA results show that the cumulative contribution rate of the above five factors can reach 90%. Meanwhile, the grey relation coefficients between key factors of fuel consumption influence and fuel consumption are all greater than 0.75. It proves that the screening of key factors of fuel consumption influenced by KPCA is effective.
- In this study, the fuel consumption model is established by SVM, and the penalty factor and kernel function parameters in SVM are optimized by CV. The SVM fuel consumption model has high stability and generalization ability, and the deviation between the predicted and true values of the model is small. In the gravel samples, its ARE is 4.91%, RMSE is 5.91, and R2 is 0.9764. While in the sand samples, the ARE is 3.49%, RMSE is 3.08, and R2 is 0.9494. The deviation between the true values and the predicted values from the SVM fuel consumption model is small.
- In this study, the optimized shoveling trajectories are obtained by IPSO for shoveling gravel and shoveling sand at three engine speeds. Validation experiments are conducted based on the optimized trajectory and compared with the sample data fuel consumption and manually controlled shoveling fuel consumption. The results show that the optimized trajectory can significantly reduce the fuel consumption of shoveling operations. For shoveling gravel, the average fuel consumption of the validation experiment is reduced by 60.93%, 45.79%, and 49.10%, respectively, compared with the sample average fuel consumption with three engine speeds. For shoveling sand, the average fuel consumption in the validation experiment is reduced by 30.93%, 35.56%, and 28.59%, respectively, compared with the sample average fuel consumption with three engine speeds. Compared with manually controlled shoveling gravel and sand, fuel consumption can be reduced by 27.66% and 24.34%, respectively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, G.J.; Xiao, C.Y. Dynamic simulation analysis on loader’s working device. Aust. J. Mech. Eng. 2018, 16, 2–8. [Google Scholar]
- Xu, J.; Yoon, H.S. A review on mechanical and hydraulic system modeling of excavator manipulator system. J. Constr. Eng. 2016, 2016, 9409370. [Google Scholar] [CrossRef]
- Koizumi, T.; Tsujiuchi, N.; Yoshida, T.; Andou, H. Evaluation process of digging performance for hydraulic excavator by bucket tip trace. J. Syst. Des. Dyn. 2011, 5, 1005–1016. [Google Scholar] [CrossRef]
- Wang, X.; Sun, W.; Li, E.; Song, X. Energy-minimum optimization of the intelligent excavating process for large cable shovel through trajectory planning. Struct. Multidisc. Optim. 2018, 58, 2219–2237. [Google Scholar] [CrossRef]
- Sarata, S.; Koyachi, N.; Sugawara, K. Field test of autonomous loading operation by wheel loader. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–28 September 2008. [Google Scholar]
- Hong, Q.G.; Chen, Y.H.; Huai, Z.P. Experimental Study on Automatic Shovel Loading of Loader. Coal Mine. Mach. 2021, 42, 195–197. [Google Scholar]
- Xu, L.C.; Ge, R.H. Optimization design of shovel depth when loader shovelling original raw soil. TELKOMNIKA Indones. J. Electr. Eng. 2013, 11, 4639–4645. [Google Scholar]
- Gong, J.; Cui, Y.X. Track planning for a wheel Loader in a digging. J. Mech. Eng. 2009, 45, 29–34. [Google Scholar] [CrossRef]
- Zhang, H.; Cao, S.J.; Kazuhiko, S. Test Investigation on Autonomous Scooping Control Strategy of Wheel Loader. Appl. Mech. Mater. 2010, 42, 156–159. [Google Scholar] [CrossRef]
- Filla, R.; Frank, B. Towards finding the optimal bucket filling strategy through simulation. In Proceedings of the 15th Scandinavian International Conference on Fluid Power, Linköping, Sweden, 7–9 June 2017. [Google Scholar]
- Meng, Y.; Fang, H.Z.; Liang, G.D.; Gu, Q.; Liu, L. Bucket trajectory optimization under the automatic scooping of LHD. Energies 2019, 12, 3919. [Google Scholar] [CrossRef]
- Yu, X.J.; Huai, Y.H.; Li, X.F.; Wang, D.W.; Yu, A. Shoveling trajectory planning method for wheel loader based on kriging and particle swarm optimization. J. Jilin Univ. (Eng. Technol. Ed.) 2020, 50, 437–444. [Google Scholar]
- Osumi, H.; Uehara, T.; Okada, N. Efficient scooping of rocks by autonomous controlled wheel loader. J. Rob. Mechatron. 2012, 24, 924–932. [Google Scholar] [CrossRef]
- Zhang, T.; Fu, T.; Song, X. Multi-objective excavation trajectory optimization for unmanned electric shovels based on pseudospectral method. Autom. Constr. 2022, 136, 104176. [Google Scholar] [CrossRef]
- Shen, W.; Jiang, J.; Su, X.; Reza Karimi, H. Control strategy analysis of the hydraulic hybrid excavator. J. Frankl. Inst. Eng. Appl. Math. 2015, 352, 541–561. [Google Scholar] [CrossRef]
- Frank, B.; Kleinert, J.; Filla, R. Optimal control of wheel loader actuators in gravel applications. Autom. Construct. 2018, 91, 1–14. [Google Scholar] [CrossRef]
- Yao, J.; Edson, C.P.; Yu, S. Bucket Loading Trajectory Optimization for the Automated Wheel Loader. IEEE Trans. Veh. Technol. 2023, 72, 6948–6958. [Google Scholar] [CrossRef]
- Liang, G.; Liu, L.; Meng, Y. Dynamic Modeling and Analysis of Loader Working Mechanism Considering Cooperative Motion with the Vehicle Body. Machines 2022, 11, 9. [Google Scholar] [CrossRef]
- Brinkschulte, L.; Hafner, J.; Geimer, M. Real-time load determination of wheel loader components. ATZheavy Duty Worldw. 2019, 12, 62–68. [Google Scholar] [CrossRef]
- Wang, S.; Yin, Y.; Wu, Y.; Hou, L. Modeling and Verification of an Acquisition Strategy for Wheel Loader’s Working Trajectories and Resistance. Sensors 2022, 22, 5993. [Google Scholar] [CrossRef] [PubMed]
- Trani, M.L.; Bossi, B.; Gangolells, M.; Casals, M. Predicting fuel energy consumption during earthworks. J. Clean. Prod. 2016, 112, 3798–3809. [Google Scholar] [CrossRef]
- Ma, W.X.; Zhang, Y.B.; Liu, C.B.; Wang, S.L. Prediction method of the fuel consumption of wheel loaders in the V-type loading cycle. Math. Prob. Eng. 2015, 2015, 538176. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Shi, G.; Zheng, T. Research on the Trajectory and Operational Performance of Wheel Loader Automatic Shoveling. Appl. Sci. 2022, 12, 12919. [Google Scholar] [CrossRef]
- Dindarloo, S.R.; Siami-Irdemoosa, E. Determinants of fuel consumption in mining trucks. Energy 2016, 112, 232–240. [Google Scholar] [CrossRef]
- Siami-Irdemoosa, E.; Dindarloo, S.R. Prediction of fuel consumption of mining dump trucks: A neural networks approach. Appl. Energy 2015, 151, 77–84. [Google Scholar] [CrossRef]
- Alamdari, S.; Basiri, M.H.; Mousavi, A.; Soofastaei, A. Application of machine learning techniques to predict haul truck fuel consumption in open-pit mines. J. Min. Environ. 2022, 13, 69–85. [Google Scholar]
- Gong, J.; Shang, J.; Li, L.; Zhang, C.; He, J.; Ma, J. A Comparative Study on Fuel Consumption Prediction Methods of Heavy-Duty Diesel Trucks Considering 21 Influencing Factors. Energies 2021, 14, 8106. [Google Scholar] [CrossRef]
- Shen, Y.C.; Song, H.; Li, G.Q.; Cherouat, A. Analysis and Prediction of Excavator Energy Consumption Based on Improved PSO-BP Neural Network. In Proceedings of the 12th International Workshop of Advanced Manufacturing and Automation, Xiamen, China, 11–12 October 2012. [Google Scholar]
- Liu, Y.H.; Zhang, Z.D.; Cai, Z.G. Research on the prediction of working fuel consumption for wheel loader based on BP neural network. Constr. Mach. 2018, 503, 81–83. [Google Scholar]
- Zhao, Y.; Zhou, M.; Wang, L. Bearing Fault Diagnosis of Single-Channel Data by a 3D DCN with Bilinear LBP and Modified KPCA. J. Electr. Eng. Technol. 2023. [Google Scholar] [CrossRef]
- Wang, Y.C.; Yang, S.J.; Guo, Q.P.; Yin, Y. Prediction of Blasting Muckpile Morphology in Throw Blasting of Coal Mine Based on MPA-SVM. Explos. Mater. 2023, 52, 58–64. [Google Scholar]
- Yuasa, T.; Ishikawa, M.; Ogawa, S. An Optimal Design Methodology for the Trajectory of Hydraulic Excavators Based on Genetic Algorithm. J. Rob. Mechatron. 2021, 33, 1248–1254. [Google Scholar] [CrossRef]
- Bi, Q.; Wang, G.; Wang, Y.; Yao, Z.; Hall, R. Digging Trajectory Optimization for Cable Shovel Robotic Excavation Based on a Multi-Objective Genetic Algorithm. Energies 2020, 13, 3118. [Google Scholar] [CrossRef]
- Zhao, X.; Jia, M. A new local-global deep neural network and its application in rotating machinery fault diagnosis. Neurocomputing 2019, 366, 215–233. [Google Scholar] [CrossRef]
- Lu, X.; Yang, C.; Wu, Q.; Wang, J.; Lu, Z.; Sun, S.; Liu, K.; Shao, D. Research on Analog Circuit Soft Fault Diagnosis Method Based on Mathematical Morphology Fractal Dimension. Electronics 2023, 12, 184. [Google Scholar] [CrossRef]
- Zhou, T.; Lu, H.L.; Wang, W.W.; Yong, X. GA-SVM based feature selection and parameter optimization in hospitalization expense modeling. Appl. Soft Comput. 2019, 75, 323–332. [Google Scholar]
- Patange, A.D.; Pardeshi, S.S.; Jegadeeshwaran, R. Augmentation of Decision Tree Model through Hyper-Parameters Tuning for Monitoring of Cutting Tool Faults Based on Vibration Signatures. J. Vib. Eng. Technol. 2022, 10, 1–19. [Google Scholar] [CrossRef]
- Bajaj, N.S.; Patange, A.D.; Jegadeeshwaran, R. Application of metaheuristic optimization based support vector machine for milling cutter health monitoring. Intell. Syst. Appl. 2023, 18, 200196. [Google Scholar] [CrossRef]
- Jain, M.; Saihjpal, V.; Singh, N.; Singh, S.B. An Overview of Variants and Advancements of PSO Algorithm. Appl. Sci. 2022, 12, 8392. [Google Scholar] [CrossRef]
- Han, D.; Yang, X.; Li, G. Highway traffic speed prediction in rainy environment based on APSO-GRU. J. Adv. Transp. 2021, 2021, 4060740. [Google Scholar] [CrossRef]
- Lin, J.; Sheng, G.; Yan, Y.; Dai, J.; Jiang, X. Prediction of Dissolved Gas Concentrations in Transformer Oil Based on the KPCA-FFOA-GRNN Model. Energies 2018, 11, 225. [Google Scholar] [CrossRef]
- Ahluwalia, R.K.; Wang, X.; Star, A.G. Performance and cost of fuel cells for off-road heavy-duty vehicles. Int. J. Hydrogen Energy 2022, 47, 10990–11006. [Google Scholar] [CrossRef]
- Cao, B.; Liu, X.; Chen, W. Intelligent energy-saving operation of wheel loader based on identifiable materials. J. Mech. Sci. Technol. 2020, 34, 1081–1090. [Google Scholar] [CrossRef]
- Li, J.; Chen, C.; Li, Y. Difficulty assessment of shoveling stacked materials based on the fusion of neural network and radar chart information. Autom. Constr. 2021, 132, 103966. [Google Scholar] [CrossRef]
- Fei, X.; Han, Y.; Wong, S.V. An Overview of and Prospects for Research on Energy Savings in Wheel Loaders. Automot. Exper. 2023, 6, 133–148. [Google Scholar] [CrossRef]
- Dong, Z.; Jiang, F.; Tan, Y.; Wang, F.; Ma, R.; Liu, J. Review of the Modeling Methods of Bucket Tooth Wear for Construction Machinery. Lubricants 2023, 11, 253. [Google Scholar] [CrossRef]
- Xiao, W.; Liu, M.; Chen, X. Research Status and Development Trend of Underground Intelligent Load-Haul-Dump Vehicle—A Comprehensive Review. Appl. Sci. 2022, 12, 9290. [Google Scholar] [CrossRef]
- Dadhich, S.; Bodin, U.; Andersson, U. Key Challenges in Automation of Earth-Moving Machines. Autom. Constr. 2016, 68, 212–222. [Google Scholar] [CrossRef]
- Azulay, O.; Shapiro, A. Wheel loader scooping controller using deep reinforcement learning. IEEE Access 2021, 9, 24145–24154. [Google Scholar] [CrossRef]
- Dadhich, S.; Sandin, F.; Bodin, U. Field test of neural-network based automatic bucket-filling algorithm for wheel-loaders. Autom. Constr. 2019, 97, 1–12. [Google Scholar] [CrossRef]
- Huang, J.; Kong, D.; Gao, G.; Cheng, X.; Chen, J. Data-Driven Reinforcement-Learning-Based Automatic Bucket-Filling for Wheel Loaders. Appl. Sci. 2021, 11, 9191. [Google Scholar] [CrossRef]






| Type of Pile | Density (kg/m3) | Angle of Repose (°) | Particle Diameter (mm) |
|---|---|---|---|
| Gravel | 2672 | 35.0 | 20–60 |
| Sand | 2392 | 36.5 | <1 |
| Type of Pile | Parameter | Insertion Phase | Scooping Phase | Stopping Phase | Lifting Phase | Total |
|---|---|---|---|---|---|---|
| Gravel | Fuel consumption (mL) | 27.12 | 49.27 | 4.10 | 15.61 | 96.10 |
| Percentage (%) | 28.22 | 51.27 | 4.27 | 16.24 | 100.00 | |
| Sand | Fuel consumption (mL) | 15.97 | 41.15 | 6.45 | 24.68 | 88.26 |
| Percentage (%) | 20.51 | 52.83 | 8.29 | 31.68 | 100.00 |
| Type of Pile | Engine Speed (RPM) | Number | Initial Velocity (m·s−1) | Displacement of Wheel Loader | Displacement of Tilt Cylinder in Scooping Phase (mm) | Displacement of Lift Cylinder | Operation Time (s) | Shoveling Weight (kg) | Fuel Consumption (mL) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Insertion Phase (mm) | Scooping Phase (mm) | Stopping Phase (mm) | Lifting Phase (mm) | Scooping Phase (mm) | Lifting Phase (mm) | ||||||||
| Gravel | 900 | 1 | 0.48 | 802 | 1431 | 259 | 182 | 27 | 301 | 281 | 13.62 | 4771 | 73.63 |
| 2 | 0.49 | 789 | 1536 | 105 | 39 | 20 | 307 | 265 | 13.31 | 5116 | 74.34 | ||
| 3 | 0.35 | 995 | 1061 | 134 | 125 | 21 | 304 | 277 | 19.04 | 4966 | 141.51 | ||
| … | … | … | … | … | … | … | … | … | … | … | … | ||
| 40 | 0.42 | 789 | 1563 | 134 | 202 | 26 | 303 | 279 | 18.58 | 4927 | 142.70 | ||
| 1200 | 1 | 0.81 | 749 | 1508 | 462 | 103 | 20 | 308 | 267 | 13.03 | 4609 | 62.54 | |
| 2 | 0.83 | 718 | 1738 | 105 | 125 | 28 | 300 | 282 | 12.64 | 4934 | 63.88 | ||
| 3 | 0.75 | 745 | 1699 | 77 | 163 | 25 | 302 | 270 | 14.99 | 5103 | 110.32 | ||
| … | … | … | … | … | … | … | … | … | … | … | … | ||
| 40 | 0.79 | 779 | 1431 | 249 | 144 | 32 | 296 | 251 | 15.79 | 4284 | 111.48 | ||
| 1500 | 1 | 1.17 | 806 | 1334 | 164 | 355 | 28 | 299 | 278 | 14.62 | 3894 | 73.49 | |
| 2 | 1.09 | 819 | 1392 | 240 | 67 | 20 | 309 | 258 | 11.73 | 4914 | 75.12 | ||
| 3 | 1.18 | 730 | 1724 | 202 | 422 | 28 | 299 | 278 | 15.96 | 3796 | 76.96 | ||
| … | … | … | … | … | … | … | … | … | … | … | … | ||
| 40 | 1.16 | 729 | 1669 | 173 | 345 | 28 | 298 | 279 | 16.57 | 3770 | 102.71 | ||
| Sand | 900 | 1 | 0.43 | 787 | 1521 | 307 | 173 | 71 | 263 | 270 | 11.22 | 5409 | 55.49 |
| 2 | 0.50 | 739 | 1651 | 183 | 230 | 93 | 241 | 260 | 13.55 | 5474 | 68.65 | ||
| 3 | 0.48 | 682 | 1787 | 39 | 537 | 89 | 244 | 225 | 17.72 | 6722 | 81.59 | ||
| … | … | … | … | … | … | … | … | … | … | … | … | ||
| 40 | 0.37 | 748 | 1632 | 173 | 250 | 90 | 243 | 271 | 15.87 | 6449 | 83.71 | ||
| 1200 | 1 | 0.86 | 707 | 1755 | 192 | 67 | 94 | 237 | 270 | 13.08 | 5864 | 62.71 | |
| 2 | 0.83 | 768 | 1579 | 221 | 134 | 73 | 261 | 276 | 12.11 | 5844 | 63.72 | ||
| 3 | 0.84 | 960 | 1110 | 96 | 105 | 23 | 328 | 275 | 16.27 | 5441 | 70.59 | ||
| … | … | … | … | … | … | … | … | … | … | … | … | ||
| 40 | 0.81 | 729 | 1684 | 240 | 211 | 68 | 265 | 275 | 14.31 | 6878 | 74.78 | ||
| 1500 | 1 | 1.16 | 682 | 1841 | 192 | 259 | 99 | 233 | 263 | 14.16 | 5909 | 61.06 | |
| 2 | 1.17 | 670 | 1899 | 96 | 250 | 94 | 237 | 265 | 12.78 | 6117 | 61.33 | ||
| 3 | 1.17 | 826 | 1418 | 144 | 96 | 94 | 239 | 270 | 11.77 | 6241 | 63.60 | ||
| … | … | … | … | … | … | … | … | … | … | … | … | ||
| 40 | 1.20 | 889 | 1234 | 173 | 364 | 91 | 237 | 271 | 13.36 | 6052 | 64.94 | ||
| Gravel | Sand | ||||
|---|---|---|---|---|---|
| Parameters | γ (%) | γ′ (%) | Parameters | γ (%) | γ′ (%) |
| Initial velocity | 31.64 | 31.64 | Initial velocity | 31.00 | 31.00 |
| Displacement of wheel loader in insertion phase | 27.04 | 58.68 | Displacement of wheel loader in insertion phase | 24.42 | 55.42 |
| Operation time | 15.36 | 74.03 | Shoveling weight | 13.99 | 69.41 |
| Shoveling weight | 15.35 | 89.39 | Operation time | 13.79 | 83.20 |
| Displacement of wheel loader in scooping phase | 6.56 | 95.95 | Displacement of wheel loader in scooping phase | 10.70 | 93.89 |
| Displacement of wheel loader in stopping phase | 2.65 | 98.60 | Displacement of wheel loader in stopping phase | 5.64 | 99.53 |
| Displacement of wheel loader in lifting phase | 1.13 | 99.73 | Displacement of wheel loader in lifting phase | 0.29 | 99.82 |
| Displacement of lift cylinder in scooping phase | 0.24 | 98.97 | Displacement of lift cylinder in scooping phase | 0.16 | 98.99 |
| Displacement of lift cylinder in lifting phase | 0.02 | 99.98 | Displacement of lift cylinder in lifting phase | 0.01 | 99.99 |
| Displacement of tilt cylinder in scooping phase | 0.01 | 100.00 | Displacement of tilt cylinder in scooping phase | 0.01 | 100.00 |
| Type of Pile | Initial Velocity | Displacement of Wheel Loader in Insertion Phase | Shoveling Weight | Operation Time | Displacement of Wheel Loader in Scooping Phase |
|---|---|---|---|---|---|
| Gravel | 0.792 | 0.782 | 0.834 | 0.789 | 0.779 |
| Sand | 0.762 | 0.795 | 0.894 | 0.846 | 0.822 |
| Type of Pile | ARE (%) | RMSE | R2 |
|---|---|---|---|
| Gravel | 4.91 | 5.91 | 0.9764 |
| Sand | 3.49 | 3.08 | 0.9494 |
| Parameters | Interval | Gravel Model | Sand Model | ||||
|---|---|---|---|---|---|---|---|
| 900 RPM | 1200 RPM | 1500 RPM | 900 RPM | 1200 RPM | 1500 RPM | ||
| Initial velocity (m·s−1) | Upper limit | 0.6 | 0.95 | 1.3 | 0.6 | 0.95 | 1.3 |
| Lower limit | 0.3 | 0.65 | 1.05 | 0.3 | 0.65 | 1.05 | |
| Displacement of wheel loader in insertion phase (mm) | Upper limit | 1000 | |||||
| Lower limit | 600 | ||||||
| Shoveling weight (kg) | Upper limit | 5526 | 5545 | 5558 | 7294 | 7441 | 7520 |
| Lower limit | 4459 | 4609 | 3913 | 5400 | 5773 | 5519 | |
| Operation time (s) | Upper limit | 25 | 23 | 21 | 25 | 26 | 23 |
| Lower limit | 12 | 12 | 10 | 11 | 12 | 10 | |
| Displacement of wheel loader in scooping phase (mm) | Calculated according to Equation (2) | ||||||
| Type of Pile | Engine Speed (RPM) | Initial Velocity (m·s−1) | Displacement of Wheel Loader in Insertion Phase (mm) | Displacement of Wheel Loader in Scooping Phase (mm) | Fuel Consumption (mL) |
|---|---|---|---|---|---|
| Gravel | 900 | 0.59 | 704 | 1778 | 55.05 |
| 1200 | 0.86 | 686 | 1843 | 59.58 | |
| 1500 | 1.16 | 698 | 1799 | 48.59 | |
| Sand | 900 | 0.48 | 839 | 1272 | 48.12 |
| 1200 | 0.79 | 749 | 1520 | 48.16 | |
| 1500 | 1.25 | 733 | 1569 | 56.87 |
| Type of Pile | Engine Speed (RPM) | Number | Initial Velocity (m·s−1) | Displacement of Wheel Loader in Insertion Phase (mm) | Displacement of Wheel loader In Scooping Phase (mm) | Operation Time (s) | Shoveling Weight (kg) | Fuel Consumption (mL) | Average Fuel Consumption (mL) |
|---|---|---|---|---|---|---|---|---|---|
| Gravel | 900 | 1 | 0.56 | 719 | 1690 | 10.99 | 4492 | 53.50 | |
| 2 | 0.53 | 713 | 1710 | 11.79 | 4602 | 51.91 | 54.50 | ||
| 3 | 0.49 | 722 | 1703 | 11.20 | 4570 | 58.09 | |||
| 1200 | 1 | 0.83 | 702 | 1804 | 12.02 | 4641 | 67.64 | ||
| 2 | 0.81 | 704 | 1785 | 12.49 | 4713 | 58.68 | 61.97 | ||
| 3 | 0.81 | 694 | 1748 | 12.55 | 4596 | 59.60 | |||
| 1500 | 1 | 1.14 | 726 | 1737 | 8.01 | 4388 | 45.09 | ||
| 2 | 1.12 | 704 | 1844 | 10.56 | 4414 | 47.30 | 44.59 | ||
| 3 | 1.09 | 725 | 1745 | 7.33 | 3770 | 41.38 | |||
| Sand | 900 | 1 | 0.52 | 826 | 1432 | 10.52 | 4232 | 49.24 | |
| 2 | 0.47 | 855 | 1342 | 9.85 | 5357 | 50.23 | 49.98 | ||
| 3 | 0.49 | 819 | 1436 | 9.90 | 5207 | 50.48 | |||
| 1200 | 1 | 0.81 | 747 | 1668 | 9.31 | 4966 | 49.78 | ||
| 2 | 0.77 | 758 | 1601 | 10.10 | 4550 | 47.54 | 50.00 | ||
| 3 | 0.87 | 730 | 1643 | 10.39 | 4843 | 52.69 | |||
| 1500 | 1 | 1.14 | 728 | 1594 | 10.65 | 6514 | 56.50 | ||
| 2 | 1.14 | 739 | 1603 | 11.12 | 6442 | 64.64 | 57.42 | ||
| 3 | 1.15 | 749 | 1488 | 11.37 | 4758 | 51.11 |
| Driver | Shoveling Operation | Fuel Consumption | Average Fuel Consumption | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Driver A | Shoveling gravel | 71.67 | 64.06 | 92.31 | 72.56 | 75.38 | 71.89 | 63.60 | 71.72 | 76.12 | 66.70 | 72.60 |
| Shoveling sand | 72.65 | 62.36 | 72.07 | 64.77 | 68.66 | 92.63 | 76.10 | 72.38 | 65.51 | 66.17 | 71.33 | |
| Driver B | Shoveling gravel | 84.85 | 65.72 | 74.56 | 77.76 | 72.16 | 74.00 | 65.73 | 68.77 | 96.22 | 78.53 | 75.83 |
| Shoveling sand | 61.17 | 57.76 | 67.28 | 61.05 | 74.34 | 66.57 | 69.00 | 74.26 | 68.23 | 74.09 | 67.38 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Shi, G.; Tan, C.; Wang, Z. Machine Learning-Based Shoveling Trajectory Optimization of Wheel Loader for Fuel Consumption Reduction. Appl. Sci. 2023, 13, 7659. https://doi.org/10.3390/app13137659
Chen Y, Shi G, Tan C, Wang Z. Machine Learning-Based Shoveling Trajectory Optimization of Wheel Loader for Fuel Consumption Reduction. Applied Sciences. 2023; 13(13):7659. https://doi.org/10.3390/app13137659
Chicago/Turabian StyleChen, Yanhui, Gang Shi, Cheng Tan, and Zhiwen Wang. 2023. "Machine Learning-Based Shoveling Trajectory Optimization of Wheel Loader for Fuel Consumption Reduction" Applied Sciences 13, no. 13: 7659. https://doi.org/10.3390/app13137659
APA StyleChen, Y., Shi, G., Tan, C., & Wang, Z. (2023). Machine Learning-Based Shoveling Trajectory Optimization of Wheel Loader for Fuel Consumption Reduction. Applied Sciences, 13(13), 7659. https://doi.org/10.3390/app13137659






