Rock Crack Types Identification by Machine Learning on the Sound Signal
Abstract
:1. Introduction
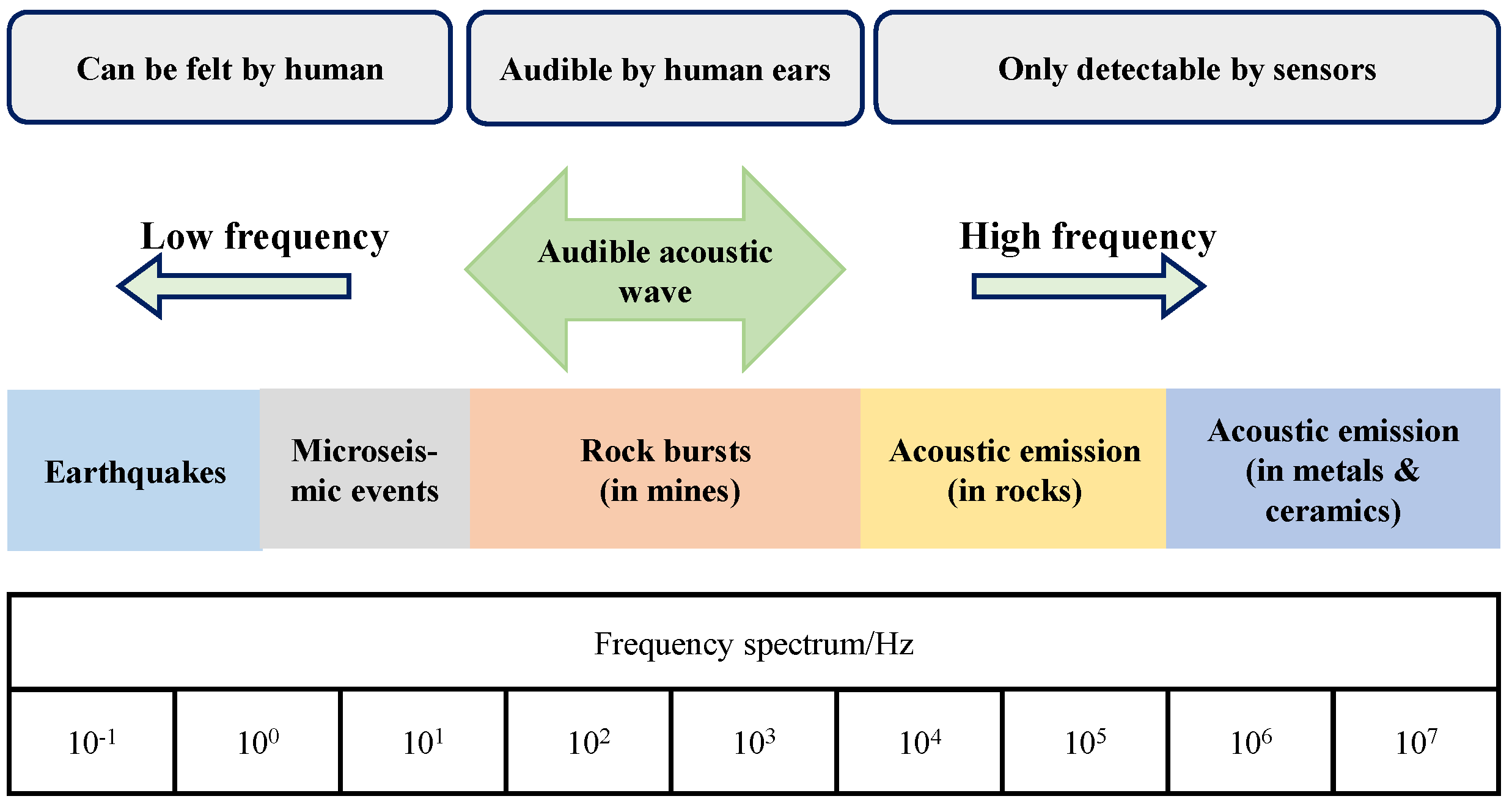
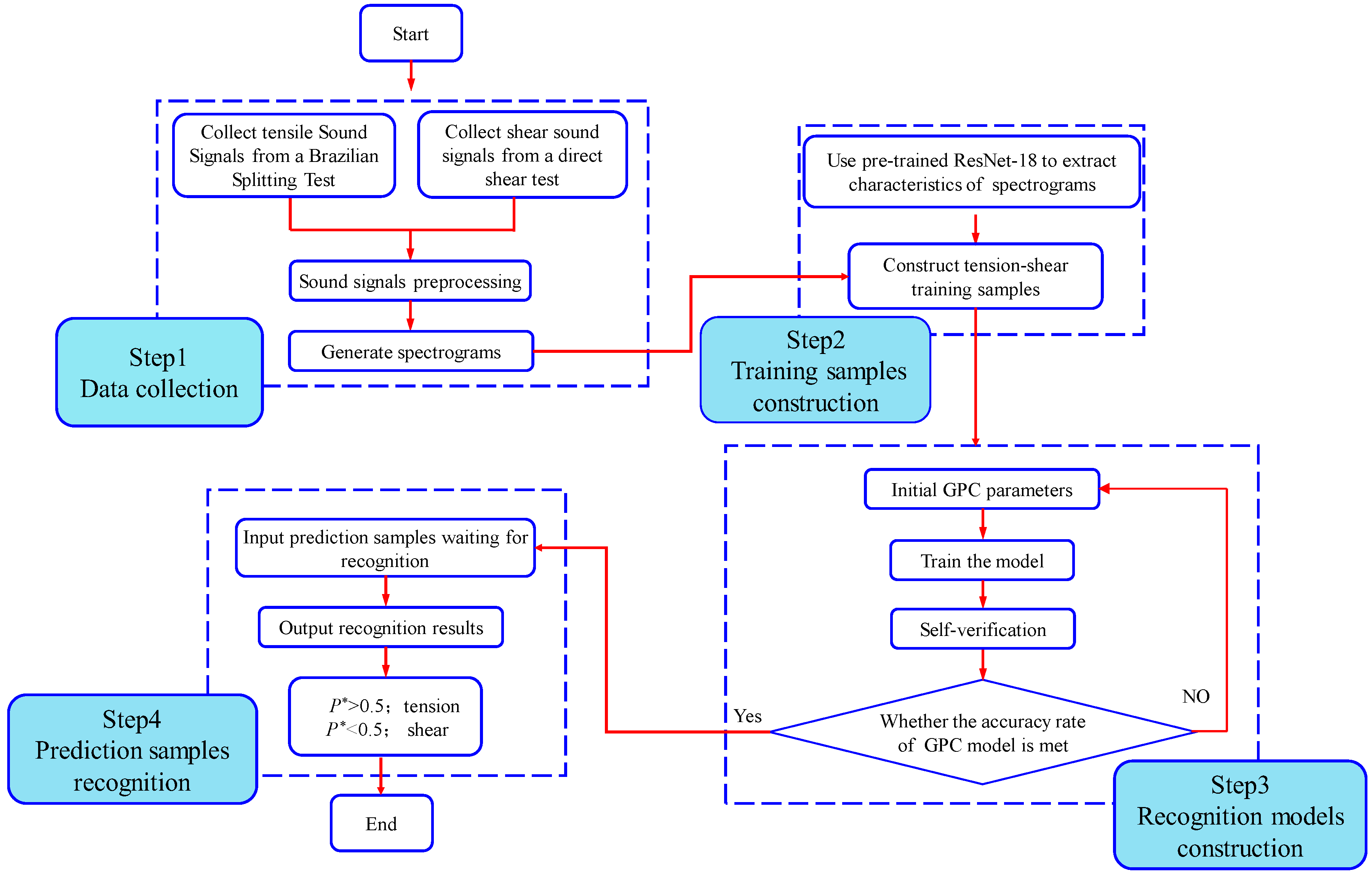
2. Automatic Recognition Method-Based Spectrograms for Hard Rock Crack Types
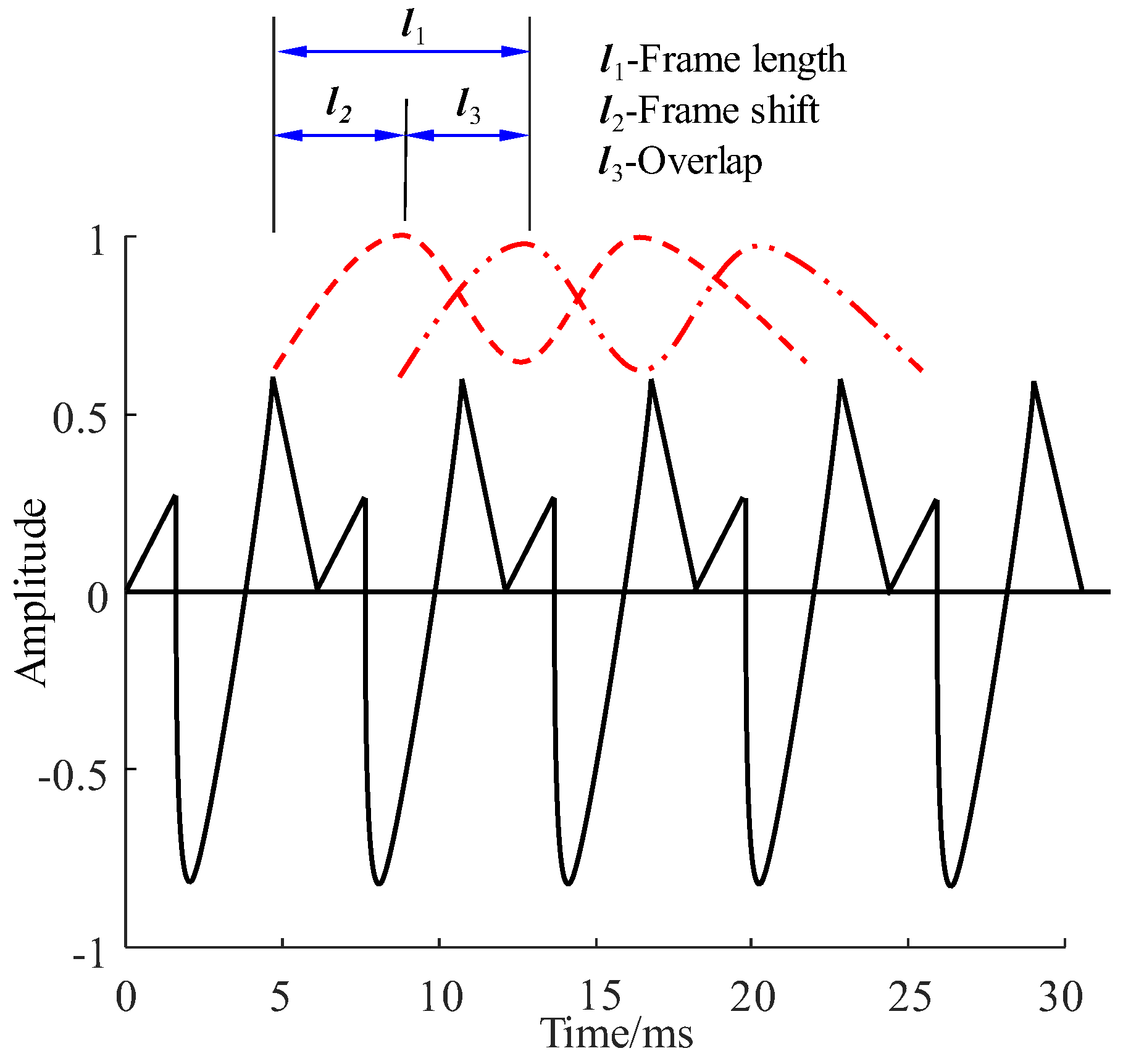
2.1. Basic Idea of the Method
2.2. Sound Signals of Tensile and Shear Cracks Collected during Rock Tests
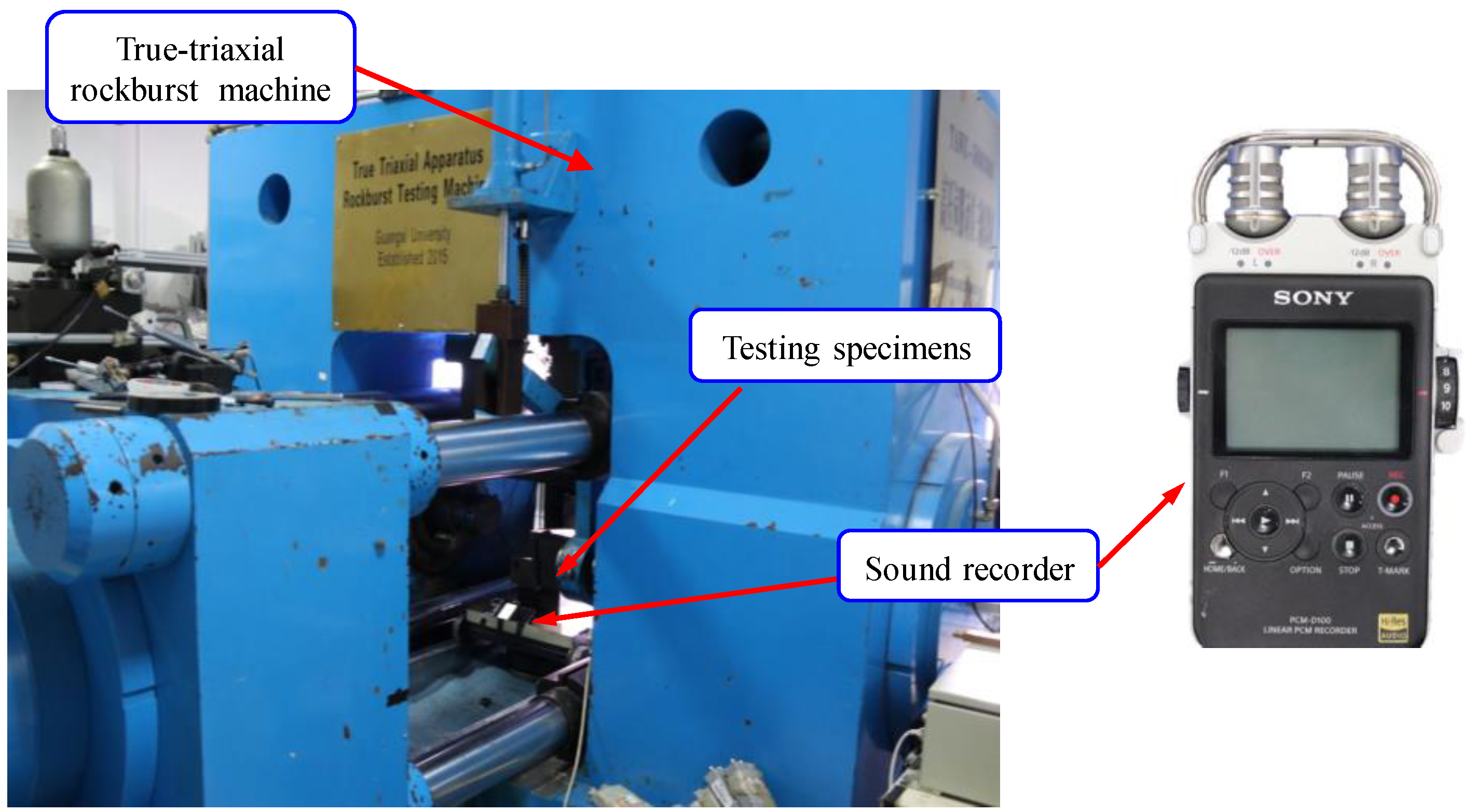
2.2.1. Rock Tests
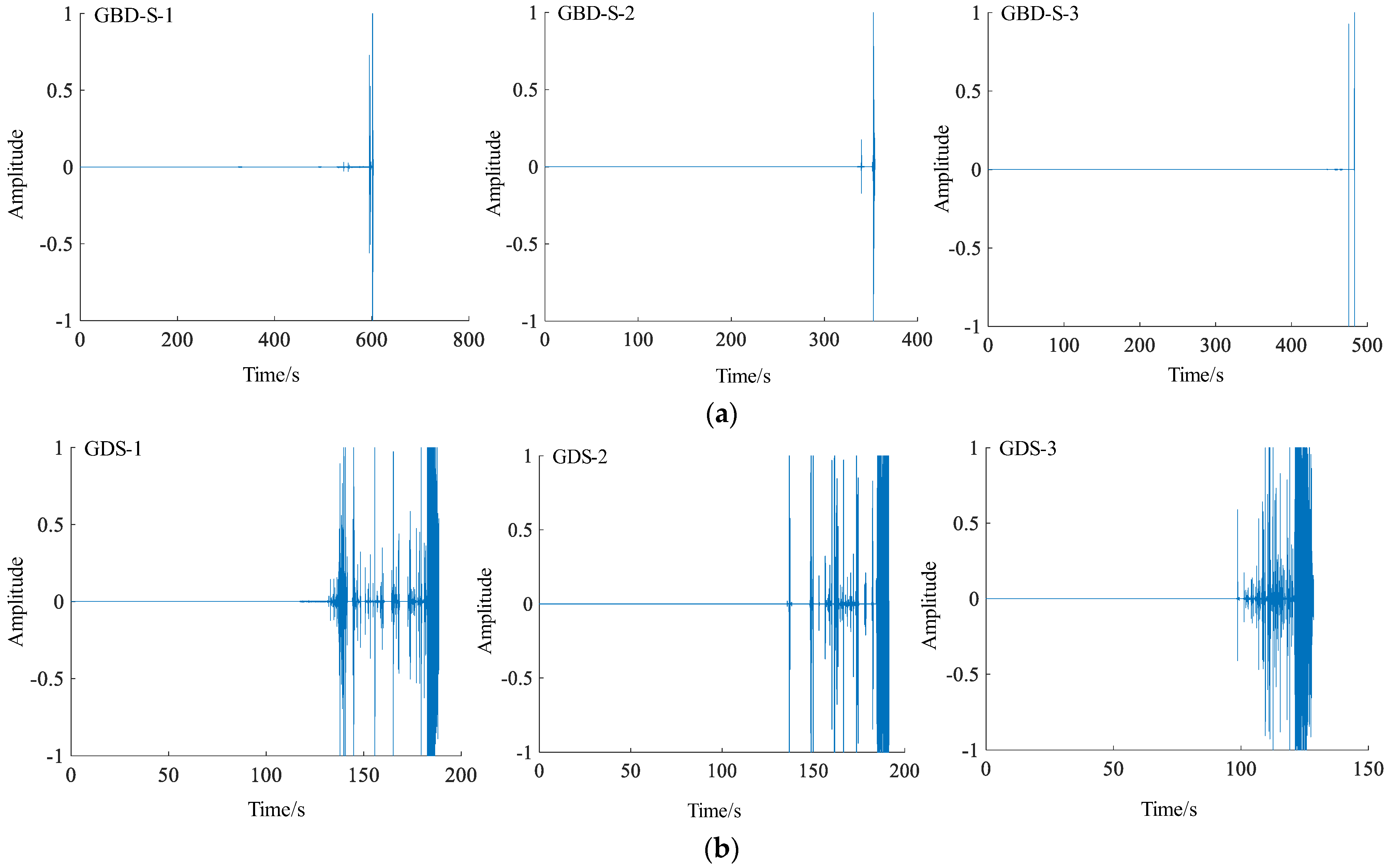
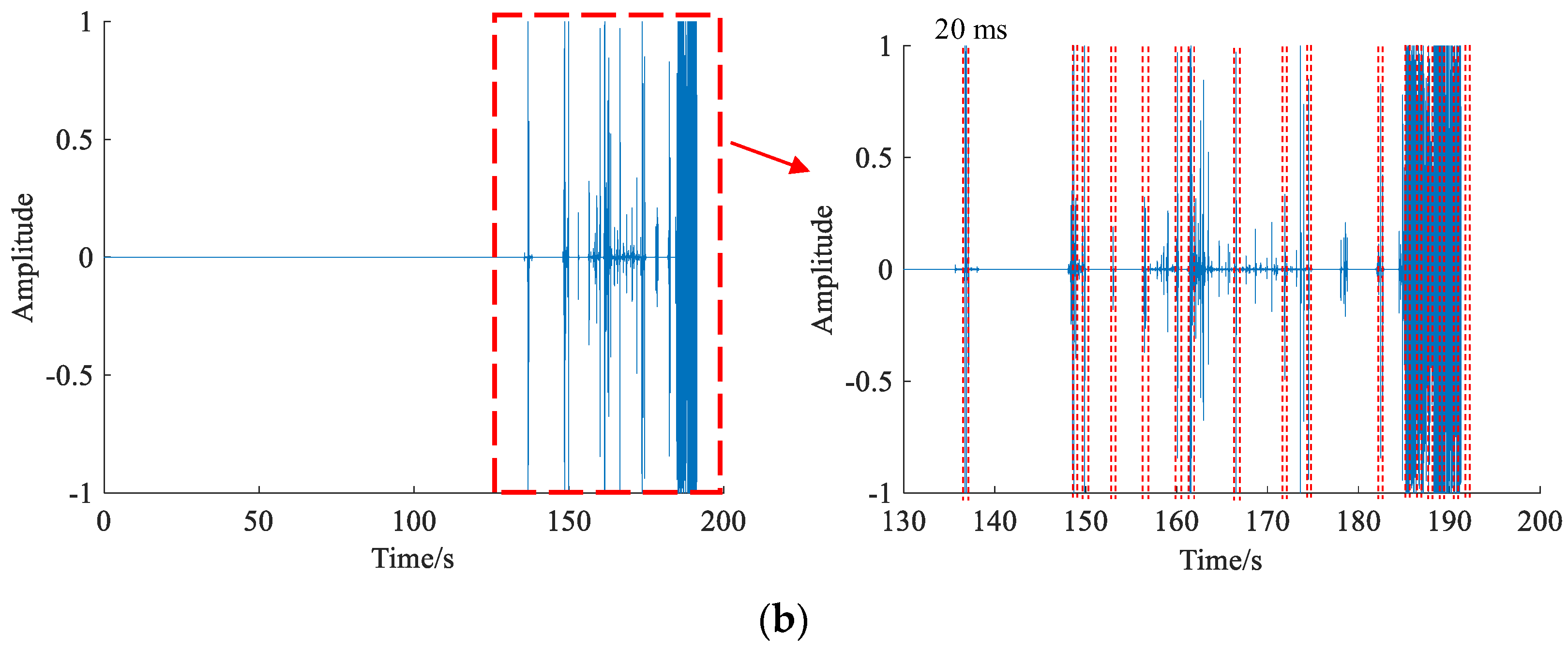
2.2.2. Sound Signals of Tensile and Shear Cracks
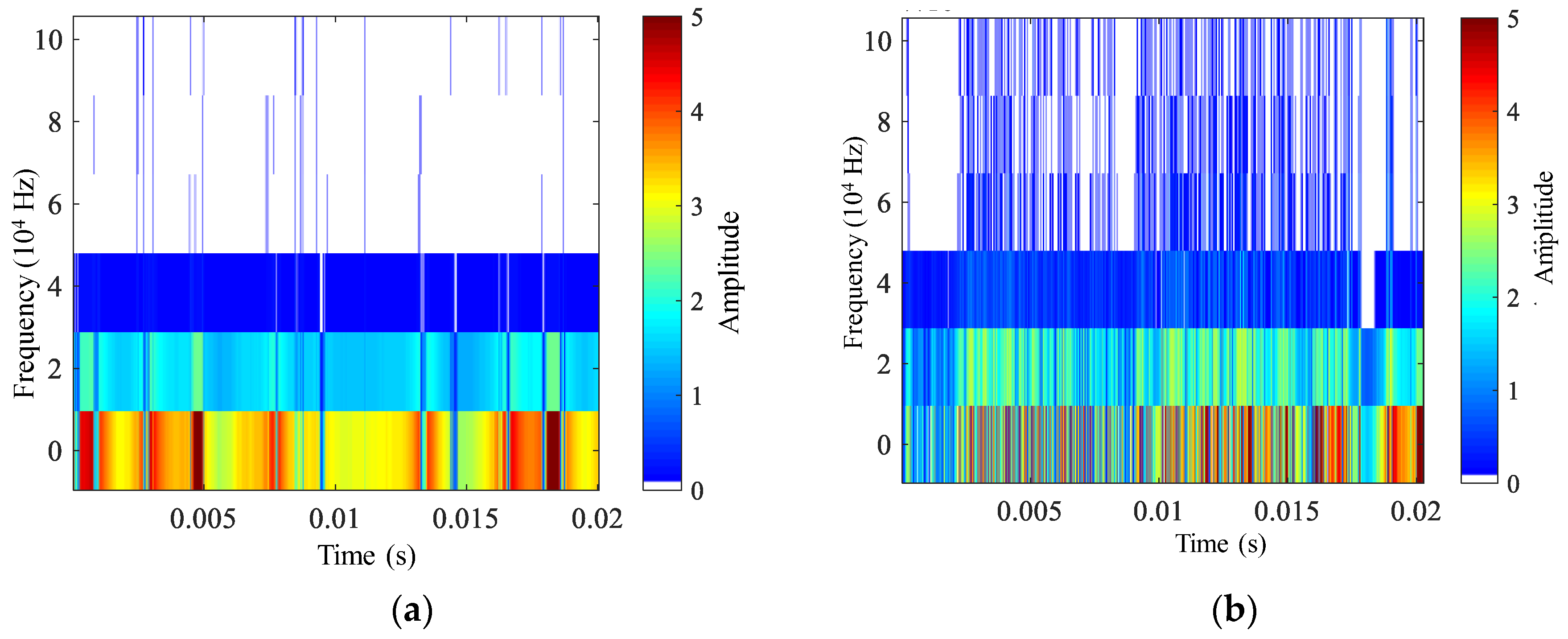
2.2.3. Extracting Spectrograms of the Tensile Cracks and Shear Cracks
2.3. Feature Extraction Using a Pre-Trained Deep Neural Network ResNet-18
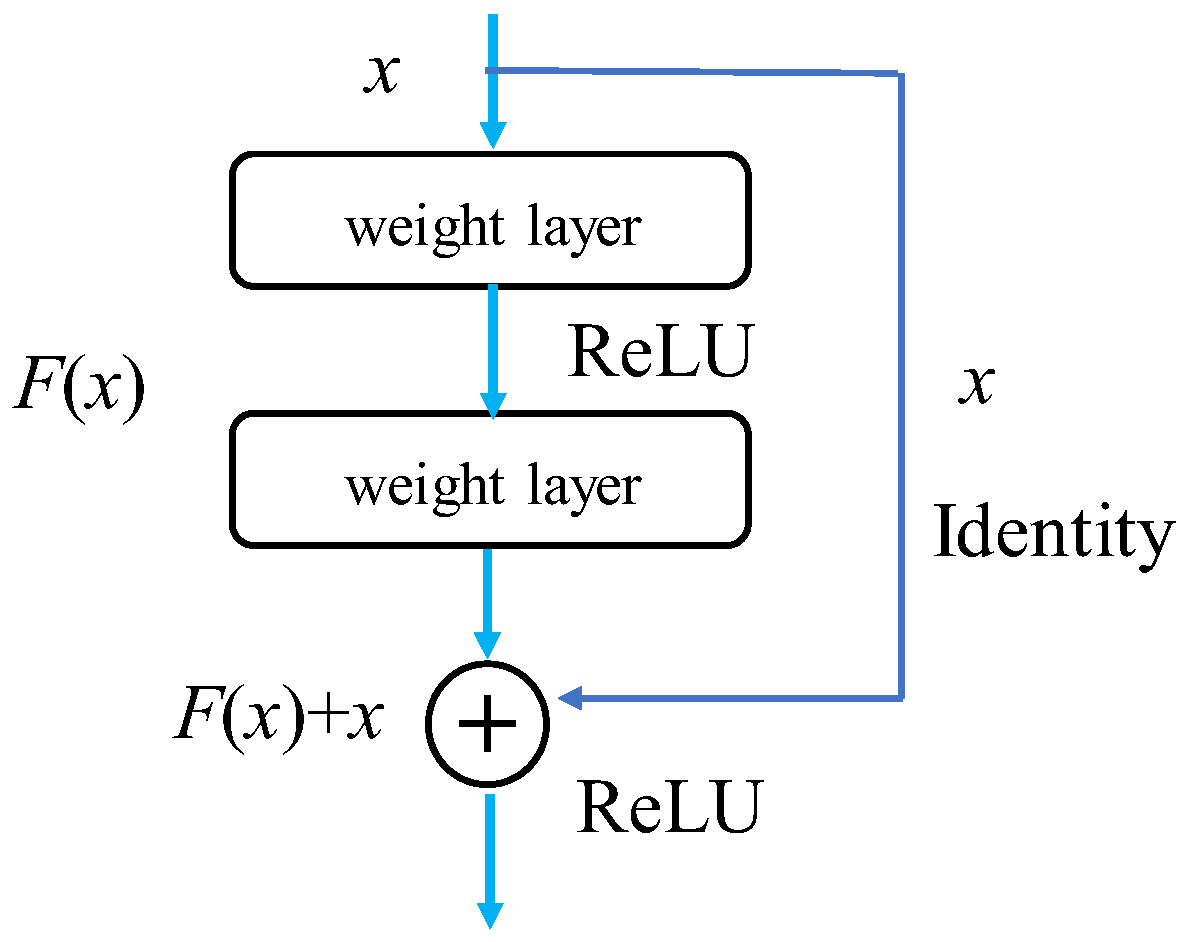
2.3.1. ResNet-18 Network
2.3.2. Feature Extraction from the Spectrograms
2.4. Identification Model for Tensile and Shear Crack Using GPC
2.4.1. Basic Principle of GPC
2.4.2. Implementation Steps
2.4.3. Verify the GPC
3. Results and Discussion
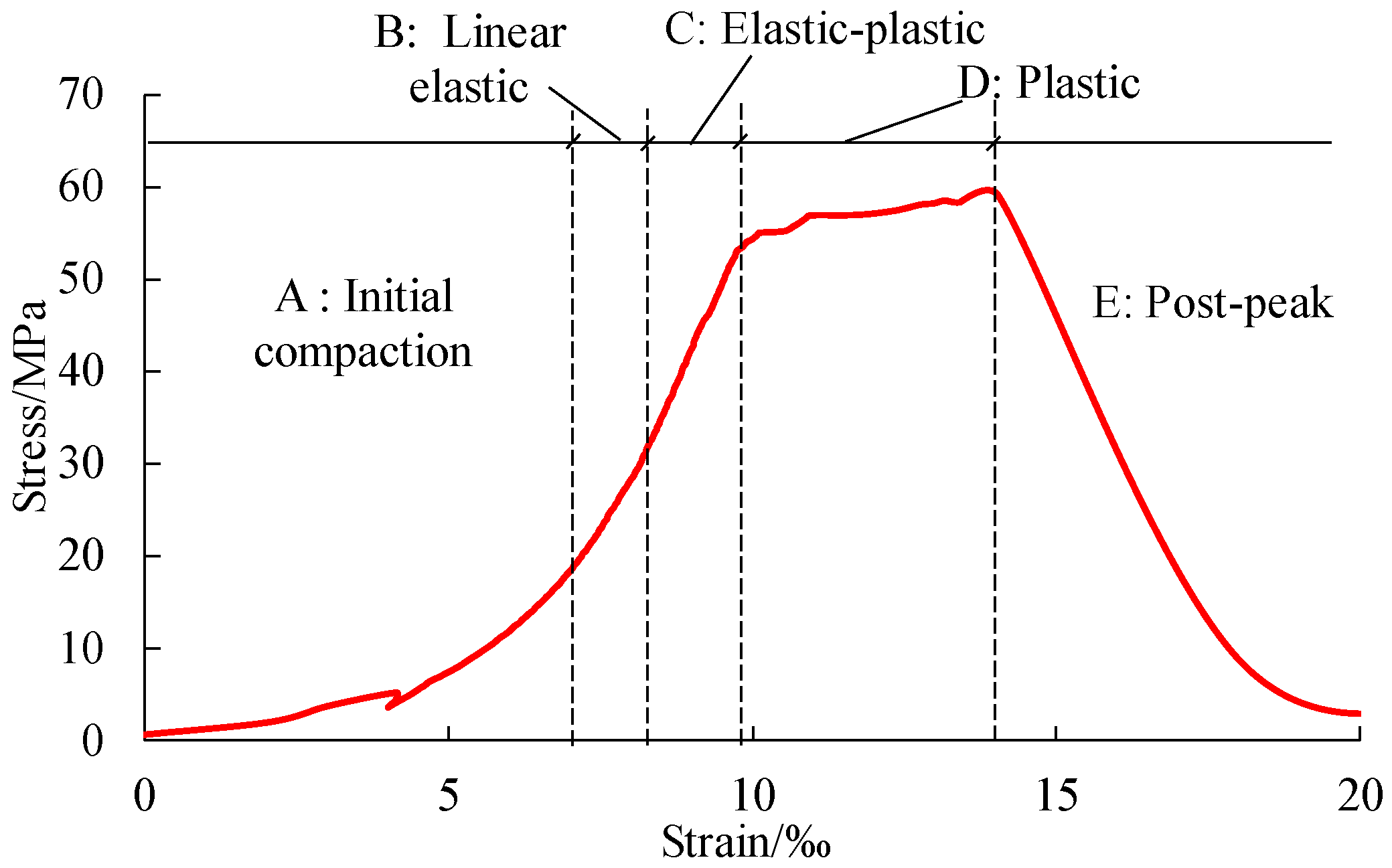
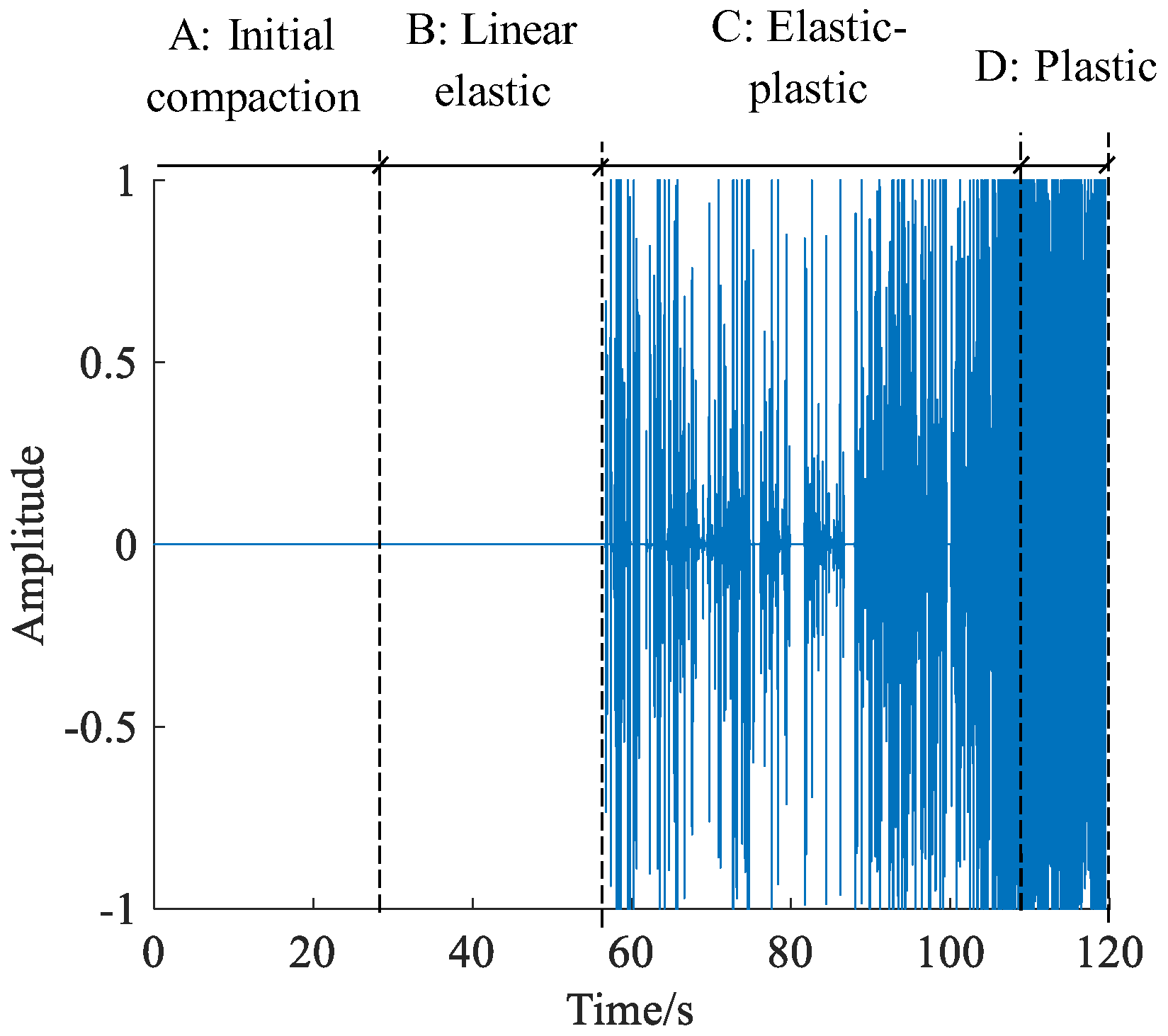
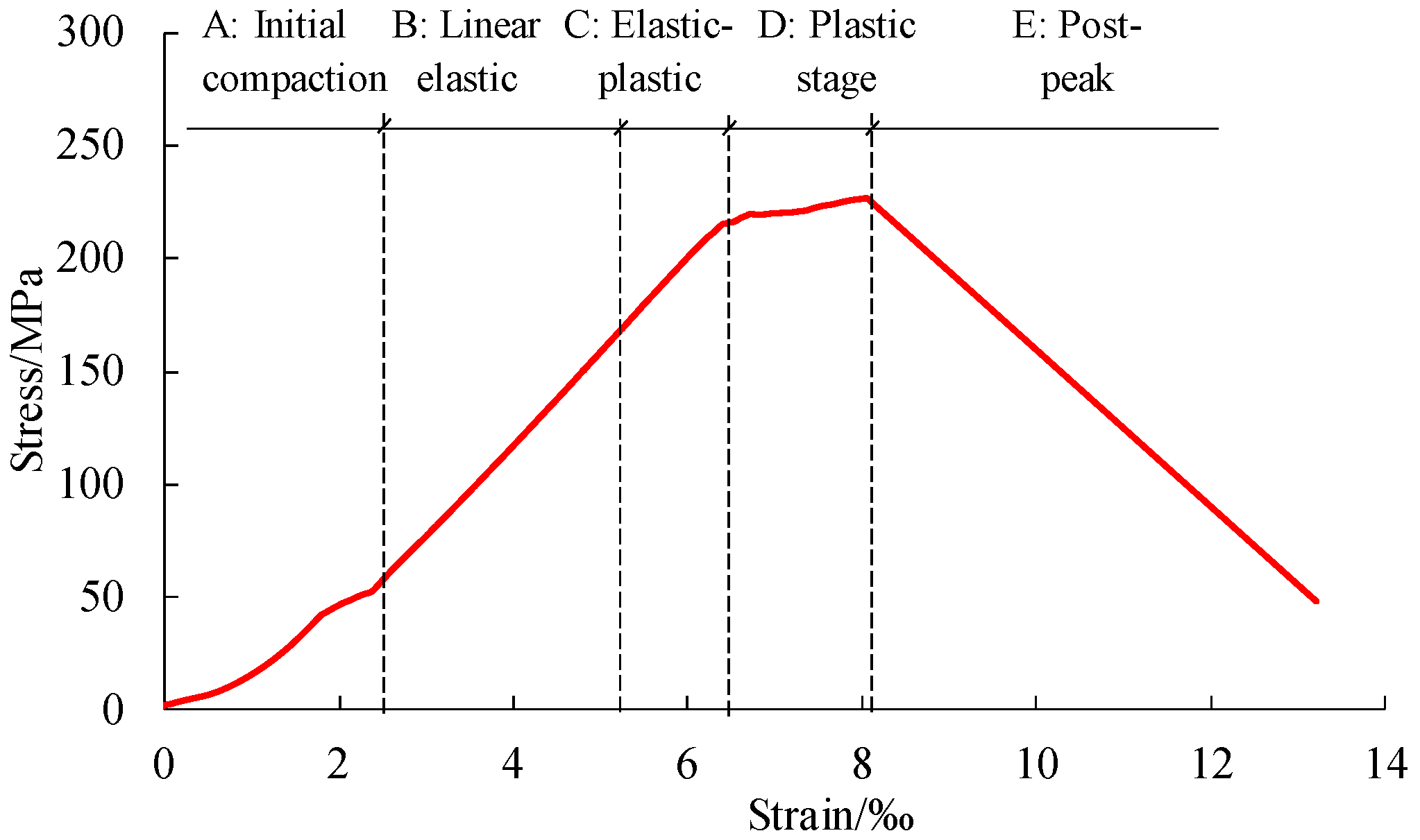
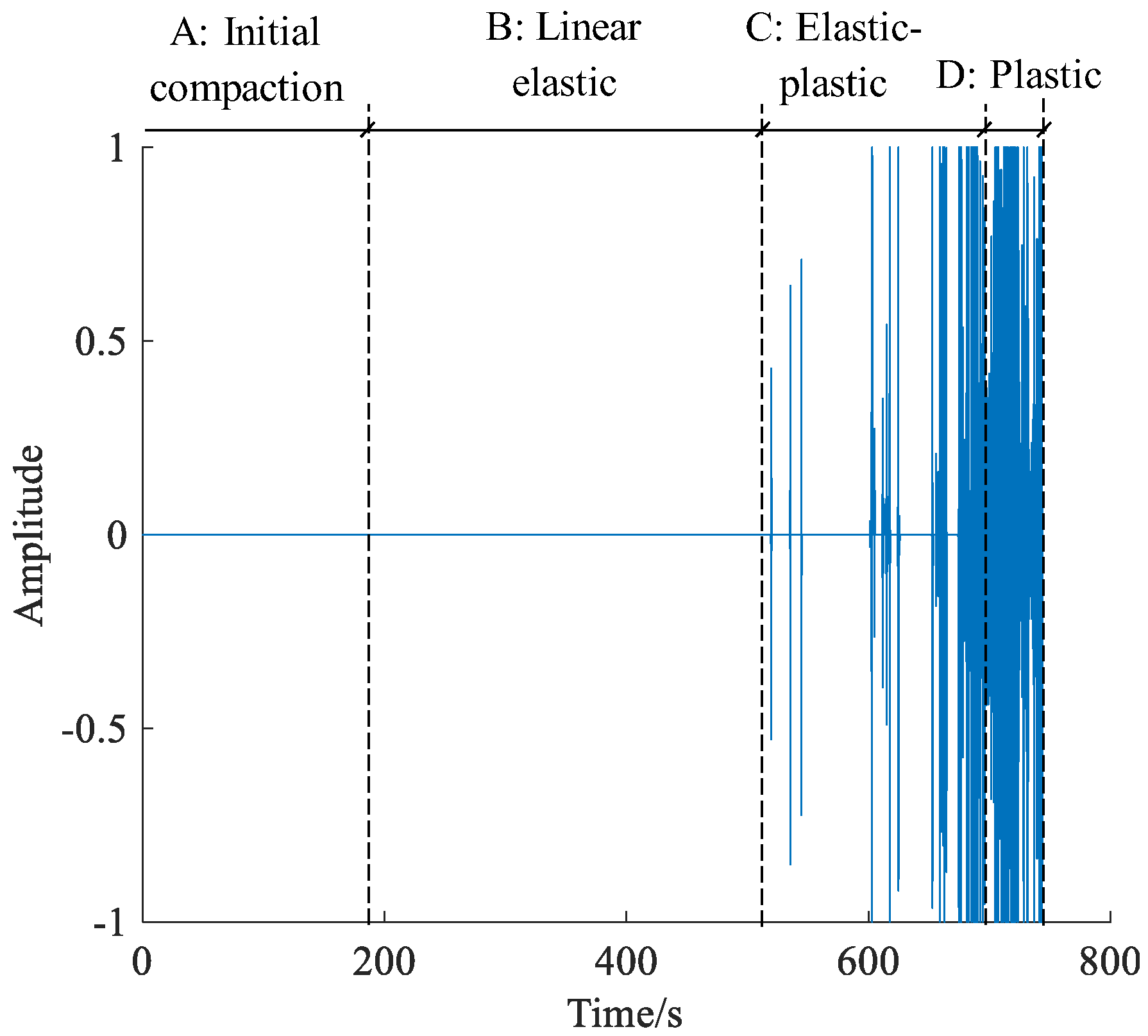
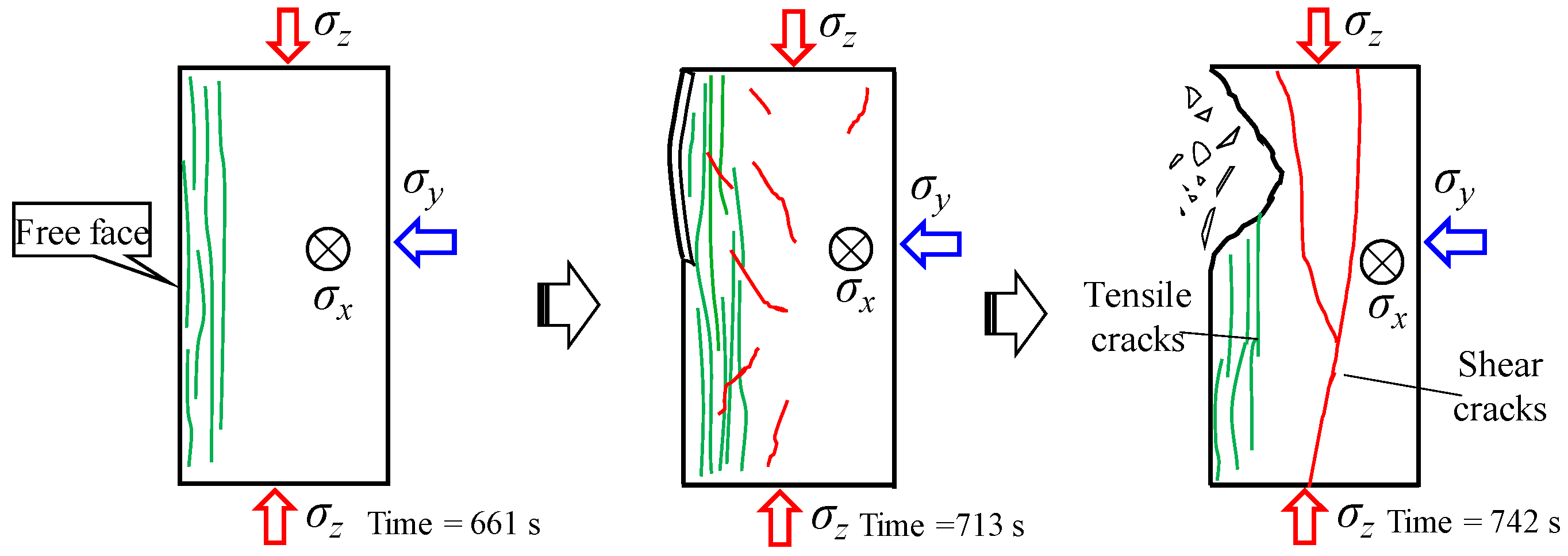
3.1. Identifying the Development of Tensile and Shear Cracks under Biaxial Compression Test
3.1.1. Biaxial Compression Test on a Granite Specimen
3.1.2. Tensile and Shear Cracks Development under Biaxial Compression Test
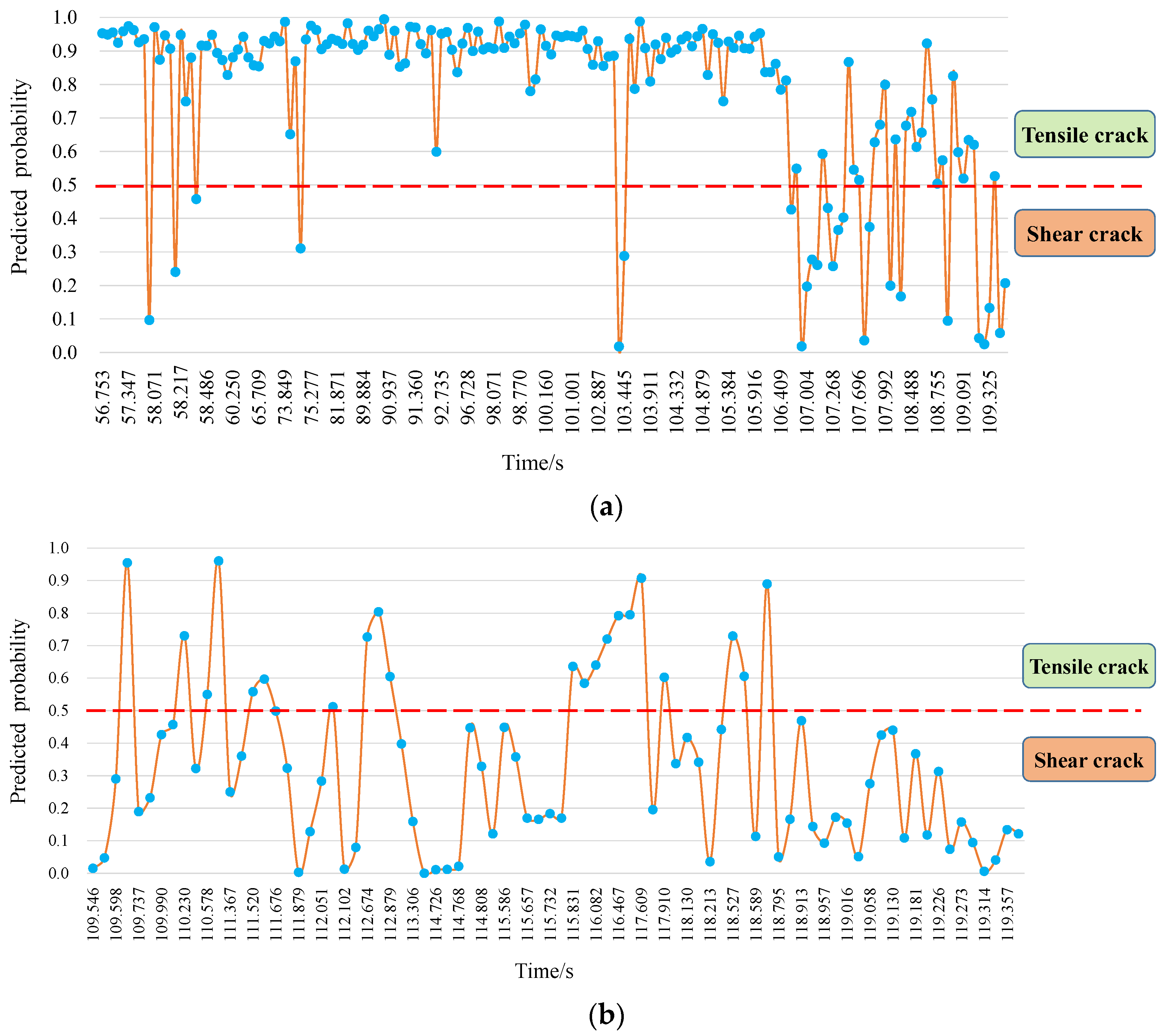
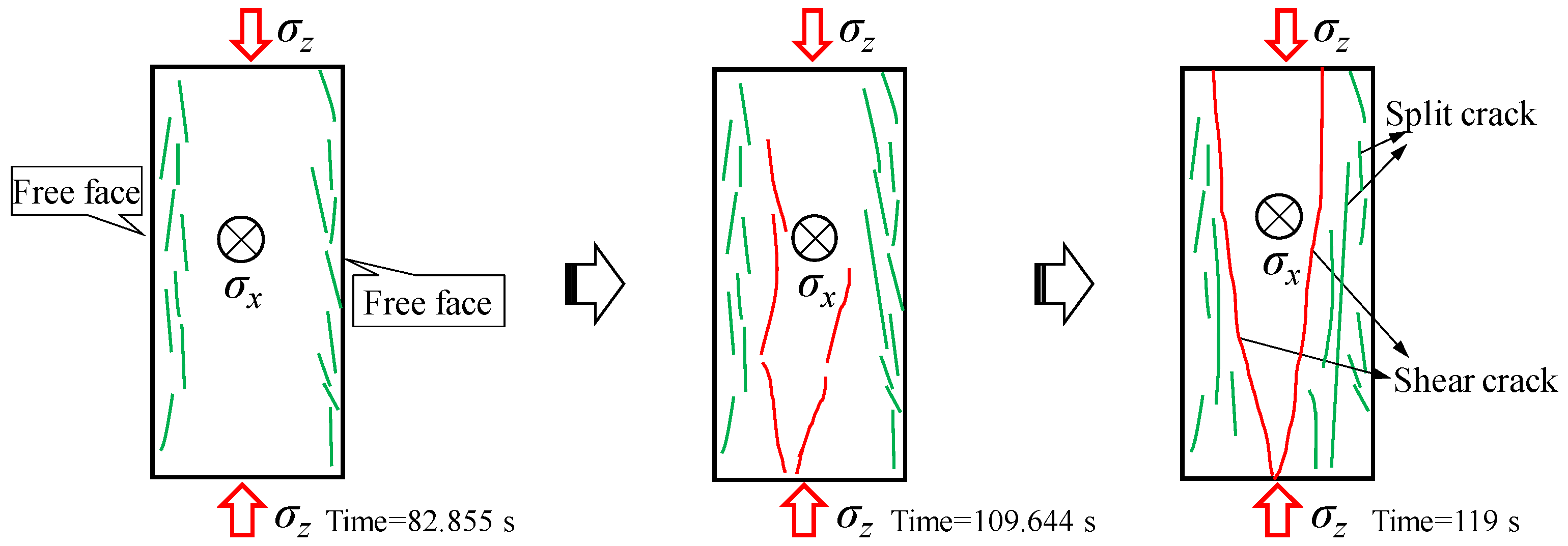
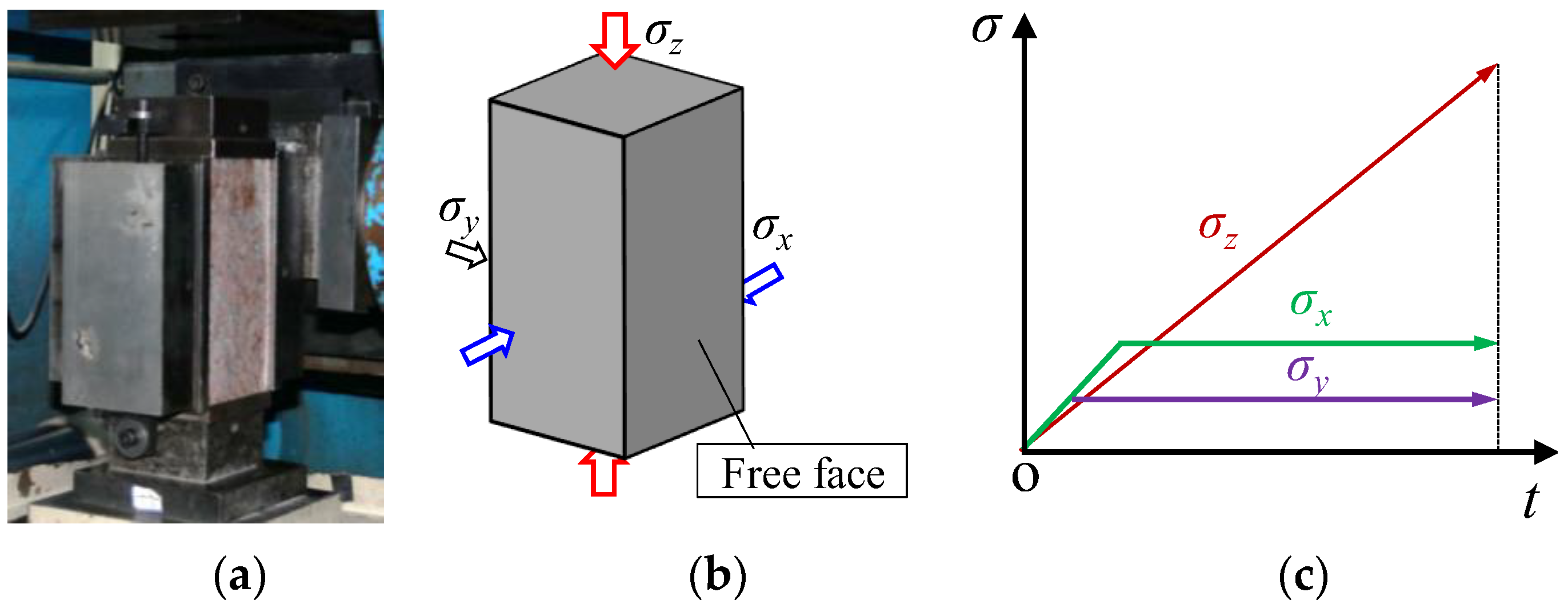
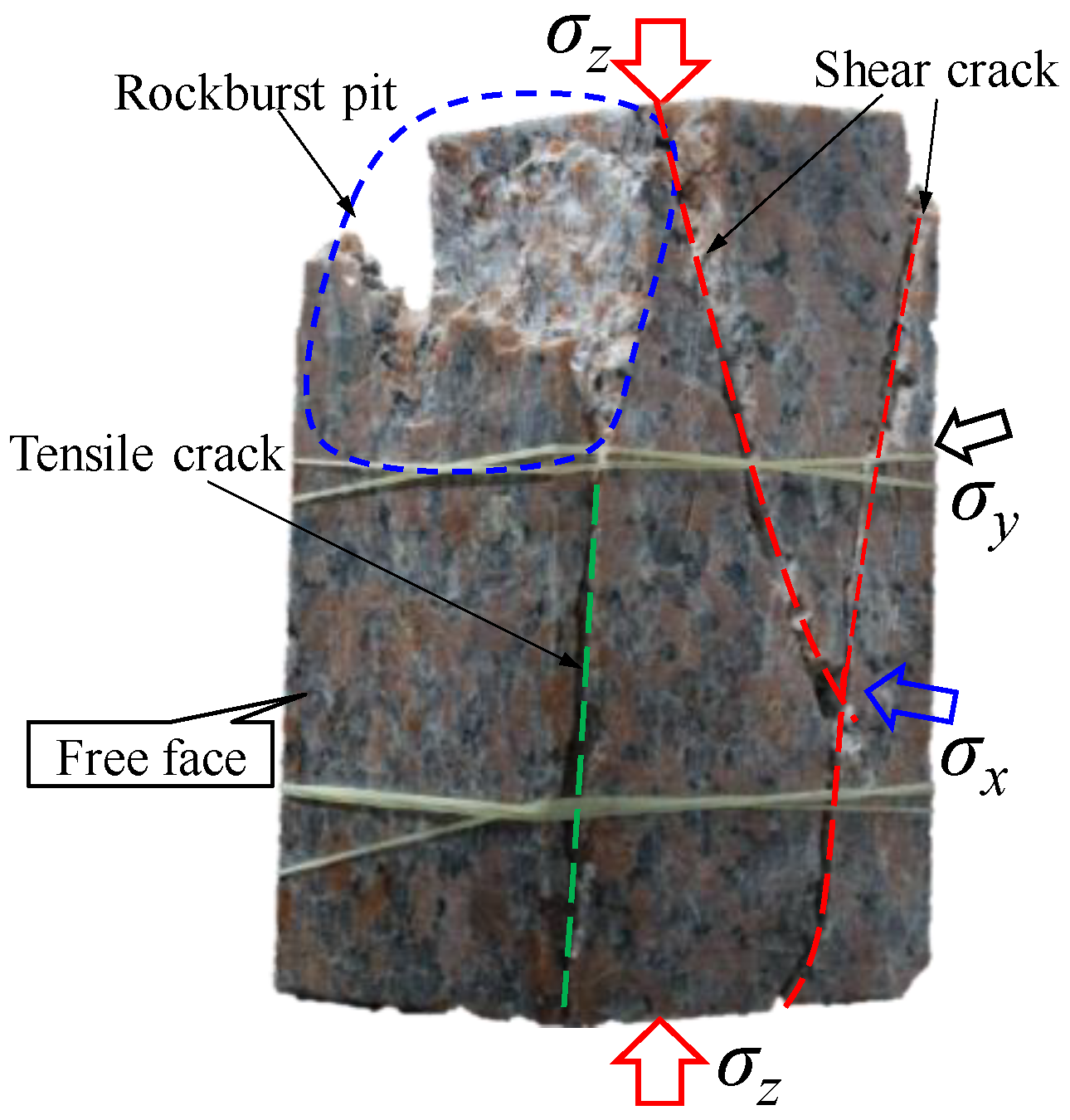
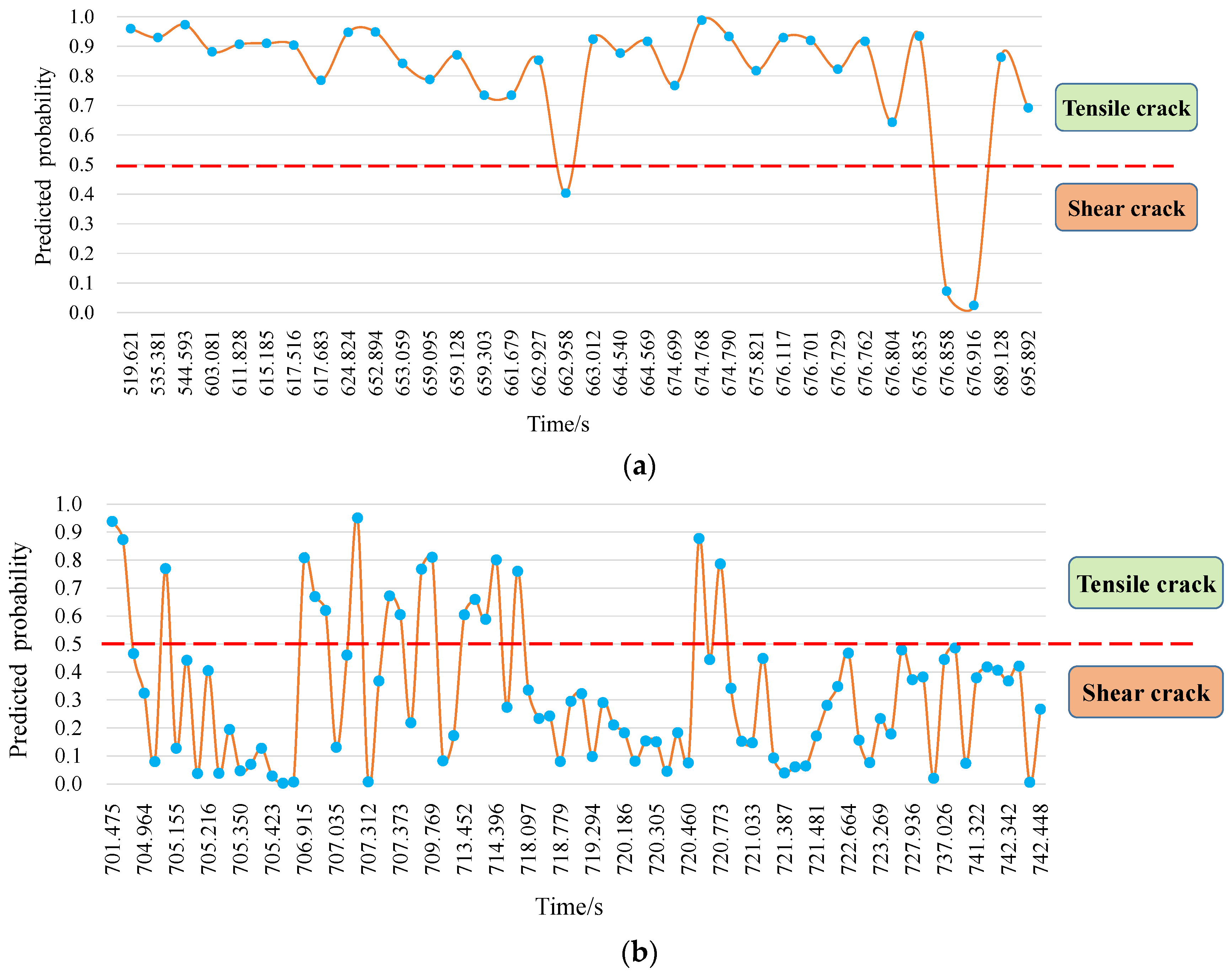
3.2. Identifying the Development of Tensile and Shear Cracks during Rockburst
3.2.1. Rockburst Test on a Granite Specimen
3.2.2. Tensile and Shear Cracks Process during Rockburst
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jiang, J.; Su, G.; Yan, Z.; Hu, X. Rock crack type identification by Gaussian process learning on acoustic emission. Appl. Acoust. 2022, 19, 108926. [Google Scholar] [CrossRef]
- Ohno, K.; Ohtsu, M. Crack classification in concrete based on acoustic emission. Constr. Build. Mater. 2010, 24, 2339–2346. [Google Scholar] [CrossRef]
- Aggelis, D.G. Classification of cracking mode in concrete by acoustic emission parameters. Mech. Res. Commun. 2011, 38, 153–157. [Google Scholar] [CrossRef]
- Aggelis, D.G.; Mpalaskas, A.C.; Matikas, T.E. Acoustic signature of different fracture modes in marble and cementitious materials under flexural load. Mech. Res. Commun. 2013, 47, 39–43. [Google Scholar] [CrossRef]
- Liu, J.; Li, Y.; Xu, X.; Xu, S.; Jing, C. Cracking mechanisms in granite rocks subjected to uniaxial compression by moment tensor analysis of acoustic emission. Theor. Appl. Fract. Mech. 2015, 75, 151–159. [Google Scholar]
- Zhou, H.; Wang, Z.; Ren, W.; Liu, Z.; Liu, J. Acoustic emission based mechanical behaviors of Beishan granite under conventional triaxial compression and hydro-mechanical coupling tests. Int. J. Rock Mech. Min. Sci. 2019, 123, 104125. [Google Scholar] [CrossRef]
- Li, D.; Wang, E.; Kong, X.; Ali, M.; Wang, D. Mechanical behaviors and acoustic emission fractal characteristics of coal specimens with a pre-existing flaw of various inclinations under uniaxial compression. Int. J. Rock Mech. Min. Sci. 2019, 116, 38–51. [Google Scholar] [CrossRef]
- Hu, X.; Su, G.; Chen, G.; Mei, S.; Feng, X.; Mei, G.; Huang, X. Experiment on Rockburst Process of Borehole and Its Acoustic Emission Characteristics. Rock Mech. Rock Eng. 2019, 52, 783–802. [Google Scholar] [CrossRef]
- Meng, F.; Zhou, H.; Wang, Z.; Zhang, L.; Kong, L.; Li, S.; Zhang, C. Influences of Shear History and Infilling on the Mechanical Characteristics and Acoustic Emissions of Joints. Rock Mech. Rock Eng. 2017, 50, 2039–2057. [Google Scholar] [CrossRef]
- Chen, B.; Feng, X.; Li, Q.; Luo, R.; Li, S. Rock Burst Intensity Classification Based on the Radiated Energy with Damage Intensity at Jinping II Hydropower Station, China. Rock Mech. Rock Eng. 2015, 48, 289–303. [Google Scholar] [CrossRef]
- Su, G.; Shi, Y.; Feng, X.; Jiang, J.; Zhang, J.; Jiang, Q. True-Triaxial Experimental Study of the Evolutionary Features of the Acoustic Emissions and Sounds of Rockburst Processes. Rock Mech. Rock Eng. 2018, 51, 375–389. [Google Scholar] [CrossRef]
- Zhang, C.; Feng, X.; Zhou, H.; Qiu, S.; Wu, W. Case Histories of Four Extremely Intense Rockbursts in Deep Tunnels. Rock Mech. Rock Eng. 2012, 45, 275–288. [Google Scholar] [CrossRef]
- Sharan, R.; Moir, T. An overview of applications and advancements in automatic sound recognition. Neurocomputing 2016, 200, 22–34. [Google Scholar] [CrossRef] [Green Version]
- Espi, M.; Fujimoto, M.; Kinoshita, K.; Nakatani, T. Exploiting spectro-temporal locality in deep learning based acoustic event detection. Eurasip J. Audio Speech Music. Process. 2015, 2015, 26. [Google Scholar] [CrossRef]
- Dahl, G.; Yu, D.; Deng, L.; Acero, A. Context-dependent pre-trained deep neural networks for large-vocabulary speech recognition. IEEE Trans. Audio Speech Lang. Process. 2011, 20, 30–42. [Google Scholar] [CrossRef] [Green Version]
- Hinton, G.; Deng, L.; Yu, D.; Dahl, G.; Mohamed, A.; Jaitly, N.; Senior, A.; Vanhoucke, V.; Nguyen, P.; Sainath, T.; et al. Deep Neural Networks for Acoustic Modeling in Speech Recognition: The Shared Views of Four Research Groups. Signal Process. Mag. IEEE 2012, 29, 82–97. [Google Scholar] [CrossRef]
- McLoughlin, I.; Zhang, H.; Xie, Z.; Song, Y.; Xiao, W. Robust Sound Event Classification Using Deep Neural Networks. IEEE/ACM Trans. Audio Speech Lang. Process. 2015, 23, 540–552. [Google Scholar] [CrossRef] [Green Version]
- Cai, M.; Kaiser, P.; Suorineni, F.; Su, K. A study on the dynamic behavior of the Meuse/Haute-Marne argillite. Phys. Chem. Earth Parts A/B/C 2007, 32, 907–916. [Google Scholar] [CrossRef]
- Meng, H.; Yan, T.; Yuan, F.; Wei, H. Speech Emotion Recognition From 3D Log-Mel Spectrograms with Deep Learning Network. IEEE Access 2019, 7, 125868–125881. [Google Scholar] [CrossRef]
- Arias-Vergara, T.; Klumpp, P.; Vasquez-Correa, J. Multi-channel spectrograms for speech processing applications using deep learning methods. Pattern Anal. Appl. 2021, 24, 423–431. [Google Scholar] [CrossRef]
- Bousetouane, F.; Morris, B. Off-the-Shelf CNN Features for Fine-Grained Classification of Vessels in a Maritime Environment; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Bar, Y.; Diamant, I.; Wolf, L.; Lieberman, S.; Konen, E.; Greenspan, H. Chest pathology identification using deep feature selection with non-medical training. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2018, 6, 259–263. [Google Scholar] [CrossRef]
- Xu, Y.; Jia, Z.; Wang, L.; Ai, Y.; Zhang, F.; Lai, M.; Chang, E. Large scale tissue histopathology image classification, segmentation, and visualization via deep convolutional activation features. BMC Bioinform. 2017, 18, 281. [Google Scholar] [CrossRef] [Green Version]
- Lopes, U.; Valiati, J. Pre-trained convolutional neural networks as feature extractors for tuberculosis detection. Comput. Biol. Med. 2017, 89, 135–143. [Google Scholar] [CrossRef] [PubMed]
- Guo, S.; Chen, S.; Li, Y. Face recognition based on convolutional neural network and support vector machine. In Proceedings of the IEEE International Conference on Information and Automation (ICIA), Ningbo, China, 1–3 August 2016; pp. 1787–1792. [Google Scholar]
- Testa, A.; Gallo, D.; Langella, R. On the Processing of Harmonics and Interharmonics: Using Hanning Window in Standard Framework. Power Deliv. IEEE Trans. Power Deliv. 2004, 19, 28–34. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Endo, Y.; Iizuka, S.; Kanamori, Y.; Mitani, J. DeepProp: Extracting Deep Features from a Single Image for Edit Propagation. Comput. Graph. Forum 2016, 35, 189–201. [Google Scholar] [CrossRef]
- Yue, J.; Zhao, W.; Mao, S.; Liu, H. Spectral–spatial classification of hyperspectral images using deep convolutional neural networks. Remote Sens. Lett. 2015, 6, 468–477. [Google Scholar] [CrossRef]
- Babenko, A.; Lempitsky, V. Aggregating Deep Convolutional Features for Image Retrieval. arXiv 2015, arXiv:1510.07493. [Google Scholar]
- Su, G.; Peng, L.; Hu, L. A Gaussian process-based dynamic surrogate model for complex engineering structural reliability analysis. Struct. Saf. 2017, 68, 97–109. [Google Scholar] [CrossRef]
- Williams, C. Prediction with Gaussian Processes: From Linear Regression to Linear Prediction and Beyond. In Learning in Graphical Models; Jordan, M.I., Ed.; Springer: Dordrecht, The Netherlands, 1998; pp. 599–621. [Google Scholar]
- Hensman, J.; Mills, R.; Pierce, S.; Worden, K.; Eaton, M. Locating acoustic emission sources in complex structures using Gaussian processes. Mech. Syst. Signal Process. 2010, 24, 211–223. [Google Scholar] [CrossRef]
- Su, G.; Jiang, J.; Yu, B.; Xiao, Y. A Gaussian process-based response surface method for structural reliability analysis. Struct. Eng. Mech. 2015, 56, 549–567. [Google Scholar] [CrossRef]
- Chen, J.; Feng, X. True triaxial experimental study on rock with high geostress. Chin. J. Rock Mech. Eng. 2006, 25, 1537–1543. [Google Scholar]
- Cai, M. Principles of rock support in burst-prone ground. Tunn. Undergr. Space Technol. 2013, 36, 46–56. [Google Scholar] [CrossRef]
- Li, T.; Cai, M.; Cai, M. A review of mining-induced seismicity in China. Int. J. Rock Mech. Min. Sci. 2007, 44, 1149–1171. [Google Scholar] [CrossRef]
- Ortlepp, W. The behaviour of tunnels at great depth under large static and dynamic pressures. Tunn. Undergr. Space Technol. 2001, 16, 41–48. [Google Scholar] [CrossRef]
- Su, G.; Jiang, J.; Zhai, S.; Zhang, G. Influence of Tunnel Axis Stress on Strainburst: An Experimental Study. Rock Mech. Rock Eng. 2017, 50, 1551–1567. [Google Scholar] [CrossRef]
- Su, G.; Feng, X.; Wang, J.; Jiang, J.; Hu, L. Experimental Study of Remotely Triggered Rockburst Induced by a Tunnel Axial Dynamic Disturbance under True-Triaxial Conditions. Rock Mech. Rock Eng. 2017, 50, 2207–2226. [Google Scholar] [CrossRef]

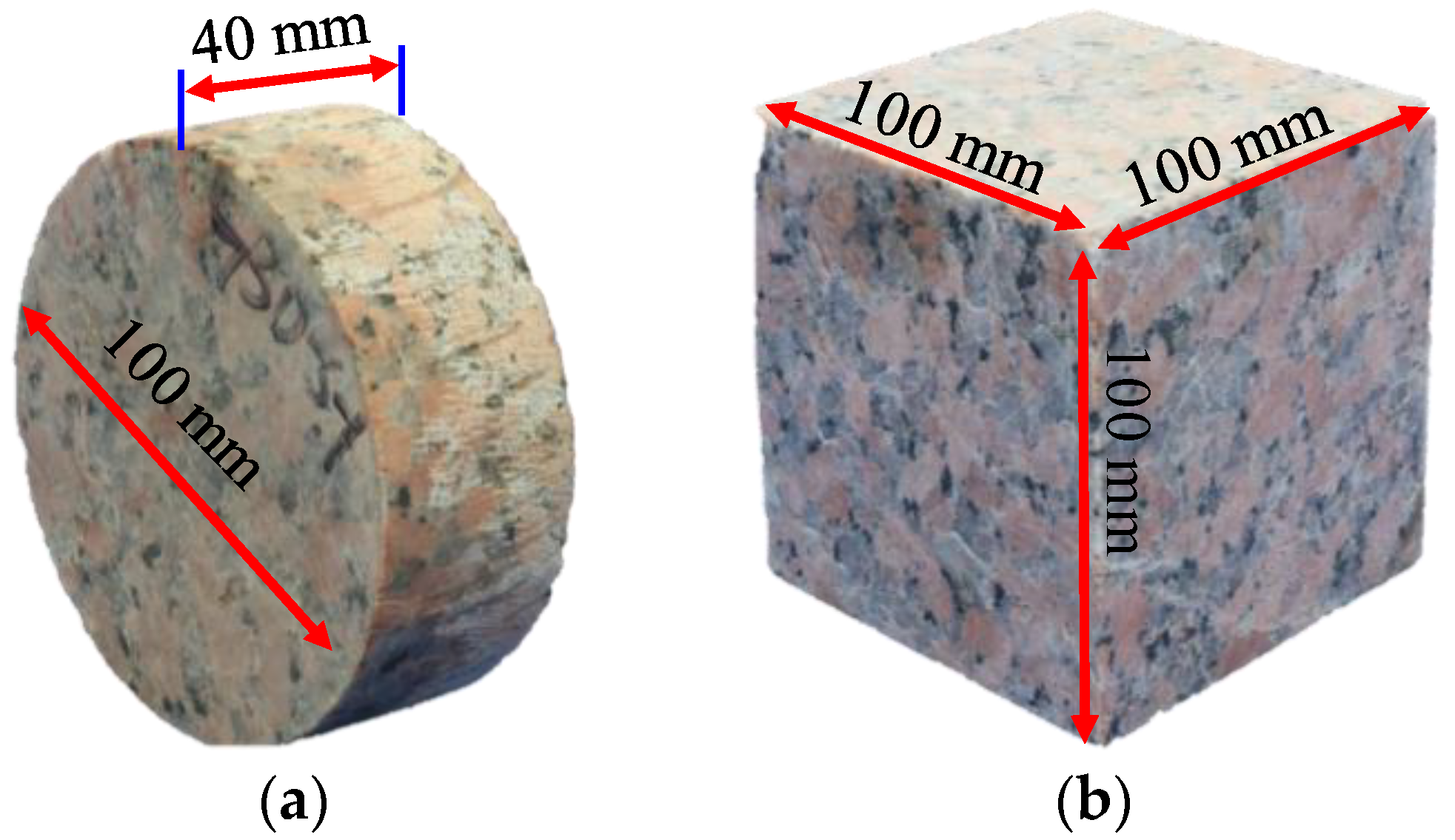





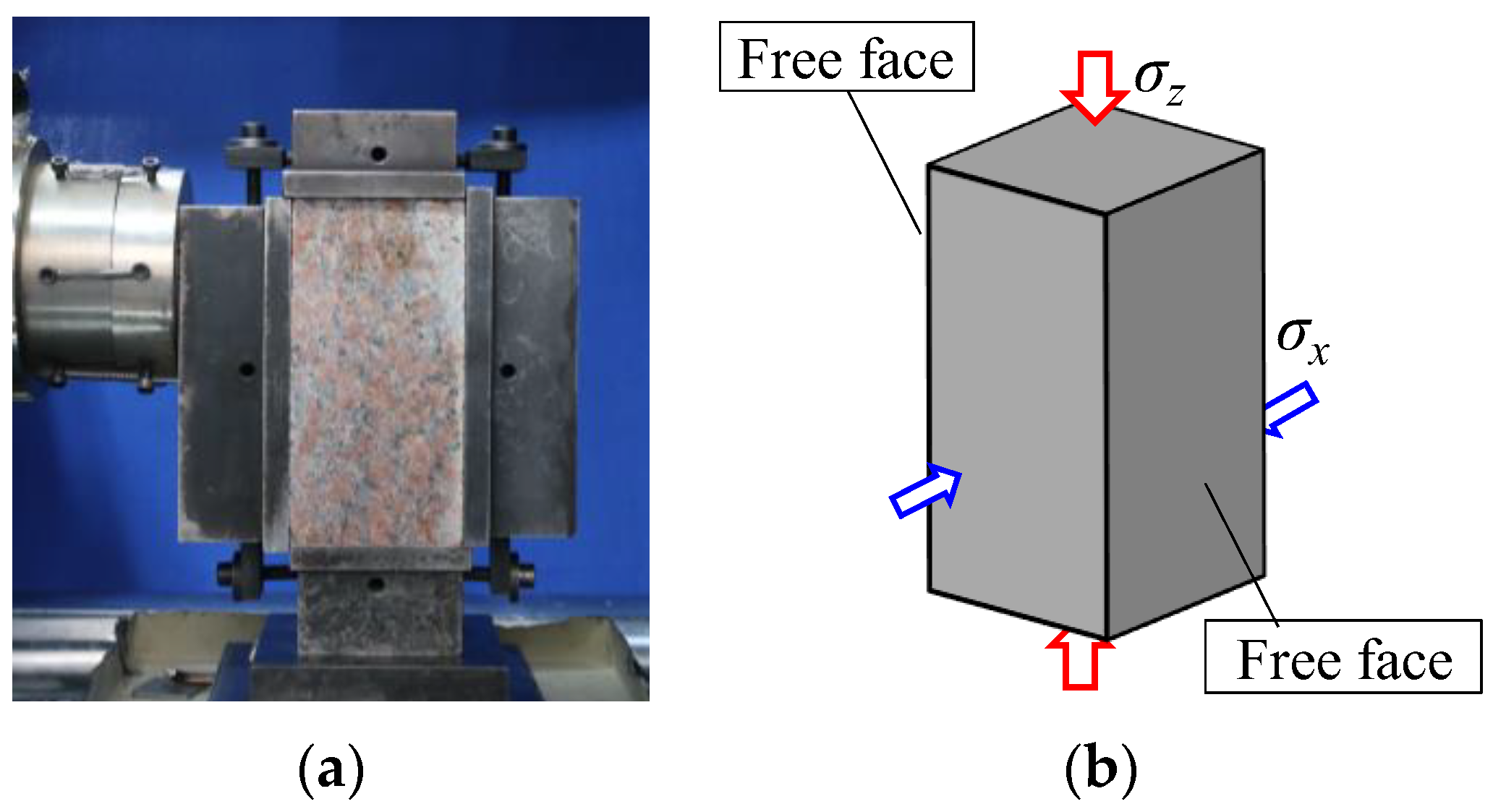
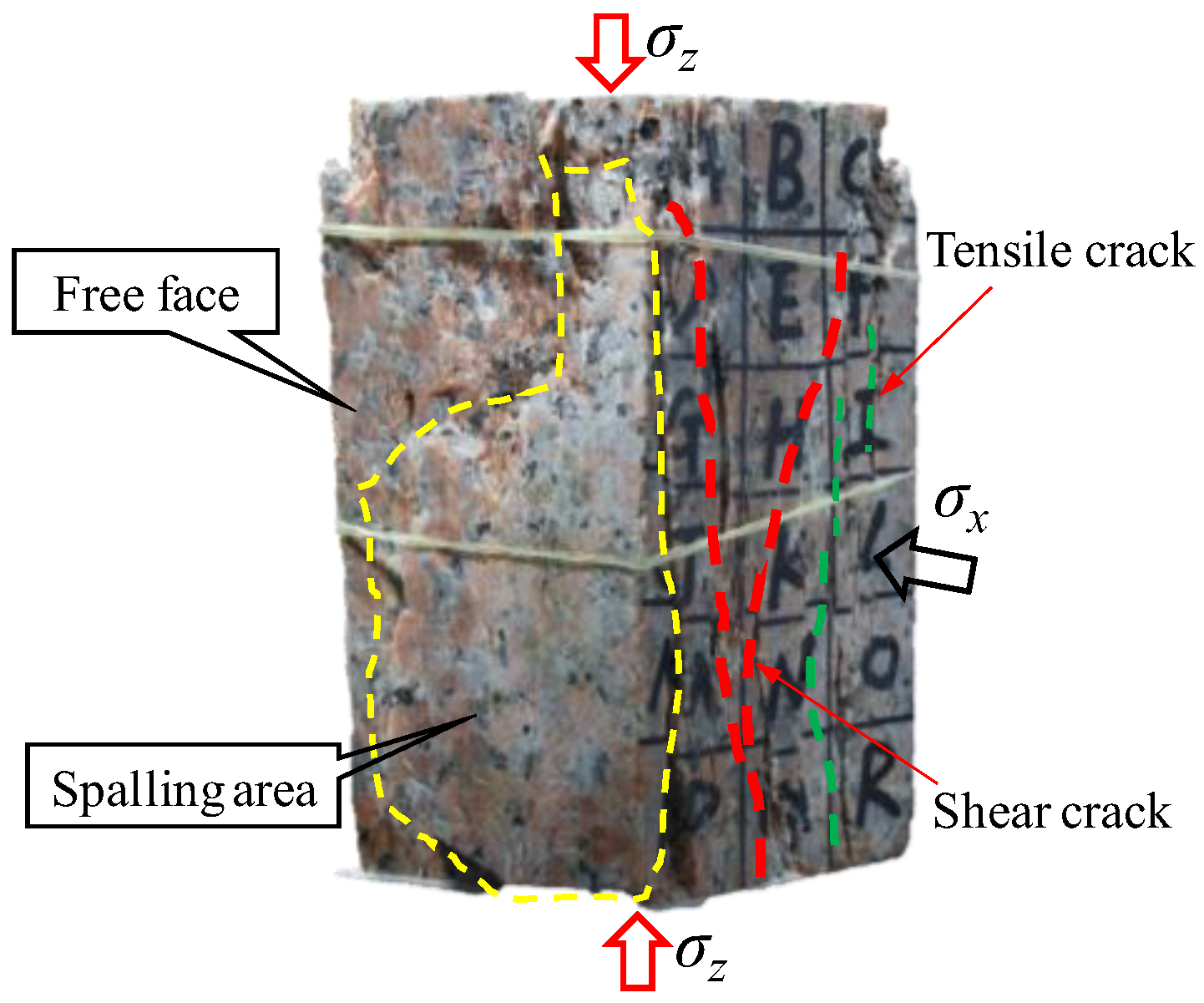
| Density (g/cm3) | Elastic Modulus (GPa) | Poisson’s Ratio | Uniaxial Compressive Strength (MPa) |
|---|---|---|---|
| 2.63 | 35.2 | 0.27 | 124 |
| Test Type | Specimen Number | Pre-Loading | Loading Rate |
|---|---|---|---|
| Brazilian splitting test | GBD-S-1 | F1: 5 kN | F1: 50 N/s |
| GBD-S-2 | |||
| GBD-S-3 | |||
| Direct shear test | GDS-1 | F1: 10 kN F2: 5 kN | F2: 500 N/s |
| GDS-2 | |||
| GDS-3 |
| Crack Type | Shape Characteristic | Frequency/kHz | Amplitude of the High Energy/dB | Duration of the High Energy/s |
|---|---|---|---|---|
| Tensile | “bar” form | 0–30 | 3–5 | 0–0.02 |
| Shear | “jungle” form | 0–100 | 4–5 | 0.005–0.02 |
| k (Times) | Accuracy (%) |
|---|---|
| 1 | 100 |
| 2 | 75 |
| 3 | 87.5 |
| 4 | 100 |
| 5 | 87.5 |
| Average accuracy | 90 |
| A (Initial Compaction Stage) | B (Elastic Period) | C (Elastic-Plastic Stage) | D (Plastic Stage) | |
|---|---|---|---|---|
| tensile crack | 0 | 0% | 85% | 25% |
| shear crack | 0 | 0% | 15% | 75% |
| A (Initial Compaction Stage) | B (Elastic Period) | C (Elastic-Plastic Stage) | D (Plastic Stage) | |
|---|---|---|---|---|
| tensile crack | 0 | 0% | 92% | 20% |
| shear crack | 0 | 0% | 8% | 80% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, H.; Jiang, J.; Su, G. Rock Crack Types Identification by Machine Learning on the Sound Signal. Appl. Sci. 2023, 13, 7654. https://doi.org/10.3390/app13137654
Jiang H, Jiang J, Su G. Rock Crack Types Identification by Machine Learning on the Sound Signal. Applied Sciences. 2023; 13(13):7654. https://doi.org/10.3390/app13137654
Chicago/Turabian StyleJiang, Hao, Jianqing Jiang, and Guoshao Su. 2023. "Rock Crack Types Identification by Machine Learning on the Sound Signal" Applied Sciences 13, no. 13: 7654. https://doi.org/10.3390/app13137654
APA StyleJiang, H., Jiang, J., & Su, G. (2023). Rock Crack Types Identification by Machine Learning on the Sound Signal. Applied Sciences, 13(13), 7654. https://doi.org/10.3390/app13137654





