Optimization of Vehicle Powertrain Mounting System Based on Generalized Inverse Cascade Method under Uncertainty
Abstract
:1. Introduction
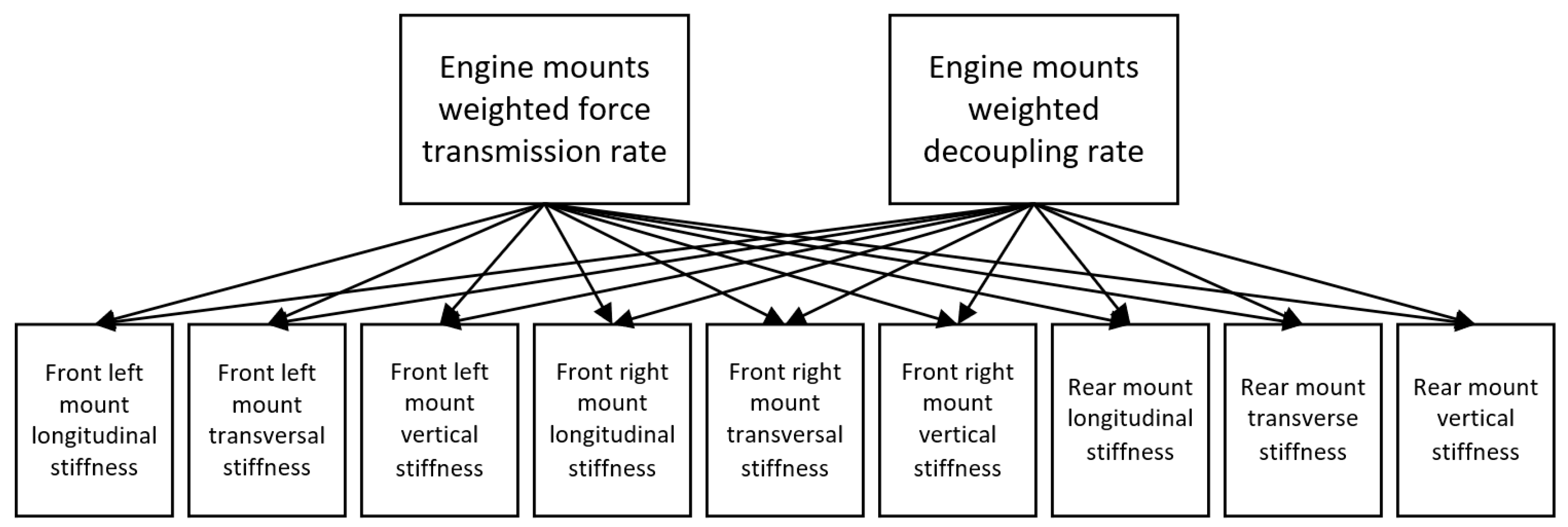
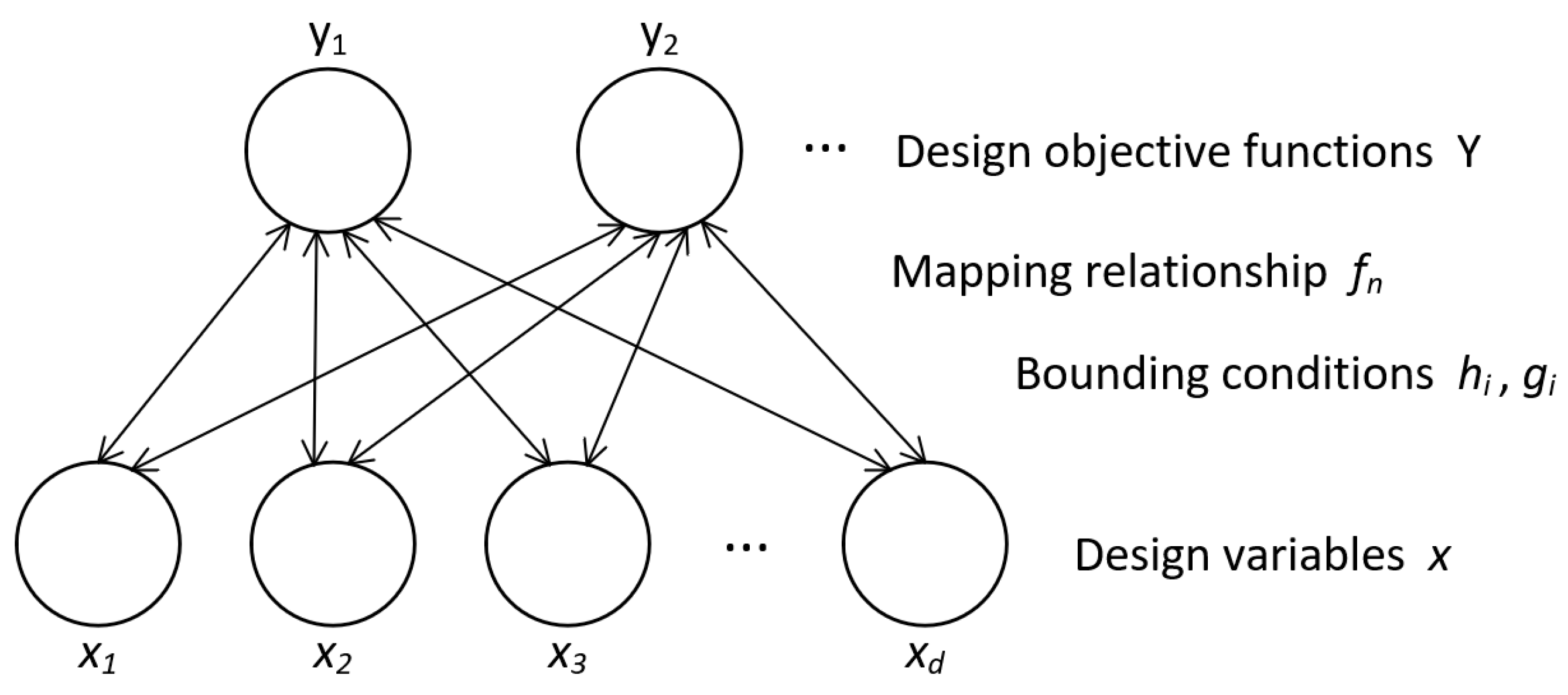
2. Multi-Objective Two-Level Model Construction
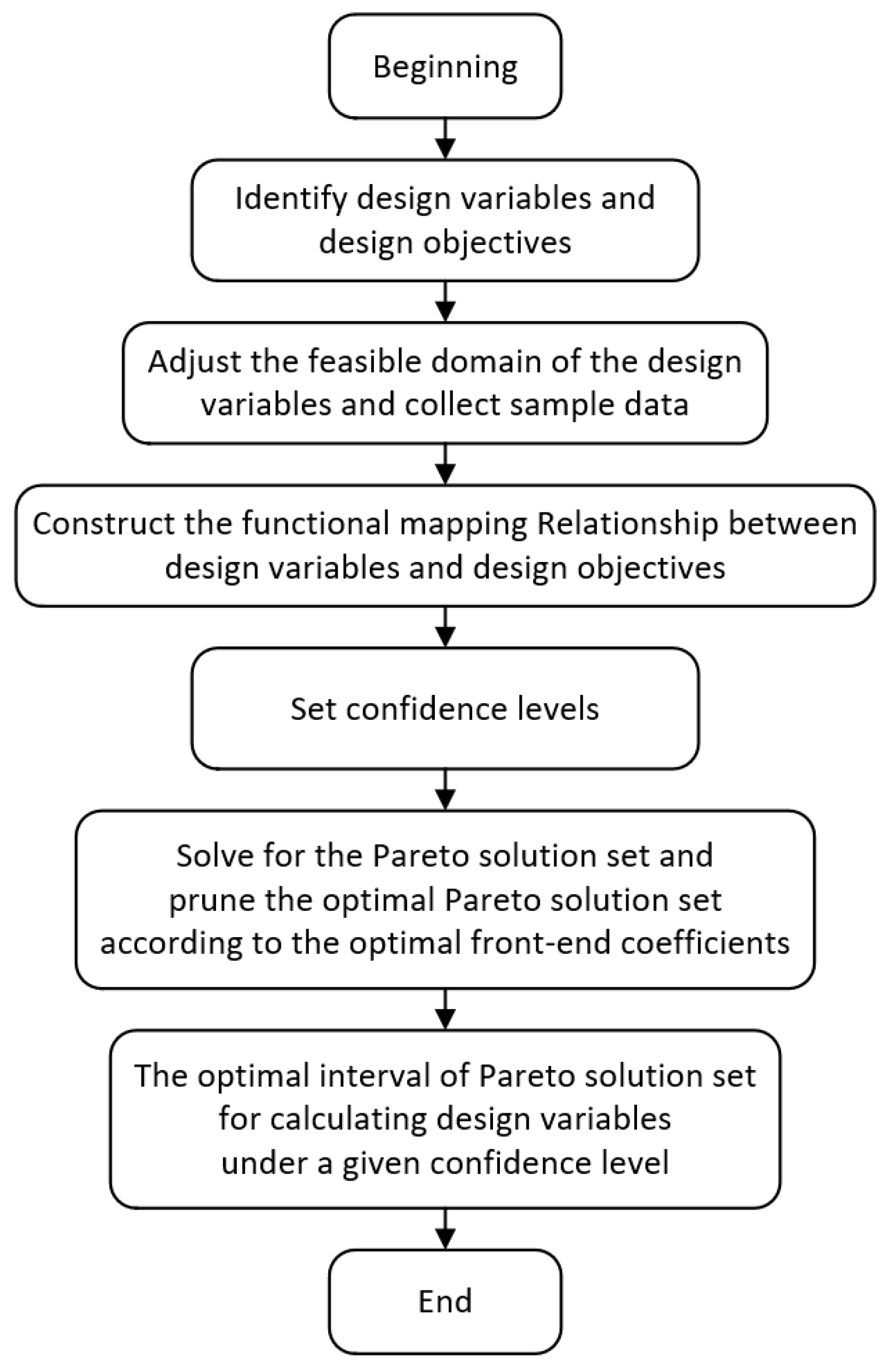
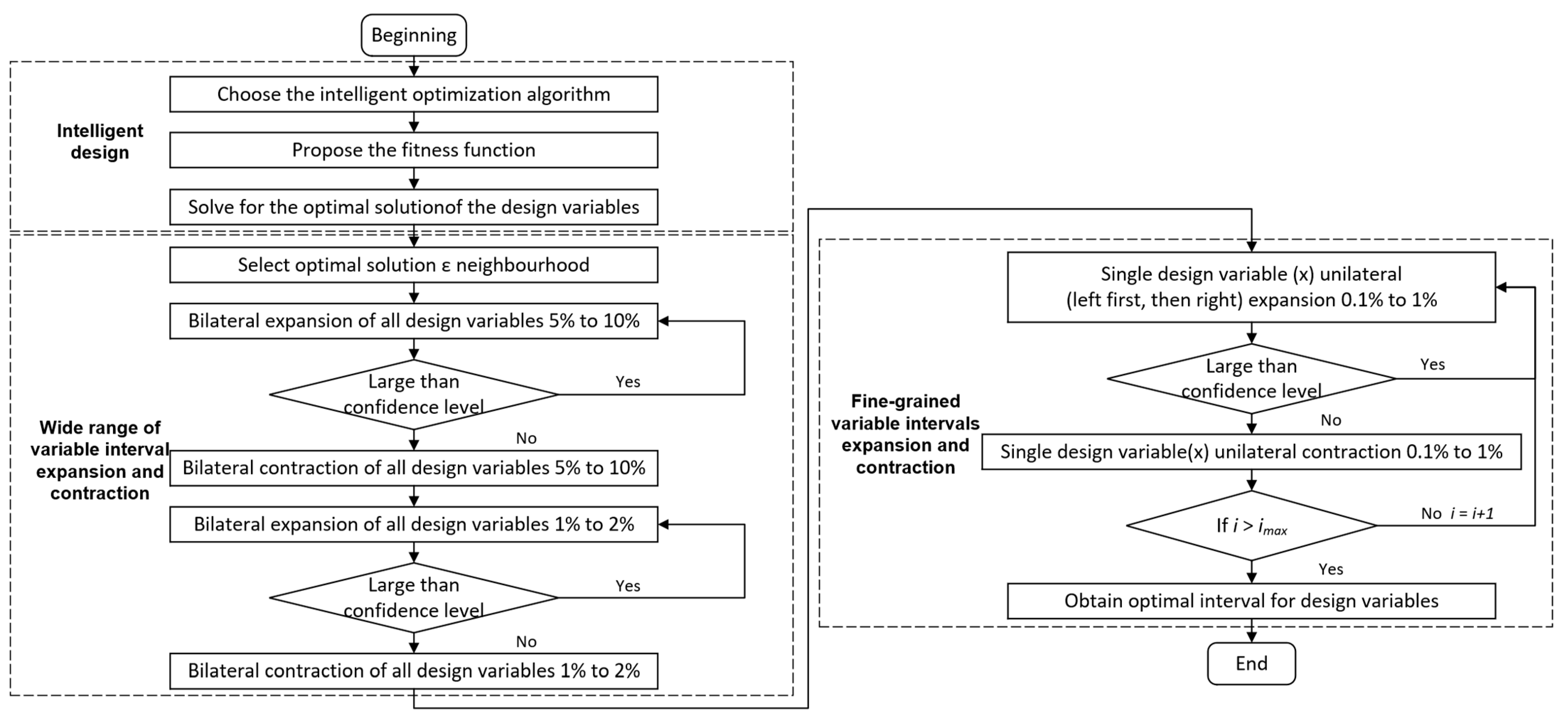
3. Introduction to the Generalized Inverse Cascade Method
| Algorithm 1: generalized inverse cascade method |
| Input: initial interval of design variables xi,1: =(ai,1, bi,1), mapping relationship fn between design variables x and design objectives Y, confidence threshold H0 Ouput: optimal interval of design variables (ai,3, bi,3) 1. Adjust the design variable feasible domain xi,2: =(ai,2, bi,2). 2. Calculate the optimal solution xi,opt for the design variables according to the intelligent optimization algorithm. 3. (ai,3, bi,3): =(xi,opt − ε, xi,opt + ε)//choose the optimal solution neighbourhood (ai,3, bi,3): =(xi,opt − ε, xi,opt + ε) 4. While Hc > H0, do 5. ai,3: =ai,3 × (90% to 95%)//Reduce the left-hand side of all design variables by 5% to 10%. 6. bi,3: =bi,3 × (105% to 110%)//Increase the right-hand side of all design variables by 5% to 10%. 7. Calculate Hc from fn. 8. end while 9. ai,3: =ai,3 × (105% to 110%)//Increase the left-hand side of all design variables by 5% to 10%. 10. bi,3: =bi,3 × (90% to 95%)//Reduce the right-hand side of all design variables by 5% to 10%. 11. While Hc > H0, do 12. ai,3: =ai,3 × (98% to 99%)//Reduce the left-hand side of all design variables by 1% to 2%. 13. bi,3: =bi,3 × (101% to 102%)//Increase the right-hand side of all design variables by 1% to 2%. 14. Calculate Hc from fn 15. end while 16. ai,3: =ai,3 × (101% to 102%)//Increase the left-hand side of all design variables by 1% to 2%. 17. bi,3: =bi,3 × (98% to 99%)//Reduce the right-hand side of all design variables by 1% to 2%. 18. for i: =1 to imax do//from the 1st design variable to the imax design variable 19. While Hc > H0, do 20. ai,3: =ai,3 × (99% to 99.9%)//0.1% to 1% reduction in the left-hand side of the ith design variable 21. Calculate Hc from fn 22. end while 23. ai,3: =ai,3 × (100.1% to 101%)//0.1% to 1% increase in the left-hand side of the ith design variable 24. While Hc >H0, do 25. bi,3: =bi,3 × (100.1% to 101%)//0.1% to 1% increase in the right-hand side of the ith design variable 26. Calculate Hc from fn 27. end while 28. bi,3: =bi,3 × (99% to 99.9%)//0.1% to 1% reduce in the right-hand side of the ith design variable 29. end for 30. Return (ai,3, bi,3) 31. End the generalized inverse cascade method. |
4. Example
4.1. Identify Design Objectives and Design Variables
4.2. A Platform for Acquiring Basic Sample Data
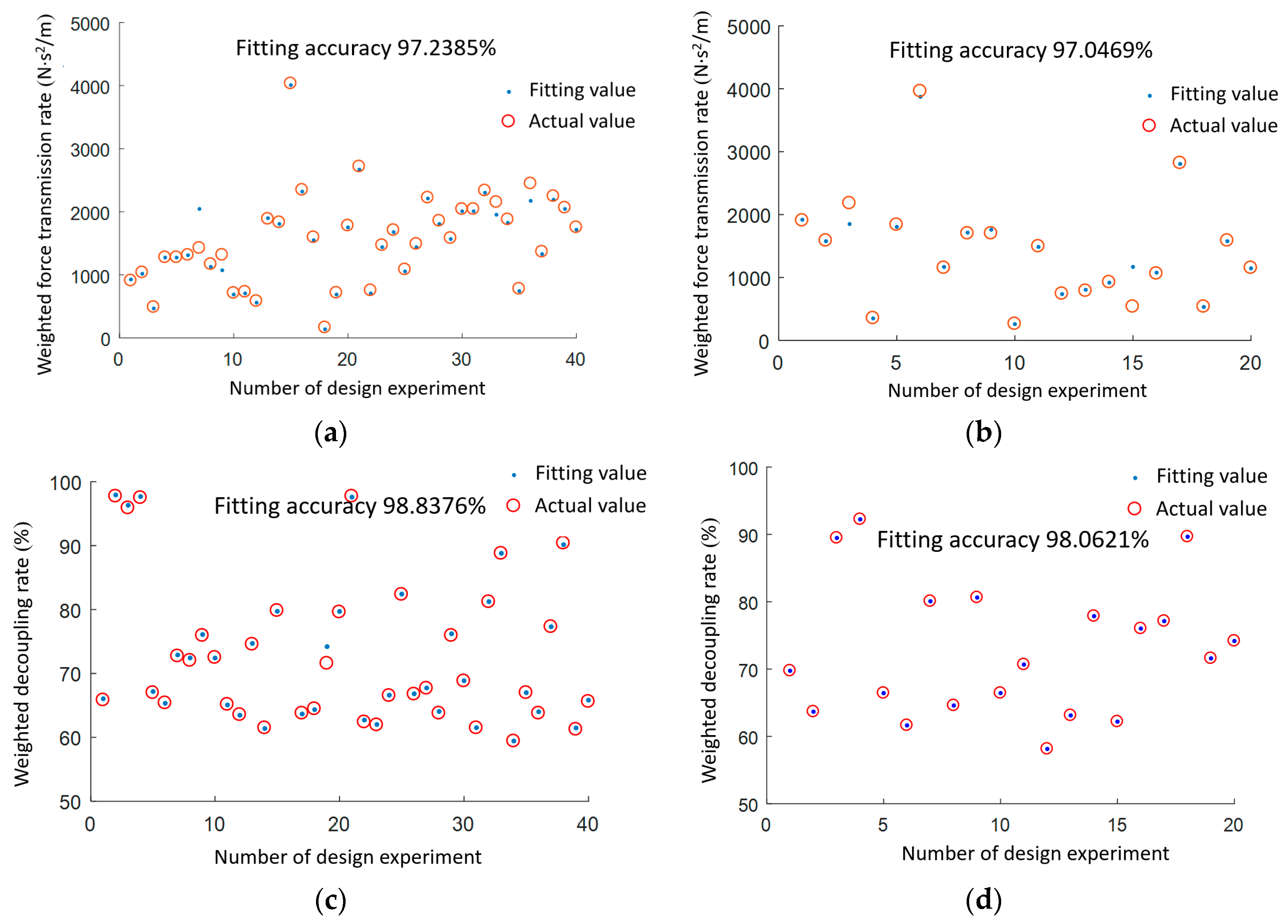
4.3. The Mapping Function for Design Variables and Design Objectives
4.4. Optimal Intervals for Design Variables Based on Generalized Inverse Calculation Solving
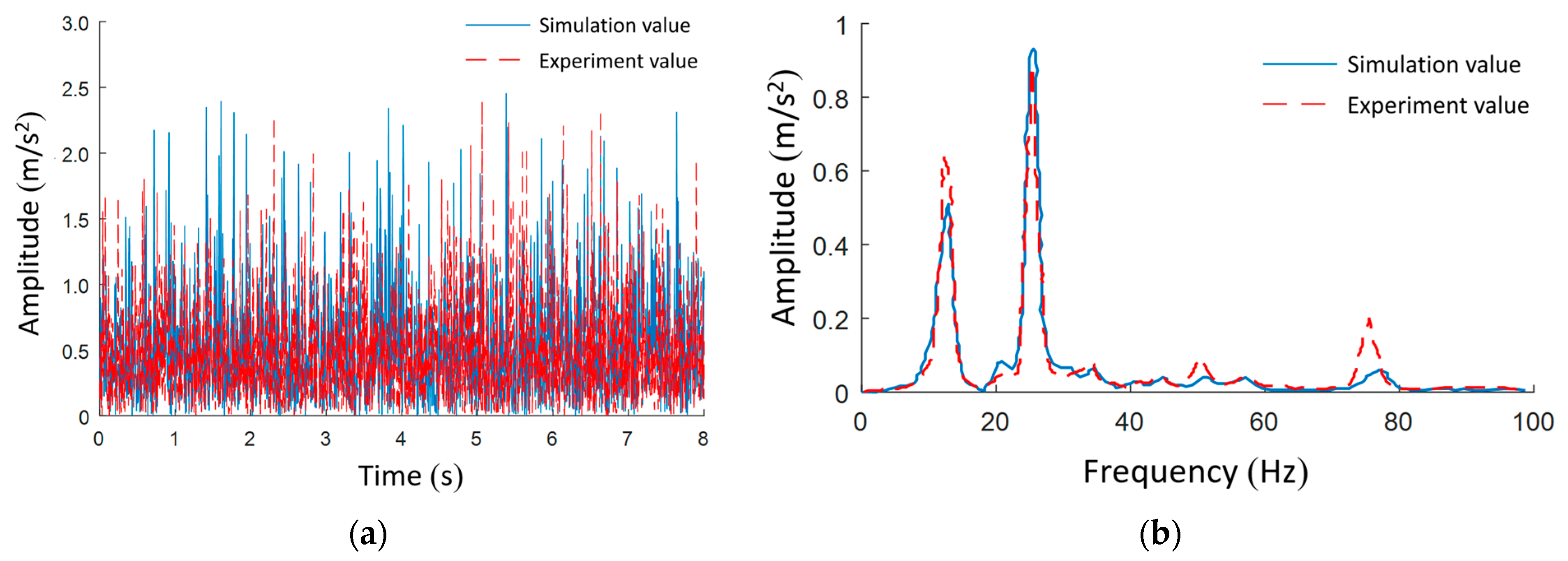
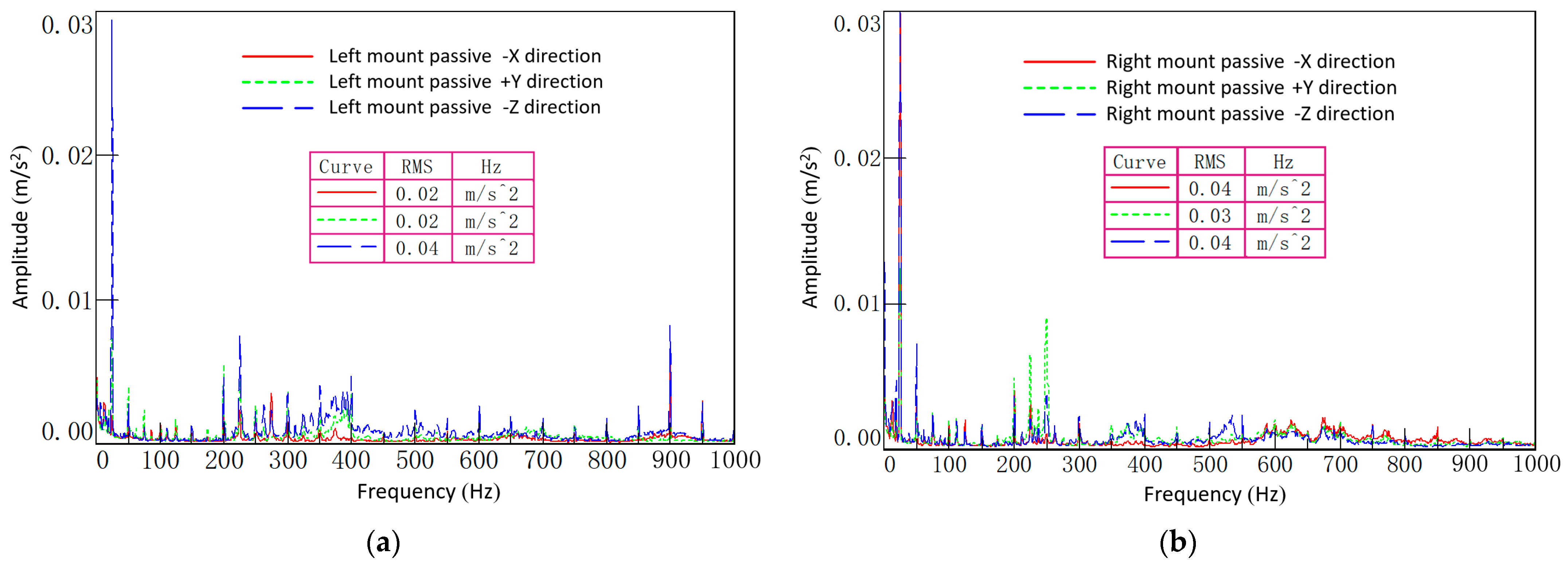
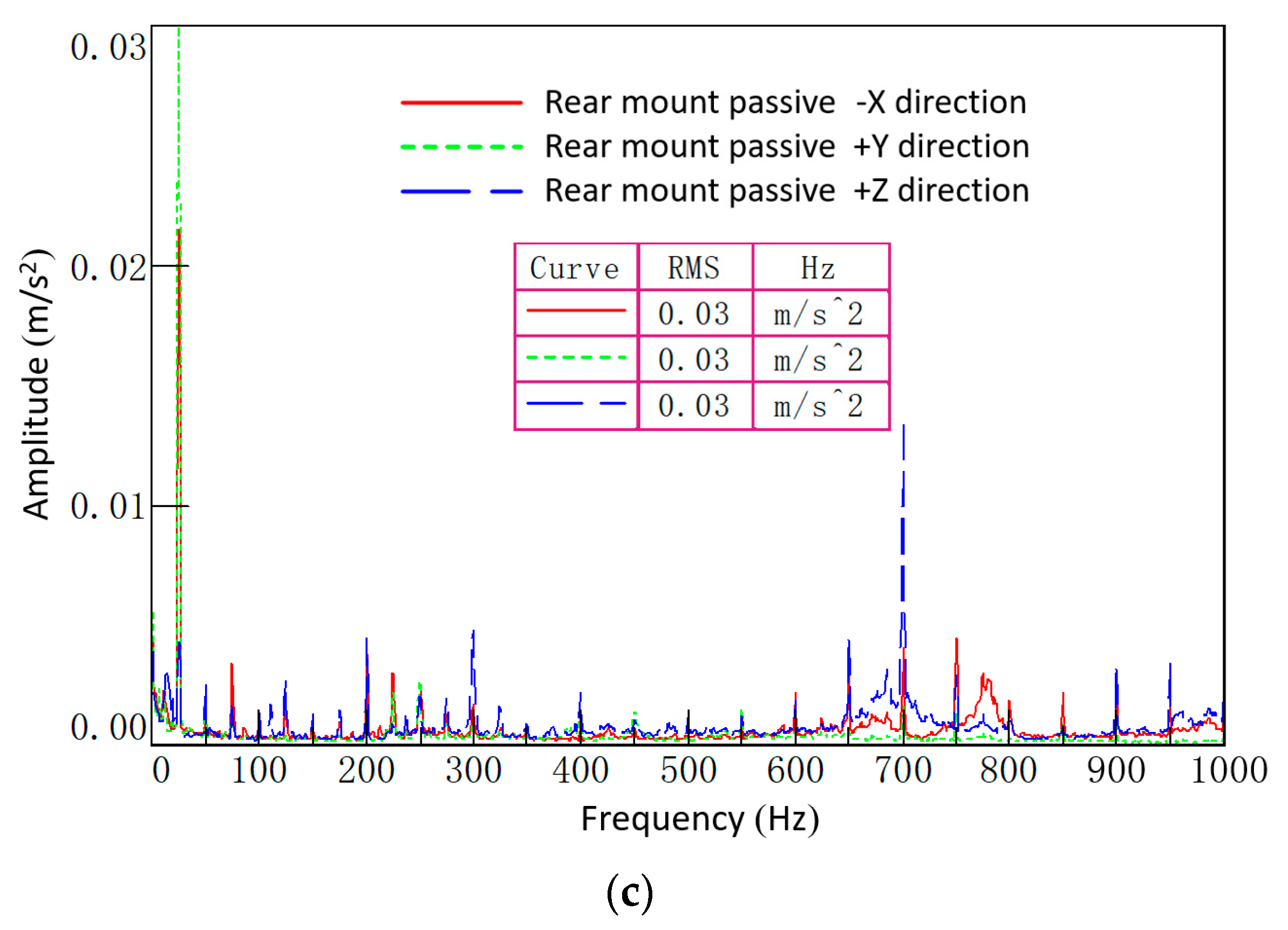
5. Experimental Verification
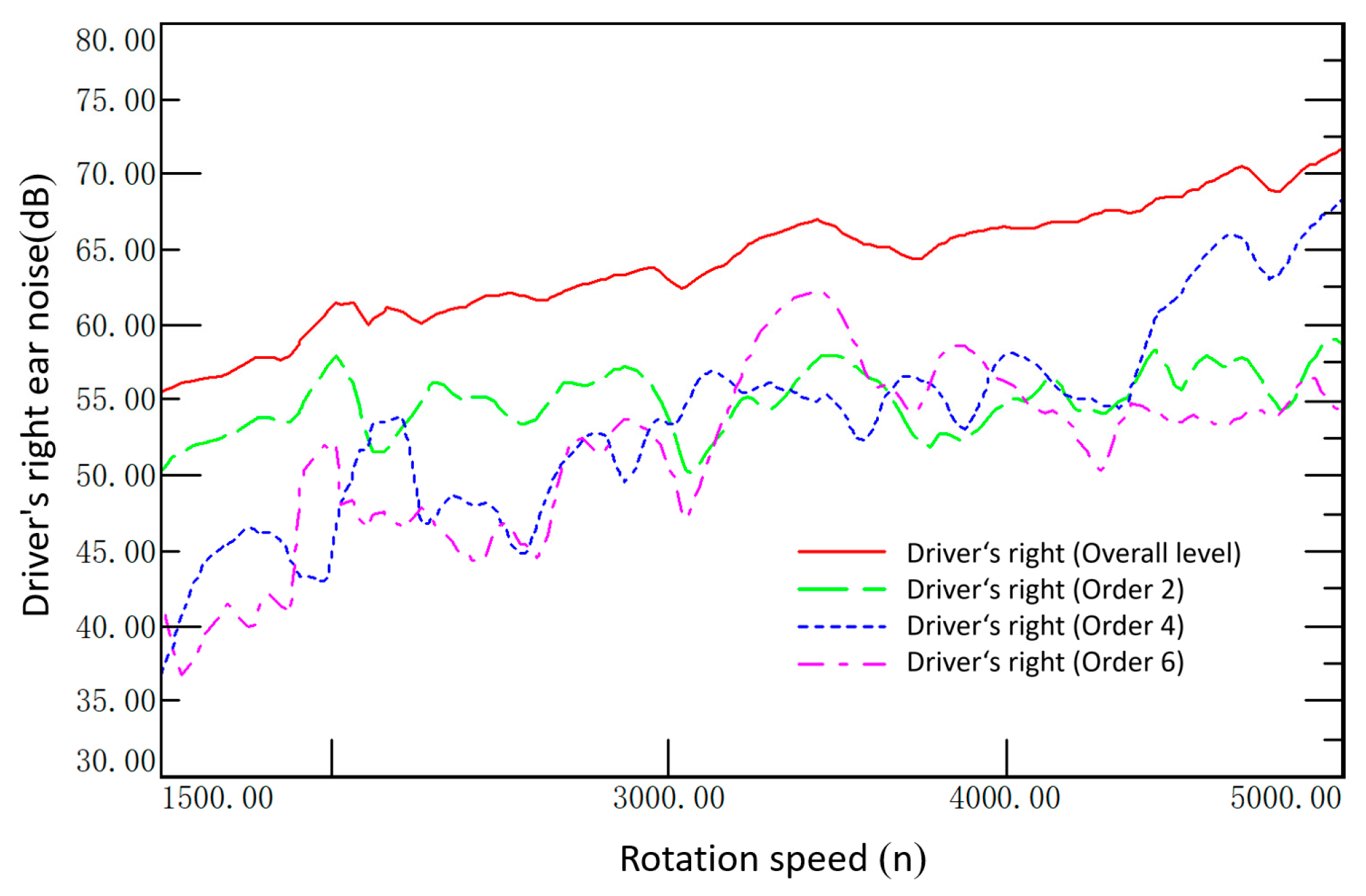
5.1. Idle Condition
5.2. Third Gear Full Throttle Acceleration Condition
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, H.; Huang, X.; Ding, W.; Zhang, S.; Pang, J. Optimization of electric vehicle sound package based on LSTM with an adaptive learning rate forest and multiple-level multiple-object method. Mech. Syst. Signal Process. 2023, 187, 109932. [Google Scholar] [CrossRef]
- Chang, L.; Jiang, A.; Rao, M.; Ma, F.; Huang, H.; Zhu, Z.; Hu, Y. Progress of low-frequency sound absorption research utilizing intelligent materials and acoustic metamaterials. RSC Adv. 2021, 11, 37784–37800. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Lu, Z. Optimal Design Method of Power-train Mounting System for Generalized Force Transmissibility Reduction. J. Mech. Eng. 2011, 47, 52–58. [Google Scholar] [CrossRef]
- Shangguan, W.; Liu, X.; Lv, Z. Design Method of Automotive Powertrain Mounting System Based on Vibration and Noise Limitations of Vehicle Level. Mech. Syst. Signal Process. 2016, 76–77, 677–695. [Google Scholar] [CrossRef]
- Huang, X.; Huang, H.; Wu, J.; Yang, M.; Ding, W. Sound quality prediction and improving of vehicle interior noise based on deep Convolutional neural networks. Expert Syst. Appl. 2020, 160, 113657. [Google Scholar] [CrossRef]
- Sun, Q.; Liu, S.; Niu, N. A Decoupling Method of Powertrain Mounting Systems and Vibration Characteristics Analysis of Complex Flexible Foundations. J. Vib. Shock 2019, 38, 258–263. [Google Scholar] [CrossRef]
- Huang, H.; Lim, T.C.; Wu, J.; Ding, W.; Pang, J. Multitarget prediction and optimization of pure electric vehicle tire/road airborne noise sound quality based on a knowledge-and data-driven method. Mech. Syst. Signal Process. 2023, 197, 110361. [Google Scholar] [CrossRef]
- Huang, H.; Huang, X.; Ding, W.; Yang, M.; Yu, X.; Pang, J. Vehicle vibro-acoustical comfort optimization using a multi-objective interval analysis method. Expert Syst. Appl. 2023, 213, 119001. [Google Scholar] [CrossRef]
- Zhou, M.; Hou, Z. Optimization on Engine Mounting Based on Genetic Algorithm. Automob. Technol. 2006, 9, 13–16. [Google Scholar]
- Zhou, G.; Jiang, W.; Wu, H. Optimal design of engine mount system by minimizing the total force transmission. J. Vib. Shock 2008, 27, 56–58. [Google Scholar] [CrossRef]
- Tong, W.; Chen, J.; Song, X. Multi-objective optimization of engine mounting system based on ADAMS. Automot. Eng. 2011, 33, 971–975. [Google Scholar] [CrossRef]
- Pan, G.; Fu, B.; Wang, G. Optimization design of a powertrain mount-system based on the TPA and genetic algorithm. J. Vib. Shock 2021, 40, 279–286. [Google Scholar] [CrossRef]
- Chen, J.; Xu, C. Optimization Design and Reliability Analysis of Engine Mount System. Automot. Eng. 2009, 31, 234–238. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, X.; Li, Y. Optimization of engine mounting system based on Pareto clustering immune evolutionary algorithm and robustness analysis. J. Hefei Univ. Technol. (Nat. Sci.) 2012, 35, 1589–1593. [Google Scholar]
- Shi, P.; Chen, W.; Gao, L. Robustness Design of Powertrain Mount System Based on Monte Carlo Method. Automot. Eng. 2010, 32, 707–711. [Google Scholar] [CrossRef]
- Zheng, G.; Dong, Z.; Hao, T. Stiffness optimization and robustness analysis of the mount system based on the RSM model. J. Mach. Des. 2020, 37, 71–77. [Google Scholar] [CrossRef]
- Wu, J.; Liu, X.; Shan, Y. Robustness Optimization of Engine Mounting System Based on Six Sigma and Torque Roll Axis Decoupling Method. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2019, 233, 1047–1060. [Google Scholar] [CrossRef]
- Chen, J.; Liu, C.; Yang, Z. Robust optimization design of engine mounting system based on Six Sigma method. J. Hefei Univ. Technol. (Nat. Sci.) 2017, 40, 1469–1473. [Google Scholar]
- Huang, H.B.; Wu, J.H.; Huang, X.R.; Yang, M.L.; Ding, W.P. A generalized inverse cascade method to identify and optimize vehicle interior noise sources. J. Sound Vib. 2020, 467, 115062. [Google Scholar] [CrossRef]
- Xin, F.; Qian, L.; Du, H. Multi-Objective Robust Optimization Design for Powertrain Mount System of Electric Vehicles. J. Low Freq. Noise Vib. Act. Control 2017, 36, 243–260. [Google Scholar] [CrossRef]
- Li, C.; Cong, Z.Z.; Bao, J.D. Robust Optimization of Powertrain Mounting System Based on Interval Analysis. In Proceedings of the Fifth Asia International Symposium on Mechatroni (AISM 2015), Guilin, China, 7–10 October 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Cai, B.; Shangguan, W.B.; Lü, H. An Efficient Analysis and Optimization Method for Powertrain Mounting Systems Involving Interval Uncertainty. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 234, 1318–1329. [Google Scholar] [CrossRef]
- Chen, J.; Li, S.; Liu, C.; Deng, Z.; Shu, H. Robustness Optimization of Powertrain Mounting Systems Based on Chebyshev Interval Method. China Mech. Eng. 2018, 29, 314–319. [Google Scholar]
- Xie, Z.; Yu, D.; Li, R. Robust Optimization Design of Engine Mount Systems Based on Interval Analysis. Automot. Eng. 2014, 36, 1503–1507+1527. [Google Scholar] [CrossRef]
- Lü, H.; Mao, H.; Huang, X. An Effective Approach for Reliability-Based Robust Design Optimization of Uncertain Powertrain Mounting Systems Involving Imprecise Information. Eng. Comput. 2021, 38, 1193–1214. [Google Scholar] [CrossRef]
- Lü, H.; Zheng, Z.; Huang, X. A Methodology for Design Optimization of Powertrain Mounting Systems Involving Hybrid Interval-Random Uncertainties. Struct. Multidiscip. Optim. 2021, 63, 1265–1285. [Google Scholar] [CrossRef]
- Xing, T. Vehicle Suspension K&C Characteristic Analysis and Its EDBS Implementation. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2015. [Google Scholar]
- Huang, H.; Huang, X.; Ding, W.; Yang, M.; Fan, D.; Pang, J. Uncertainty optimization of pure electric vehicle interior tire/road noise comfort based on data-driven. Mech. Syst. Signal Process. 2022, 165, 108300. [Google Scholar] [CrossRef]
- Zhuang, C.; Wen, H.; Ni, X.; Zhang, D.; Bao, Y.; Huang, H. Optimization of Cab Vibration Comfort for Construction Machinery Based on Multi-Target Regression Forests. Machines 2022, 10, 1148. [Google Scholar] [CrossRef]
- Cheng, L.; Wen, H.; Ni, X.; Zhuang, C.; Zhang, W.; Huang, H. Optimization Study on the Comfort of Human-Seat Coupling System in the Cab of Construction Machinery. Machines 2023, 11, 30. [Google Scholar] [CrossRef]
- Luo, J. Simulation Analysis and Optimization Study of a Vehicle Powertrain Mounting System. Master’s Thesis, South China University of Technology, Guangzhou, China, 2021. [Google Scholar]


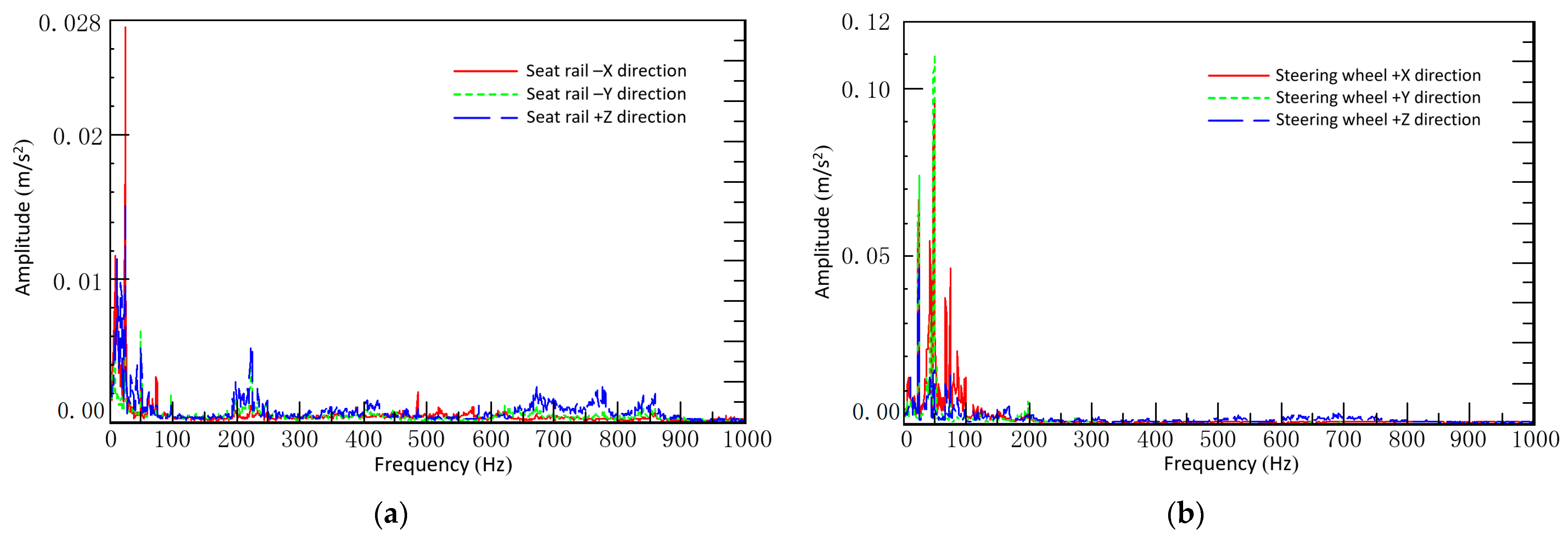

| Mount Direction | Mount Stiffness (N/mm) |
|---|---|
| Front left longitudinal mount (X-direction) | 28 ≤ SFL,X ≤ 52 |
| Front left transversal mount (Y-direction) | 35 ≤ SFL,Y ≤ 65 |
| Front left vertical mount (Z-direction) | 210 ≤ SFL,Z ≤ 390 |
| Front right longitudinal mount (X-direction) | 28 ≤ SFR,X ≤ 52 |
| Front right transversal mount (Y-direction) | 35 ≤ SFR,Y ≤ 65 |
| Front right vertical mount (Z-direction) | 210 ≤ SFR,Z ≤ 390 |
| Rear longitudinal mount (X-direction) | 36.4 ≤ SRR,X ≤ 67.6 |
| Rear transversal mount (Y-direction) | 117.6 ≤ SRR,Y ≤ 218.4 |
| Rear vertical mount (Z-direction) | 176.4 ≤ SRR,Z ≤ 327.6 |
| Sample | SFL,X (N/mm) | SFL,Y (N/mm) | SFL,Z (N/mm) | SFR,X (N/mm) | SFR,Y (N/mm) | SFR,Z (N/mm) | SRR,X (N/mm) | SRR,Y (N/mm) | SRR,Z (N/mm) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 48 | 41 | 358 | 44.1 | 62.7 | 260 | 53.7 | 126 | 224 |
| 2 | 28.3 | 49 | 364 | 32.8 | 47.5 | 378 | 53.3 | 160 | 306 |
| … | … | … | … | … | … | … | … | … | … |
| 59 | 37.7 | 53.2 | 328 | 51 | 37.6 | 360 | 62.4 | 178 | 298 |
| 60 | 52 | 61.2 | 314 | 34 | 60.4 | 323 | 51 | 138 | 293 |
| Design Variable | Lower Limit of the Optimization Interval (N/mm) | Upper Limit of the Optimization Interval (N/mm) |
|---|---|---|
| SFL,X | 28 | 38 |
| SFL,Y | 36 | 49 |
| SFL,Z | 233 | 271 |
| SFR,X | 28 | 35 |
| SFR,Y | 35 | 48 |
| SFR,Z | 229 | 282 |
| SRR,X | 51 | 62 |
| SRR,Y | 172 | 207 |
| SRR,Z | 178 | 327 |
| Design Variable | Lower Limit of the Optimization Interval (N/mm) | Upper Limit of the Optimization Interval (N/mm) |
|---|---|---|
| SFL,X | 28 | 36 |
| SFL,Y | 39 | 51 |
| SFL,Z | 256 | 311 |
| SFR,X | 28 | 41 |
| SFR,Y | 40 | 50 |
| SFR,Z | 265 | 304 |
| SRR,X | 57 | 66 |
| SRR,Y | 203 | 213 |
| SRR,Z | 199 | 325 |
| Mount Direction | Mount Element Stiffness Value (N/mm) | ||||
|---|---|---|---|---|---|
| Original Stiffness Value | Median Value of Pareto Optimal Solution Set #1 | Median Value of Pareto Optimal Solution Set #2 | Minimum Value of Pareto Optimal Solution Set #1 | Maximum Value of Pareto Optimal Solution Set #1 | |
| SFL,X | 40 | 33 | 32 | 28 | 38 |
| SFL,Y | 50 | 42.5 | 45 | 36 | 49 |
| SFL,Z | 300 | 252 | 283.5 | 233 | 271 |
| SFR,X | 40 | 31.5 | 34.5 | 28 | 35 |
| SFR,Y | 50 | 41.5 | 45 | 35 | 48 |
| SFR,Z | 300 | 255.5 | 284.5 | 229 | 282 |
| SRR,X | 52 | 56.5 | 61.5 | 51 | 62 |
| SRR,Y | 168 | 189.5 | 208 | 172 | 207 |
| SRR,Z | 252 | 252.5 | 262 | 178 | 327 |
| Mount Direction | Force Transmission Rate (N·s2/m) | ||||
|---|---|---|---|---|---|
| Original Stiffness Value | Median Value of Pareto Optimal Solution Set #1 | Median Value of Pareto Optimal Solution Set #2 | Minimum Value of Pareto Optimal Solution Set #1 | Maximum Value of Pareto Optimal Solution Set #1 | |
| SFL,X | 700 | 599 | 638 | 615 | 668 |
| SFL,Y | 4560 | 3872 | 4053 | 4096 | 3989 |
| SFL,Z | 956 | 860 | 816 | 890 | 877 |
| SFR,X | 1400 | 1182 | 1226 | 1207 | 1266 |
| SFR,Y | 4606 | 4179 | 4110 | 4197 | 4050 |
| SFR,Z | 923 | 825 | 807 | 807 | 798 |
| SRR,X | 1200 | 1004 | 1128 | 1120 | 1156 |
| SRR,Y | 800 | 716 | 681 | 696 | 749 |
| SRR,Z | 736 | 618 | 695 | 688 | 638 |
| Weighted force transmission rate | 1385 | 1212 | 1233 | 1253 | 1235 |
| Mount Direction | Decoupling Rate of Main Vibration Mode (%) | ||||
|---|---|---|---|---|---|
| Original Stiffness Value | Median Value of Pareto Optimal Solution Set #1 | Median Value of Pareto Optimal Solution Set #2 | Minimum Value of Pareto Optimal Solution Set #1 | Maximum Value of Pareto Optimal Solution Set #1 | |
| X | 70.71 | 83.28 | 79.76 | 80.22 | 81.46 |
| Y | 74.51 | 81.75 | 83.68 | 80.11 | 78.60 |
| Z | 84.43 | 91.91 | 90.90 | 86.08 | 89.46 |
| θx | 76.80 | 83.05 | 80.63 | 88.57 | 77.69 |
| θy | 72.27 | 79.45 | 81.46 | 77.00 | 86.42 |
| θz | 63.06 | 83.70 | 78.54 | 81.11 | 79.58 |
| Weighted decoupling rate | 72.26 | 83.31 | 82.20 | 81.50 | 80.91 |
| Mount Direction | Vibration Isolation Rate before Optimization (dB) | Vibration Isolation Rate after Optimization (dB) |
|---|---|---|
| SFL,X | 22.72 | 26.83 |
| SFL,Y | 15.15 | 18.24 |
| SFL,Z | 23.34 | 24.50 |
| SFR,X | 20.45 | 20.51 |
| SFR,Y | 14.84 | 17.62 |
| SFR,Z | 23.75 | 24.67 |
| SRR,X | 20.38 | 22.75 |
| SRR,Y | 24.72 | 23.42 |
| SRR,Z | 23.89 | 26.53 |
| Position | X-Direction (m/s2) | Y-Direction (m/s2) | Z-Direction (m/s2) | RSS Test Value (m/s2) | RSS Limit Value (m/s2) |
|---|---|---|---|---|---|
| Seat rail | 0.0261 | 0.0134 | 0.0254 | 0.039 | 0.05 |
| Steering wheel | 0.1 | 0.1 | 0.0532 | 0.15 | 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shui, Y.; Wen, H.; Zhao, J.; Wu, Y.; Huang, H. Optimization of Vehicle Powertrain Mounting System Based on Generalized Inverse Cascade Method under Uncertainty. Appl. Sci. 2023, 13, 7615. https://doi.org/10.3390/app13137615
Shui Y, Wen H, Zhao J, Wu Y, Huang H. Optimization of Vehicle Powertrain Mounting System Based on Generalized Inverse Cascade Method under Uncertainty. Applied Sciences. 2023; 13(13):7615. https://doi.org/10.3390/app13137615
Chicago/Turabian StyleShui, Yongbo, Hansheng Wen, Jian Zhao, Yudong Wu, and Haibo Huang. 2023. "Optimization of Vehicle Powertrain Mounting System Based on Generalized Inverse Cascade Method under Uncertainty" Applied Sciences 13, no. 13: 7615. https://doi.org/10.3390/app13137615
APA StyleShui, Y., Wen, H., Zhao, J., Wu, Y., & Huang, H. (2023). Optimization of Vehicle Powertrain Mounting System Based on Generalized Inverse Cascade Method under Uncertainty. Applied Sciences, 13(13), 7615. https://doi.org/10.3390/app13137615






