A Logic-Tree Approach for Probabilistic Seismic Hazard Assessment in the Administrative Region of Attica (Greece)
Abstract
1. Introduction
2. Materials and Methods
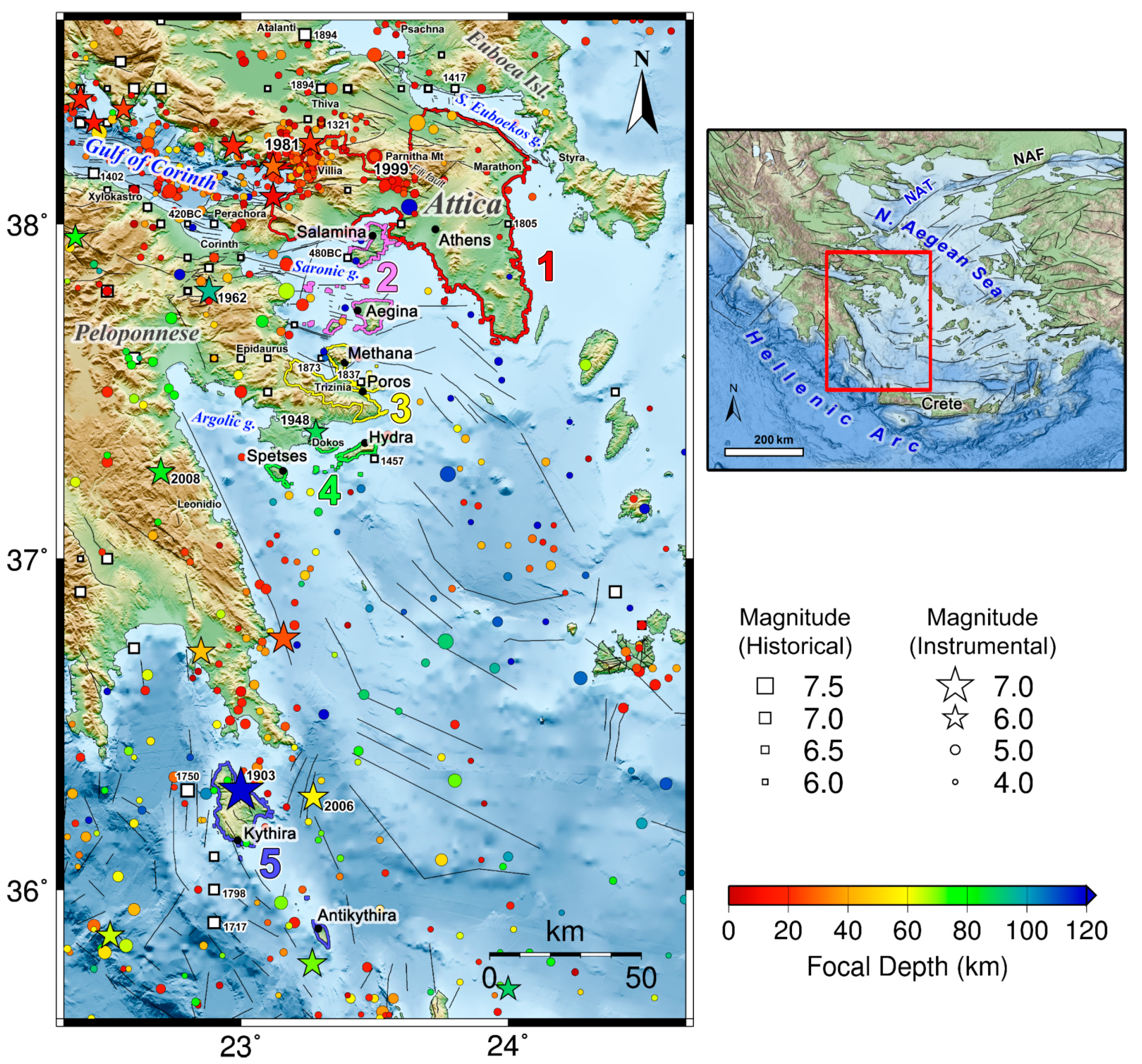
2.1. Earthquake Catalog
2.2. Seismogenic Source Zones and Seismic Parameters
2.3. Ground Motion Prediction Equations (GMPEs)
2.4. Evaluation of the Predictive Perfomance of GMPEs—GMPE Ranking
2.5. Logic Tree Approach/Structure and PSHA Calculations
3. Results
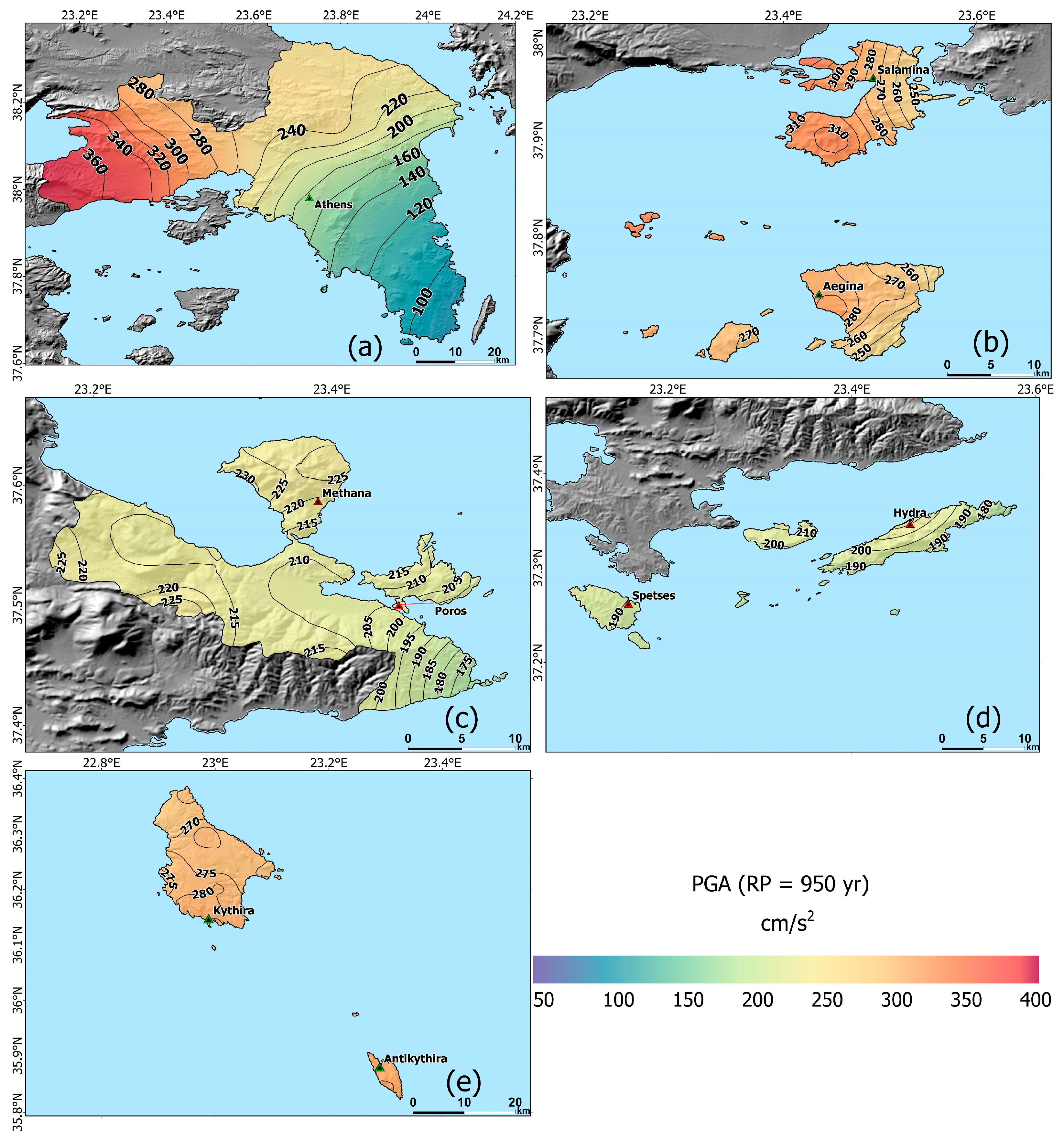
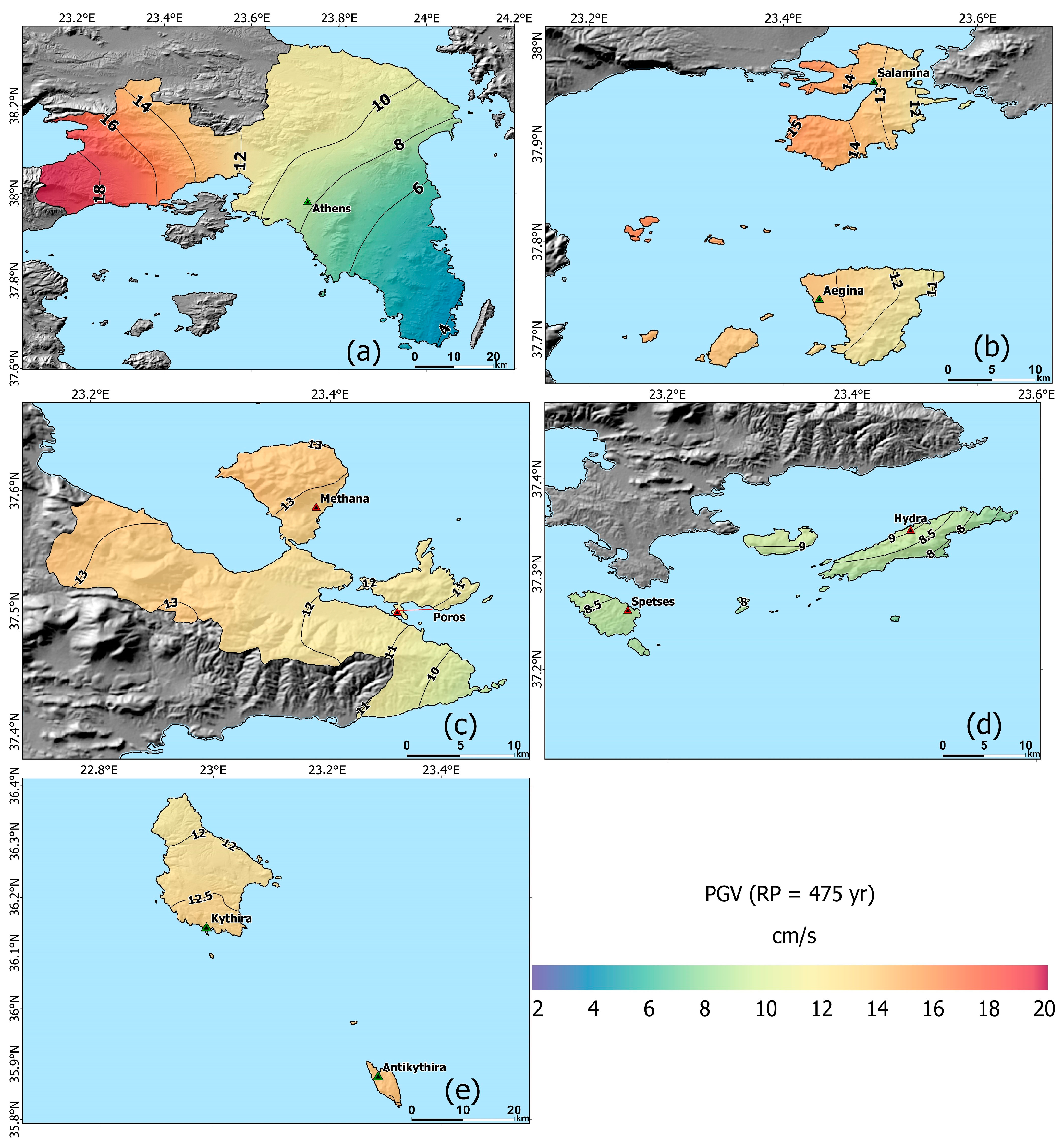
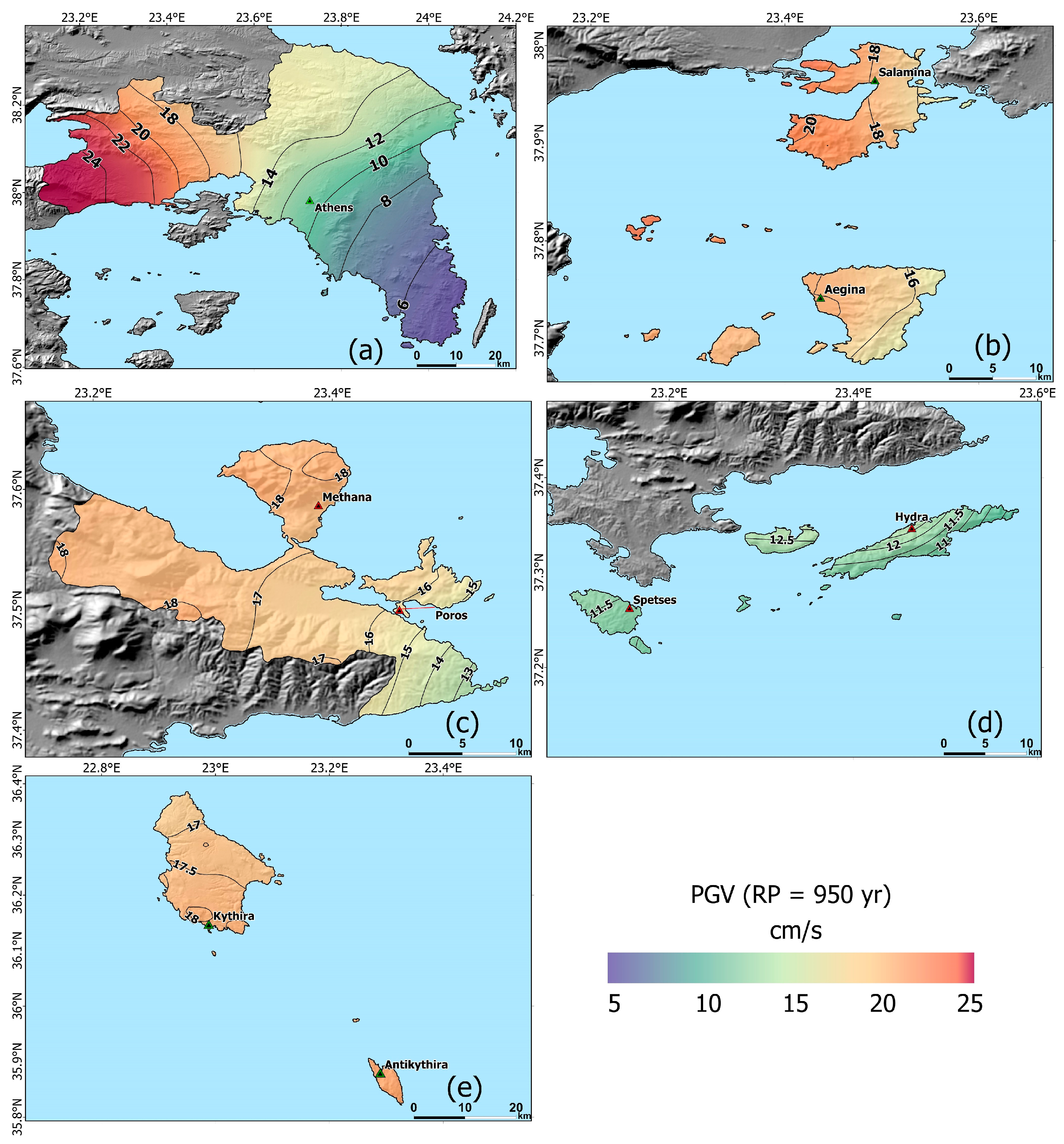
3.1. Spatial Distribution of PGA and PGV
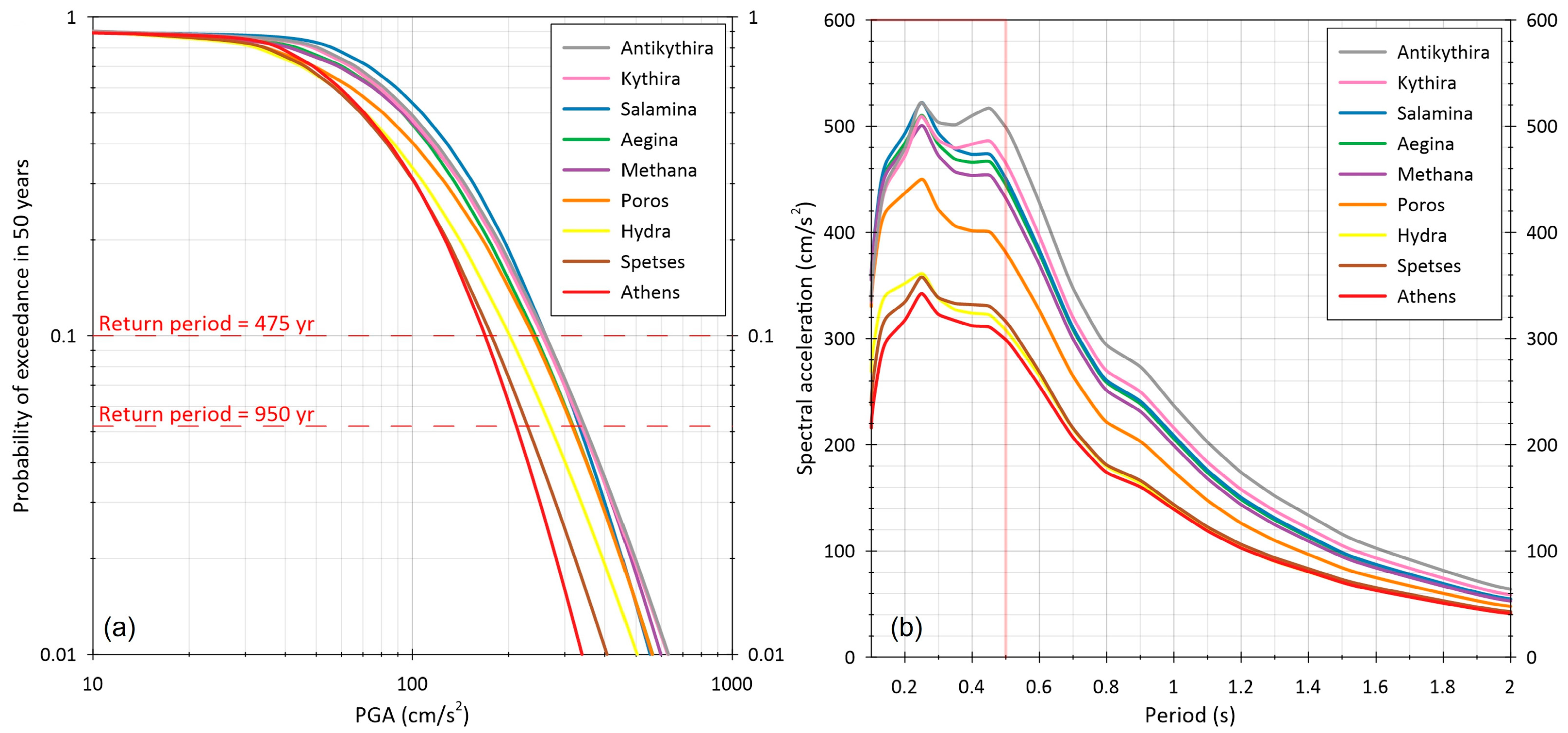
3.2. Hazard Curves and Uniform Hazard Spectra (UHS)
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Båth, M. The Seismology of Greece. Tectonophysics 1983, 98, 165–208. [Google Scholar] [CrossRef]
- Papazachos, B.C.; Papazachou, C. The Earthquakes of Greece; Ziti Publ. Co.: Thessaloniki, Greece, 2003. [Google Scholar]
- Stucchi, M.; Rovida, A.; Gomez Capera, A.A.; Alexandre, P.; Camelbeeck, T.; Demircioglu, M.B.; Gasperini, P.; Kouskouna, V.; Musson, R.M.W.; Radulian, M.; et al. The SHARE European Earthquake Catalogue (SHEEC) 1000–1899. J. Seismol. 2013, 17, 523–544. [Google Scholar] [CrossRef]
- Makropoulos, K.; Kaviris, G.; Kouskouna, V. An Updated and Extended Earthquake Catalogue for Greece and Adjacent Areas since 1900. Nat. Hazards Earth Syst. Sci. 2012, 12, 1425–1430. [Google Scholar] [CrossRef]
- Evangelidis, C.P.; Triantafyllis, N.; Samios, M.; Boukouras, K.; Kontakos, K.; Ktenidou, O.; Fountoulakis, I.; Kalogeras, I.; Melis, N.S.; Galanis, O.; et al. Seismic Waveform Data from Greece and Cyprus: Integration, Archival, and Open Access. Seismol. Res. Lett. 2021, 92, 1672–1684. [Google Scholar] [CrossRef]
- Ganas, A.; Oikonomou, A.; Tsimi, C. NOAfaults: A Digital Database for Active Faults in Greece. Bull. Geol. Soc. Greece 2017, 47, 518. [Google Scholar] [CrossRef]
- Albini, P.; Pantosti, D. The 20 and 27 April 1894 (Locris, Central Greece) Earthquake Sources through Coeval Records on Macroseismic Effects. Bull. Seismol. Soc. Am. 2004, 94, 1305–1326. [Google Scholar] [CrossRef]
- Kouskouna, V.; Ganas, A.; Kleanthi, M.; Kassaras, I.; Sakellariou, N.; Sakkas, G.; Valkaniotis, S.; Manousou, E.; Bozionelos, G.; Tsironi, V.; et al. Evaluation of Macroseismic Intensity, Strong Ground Motion Pattern and Fault Model of the 19 July 2019 Mw5.1 Earthquake West of Athens. J. Seismol. 2021, 25, 747–769. [Google Scholar] [CrossRef]
- Lekkas, E. The Athens Earthquake (7 September 1999): Intensity Distribution and Controlling Factors. Eng. Geol. 2001, 59, 297–311. [Google Scholar] [CrossRef]
- Papadimitriou, P.; Voulgaris, N.; Kassaras, I.; Kaviris, G.; Delibasis, N.; Makropoulos, K. The Mw = 6.0, 7 September 1999 Athens Earthquake. Nat. Hazards 2002, 27, 15–33. [Google Scholar] [CrossRef]
- Papadopoulos, G.A.; Drakatos, G.; Papanastassiou, D.; Kalogeras, I.; Stavrakakis, G. Preliminary Results about the Catastrophic Earthquake of 7 September 1999 in Athens, Greece. Seismol. Res. Lett. 2000, 71, 318–329. [Google Scholar] [CrossRef]
- Kapetanidis, V.; Karakonstantis, A.; Papadimitriou, P.; Pavlou, K.; Spingos, I.; Kaviris, G.; Voulgaris, N. The 19 July 2019 Earthquake in Athens, Greece: A Delayed Major Aftershock of the 1999 Mw = 6.0 Event, or the Activation of a Different Structure? J. Geodyn. 2020, 139, 101766. [Google Scholar] [CrossRef]
- Jackson, J.A.; Gagnepain, J.; Houseman, G.; King, G.C.P.; Papadimitriou, P.; Soufleris, C.; Virieux, J. Seismicity, Normal Faulting, and the Geomorphological Development of the Gulf of Corinth (Greece): The Corinth Earthquakes of February and March 1981. Earth Planet. Sci. Lett. 1982, 57, 377–397. [Google Scholar] [CrossRef]
- Papazachos, B.C.; Comninakis, P.E.; Papadimitriou, E.; Scordilis, E. Properties of the February-March 1981 Seismic Sequence in the Alkyonides Gulf in Central Greece. Ann. Geophys. 1984, 2, 537–544. [Google Scholar]
- King, G.C.P.; Ouyang, Z.X.; Papadimitriou, P.; Deschamps, A.; Gagnepain, J.; Houseman, G.; Jackson, J.A.; Soufleris, C.; Virieux, J. The Evolution of the Gulf of Corinth (Greece): An Aftershock Study of the 1981 Earthquakes. Geophys. J. Int. 1985, 80, 677–693. [Google Scholar] [CrossRef]
- Michas, G.; Kapetanidis, V.; Spingos, I.; Kaviris, G.; Vallianatos, F. The 2020 Perachora Peninsula Earthquake Sequence (Εast Corinth Rift, Greece): Spatiotemporal Evolution and Implications for the Triggering Mechanism. Acta Geophys. 2022, 70, 2581–2601. [Google Scholar] [CrossRef]
- Spingos, I.; Kapetanidis, V.; Michas, G.; Kaviris, G.; Vallianatos, F. Shear-Wave Splitting Patterns in Perachora (Eastern Gulf of Corinth, Greece). Ann. Geophys. Accept. 2023, 66, 1–6. [Google Scholar] [CrossRef]
- Papadimitriou, E.; Bonatis, P.; Bountzis, P.; Kostoglou, A.; Kourouklas, C.; Karakostas, V. The Intense 2020–2021 Earthquake Swarm in Corinth Gulf: Cluster Analysis and Seismotectonic Implications from High Resolution Microseismicity. Pure Appl. Geophys. 2022, 179, 3121–3155. [Google Scholar] [CrossRef]
- Kaviris, G.; Kapetanidis, V.; Kravvariti, P.; Karakonstantis, A.; Bozionelos, G.; Papadimitriou, P.; Voulgaris, N.; Makropoulos, K. Anisotropy Study in Villia (E. Corinth Gulf, Greece). In Proceedings of the 2nd European Conference on Earthquake Engineering and Seismology, Istanbul, Türkiye, 25–29 August 2014. [Google Scholar]
- Elias, P.; Spingos, I.; Kaviris, G.; Karavias, A.; Gatsios, T.; Sakkas, V.; Parcharidis, I. Combined Geodetic and Seismological Study of the December 2020 Mw = 4.6 Thiva (Central Greece) Shallow Earthquake. Appl. Sci. 2021, 11, 5947. [Google Scholar] [CrossRef]
- Kaviris, G.; Kapetanidis, V.; Spingos, I.; Sakellariou, N.; Karakonstantis, A.; Kouskouna, V.; Elias, P.; Karavias, A.; Sakkas, V.; Gatsios, T.; et al. Investigation of the Thiva 2020–2021 Earthquake Sequence Using Seismological Data and Space Techniques. Appl. Sci. 2022, 12, 2630. [Google Scholar] [CrossRef]
- Kaviris, G.; Spingos, I.; Millas, C.; Kapetanidis, V.; Fountoulakis, I.; Papadimitriou, P.; Voulgaris, N.; Drakatos, G. Effects of the January 2018 Seismic Sequence on Shear-Wave Splitting in the Upper Crust of Marathon (NE Attica, Greece). Phys. Earth Planet. Inter. 2018, 285, 45–58. [Google Scholar] [CrossRef]
- Kapetanidis, V.; Kassaras, I. Contemporary Crustal Stress of the Greek Region Deduced from Earthquake Focal Mechanisms. J. Geodyn. 2019, 123, 55–82. [Google Scholar] [CrossRef]
- Karakonstantis, A.; Papadimitriou, P.; Millas, C.; Spingos, I.; Fountoulakis, I.; Kaviris, G. Tomographic Imaging of the NW Edge of the Hellenic Volcanic Arc. J. Seismol. 2019, 23, 995–1016. [Google Scholar] [CrossRef]
- Kiratzi, A.; Benetatos, C. The 6 January 2008 (Mw 6.2) Leonidio (Southern Greece) Intermediate Depth Earthquake: Teleseismic Body Wave Modeling; Technical Report; EMSC (European Mediterranean Seismological Centre): Bruyères-le-Châtel, France, 2008; p. 6. [Google Scholar]
- Zahradnik, J.; Gallovic, F.; Sokos, E.; Serpetsidaki, A.; Tselentis, A. Quick Fault-Plane Identification by a Geometrical Method: Application to the MW 6.2 Leonidio Earthquake, 6 January 2008, Greece. Seismol. Res. Lett. 2008, 79, 653–662. [Google Scholar] [CrossRef]
- Papadimitriou, E.E.; Karakostas, V.G. Rupture Model of the Great AD 365 Crete Earthquake in the Southwestern Part of the Hellenic Arc. Acta Geophys. 2008, 56, 293–312. [Google Scholar] [CrossRef]
- Ambraseys, N. Earthquakes in the Mediterranean and Middle East: A Multidisciplinary Study of Seismicity up to 1900; Cambridge University Press: Cambridge, UK, 2009; ISBN 978-0-521-87292-8. [Google Scholar]
- Papadopoulos, G.A. A Seismic History of Crete: Earthquakes and Tsunamis, 2000 B.C.–A.D. 2010; Ocelotos Publishing: Ocelotons, Athens, 2011; Volume 415. [Google Scholar]
- Konstantinou, K.I.; Kalogeras, I.S.; Melis, N.S.; Kourouzidis, M.C.; Stavrakakis, G.N. The 8 January 2006 Earthquake (Mw 6.7) Offshore Kythira Island, Southern Greece: Seismological, Strong-Motion, and Macroseismic Observations of an Intermediate-Depth Event. Seismol. Res. Lett. 2006, 77, 544–553. [Google Scholar] [CrossRef]
- Papanikolaou, D. The Geology of Greece; Springer: Berlin/Heidelberg, Germany, 2021; Volume 345. [Google Scholar]
- Mariolakos, I.; Papanikolaou, D.; Symeonidis, N.; Lekkas, S.; Karotsieris, Z.; Sideris, C. The Deformation of the Area around the Eastern Korinthian Gulf, Affected by the Earthquakes of February–March 1981. In Proceedings of the International Symposium on the Hellenic Arc and Trench (HEAT), Athens, Greece, 8–10 April 1982; Volume 1, pp. 400–420. [Google Scholar]
- Papanikolaou, D.; Mariolakos, I.; Lekkas, E.; Lozios, S. Morphotectonic Observations on the Asopos Basin and the Coastal Zone of Oropos. Contribution on the Neotectonics of Northern Attica. Bull. Geol. Soc. Greece 1988, 20, 252–267. [Google Scholar]
- Mariolakos, I.; Fountoulis, I.; Sideris, C.; Chatoupis, T. Morphoneotectonic Structure of the Parnis Mt. (Athens, Greece). Bull. Geol. Soc. Greece 2001, 34, 183–190. [Google Scholar] [CrossRef]
- Mariolakos, I.; Fountoulis, I.; Theocharis, D. The Neotectonic Structure and Evolution of the Salamis Island (Athens, Greece). Bull. Geol. Soc. Greece 2001, 34, 165–173. [Google Scholar] [CrossRef]
- Theocharis, D.; Fountoulis, I. Morphometric Indices and Tectonically Active Structures: The Case of Salamis Island. In Proceedings of the 6th Panhellenic Geographical Congress, Thessalon, Greece, 3–6 October 2002; Volume 1, pp. 97–106. [Google Scholar]
- Chatoupis, T.; Fountoulis, I. The Neotectonic Deformation of N. Parnis Mt. (Attica, Greece). Bull. Geol. Soc. Greece 2004, 36, 1588–1597. [Google Scholar]
- Papanikolaou, I.; Papanikolaou, D.; Lekkas, E. Low Slip-Rate Faults around Big Cities: A Challenging Threat. The Afindai Fault as a Case Study for the City of Athens. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Lekkas, E.; Papanikolaou, I.; Papanikolaou, D.; Danamos, G. Correlating the Damage Pattern and the Geological Structure. Local Site Effects from the 2006 Mw = 6.7 Kythira Island Intermediate Depth Event, SW Greece. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- de Gelder, G.; Fernández-Blanco, D.; Öğretmen, N.; Liakopoulos, S.; Papanastassiou, D.; Faranda, C.; Armijo, R.; Lacassin, R. Quaternary E-W Extension Uplifts Kythira Island and Segments the Hellenic Arc. Tectonics 2022, 41, e2022TC007231. [Google Scholar] [CrossRef] [PubMed]
- Veliz-Borel, V.; Mouslopoulou, V.; Nicol, A.; Begg, J.; Oncken, O. Normal Faulting Along the Kythira-Antikythira Strait, Southwest Hellenic Forearc, Greece. Front. Earth Sci. 2022, 9, 1325. [Google Scholar] [CrossRef]
- Deligiannakis, G.; Papanikolaou, I.D.; Roberts, G. Fault Specific GIS Based Seismic Hazard Maps for the Attica Region, Greece. Geomorphology 2018, 306, 264–282. [Google Scholar] [CrossRef]
- Konstantinou, K.I.; Mouslopoulou, V.; Saltogianni, V. Seismicity and Active Faulting around the Metropolitan Area of Athens, Greece. Bull. Seismol. Soc. Am. 2020, 110, 1924–1941. [Google Scholar] [CrossRef]
- Iezzi, F.; Roberts, G.; Faure Walker, J.; Papanikolaou, I.; Ganas, A.; Deligiannakis, G.; Beck, J.; Wolfers, S.; Gheorghiu, D. Temporal and Spatial Earthquake Clustering Revealed through Comparison of Millennial Strain-Rates from 36Cl Cosmogenic Exposure Dating and Decadal GPS Strain-Rate. Sci. Rep. 2021, 11, 23320. [Google Scholar] [CrossRef] [PubMed]
- Danamos, G. Contribution to the Geology and Hydrogeology of the Island of Kythira. Ph.D. Thesis, University of Athens, Athens, Greece, 1992. [Google Scholar]
- Mariolakos, I.; Fountoulis, I. The Athens Earthquake September 7, 1999: The Neotectonic Regime of the Affected Area. Ann. Géologiques Pays Hell. 2000, 38, 165–174. [Google Scholar]
- Wang, Z. Seismic Hazard Assessment: Issues and Alternatives. Pure Appl. Geophys. 2011, 168, 11–25. [Google Scholar] [CrossRef]
- Wang, Z. A Clear Definition of Seismic Hazard and Risk: A Basis for Hazard and Risk Assessment, Communication, and Management. In AGU Fall Meeting Abstracts, 2005; AGU: Washington, DC, USA, 2005; p. S53B-1110. [Google Scholar]
- Wang, Z. Understanding Seismic Hazard and Risk Assessments: An Example in The New Madrid Seismic Zone of The Central United States. In Proceedings of the 8th National Conference on Earthquake Engineering, San Francisco, CA, USA, 18–22 April 2006; Volume 416. [Google Scholar]
- Musson, R.M.W. PSHA Validated by Quasi Observational Means. Seismol. Res. Lett. 2012, 83, 130–134. [Google Scholar] [CrossRef]
- Mulargia, F.; Stark, P.B.; Geller, R.J. Why Is Probabilistic Seismic Hazard Analysis (PSHA) Still Used? Phys. Earth Planet. Inter. 2017, 264, 63–75. [Google Scholar] [CrossRef]
- Makropoulos, K.C.; Burton, P.W. Seismic Hazard in Greece. II. Ground Acceleration. Tectonophysics 1985, 117, 259–294. [Google Scholar] [CrossRef]
- Banitsiotou, I.D.; Tsapanos, T.M.; Margaris, V.N.; Hatzidimitriou, P.M. Estimation of the Seismic Hazard Parameters for Various Sites in Greece Using a Probabilistic Approach. Nat. Hazards Earth Syst. Sci. 2004, 4, 399–405. [Google Scholar] [CrossRef]
- Tselentis, G.-A.; Danciu, L. Probabilistic Seismic Hazard Assessment in Greece—Part 1: Engineering Ground Motion Parameters. Nat. Hazards Earth Syst. Sci. 2010, 10, 25–39. [Google Scholar] [CrossRef]
- Bonatis, P. Strong Ground Motion Simulation in the Central Ionian Islands Using a Hybrid (Deterministic and Stochastic) Approach. Master’s Thesis, Aristotle University of Thessaloniki, Thessaloniki, Greece, 2020. [Google Scholar]
- Bonatis, P.; Akinci, A.; Karakostas, V.; Papadimitriou, E.; Kaviris, G. Near-Fault Broadband Ground Motion Simulation Applications at the Central Ionian Islands, Greece. Pure Appl. Geophys. 2021, 178, 3505–3527. [Google Scholar] [CrossRef]
- Pavlou, K.; Κaviris, G.; Kouskouna, V.; Sakkas, G.; Zymvragakis, A.; Sakkas, V.; Drakatos, G. Minor Seismic Hazard Changes in the Broader Area of Pournari Artificial Lake after the First Filling (W. Greece). Results Geophys. Sci. 2021, 7, 100025. [Google Scholar] [CrossRef]
- Kaviris, G.; Zymvragakis, A.; Bonatis, P.; Sakkas, G.; Kouskouna, V.; Voulgaris, N. Probabilistic Seismic Hazard Assessment for the Broader Messinia (SW Greece) Region. Pure Appl. Geophys. 2022, 179, 551–567. [Google Scholar] [CrossRef]
- Kaviris, G.; Zymvragakis, A.; Bonatis, P.; Kapetanidis, V.; Voulgaris, N. Probabilistic and Scenario-Based Seismic Hazard Assessment on the Western Gulf of Corinth (Central Greece). Appl. Sci. 2022, 12, 11152. [Google Scholar] [CrossRef]
- Anonymous. ELSTAT Census Results of Population and Housing 2021; Hellenic Statistical Authority: Piraeus, Greece, 2021; p. 64. [Google Scholar]
- Cornell, C. Engineering Seismic Risk Analysis. Bull. Seismol. Soc. Am. 1968, 58, 1583–1606. [Google Scholar] [CrossRef]
- McGuire, R.K. FORTRAN Computer Program for Seismic Risk Analysis; Open-File Report; US Geological Survey: Washington, DC, USA, 1976.
- Marzocchi, W.; Taroni, M. Some Thoughts on Declustering in Probabilistic Seismic-Hazard Analysis. Bull. Seismol. Soc. Am. 2014, 104, 1838–1845. [Google Scholar] [CrossRef]
- Taroni, M.; Akinci, A. A New Smoothed Seismicity Approach to Include Aftershocks and Foreshocks in Spatial Earthquake Forecasting: Application to the Global Mw ≥ 5.5 Seismicity. Appl. Sci. 2021, 11, 10899. [Google Scholar] [CrossRef]
- Woessner, J.; Laurentiu, D.; Giardini, D.; Crowley, H.; Cotton, F.; Grünthal, G.; Valensise, G.; Arvidsson, R.; Basili, R.; Demircioglu, M.B.; et al. The 2013 European Seismic Hazard Model: Key Components and Results. Bull. Earthq. Eng. 2015, 13, 3553–3596. [Google Scholar] [CrossRef]
- Danciu, L.; Nandan, S.; Reyes, C.; Basili, R.; Weatherill, G.; Beauval, C.; Rovida, A.; Vilanova, S.; Sesetyan, K.; Bard, P.-Y.; et al. ESHM20—EFEHR Technical Report the 2020 Update of the European Seismic Hazard Model—ESHM20: Model Overview; EFEHR European Facilities of Earthquake Hazard and Risk; ETH Library: Zurich, Switzerland, 2021. [Google Scholar]
- Ordaz, M.; Salgado-Gálvez, M.A.; Giraldo, S. R-CRISIS: 35 Years of Continuous Developments and Improvements for Probabilistic Seismic Hazard Analysis. Bull. Earthq. Eng. 2021, 19, 2797–2816. [Google Scholar] [CrossRef]
- Gutenberg, B.; Richter, C.F. Frequency of Earthquakes in California. Bull. Seismol. Soc. Am. 1944, 34, 185–188. [Google Scholar] [CrossRef]
- Wiemer, S.; Wyss, M. Minimum Magnitude of Completeness in Earthquake Catalogs: Examples from Alaska, the Western United States, and Japan. Bull. Seismol. Soc. Am. 2000, 90, 859–869. [Google Scholar] [CrossRef]
- Aki, K. Maximum Likelihood Estimate of b in the Formula LogN a − BM and Its Confidence Limits. Earthq. Res. Inst. Univ. Tokyo 1965, 43, 237–239. [Google Scholar]
- Wiemer, S. A Software Package to Analyze Seismicity: ZMAP. Seismol. Res. Lett. 2001, 72, 373–382. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhou, S.; Zhuang, J. A Test on Methods for MC Estimation Based on Earthquake Catalog. Earth Planet. Phys. 2018, 2, 150–162. [Google Scholar] [CrossRef]
- Kijko, A.; Sellevoll, M.A. Estimation of Earthquake Hazard Parameters for Incomplete and Uncertain Data Files. Nat. Hazards 1990, 3, 1–13. [Google Scholar] [CrossRef]
- Wheeler, R. Methods of Mmax Estimation East of the Rocky Mountains; US Department of the Interior, Geological Survey: Washington, DC, USA, 2009; Volume 1018, p. 44.
- Kijko, A.; Singh, M. Statistical Tools for Maximum Possible Earthquake Magnitude Estimation. Acta Geophys. 2011, 59, 674–700. [Google Scholar] [CrossRef]
- Margaris, B.; Papazachos, C.; Papaioannou, C.; Theodulidis, N.; Kalogeras, I.; Skarlatoudis, A. Empirical Attenuation Relations for the Horizontal Strong Ground Motion Parameters of Shallow Earthquakes in Greece. In Proceedings of the Twelfth European Conference on Earthquake Engineering, London, UK, 9–13 September 2002; p. 11. [Google Scholar]
- Skarlatoudis, A.A.; Papazachos, C.B.; Margaris, B.N.; Theodulidis, N.; Papaioannou, C.; Kalogeras, I.; Scordilis, E.M.; Karakostas, V. Empirical Peak Ground-Motion Predictive Relations for Shallow Earthquakes in Greece. Bull. Seismol. Soc. Am. 2003, 93, 2591–2603, Erratum in Bull. Seismol. Soc. Am. 2007, 97, 2219–2221. [Google Scholar] [CrossRef]
- Danciu, L.; Tselentis, G.-A. Engineering Ground-Motion Parameters Attenuation Relationships for Greece. Bull. Seismol. Soc. Am. 2007, 97, 162–183. [Google Scholar] [CrossRef]
- Sakkas, G. Calculation and Analysis of the Seismic Motion Rotational Components in Greece. Ph.D. Thesis, Department of Geophysics and Geothermics, National and Kapodistrian University of Athens, Athens, Greece, 2016. [Google Scholar] [CrossRef]
- Chousianitis, K.; Del Gaudio, V.; Pierri, P.; Tselentis, G.-A. Regional Ground-Motion Prediction Equations for Amplitude-, Frequency Response-, and Duration-Based Parameters for Greece. Earthq. Eng. Struct. Dyn. 2018, 47, 2252–2274. [Google Scholar] [CrossRef]
- Skarlatoudis, A.A.; Papazachos, C.B.; Margaris, B.N.; Ventouzi, C.; Kalogeras, I.; the EGELADOS Group. Ground-Motion Prediction Equations of Intermediate-Depth Earthquakes in the Hellenic Arc, Southern Aegean Subduction Area. Bull. Seismol. Soc. Am. 2013, 103, 1952–1968. [Google Scholar] [CrossRef]
- Boore, D.M.; Stewart, J.P.; Skarlatoudis, A.A.; Seyhan, E.; Margaris, B.; Theodoulidis, N.; Scordilis, E.; Kalogeras, I.; Klimis, N.; Melis, N.S. A Ground-Motion Prediction Model for Shallow Crustal Earthquakes in Greece. Bull. Seismol. Soc. Am. 2020, 111, 857–874. [Google Scholar] [CrossRef]
- Mosca, I.; Sargeant, S.; Baptie, B.; Musson, R.M.W.; Pharaoh, T.C. The 2020 National Seismic Hazard Model for the United Kingdom. Bull. Earthq. Eng. 2022, 20, 633–675. [Google Scholar] [CrossRef]
- Scaria, A.; Gupta, I.D.; Gupta, V.K. An Improved Probabilistic Seismic Hazard Mapping of Peninsular Shield Region of India. Soil Dyn. Earthq. Eng. 2021, 141, 106417. [Google Scholar] [CrossRef]
- Sotiriadis, D.; Margaris, B. Evaluation of the Predictive Performance of Regional and Global Ground Motion Predictive Equations against Greek Strong Motion Data. Soil Dyn. Earthq. Eng. 2023, 165, 107656. [Google Scholar] [CrossRef]
- Scherbaum, F.; Cotton, F.; Smit, P. On the Use of Response Spectral-Reference Data for the Selection and Ranking of Ground-Motion Models for Seismic-Hazard Analysis in Regions of Moderate Seismicity: The Case of Rock Motion. Bull. Seismol. Soc. Am. 2004, 94, 2164–2185. [Google Scholar] [CrossRef]
- Kale, Ö.; Akkar, S. A New Procedure for Selecting and Ranking Ground-Motion Prediction Equations (GMPEs): The Euclidean Distance-Based Ranking (EDR) Method. Bull. Seismol. Soc. Am. 2013, 103, 1069–1084. [Google Scholar] [CrossRef]
- Scherbaum, F.; Delavaud, E.; Riggelsen, C. Model Selection in Seismic Hazard Analysis: An Information-Theoretic Perspective. Bull. Seismol. Soc. Am. 2009, 99, 3234–3247. [Google Scholar] [CrossRef]
- Luzi, L.; Puglia, R.; Russo, E.; D’Amico, M.; Felicetta, C.; Pacor, F.; Lanzano, G.; Çeken, U.; Clinton, J.; Costa, G.; et al. The Engineering Strong-Motion Database: A Platform to Access Pan-European Accelerometric Data. Seismol. Res. Lett. 2016, 87, 987–997. [Google Scholar] [CrossRef]
- Beauval, C.; Tasan, H.; Laurendeau, A.; Delavaud, E.; Cotton, F.; Guéguen, P.; Kuehn, N. On the Testing of Ground-Motion Prediction Equations against Small-Magnitude Data. Bull. Seismol. Soc. Am. 2012, 102, 1994–2007. [Google Scholar] [CrossRef]
- Wald, D.J.; Allen, T.I. Topographic Slope as a Proxy for Seismic Site Conditions and Amplification. Bull. Seismol. Soc. Am. 2007, 97, 1379–1395. [Google Scholar] [CrossRef]
- Lemoine, A.; Douglas, J.; Cotton, F. Testing the Applicability of Correlations between Topographic Slope and VS30 for Europe. Bull. Seismol. Soc. Am. 2012, 102, 2585–2599. [Google Scholar] [CrossRef]
- Bommer, J.J.; Scherbaum, F. The Use and Misuse of Logic Trees in Probabilistic Seismic Hazard Analysis. Earthq. Spectra 2008, 24, 997–1009. [Google Scholar] [CrossRef]
- Atkinson, G.M.; Bommer, J.J.; Abrahamson, N.A. Alternative Approaches to Modeling Epistemic Uncertainty in Ground Motions in Probabilistic Seismic-Hazard Analysis. Seismol. Res. Lett. 2014, 85, 1141–1144. [Google Scholar] [CrossRef]
- Marzocchi, W.; Taroni, M.; Selva, J. Accounting for Epistemic Uncertainty in PSHA: Logic Tree and Ensemble Modeling. Bull. Seismol. Soc. Am. 2015, 105, 2151–2159. [Google Scholar] [CrossRef]
- National Building Code. EAK Greek Seismic Code; Earthquake Planning and Protection Organization: Athens, Greece, 2003.
- Tselentis, G.-A.; Danciu, L.; Sokos, E. Probabilistic Seismic Hazard Assessment in Greece—Part 2: Acceleration Response Spectra and Elastic Input Energy Spectra. Nat. Hazards Earth Syst. Sci. 2010, 10, 41–49. [Google Scholar] [CrossRef]
- Panakkat, A.; Adeli, H. Neural Network Models for Earthquake Magnitude Prediction Using Multiple Seismicity Indicators. Int. J. Neural Syst. 2007, 17, 13–33. [Google Scholar] [CrossRef]
- Chattopadhyay, G.; Chattopadhyay, S. Dealing with the Complexity of Earthquake Using Neurocomputing Techniques and Estimating Its Magnitudes with Some Low Correlated Predictors. Arab. J. Geosci. 2009, 2, 247–255. [Google Scholar] [CrossRef]
- Wessel, P.; Smith, W.H.F. New, Improved Version of Generic Mapping Tools Released. Eos Trans. Am. Geophys. Union 1998, 79, 579. [Google Scholar] [CrossRef]
- Esri ArcGIS Pro, version 3.1.0; Esri: Redlands, CA, USA, 2023.
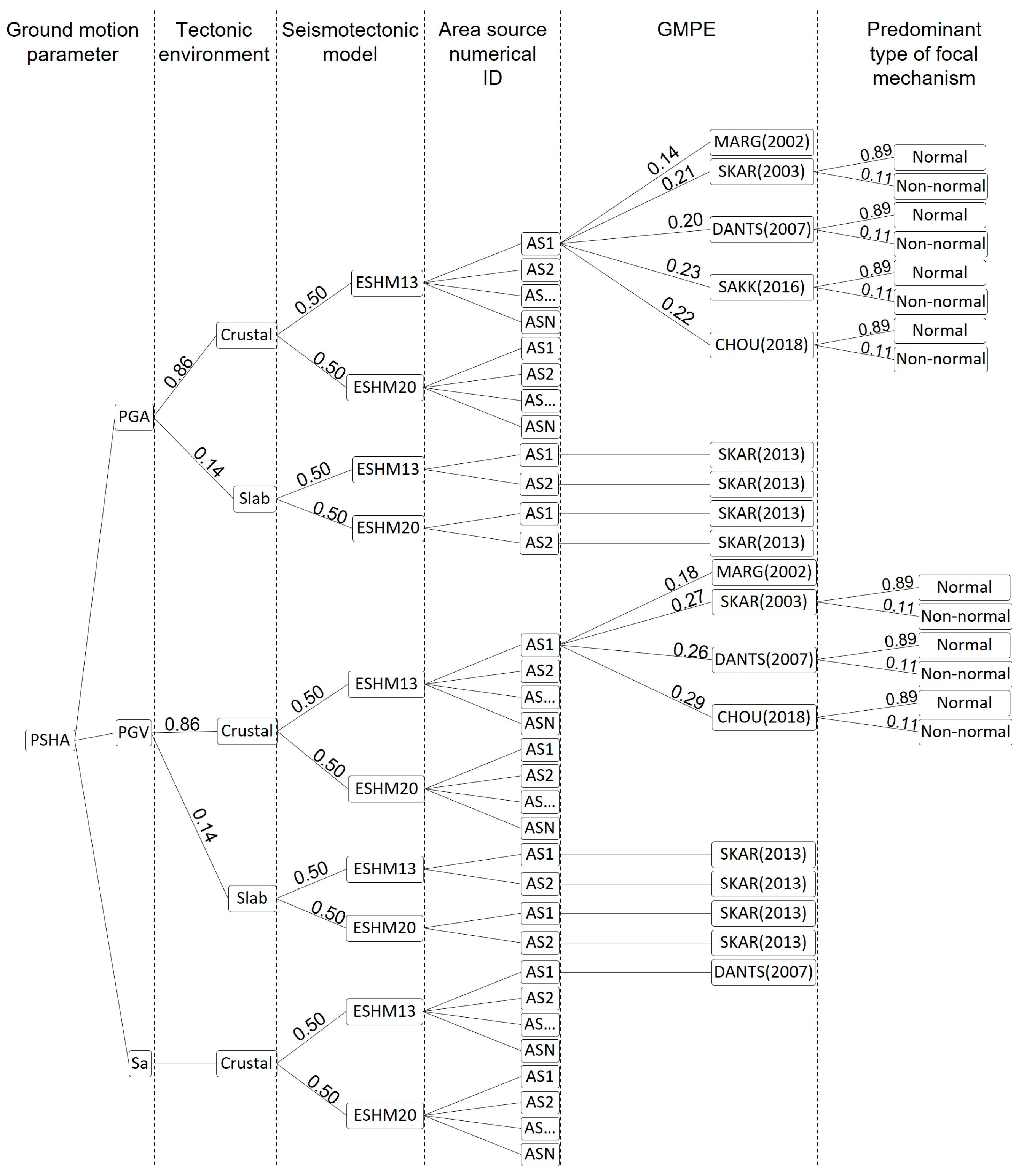

| Reference | Functional Form | PGA Weight | PGV Weight |
|---|---|---|---|
| [76] | 0.14 | 0.18 | |
| [77] | 0.21 | 0.27 | |
| [78] | 0.20 | 0.26 | |
| [79] | 0.23 | - | |
| [80] | 0.22 | 0.29 |
| Site | PGAr (cm/s2) | PGAs (cm/s2) |
|---|---|---|
| Athens | 141 | 169 |
| Salamina | 218 | 261 |
| Aegina | 225 | 243 |
| Methana | 167 | 240 |
| Poros | 155 | 239 |
| Hydra | 168 | 202 |
| Spetses | 148 | 178 |
| Kythira | 212 | 254 |
| Antikythira | 219 | 263 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaviris, G.; Zymvragakis, A.; Bonatis, P.; Kapetanidis, V.; Spingos, I.; Mavroulis, S.; Kotsi, E.; Lekkas, E.; Voulgaris, N. A Logic-Tree Approach for Probabilistic Seismic Hazard Assessment in the Administrative Region of Attica (Greece). Appl. Sci. 2023, 13, 7553. https://doi.org/10.3390/app13137553
Kaviris G, Zymvragakis A, Bonatis P, Kapetanidis V, Spingos I, Mavroulis S, Kotsi E, Lekkas E, Voulgaris N. A Logic-Tree Approach for Probabilistic Seismic Hazard Assessment in the Administrative Region of Attica (Greece). Applied Sciences. 2023; 13(13):7553. https://doi.org/10.3390/app13137553
Chicago/Turabian StyleKaviris, George, Angelos Zymvragakis, Pavlos Bonatis, Vasilis Kapetanidis, Ioannis Spingos, Spyridon Mavroulis, Evelina Kotsi, Efthymios Lekkas, and Nicholas Voulgaris. 2023. "A Logic-Tree Approach for Probabilistic Seismic Hazard Assessment in the Administrative Region of Attica (Greece)" Applied Sciences 13, no. 13: 7553. https://doi.org/10.3390/app13137553
APA StyleKaviris, G., Zymvragakis, A., Bonatis, P., Kapetanidis, V., Spingos, I., Mavroulis, S., Kotsi, E., Lekkas, E., & Voulgaris, N. (2023). A Logic-Tree Approach for Probabilistic Seismic Hazard Assessment in the Administrative Region of Attica (Greece). Applied Sciences, 13(13), 7553. https://doi.org/10.3390/app13137553










